Article information

Abstract

Trans Abstract

1. 서 론

2011년 3월 동일본 대지진과 2018년 9월 인도네시아 술라웨시 지진의 사례에서 볼 수 있듯이 지진 및 지진해일은 발생하면 큰 규모의 인명 피해와 재산손실을 야기할 수 있다. 지진은 일반적으로 대륙판이 서로 만나는 경계, 예를 들면 불의 고리라 불리는 환태평양 조산대 상에 위치한 해구를 따라 빈번하게 발생한다. 그러나 판 경계가 아니더라도 지진은 발생할 수 있으며(2018년 포항 지진), 언제 어느 규모로 발생하는지 정확히 예측하기 매우 어렵다. 2009년 이탈리아 과학자들이 이탈리아 라퀼라(L’Aquila)시에 대하여 ‘큰 규모의 지진으로 발전할 가능성이 낮다고’ 발언한지 엿새 만에 Mw 6.3의 지진이 발생하여 300여명의 사상자가 발생한 바 있다. 또한 2011년 동일본 대지진의 경우도 종래의 예측 범위를 초월한 규모의 지진이였고 실제 사망자의 65% 이상이 가능최대규모를 가정하여 범람피해가 예상되지 않는다고 예상했던 지역에서 발생하였다(Mori et al., 2018). 이런 사례는 지진의 발생시기와 규모를 예측하는 일이 어렵다는 것을 시사한다. 지진이 해저에서 발생하여 동반되는 지진해일 또한 예측하기 어렵다. 지진해일의 피해규모를 예상하고 방재대책을 수립한 종래의 연구는 주로 결정론적인 접근법을 사용한 경우가 많다. 어떤 장소에서 특정 파라미터를 가진 지진이 발생한다고 가정하되 보수적 결과를 위해 가능최대규모를 적용하거나, 그보다 작은 재난에 대해 정량적으로 대응하기 위해 보다 잦은 빈도로 발생하는 지진을 Gutenberg-Richter 관계를 통해 산정하여 결과를 얻는 방식을 사용했다. 결정론적으로 수행되는 연구는 지진해일 발생조건과 해일고 결과가 1대1로 대응된다는 면에서 조건에 따라 결과를 활용하는 데 용이할 수 있으나 실제 자연에서 예상범주 밖의 지진 또는 지진해일이 발생할 경우, 2011년의 사례와 같이 본래 의도한 기능을 상실할 가능성이 크다. 이러한 이유로 여러가지 경향의 지진이 발생하는 경우를 고려하여 지진 및 지진해일 재난에 대비하기 위한 연구가 진행되었다.

확률론적 지진해일 재해도 분석(Probabilistic Tsunami Hazard Analysis, PTHA)은 Cornell(1968)이 제안한 확률론적 지진재해도 분석(Probabilistic Seismic Hazard Analysis, PSHA)에서 파생된 방법으로 지진의 불확실성을 고려하여 지진해일고의 재해도(연초과확률)를 평가 및 분석하는 방법이다. PTHA를 수행하는 데 있어서 지진의 불확실성을 고려하는 것은 매우 중요한 요소이며, 이를 고려하는 방법으로 (1) 역사지진에 기반한 시나리오를 활용, (2) 로직트리 작성, (3) 가상의 단층변위분포를 생성하는 방식이 있다. 두 번째 방법인 로직트리는 지진발생역과 어떤 발생역에서 일어나는 지진특성(지진해일 모의의 입력자료)에 관한 불확실성을 제어하고 분석하는 간단한 방법이다. 로직트리를 활용한 PTHA는 미국 동부해안(Park and Cox, 2016), 인도네시아(Horspool et al., 2014), 남유럽(Lorito et al., 2014) 등 지진재난이 잦은 곳에 대해 수행된 바 있으며, 우리나라와 가까이 있는 일본에서도 로직트리를 사용하여 많은 연구가 수행되고 있다(Annaka et al., 2007; Fukutani et al., 2015; Sugino et al., 2015; Japan Society of Civil Engineers, 2016). Japanese Society of Civil Engineers(2016)는 일본 열도에 영향을 끼칠 수 있는 모든 지역에 대하여(류큐제도 제외) 로직트리를 작성하고 이에 따라 PTHA를 수행하였다. 해당 보고서에는 우리나라에 영향을 미칠 수 있는 지진해일이 발생 가능한 동해 동연부에 대한 로직트리를 제시하고 있다. 그러나 일본의 관점에서 동해 동연부 지진은 연근해에서 발생하는 지진에 해당하며, 원지지진으로서 고려해야 하는 우리나라에서는 실정에 맞게 재구성할 필요가 있다. 작성된 로직트리를 근거로 하여 수행한 지진해일 수치모의 결과를 바탕으로 지진해일 재해곡선 및 프랙타일 곡선을 산출하게 된다. 프랙타일 곡선을 산출하는 과정에서 연 초과확률 값들을 크기순으로 정렬하는 연산이 요구된다. 로직트리로 설명하고자 하는 불확실성의 범위가 넓어지거나 고려할 지진발생역이 늘어난다면 분기조합 수는 기하급수적으로 증가하게된다. 크기순으로 정렬하는 알고리즘은 평균적으로 α개의 요소를 가진 배열에 대하여 αlog(α)의 시간복잡도 증가율을 가지므로 프랙타일 산출에 소요되는 시간은 비선형적으로 증가하게 된다. 따라서 연구에 사용되는 컴퓨터 자원이 충분하지 않다면 계산결과 값을 얻는 것이 불가능할 수 있다. 본 연구에서는 Japan Society of Civil Engineers(2016)의 내용을 기반으로 확률론적 지진해일의 일반적 개념과 로직트리 작성 과정을 설명하고, 제시된 로직트리를 우리나라 실정에 맞게 재구성하였으며, 우리나라 부산광역시 소재 연안해역의 1개소에 대하여 기초적인 PTHA를 수행하였다. 또한, 프랙타일 곡선을 산출하는 데 있어 모든 분기를 고려하면서도 시간효율을 개선하기 위한 방법을 제안하였으며, 새로 제안된 방법의 사용 조건에 따른 정확성과 시간효율을 기존 방법과 비교 평가하였다.

2. 지진해일 발생지역 및 로직트리 구성

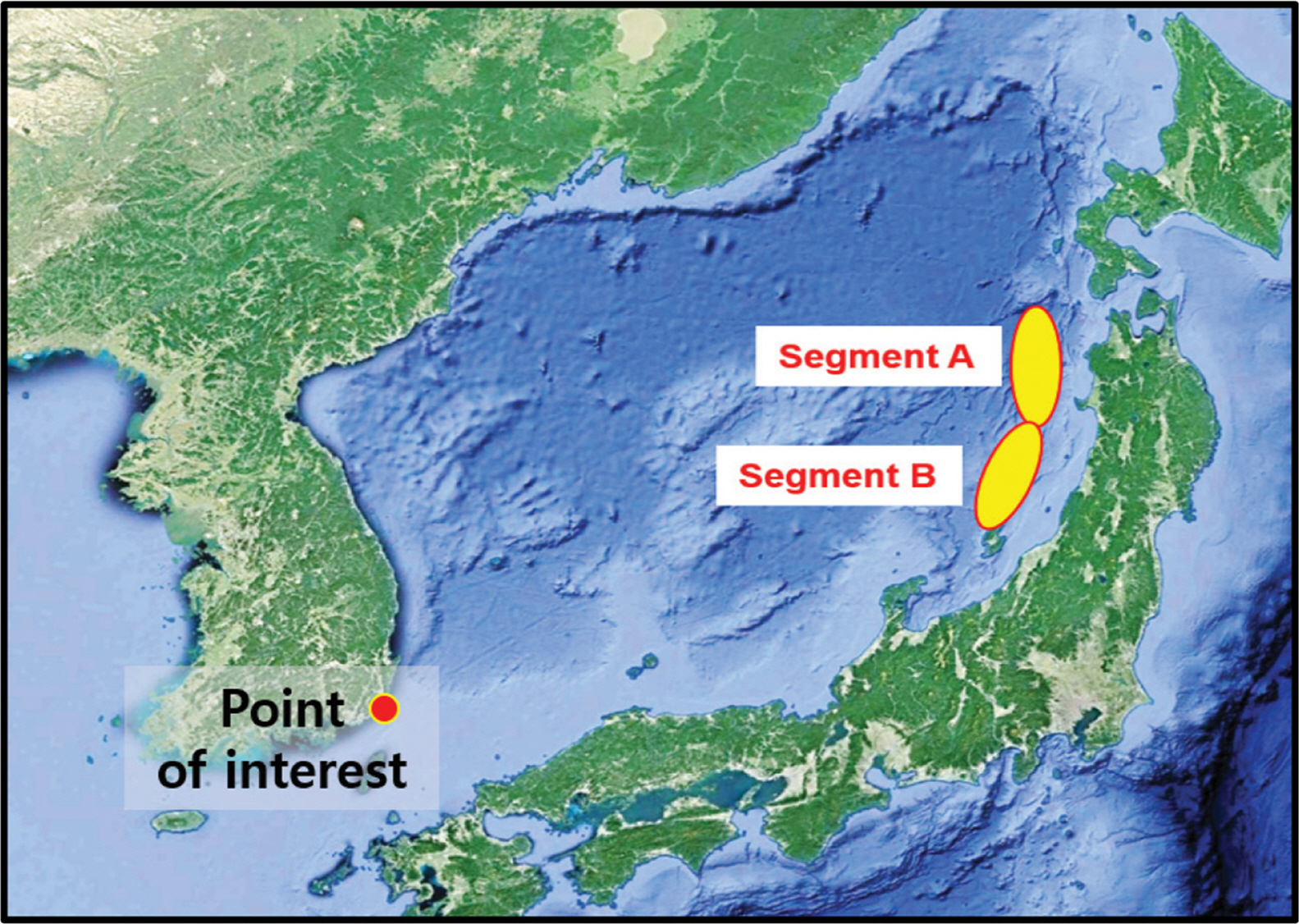
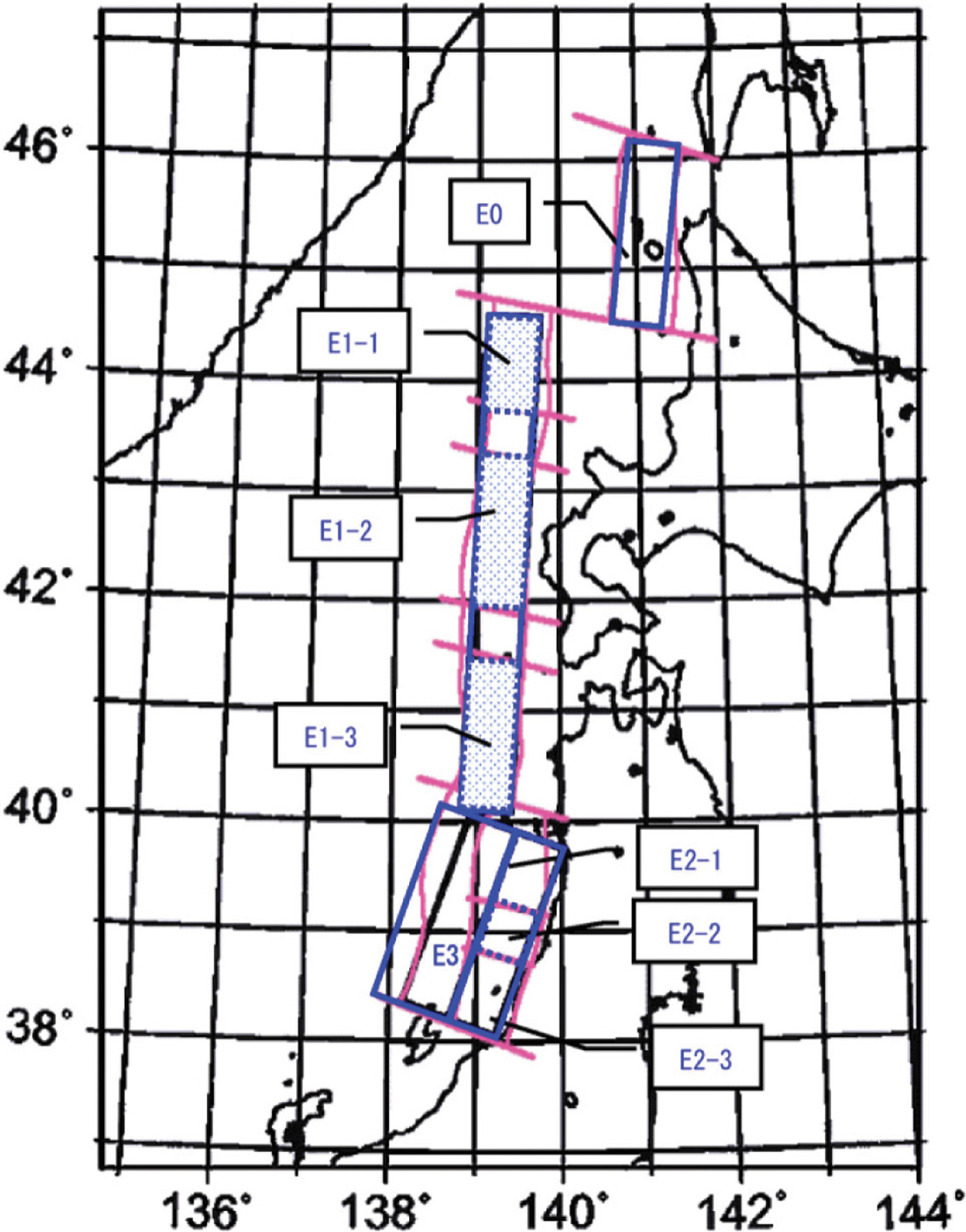
Japan Society of Civil Engineers(2016)는 Fig. 1에 보인 바와 같이 동해 동연부상에서 지진발생 가능지역을 크게 4개의 단층으로, 상세하게는 8개의 단층 즉 세그먼트(segment)로 나누었다. 본 연구에서는 8개의 세그먼트 중 1983년에 지진해일이 발생한 지역인 세그먼트 A(E1-3)와 우리나라에 큰 영향을 주는 지진발생역인 세그먼트 B(E3), 총 2개 소 만을 고려하여 부산광역시 소재 연안해역 1개소에 대한 PTHA를 수행하고 이를 예시로 PTHA의 수행 과정과 결과를 기술한다(Fig. 2). 복수의 세그먼트가 고려되는 방식은 크게 두가지가 있다. 복수의 세그먼트가 서로 독립적으로 거동하는 경우와 서로 연동하는 경우이다. 독립적 거동의 경우는 세그먼트간 영향이 없이 각 세그먼트가 별개로 활동한다고 생각하는 것이다. 이 경우 특정해일고를 유발시킬 수 있는 지진 발생장소의 수가 증가하는 방식으로 해석된다. 반면, 연동에 의한 경우는 두 세그먼트에서 동시에 거동하여 지진이 발생하며 하나의 지진으로 간주된다. 본 연구에서는 2개의 세그먼트가 단독으로 거동할 경우 만을 가정하여 연구를 진행하였다.

Fig. 1.

Active faults along the eastern margin of East Sea (JSCE, 2016).

Fig. 2.

Tsunamigenic areas and point of interest in this study.

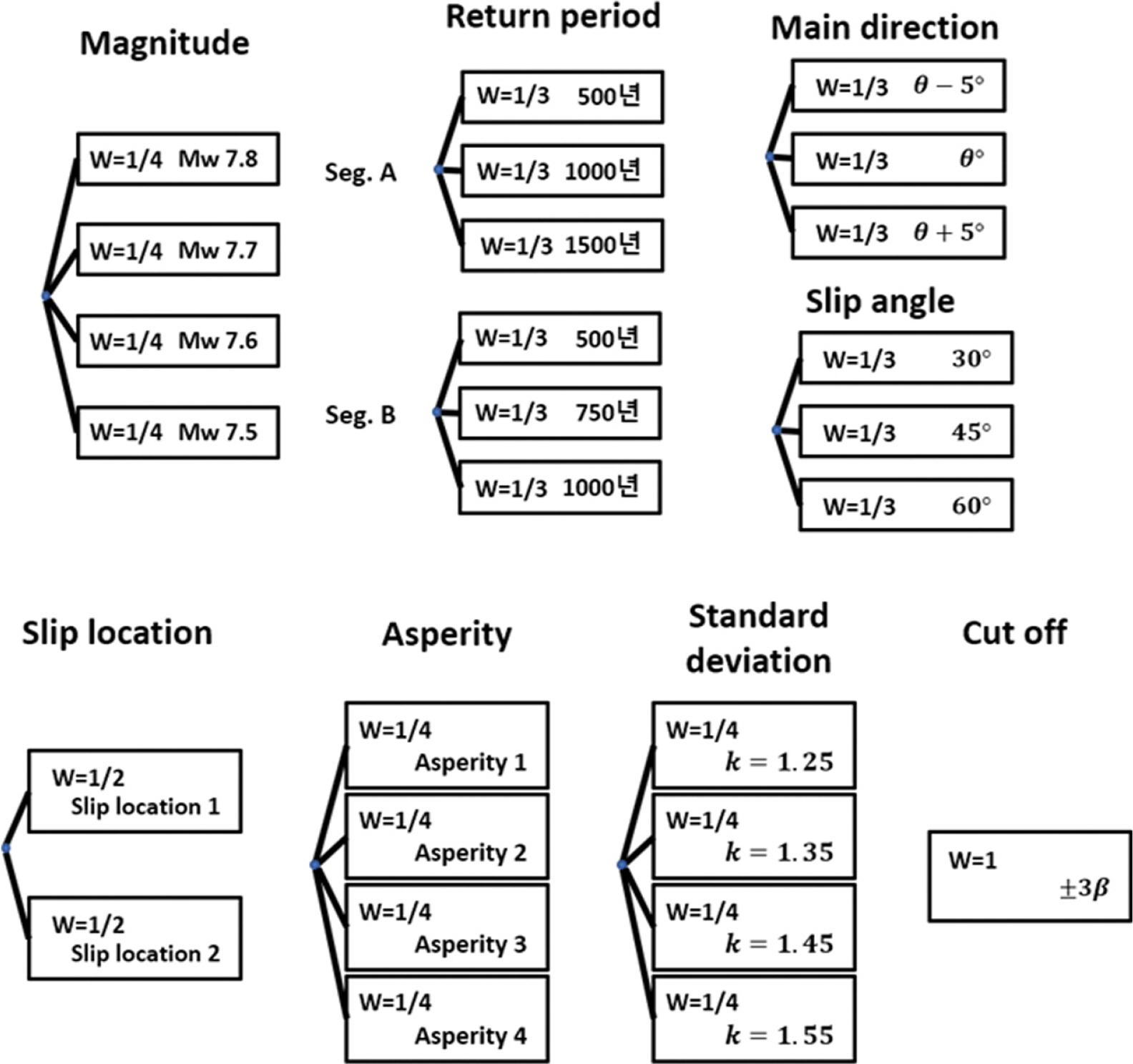
지진의 불확실성을 설명하는 로직트리의 구성요소는 지진의 강도와 재현기간 및 지진해일의 초기수면에 영향을 줄 수 있는 인자들로 구성되며 연구자가 사용한 수면변위 재현모델의 특성에 따라 변동될 수 있다. 또한 각 요소의 분기도 연구자 경향에 따라 다르게 구성될 소지가 존재한다. 예를 들면 과거 최대지진규모를 넘어서는 지진을 로직트리에 반영할 때 그 강도를 + 0.1Mw 수준으로 할 것인지 아니면 + 0.2Mw 수준까지 고려 할 것인지에 관한 이론적 규범이 확립되어 있지 않다. 이 경우 Japan Society of Civil Engineers(2008)와 같이 전문가를 대상으로한 설문조사를 통해 분기항목과 그 가중치를 결정한 사례도 있다.

Japan Society of Civil Engineers(2016)에서 동해 동연부 로직트리 작성을 위해 고려한 요소는 지진규모, 재현기간, 경사각, 경사방향, 경사위치, 변위분포와 해일고 분포의 표준편차와 분포의 타절범위 등 총 8가지이다. 본 연구에서 작성한 트리의 구성과 논리 분기가 설명하는 지진의 스케일링 법칙은 Japan Society of Civil Engineers(2016)의 방식을 토대로 하였다. 본 연구에서 고려한 지진발생역인 세그먼트 A와 세그먼트 B에서 발생하는 지진의 재현기간은 각각 500년~1500년, 500년~1000년이며, 각 지역에서 발생가능한 지진의 최대 규모는 Mw 7.8이다(The Headquarters for Earthquake Research Promotion, 2003). 지진의 규모는 Mw 7.5부터 0.1 간격으로 Mw 7.8까지 총 4개의 분기로 구성하였다. 재현기간에 대해서는 각 세그먼트의 최대값, 평균값, 최소값으로 3개의 분기를 설정하였다. 규모와 재현기간에 있어서 Gutenberg-Richter 관계에 의거하여 강도와 재현기간이 함께 증가하는 경향을 분기에 반영할 수 있다. 그러나 Japan Society of Civil Engineers(2016)에서는 각 세그먼트에서 지진의 최대규모는 과거기록을 바탕으로 결정하였고, 재현기간은 해저 퇴적물 조사를 통해 규모와는 독립적으로 추정하였다. 본 연구에서는 Japan Society of Civil Engineers(2016)의 방법을 차용하였으므로 제시된 재현기간과 지진의 강도는 서로 독립적이다.

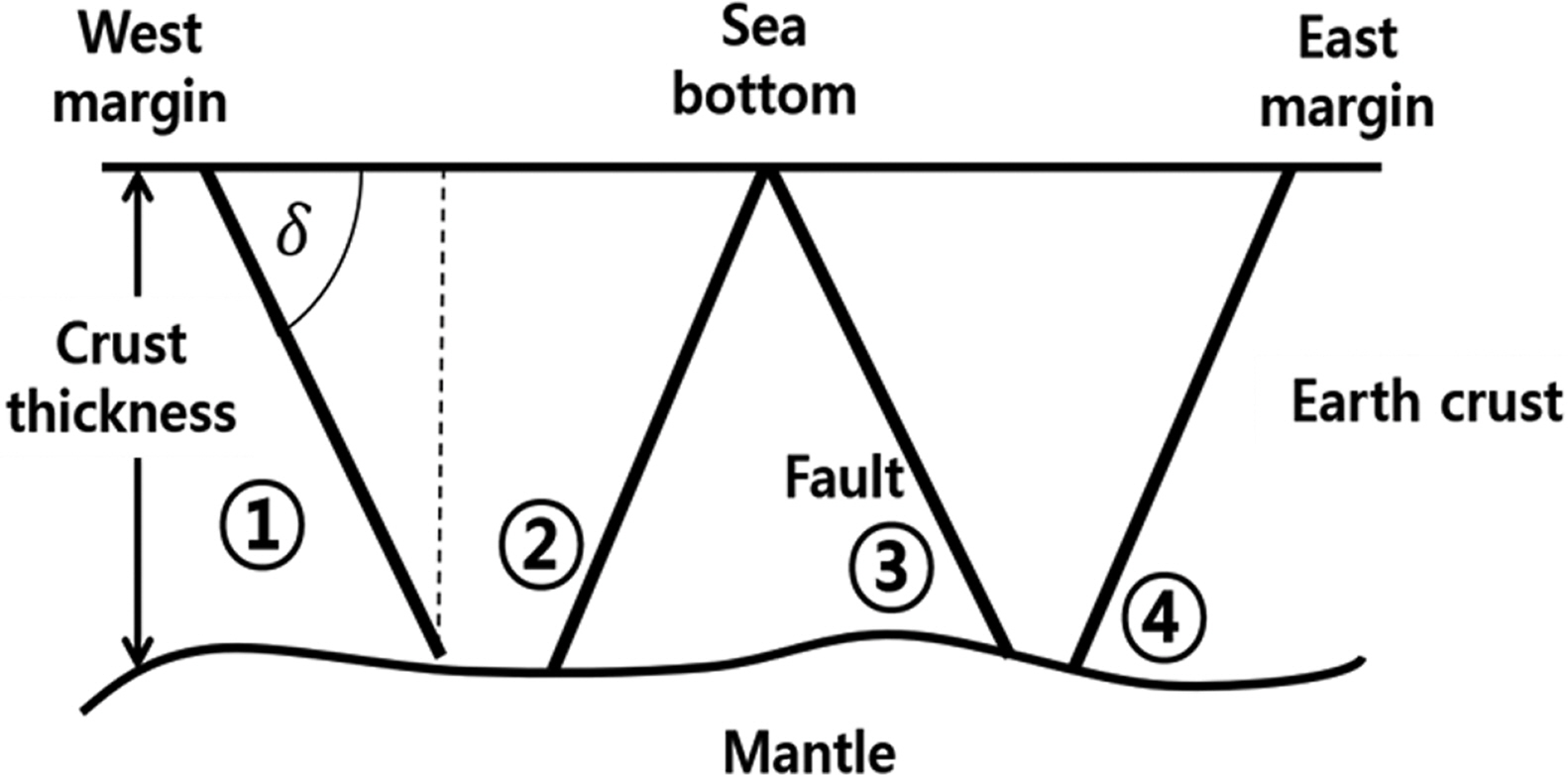
단층경사의 위치, 방향, 경사각도는 Fig. 3과 같이 경사각(δ) 별로 1번~4번까지 4가지 조건으로 설정되어 있다. 단층경사각은 본래 30도와 60도 두 가지 경우만을 고려하고 있으나, 지진 파라미터를 산정하는 스케일링 과정에서 단층경사각은 단층의 길이와 폭을 결정하는 요소이며, 단층의 길이와 폭은 지진해일 초기수면 형상 및 지진해일의 파장에 매우 중요한 변수로 작용하므로 45도를 추가하여 기존 2개 분기에서 3개 분기로 세밀하게 고려하였다. 일본 서해안에 근접한 요소 2건(3번, 4번 위치)에 대해서는 우리나라 기준으로 상대적으로 더 먼 거리이며 얕은 지역에서 발생하여 그 영향력이 1번, 2번 위치에 비해 작으므로 본 연구에서는 보수적 평가관점에서 고려하지 않았다.

Fig. 3.

Conceptual sketch showing slip positions and directions given by Japanese Society of Civil Engineers (2016).

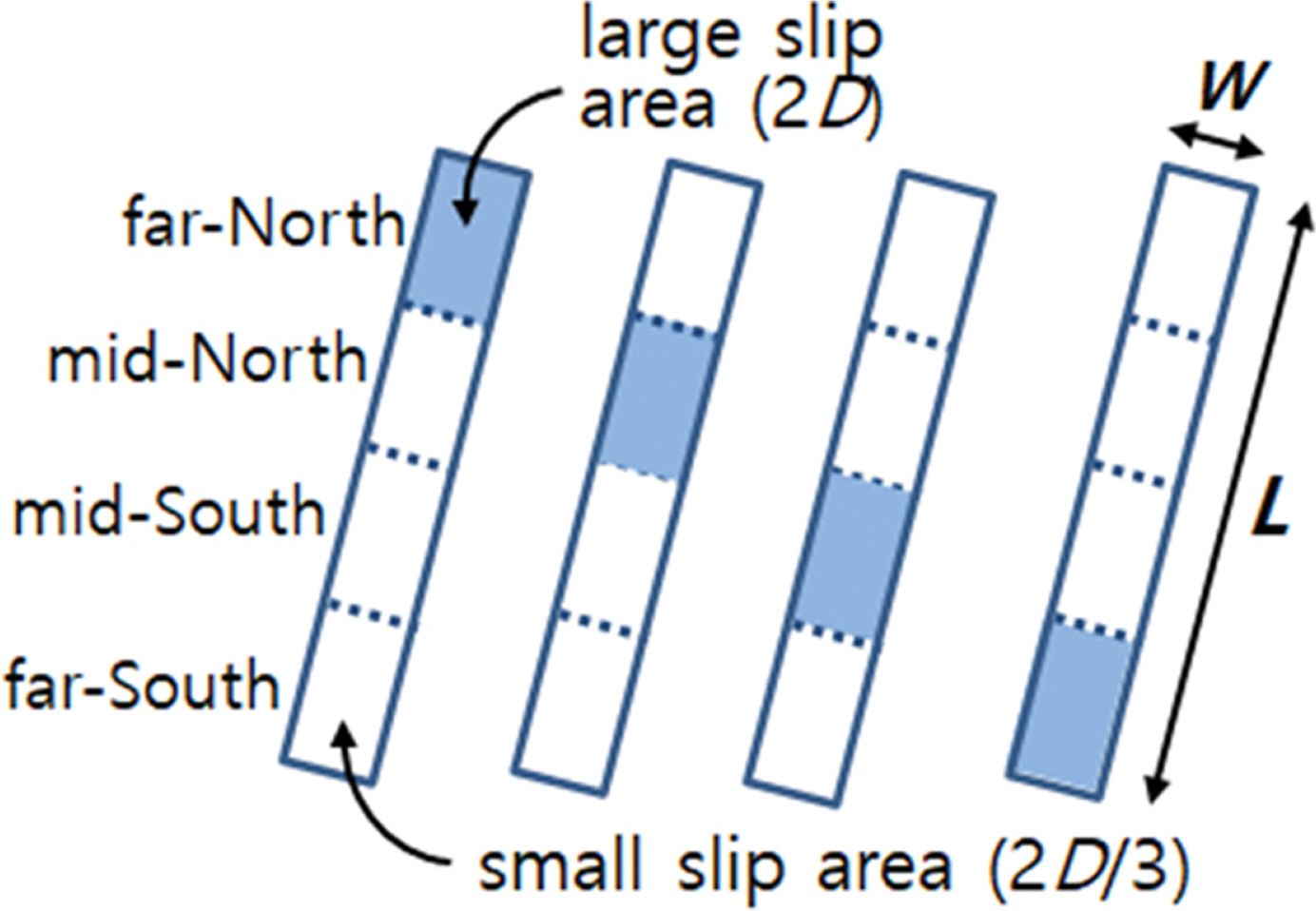
지진규모가 크고 단층의 길이가 길어질 경우, 단층의 변위분포에 따라 지진해일의 전파경향과 지진해일고 계산값이 달라지게 된다. 단층 변위량의 불균일성(asperity)을 고려하기 위해서는 전체 단층 길이를 4등분하여 그 중 1/4 면적에 대해 평균 활동량(D)의 2배를, 나머지 3/4면적에 대해 2/3배를 적용하였다. 활동량이 큰 영역은 Fig. 4에 보인 바와 같이 4가지 경우로 고려하였다. 또한 우리나라 동해안에 영향을 미치는 동해 동연부 지진해일은 원지지진해일이라는 점에 착안하여 주향각 요소를 추가하였다. 동해 동연부에서 같은 규모의 지진이 발생하더라도 지진해일이 먼 거리를 전파하는 경우 진행하는 방향의 작은 차이는 원지에서 큰 차이를 유발할 수 있다(Rhee et al., 2014). 본 연구에서는 Japan Society of Civil Engineers(2016)에서 제시한 주향각에 대해 ± 5도의 분기를 추가하여 3가지 경우로 나누어 고려하였다.

Fig. 4.

Deployment of large displacement component over active fault.

지진해일고의 분포와 관련된 사항에 대해서는 해일고 분포의 표준편차와 타절 범위가 로직트리에 고려된다. 발생가능한 해일고의 분포는 대수정규분포를 따르며(Aida, 1978), 이대수정규분포는 특정 계산점에서 산출된 해일고의 최대값과 표준편차 β를 모수로 가진다. 표준편차 β는 수심자료, 지형자료의 분해능 조건이나 국지적인 지형의 효과에 의한 계산 해일고와 실제 관측해일고의 차이를 고려하기 위한 것이다. 본 연구에서 설정한 표준편차의 분기 값은 Japan Society of Civil Engineers(2016)를 따랐으며, 다음과 같은 식(1)에 의해 산정된다(Sugino et al., 2015).

R_i는 관측된 해일고, h_i는 모의된 해일고이며, i는 해일고 관측지점을 의미한다. Hi는 i번째 관측지점에서 관측된 해일고와 모의된 해일고의 비를 나타내며 ln(H)는 Hi 값의 대수평균 값이다. ln(Hi)의 표준편차가 β가 되며 자연로그를 취할시 β가 되는 값을 k라 한다.

두 모수를 기반으로 만들어진 해일고 확률밀도곡선은 그 범위를 설정하지 않는다면 수학적으로 무한하게 크거나 작은 해일고를 포함하게 된다. 매우 작은 해일고와 매우 큰 해일고는 현실적으로 발생하기 어렵거나, 공학적으로 의미가 없는 해일고이므로 타절 범위를 정하여 배제한다. 역사적으로 발생한 지진해일의 수치모의 계산치와 실제 관측값의 비를 고려한 연구에 따르면 관측된 해일고는 분포의 중앙에서 표준편차의 3배 이내 범위에 약 99.9%가 존재하게 된다(Japan Society of Civil Engineers, 2016). 따라서 본 연구에서는 표준편차의 3배되는 값으로 타절 범위를 상정하였다. 언급된 모든 요소들을 정리하면 Fig. 5에 나타낸 바와 같으며, 하나의 세그먼트에 대해 강도분기 4개, 재현기간 분기 3개, 주향 분기 3개, 경사각 분기 3개, 경사위치 분기 2개, 단층변위 분포 분기 4개, 해일고분포의 표준편차 분기 4개와 타절범위 1분기를 고려한 각 세그먼트를 설명하는 로직트리의 총 분기 수는 3,456(= 4 × 3 × 3 × 3 × 2 × 4 × 4 × 1)개가 되며, 앞서 언급한 바와 같이 본 연구에서는 2개의 지진원이 단독거동한다고 가정하였으므로 총 3,4562개, 약 1,200만 가지 경우를 고려하였다.

Fig. 5.

Branch structures of logic tree.

작성된 로직트리와 Mansinha and Smylie(1971)의 해석해를 사용하여 각 분기에 의한 지진해일 초기수면을 구할 수 있다. 초기수면 재현에 필요한 단층의 길이 L과, 폭 W를 구하기 위해 먼저 식(2)를 이용하여 지진 모멘트 M₀를 구하고, 이를 스케일링 법칙인 식(3)에 대입하여 단층 면적 S를 구한다.

단층면적이 산출되고 나면 식(4)에 제시한 바와 같이 단층면적(S)을 그 폭(W)으로 나누어 단층의 길이(L)을 산출한다. 여기서, 단층의 폭은 식(5)와 같이 단층의 두께를 로직트리에서 제공하는 단층경사각을 이용하여 구한다. 평균단층 변위량 D는 식(6)과 같이 지진모멘트(M₀)를 면적과 평균변위량, 단층대의 강성률의 관계를 이용하여 산출한다.

변위량은 앞서 언급된 로직트리의 단층변위 분포 분기에 맞추어 재조정한다. 지진해일 전파 수치모의는 Yoon et al.(2007)에서 사용된 모델을 사용하였다. Yoon et al.(2007)의 지진해일 전파 수치모델은 천수방정식을 기반으로 하고 있으며 수치분산오차 보정을 통해 지진해일의 분산효과를 구현하여 원지지진해일에 대해서도 정도 높은 모의가 가능하다. 각 세그먼트 별로 288가지(= 4 × 3 × 3 × 2 × 4, 강도 4분기, 주향각 3분기, 경사각 3분기, 경사위치 2분기, 단층변위분포 4분기) 경우에 대한 지진해일 전파 수치모의가 수행되었다. 이는 세그먼트 당 3,456개의 분기 중 표준편차와 타절범위, 재현기간 분기에 의한 증가분을 제외한 경우에 해당하며, 3개의 변수는 수치모의에 반영되는 입력자료가 아니라 통계처리 과정에서 사용되는 변수이기 때문에 지진해일 모의시행 수에 영향을 주지 않는다. 본 연구에서 PTHA 수행을 위해 해일고를 추출한 지점과 계산조건 및 계산영역에 대한 사항은 Fig. 6과 Table 1에 나타낸 바와 같다.

Fig. 6.

Compuational domains for PTHA on South-East region in Korea.

Table 1.

Details on computational domains and conditions

3. 지진해일 재해도 산정

각각의 분기에 대하여 지진해일 전파 수치모의를 수행하게 되면, Fig. 7에 보인 바와 같이 관심지역에서의 최대 해일고값 h0를 얻을 수 있다. 최대해일고 값과 분기에서 선택된 표준편차 β를 통해 어떤 지점에서 발생 가능한 해일고의 확률밀도를 얻을 수 있다. 설정된 타절 범위를 적용하여 너무 크거나 작은 값을 제거한 후 누적확률분포를 산출한다.

Fig. 7.

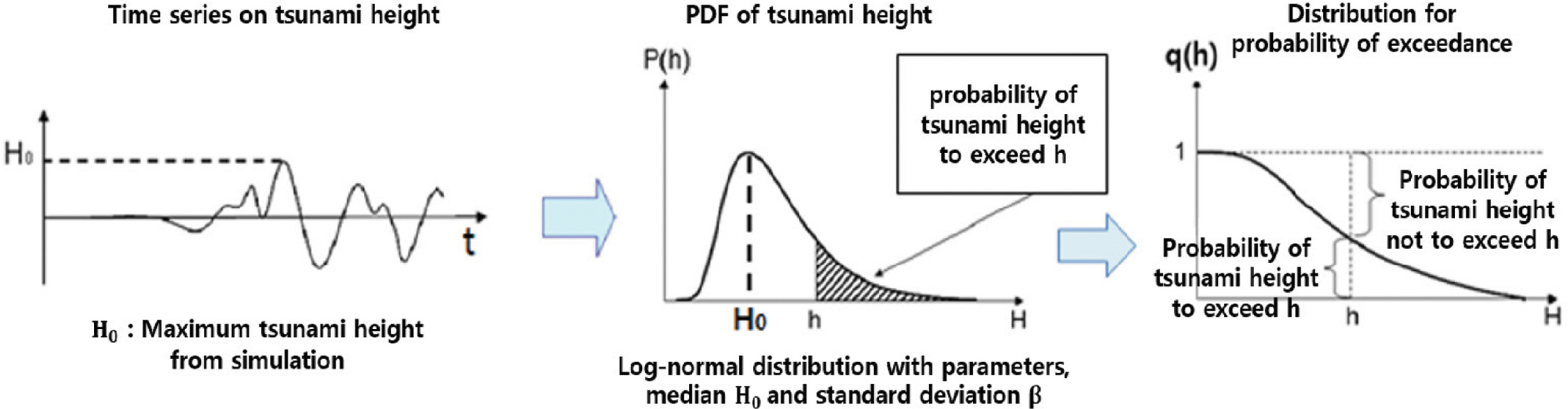
Construction of tsunami hazard curve from tsunami height (Japanese Society of Civil Engineers, 2016).

누적확률분포 값을 1에서 감해주면 각 해일고에 대한 초과확률분포(재해곡선)를 얻을 수 있다. 이 초과확률분포에 연 1회 이상 지진이 발생할 확률을 곱해주면, 로직트리의 분기가 설명하는 지진에 대한 수위별 재해곡선이 얻어진다. 지진의 발생확률을 산정하는 방식은 크게 포아송분포 또는 BPT(Brownian Passage Time) 분포를 이용하는 두 가지 방법 있으며 전자는 장기평가(발생하는 두 지진이 서로 영향이 없다고 간주할 경우), 후자는 현시점 평가(지진발생 후 특정기간 내에 지진이 다시 발생할 경우를 평가)를 수행하는 데 사용된다. 동해 동연부는 큰 규모의 지진이 빈번하게 발생하는 곳은 아니므로 본 연구에서는 포아송 분포만을 사용하였다. 포아송 분포에 의하여 지진이 관심기간 동안 1회 이상 발생할 확률은 다음의 식과 같이 산정된다.

여기서 ν는 대상기간동안 평균발생횟수, t는 대상기간이다. 재해곡선은 논리분기 요소별로 부여된 가중치의 곱으로써 산출되는 가중치를 가지고 있으며 이 가중치를 이용하여 프랙타일 곡선을 추출한다(Fig. 8 참조). 재해곡선 산출의 기반이 되는 로직트리의 분기가 가진 가중치는 해당 분기의 지진이 발생하는 빈도를 나타내는 것이 아니며 전문가 집단에서 부여한 분기별 신뢰도이므로 분기의 가중치에 기반한 가중평균값은 평균적인 발생확률으로서 객관적인 의미가 없다. 따라서 로직트리의 결과를 다수의 프랙타일 곡선으로 표현함으로써 재해도(연초과확률)산출 결과의 범위를 제시한다. 0.8 프랙타일곡선 상에 위치한 값은 80%의 전문가가 생각하는 연초과확률의 최대값을 의미한다.

Fig. 8.

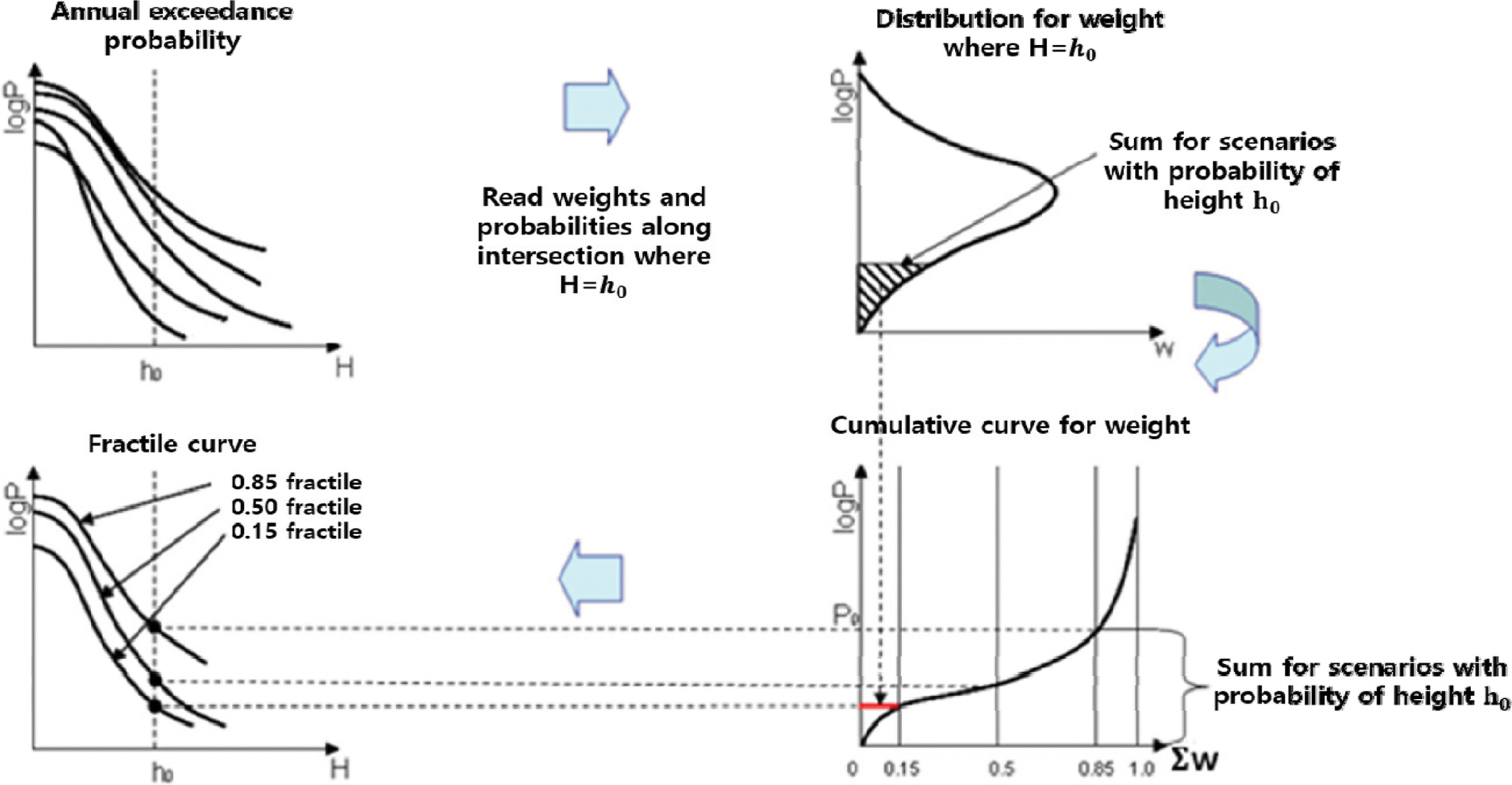
Procedure on construction of fractile curves from hazard curves (Japanese Society of Civil Engineers, 2016).

3.2 이산가중치분포법(Discrete Weight Distribution)

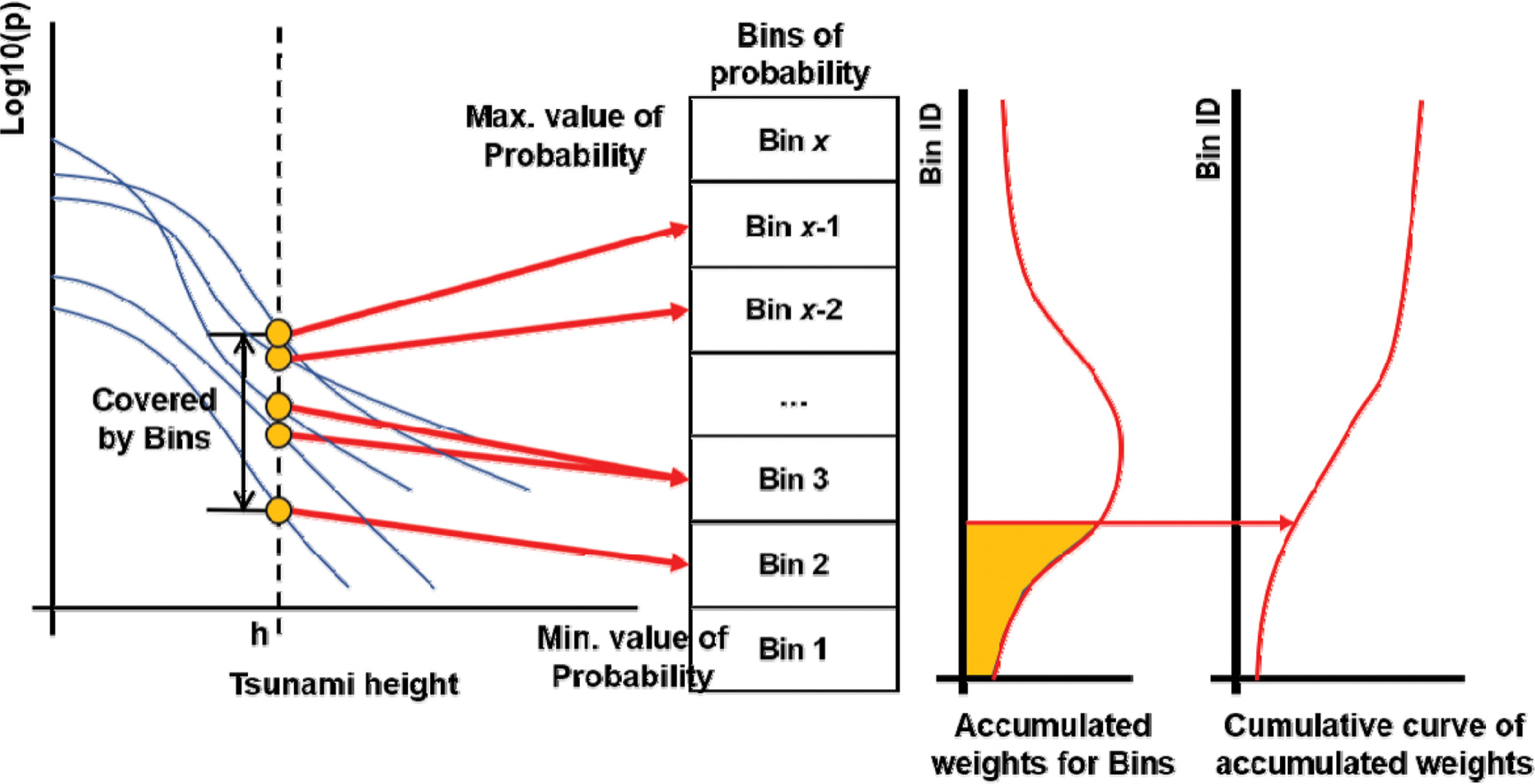
프랙타일 곡선 산출과정에서 크기순으로 정렬하게 되는 이유는 논리분기 순서가 확률의 크기와 무관하기 때문에 그래프 축 상에 표현되는 연초과확률과 자료의 순서를 맞추어 프랙타일곡선을 산출하기 위함이다. 정렬과정에 있어서 최소 2개의 값에 대한 크기 비교가 이루어지며, 여기에 사용되는 조건문(IF) 연산은 시간이 많이 소요되는 구문 중 하나이다. 본 연구에서는 조건문 사용을 최소화하기 위해 전체 확률구간을 대수확률등급으로 이산화하고 각각의 대수확률등급에 속차는 연초과확률의 가중치를 누적하는 이산가중치분포법(Discrete Weight Distribution, DWD)을 개발하였으며 그 개념도를 Fig. 9에 나타내었다. 이를 통해 정렬연산이 자동적으로 수행되어 조건문 사용을 줄임으로써 계산시간을 단축시킬 수 있다. 먼저, 1번 논리분기부터 마지막 논리분기까지 각 분기는 한번씩 조회되어 연초과확률의 수준에 따라 적합한 식별번호가 부여된다. 식별번호에 따라 논리분기가 제공하는 연초과확률의 가중치가 적합한 구간에 누적된다. 대수확률구간의 상한과 하한은 각각 10⁻²과 10⁻³⁰으로 설정하여 가능한 모든 범위에서 매끄러운 프랙타일 곡선을 산출할 수 있게 하였다. 재해곡선이나 프랙타일 곡선은 y축(연초과확률 축)에 관하여 로그스케일로 표현되므로 로그스케일상 일정한 간격이 되도록 구간을 등분하였다. 각 구간의 가중치가 누적된 결과가 분포곡선을 나타내게 되면 이에 대한 누적곡선을 산출하고, 정렬방법과 같은 방식으로 프랙타일 곡선을 산출한다.

Fig. 9.

Construction of fractile curves using discrete weight distribution.

3.3 몬테카를로 기법

PTHA에서 2개 이상의 세그먼트에서 발생하는 지진이 독립적으로 발생하고 서로 연동하지 않는다고 할 때, 특정 해일고가 발생할 확률은 각 세그먼트에서 제공하는 특정 해일고의 연초과확률들을 선형 중첩하여 산정한다. 따라서 해일고의 재현확률을 조합하는 과정은 몬테카를로 기법을 사용하여 수행될 수 있다. 확률론적 접근법에 몬테카를로 기법을 적용한 연구는 Shapira(1983), Cramer et al.(1996), Musson(1999, 2000), Assatourians and Atkinson(2013) 등에 의해 수행된 바 있으나, 이들 연구는 모두 지진에 관하여 확률론적으로 접근한 연구이며, 지진의 불확실성을 고려하기 위한 로직트리 기법의 대안으로서 몬테카를로 기법을 사용하였다. 몬테카를로 방법은 지진강도, 발생위치 등에 관하여 역사지진 연구를 통해 구체화된 범위 내에서 각 변수들을 무작위로 조합하여 가상의 지진 카탈로그를 생성하기 위해 사용되었다. Japan Society of Civil Engineers(2016)에서는 앞서 언급된 연구에서 적용된 방법과는 다소 다르게 이미 생성된 로직트리의 분기 중 일부를 무작위로 추출하는 데 몬테카를로 방법을 적용하였으며, 선택된 분기를 활용하여 프랙타일 곡선을 산출하는 방법을 제안하였다(Fig.10). 먼저, 각 분기의 가중치를 누적하여 0에서 1에 이르는 누적곡선을 생성한다. 여기에 0에서 1 사이 크기의 난수를 발생시켜 난수가 해당하는 구간에 대응하는 분기를 선택한다. 이러한 방식으로 각 세그먼트별로 일정한 수의 논리분기(해저드곡선)를 무작위로 선택하고, 세그먼트 별로 추출된 해저드곡선을 선형조합하고 프랙타일 곡선을 산출한다. 선형조합의 결과로 산출된 해저드곡선은 (1/무작위 추출 시행 수)의 가중치를 가지게 된다. 단순정렬기법이나 이산가중치분포법과 달리 몬테카를로 기법의 최대 장점은 세그먼트 개수가 증가하여도 다루게 되는 총 재해곡선수가 비선형적으로 증가하지 않고 선형증가한다는 점이다. 몬테카를로 기법의 무작위 추출 횟수를 m이라 할 때, 세그먼트 개수 n의 경우 총 재해곡선수는 n × m개로서 기존 방법에 비해 획기적으로 감소한다. 동해동연부의 예시에서 8개의 세그먼트(n = 8)에 대하여 무작위 추출을 800회 수행(m = 800)하면, 8 × 800 = 6,400개의 재해곡선을 추출하여 사용하게 된다.

Fig. 10.

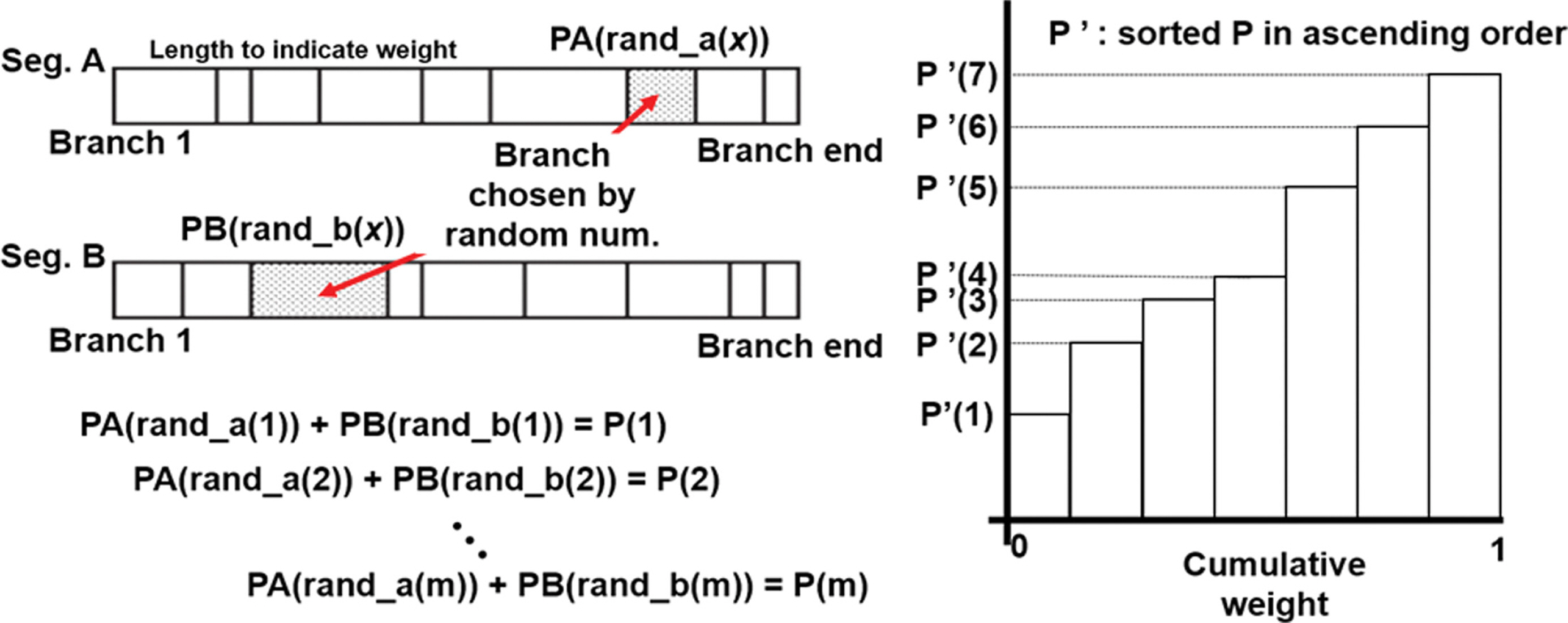
Procedures for constructing hazard-weight curve to gain fractile curve based on Monte Carlo method (Japanese Society of Civil Engineers, 2016).

3.4 기법 비교 검토

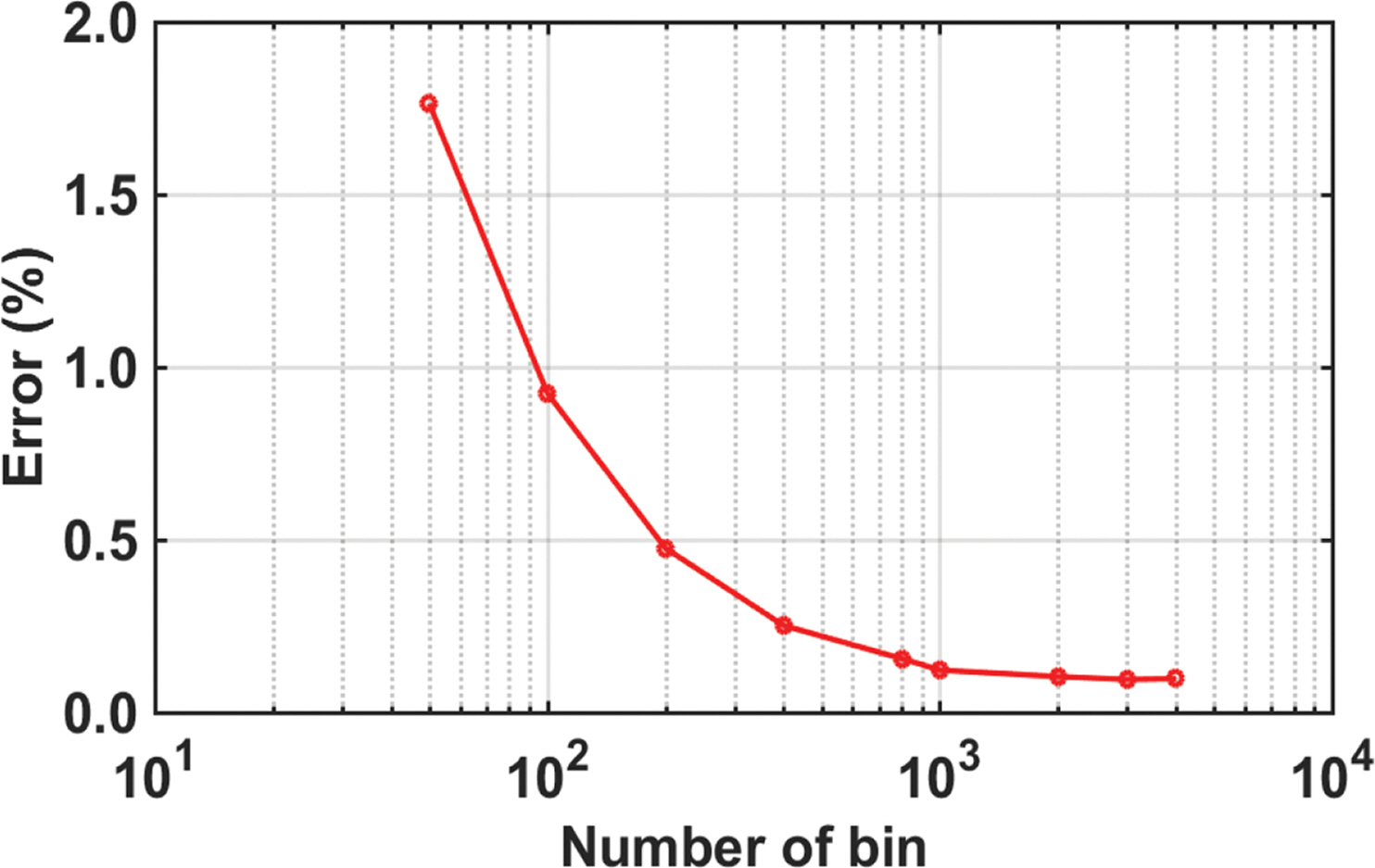
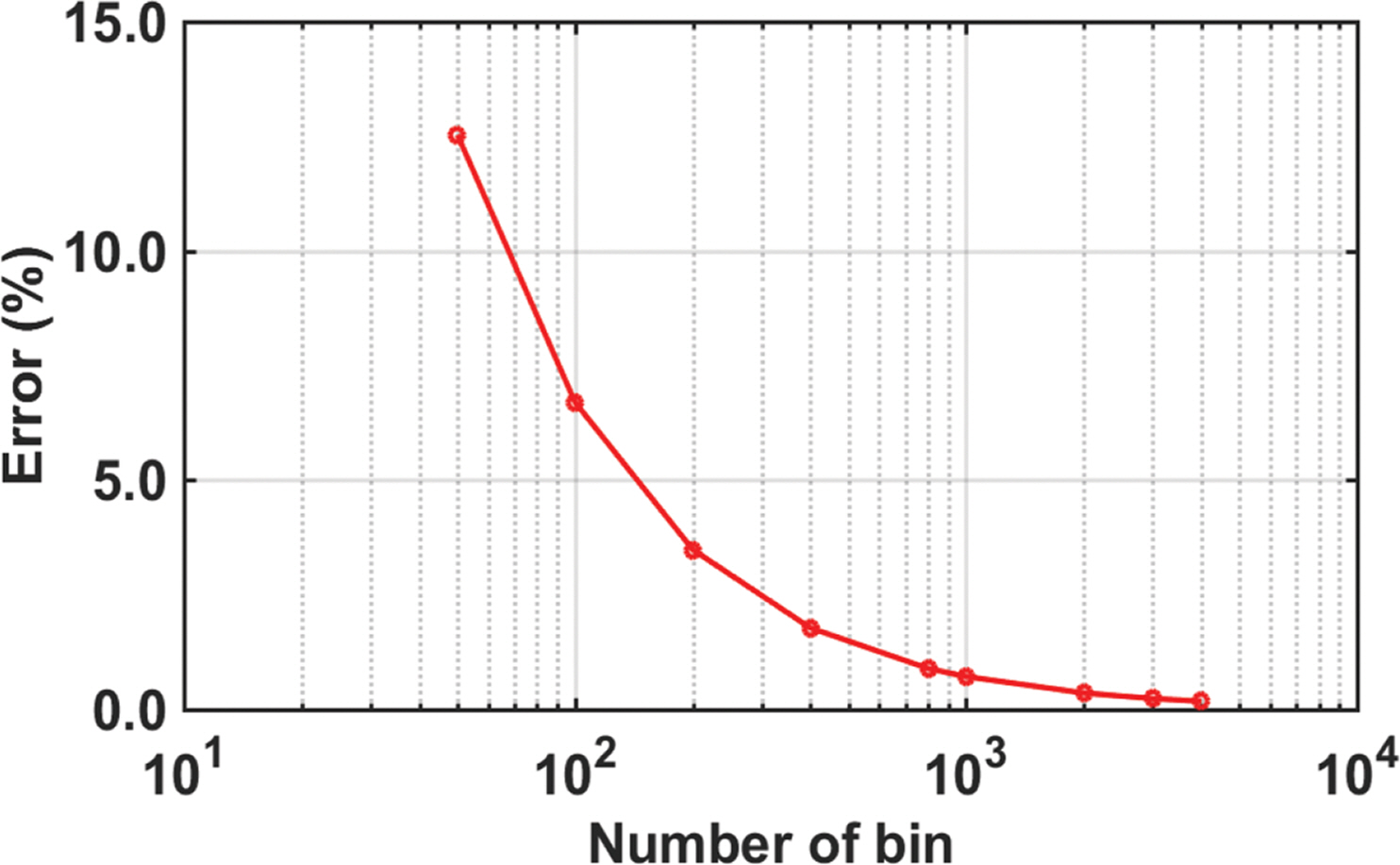
이산가중치분포법에서 확률구간의 분할 수에 대한 프랙타일 산출 결과의 변동성을 확인하기 위해 50개, 100개, 200개 400개, 800개, 1,000개, 2,000개, 4,000개로 구간을 분할하여 프랙타일 곡선을 산출하였으며, 크기순 정렬기법을 사용하여 얻은 결과와 비교하였다. Fig. 11은 발생원 1개소(세그먼트 A)에 대한 총 3,456개의 재해곡선으로부터 이산가중치분포법으로 얻은 프랙타일 곡선을 정렬기법에 의해 얻은 결과와 비교한 그림이다. 확률구간을 50개로 나누었을 경우, 0.86 및 0.95 프랙타일 곡선은 정렬기법의 결과와 다소 큰 차이를 보여주었으나, 확률구간을 200개로 나누면 정확도가 크게 개선되었다. 오차는 확률구간 분할 수가 증가할수록 점차 개선되며 800개 이상의 경우에 대해서 오차 감소율이 크게 줄어들었다. 구간 분할 수에 대한 오차의 변화는 Fig. 12에 제시하였다. 세그먼트를 2개 고려할 경우 논리분기 조합 수는 약 1,200만 개가 되며 이에 대한 결과는 Fig. 13에 나타냈다. 지진해일 발생원이 2개소이므로 단일 세그먼트와 비교 시 특정 해일고에 대한 재해곡선이 전반적으로 상승된 것을 확인 할 수 있다. Fig. 14에 보인 바와 같이 50개의 확률구간으로 나눌 경우의 오차는 약 13%에 이르렀으나 800개의 확률구간으로 나눈 경우부터는 1% 미만의 오차율을 보여주었다. 오차가 어느 정도 수렴성을 보이기 시작하는 구간분할 수는 1,000여개 수준이다. 한편, 몬테카를로 기법으로 산출한 프랙타일 곡선의 결과를 크기순 정렬기법과 이산가중치분포법으로 산출된 결과와 비교하였다(Fig. 15). 몬테카를로 기법의 결과는 난수 추출수를 각 세그먼트별로 800회로 설정한 경우이고 이산가중치분포법은 구간을 1,000개로 나눈 결과이다. 세 가지 방법 모두 서로 동일한 결과를 제공하는 것을 보아 몬테카를로 기법 또한 일관적인 결과를 보여줄 수 있음을 확인할 수 있다.

Fig. 11.

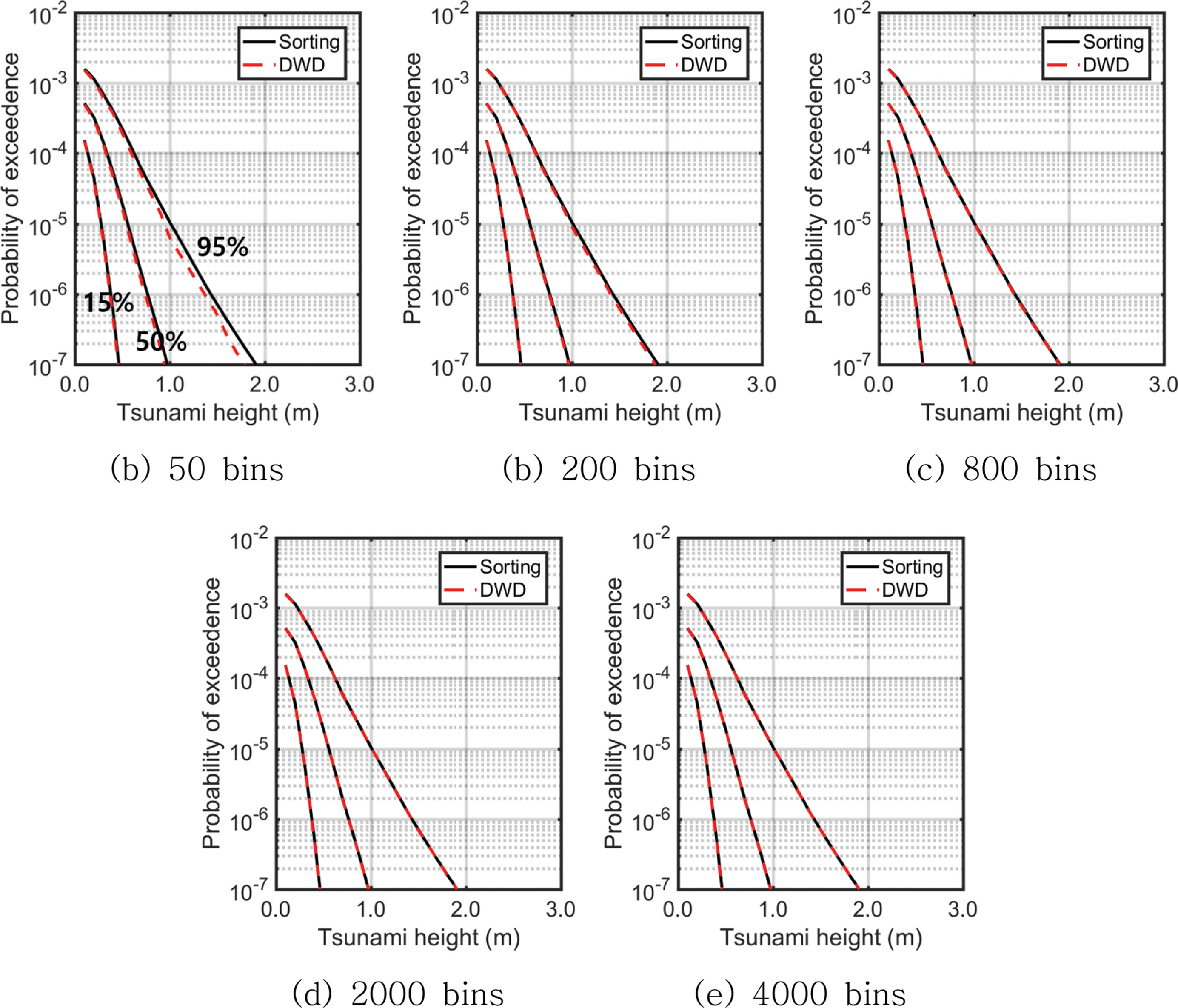
Variation of fractile curves with increase of discretization and its comparison with the results obtained using sorting method (single segment).

Fig. 12.

Error of DWD method for the case of single segment with increase of discretization.

Fig. 13.

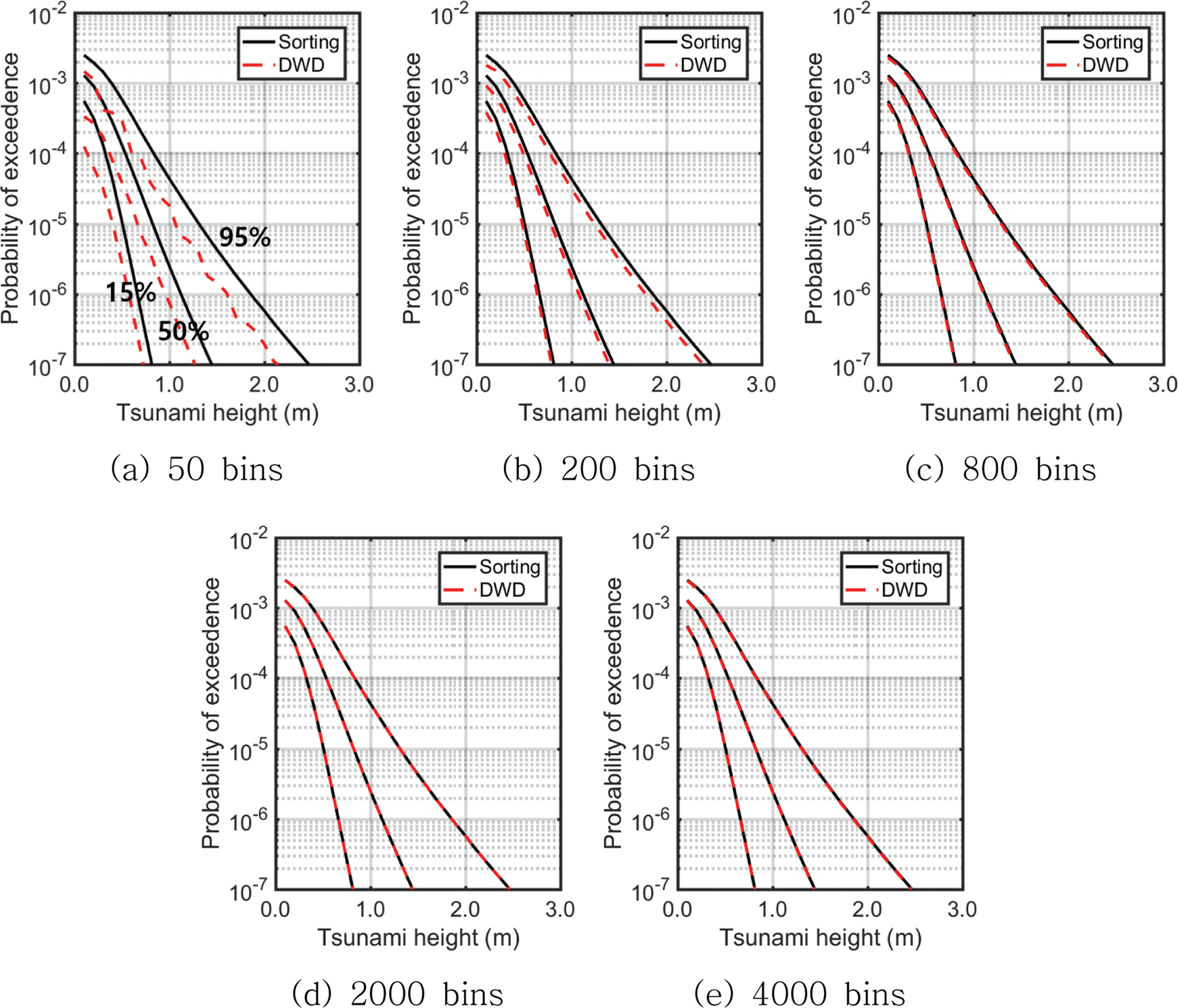
Variation of fractile curves with the increase of discretization and its comparison with the results obtained using sorting method (double segments).

Fig. 14.

Error of DWD method for the case of double segments with increase of discretization.

Fig. 15.

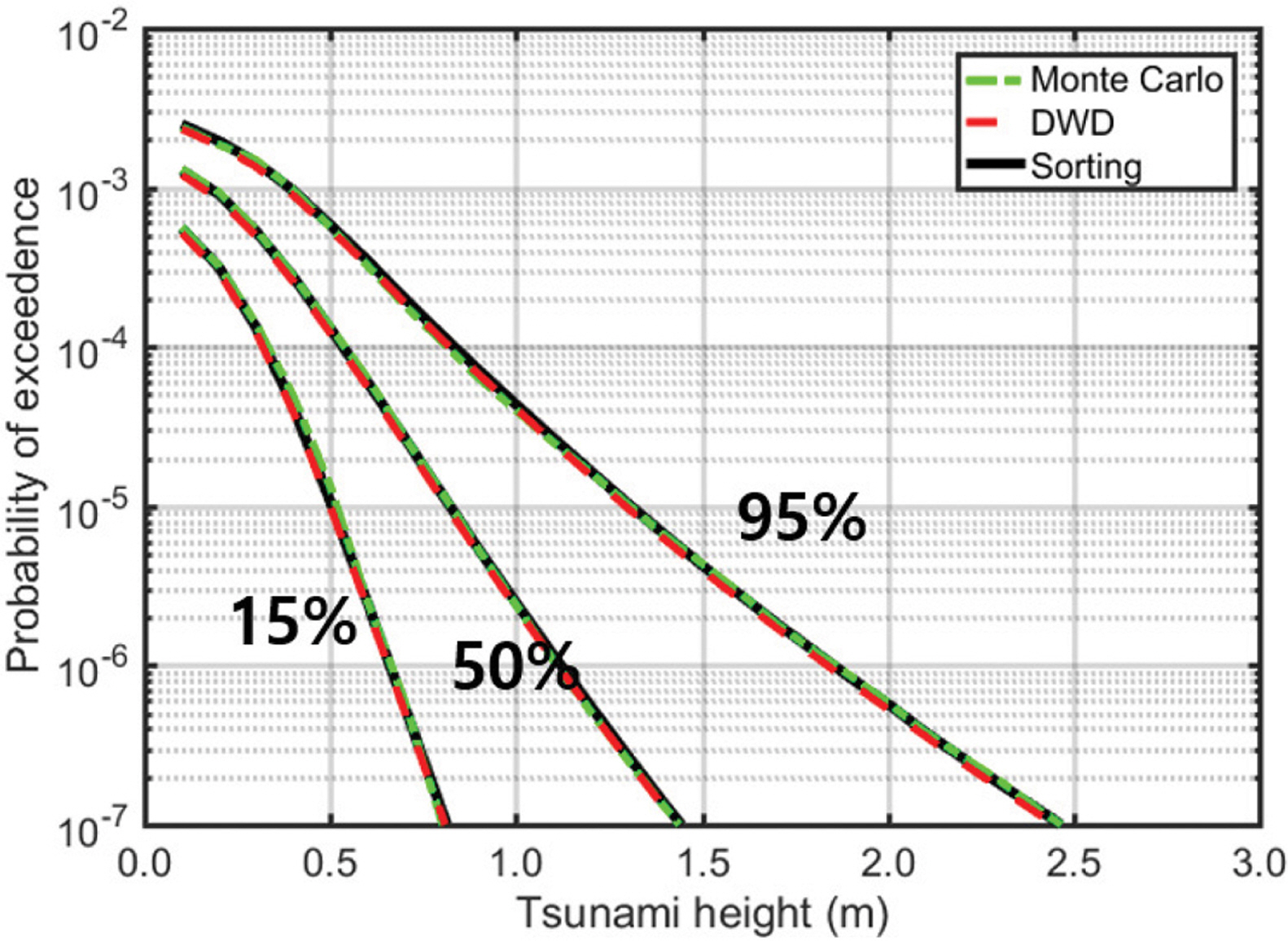
Fractile curves obtained using Monte Carlo (green), Sorting (black), DWD (red) method; 800 random numbers for each segment (Monte Carlo) and 1,000 bins (DWD method) are employed.

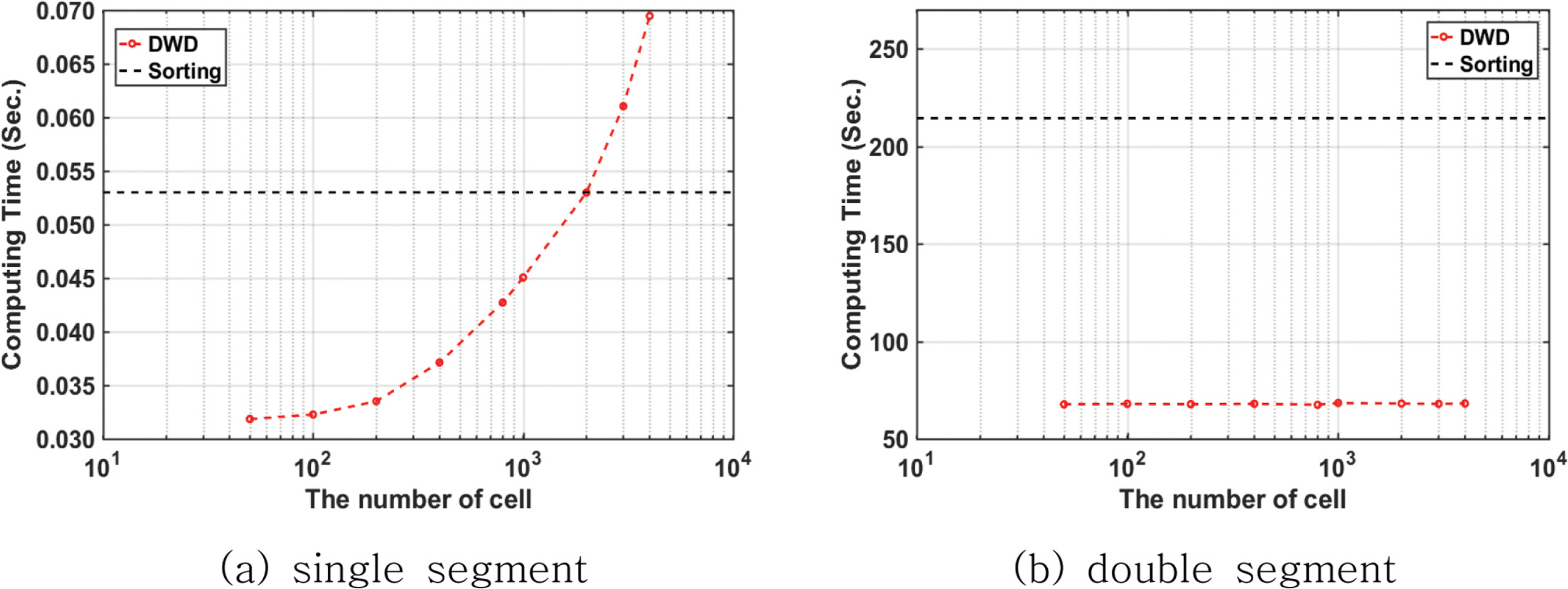
세그먼트의 수와 확률구간의 이산화 수준에 따른 방법별 계산 소요시간을 Fig. 16에 나타내었다. 소요시간 측정은 Intel i5-6500 3.2 Ghz의 CPU와 32 GB 메모리, Win10 64x 운영체제 환경에서 수행되었다. 본 연구에서 작성한 3,456개의 논리분기에 대해 정렬기법을 사용할 경우 프랙타일 산출 소요시간은 0.053초이며, 앞서 언급된 확률구간 수에 대한 이산가중치분포법의 소요시간은 0.032초(50개)에서 0.069초(4,000개)까지 증가한다. 2,000개 이상으로 분할할 경우 이산가중치분포법을 사용한 경우가 시간소요 측면의 이점을 상실하였다. 3,456개의 논리분기를 처리하는 데 있어 정렬기법을 사용한 경우나 이산가중치분포법의 결과 간에 절대적인 시간차이는 무시할 수 있을 수준으로 작다고 할 수 있으나, 세그먼트가 두 개인 경우에 대해서는 이산가중치분포법이 크기순정렬기법을 사용했을 때의 1/3 수준이다. 세그먼트 1개의 경우에 비해 2개의 세그먼트에 대하여 분할 수 변화에 따른 시간변동이 크지 않은 것은 분기 수가 많을 경우 논리분기를 조회하는 데 소요되는 시간이 더 지배적이기 때문이며 구간을 생성하는 소요시간의 절대적인 크기가 매우 작기 때문이다.

Fig. 16.

Comparison of computing time with increase of discretization.

Fig. 17은 각 세그먼트별 논리분기 수를 3,456개로 고정하고 세그번트의 수가 증가함에 따른 방법별 소요시간 변화를 비교한 것이다. 이산가중치분포법 적용 시 확률구간을 1,000개로 분할하였으며, 몬테카를로 방법의 경우 세그먼트 별로 800개의 난수를 사용하였다. 세그먼트 1개를 고려한 경우, 이산가중치분포법, 정렬기법, 몬테카를로 방법 순으로 빠르게 결과를 산출할 수 있었다. 2개 이상의 지진원이 고려된 경우 모든 분기를 고려하게 되는 두 방법(정렬방법, 이산가중치분포법)은 몬테카를로 방법에 비해 소요시간이 크게 증가한 것을 확인할 수 있다. 또한 몬테카를로 기법의 소요시간은 고려되는 세그먼트 수의 증가에 따라 비교적 선형적으로 증가하는 것을 볼 수 있다. 몬테카를로 방법의 소요시간(3.698초)이 세그먼트 1개에 대해서 다른 두 방법(정렬기법 0.053초; 이산가중치분포법 0.043초)에 비해 소요시간이 크게 차이가 나는 것은 난수를 생성하는 과정에서 발생한다.

Fig. 17.

Elapsed time for constructing fractile curves as the increase of considered segments; 800 random numbers for each segment (Monte Carlo) and 1,000 bins (DWD method) are employed.

4. 결 론

우리나라에 영향을 주는 지진해일의 발생역인 동해 동연부에 대해 로직트리를 작성하고 프랙타일 곡선을 산출하는 방법을 제안하였으며 기존의 방법과 비교하였다. 로직트리를 작성하는 데 있어 우리나라에 내습하는 지진해일은 모두 원지 지진해일이라는 점에 착안하여 주향각에 대한 불확실성을 추가하였으며, 단층경사 방향 및 위치(경도방향)에 대해서도 일본 서해안에 근접한 발생원은 배제하였다. 연초과확률 정렬 처리 단계에서 발생하는 시간소요는 대수적으로 등간격으로 분할된 확률구간을 활용하여 프랙타일을 산출하는 방법을 통해 작업량이 많은 경우(2~3개 세그먼트가 고려된 사항)에 대해 약 2~3배의 시간을 단축시킬 수 있었다. 이는 정렬기법 대비 데이터 조회수 및 조건문 연산을 줄여 시간효율을 개선시켰기 때문인 것으로 판단된다. 세그먼트가 1개일 경우는 이산가중치분포법이, 세그먼트가 2개 이상인 경우는 몬테카를로 방법을 사용하는 것이 가장 신속하게 결과를 얻을 수 있는 방안이라 판단된다. 몬테카를로 기법은 고려하는 세그먼트 수에 따라 시간이 선형적으로 증가하므로 많은 수의 세그먼트가 고려될 경우 매우 유용할 것으로 판단되나 모든 분기가 반영된 결과가 아님에 유의해야 한다.

Article information Continued