불연속 갤러킨 음해법의 천수방정식 적용
Applications of Implicit Discontinuous Galerkin Method to Shallow Water Equations
Article information
Abstract
천수방정식에 대한 불연속 갤러킨 기법 (DG)은 주로 양해법 기반으로 개발되어 적용되어 왔으나, 바닥마찰항의 처리, 과도한 CFL 조건 등의 불리한 점이 지적되어 왔다. 이에 대한 대안으로써, 본 연구에서는 음해법 기반의 모형을 개발하고 이를 적용하여 향후 가능성을 입증하였다. 본 논문에서 연구한 사례에서는 선형 삼각형 요소를 사용하였고, 수치흐름률로서 Roe 흐름률을 이용하였으며, TVD 특성 보존을 위한 기울기 제한자를 적용하였다. 적용 사례로서 실린더 주변의 흐름과 댐 붕괴류 문제 등에 대하여 적용하고, 기존의 실험치, 수치해와 비교하여 잘 일치함을 확인하였다.
Trans Abstract
Though the discontinuous Galerkin (DG) method has been developed and applied to shallow water equations mainly in explicit schemes, they have been criticized for the limitation in treatment of bottom friction terms and severe CFL conditions. In this study, an implicit scheme is devised and applied to some representative benchmark problems. The linear triangular elements were employed and the Roe numerical fluxes were adopted for convective fluxes. To preserve TVD property, the slope limiter was employed. As the case studies, the model is applied to the flow around the cylinders and the dam-break flow. Then, the results are compared with the experimental and numerical data of previous studies and good agreements were observed.
1. 서 론
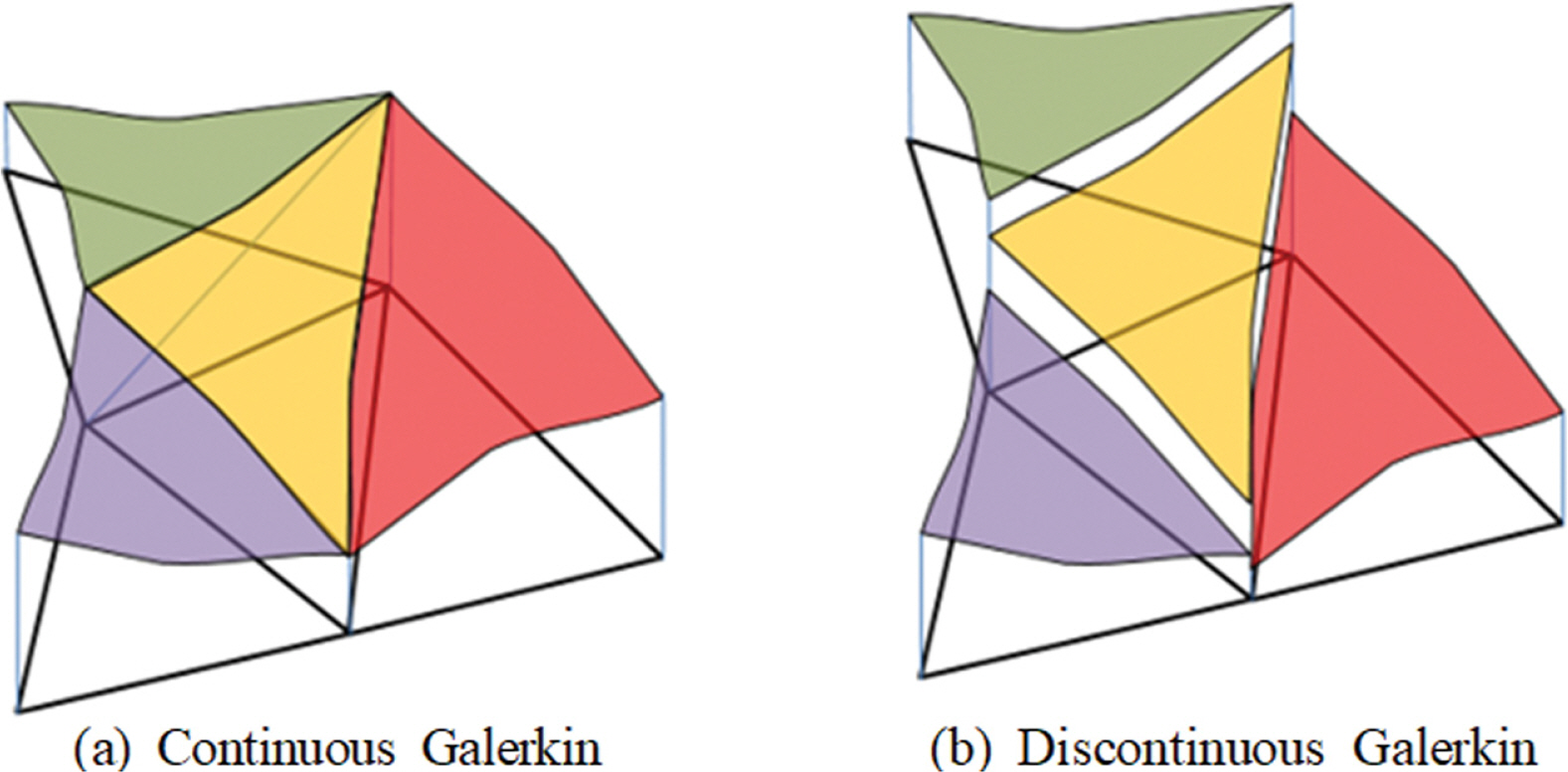
불연속 갤러킨 기법은 Reed and Hill(1973)에 의하여 중성자 이송방정식의 모의에 적용된 이래로, 1990년대 이후 Runge-Kutta 불연속 갤러킨(RKDG) 유한요소법으로 적용이 점차 증가하고 있다. 개별 요소에 대한 약형식(weak form)의 결과로서 나타나게 되는 요소 경계에 수직인 흐름률(flux)은 근사 리만해법(approximate Riemann solver)을 이용하여 구하는 것이 일반적이다. 기존의 안정화(stabilized) 유한요소법(예를 들면, SUPG, 특성선 기반 유한요소법(characteristic Galerkin Method) 등)과는 달리, Fig. 1에 보인 바와 같이 각 요소 사이의 경계에서 불연속을 허용하므로, 불연속적인 흐름의 모의에 유리한 것이 장점으로 알려져 있다. 또한, 이송방정식의 처리에 있어서, 상류이송기법에 의하여 산정되는 흐름률 자체가 필요한 안정성을 제공하기 때문에 추가적인 안정항이 필요하지 않다는 것이 장점이라고 할 수 있다. 최근 국내의 연구로는 Lee and Lee(2016) 등이 천수방정식의 연구에 적용한 바 있으며, 국외에서는 Engsig-Karup et al.(2006)이 Boussinesq 방정식에 적용한 바 있다.
Continuous and discontinuous Galerkin method.
천수방정식은 압축성 유동에 대한 나비에-스토크스 방정식과 수학적으로 밀접한 유사성을 갖는 것이 오래 전부터 알려져 왔으며(Orlin et al., 1947), 이에 대한 해석을 위해서는 충격파(단파(bore) 등), 접촉불연속(contact discontinuity), 전단파(shear wave), 와동(vortex), 젖음-마름 이동경계(wet-dry moving boundary) 등 압축성 유동에 대응하는 다양한 불연속적인 해를 해석할 수 있는 수치기법이 요구된다. 불연속 갤러킨 기법은 압축성 유동의 해석에 많이 사용되어 왔으며, 천수방정식의 해석에 적용할 수 있는 효과적인 방법으로 최근의 관심과 함께, 이에 대한 적용도 증가하고 있다. 최근, LeVeque and George(2007)의 천수방정식에 대한 리만해법 연구는, 유한체적법에 적용되어 불규칙한 실제 지형이나 수위가 낮아져서 노출되는 마른(dry) 영역에 대한 흐름을 모의하였으며, 그 후 유한체적법/불연속 갤러킨 기법 기반의 고차 정확도 모델 개발로 이어지게 되었다. 본 연구에서는 최근 개발된 음해법(Lee, 2019)을 실린더 주변의 흐름 해석과 댐 붕괴류 해석에 적용하였다.
천수방정식에 대한 불연속 갤러킨 기법의 적용은 저차(low order) 시간적분법에서 고차(high order) Runge-Kutta 시간적분법으로 양해법 기반의 해법이 개발되고 적용되어 왔다. 최근에는 젖음-마름 이동경계, 수치흐름률(numerical flux)과 생성항(source term)을 포함한 균형성 (well-balancedness)에 대한 연구까지 발전하고 있다(Lee and Lee, 2016). 다만, 양해법의 불연속 갤러킨 기법의 천수방정식에 대한 적용은 두가지 문제점을 제기한다. 첫째, 불연속 갤러킨 기법의 엄격한 CFL 조건 제한은 모델의 경쟁력을 제한하는 요소가 된다(Lee, 2014). 과거, Lee and Lee(2016)는 바닥마찰항에만 음해법을, 그 이외의 항에 대해서는 양해법을 적용하는 점-음해법(pointimplicit method)을 적용하여 문제점을 극복하였으나, CFL 조건을 완화시킬 수는 없었다. 둘째, 젖음-마름 이동경계 문제에서와 같이 수심이 매우 작은 영역에서는 바닥마찰항의 처리에 어려움이 있다. 따라서, 음해법 모델의 개발과 적용이 요구되고 있으나, 압축성 유체 유동에 대한 음해법 모델(예를 들면, Qin and Shu(2018) 등) 관련 연구가 활발한 반면에 천수방정식에 대한 연구 사례는 찾아보기 어렵다(Lee, 2019).
본 논문에서는 우선 지배방정식과 공간/시간 이산화 기법, 기울기 제한자(slope limiter)에 대하여 간략하게 설명한다. 관련된 몇가지 적용사례를 제시하고, 결론 및 향후 연구방향에 대하여 기술한다.
2. 지배방정식 및 모델화
2.1 지배방정식과 이산화
지배방정식으로서 천수방정식은 나비에-스토크스 방정식을, 정수압 가정하에 연직방향으로의 유속을 무시하고, 수심적분하여 다음과 같은 형태를 취한다.
여기서
로 표현되며, h는 수심, u와 v는 각각 x-와 y- 방향으로 수심평균된 유속이다. g는 중력가속도(9.81 m/s2)이며, ρ는 물의 밀도, zb는 기준면(reference/datum level)에서 연직상방으로 측정한 하상의 높이이며 이를 공간미분한 항 (S0x, S0y) = (- ∂zb/∂x, - ∂zb/∂y)이 바닥 경사항으로 사용된다.
수치적 근사해 Uh는 다음과 같이 기저함수(basis function)을 사용하여 표현할 수 있다.
여기서 ndof는 자유도(degree of freedom)이고, ϕ(x)는 기저함수이다. 불연속 갤러킨 기법에서는 Uh가 지역적(local)이며, 따라서, 요소간 경계에서 연속성이 강제되지 않는다. 갤러킨 근사에서 가중함수(weight function)은 기저함수와 같은 함수를 사용하기 때문에, 식(1)에 대한 공간차분형은 다음과 같다.
여기서 K는 각 요소의 영역이며, ∂K는 요소의 경계이다. 아래첨자 i, i = {1, 2, 3}는 각각 천수방정식 식(1)의 번호, p, q = {1, ..., ndof}는 기저함수의 번호를 나타낸다. 위첨자 ‘-’와 ‘+’는 각각 내부요소(owner call)과 외부요소(neighbor cell)에 연관된 변수라는 것을 의미한다. n은 요소의 경계에서 법선방향으로 외부요소에 향하는 단위벡터(outward unit normal vector)이다. H(i) (
2.2 시간적분법 - 음해법의 적용
선형 삼각형 요소에 대한 자유도는 ndof = 3이 되며, 공간 차분은 다음과 같다.
여기서 각 항은 다음과 같이 정의된다.
양해법을 적용한다면, R(i)p는
여기서
명백하게 위 방정식은 블록 행렬 구조를 갖게 되어(Lee, 2019), 행렬형태로는 다음과 같다.
여기서 ∆U(i)와 R(i)는 열 벡터(column vector)로서, 각각 미지수와 잔차(residuals)를 나타내며, i-번째 요소에 대해서 다음과 같다.
아래첨자 1, 2, 3은 선형 삼각형 요소의 각 노드 번호이다. 조립과정으로 만들어진 행렬 K는 CSR(Compressed Sparse Row) 형식으로 저장되며, 연립방정식은 BiCGStab 알고리즘(Saad, 2003)으로 해를 구하였다.
2.3 기울기 제한자
대체로 많은 천수방정식 모델에서와 같이, TVD(Total Variation Diminishing) 특성을 보존하기 위하여, 본 연구에서도 기울기 제한자(slope limiter)를 적용하였다. 기존에 많이 사용되고 있는, 잘 알려진 MINMOD 제한자가 다소 소산적(dissipative)인 것으로 알려져 그 대안으로 많은 기법이 시도되어 왔다. 본 연구에서 적용된 제한자는, 2차원 삼각형 요소에 대하여, Tu and Aliabadi(2005)에 의하여 제한된 것으로서 각 시간 단계에서 수심(h), 유속흐름률(hu, hv)에 대하여 적용된다. 기본적으로 van Albada 형 제한자의 미분형으로서, 유한체적법(FVM)에서 많이 사용되는 유사형태 기울기 제한자를 불연속 갤러킨 기법에 맞도록 재설계한 것이라 할 수 있다. 각 요소의 독립변수(Uh)의 기울기(gradient)를 요소의 각 변에서의 계산한 기울기(face gradients)의 가중치를 이용하여 제한하는 기법이다. 여기서, 변에서 기울기는 각 변을 공유하는 요소의 면적 가중치를 이용하여 계산한다. 이 과정을 단계별로 요약하면 다음과 같다.
[단계 1] 삼각형 요소의 각 변에 대한 기울기(gradients) 산정.
삼각형 요소 abc(Fig. 2)에서 변수 f에 대한 기울기 (∆f)ab, (∆f)bc, (∆f)ca를 산정한다. 본 연구와 같이 2차원 천수방정식 문제에서는 ∆f = (∂f/∂x, ∂f/∂y)로 정의된다.
Application of the slope limiter of Tu and Aliabadi (2005).
[단계 2] 각 요소에서 제한되기 전 단계 초기 기울기(unlimited gradient) 계산.
요소 0(Fig. 2)의 초기 기울기의 계산은 면적 가중치를 이용하여 각 변의 기울기를 조합하여 다음과 같이 구한다.
여기서 A0a3b, A0b1c, A0c2a는 각 사각형의 면적이다.
[단계 3] 각 요소에서 제한 된 기울기의 산정.
요소 0의 제한된 기울기는 다음과 같다.
여기서
가중치 산정에 필요한 g1, g2, g3는 초기 기울기의 L2 놈(norm)에 대한 제곱으로 다음과 같이 각 주변 요소에 대하여 계산한다.
파라메터 ε는 수치적 안정을 위하여 필요한 작은 수로서, Tu and Alibadi(2005)는 ε = 10-10를 제안하였으나, 충분히 작은 값이라면 문제가 되지 않는다.
[단계 4] 각 노드에서 변수의 제한된 기울기의 산정.
요소 0(Fig. 2)에 대한 노드의 제한된 변수값
여기서 ϕa, ϕb, ϕc는 선형 기저함수(linear basis functions)이다. 각 단계[1~4]를 모든 요소에 적용하여야 하며, 불연속 갤러킨 음해법의 적용에 대한 상세한 사항에 대해서는 Lee (2019)를 참고하기 바란다.
3. 모델의 적용 및 결과
본 연구에서 개발된 모델의 적용성을 확인하기 위하여 실린더 주위의 흐름과 댐 붕괴류에 적용하였다. 두 가지 적용 사례에서 CFL 수
3.1 실린더 주위 흐름
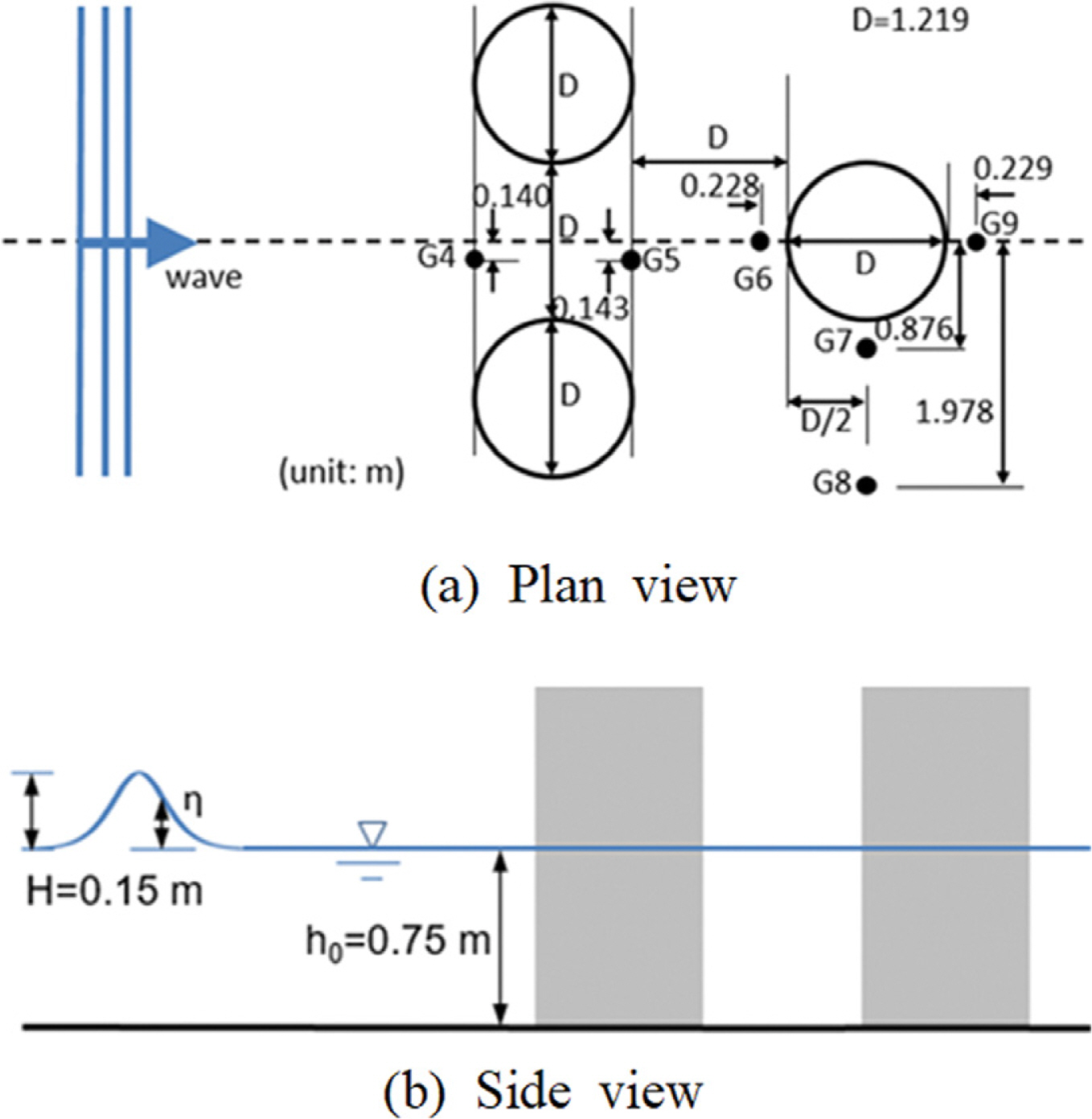
Zhang(2009)는 파랑-구조물 상호작용에 대한 연구의 하나로서 고립파에 대한 실린더 구조물의 주위의 흐름을 실험적으로 연구하였다(Fig. 3). 본 연구에서는 파고와 수심의 비 H/h0 = 0.20, 수심과 실린더 지름의 비 h0/D = 0.62, 고립파 파고 H = 0.15 m, 수심 h0 = 0.75 m인 경우를 선택하여 모델을 적용하였다. 세개의 실린더는 모두 같은 크기이다. 입력파로서 1차 고립파(first-order solitary wave)를 적용하였으며, 파형은 Li and Raichlen(2002)이 제시한 바와 같이 다음 파고와 유속을 적용하였다.
Layout of the experiment (D = 1.219 m (= 4 ft)).
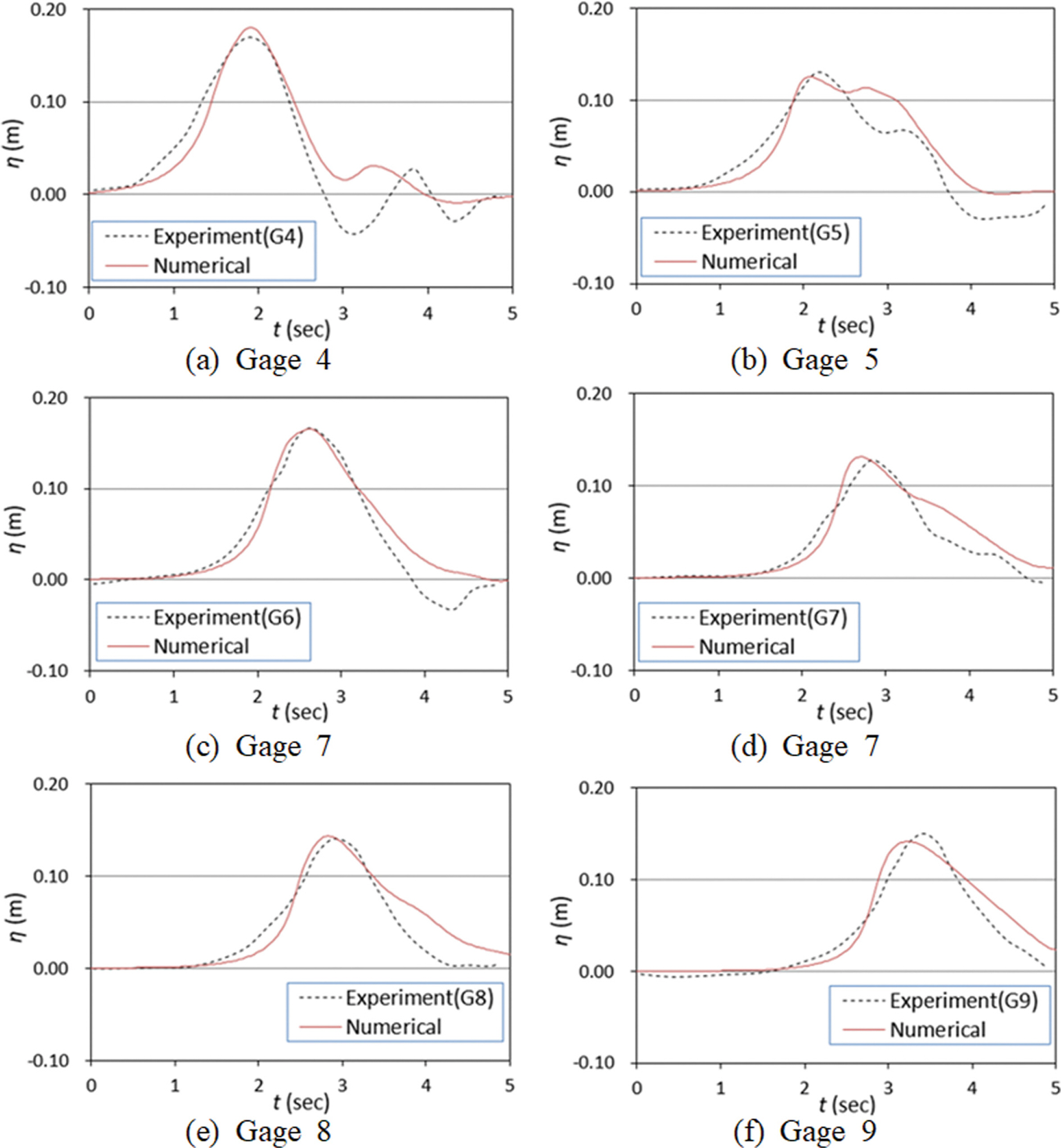
여기서 x0 는 초기 고립파의 파고점의 위치이다. Fig. 4은 Fig. 3에 보인 선택된 파고계에서 계측된 실험치(Zhang, 2009)와 본 연구의 수치해를 비교한 것으로서 대체로 잘 일치하는 것으로 보인다. 실린더 후면에서 불일치가 현저하게 보이는 경우가 있으나, 이는 비정수압 효과, 분산특성 등을 잘 반영하지 못하는 천수방정식 자체의 한계로 보인다.
Comparison of experimental and numerical results at selected gage locations.
3.2 댐 붕괴류 흐름
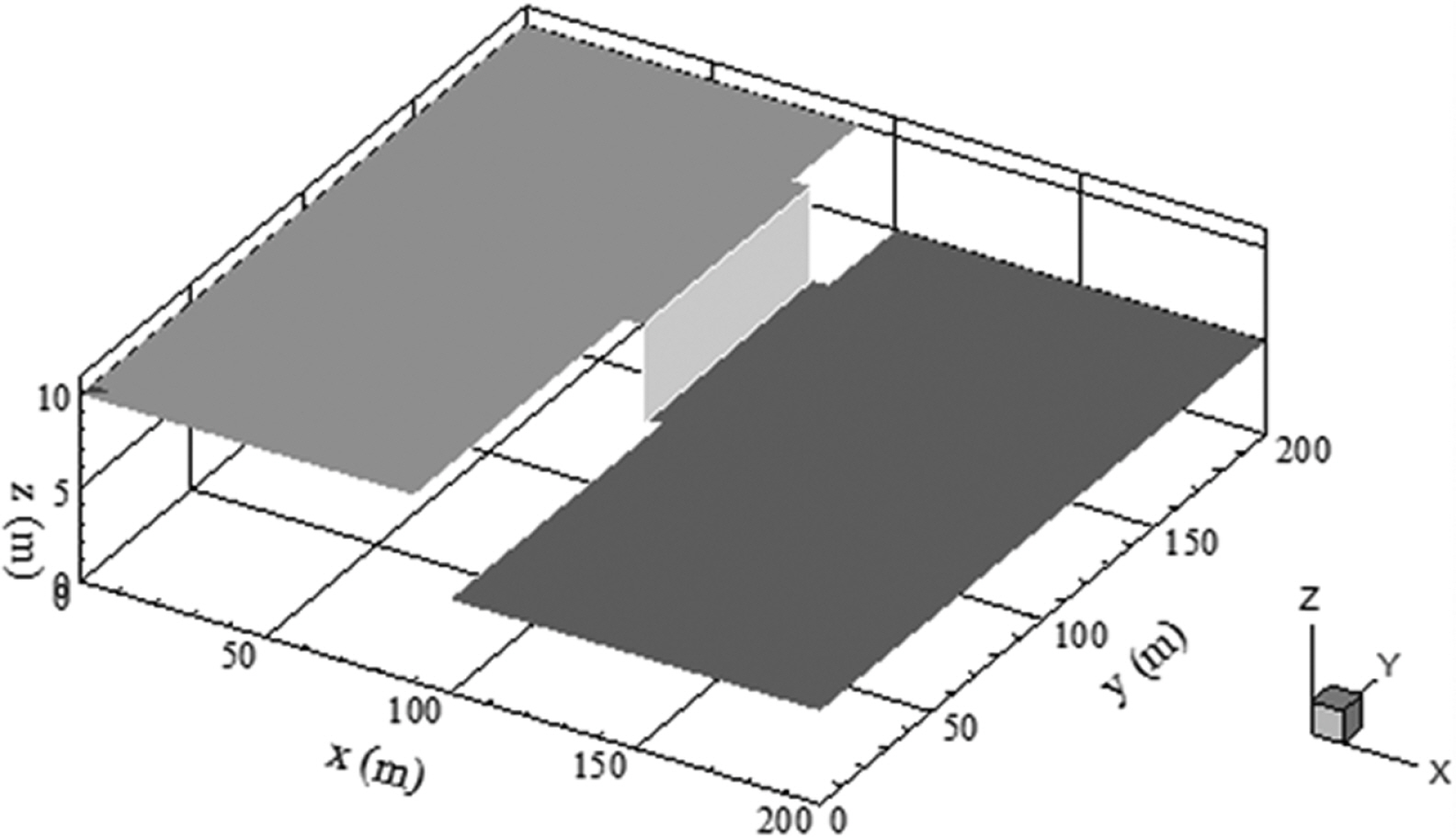
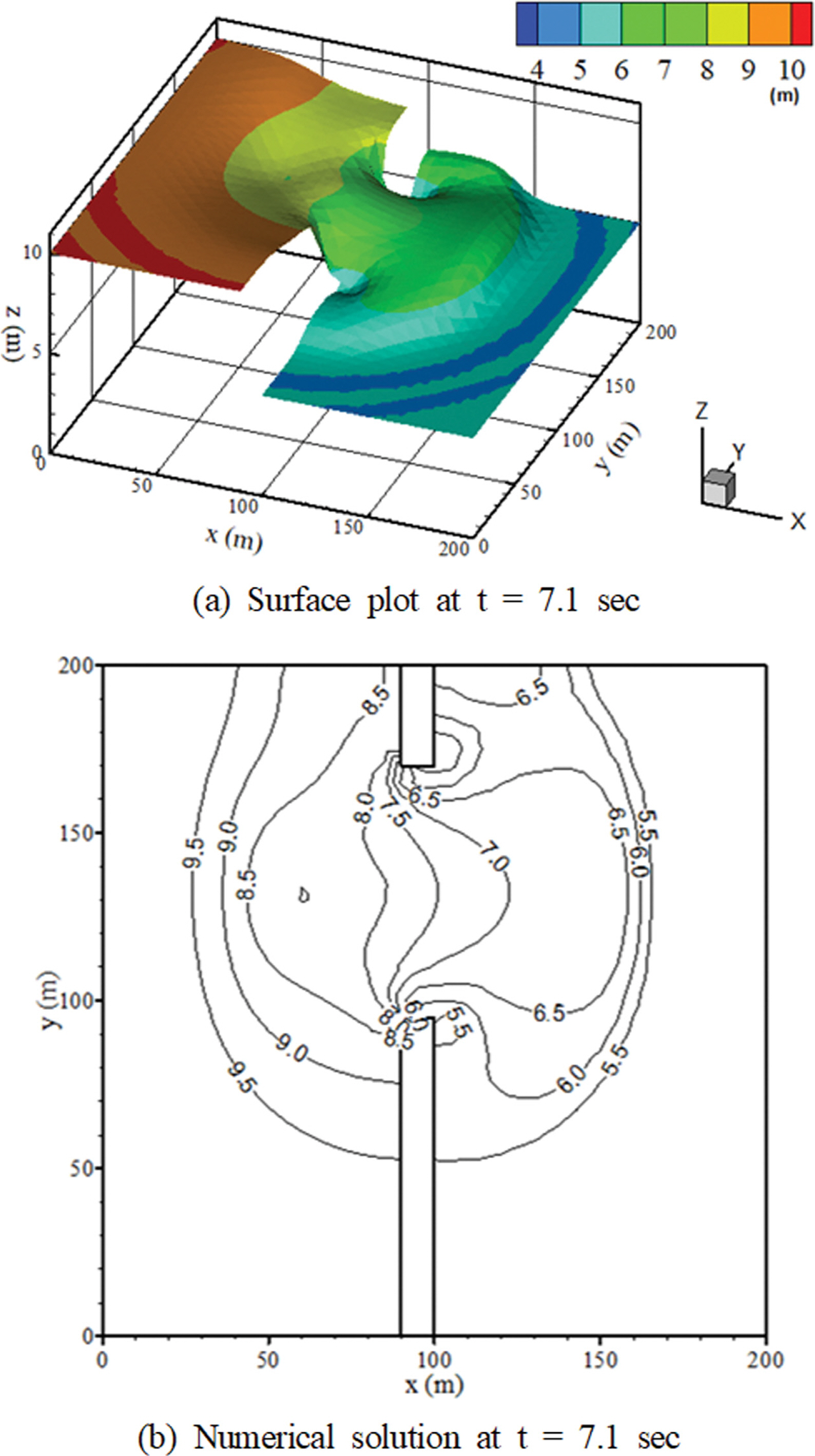
국부적인 비대칭 댐 붕괴류 문제는 Fennema and Chaudhry (1990)에 의하여 처음시도되었다. 전체 계산영역은 200 m 길이, 200 m 폭의 수로이다. 영역은 폭 10 m의 댐으로 구분이 되어 있으며, 초기 조건으로서 댐 하류부(tail)와 상류부(reservoir) 수심의 비는 ht/hr = 0.5이며, 전 영역의 초기 유속은 0으로 주어진다(Fig. 5). 비대칭적인 댐 파괴부는(두께 10 m 댐의) 폭이 75 m이고, 내부 저수지에서 길이방향으로 흐름을 유도한다. 문제를 단순화하기 위하여 많은 연구자들이 마찰과 경사가 없는 수로를 가정하였다.
Initial condition with a dam.
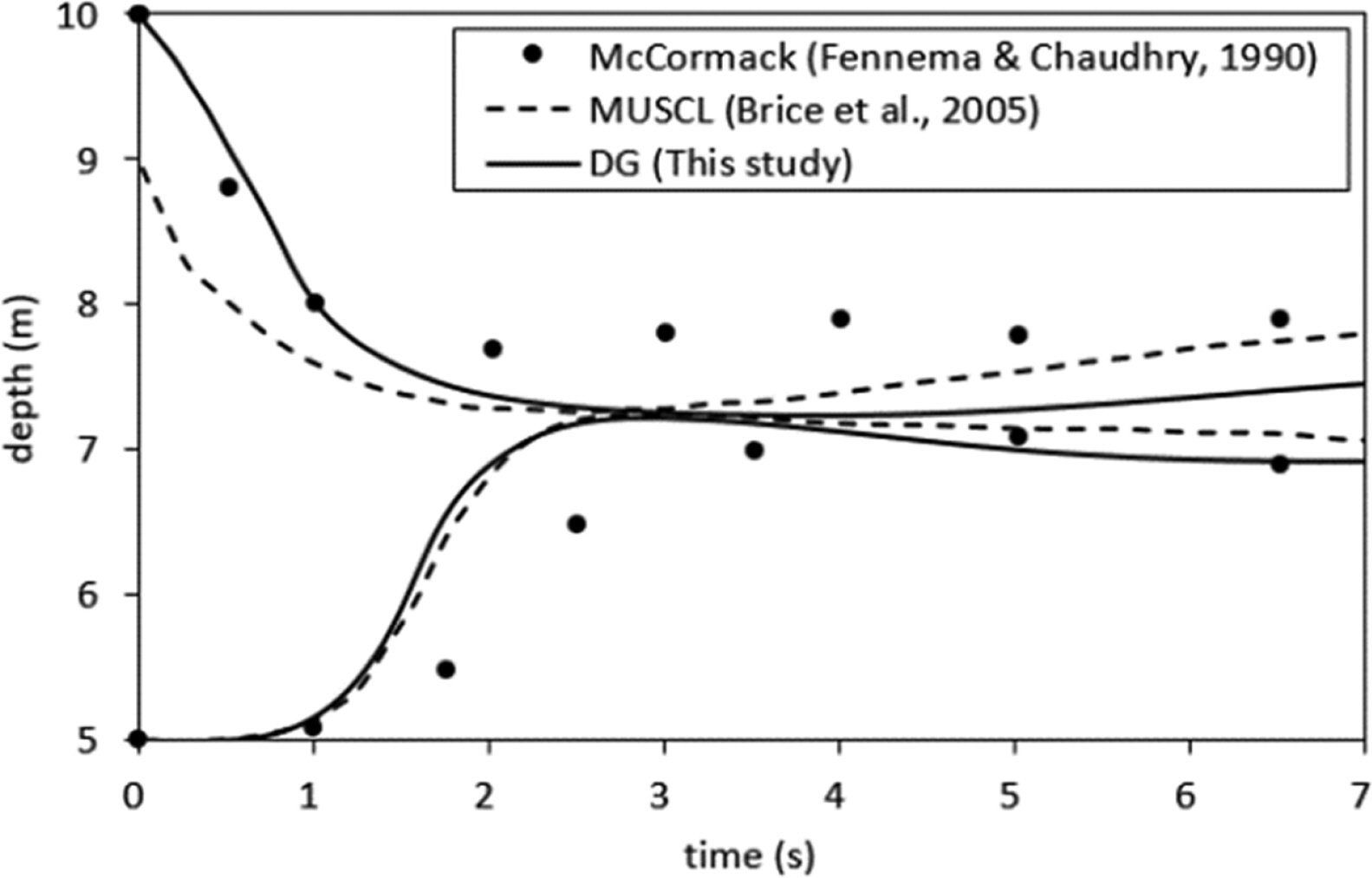
Fig. 6는 댐 붕괴후 7.1 초 후의 수표면을 보인 것이며, Fig. 7은 선행 연구 사례로서 Fennema and Chaudhry(1990)와 Brice et al.(2005)의 수치해석 결과를 본 연구의 결과와 비교한 것이다. 전체 영역에서 위치 좌표 (95,130)과 (115,130)의 시간에 따른 수심변화를 보인 것으로서, 기존 두 연구결과와 비교적 잘 일치함을 알 수 있다.
Plots of numerical solution of dam break.
4. 결론 및 향후 연구
불연속 갤러킨 음해법(Implicit Discontinuous Galerkin)을 천수방정식에 적용하고, 이를 몇가지 사례에 적용하여 대체로 기존 연구의 결과와 잘 일치함을 확인하였다. 일반적으로 계산수리학과 전산유체역학 분야에서는 음해법이 양해법에 비하여 보다 효과적인 방법이나, 알고리즘이 복잡하다는 점이 알려져 있다. 불연속 갤러킨 기법의 적용에서도, 음해법은 양해법보다 수치적 알고리즘이 더 복잡하며, 특히, 잔차의 자코비안(Jacobian) 계산에 노력이 필요하다. 또한, 양해법에서 필요하지 않았던 강성행렬(stiffness matrix)의 조립과정(assembly)이 필요하고, 전역행렬(global matrix)을 풀어 해를 구하여야 한다는 점 때문에 적용이 많지 않았던 것으로 보인다. 그러나, 음해법을 적용함으로써, 보다 더 안정적이며, 관련된 CFL 조건의 완화로 인한 사용성에서 유리한 모델에 이르게 된다는 점에 대해서는 관련 연구자들이 동의하는 바이기 때문에, 향후 음해법의 적용이 증가할 것으로 기대된다.
천수방정식에 대한 젖음-마름 이동 경계의 처리에는 음해법 모델이 필수적이므로(Lee and Lee, 2016), 현재 개발된 모델에 대한 관련 연구가 진행 중이다. 개발된 코드를 실제 문제에 구현하기 위해서는 장시간의 모의가 필요하기 때문에 코드의 병렬화에 대한 연구도 필요할 것으로 사료된다. 불연속 갤러킨 기법이 가진 장점의 하나로서 고차 요소로의 확장도 필요하다고 생각되며, 오염물질 이동 등의 모의를 위한 모델 확장도 고려하고 있다.
Acknowledgements
본 결과물은 환경부의 재원으로 한국환경산업기술원 수생태계 건강성 확보 기술개발사업의 지원을 받아 연구되었습니다(2020003050002).