1. 서 론
사회가 발전함에 따라 항만 구조물과 같은 사회기반 시설물에 요구되는 안전성에 대한 국민적 기대치가 점점 높아지고 있다. 따라서 건설비용이 많이 들고 파괴에 따른 사회적 손실비용이 크게 발생하는 항만 구조물의 사용 기간 경과에 따른 안전성에 대한 관리가 매우 중요하다. 특히 기후변화에 따른 해양환경은 점점 더 불확실해지고 항만 구조물의 노후화는 빠르게 가속화되고 있다. 이는 시간의 진행에 따라 항만 구조물이 기능적으로 그리고 역학적으로 손상된다는 의미이다. 따라서 노후화에 따른 손상의 정도를 정확히 예측하여 갑작스러운 파괴가 발생하지 않도록 해야 하고, 또한 최초 설계시 부여된 기능성과 안전성이 올바로 유지되도록 예방적 유지관리(preventive maintenance)가 실시되어야 한다. 구조물의 생애주기 동안 최소의 비용으로 최대의 성능, 기능성과 안전성을 확보하기 위하여 언제 어떤 유지관리 행위가 수행되어야 하는지를 결정해야 한다. 항만 구조물과 같은 대부분의 중요 시설물의 경우 파괴사건의 발생도 아주 드물고 그에 대한 피해상태 등과 같은 자료가 거의 없기 때문에 재령기반 유지관리(age-based maintenance) 모형을 사용할 수가 없다. 따라서 조건기반 유지관리(Condition-Based Maintenance: CBM) 모형이 적용되는데, 이를 위해서는 미래 시간에 대한 피해의 진행 과정과 크기를 추적할 수 있어야 하고 또한 재령에 따른 잔류수명(Residual Useful Life : RUL)을 올바로 추정하는 것이 필요하다(Cui et al., 2004; Wang, 2007; Pecht and Jaai, 2010; Gasperin et al., 2011; Ahmad and Kamaruddin, 2012, Ye et al., 2012).
구조물이 그 기능을 수행하기 시작하는 최초 시점에서부터 파괴시까지의 시간 간격으로 정의되는 내구수명(lifetime)과 다르게 잔류수명은 일정 재령이 경과한 기준시점에서부터 미래 파괴가 발생되는 시점까지의 시간 간격으로 정의된다. 따라서 잔류수명을 올바로 추정하기 위해서는 먼저 기준시점에서의 피해상태가 올바로 파악되어야 하고, 다음으로 미래의 피해 진행 과정이 정확히 예측 산정되어야 한다. 이와 같은 예측과 산정과정은 기준시점 이전의 과거 피해에 대한 관측자료를 기반으로 접근(statistical data-driven approach) 되어야 한다. 따라서 과거의 관측자료 속에 내포된 피해의 거동특성과 미래 시간의 경과에 따른 불확실성이 올바로 고려되어야 한다. 현재까지 시간의 함수로 불확실성을 고려하면서 피해의 진행 과정을 해석하는데 가장 적합한 확률모형이 추계학적 확률과정(stochastic process)이다. 감마 확률과정(Gamma Process: GP)과 위너 확률과정(Wiener Process: WP)이 많은 연구자들에 의하여 사용되고 있다(van Noortwijk, 2009; Gorjian et al., 2009; Si et al., 2011; Shahraki et al., 2017; Lee, 2019). 먼저 Singpurwalla(1995), Wang et al.(2000), Bagdonavicius and Nikulin(2000), Dieulle et al.(2003), Crowder and Lawless (2007), van Noortwijk et al.(2007), Ebrahimi(2009), Kuniewslci et al.(2009), Nicolai et al. (2009), Pandey et al.(2009), Lee(2015, 2019) 등이 추계학적 감마 확률과정을 이용하여 시간에 따른 피해 경로를 해석하였다. 방파제의 대표적 형식인 경사제를 해석한 Lee(2015, 2019)의 연구를 제외한 대부분의 연구들은 전자 기계 장치에 대한 연구이다. 또한 피해가 단조 증가해야 하는 등 여러 가지 특징과 제약성이 있지만 잔류수명의 관점에서 보면 감마 확률과정은 잔류수명의 거동특성을 해석하기 보다는 잔류수명의 평균(Mean Residual Life: MRL)을 정량적으로 산정하는데 주로 적용된다. 따라서 잔류수명에 대한 거동특성을 해석하기 위하여는 확률밀도함수 등을 수학적으로 정의할 수 있어야 하는데 이에 더 적합한 확률과정이 추계학적 위너 확률 과정이다. Cox and Miller(1965)의 연구를 시작으로 Chhikara and Folks(1977), Doksum and Hoyland(1992), Whitmore (1995), Whitmore and Schenkelberg (1997), Tseng et al. (2003), Gebraeel et al.(2005), Tseng and Peng(2007), Elwang and Gebraeel(2009), Peng and Tseng(2009), Wang(2010), Wang et al.(2010), Tsai et al.(2011), Guo et al.(2013), Jin et al.(2013), Le Son et al.(2013), Wang et al.(2013), Wang et al.(2014), Li et al.(2017, 2019) 등 상당히 많은 연구자들이 위너 확률과정의 적용성에 대하여 활발히 연구하였다. 수학적으로 보면 피해의 진행이 선형이냐 비선형이냐에 따라 해석하는 방법을 달리한 연구들이다. 또한 시간에 따른 불확실성을 다르게 고려할 수 있는 다양한 접근법을 제시하였다. 그러나 콘크리트 빔 교량의 균열에 대한 물리적 구성방정식을 활용한 Wang(2010)의 연구를 제외한 대부분의 연구들은 전자 기계 장치나 임의로 설정한 가상적 상황에 대하여 MCS(Monte-Carlo Simulation) 기법을 활용한 수치적 모의에 대한 것들이다. 기후변화에 따른 해양환경이 점점 더 불확실해지고 노후화가 빠르게 진행되고 있는 중요한 사회기반 시설물인 항만 구조물에 대한 연구는 아직 수행되지 않고 있다. 따라서 본 연구에서는 위너 확률과정을 이용하여 처음으로 경사제 피복재에 대한 피해 경로와 파괴확률 그리고 그에 따른 잔류수명의 거동특성을 해석하고자 한다.
본 논문의 구성은 다음과 같다. 먼저 제 2절에 일반화된 WP를 이용하여 구조물의 시간에 따른 피해경로를 추적할 수 있고 누적피해와 내구수명의 분포함수를 해석할 수 있는 추계학적 모형을 수립하였다. 또한 변수변환 기법을 활용하여 구조물의 잔류수명을 해석할 수 있는 일반화된 추계학적 모형이 제 3절에 제시되었다. 한편 제 4절에서는 최소자승법과 최우도법을 이용하여 모형에 포함된 파라미터를 추정할 수 있는 방법을 설명하였으며, 제 5절에서는 기존에 해석된 조건에 대하여 모형을 검증한 후, 경사제에 적용하여 시간에 따른 피해의 거동특성과 잔류수명에 대한 여러 가지 특성들을 분석하였다. 마지막으로 제 6절에 결론을 제시하였다.
2. 피해경로 추적 모형
시간 t의 진행에 따른 항만 구조물의 피해를 X(t)라 정의하면 일반화된 위너 확률과정(Wiener Process: WP)은 다음 식 (1)과 같이 정의된다(Si et al., 2012; Wang et al., 2014; Li et al., 2017, 2019).
여기서 X(0)는 초기 피해, a는 피해 진행의 기울기(slope of drift), λ(u; θ → θ → γ → γ →
식(1)에 의하여 정의된 추계학적 확률과정을 일반화된 WP라 정의하며, X(t)는 정상적이면서 독립된 증분(stationary and independent increments)을 갖는 연속인 확률과정이다. 따라서 다음 식(2)를 이용하면 피해의 증분은 위에서 정의된 BM 확률과정에 의하여 dX(t) ~ N{a[Λ(t + dt; θ → θ → σ B 2 γ → γ →
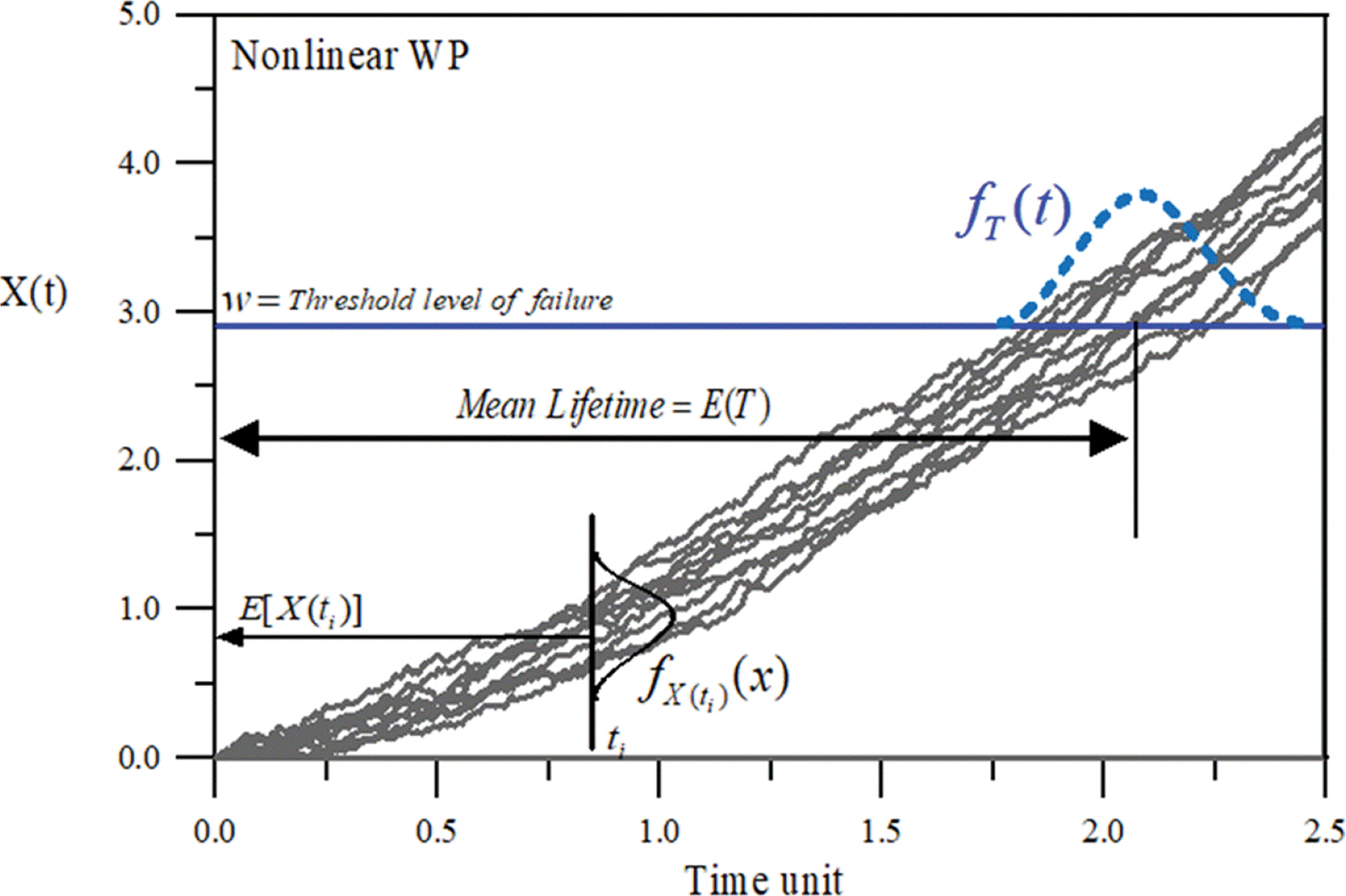
따라서 식(1)과 식(2)를 이용하면 시간에 따른 불확실성을 고려하면서 피해경로를 Fig. 1과 같이 추적할 수 있다. Fig. 1에서 볼 수 있듯이 다양한 피해경로가 나타나고 있을 뿐만 아니라 시간에 따라 불확실성이 다르게 나타나고 있다. 이를 해석하기 위해서는 시간에 따라 각기 다르게 나타나는 누적피해 X(t)의 확률밀도함수를 산정할 수 있어야 한다.
식(2)에서 피해의 증분 dX(t)가 정규분포를 따르기 때문에 전 확률정리에 의하여 X(t)도 평균 μX(t) = aΛ(t; θ → σ X ( t ) 2 = σ B 2 ζ ( t ; γ → )
따라서 식(4)를 이용하면 시간에 따른 파괴확률, Pf(t)와 신뢰도, R(t)를 다음 식(5)로 부터 쉽게 산정할 수 있다. 임의 시간에서 누적피해가 파괴한계를 초과한다는 개념이다.
여기서 w는 Fig. 1에서 알 수 있듯이 파괴한계(threshold level of failure)를 의미한다. 따라서 식(1)에 정의된 일반화된 WP를 이용하면 시간의 진행에 따른 피해경로도 추적할 수 있고 파괴확률도 쉽게 산정할 수 있다.
한편 Fig. 1을 보면 피해경로가 각기 다른 시간에 파괴한계를 통과하는 것을 쉽게 알 수 있다. 이를 구조물의 내구수명 또는 사용수명(lifetime)이라 한다. 내구수명은 잔류수명과 다르게 구조물이 그 기능을 발휘하는 최초 시점에서부터 파괴시까지의 시간 간격을 의미한다. 따라서 내구수명, T는 다음 식(6)과 같이 정의된다.
여기서 inf는 하한(infimum) 또는 최대하계(greatest lower bound)를 의미한다. 일반적으로 추계학적 확률과정에서 내구수명을 FHT(First Hitting Time), FPT(First Passage Time) 또는 FTTF(First Time To Failure)라 정의한다. 가장 간단한 경우로서 식(1)과 식(2)에서 Λ(t; θ → γ →
한편 Λ(t; θ →
그러나 식(8)은 ζ(t; γ → γ → γ →
그러므로 식(8)을 적용하면 변수 변환된 내구수명 S = inf{s: Y(s) ≥ w}에 대한 확률밀도함수 gS(s)를 구할 수 있고, 이를 다시 치환하면 다음 식(11)을 얻을 수 있다(Wang et al., 2014).
3. 잔류수명 산정 모형
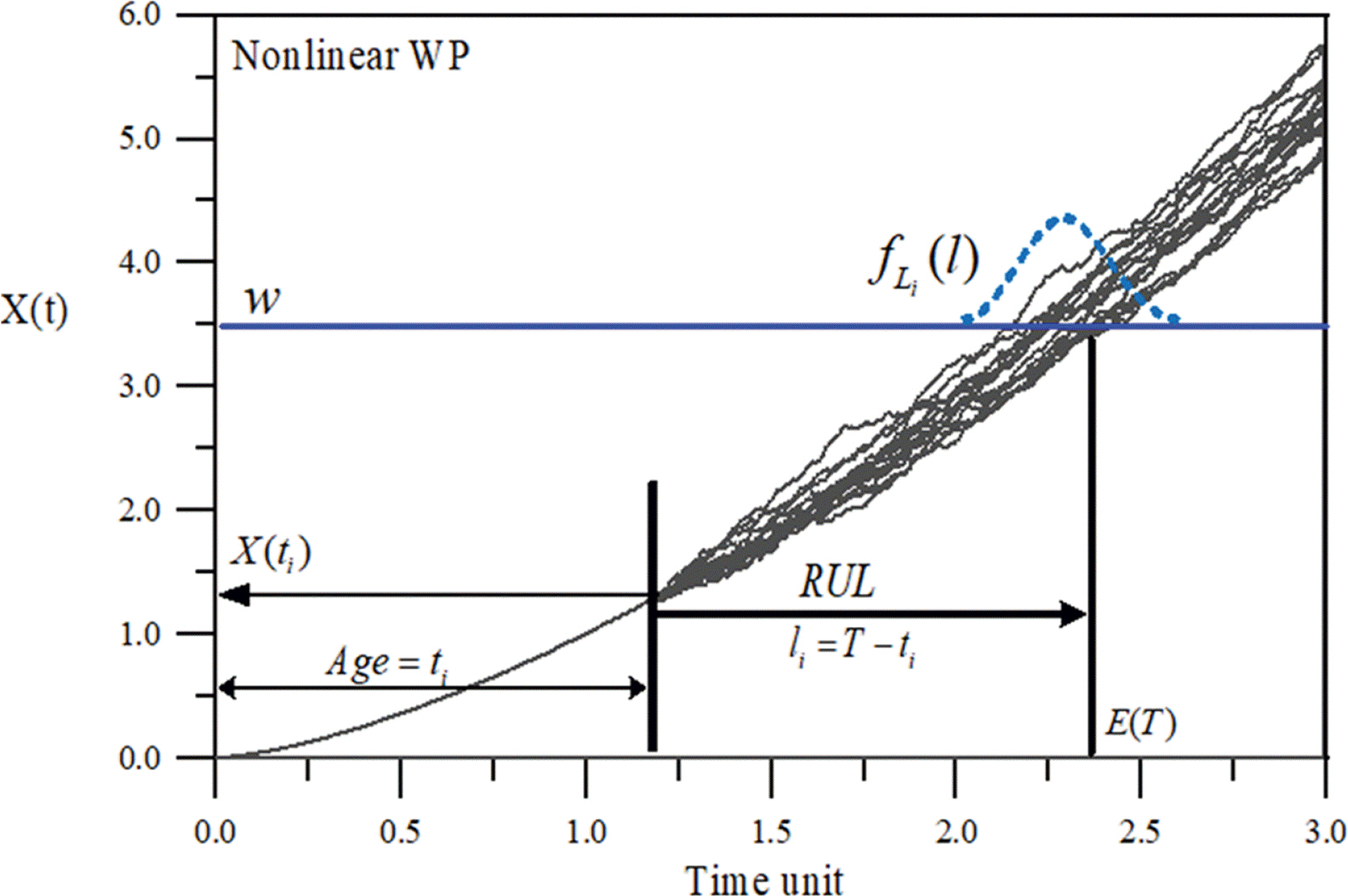
이상에서 일반화된 WP를 이용하여 시간에 따른 피해경로와 불확실성에 대한 비선형성을 고려할 수 있는 수학적 모형을 수립하였다. 즉, 시간에 따른 피해경로를 비선형적으로 추정할 수 있으며, 각각의 시간에서의 누적피해의 확률밀도함수를 산정하여 파괴확률도 추정할 수 있다. 또한 구조물이 그 기능을 수행하기 시작하는 최초 시점에서부터 파괴시까지의 시간 간격인 내구수명에 대한 확률밀도함수도 구할 수 있었다. 따라서 이하에는 재령이 이미 일정 시간 경과한 기존 항만 구조물의 잔류수명(Residual Useful Life: RUL)을 산정할 수 있는 수학적 모형을 수립하였다. 잔류수명은 Fig. 2에 제시된 바와 같이 구조물의 재령과 현재까지의 피해 그리고 장래 피해 진행 상황에 의존한다.
수학적으로 식(12)에서 ti = 0인 경우 Li = T와 같이 정의되어 잔류수명은 내구수명이 된다. 즉, 수학적으로 내구수명은 잔류수명의 극한에 해당하는 경우이다. 식(12)의 정의를 이용하여 잔류수명을 확률론적으로 해석하기 위해서는 현재 재령에서의 누적피해도 X(ti)를 정확히 알아야 하고, ti 이후의 li 진행에 따른 피해경로를 올바로 예측할 수 있어야 한다. 따라서 식(12)를 다음 식(13)과 같이 변환하면 식(6)에서 적용된 개념을 그대로 적용할 수 있다.
먼저 선형의 WP, 즉, Λ(t; θ → γ →
그러나 식(14)는 선형의 WP에 대한 결과로서 항만 구조물과 같이 피해 진행이 복잡하면서 비선형인 경우에는 적용할 수가 없다. 따라서 이하에 Wang et al.(2014)의 접근법에 따라 Λ(t; θ → γ →
이때 ζ(ti + l; γ → γ → γ → γ →
Yi(si) = X[η-1(si; γ → θ → γ → θ → θ →
여기서 ψ(si; θ → θ →
현재까지 연구된 대부분의 문제들은 Λ(t; b) = tb, ζ(t; c) = tc의 비선형 멱함수를 이용하여 해석되고 있다. 수학적으로 약간 복잡하지만 이를 식(19)에 대입하고 정리하면 다음 식(20)을 얻을 수 있다.
(20)
본 연구에서 유도된 식(20)을 검증하기 위하여 다음 두 가지 경우에 대하여 수학적으로 분석하였다. 하나는 일반적으로 알려진 b = c = 1인 선형의 WP에 대한 경우이고, 다른 하나는 b ≠ 1, c = 1인 일부 비선형 WP인 경우이다. 먼저 전자의 경우 b = c = 1을 대입하여 정리하면 식(20)은 정확히 식(14)와 같아진다. 따라서 식(20)은 선형의 WP에 대한 잔류수명을 포함한다. 나머지 다른 하나 b ≠ 1, c = 1인 경우에 대하여 정리하면 잔류수명의 확률밀도함수는 Si et al.(2012)이 제시한 다음 식(21)과 같아진다. 한편 b ≠ 1, c ≠ 1인 조건에서의 검증은 제 5절의 MCS 기법을 활용한 수치해석 결과와의 비교를 통해서 수행되었다.
4. 최우도법에 의한 모형 파라미터 추정
추계학적 WP을 이용하여 구조물의 잔류수명을 확률론적으로 해석할 수 있는 수학적 모형을 수립하였다. 시간에 따른 피해 진행과 그에 따른 불확실성을 모두 비선형적으로 고려할 수 있는 모형이다. 따라서 모형을 임의의 구조물에 적용하기 위해서는 모형에 포함된 파라미터들을 올바로 추정해야 한다. 이를 위해 본 연구에서는 최소자승법(least square method)과 최우도법(maximum likelihood method)을 이용하였다.
먼저 현재의 재령 ti 이전에 일정 시간 간격으로 n개의 누적피해 X(t1 = dt) = X1, X(t2 = 2dt) = X2, ..., X(ti = ndt) = Xn가 관측되었다고 생각하면, Lee(2019)에 제시된 바와 같이 최소자승법을 이용하여 다음 식(22)를 얻을 수 있다.
한편 0 ≤ t1 < t2 … < ti에서 X ^ 1 - X ^ 2
여기서 ∆ X j = X j - X j - 1 , ∆ t j b ^ = t j b ^ - t j - 1 b ^ , ∆ t j c = t j c - t j - 1 c ∂ ln L ( a , b ^ , c , σ B | ∆ X 1 , . . . , ∆ X n ) / ∂ a = 0 , ∂ ln L ( a , b ^ , c , σ B | ∆ X 1 , . . . , ∆ X n ) / ∂ c = 0 , ∂ ln L ( a , b ^ , c , σ B | ∆ X 1 , . . . , ∆ X n ) / ∂ σ B = 0
따라서 MATLAB(Moler, 2004) 등을 이용하면 모형에 포함된 파라미터들을 쉽게 추정할 수 있다. 서론에서 언급된 많은 연구에서는 실험자료나 관측자료와 비교하여 시간에 따른 불확실성이 시간 진행에 선형적으로 의존한다고 가정하였다. 비록 시간에 따른 불확실성을 비선형적으로 고려하는 경우에도 ζ(t; γ → θ → γ → θ → θ → γ →
5. 경사제에 대한 해석
일반화된 WP를 이용하여 임의 구조물의 피해경로를 실시간으로 추적할 수 있을 뿐만 아니라 재령에 따른 잔류수명을 수학적으로 또는 수치적으로 해석할 수 있는 추계학적 모형을 수립하였다. 또한 최소자승법과 최우도법을 이용하여 모형에 포함된 파라미터를 추정할 수 있는 방법도 제시하였다. 따라서 이하에 수립된 모형을 먼저 검증하고, 경사제 피복재에 적용하였다.
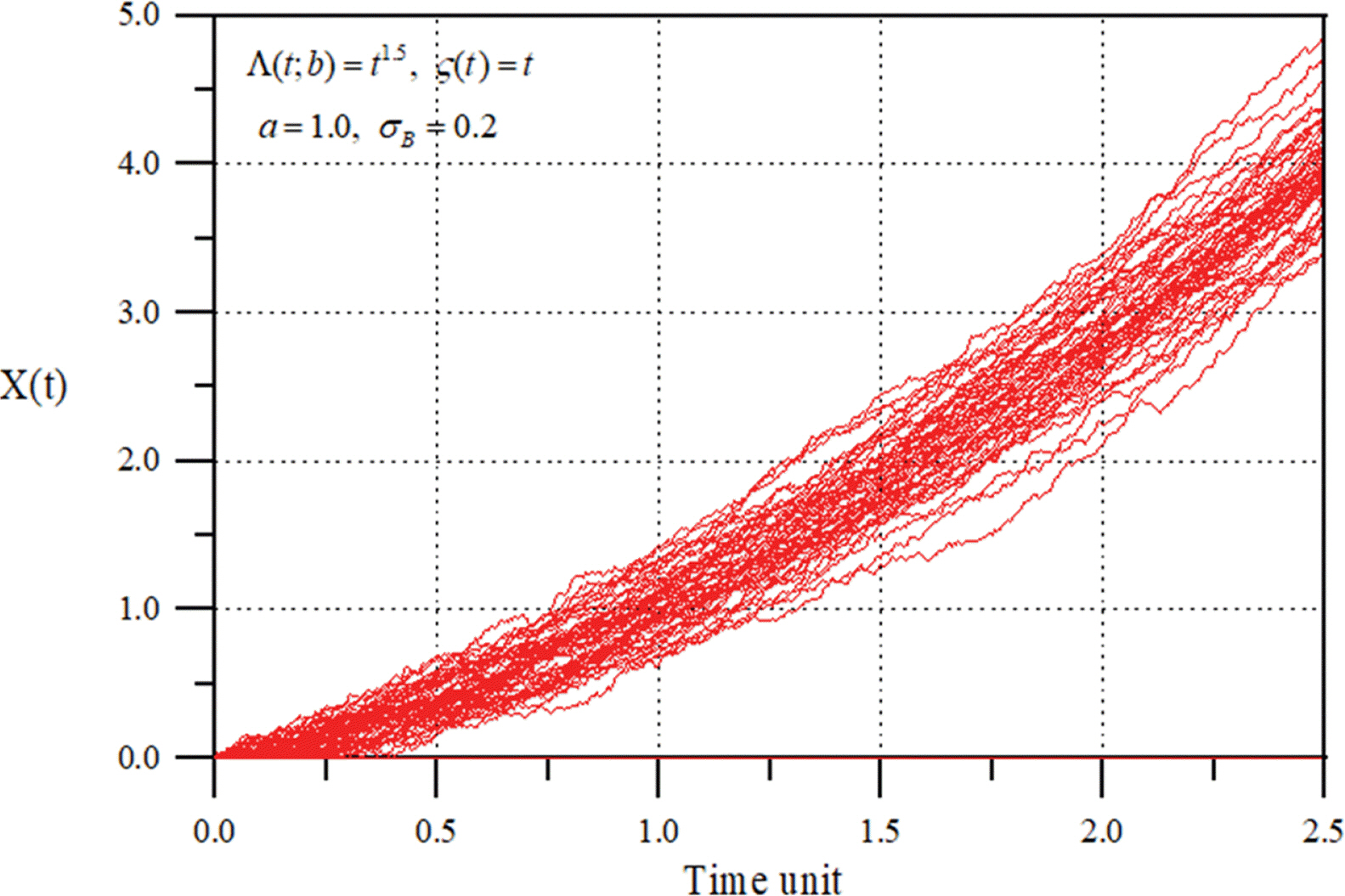
Si et al.(2012)은 a = 1.0, σB = 0.2 그리고 Λ(t; θ → γ →
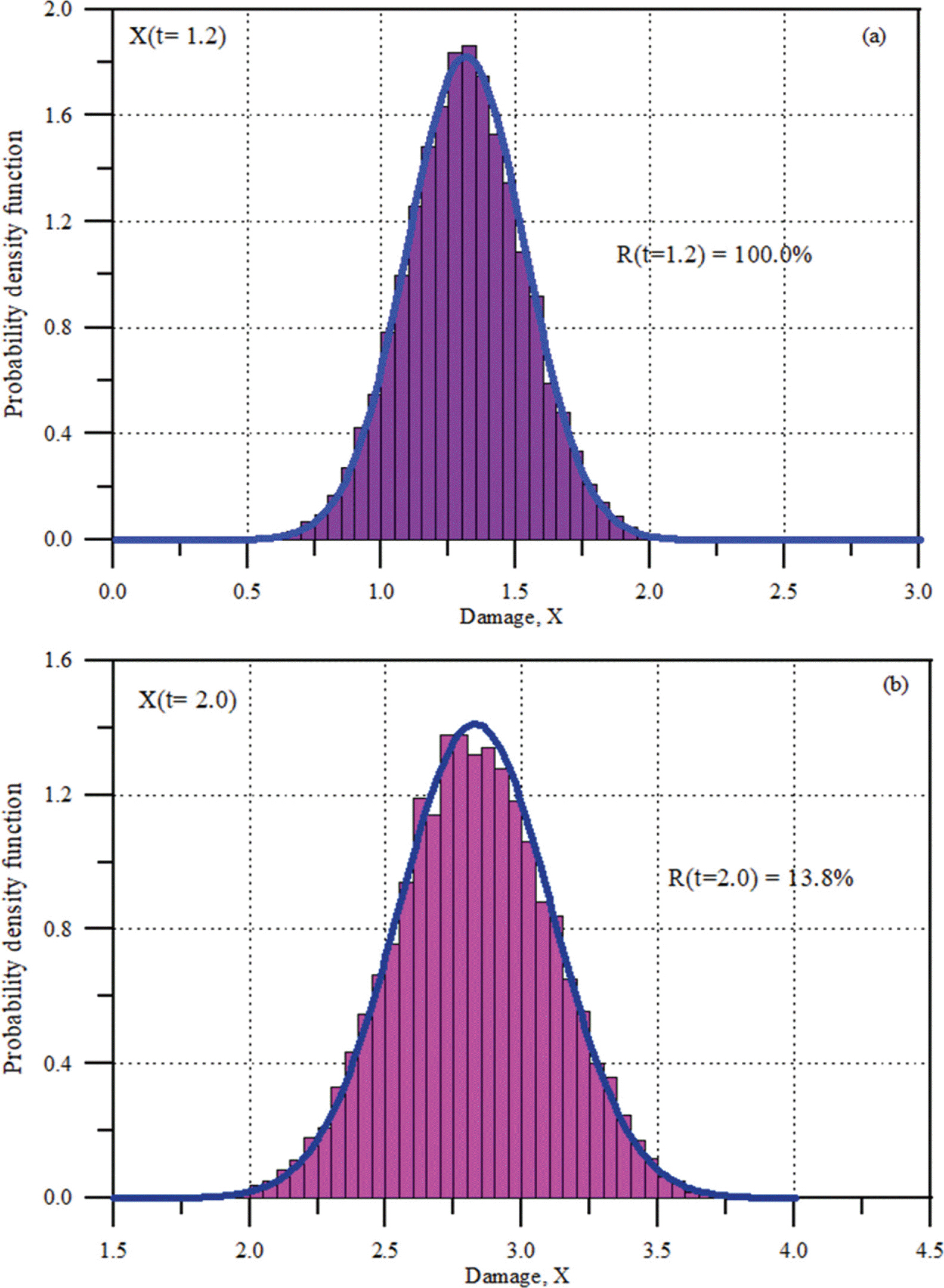
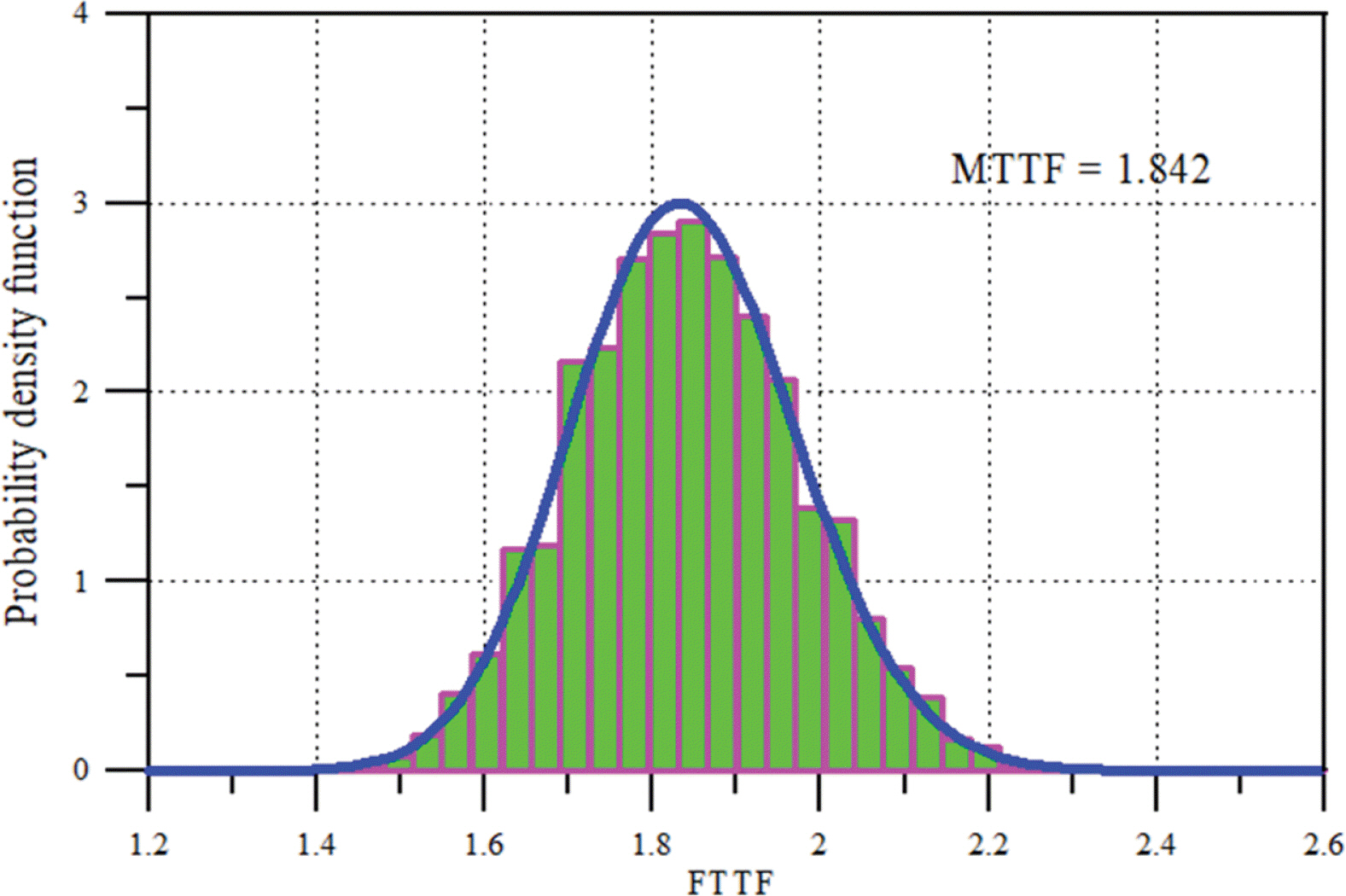
또한 Fig. 4는 t = 1.2와 t = 2.0에서 피해의 확률밀도함수를 나타낸 것이다. 그림에서 막대그래프는 MCS의 결과이고 실선은 식(4)에 의한 결과이다. 그림에서 볼 수 있듯이 매우 잘 일치하고 있다. 또한 w = 2.5에 대하여 식(5)에 의하여 산정된 R(t)를 함께 제시하였는데 시간이 진행될수록 신뢰도는 감소하고 파괴확률은 증가하는 것을 알 수 있다. 동일하게 내구수명에 대한 확률밀도함수도 Fig. 5에 제시하였는데 MCS 결과가 식(11)에 의하여 계산된 실선의 결과와 매우 잘 일치하고 있다. 그림에서 MTTF(Mean Time To Failure)는 내구수명의 평균을 의미한다. 피해가 최초 시간에서 파괴한계 w = 2.5 이상이 되는데 걸리는 평균 시간이 1.842라는 의미이다. Si et al.(2012)도 Fig. 5와 동일한 결과를 제시하였다.
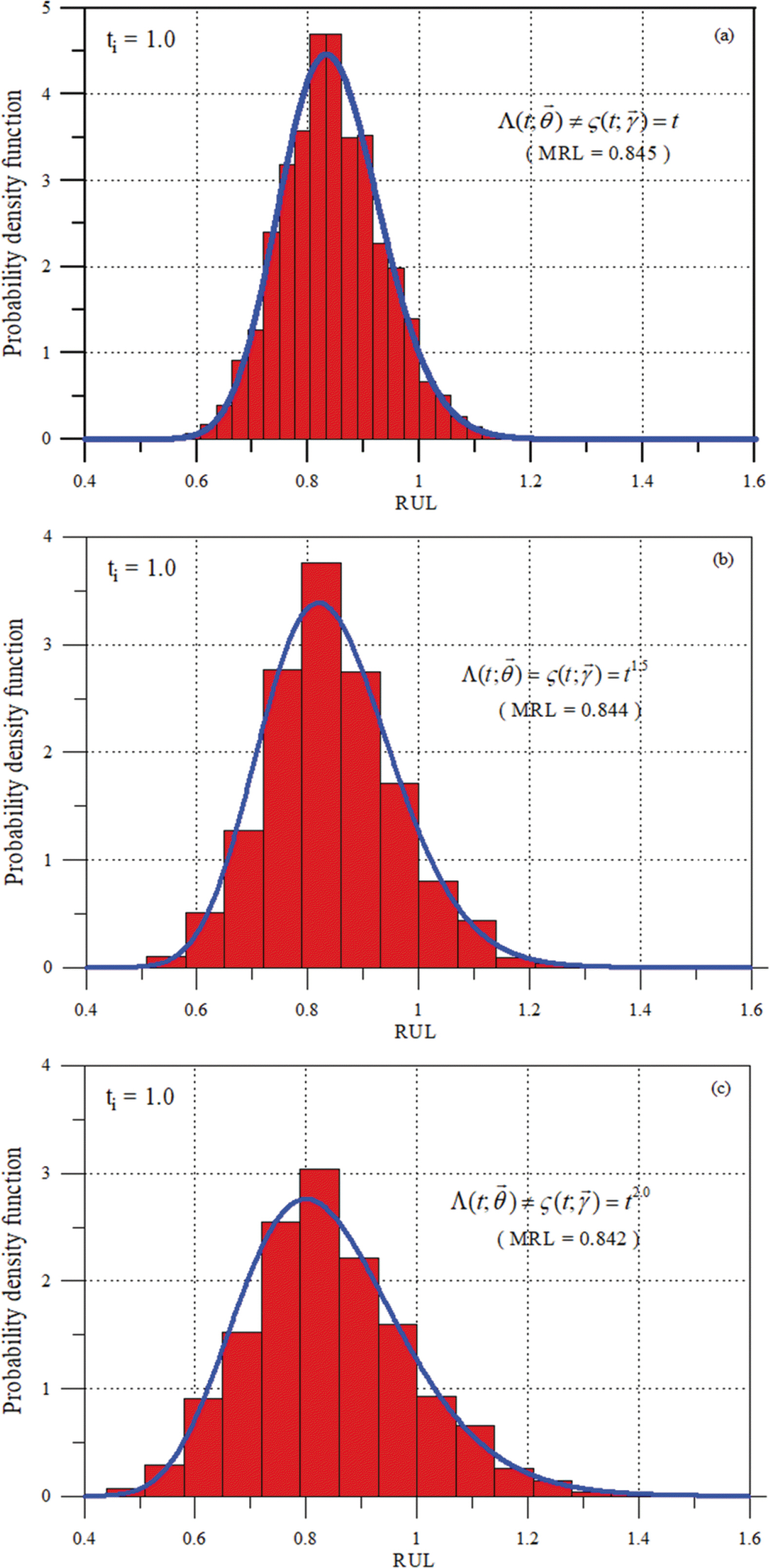
마지막으로 잔류수명에 대한 확률밀도함수를 해석하였다. 먼저 재령 ti = 1.0에서 잔류수명의 확률밀도함수를 Fig. 6에 제시하였다. 불확실성을 고려하는 방법, ζ(t; γ → γ → θ → θ → γ → γ →
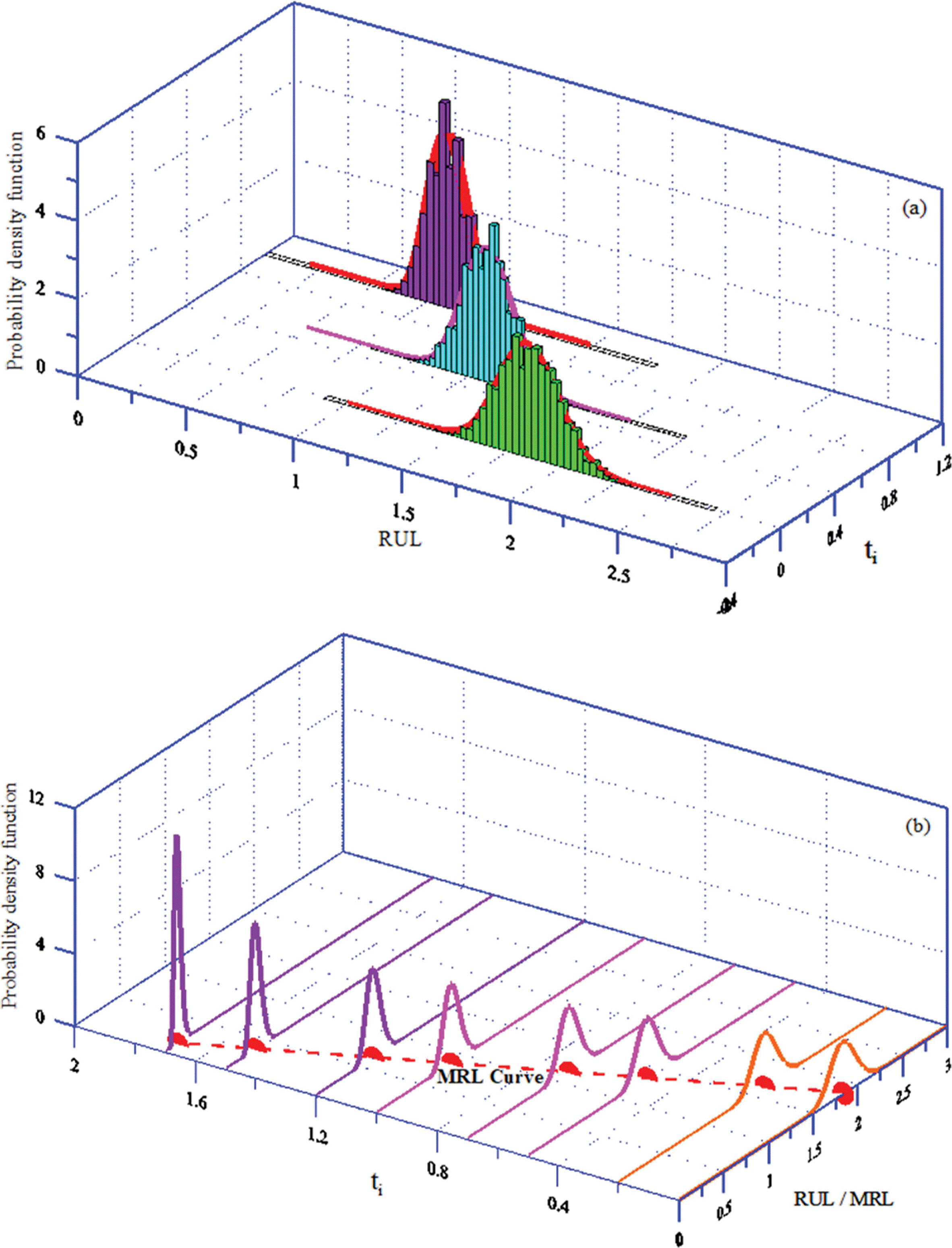
비교 목적으로 각기 다른 재령 ti에 따른 잔류수명의 밀도함수를 Fig. 7에 제시하였다. 다른 재령에서도 식(20)의 결과가 MCS의 결과와 매우 잘 일치하고 있다. 특히 Fig. 7(b)의 결과에는 MRL 곡선도 함께 제시하였는데 재령의 증가에 따라 잔류수명이 급격하게 감소하는 것을 알 수 있다. 따라서 본 연구에서 수립된 모형에 대한 검증이 올바로 수행되었다.
한편 경사제에 대한 잔류수명을 해석하기 위해서는 경사제 파괴모드 중 어떤 파괴를 대상으로 할 것인가를 먼저 결정하여야 한다. 본 연구에서는 CEM(2006)에 제시된 바와 같이 경사제 전면의 피복재의 피해를 대상으로 하였다. 파랑과 직접적으로 만나는 전면에 거치된 피복재의 연속적인 피해에 의하여 경사제 파괴가 발생된다는 의미이다. 파라미터를 추정하기 위해서는 피복재의 피해에 대한 관측자료가 있어야 하는데, 본 연구에서는 Melby(1999)에 의하여 수행된 모형실험 자료를 활용하였다. Melby(1999)는 Series A’에서부터 Series G’까지 모두 7가지 조건에 대하여 실험을 실시하였다.
식(22)와 식(25)를 이용하여 산정된 파라미터 추정 결과를 Table 1에 제시하였다. 따라서 추정된 파라미터를 이용하면 피복재의 시간에 따른 피해경로와 분포함수 그리고 파괴확률을 산정할 수 있다. 또한 임의 재령에서의 잔류수명에 대하여도 해석할 수 있다. 본 연구에서는 Series A’을 중심으로 해석하였다.
먼저 Fig. 8에 ζ(t; γ → b ^ a ^ σ ^ B γ → θ → γ → γ → γ → θ →
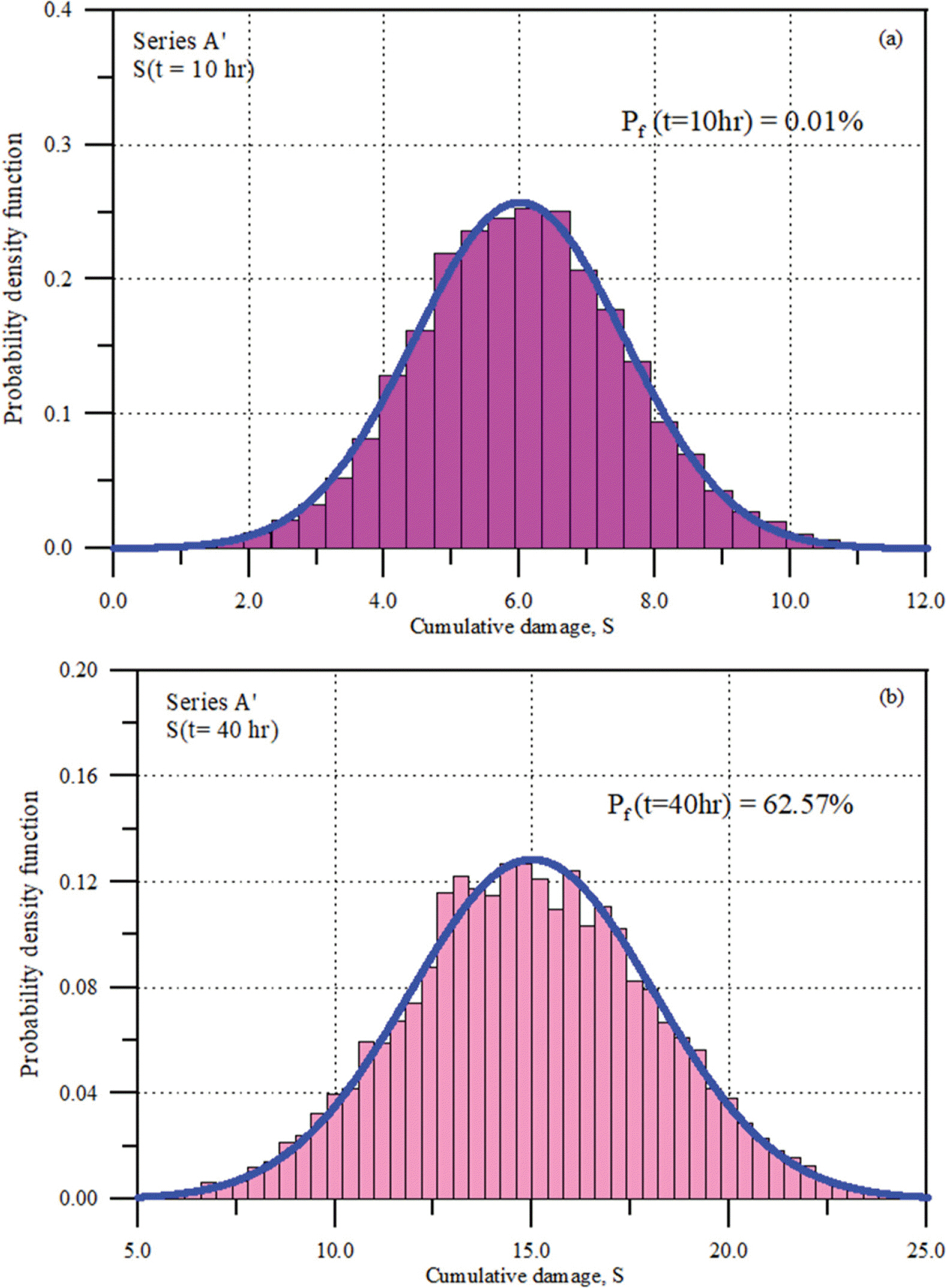
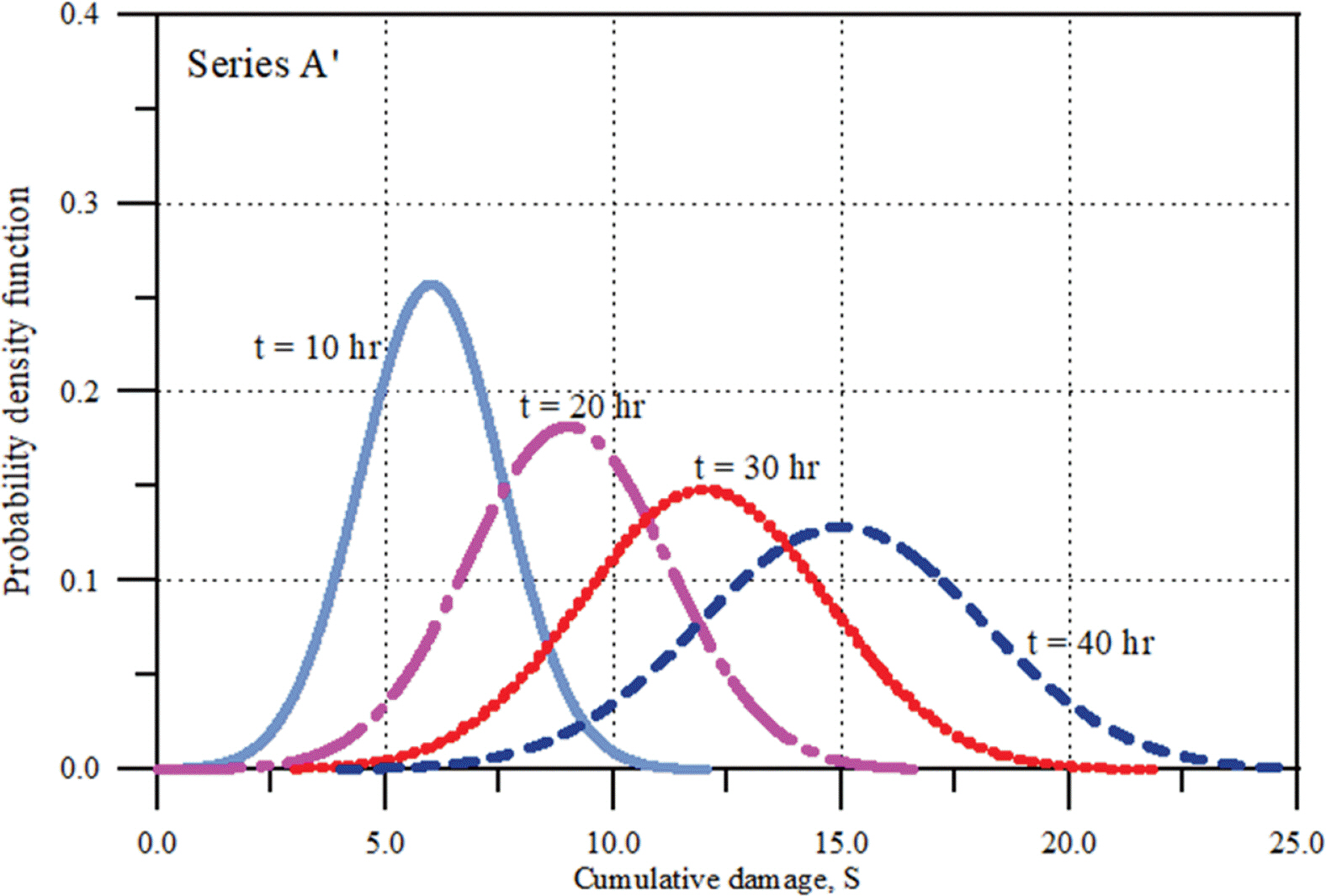
또한 Fig. 10에 t = 10 hr과 t = 40 hr에서 누적피해의 확률밀도함수와 파괴확률 Pf(t)를 함께 제시하였다. 그림에서 볼 수 있듯이 분포함수의 특성이 MCS 결과와 매우 잘 일치하고 있으며, 파괴확률도 시간의 진행에 따라 커지는 현상을 잘 묘사하고 있다. 이때 파괴한계는 PIANC(1992), CEM(2006)에서 제시한 w = 14를 사용하였다.
이를 자세히 살펴보기 위하여 Fig. 11에 임의 시점에서 누적피해의 확률밀도함수를 비교하였다. 그림에서 볼 수 있듯이 경과시간이 클수록 우측으로 이동하면서 불확실성이 커지고 있다. 따라서 파괴한계 w = 14를 넘는 영역인 파괴확률도 증가하고 있다. 정량적으로는 Pf(t = 20 hr) = 1.13%이고 Pf(t = 30 hr) = 22.79%이다.
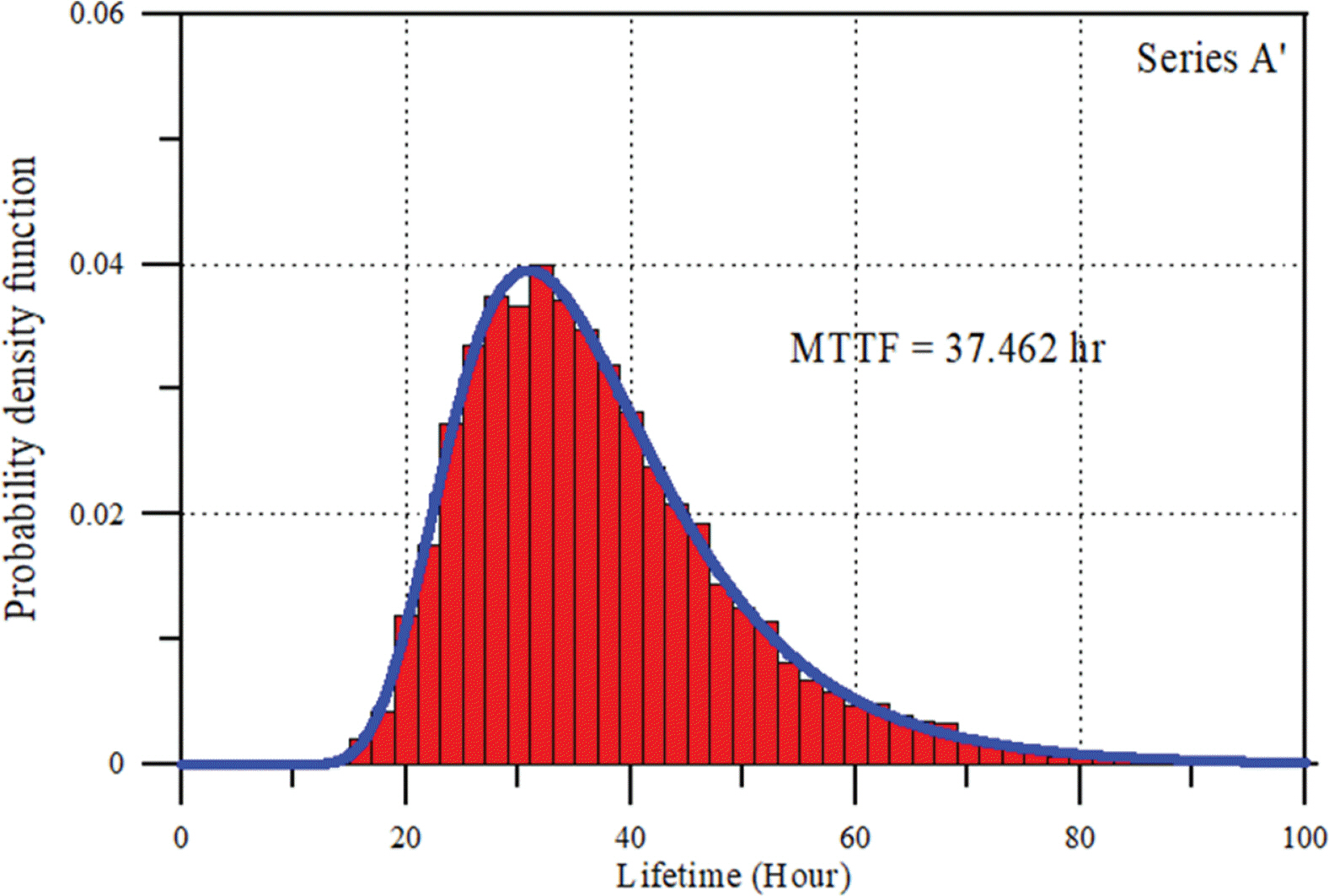
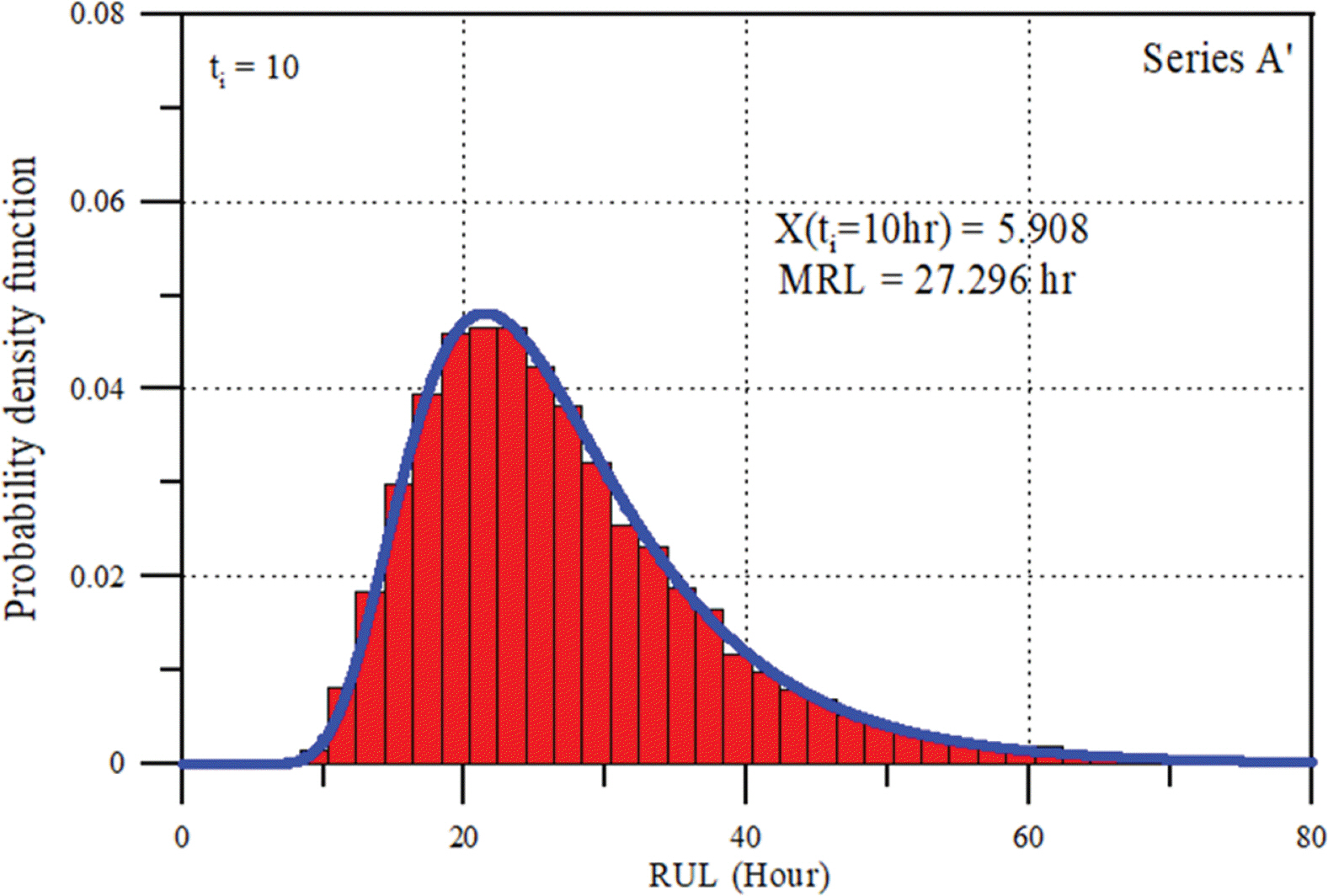
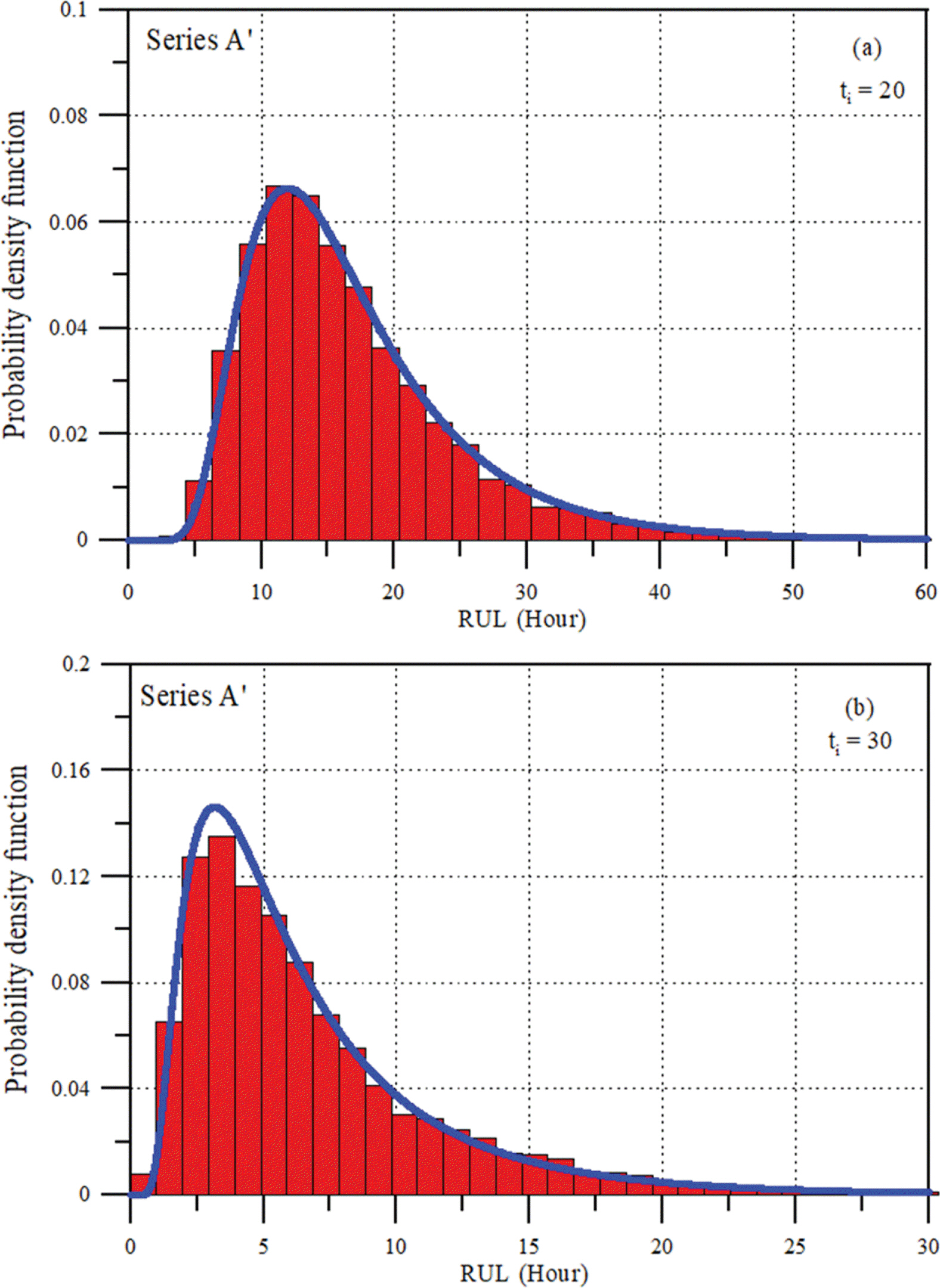
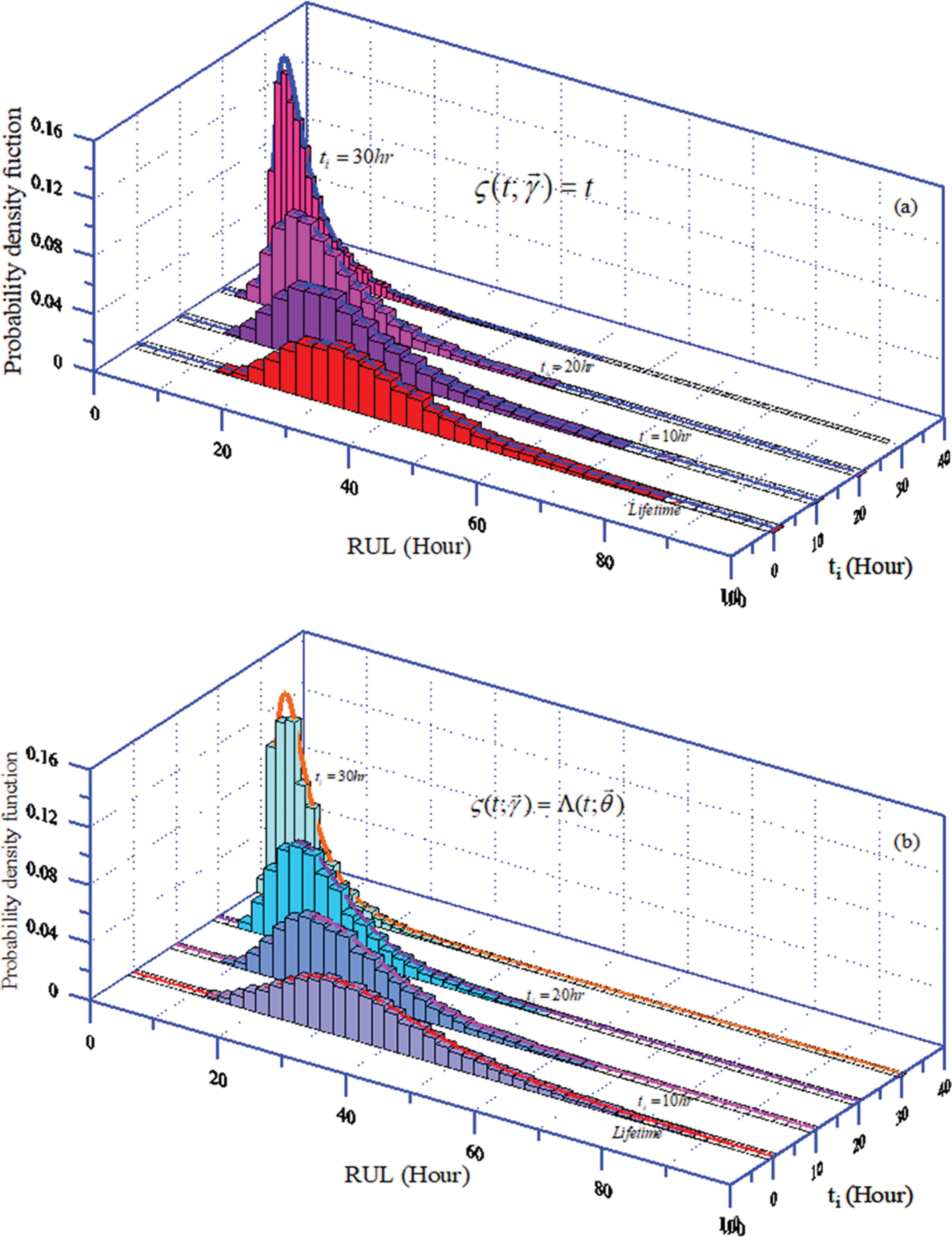
마지막으로 재령에 따른 잔류수명의 거동특성을 해석하였다. 먼저 Fig. 12에 내구수명에 대한 밀도함수를 제시하였다. 그림에서 볼 수 있듯이 우측 꼬리 부분이 길게 형성되는 특성을 포함하면서 분포함수가 MCS 결과와 매우 잘 일치한다. 이는 경사제 피복재의 피해가 완만히 증가하는 현상을 반영한 것으로 판단된다. 그림에서 실선은 재령 ti = 0인 조건에서 식(20)으로 부터 산정된 결과이다. Series A’의 평균 내구수명, MTTF = 37.462 hr로 산정되었다. 이는 경사제가 그 기능을 수행하기 시작하는 최초의 시점에서 평균적으로 약 37 hr 후에 피복재의 피해가 파괴한계, w = 14에 도달한다는 의미이다. 동일한 개념으로 경사제의 재령에 따른 잔류수명을 해석하였다. 먼저 ti = 10 hr에서 잔류수명의 밀도함수를 Fig. 13에 제시하였다. MCS 결과를 함께 제시하였는데 잘 일치하고 있다. 그림에서 X(ti = 10 hr) = 5.908은 현재 재령 ti = 10 hr에서 피복재 피해의 크기, MRL = 27.296 hr는 평균 잔류수명을 의미한다. 물리적으로 현재 재령 ti = 10 hr 기준으로 경사 제의 피복재 피해는 27.296 hr 후에 파괴한계 w = 14에 도달 한다는 의미이다. 피해의 진행에 불확실성이 없다고 가정하는 결정론적 해석에서는 MRL과 재령 ti의 합은 이론적으로 MTTF가 되어야 한다. 그러나 결과를 보면 MTTF = 37.462 hr인데 비해 MRL + ti = 37.296 hr로 차이를 보이고 있다. 이는 현재 재령 ti 이후, 미래에 대한 피해를 예측하는 과정에 포함된 불확실성의 영향이다. 이와 같은 현상을 더 확인하기 위하여 ti = 10 hr 보다 더 오래된 재령, ti = 20 hr와 ti = 30 hr에서 잔류수명의 밀도함수를 산정하여 Fig. 14와 Table 2에 제시하였다.
그림에서 볼 수 있듯이 오래된 재령에서도 우측 꼬리 부분의 특성이 나타나면서 분포함수가 MCS 결과와 매우 잘 일치한다. 또한 재령이 오래되면 잔류수명의 분포가 좌측으로 이동하는 경향을 나타내고 있다. 또한 Table 2를 보면 재령이 오래 될수록 MRL + ti가 MTTF와 크게 차이를 보이고 있다. 이는 앞에서 언급한 현재 재령 이후 미래에 대한 피해 진행을 예측하는 과정에 나타날 수 있는 불확실성에 의한 영향이다. 특히 Table 2에는 불확실성을 고려하는 두 가지 방법 ζ(t; γ → γ → θ →
일반적으로 잔류수명을 예측할 때 현재 재령의 피해는 현장 관측으로부터 알고 있다고 생각한다. 그러나 미래 재령을 기준으로 잔류수명을 예측하는 경우는 앞에서 언급한 수치모의 결과를 이용하면 된다. 이상에서 언급된 경사제의 잔류수명에 대한 결과들을 좀 더 쉽게 이해하기 위하여 Fig. 15에 함께 비교하였다.
6. 결 론
기후변화에 따른 해양환경은 점점 더 불확실해지고 기존 항만 구조물의 노후화가 빠르게 가속화되고 있는 상황에서, 건설비용이 많이 들고 파괴에 따른 사회적 손실비용이 크게 발생하는 항만 구조물의 안전성에 대한 국민적 기대치가 점점 높아지고 있다. 따라서 시간의 진행에 따라 최초 설계시 부여된 기능성과 안전성이 올바로 유지되도록 생애주기 관점에서 예방적 유지관리가 실시되어야 한다. 이를 위해서는 먼저 시간의 진행에 따른 항만 구조물의 노후화 정도인 피해를 정확히 예측할 수 있어야 한다. 또한 항만 구조물의 생애주기 동안 최소의 비용으로 최대의 성능을 확보하기 위하여 언제 어떤 유지관리 행위가 수행되어야 하는지를 결정해야 한다. 따라서 시간에 따른 피해 진행의 크기와 그에 따른 잔류수명에 대한 추정이 반드시 필요하다.
본 연구에서는 추계학적 WP을 이용하여 항만 구조물의 시간에 따른 피해경로의 비선형성과 불확실성을 고려할 수 있는 확률모형을 수립하였다. 실시간에 따라 피해경로를 추정할 수 있으며 각각의 시간에서 누적피해의 확률밀도함수도 산정하여 파괴확률과 신뢰도를 추정할 수 있다. 또한 구조물이 그 기능을 수행하기 시작하는 최초 시점에서부터 파괴될 때 까지의 시간 간격인 내구수명에 대한 확률밀도함수도 구할 수 있다. 그러나 내구수명은 사용기간, 재령이 이미 일정시간 경과한 기존 구조물에는 적용할 수 없다. 이를 해결하기 위하여 잔류수명을 산정할 수 있는 모형을 제시하였다. 잔류수명이란 일정 재령이 경과한 구조물의 현재 피해상태로부터 파괴가 발생하는 미래 임의 시점까지의 시간 간격으로 정의된다. 따라서 현재까지의 피해상태와 미래에 발생될 피해 진행과정에 불가피하게 포함되는 불확실성을 고려할 수 있는 확률론적 모형이다. 또한 최소자승법과 최우도법을 이용하여 모형에 포함된 파라미터를 추정할 수 있는 방법도 제시하였다.
이전의 연구자들이 수행한 단순한 조건에 대하여 모형의 검증을 먼저 수행하고, 경사제에 적용하였다. MCS 기법을 이용하여 피해경로를 추적하면서 시간의 진행에 따른 누적피해와 잔류수명에 대한 확률밀도함수를 산정하고 해석하였다. 검증 조건에서 이론적으로 산정된 결과들이 수치 해석 결과와 매우 잘 일치하였다. 불확실성을 고려하면서 시간의 진행에 따른 비선형적인 피해 진행 경로를 잘 추적할 수 있었다. 내구수명이나 잔류수명에 대한 확률밀도함수의 거동과 MTTF와 MRL이 정량적으로 잘 일치하였다. 한편 수립된 모형을 경사제에 적용하였는데, 파랑과 직접적으로 만나는 경사제 전면에 거치된 피복재의 연속적인 피해에 의해 파괴가 발생한다는 개념을 이용하였다. 재령에 따른 경사제 피복재의 피해에 대한 현장 관측자료가 없어서 본 연구에서는 Melby(1999)에 의하여 제시된 수리모형 실험자료를 활용하였다. 먼저 모두 7가지의 조건에 대하여 모형의 파라미터를 추정하여 제시하였다. WP의 시간 진행에 따른 불확실성을 고려하는 방법을 달리하여 추정하였다. 또한 추정된 파라미터를 이용하여 MCS 기법을 이용하여 수치적으로 피해경로를 추적하면서 시 간의 진행에 따른 누적피해를 산정하고 잔류수명에 대한 확률밀도함수를 얻을 수 있었다. 수치적으로 모의된 결과는 시 간의 진행에 따라 누적피해가 완만하게 증가하는 실험자료와 거의 동일한 거동을 보이면서 피해의 진행에 따른 불확실성도 잘 재현하고 있다. 특히 피해의 불확실성을 선형적으로 고려할 수 있다는 것이 확인되었다. 이는 해석적으로 상당한 편의를 가져올 수 있다. 한편 시간의 진행에 따른 누적피해의 확률밀도함수와 파괴확률을 산정하였는데 이론적인 결과가 MCS의 결과와 매우 잘 일치하였다. 경과시간이 클수록 밀도함수가 우측으로 이동하면서 불확실성이 커지고 있다. 따라서 파괴확률도 급격하게 증가하였다. 마지막으로 재령에 따른 잔류수명의 거동특성을 해석하였다. 먼저 잔류수명의 분포함수에서 좌측보다는 우측 꼬리 부분이 길게 형성되는 것을 확인할 수 있었다. 이는 경사제 피복재의 피해가 완만하게 증가하는 현상을 반영한 것으로 판단된다. 특히 본 연구에서는 재령과 내구수명 그리고 잔류수명의 관계를 해석하였는데 재령이 오래될수록 재령과 MRL의 합이 MTTF와 큰 차이를 보이고 있다. 이는 재령이 증가하면 잔류수명의 평균인 MRL이 불확실성에 의하여 급격히 감소하기 때문이다. 따라서 구조물의 예방적 생애주기 관리를 위해서는 반드시 잔류수명에 대한 해석이 필요하다.
이상에서 제시한 방법은 추계학적 모형을 이용하여 피해경로를 추적하고 잔류수명을 추정하는 절차를 설명한 것이다. 따라서 현장 실측자료만 확보되면 실제 경사제에 대한 해석도 가능하다. 한편 본 연구에서는 피해진행의 기울기를 나타내는 파라미터, a를 상수로 고려하였다. 따라서 이를 확률변수로 고려하여 해석하는 것도 생각할 수 있다. 이는 피해의 관측 자료가 작은 경우에는 파라미터 추정에 오차가 포함될 수 있기 때문이다.