1. 서 론
사석 방파제를 고파랑에 의한 침식으로부터 보호하기 위하여 경사면을 피복재로 피복한다. 크기가 큰 원석을 구할 수 없는 경우에는 콘크리트로 만든 소파 블록을 사용하는 경우가 종종 있다. Tetrapod는 가장 오래 된 소파 블록이지만 아직도 전 세계적으로 널리 사용되고 있다. Tetrapod는 그 이름이 나타내는 바와 같이 정사면체의 중앙으로부터 그 꼭지점들을 향하여 네 개의 다리가 뻗어 있는 방사형 형태를 가지고 있다. 나중에 이와 비슷한 형태를 가지는 Dimple, Rakuna-IV, Tetra-Neo 같은 소파 블록들이 개발되었다.
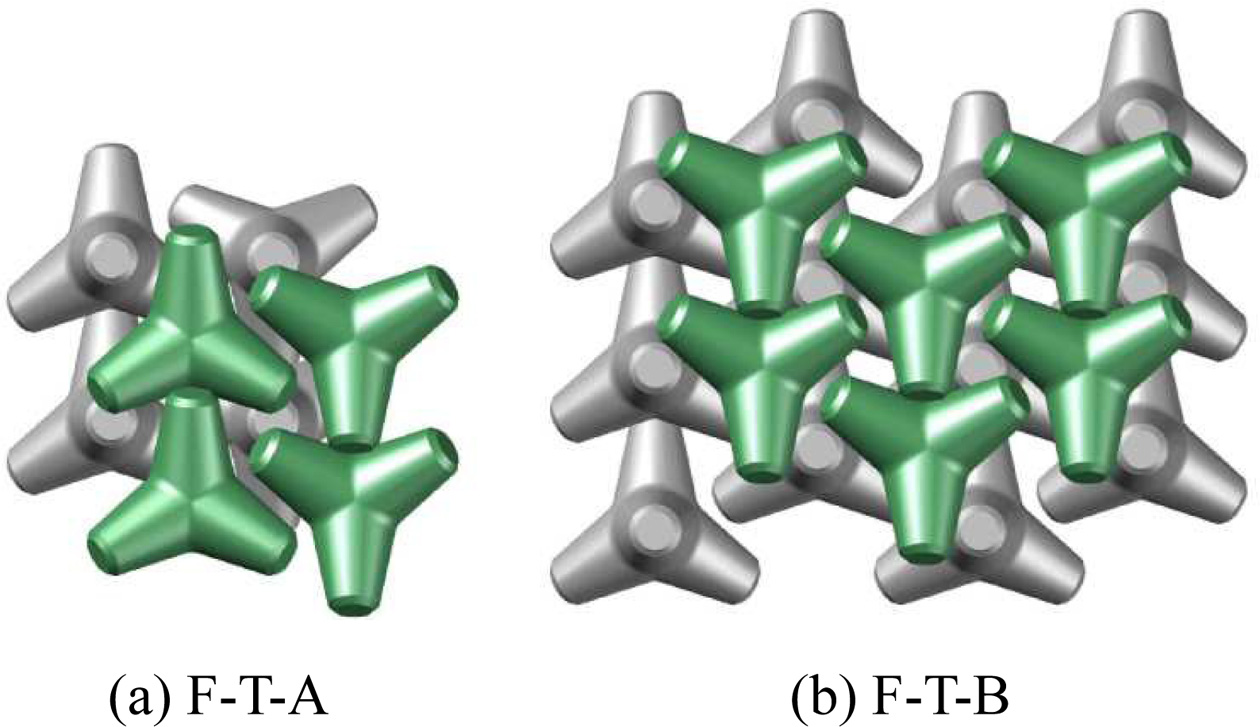
소파 블록의 안정성은 블록의 피복 방법(정적 또는 난적)에 따라 달라진다. 우리나라에서는 정적 방법이 자주 사용된다. 소파 블록의 안정성을 나타내는 지수로 Hudson(1959) 공식의 안정계수가 널리 사용된다. 여러 가지 소파 블록에 대한 안정계수 값들이 Shore Protection Manual(U.S. Army, 1984)에 제시되어 있다. 하지만, 이 값들은 규칙파 실험에 근거하여 제안되었고 콘크리트 소파 블록에 대해서는 난적에 대한 값만 제시되어 있기 때문에 정적에 대해서는 그 적용성에 한계가 있다. 최근에 Gürer et al.(2005)과 Fabião et al.(2013) 등이 Fig. 1 및 Fig. 2에 보인 바와 같이 Tetrapod의 정적 방법을 제안한 바 있으나, 각 방법에 대한 안정계수를 제안하지는 않았다. Dimple과 Rakuna-IV의 정적 방법에 대한 안정성에 대해서는 자세한 연구가 수행된 바 없다. 또한, 여러 종류의 소파 블록에 대한 안정성을 상호 비교하기 위해서는 같은 연구자가 동일한 장비를 이용하여 실험을 수행함으로써 실험 자료의 일관성을 유지하는 것이 무엇보다 중요하다.
본 연구에서는 사석 방파제에 피복된 Tetrapod, Rakuna-IV 및 Dimple에 대하여 수리실험을 수행하여 서로 다른 정적 방법을 사용했을 때의 안정계수를 결정하였다. 각각의 피복 블록에 대하여 두 가지의 정적 방법을 제안하였다. 각 피복 방법에 대하여 유의파고를 단계적으로 증가시키면서 소파 블록의 피해가 발생할 때까지 실험을 계속하였다. 안정계수는 최초로 피해가 발생하였을 때의 유의파고를 이용하여 Hudson(1959) 공식으로부터 계산하였다.
2. 피복 방법
Tetrapod, Rakuna-IV 및 Dimple에 대한 정적 피복 방법을 Fig. 3부터 Fig. 5까지 제시하였다. 각 소파 블록에 대하여 두 가지의 서로 다른 피복 방법을 사용하였다. 각 그림에서 왼쪽 사진은 일층만 피복했을 때를 나타내며, 오른쪽 사진은 이층까지 피복을 완료한 상태를 나타낸다. Tetrapod에 대한 Fig. 3에서, 두 방법 모두 일층 소파 블록은 블록의 다리 하나가 방파제 사면으로부터 직각으로 밖으로 향하도록 배열되어 있다. 이층 소파 블록은 블록의 다리 하나가 방파제 사면을 향하여 직각으로 안으로 향하도록 배열되어 있다. T-A 방법에서는 각 층에서 나머지 세 개의 다리의 방향이 일정하게 되도록 배치한 반면, T-B 방법에서는 한 열의 방향이 인접한 열의 방향과 반대가 되도록 배치하였다. 두 방법 모두 인접한 열 또는 인접한 행의 Tetrapod를 지그재그 형태로 배치하여 다이아몬드 격자 패턴이 되도록 하였다. 이 방법들은 Tetrapod를 정사각형 격자 패턴으로 배치한 Gürer et al.(2005)의 방법과 다르다 (Fig. 1 참조). T-A 방법은 Fabião et al.(2013)의 F-T-B 방법과 동일하다 (Fig. 2 참조). Rakuna-IV의 피복 방법은 Tetrapod와 동일하다.
본 연구에서 제안한 Dimple의 피복 방법은 Tetrapod 및 Rakuna-IV의 피복 방법과 다르며, Dimple을 개발한 Chisui사의 카탈로그에 제시된 방법과도 다르다. 결과를 제시하지는 않았지만, Chisui 사의 카탈로그에 제시된 방법은 본 연구에서 제안한 방법보다 불안정하다는 것을 확인하였다. Dimple에 대해서도 두 가지 서로 다른 방법을 제안하였다. 두 방법 모두 일층 소파 블록은 블록의 다리 하나가 방파제 사면으로부터 직각으로 밖으로 향하도록 배열되어 있으며, 이층 소파 블록은 블록의 다리 하나가 방파제 사면을 향하여 직각으로 안으로 향하도록 배열되어 있다. 두 방법의 차이는 이층 소파 블록의 나머지 세 개 다리의 방향에서 찾아 볼 수 있다. 첫 번째 방법에서는 Dimple의 다리 하나가 위로 향하도록 배치한 반면, 두 번째 방법에서는 아래로 향하도록 배치하였다. D-B 방법은 Fig. 1의 Tetrapod에 대한 G-T-A 방법과 동일하다. Dimple의 피복 방법은 앞에서 설명한 Tetrapod 및 Rakuna-IV의 피복 방법과 다르다. Dimple의 경우, Fig. 5에서 볼 수 있는 바와 같이 피복층의 두께가 소파블록의 높이와 거의 같다. 이러한 피복 방법은 Accropode나 X-bloc같은 일층 피복 블록과 유사한 거동을 보인다.
3. 수리 실험
3.1 실험 기기
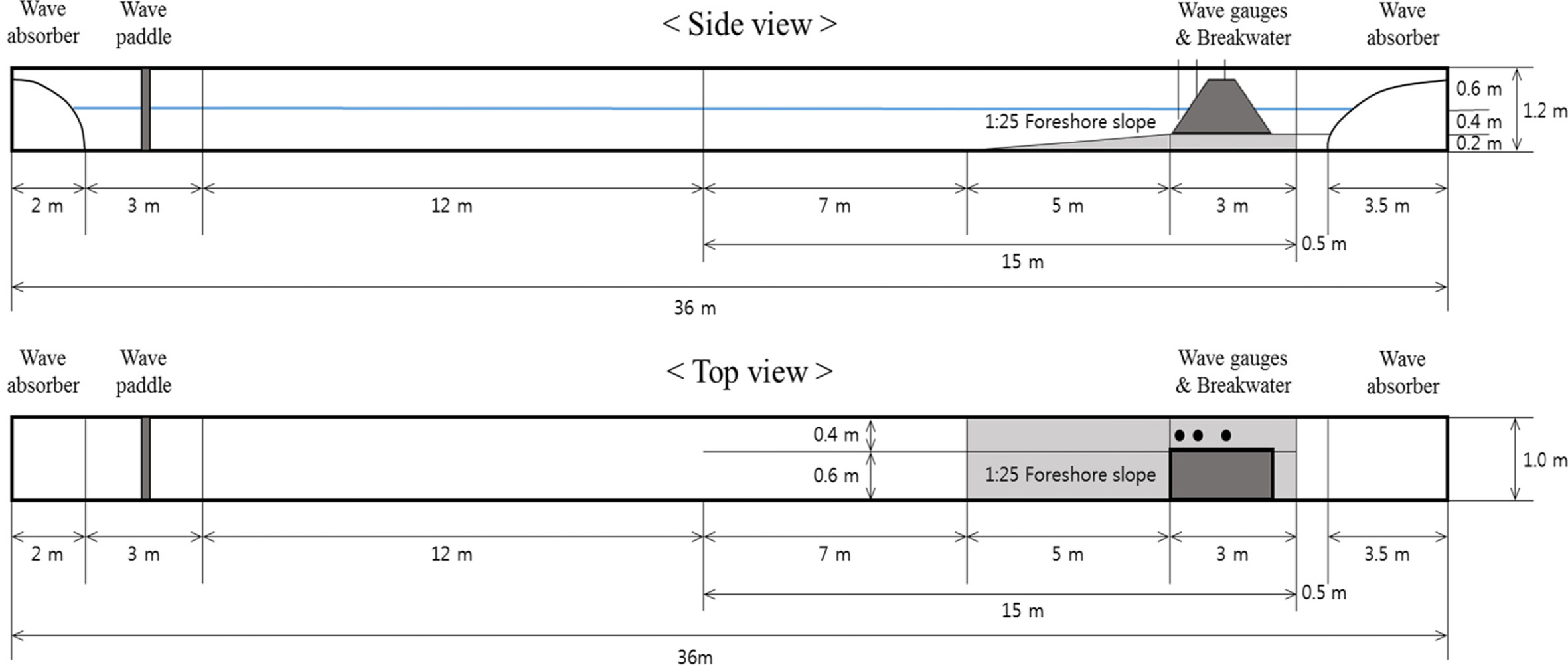
수리실험은 Fig. 6에 보인 바와 같이 서울대학교 수리해안 실험실에 있는 길이 36 m, 폭 1.0 m, 그리고 높이 1.2 m의 조파수조에서 수행되었다. 조파기는 Piston 식으로 조파수조의 한쪽 끝에 설치되어 있으며, 조파기로부터 20 m 떨어진 곳부터 해안 구조물 설치 지점의 전형적인 해저경사로 볼 수 있는 1:25의 바닥경사가 5 m 구간에 걸쳐 0.2 m 높이까지 설치되어 있다. 조파기로부터 13 m 떨어진 구간부터는 수조를 폭 0.6 m와 0.4 m 두 수로로 나누어 폭 0.6 m 수로에는 구조물을 설치하여 실험을 수행하였고, 폭 0.4 m 수로에는 파고계를 설치하여 입사파고를 측정하였다. 이렇게 함으로써 설치된 방파제에 의한 반사파의 영향이 없는 곳에서 입사파를 관측할 수 있다. 조파수조의 양 끝을 제외한 부분은 투명 강화유리로 구성되어 있어 실험 중 모든 구간에서 관측이 가능하다. 본 실험에 사용된 파고계는 용량식 파고계로서, 절연 피복선을 수중에 넣어 연직으로 설치되어 있는 전선과 수면 사이의 전기적 용량의 변화를 측정하여 수면변위를 계산한다. 파고계는 선형성과 응답성이 좋은 길이 0.8 m의 파고계로서, 수위 측정 가능 범위는 정수면 기준 ±0.4 m이다.
3.2 실험 모형 및 방법
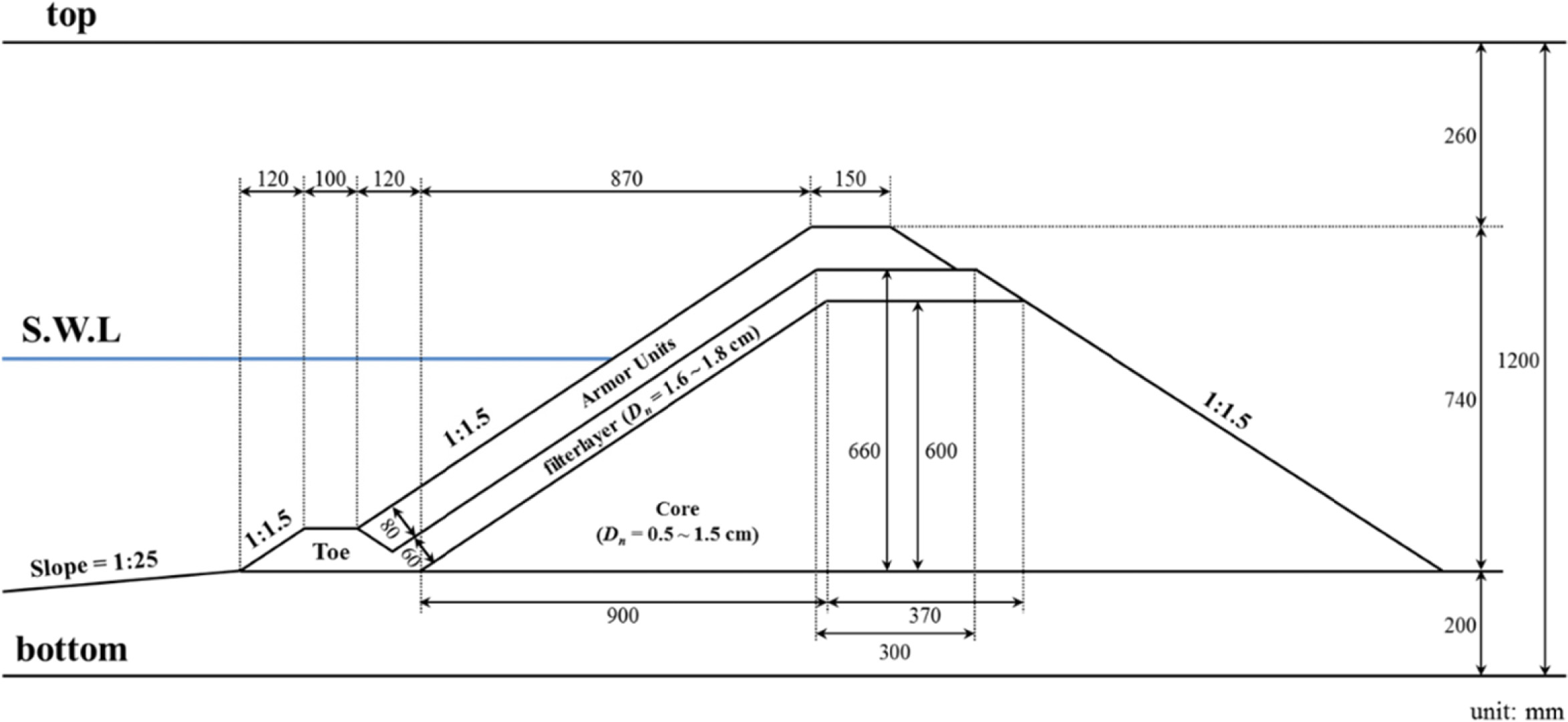
본 실험에 사용한 방파제는 경사식 방파제로서 경사는 국내에서 가장 빈번히 사용되는 1:1.5 경사를 사용하였다. 제체는 Fig. 7에 보인 바와 같이 공칭길이 1.5 cm 이하의 쇄석으로 구성되어 있는 코어와 공칭길이가 1.6~1.8 cm이고 평균 중량이 약 13.5 g 인 필터층과 Toe로 구성되어 있으며, 필터층위에 소파 블록을 2층으로 피복하였다. 방파제 마루높이는 34 cm로 하여 월파가 거의 발생하지 않도록 하였다.
실험에 사용된 Tetrapod는 32 ton 급을 1:50의 축척으로 만든 모델로, 높이(h) 7.1 cm, 공칭길이(Dn) 4.64 cm, 그리고 밀도(ρa) 2.23 g/cm3로 제작되었으며, 포화중량(W)은 약 223.5 g이다. 16 ton 급 모델인 Rakuna-IV의 제원은 공칭길이 3.80 cm, 포화중량은 127.1 g이며, 20 ton 급으로 제작한 Dimple의 경우, 공칭길이 4.10 cm, 포화중량은 151.0 g이다 (Table 1). 각 블록의 현장 환산 무게가 서로 다른 이유는 본 연구만을 위해서 모든 블록을 다시 새롭게 제작할 수가 없어서 이전에 다른 목적으로 제작되었던 블록들을 사용하였기 때문이다. 하지만 무게가 다른 Tetrapod에 대해서 실험한 결과 거의 비슷한 안정계수를 얻었기 때문에 무게 차이로 인한 영향은 거의 없을 것으로 생각된다 (Min 2015 참조). 또한 일반적으로 콘크리트의 밀도는 2.3 g/cm3를 사용하는데, 본 연구에서는 민물을 사용하여 실험하였으므로 비중 1.035인 해수의 영향을 고려하기 위하여 좀 작은 밀도를 사용하였다.
조파판에서 13 m 떨어진 지점부터 15 m 구간은 수조를 0.6 m와 0.4 m의 두 수로로 나누는 분할판이 설치되어 있으며, 폭 0.6 m 수로에는 방파제를, 폭 0.4 m 수로에는 파고계를 설치하였다. 방파제는 조파기로부터 25 m 떨어진, 1:25의 바닥경사가 끝나는 지점에 설치하였다. 방파제가 설치되는 0.6 m 폭은 대략 Tetrapod 9개, Rakuna-IV 11개, Dimple 8개의 너비에 해당되는 길이이다. 하지만 양 쪽 벽에 접하고 있는 소파 블록은 맞물림 효과(interlocking effects)가 상대적으로 적게 작용하게 된다. 이에 본 실험에서는 양 쪽 벽에 위치한 소파 블록이 이탈하지 않도록 단단하게 고정시켰다. 소파 블록은 2층으로 피복하였으며, 용이한 피해 관측을 위해 두 열씩 다르게 도색한 소파 블록을 피복하였다.
Table 1.
Size of armor units, filter layer, toe and core assuming 1:50 scale
조파기에서 생성된 파가 방파제에 도달했을 때의 입사파를 측정하기 위해 방파제와 같은 위치의 0.4 m 폭의 수로에 파고계를 설치하였다. 폭 0.4 m 수로에는 방파제가 설치되지 않지만 수조 끝의 소파장치로부터 약간의 반사파가 발생한다. 3점 분리법(Suh et al., 2001)을 이용하여 입사파와 반사파를 분리하기 위해 총 3개의 파고계를 설치하였다. 입사파와 반사파 분리를 위해서는 파고계 간의 간격이 한 파장 내에 위치해야 한다. 따라서 파고계 간의 거리는 첫 번째와 두 번째 파고계 사이의 거리는 0.3 m, 두 번째와 세 번째 파고계 사이의 거리는 0.5 m로 설정하였다. 파고계 위치에서의 파장은 3.35 m이다.
3.3 실험 조건
본 실험에서 축척은 1:50으로 가정하여 Froude 상사법칙을 적용하여 유의주기와 유의파고를 산정하였다. 유의주기(Ts)는 현장 값으로 13 s, 실험실 값으로는 1.84 s에서 실험을 수행하였으며, 유의파고(Hs)는 현장 값 5.6 m~8.4 m, 실험실 값 11.2 cm~16.8 cm로 적용하였다. 구조물 전면에서의 파랑경사는 0.033~0.05로서 풍파를 나타낸다. 구체적인 유의파고의 범위는 각 소파 블록마다 달리 적용하여 실험을 진행하였다 (Table 2). Van der Meer(1987, 1988, 2000), Suh and Kang(2012) 등 피복재의 안정공식을 구하기 위한 연구에서는 주기의 영향을 고려하였으나, 본 연구에서 안정계수를 계산하기 위해 사용한 Hudson(1959) 공식에는 주기가 포함되어 있지 않기 때문에 하나의 주기만을 사용하였다.
본 실험에서는 식 (1)의 Modified Bretschneider-Mitsuyasu spectrum(Goda, 2010)을 사용하였으며, 이는 Pierson-Moskowitz spectrum과 동일하다.
Table 2.
Wave condition
여기서 S(f)=파랑스펙트럼 밀도함수, f = 주파수, Hs= 유의파고, Ts=유의주기이다.
3.4 실험 절차
본 실험은 다음과 같은 절차에 따라 수행하였다.
① 수조의 물을 뺀 상태에서 경사 1:1.5의 방파제의 Core와 필터층, 그리고 Toe를 설치한다.
② 조파수조에 0.6 m까지 물을 채운다.
③ 소파 블록을 설치한다.
④ 방파제 옆 채널에 파고계를 설치한 후 매 실험마다 파고계를 보정한다.
⑤ 방파제와 소파 블록의 안정화를 위해 다짐파(Ts= 1.83 s, Hs= 0.11m)를 약 500초 간 조파한다.
⑥ 보정된 스펙트럼을 이용하여 조파한다.
⑦ 조파를 시작한 후 조파된 파랑이 조파수조의 끝까지 전달되어 안정화되었다고 볼 수 있을때부터(약 100 s 후) 파랑 데이터를 취득하기 시작한다.
⑧ 500파를 조파한 후 피해를 판정하고 피해가 발생하지 않았을 경우 파고를 0.2 m(현장 값) 증가시켜 조파를 실시한다. 일반적으로 한 폭풍의 지속시간을 재현하기 위해 1,000 파를 사용하지만, 본 연구에서는 같은 조건의 실험을 5회 반복하기 때문에 실험 시간을 단축하기 위하여 500파를 조파하였다.
⑨ 피해가 발생할 때까지 0.2 m씩 파고를 계속 증가시키며 실험을 수행한다. 본 실험에서는 소파 블록이 한 공칭 길이 이상 움직이거나, 다른 곳으로 이동했다가 원래 위치로 돌아오는 경우, 또는 그 자리에서 180 o 이상 회전하는 경우를 피해로 간주하였다. 파고를 단계적으로 증가시킴으로써 소파 블 록의 안정성에 영향을 미칠지도 모르는 관성 효과는 무시하였다.
⑩ 피해 발생 시 실험을 중단하고 취득한 파랑자료로부터 3점 분리법(Suh et al., 2001)을 이용하여 입사파와 반사파를 분리한다.
⑪ Zero-upcrossing method를 이용하여 유의파고와 유의주기를 산정한다.
⑫ 최초로 피해가 발생한 파고보다 0.2 m 더 큰 파고의 파랑을 발생시켜 피해가 증가하는지 확인한다.
⑬ Hudson(1959) 공식을 이용하여 안정계수를 산정한다.
여기서 γa = 소파 블록의 단위 중량, Hsi= 피해가 최초로 발생한 시점의 유의파고, S = 소파 블록의 비중, θ = 방파제의 사면 경사각이다. Shore Protection Manual의 안정계수는, 일반적으로 no-damage 조건이라고 일컬어지는, 0~5% 피해에 근거하여 계산되었다. 하지만, 본 연구에서는 최초 피해에 해당하는 파고 Hsi를 사용하여 안정계수를 계산하였는데, 이는 실제 현장에서의 불확실성이 실험실에서보다 크고 또한 실험실 실험에서는 소파 블록의 파손에 의한 피해를 재현할 수 없기 때문에 실험실 자료를 사용할 경우 좀 더 보수적인 기준을 사용해야 하기 때문이다.
소파블록 제거 후 다시 축조하여 같은 조건으로 실험을 총 5회 반복 수행한다.
4. 결과 및 토의
각 피복 방법에 대한 안정계수의 평균, 표준편차, 변동계수 등을 소파 블록의 공극률과 함께 Table 3에 제시하였다. 5회의 반복 실험에 대한 자세한 실험 결과는 Min(2015)의 논문에 수록되어 있다. 소파 블록의 공극률은 Fig. 7의 피복층(Armor Units)의 부피와 거기에 들어가는 블록의 개수로부터 계산하였다. 피복층의 아랫면은 일정하지만 윗면은 블록의 종류 및 거치방법에 따라 달라진다.
Table 3.
Experimental results
Tetrapod에 대한 두 가지 피복 방법은 안정계수도 비슷하고 공극률도 비슷하다. 본 연구에서 계산된 안정계수는 Shore Protection Manual에 난적에 대하여 주어진 값 7.0보다 약간 크다. 난적 대비 안정계수의 증가율은 T-A의 경우 7%, T-B의 경우 4%이다. Rakuna-IV 역시 피복 방법에 상관 없이 비슷한 안정계수와 공극률을 보였다. 계산된 안정계수 또한 Rakuna-IV를 개발한 Nikken Kogaku 사의 카탈로그에 제시된 난적의 안정계수 9.44보다 크다. 난적 대비 안정계수의 증가율은 R-A의 경우 12%, R-B의 경우 8%이다. 따라서 Tetrapod나 Rakuna-IV의 난적에 대하여 제시된 안정계수를 정적의 경우에 적용한다면 결과적으로 보다 안정적인 설계가 될 것이다.
Dimple의 경우에는 피복 방법에 따라 다소 다른 안정계수를 보였으며, D-B 방법의 안정계수가 D-A 방법보다 컸다. D-B 방법의 경우, 본 연구에서 사용한 조파수조에서 발생시킬 수 있는 최대 파고에서도 피해가 발생하지 않았다. 최대 파고는 8.31 m였으며, 이에 상응하는 안정계수는 23.80이다. 따라서 D-B 방법에 대한 Dimple의 안정계수는 23.8보다 클 것이다. 계산된 안정계수는 난적에 대하여 Chisui 사의 카탈로그에 제시된 값 10.0보다 훨씬 크다. 또한 Chisui 사의 카탈로그에는 정적 방법도 제시되어 있다. 본 연구에서 이 정적 방법에 대하여 수리실험을 수행한 결과 (결과는 제시하지 않음), 8.0~9.0 사이의 아주 작은 안정계수를 보였다. 본 연구에서 사용한 정적 방법이 큰 안정계수를 나타내는 이유는 아마도 소파 블록이 (작은 공극률로) 매우 조밀하게 쌓여져서 일층 피복 블록과 비슷한 거동을 보이기 때문일 것이다. 일층 피복 블록의 특징 중 하나는 초기 안정성은 높은 반면 급작스러운 피해를 나타내기 때문에 큰 안전율을 사용한다는 것이다. 예를 들어 Van der Meer(2000)는 일층 피복 블록 Accropode에 대하여 1.5의 안전율을 사용하였다. D-A 방법과 D-B 방법은 공극률도 같고 단지 위 층의 블록 방향이 반대일 뿐인데, 안정계수의 차이를 보이는 이유는 명확하지 않다.
세 가지 소파 블록의 안정계수를 비교한 결과, Dimple이 가장 안정적이고, Rakuna-IV가 그 다음이며, Tetrapod가 가장 불안정함을 보였다. 모든 소파 블록에 대하여 안정계수의 변동계수가 0.06 이하로서, 5회 반복 실험의 실험 오차가 매우 작음을 나타낸다. 정적으로 쌓은 Tetrapod나 Rakuna-IV의 공극률은 난적의 공극률 (Tetrapod 50% 및 Rakuna-IV 56.5%)과 크게 다르지 않은 반면, 정적한 Dimple의 공극률은 난적의 공극률 56%보다 훨씬 작다. 이는 아마도, 전술한 바와 같이, Dimple을 너무 촘촘히 쌓아서 피복층의 두께가 블록의 높이와 거의 같기 때문일 것이다 (Fig. 5 참조).
소파 블록 피복층의 공극률은 경제성과 밀접한 관계가 있기 때문에 방파제 설계에 중요한 요소 중의 하나이다. 즉, 공극률이 커질수록 소요되는 소파 블록의 개수가 작아지고, 따라서 더 경제적이다. Rakuna-IV는 공극률이 57% 이상이고 안정계수도 10보다 크기 때문에 경제성과 안정성에서 우수한 블록이다. Dimple은 20 이상의 안정계수를 보였지만, 매우 조밀하게 쌓은 결과 공극률이 44% 밖에 되지 않는다. 본 연구에서 실험한 블록들처럼 방사형 형상을 갖는 소파 블록을 사용하는 경우, 공극률이 너무 작다면 특별한 주의를 요하는데, 이러한 피복층은 일층 피복 블록과 비슷한 거동을 보여 급작스러운 피해가 발생할 수 있기 때문이다.
5. 결 론
사석 방파제의 대표적 방사형 소파 블록인 Tetrapod, Rakuna-IV 및 Dimple 각각에 대하여 두 가지씩 서로 다른 정적 피복 방법을 제안하였으며, 이에 상응하는 안정계수를 수리 실험을 통하여 결정하였다 (Table 3 참조). Tetrapod와 Rakuna-IV는 피복 방법에 상관 없이 비슷한 안정계수를 보인 반면, Dimple은 피복 방법에 따라 약간 다른 안정계수를 보였다. Dimple이 가장 큰 안정계수를 보인 반면, Tetrapod는 가장 작은 값을 보였다. Tetrapod와 Rakuna-IV는 정적일 때의 안정계수가 난적보다 약간 큰 값을 보인 반면, Dimple은 정적 시의 안정계수가 난적보다 훨씬 큰 값을 보였다. 하지만, 본 연구에서 제안한 Dimple의 정적 방법은 일층 피복블록처럼 거동하여 급작스러운 파괴를 야기할 수 있기 때문에 주의를 요한다.
본 연구에서 계산된 안정계수는 소파 블록의 피해가 시작되는 (즉, 0 퍼센트 피해) 파고를 기준으로 하기 때문에, 일반적으로 안정계수 계산에 사용되는 0 내지 5 퍼센트 피해에 해당하는 값보다 약간 작을 것이다. 그러나 실험실에서보다 현장에서 소파 블록 거치의 불확실성이 더 크고 실험실 실험에서는 소파 블록의 파손에 의한 피해를 고려할 수 없음을 감안할 때 실험실에서의 0 퍼센트 피해 파고를 기준으로 안정계수를 계산하는 것이 합리적이라고 생각된다.
본 연구에서 Tetrapod에 대해서 제안된 피복 방법은 원래 Sotramer(1978)에서 제안한 Gürer et al.(2005)의 방법들과 다르다. Tetrapod에 대하여 이들의 방법과 비교하는 추가 연구가 필요하다. 또한 이 방법들은 Rakuna-IV와 Dimple에 대해서도 적용할 수 있을 것으로 보이며, 이것들에 대한 추가실험이 필요하다.