A Study on Trend Analysis in Sea Level Data Through MK Test and Quantile Regression Analysis

Sumiya Uranchimeg; Yong-Tak Kim; Hyun-Han Kwon; Kyu-Nam Hwang

doi:10.9765/KSCOE.2015.27.2.94

Abstract

Population and urban development along the coast is growing in South Korea, and particularly sea level rise is likely to increase the vulnerability of coastal areas. This study aims to investigate the sea level rise through Mann-Kendall(MK) test, ordinary linear regression(OR) and quantile regression analysis(QRA) with sea level data at the 20 tide stations along the coast of Korean Peninsula. First, statistically significant long-term trends were analysed using a non-parametric MK test and the test indicated statistically significant trends for 18 and 10 stations at the 5% significance level in the annual mean value of sea level and the annual maximum value of sea level, respectively. The QRA method showed better performance in terms of characterizing the degree of trend. QRA showed that an average annual rise in mean sea level is about 1-6 mm/year, and an average rise in maximum sea level is about 1-20 mm. It was found that upward convergent and upward divergent were a representative change given the nine-category distributional changes. We expect that in future work we will address nonstationarities with respect to sea level that were identified above, and develop a nonstationary frequency analysis with climate change scenarios.

핵심용어: Trend Analysis, MK Test, Quanitle Regression, Sea Level Rise, Climate Change, 경향성 분석, 분위회귀분석, 해수면 상승, 기후변화

Abstract

우리나라의 연안은 도시개발, 인구증가가 지속적으로 나타나고 있으며, 이러한 점에서 해수면 상승으로 인한 연안재해 취약성이 가중될 것으로 전망되고 있다. 본 연구에서는 우리나라 연안의 20개 지역의 조위자료를 바탕으로 Mann-Kendall(MK) 검정, 선형회귀분석(OR), 분위회귀분석(QRA) 등을 이용하여 해수면상승에 대한 분석을 수행하였다. MK 검정결과 연평균조위의 경우 18개 지점에서 경향성이 통계적으로 유의한 것으로 분석되었으며, 연최대치의 경우에도 10개 지점에서 경향성이 통계적으로 유의(p < 0.05)한 것으로 평가되었다. QRA 방법을 이용하여 해수면의 경향성을 분위별로 평가한 결과 기존 회귀분석 방법에 비해 다각적인 경향성 검토가 가능하였다. QRA분석 결과 연평균해수면은 매년 1-6 mm의 범위에서 상승하고 있으며, 연최대해수면의 경우 1-20 mm의 범위에서 증가경향이 나타나고 있음을 확인할 수 있었다. 우리나라의 해수면상승의 경우 대부분 상향수렴 및 상향발산의 형태를 가지는 경향성을 나타내고 있었다. 향후 연구로서 이러한 경향성을 기반으로 연최대해수면 자료에 대한 비정상성빈도해석 절차의 개발 및 적용이 필요할 것으로 판단된다.

핵심용어: Trend Analysis, MK Test, Quanitle Regression, Sea Level Rise, Climate Change, 경향성 분석, 분위회귀분석, 해수면 상승, 기후변화

1. 서 론

우리나라의 연안지역은 꾸준히 개발이 이루어지고 있으며 이로 인한 인구증가와 더불어 해일 등과 같은 극치해수면으로 피해가 우려되고 있다. 전 세계적으로 연안도시에 대한 연구에서 4천만 명이 100년 빈도를 초과하는 홍수에 노출되어 있는 것으로 알려지고 있다(Nicholls et al., 2008). 미국의 경우 평균해수면기준 1 m이하의 육지 비율이 60%에 이르고 있으며 해안지역에서 빈번하게 발생하는 극치사상들로 인한 취약성이 증가하고 있다고 알려지고 있다(Titus et al., 2009). 극치해수면의 발생은 천문학적인 조수(tide), 파도(wave), 해류(current), 극치기상(extreme weather), 엘니뇨와 같은 전 지구적 원격상관관계(tele-connection) 등 다양한 원인의 복합 적인 요인으로 인하여 발생한다. 이러한 극치발생은 육지로부터의 담수 유입, 빙하의 융해 등 해양의 장기적 체적 변화로 기인하는 해수면 상승(sea level rise, SLR)과 매우 관련이 깊다. 이 밖에도 여러 요인에 의해 발생하는 융기 및 침하로 인한 지각의 수직 변동(vertical land movement, VLM)과도 관계가 있다.

삼면이 바다로 둘러싸인 우리나라의 연안은 도시개발, 인구증가 등 해수면 상승으로 인한 위험도를 가중시키는 다양한 불확실성 요소가 존재하며 이에 대한 검토가 필수적으로 요구되고 있다. 장기적으로 연안에 영향을 주는 대표적인 요인은 전지구적 SLR로서 다양한 문제점을 발생시킬 것으로 전망되고 있다. 이에 대한 대책을 장기적으로 고려하지 않으면 우리나라뿐만 아니라 전 지구적으로 심각한 피해가 초래될 것이다. 조위계에 의한 20세기 평균 지구 해수면 상승률(mean sea level rise, MSLR)은 연 1.7 mm로 20세기 말부터는 2.3 mm로 증가하였으며 위성고도계(satellite altimeter)를 사용한 관측자료에 의해 1993년 이후 약 3 mm의 MSLR이 확인되고 있다. 점차 4-6 mm의 상승률이 나타날 것으로 예상되고 있으며(Yuk et al., 2011) 이로 인한 연안의 범람 및 침식 등과 같은 직접적인 피해에서 나아가 사회적이고 경제적인 문제 및 법적 문제에 대한 대비책이 시급하다. 현재 해수면 상승의 위험에 대한 다수의 연구가 시행되고 있으며 그 목적에 따른 분석을 위해 조위 시계열 자료의 검정과 특성 분 석이 필수적으로 요구된다. SLR의 영향을 연안지역 구조물에 대해서 적용하기 위해서는 자료가 시간에 따라 변화하는 특성 즉 비정상성(nonstationarity)를 고려한 해석이 필요하다. 이러한 점에서 자료가 가지고 있는 경향성에 대한 통계적 유의성을 종합적으로 평가하는 것이 우선적으로 요구되며, 해석 결과는 다른 연구의 기초 자료로 활용될 수 있다.

IPCC(Climate Change WGI, 2013)는 과정기반 모델과 빙하 및 빙상 기여도에 대한 문헌 평가를 결합하여 CMIP5 기후전망으로부터 2081~2100년 기간의 전지구 평균해수면은 1986~2005 년보다 RCP2.6에서 0.26~0.55m, RCP4.5에서 0.32~0.63m, RCP6.0에서 0.33~0.63m, RCP8.5에서 0.45~0.82m 상승할 것으로 전망하였으며 2081~2100년 동안 해수면 상승률은 8~16 mm/yr로 전망되고 있다. Jang and Hong(1991)은 해수면 상승의 원인을 파악하고 항만, 시설 및 간척지의 피해에 대해 분석하였으며 해안선의 후퇴로 인한 경제국토의 감소를 예상하였다. Park, Y.K.(2012)은 해수면 상승에 따라 나타나 는 기선의 이동을 중심으로 나타나는 해양 관할권 문제와 기선의 동결이라는 관습국제법의 형성에 대하여 논의하였다. 또한 해양경계 변화 가능성과 섬의 법적 지위 및 기타 섬에 미치는 법적인 쟁점에 대하여 연구하였다(Kim, M.S., 2013). Cho and Maeng(2007)은 해수면 상승으로 인한 자연생태계와 사회경제시스템에 미치는 영향에 대해 열거하였으며 해수면 상승에 대응하기 위한 온실가스 감축 및 적응 두 가지면에서 접근하였다. 우리나라의 부산지역에 관한 Lee and Choi(2011)의 연구는 토지손실비용, 주택손실비용 및 사회간접자본의 재건설 비용 등 경제적인 손실 측면에서 해수면 상승의 피해를 바라보았으며, Lee and Bu(2011)는 제주 연안 지역에서의 해수면상승 시나리오를 구축하고 연안 구조물피해와 침수피해에 관하여 연구하였다.

수문 및 기상 시계열 자료가 내포하고 있는 변동 특성은 추세, 변동점 및 장단기 주기 등 자료 자체에 대하여 가시적으로 판단할 수 있는 부분이 대다수이며, 이러한 변동특성은 각종 통계기법으로 정량화할 수 있다(Kim, G.S., 2006). 경향성 분석 기법으로는 Mann-Kendall(MK) 검정, Hotelling-Pabst 검정, Spearman’s Rho 검정, Linear regression 검정, CUSUM 검정, Cumulative Deviation 검정, Worsley likelihood 검정, Rank-Sum 검정 및 Student’s-t 검정이 있으며 다양한 수문기상자료를 통해 경향성을 파악하였다(Oh et al., 2005). 이중에서 MK 검정 방법이 가장 일반적인 방법으로 활용되고 있다. Kendall and Gibbons(1990)는 MK 분석 은 표본자료의 특성에 영향을 받지 않고 모평균의 분포가 연속적인 모평균을 가진다는 가정아래 검정을 실시한다고 제시 하였다. Khaled and Rao(1998)는 MK 검정을 사용하여 자기 상관적 시계열 자료를 분석하였으며, Zhao et al.(2007)은 황 하강의 약 50년 자료를 이용하여 4개 지점에 대한 하천유량을 MK 검정으로 경향성 판단을 하였다. 또한, 미국 캔자스주 내 강의 수질 측정 데이터를 사용하여 MK 검정을 실시 하였다(Yu et al., 1993).

그러나 MK검정 방법은 주로 시계열자료의 평균적인 변동성에 초점이 맞추어져 있어, 극소, 극대 부분에 대한 경향성을 검정하는데 있어서 어려움이 있다. 이러한 점에서 분위회귀분석(quantile regression analysis, QRA)을 통하여 자료의 확률분포의 다양한 관점에서 경향성을 평가할 수 있는 방법이 활용되고 있다(So et al., 2012). QRA방법은 경향성을 평가하는데 있어서 평균뿐만 아니라 원하는 분위에서 경향성을 평가할 수 있는 방법으로서 시계열의 다양한 특성을 평가할 수 있다. 본 연구에서는 우리나라 연안의 20개 지역의 조위 자료를 바탕으로 표본자료의 특성에 영향을 받지 않고 경향성을 판단할 수 있는 MK 검정을 통해 경향성 분석을 수행함과 동시에 QRA방법을 통하여 다양한 분위에 대한 경향성을 종합적으로 평가하고자 한다. 본 논문의 구성은 2장에서 경향성 평가 방법에 대한 이론적 배경을 간략히 소개하고, 3장에서는 MK검정과 QRA검정 방법을 기준으로 경향성을 평가하였다. 4장에서는 이를 토대로 결론 및 토의를 실시하였다.

2. 경향성 평가 기법

2.1 MK 검정 방법

시계열 자료의 경향성을 판단하는 통계학적 방법들은 크게 비매개변수적 방법과 매개변수적 방법으로 나눌 수 있다. 매개변수적 방법은 매개변수에 대한 추론을 할 때 모집단분포 (distribution)에 대한 가정을 포함하는 것이고, 반대로 모집단 분포에 대한 가정을 하지 않고 분석하는 검정을 비매개변수적 방법이라고 한다. 비매개변수적 경향성 검정 기법은 순위 (rank)에 기반한 검정과 더불어, 모든 자료간의 관계를 종합적으로 분석할 수 있기 때문에 관측시계열에서 종종 나타나는 결측값이나 계절성 등을 유연하게 고려할 수 있으며, 매개변수적 경향성 검정에 비해 많이 이용된다(Hirsch and Slack, 1984). 비매개변수적 경향성 검정에 널리 이용되는 분석 방법으로는 MK 검정법으로 시계열 자료의 단조 경향 (monotonic trend)을 분석하는데 유용하게 사용되어지고 있다. MK 검정의 귀무가설(null hypothesis)은 분석대상 시계열에 경향성이 존재하지 않는다는 것이며 검정 통계량 S를 정의하면 아래와 같다(Mann, 1945; Kendall, 1975). Mann- Kendall 통계치(S)는

(2.1)

S=∑i=1n−1∑j=i+1nsgn(xj−xi)

으로 나타낸다. 여기서 sgn(x_j–x_i) 는

(2.2)

sng(xj−xi)=1if(xj−xi)>00if(xj−xi)=0−1if(xj−xi)<0

이며, S의 분산 σ_s² 는 다음과 같이 정의된다.

(2.3)

σs2=118[n(n−1)(2n+5)−∑i=1gti(ti−1)(2ti+5)]

여기서 n은 자료의 개수, x_j와 x_i는 순차적인 자료의 값이며 g 는 연결 그룹(tied group) 개수 (연결 그룹은 동일한 값을 갖은 자료의 집합)이며 t_i는 i 번째 연결 그룹의 자료개수를 말한다. 본 연구에서는 자료의 특성을 반영하여 연결 그룹을 고려하지 않았다.

정규화된 검정통계량 Z 는 다음 식과 같이 계산되며 Z 값의 부호는 경향성의 증가 또는 감소를 나타낸다.

(2.4)

Z=S−1[σS2]1/20S+1[σS2]1/2ifS>0ifS=0ifS<0

(2.5)

p=0.5−Φ(Z)

(2.6)

ΦZ=12π∫0Ze−t22dt

p는 유의수준을 나타내며, 일반적으로 p ≤ 0.05 이면 유의수준 5%에서 자료에 경향성이 존재하고 있음을 판단할 수 있다.

2.2 분위회귀분석(QRA) 방법

대부분의 통계학적 연구는 자료에 대해서 선형회귀분석, MK 경향성 분석 등을 적용하여 경향성 존재 여부와 유의성을 검정하려 한다. 그러나 최소자승법(Least-Squares Method, LSM)에 근거한 일반적 회귀분석은 종속변수와 회귀인자의 평균 관계를 요약하는데 유용한 도구이지만, LSM 회귀분석은 종속변수와 회귀인자의 평균 관계만을 파악한다는 점에서 부분적인 정보만을 제공하게 된다는 단점을 가지고 있다(So et al., 2012). 즉, 변수간의 관계를 종합적으로 평가하기 위해서 는 종속변수의 조건부 분포에서 여러 분위(quantile)에 대해서 회귀인자의 영향을 파악할 수 있는 QRA 분석이 필요하다. 즉, QRA는 자료의 경향성 측면에서 매우 풍부한 정보를 얻을 수 있는 방법 중 하나라 할 수 있다(Koenker, 2005; Hao and Naiman, 2007). 본 절에서는 QRA 방법에 대한 이론적 배경, 매개변수 추정 등에 대해서 요약 정리하였다. 확률분포(probability distribution function, pdf)를 가지는 무작위 변량에 대한 누가 확률은 다음과 같이 정의될 수 있다.

(2.7)

F(y)=prob(Y≤y)

무작위 변량Y의 τ에 해당하는 분위 Q는 다음과 같은 역함수로 정의된다.

(2.8)

Q(τ)=F(τ)−1=inf{y:F(y)≥τ}

여기서, 0 < τ < 1 이며 특히 중앙값의 경우 τ = 0.5의 값을 갖게 된다.

무작위 변량의 무작위 표본 {y₁ ,…,y_n }에 대해서 표본의 중앙값은 절대편차(absolute deviation)의 합을 다음과 같이 최소화함으로써 추정이 가능하다.

(2.9)

argminξ∊R∑i=1nyi−ξ

동일하게 τ 에 해당하는 표본 분위 ξ(τ) 은 다음과 같은 최적화문제로 나타낼 수 있다. argmin은 함수의 최소값을 얻을 수 있는 인자선정을 나타낸다.

(2.10)

argminξ∊R∑i=1nρτ(yi−ξ)

여기서, ρ_τ (z) = z(τ – I (z < 0)), 0 < τ < 1.I (•)는 지시함수 (indicator function)를 나타낸다. 평균은 잔차제곱합을 최소화함으로써 표본평균 μ^ 추정이 가능하며 다음과 같이 나타낼 수 있다.

(2.11)

μ̂=argminμ∊R∑i=1n(yi−μ)2

또한 선형 조건부 평균 함수(linear conditional mean function) E(Y|X= x)= x′b 를 도입하여 다음 식과 같이 확장 가능하다.

(2.12)

b̂=argminb∊Rp∑i=1n(yi−xi'b)2

선형조건부 분위 함수 Q(τ|X=x) = x′b(τ) 는 아래 식과 같이 규정할 수 있으며 최적화 과정을 통해 추정이 가능하다.

Table 1.

Summaries of the nine-category distributional changes

Category	Changes of quantile regression lines	Changes of PDF
Category	Changes of quantile regression lines	Scale	Location
I	상향 수렴	Yes (피크)	Yes (오른쪽)
II	상향 평행	No	Yes (오른쪽)
III	상향 발산	Yes (평면)	Yes (오른쪽)
IV	수평 수렴	Yes (피크)	No
V	수평 평행	No	No
VI	수평 발산	Yes (평면)	No
VII	하향 수렴	Yes (피크)	Yes (왼쪽)
VIII	하향 평행	No	Yes (왼쪽)
IX	하향 발산	Yes (평면)	Yes (왼쪽)

(2.13)

b̂(τ)=argminb∊Rp∑i=1nρτ(y−xi'b)

최종적으로 분위회귀분석을 수행하기 위한 다음 식은 최대· 최소화를 위한 쌍대문제(dual problem) 형의 일반적인 선형 프로그래밍(linear programming)으로 나타낼 수 있다(So et al., 2012).

(2.14)

limb∊Rp[∑i∊{i:yi≥xi'b}τyi−xi'b+∑i∊{i:yi<xi'b}(1−τ)yi−xi'b]

2.3 분포 변화에 따른 분류법

경향성을 평가하는데 있어서 기울기 및 부호는 고려되는 분위에 따라 달라질 수 있으며 이로 인하여 매년 추정되는 확률분포도 달라질 수 있다. 본 연구에서는 분위회귀분석을 활용하여 경향성을 평가하는데 있어서 분석 시작년도에 해당하는 경험적 분포와 분석 최종년도의 경험적 분포의 모양을 비교하여 해수면 상승의 변화 여부를 판단하였다. 즉, 확률분포 의 위치 및 퍼짐 정도를 가지고 경향성을 평가하고자 한다. 선형 분위회귀분석의 회귀 상수는 조밀한 분위에서 가장 먼저 추정된다. 본 연구에서는 주어진 년(X)은 조위지수(Y)의 조건부 분위수를 계산하는데 있어서, 조위지수를 0.05에서 0.95까지 0.05씩 증가시키면서 분석을 수행하였다. 해당 분위와 관련되어 추정된 조건부 조위 특성은 누적확률밀도함수 (cumulative distribution function, CDF)와 확률밀도함수 (probability density function, PDF)로 평가된다. 본 연구에서는 Table 1과 같이 분포특성에 따른 경향성의 범주화를 수행하고자 하며, 총 9개의 범주로 구분된다.

3. 조위자료의 경향성 평가

3.1 대상지역 및 자료의 특성

본 연구에서는 극치사상을 추출하기 위해 국립해양조사원 (www.khoa.go.kr, Korea Hydrographic and Oceanographic Administration, KHOA)에서 관리한 45개 조위관측소의 시조위 자료를 이용하였다. 예보기준면이 적용된 KHOA의 45개 조위관측소의 한 시간 단위 자료로부터 연평균 및 연최대 조위계열 (annual average and annual maximum sea level series)을 추출하였다. 본 연구에서는 한반도 해안을 동해안, 서해안, 남해안, 제주 권역으로 구분하고 통계분석의 신뢰성을 만족하기 위해 자료 기간이 20년 이상인 20개 지점을 선정하였으며, 2013년까지 자료를 활용하여 연 최대치 및 연 평균치를 추출하였다. 20개 지점의 자료연한은 짧게는 26년에서 길게는 51년의 범위를 가지고 있다. Fig. 1은 본 연구에서 선정된 20개 지점에 대한 위치이며, Table 2는 선정된 20개 조위관측소에 대한 현황이다.

Fig. 1.

Tide stations used in this study.

Table 2.

Locations and data lengths of tide stations used in this study

Number	Station Name	Location		Data Period
Number	Station Name	Latitude(^oN)	Longitude(^oE)	Start	End
1	Anheung	36.674	126.132	Jan-87	Dec-13
2	Boryeoung	36.406	126.486	Jan-86	Dec-13
3	Busan	35.096	129.035	Jan-62	Dec-13
4	Chujado	33.962	126.300	Jan-86	Dec-13
5	Daeheuksando	34.684	125.436	Jan-70	Dec-13
6	Gadukdo	35.024	128.811	Jan-77	Dec-13
7	Geomundo	34.028	127.309	Jan-82	Dec-13
8	Gunsan	35.975	126.563	Jan-80	Dec-13
9	Jeju	33.527	126.543	Jan-64	Dec-13
10	Mokpo	34.780	126.376	Jan-80	Dec-13
11	Mukho	37.550	129.116	Jan-65	Dec-13
12	Pohang	36.047	129.384	Jan-77	Dec-13
13	Seogwipo	33.240	126.561	Jan-85	Dec-13
14	Sokcho	38.207	128.594	Jan-77	Dec-13
15	Tongyoung	34.828	128.434	Jan-76	Dec-13
16	Ulleungdo	37.491	130.914	Jan-78	Dec-13
17	Ulsan	35.502	129.387	Jan-63	Dec-13
18	Wando	34.315	126.759	Jan-83	Dec-13
19	Wido	35.618	126.302	Jan-85	Dec-13
20	Yeosu	34.747	127.766	Jan-68	Dec-13

Table 3.

Results of Mann-Kendall nonparametric trend test to annual average sea level

Station Name	p-value	M-K test statistic	Station Name	p-value	M-K test statistic
Anheung	5.00×10^-2	1.96	Mukho	3.11×10^-6	4.66
Boryeoung	3.83×10^-7	5.08	Pohang	4.56×10^-12	6.92
Busan	1.81×10^-13	7.36	Seogwipo	3.60×10^-6	4.63
Chujado	3.00×10^-4	3.62	Sokcho	1.95×10^-11	6.71
Daeheuksando	4.86×10^-2	1.97	Tongyoung	3.17×10^-8	5.53
Gadukdo	1.09×10^-8	5.72	Ulleungdo	1.48×10^-2	2.44
Geomundo	2.02×10^-6	4.75	Ulsan	3.28×10^-3	2.94
Gunsan	1.11×10^-3	3.26	Wando	2.78×10^-3	2.99
Jeju	0.00	8.78	Wido	8.37×10^-1	-0.21
Mokpo	1.54×10^-7	5.25	Yeosu	2.85×10^-5	4.18

Table 4.

Results of Mann-Kendall nonparameric trend test to annual maximum sea level

Station Name	p-value	M-K test statistic	Station Name	p-value	M-K test statistic
Anheung	2.07×10^-2	2.31	Mukho	8.03×10^-1	0.25
Boryeoung	4.82×10^-2	1.98	Pohang	4.01×10^-3	2.88
Busan	2.32×10^-3	3.05	Seogwipo	1.90×10^-2	2.34
Chujado	1.33×10^-1	1.50	Sokcho	5.13×10^-2	1.95
Daeheuksando	8.76×10^-4	3.33	Tongyoung	6.78×10^-1	0.41
Gadukdo	5.92×10^-1	0.54	Ulleungdo	5.13×10^-1	0.65
Geomundo	1.01×10^-1	1.64	Ulsan	7.01×10^-2	1.81
Gunsan	2.02×10^-1	1.27	Wando	8.60×10^-2	-1.72
Jeju	6.74×10^-7	4.97	Wido	4.09×10^-2	2.04
Mokpo	2.48×10^-7	5.16	Yeosu	3.39×10^-2	-2.12

3.2 MK검정 결과

경향성 분석은 장기간의 수문자료에 대해 변화 양상을 판단 하여 용도에 따라 자료를 분석할 수 있는 유용한 방법이다. 일반적으로 가설검증 시 유의수준 α를 0.05 또는 0.01로 설정하고 샘플집단의 p-value를 계산하여 유의수준 0.05 또는 0.01보다 작으면 귀무가설은 기각된다. 여기서 귀무가설 H₀은 “자료의 경향성이 존재하지 않음”을 의미한다. 즉, 귀무가설이 기각 된다는 것은 “자료의 경향성이 존재”함을 의미한다. 본 연구에서는 비매개변수적 경향성 분석 방법인 MK 검정법을 유의 수준 5%에서 수행하였으며 Table 3과 4는 각각 20개 지점의 연 평균 및 연 최대 조위의 분석 결과이다.

Fig. 2.

Sighificance test of trend of annual maximum sea level and annual mean sea level.

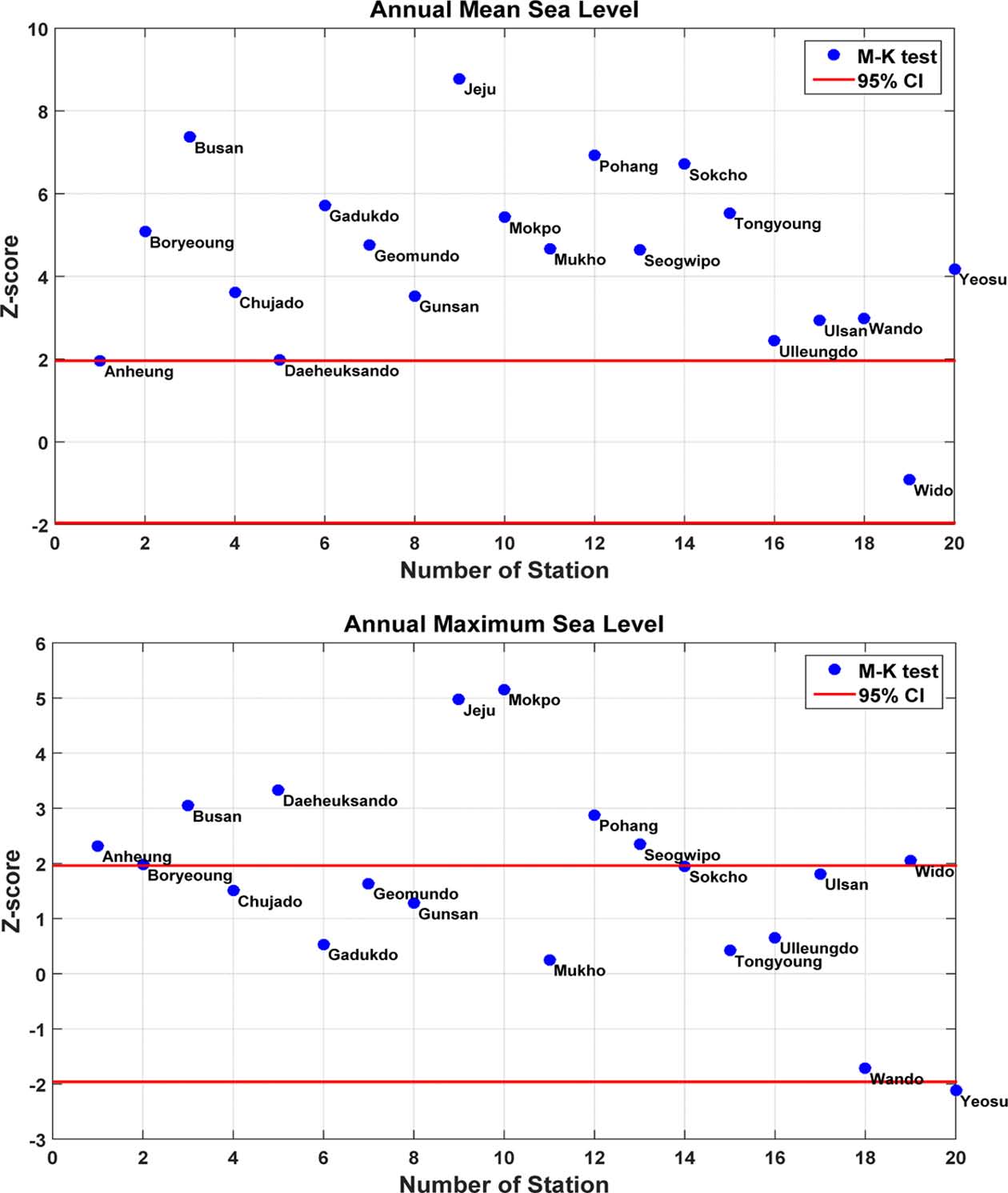
아래 표에서 p-value가 0.05보다 작을 때 귀무가설이 기각되어 유의수준 5%에서 경향성이 있다고 판단한다. 본 연구 에 사용된 20개 지점의 경향성 분석시 연평균조위의 경우 위도, 안흥을 제외한 18개 지점에서 경향성이 있는 것으로 분석되었으며, 연최대조위의 경우 포항, 제주, 대흑산도, 부산 등 10개 지점에서 경향성이 있는 것으로 나타났다.

3.3 분위회귀분석 결과

3.3.1 연평균조위자료 분석

본 연구에서는 분위회귀분석(QRA) 방법을 이용하여 시간에 따른 연평균조위의 경향성을 평가 및 비교하기 위하여 일반적으로 사용되는 시계열의 평균에 대한 회귀분석 Ordinary Regression (이하 OR) 방법을 이용하였다. QRA 방법의 적용은 5% 간격으로 5%부터 95%까지 Quantile에 대하여 식. 2.14를 이용하여 회귀계수 b를 추정하였으며, OR 방법의 경우 LSM 기법을 이용하여 회귀계수 b를 추정하였다. QRA 방법의 경우 분위별로 경향성이 다르게 나타나고 있다. 또한 OR 방법의 경향성과 QRA방법의 평균경향성은 유사한 기울기를 가지는 것을 확인할 수 있으며, 평균적으로 매년 1~6 mm범위에서 해수면이 상승하고 있음을 확인할 수 있었다.

Fig. 3에서는 유의수준 5%를 기준으로 지점별로 경향성의 유의성을 평가하여 나타내었다. 제주 및 목포 지점의 경우 높은 분위로 갈수록 증가경향이 감소하는 것을 확인할 수 있었다. 반면 포항 및 완도의 경우에는 높은 분위로 갈수록 증가 경향이 크게 나타나고 있다. 안흥, 대흑산도, 위도를 제외한 대부분의 지역은 유의수준 5%에서 모든 분위에서 경향성이 유의성을 가지는 것으로 분석되었다.

Table 5.

Regression coefficients from QRA for annual average sea level

Station	Slope b (mm/year)
	Quantile Regression										Ordinary Regression
	10	20	30	40	50	60	70	80	90	Ave.	Ordinary Regression
Anheung	3.23	3.53	1.37	1.28	0.66	0.49	0.30	0.96	1.30	1.46	1.91
Boryeoung	5.77	5.86	5.44	5.70	5.96	5.34	6.58	6.85	9.50	6.34	6.42
Busan	2.47	2.66	2.65	2.62	2.62	2.81	2.68	2.59	2.14	2.58	2.54
Chujado	2.39	1.32	1.93	2.28	2.08	2.08	1.91	2.37	2.30	2.07	2.11
Daeheuksando	0.57	0.61	0.28	0.39	0.55	0.46	0.41	0.63	0.14	0.45	0.56
Gadukdo	1.67	2.42	2.43	2.21	2.17	2.22	2.85	2.77	3.05	2.42	2.57
Geomundo	3.12	3.51	4.21	4.37	4.79	4.36	4.72	4.36	3.33	4.09	4.00
Gunsan	2.28	2.07	2.19	2.11	1.61	1.54	1.92	1.71	1.67	1.90	1.84
Jeju	6.36	6.43	5.61	5.74	6.01	5.99	5.92	5.83	5.32	5.91	6.17
Mokpo	10.96	10.00	9.35	8.99	6.96	6.01	6.02	6.44	5.89	7.85	8.52
Mukho	2.62	2.66	2.21	1.75	1.68	1.43	1.13	0.66	0.63	1.64	1.14
Pohang	2.44	3.40	3.75	5.11	5.19	5.45	5.97	6.31	6.43	4.89	5.73
Seogwipo	3.42	3.97	3.43	4.30	4.69	5.03	5.01	4.23	4.50	4.29	3.75
Sokcho	2.47	2.48	2.59	2.93	2.79	2.70	2.74	2.39	2.71	2.64	2.66
Tongyoung	1.69	1.53	1.92	1.88	2.07	1.93	1.80	1.85	2.00	1.85	1.83
Ulleungdo	4.25	2.32	2.33	1.65	1.48	2.34	1.97	3.87	3.66	2.65	2.58
Ulsan	1.77	0.99	0.58	0.90	1.00	1.03	0.78	0.89	0.38	0.93	1.01
Wando	1.09	0.83	1.19	1.29	1.42	1.75	2.03	1.89	2.46	1.55	1.38
Wido	-1.41	-0.99	-0.52	-0.75	-0.14	-0.60	-1.03	-0.90	0.61	-0.64	-0.60
Yeosu	0.94	1.70	1.47	1.72	1.67	1.44	1.37	1.54	1.51	1.48	1.37

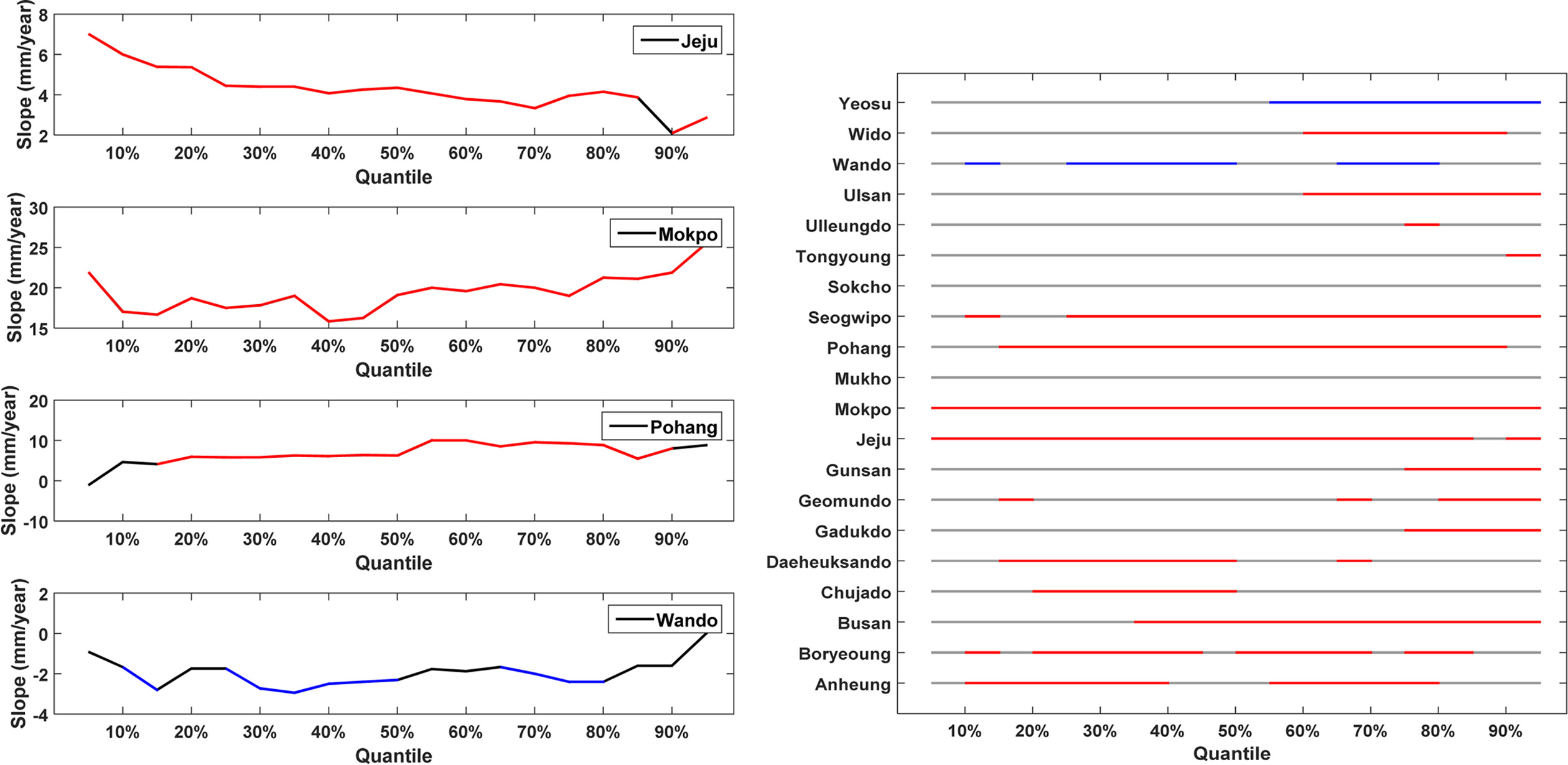
Fig. 3.

Significant-trend plots beyween quantile of 0.05 and 0.95 of annual average sea level for 20 selected stations, shere red, blue, and gray segments respecticely denote significant positive, significant negative, and insignificant trends gicen 5% significance level.

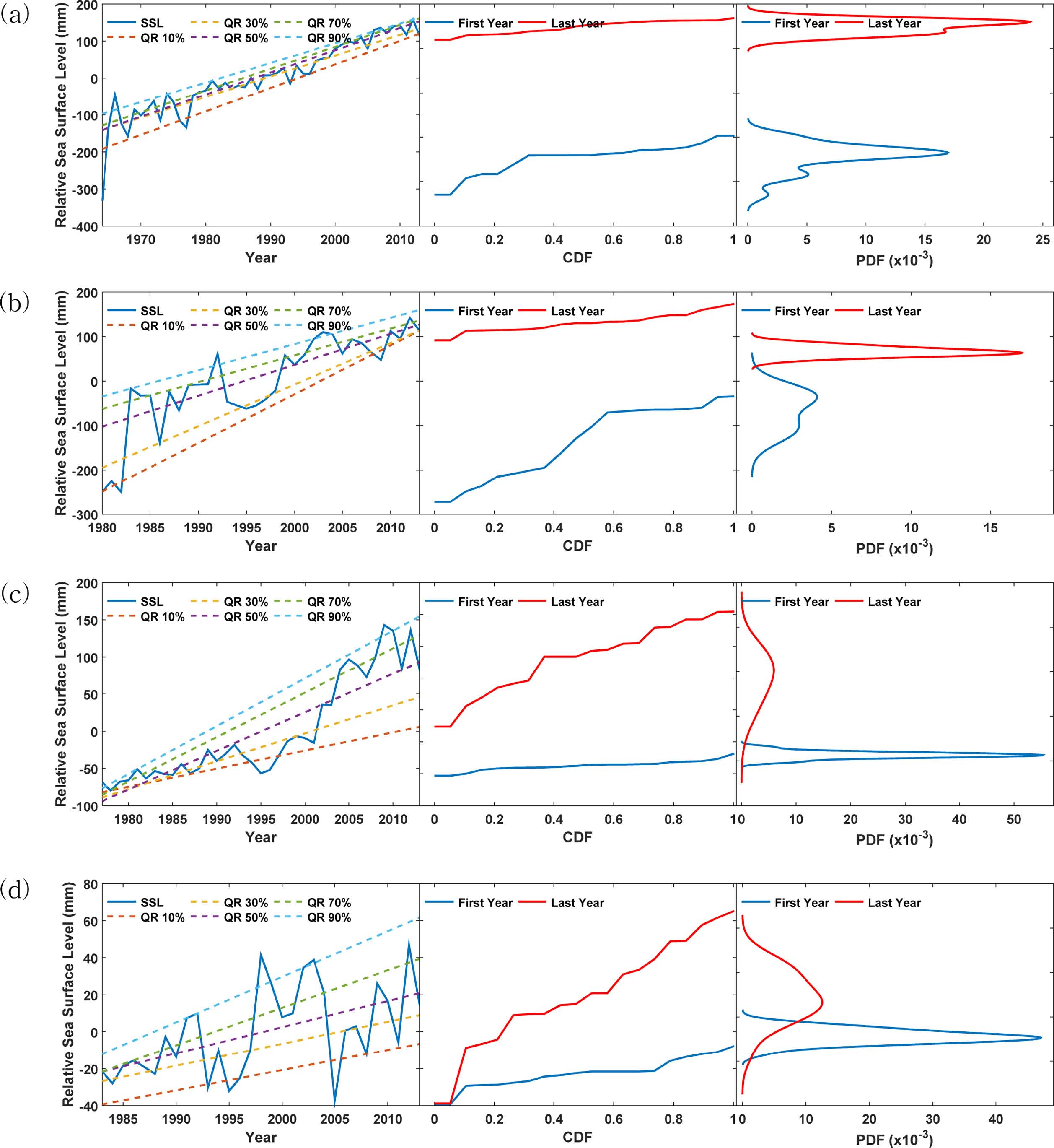
Fig. 4는 QRA 방법을 토대로 경향성을 범주화 과정을 설명하기 위하여 제주, 목포, 포항, 완도 등 4개 지점을 기준으로 분석 결과를 도시하여 나타내었다. 범주화 기준은 Table 1에서 나타내었듯이 9개로 구분되며, 구분 기준으로 분석 첫 해와 마지막 해의 확률밀도함수를 비교하는 방식으로 이루어진다. 예를 들어 제주지점(Fig. 4(a))의 경우 상향 수렴의 형태를 가지며 범주 1에 해당한다. 즉, 퍼짐 정도가 약하고 평균이 오른쪽으로 이동하는(커지는) 형태를 나타낸다. 반면 포항지점(Fig. 4(c))의 경우 분석 마지막 해의 확률밀도함수의 퍼짐정도가 크며 평균이 오른쪽으로 이동하는(커지는) 형태를 나타나고 있으며 범주 3에 해당한다. 이러한 방법으로 20개 지점을 분석하여 Table 6에 나타내었다. 대부분의 지역이 범주 1과 3으로 분류되고 있다. 즉, 상향수렴 및 상향발산 형태의 증가경향이 대표적인 특성으로 분석되었다. Table 6은 QRA분석으로부터 추정된 회귀계수 b에 대하여 p-value 값을 보여준다. QRA 방법의 p-value는 관측소별로 적용한 19개 분위로부터 추정된 pvalue 중 통계적으로 가장 유의한 p-value만을 표시하였다.

Fig. 4.

Obserced trend of annual average sea lecel associated with quantile regression(0.1, 0.3, 05, 0.7, and 0.9 from top to bottom), CDF and PDF for (a) Jeju, (b) Mokpo, (c) Pohang, and (d) Wando stations.

3.3.2 연최대조위분석 결과

본 절에서는 연 평균 조위자료와 동일하게 연최대조위 자료에 대해서도 동일한 분석을 수행하였다. Table 7에서는 QRA 방법을 이용하여 시간에 따른 연최대조위의 경향성을 평가 및 비교하기 위하여 일반적으로 사용되는 시계열의 평균에 대한 회귀분석 OR방법을 이용하였다. 연평균조위와 동일하게 OR방법의 경향성과 QRA방법의 평균경향성은 유사한 기울기를 가지는 것을 확인할 수 있으며, 평균적으로 매년 1~20 mm범위에서 연최대해수면이 상승하고 있음을 확인 할 수 있었다. Fig. 5에서는 유의수준 5%를 기준으로 지점별로 연최대조위 경향성의 유의성을 평가하여 나타내었다. 연 평균조위와는 다르게 분위에 따른 경향성의 변동은 크지 않게 나타나고 있다. 서귀포, 포항, 목포, 제주, 부산, 보령, 안 흥은 대부분의 분위에서 증가하는 경향성을 확인할 수 있었으나, 나머지 지점의 경우 증가경향이 통계적으로 유의하지 않은 결과를 보여주었다. 여수 및 완도의 경우 연최대조위가 감소하는 경향을 나타내고 있다.

Table 6.

Comparison of statisrical significance test from 3 different methods for annual average sea level

ST.No	Quantile Regression		Ordinary Regression		Mann-Kendal Test		Distribution Category
ST.No	t-Test	p-value	t-Test	p-value	H	Z-score	Distribution Category
Anheung	O.K	2.45×10 ^-3	O.K	4.90×10 ^-3	X	1.96	1
Boryeoung	O.K	3.06×10 ^-8	O.K	6.05×10 ^-9	O.K	5.08	3
Busan	O.K	0.00	O.K	0.00	O.K	7.36	1
Chujado	O.K	9.34×10 ^-6	O.K	2.46×10 ^-5	O.K	3.62	3
Daeheuksando	O.K	1.64×10 ^-2	O.K	2.39×10 ^-2	O.K	1.97	3
Gadukdo	O.K	5.37×10 ^-11	O.K	3.38×10 ^-11	O.K	5.72	3
Geomundo	O.K	2.25×10 ^-10	O.K	3.56×10 ^-9	O.K	4.75	3
Gunsan	O.K	2.11×10 ^-5	O.K	1.10×10 ^-4	O.K	3.53	1
Jeju	O.K	0.00	O.K	0.00	O.K	8.78	1
Mokpo	O.K	1.75×10 ^-10	O.K	4.20×10 ^-10	O.K	5.43	1
Mukho	O.K	1.05×10 ^-8	O.K	1.88×10 ^-5	O.K	4.66	1
Pohang	O.K	2.11×10 ^-13	O.K	1.91×10 ^-14	O.K	6.92	3
Seogwipo	O.K	6.98×10 ^-8	O.K	1.17×10 ^-6	O.K	4.63	3
Sokcho	O.K	1.11×10 ^-16	O.K	5.55×10 ^-16	O.K	6.71	3
Tongyoung	O.K	1.16×10 ^-11	O.K	1.67×10 ^-10	O.K	5.53	3
Ulleungdo	O.K	2.58×10 ^-3	O.K	1.74×10 ^-3	O.K	2.44	1
Ulsan	O.K	5.35×10 ^-4	O.K	6.29×10 ^-4	O.K	2.94	1
Wando	O.K	6.50×10 ^-5	O.K	9.42×10 ^-4	O.K	2.99	3
Wido	O.K	2.78×10 ^-2	X	2.94×10 ^-1	X	-0.92	3
Yeosu	O.K	2.47×10 ^-5	O.K	3.79×10 ^-4	O.K	4.18	1

Table 7.

Regression coefficients from QRA for annual maximum sea level

Station	Slope b (mm/year)
	Quantile Regression										Ordinary Regression
	10	20	30	40	50	60	70	80	90	Ave.	Ordinary Regression
Anheung	7.00	7.37	7.50	8.75	5.26	6.30	9.57	7.62	1.77	6.79	5.59
Boryeoung	5.56	7.14	8.64	8.57	5.60	7.50	7.14	8.33	-5.00	5.94	7.41
Busan	1.00	1.28	1.54	1.82	2.11	2.73	3.55	3.10	2.35	2.16	2.56
Chujado	0.00	3.33	3.89	3.33	4.38	1.67	1.25	0.00	2.50	2.26	1.02
Daeheuksando	2.50	3.87	4.00	4.52	4.29	2.69	3.95	2.69	3.68	3.58	5.20
Gadukdo	1.33	0.83	-0.77	-0.94	-0.56	0.80	0.74	2.69	3.93	0.90	1.38
Geomundo	2.22	3.46	1.43	1.00	1.67	0.91	2.63	2.22	3.50	2.12	2.05
Gunsan	3.42	2.17	2.78	3.20	3.15	1.05	4.40	6.25	14.12	4.50	3.52
Jeju	6.00	5.37	4.40	4.07	4.35	3.78	3.33	4.15	2.09	4.17	4.22
Mokpo	17.04	18.70	17.83	15.83	19.09	19.58	20.00	21.25	21.88	19.02	19.28
Mukho	2.11	1.94	0.46	0.54	0.00	-1.00	-1.36	0.00	-0.39	0.25	-0.02
Pohang	4.64	5.94	5.83	6.11	6.25	10.00	9.55	8.85	8.00	7.24	6.84
Seogwipo	3.46	3.50	3.68	4.00	5.00	6.00	5.79	8.10	10.00	5.50	4.72
Sokcho	2.00	2.65	2.67	1.33	1.30	2.11	0.00	2.35	2.50	1.88	2.15
Tongyoung	-1.20	-0.80	0.39	0.00	0.00	0.71	0.00	0.46	3.81	0.38	3.59
Ulleungdo	-0.87	0.00	1.43	0.59	0.83	1.25	2.27	5.19	2.42	1.46	1.34
Ulsan	0.65	1.11	0.23	0.00	0.44	1.36	3.21	4.86	7.14	2.11	3.00
Wando	-1.67	-1.74	-2.73	-2.50	-2.31	-1.88	-2.00	-2.40	-1.60	-2.09	-1.65
Wido	1.74	2.22	3.33	3.50	2.92	4.29	6.92	5.42	18.33 ff	5.41	3.71
Yeosu	-1.36	-1.48	-1.36	-1.25	-1.25	-2.94	-2.96	-3.00	-3.33	-2.11	-2.14

Fig. 5.

Significnat-trend plots between quantile of 0.05 and 0.95 of annual maximum sea lecel for 20 selected stations, where red, blue, and gray segments repecticely denote significant positive, significant negatice, and insgnificant trends given 5% significance level.

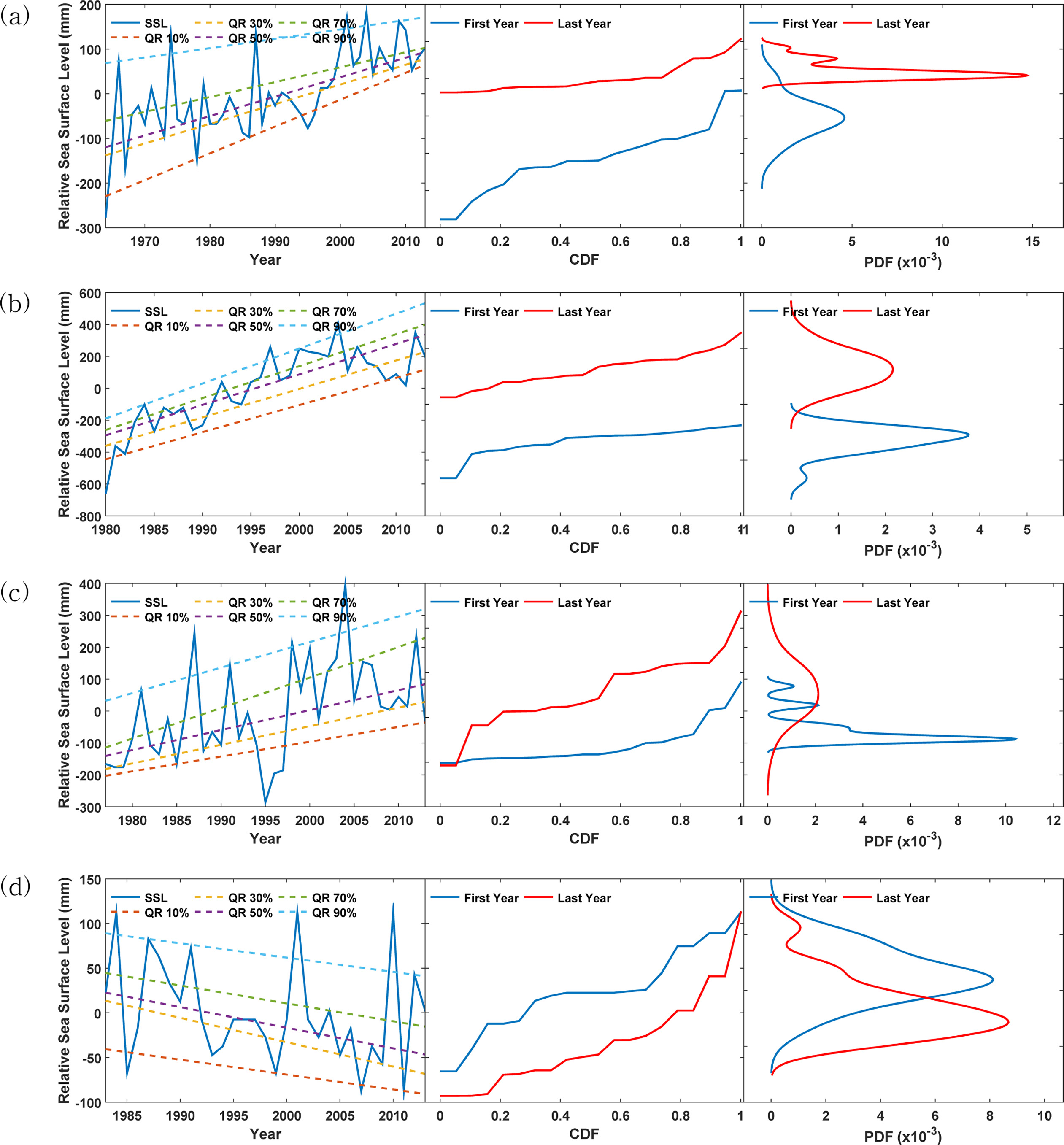
연평균조위와 동일하게 경향성을 9개의 범주로 분석하였으며, Fig. 6과 Table 8에 나타내었다. 범주화 결과 상향수렴 및 상향발산의 형태를 가지는 지역이 대부분인 것으로 분석되었으나, 추자도, 속초, 완도, 여수는 수평수렴의 형태를 가지는 범주 4로 평가되었다. 위도의 경우 범주 4로 분류되었으며 수평발산의 형태를 가지는 경향성으로 평가되었다.

Table 8.

Comparison of statistical significance test form 3 different methods for annual maximum sea level

ST.No	Quantile Regression		Ordinary Regression		Mann-Kendal Test		Distribution Category
ST.No	t-Test	p-value	t-Test	p-value	H	Z-score	Distribution Category
Anheung	O.K	0.01	X	0.05	O.K	2.31	1
Boryeoung	X	0.02	O.K	0.02	O.K	1.98	1
Busan	O.K	0.00	O.K	0.00	O.K	3.05	3
Chujado	O.K	0.01	X	0.27	X	1.50	4
Daeheuksando	O.K	0.02	O.K	0.01	O.K	3.33	3
Gadukdo	O.K	0.00	X	0.15	X	0.54	3
Geomundo	O.K	0.03	X	0.06	X	1.64	3
Gunsan	O.K	0.00	X	0.08	X	1.28	3
Jeju	O.K	0.00	O.K	0.00	O.K	4.97	1
Mokpo	O.K	0.00	O.K	0.00	O.K	5.16	3
Mukho	X	0.07	X	0.49	X	0.25	1
Pohang	O.K	0.00	O.K	0.00	O.K	2.88	3
Seogwipo	O.K	0.00	O.K	0.00	O.K	2.35	3
Sokcho	X	0.08	X	0.09	X	1.95	4
Tongyoung	O.K	0.01	X	0.12	X	0.42	3
Ulleungdo	O.K	0.01	X	0.20	X	0.65	3
Ulsan	O.K	0.00	O.K	0.01	X	1.81	3
Wando	O.K	0.01	X	0.07	X	-1.72	4
Wido	O.K	0.00	X	0.09	O.K	2.05	6
Yeosu	O.K	0.00	O.K	0.01	O.K	-2.12	4

Fig. 6.

Observed trend of annual maximum sea level associated with quntile regresttion (0.1, 0.3, 0.5, 0.7, and 0.9 from top to bottom), CDF and PDF for (a) Jeju, (b) Mokpo, (c) Pohang, and (d) Wando stations.

4. 결론 및 토의

우리나라의 연안은 도시개발, 인구증가가 지속적으로 나타나고 있으며, 이러한 점에서 해수면 상승으로 인한 연안재해 취약성이 가중될 것으로 전망되고 있다. 본 연구에서는 우리나라 연안의 20개 지역의 조위자료를 바탕으로 MK 검정, OR, QRA 등을 이용하여 해수면상승에 대한 다양한 분석을 수행하였다. 본 연구를 통해 얻은 결론은 다음과 같다.

첫째, MK 검정을 통하여 연평균조위와 연최대조위자료에 대한 경향성의 유의검정을 수행하였다. 연평균조위의 경우에 위도, 안흥을 제외한 18개 지점에서 경향성이 통계적으로 유의한 것으로 분석되었으며, 연최대치의 경우 포항, 제주, 대 흑산도, 부산 등 10개 지점에서 경향성이 통계적으로 유의한 것으로 평가되었다.

둘째, QRA 방법을 이용하여 연평균조위와 연최대조위의 경향성을 분위별로 평가하였다. QRA 방법은 시계열의 여러 분위에서 다양한 경향성을 평가할 수 있는 방법으로서, 기존 회귀분석 방법에 비해 다각적인 경향성 검토가 가능하였다. QRA분석 결과 연평균해수면의 경우 매년 1~6 mm의 범위에서 해수면이 상승하고 있으며, 연최대해수면의 경우 1~20 mm의 범위에서 증가경향이 나타나고 있음을 확인할 수 있었다.

셋째, QRA 결과를 토대로 9개 범주로 경향성을 범주화시켰으며, 우리나라의 연평균해수면의 경우 대부분 상향수렴 및 상향발산의 형태를 가지는 경향성을 나타내고 있었다. 연최대해수면의 경우에도 상향수렴 및 상향발산의 형태를 가지는 지역이 대부분인 것으로 분석되었으나, 추자도, 속초, 완도, 여수 등 일부지점에서는 수평수렴의 경향성을 나타내고 있다.

전반적으로 우리나라의 해수면은 상승하는 경향성을 보여주고 있으며 통계적으로도 유의한 경향성을 가지는 것으로 분석되었다. 향후 이러한 경향성을 기반으로 연최대해수면 자료를 활용한 비정상성빈도해석 절차의 개발 및 적용이 필요할 것으로 판단된다.