파일형 선박충돌방호공에 대한 간이충돌모델의 개발과 검증
요약
본 연구에서는 선박충돌로부터 교량을 방호하는 파일형 선박충돌방호공과 충돌선박의 간이충돌모델을 개발하고 이를 검증하였다. 선박은 선수의 비선형반력을 고려하여 모델링하였다. 충돌방호공의 모델은 파일에서 상부 슬래브의 하단과 지중에 2개의 소성힌지가 발생하는 것으로 구성하였다. 충돌중 발생하는 운동에너지와 위치에너지 및 변형에너지를 고려하여 운동방정식을 유도하고 이를 해석하는 시스템을 개발하였다. 선박과 구조물에 대한 정밀충돌해석을 수행하여 개발된 간이모델이 충돌거동을 정확히 모사할 수 있음을 보였다.
핵심용어: 파일형 선박충돌 방호공, 간이모델, 비선형 운동방정식, 소성힌지, 충돌에너지
Abstract
In this study, a simplified collision model of pile protective structures against a navigation vessel was proposed and verified. The model of pile protective structure were composed by two plastic hinges at below of cap slab and the inside of ground. A nonlinear equation of motions was developed in consideration of the kinematic energy, potential energy and deformation energy in collision event. The developed simplified model were verified by the precise finite element collision analysis of the vessel and the protective structure.
Keywords: pile protective structure, simplified model, nonlinear equation of motion, plastic hinge, collision energy
1. 서 론
교량기술의 발전에 따라 대형화된 교량들이 항로를 가로 질러 건설되는 경우가 늘면서 이에 대한 설계기법이 새롭게 시방서에 채택되고 다양한 충돌방호시설도 계획, 시공되고 있다. 여러 가지 충돌방호시설중 파일의 소성힌지에 의한 에너지 소산메카니즘을 가지고 있는 파일형 충돌방호공은 시공시 장비운용의 효율성과 소산에너지량을 손쉽게 조정할 수 있는 장점이 있다. 하지만 파일과 지반과의 상호작용 및 내부충진재와 철근의 비선형 거동, 상부구속슬래브의 영향 등을 고려해야하기 때문에 전체적인 정밀충돌해석은 매우 큰 해석모델 및 긴 해석시간을 요구하게 된다. 이러한 난점은 구조물의 비선형거동특성을 나타내면서도 자유도를 최소화한 간이충돌모델(simplified collision model)을 이용하여 해결할 수 있다. 또한 이러한 간이모델을 이용하여 다양한 매개변수들의 영향을 일련의 반복해석을 통해 분석하여 비선형거동에 대한 설계방법론을 개발할 수 있다.
선박충돌에 대한 간이모델의 개발은 주로 조선공학에서 다양하게 이루어졌다.( Sadjdak, 2004; Tabri, 2010;) 이들의 연구는 주로 선박과 선박의 충돌에 있어서 충돌시 발생하는 선측의 관통이나 충돌전후의 운동의 변화 등에 대한 간이모델을 제시하였다. 선박과 교량의 충돌해석에 대한 간이모델은 국내에서는 교량과 부선의 상부구조에 대한 충돌해석에서 사용된 예가 있다.( Lee, 2011) 국외에서는 Patsch et al.(2002)이 사장교의 교각을 100000DWT 선박에 대하여 방호하기 위하여 파일형 충돌방호공을 설계하는 과정에서 1/15의 축소모델에 대하여 수치해석과 현장시험을 수행하였다. 이들은 수치해석을 통하여 충분히 정확하게 파일의 거동을 모사할 수 있다는 것을 보였다. 최근 Zhu et al.(2012)은 대형토조에서 선박충돌방호공을 시공을 위한 파일의 횡방향 내하능력을 평가하였다. 이 들은 진자운동을 이용한 동적충격하중과 케이블을 이용한 정적하중을 재하하여 각 결과로부터 정적 및 동적 p-y곡선을 산정하였다. 3가지 종류의 이론적인 동적 p-y곡선과 실험에서 얻어진 동적 p-y곡선을 비교하고 파일의 동적 p-y곡선과 일정한 감쇠비를 사용한 충격해석을 사용하는 것이 타당하다는 결론을 얻었다. 이때 사용하는 감쇠비는 선형동적해석에서 얻은 감쇠비를 사용하였다. 교량의 설계기준에서 선수충돌력은 선박의 질량과 속도의 함수로 제시되어있다.( Chang, 2006) 그러나 설계기준에 제시된 충돌력은 충돌에 대한 충분한 이해가 부족했던 시점에서 제시된 식이기 때문에 충돌조건에 따라 일정하지 않은 보수성을 보인다. 이러한 선수충돌력에 대하여 실제 선박을 모델링하고 다양한 조건에 대한 유한요소 충돌해석을 통하여 설계기준의 설계충돌력을 평가한 연구결과가 제시되었다.( Lee and Hong, 2011) 최근 Fan et al.(2011)은 선박과 사장교의 충돌설계를 위하여 교량기초에 직접 충돌하는 선박선수모델을 질량과 비선형 스프링을 가진 단자유도계로 가정하고 이때 충돌속도에 따른 비선형 스프링의 특성을 산정하는 방법을 제안하였다. 이들의 연구에서는 강재로 이루어진 선수가 변형속도에 따라 다른 강도를 갖는 것에 주목하고 충돌중에 발생하는 변형속도의 변화를 고려한 선수강도곡선을 제안하였다. 하지만 이 연구에서는 선박은 교량의 기초에 직접 충돌하는 조건을 전제하였으므로 교량구조물은 간이모델이 아닌 일반적인 유한요소로 모델링되었다. 본 연구에서는 파일형 선박충돌 방호공의 충돌거동을 효과적으로 해석하기 위한 간이충돌모델의 운동방정식을 유도하고 이를 정밀충돌해석모델의 결과와 비교하여 검증하였다. 개발된 간이충돌모델에서 사용된 에너지 소산기구의 충돌거동은 정밀해석모델에서 얻어진 값을 사용하였다.
2. 간이모델의 개발
2.1 개요
파일형 충돌방지공의 충돌 간이모델의 작성에 있어서 다음과 같은 조건을 가정한다.
- 충돌은 평면에서 일어난다. - 선수나 파일은 탄소성거동한다. - 선수와 파일의 소성거동은 집중되어 일어난다. 파일형 충돌방호공의 간이충돌모델의 운동방정식을 유도하기 위한 충돌모델의 개략적인 형상을 Fig. 1에 나타내었다. 충돌선박은 충돌질량(mv)과, 선수의 변형에 따른충돌력을 나타내는 선수스프링으로 단순화 되었다. 파일형 충돌방호공은 상부의 구속슬래브(capping slab, 이하 슬래브)와 파일로 구성된다. 여기서 슬래브는 다수의 파일의 두부가 동일한 거동을 하도록 구속하고 충돌력을 파일로 전달하는 역할을 한다. 슬래브는 여러 개의 파일두부와 일체화되어 있으므로 자체의 회전자유도는 구속된다. 슬래브의 질량(ms)은 충돌시 관성력에 의해 충돌에 저항하는 질량을 의미한다. 방호공을 구성하는 파일군은 집중된 특성을 가진 것으로 가정하였다.
2.2 충돌중 힘의 평형
충돌중 선박과 방호공에 작용하는 힘은 Fig. 2에서 보이는 바와 같이 나타낼 수 있다. 충돌중 선박에는 관성력과 선수의 변형에 의한 반력이 작용한다. 이에 대한 평형방정식은 다음과 같다.
여기서 mv는 수리동역학적 부가질량을 포함한 선박의 충돌질량이고, fb는 선수의 변형에 의해 발생하는 비선형반력이다. 이 반력은 선박변위(xv)와 방호공의 변위(xp)간의 상대값인 선수변형량에 종속인 함수이다.
충돌과정중 선박과 방호공의 운동은 다음 조건에 따른다.
여기서 ms는 슬래브의 질량(관성저항질량)이고, mp는 파일군의 질량이다. “′ ”가 붙은 질량은 수중에서 부력을 고려한 중량을 산정하기 위한 질량이다.
x¨p
는 슬래브의 가속도이다. h′는 지면으로 부터 수직한 하부의 소성힌지로부터 충돌점 사이의 모멘트팔의 길이이다. 이 모멘트팔의 길이는 다음과 같다.
여기서 hp는 상하부 소성힌지간의 거리이다. 충돌중에 상부와 하부소성힌지의 소성회전모멘트(ku, kb)가 선박의 선수충돌력과 관성력에 의해서 발생하는 모멘트와 변위에 따른 발생하는 방호공의 2차모멘트의 합보다 작은 경우에는 방호공의 변위는 변하지 않는 소성거동을 한다. 이 때 소성힌지의 소성회전강성 ku, kb는 방호공의 변위 xp의 함수이다. 이 과정에서 충돌점에서 계산되는 모멘트(Mp)는 다음과 같다.
이 모멘트가 평형을 이루는 충돌방향의 수평력은 다음과 같다.
이들 관계를 이용하여 방호공에 작용하는 동적평형식인 식 (2)를 다시 쓰면 다음과 같다.
여기서 방호공의 수평력 fb는 방호공의 변위xp의 함수이고 선수의 작용력 fb는 방호공과 선박의 상대변위, 즉 선수의 변형에 따른 함수이다.
식(1)과 식(6)을 연계하여 해석하기 위하여 다음과 같이 변수를 가정한다.
위의 식에 식(1)과 식(6)의 변수값을 대입하면 다음과 같이 나타낼 수 있다.
유도된 미분방정식 식(8)은 다수의 비선형 항을 포함하기 때문에 대수적인 방법으로는 해를 산정하기 어려우므로 수치적인 방법으로 해를 산정하였다. 이를 위하여 미분방정식을 수치해석기법인 4차의 Runge-Kutta 방법을 사용하였다. 이 방법의 적용은 수치해석 패키지 GNU Octave( Eaton et al., 2013)의 함수인 lsode45를 이용하였다.
3. 개발모델의 검증
3.1 정밀충돌해석
개발된 간이 모델의 정확성을 검증하기 위해 선박과 방호공 및 지반을 정밀모델링하고 상용프로그램인 ABAQUS(SIMULIA,2010)를 이용하여 비선형동적 충돌해석을 수행하였다. 특히 대규모 자유도를 가진 비선형 거동에 대하여 효율성이 좋은 것으로 알려진 양해법(explicit method)를 사용하였다. 해석에 사용된 선박은 7000GT의 크기를 가진 차량운반선으로 선수부는 충돌거동시 재료 및 기하학적인 비선형거동이 집중되는 것을 고려하여 상세하게 쉘(Shell)요소로 모델링하였다.( Fig. 3(a)) 선체 및 선미부도 쉘요소를 이용하여 모델링하였으나 선수부에 비하여 상대적으로 거친 요소망을 사용하였고, 선수에만 비선형거동이 발생하는 것으로 가정하여 탄성체로 모델링하였다. 선수부의 재료는 탄소성 거동을 가정하였으며 변형속도에 따른 재료거동의 변화를 다음과 같이 식으로 고려하였다. 여기서
σ¯
는 동적응력(dynamic flow stress),
σ0
는 정적응력(static flow stress),
εpl˙
은 변형속도이고 D, n은 재료에 따르는 상수들이다. 본 연구에서는 D = 40.4/sec, n = 5 를 사용하였다.( SIMULIA, 2010) 유체중에서 움직이는 물체에 추가하는 부가질량은 기존의 설계기준( AASHTO,2010)을 따라 산정하였다. 조밀한 요소망으로 구성된 선수부분에 대해서는 해석의 효율성을 위하여 재료의 밀도를 변화시켜 한계시간간격을 증가시키는 기법인 Mass scaling을 사용하였다. 기타 선박의 상세 모델링 기법은 기존 연구( Lee and Hong, 2011)에 개발된 방법을 따랐다. 파일형 충돌방호공의 주 에너지 소산기구인 파일은 반지름 R = 1.0 m인 강관으로 가정하여 모델링하였다. 파일의 길이는 30m로 가정하였고 상부는 탄성재료로 가정한 콘크리트슬래브에 강결되고 하부는 지반에 관입된 상태에서 하부기반암에 고정되어 있는 것으로 가정하였다. 이 때 파일이 관입된 지반은 점토와 사질토로 구성된 3개의 지층이 총 10 m로 적층된 것으로 가정하였다. 파일은 SS400 강재로 모델링하였고 재료 비선형 거동을 고려하였다. 파일을 횡방향으로 지지하고 있는 주변 지반은 비선형 지반 스프링을 이용하여 지반의 비선형성을 고려하였다. 생성된 지반스프링은 파일의 중심선을 따라 고정되는 것을 가정하였다.( Lee et al., 2012) 충돌방호공은 모두 18개의 파일을 설치하고 상부에 이를 구속하는 슬래브가 설치되어 선박의 충돌에너지를 파일에 분포시키는 것으로 모델링하였다.( Fig. 3(b)) 선박은 편심이 발생하지 않도록 방호공의 중앙에 5 m/sec의 속도로 충돌하는 것으로 가정하였다. 충돌 중 발생하는 각 구성요소들의 거동과 시스템의 에너지 소산을 검토하였다. 충돌후 얻어진 선수부의 변형형상은 Fig. 4(a)에서 보이는 바와 같다. 충돌부위는 구상선수부분으로 압괴로 인하여 슬래브의 형상이 압인되어 있는 것을 볼 수 있다. 본 해석에서 사용한 충돌방지공의 슬래브 두께는 선수부에 비해 상대적으로 작은 크기이기 때문에 슬래브와의 접촉변형은 선수부의 상단에서만 발생하였지만 구상선수 전체가 일체로 거동하여 압괴현상을 보이는 것을 알 수 있다. 충돌방호공에 발생한 변형형상은 Fig. 4(b)에 나타난 바와 같다. 슬래브의 구속효과 때문에 전체 파일이 동일한 거동을 보이는 것을 볼 수 있다. 간이모델의 개발시 기본가정과 동일하게 소성힌지는 슬래브의 하단과 지중에서 발생한다.
3.2 간이모델해석
간이충돌모델을 검증하기위하여 정밀해석에서 수행된 충돌조건과 동일한 조건에 대하여 해석을 수행하고 두 개의 응답을 비교하였다.
충돌해석에서 방호공과 선체는 모두 가속운동을 하는 물체이므로 두 물체사이에 작용하는 힘은 관성력을 고려하여 산정되어야 한다. 본 연구에서는 검증해석의 결과에서 선체의 속도변화로부터 가속도를 구하고 이로부터 충돌중 발생하는 힘의 시간이력을 산정하였다.( Fig. 5) 이러한 방법은 기존의 연구에서 선박의 충돌력을 산정하는데 사용되었다.( Lee and Hong;2011) 다른 방법으로는 선체를 고정시키고 무질량강체를 이동시키면서 얻어지는 강체의 반력으로 충돌력을 산정할 수 있다. 선수의 반력을 포함한 방호공의 저항력의 산정에 대한 내용은 다른 논문에 상세히 서술하였다.( Lee, 2016) 충돌방호공의 저항력에서 변위에 따른 슬래브자중의 모멘트의 영향은 변위가 커질수록 증가지만 본 검증해석에서는 이와 같은 변위에 의한 모멘트의 영향은 고려하지 않았다. 간이충돌 모델에 적용하기 위한 해석매개변수들은 정밀충돌해석의 해석결과에서 얻어졌으며 Table 1에 나타난 바와 같다. 단 소성힌지간 거리산정에 있어서 소성힌지의 발생위치는 정밀해석에서 회전변형을 일으키지 않는 파일부분의 중심선을 연장하여 얻어진 교차점으로 하였다. 총 해석시간은 정밀해석결과 약 3.6초경에 충돌이 종료되므로 4초간 해석을 수행하였다. 해석도중 시간간격은 각 단계에서의 오류수준에 따라 자동적으로 조정된다.
3.3 응답비교
해석결과 얻어진 선박과 방호공의 거동을 정밀해석에서 얻어진 거동과 비교하여 그래프를 작성하였다.( Fig. 6) 간이모델에서 얻어진 선박의 충돌응답은 Fig. 6(a)에 나타내었다. 모 든 응답에서 정밀해석의 결과와 유사한 결과를 보여준다. 다만 속도응답에 있어서는 정밀해석을 기준으로 진동하는 거동을 보여 정밀해석에서는 약 3.6초 시점에서 충돌이 종료되고 반동이 일어난다. 간이모델의 결과로는 약4초경에 충돌이 종료되었다. 하지만 전반적으로 간이모델의 해석결과는 선박의 거동에 대하여 충분한 정확도를 보인다고 판단된다. 방호공의 충돌거동도 선박의 충돌거동과 유사하다. 다만 속도거동에 있어서 선박의 경우보다 진동현상이 더욱 두드러지게 나타났다. 하지만 전체적인 경향은 동일하게 나타났으며 변위거동도 충분한 정확도를 보였다.
충돌중 발생하는 에너지의 변화는 Fig. 7에 나타내었다. 충돌 시점에서 모든 에너지는 선박의 운동에너지의 형태로 존재하지만 충돌 초기에는 선수의 소성변형에 의해서 에너지가 소산되고 이후로는 방호공의 소성변형에 의하여 에너지가 주로 소산된다. 반면 방호공의 운동에너지는 충돌초기를 제외하고는 에너지 소산 거동에 큰 영향을 미치지 못한다. 간이충돌모델에 의한 선박의 에너지변화는 앞에서 언급하였던 속도거동의 진동현상에 의한 운동에너지의 진동 및 오차를 제외하고는 정밀해석의 경우와 매우 유사한 거동을 보이지만 전반적으로 간이충돌모델의 결과가 방호공의 에너지소산능력을 약간 크게 평가하는 결과를 보였다.
4. 결 론
본 연구에서는 파일형 충돌방지공이 효율적인 충돌해석을 위하여 간이충돌모델을 제안하고 이에 대한 검증해석을 수행하였다. 제안된 파일형 충돌방호공은 상부의 구속슬래브하단과 지중에 2개의 소성힌지를 가지는 것으로 모델링하였다. 이러한 조건하에 선수의 변형에 의한 비선형 거동과 방호공의 비선형 거동을 포함하는 운동방정식을 유도하였다. 유도된 운동방정식을 Runge-Kutta방법을 이용하여 수치적으로 해석하고 선박과 방호공의 거동을 산정하는 시스템을 개발하였다. 선박충돌시 발생하는 비선형거동들을 고려한 정밀충돌모델을 작성하여 해석을 수행하고 이를 개발된 간이모델에 대입하여 검증을 수행하였다. 검증결과 제시된 간이충돌해석모델은 파일형충돌방호공의 충돌거동을 적절히 모사하는 것으로 나타났다.
감사의 글
이 논문은 2010년도 정부(교육과학기술부)의 재원으로 한국연구재단의 기초연구사업 지원을 받아 수행되었으며, 이에 감사드립니다. (No.20100021227).
Fig. 1.
Simplified Collision Model. 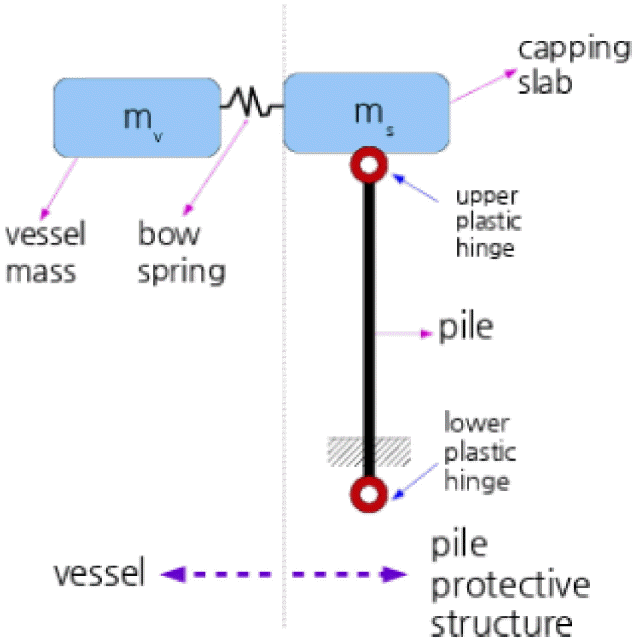
Fig. 2.
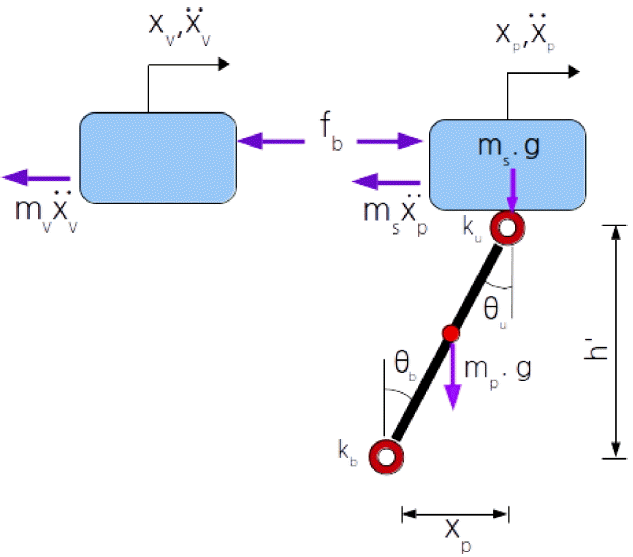
Fig. 3.
Details of Verification Model. 
Fig. 4.
Deformations after Collision. 
Fig. 5.
Force Curves Used in Simplified Analysis. 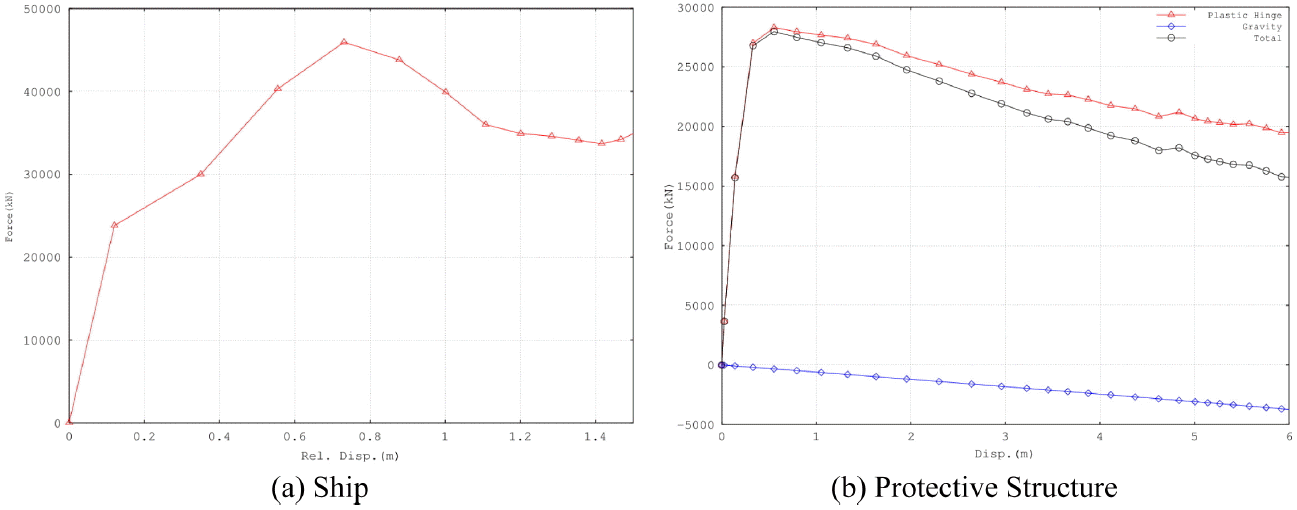
Fig. 6.
Response Comparisons between Verfication Model(RM) and Simplified Model(SM). 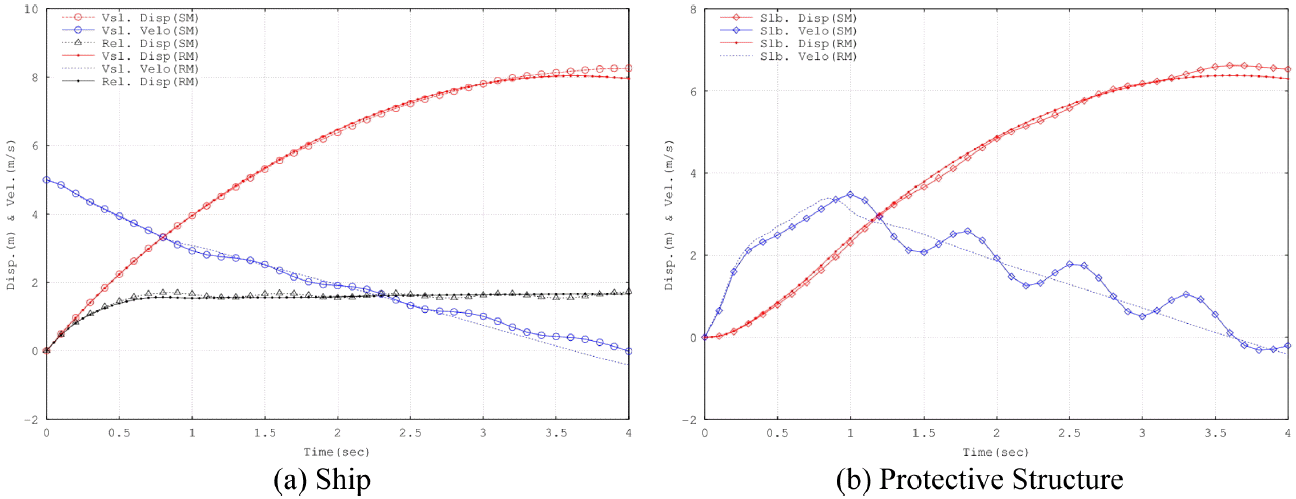
Fig. 7.
Energy Comparisons between Verification Model(RM) and Simplified Model(SM). 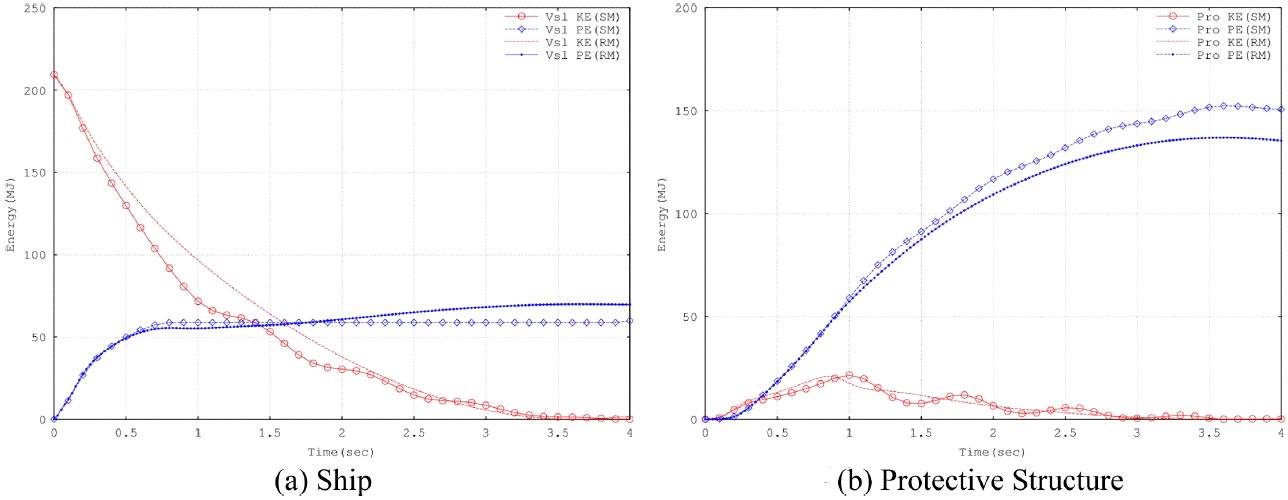
Table 1.
Parameters Used in Simplified Collision Model
|
Mass of Ship (mv) |
16748297.4 kg |
|
Mass of Capping Slab(ms) |
3542939.5 kg |
|
Mass of Piles (mp) |
394426.0 kg |
|
Distance between Plastic Hinges (hp) |
23.96 m |
|
Collision Velocity (v0) |
5 m/s |
References
ABAQUS 6.10 User Manual, Simulia,. 2010.
AASHTO LRFD Bridge Design Specifications, AASHTO. 2010.
Chang, S.P.. (2006). Design Guides of Cable Steel Bridges, Korean Society of Civil Engineers. (in Korean).
Fan, W., Yuan, W., Yang, Z., Fan, Q. (2011). Dynamic Demand of Bridge Structure Subjected to Vessel Impact Using Simplified Interaction Model Analysis and Testing of Piles for Ship Impact Defenses, ASCE Journal of Bridge Engineering, ASCE, 16(1):117-126.
Lee, G.H. (2011). A Simplified Bridge-vessel Collision Model Considering with the Rotational Motions of the Vessel, Journal of Korean Society of Civil Engineers, 31(2A):43-49 (in Korean).
Lee, G.H. (2016). A study on behaviors of pile protective structures by simplified collision model, Journal of Korean Society of Civil Engineers, in press. (in Korean).
Lee, G.H., Hong, K.Y. (2011). A Study for the Evaluation of Ship Collision Forces for the Design of Bridge Pier I: Mean Collision Force, Journal of Korean Society of Civil Engineers, 31(3A):199-206 (in Korean).
Lee, G.H., Park, J.S., Hong, K.Y. (2012). Ship Collision Behaviors of Offshore Wind Tower on Bucket Foundation, Journal of the Korea Society of Disaster Information, 8(2):138-147 (in Korean).
Patsch, A., Gerbaudo, C.F., Carlos, A.P. (2002). Analysis and Testing of Piles for Ship Impact Defenses, ASCE Journal of Bridge Engineering, ASCE, 7(A):236-244.
Sajdak, J.A.W.. (2004). Analyses of Ship Collisions: Determination of Longitudinal Extent of Damage and Penetration, PhD. Thesis, Virginia Tech.
Tabri, K. (2010). Dynamics of ship collisions, PhD. Thesis, Aalto Univ.
Zhu, B, Chen, R. P., Guo, F. J., Kong, L. G., Chen, Y. M. (2012). Large-Scale Modeling and Theoretical Investigation of Lateral Collisions on Elevated Piles, ASCE Journal of Geotechnical and Geoenvironmental Engineering, 138(4):461-471.
|
|
















