1. 서 론
극치해면고 산정방법의 대표적인 방법으로 확률분포함수를 토대로 하여 매개변수 추정을 통해 빈도별 해면고를 산정하는 방법이 있다. 그러나 이 방법은 매년 한 개 정도의 고극조위 자료만 사용하므로 자료의 낭비가 심하고 대규모 해일이 높지 않은 조위상황에서 발생한 경우 결과에 반영되지 않을 수 있다는 단점이 있다(Toro et al., 2010). 이러한 단점을 극복하기 위한 방법으로 과거사상을 비모수적 방법으로 해석하는 EST(empirical simulation technique) 기법(Scheffner et al., 1999)이 최근 널리 사용되고 있다. 여기에 부가하여 조석이 지배적인 해역에 적용가능한 방법이 제안된 바 있고(Goring et al., 2011), 국내에서도 개량된 방법이 목포해역에 적용된 바 있다(Kang et al., 2012). 이 방법은 조위조건을 토대로 한 후 태풍 및 비태풍 해일고를 독립적으로 모의하여 이들을 합산함으로써 극치해면고를 산정하는 방법이다. 이때 과거 발생했던 태풍자료를 근간으로 트레이닝세트가 구성되는데 과거자료의 한계성을 탈피하기 위해 가상태풍을 모의하여 그 결과를 트레이닝세트에 포함시켜 해석할 수 있다(Divoky and Resio, 2007). 여기서 가상태풍은 향후 발생할 수 있는 매우 큰 규모의 태풍을 대상으로 한다는 빈도개념이 결여된 다소 막연한 개념으로 설정되고 있다.
해일고와는 달리 최대풍속은 태풍조건으로부터 개략적으로 산출이 가능하며 관측자료도 풍부하다. 따라서 본 연구에서는 EST기법의 트레이닝세트에 포함되는 가상태풍 또는 설계태풍의 빈도를 설정하기 위하여 각 태풍에 의해 유발되는 최대풍속자료를 활용하고자 한다. 이를 위해 먼저 태풍에 의해 발생된 빈도별 최대풍속을 산정한 후 해당 최대풍속을 유발한 태풍환경을 역추적하여 일명 ‘표준태풍’을 생성하기 위한 매개변수를 추출한다. 즉, 빈도별 풍속과 일맥상통하는 빈도별 해일고를 발생시키는 대표적인 빈도별 태풍인 표준태풍의 매개변수를 해당지역에서 생성한다. 태풍 진행방향에 따라 몇 개 지점에서 이러한 태풍 매개변수를 설정함으로써 표준태풍의 경로와 기압강하량 등을 비롯한 제반 태풍정보를 확정하여 궁극적인 표준태풍을 확립할 수 있다. 이렇게 함으로써 EST 기법에 포함되는 가상태풍에 빈도를 설정할 수 있을 뿐 아니라 조석이 지배적이지 않은 동해안과 같은 해역에서는 표준태풍 자체를 설계태풍으로 취하여 해당 빈도의 해일 모의도 가능하게 된다.
태풍에 의해 계측된 풍속은 이벤트 성질을 띠기 때문에 연 최고풍속을 이용한 극치해석은 시행하지 않고 몬테칼로(Monte Carlo) 시뮬레이션과 같은 간접적인 방법을 통해 추정하는 것이 일반적이라고 알려져 있다(Lee et al., 2007). 태풍의 몬테칼로 시뮬레이션 방법은 Russell(1971)이 멕시코만에서 발생한 허리케인이 텍사스 연안의 해양석유시설에 미치는 영향을 파악하기 위해 처음 개발되었다. 본 연구에서도 몬테칼로 시뮬레이션을 통해 빈도별 최대풍속을 산정하고자 하는데, 국외 연구사례(Batts et al., 1980; Vickery and Twisdale, 1995)뿐 아니라 국내에서도 연구사례(Kim et al., 2005; Lee et al., 2007; Kwon and Lee, 2008)는 풍부한 편이다.
2. 자료분석
일본 기상청에서 운영하는 RSMC(Regional Specialized Meteorological Center)-Tokyo에서는 1951년 이후의 태풍정보를 최적경로자료 형태로 제공하고 있다. 본 연구에서는 이 자료 중 자료의 신뢰도 및 동질성을 감안하여 1978년 이후 자료에 대해서만 한반도에 영향을 미친 태풍 중 TY급 및 STS급 태풍을 해석대상으로 선정하였다. 인천, 군산, 목포 등 서해안 지역과 제주의 표준태풍을 설정하기 위해 해당 4개 지역 외에 이어도 지점을 추가로 분석하였다.
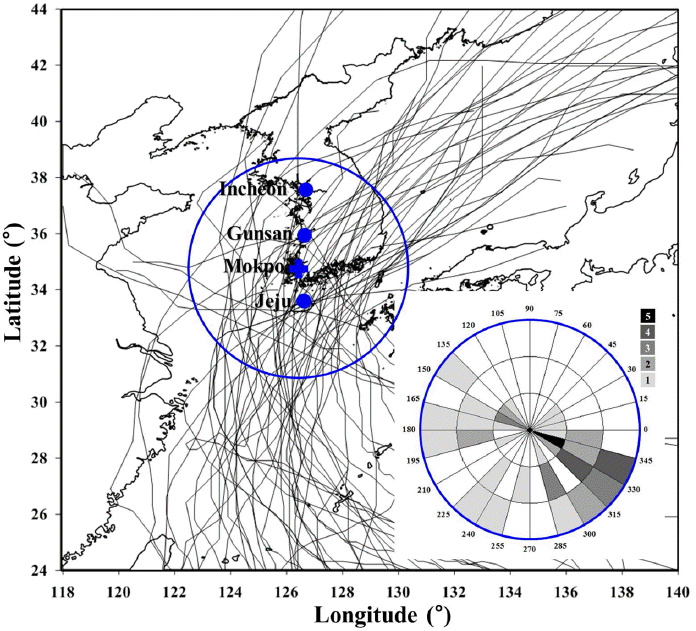
한편 몬테칼로 시뮬레이션에서 최적영향반경 설정에 관한 연구결과(Cho and Kim, 2009)에 따르면 해당 지점에서 임의의 반경을 설정한 후 여기를 통과하는 태풍을 선정하게 되는데 반경의 크기는 최소 150 km이어야 하며 300~500 km가 적절하다는 결론을 제시한 바 있다. 반경이 커질수록 다양한 태풍을 포함할 수 있다는 장점이 있는 반면 현실적으로 발생하기 어려운 태풍까지 포함하게 된다는 단점이 함께 내재되어 있다. 목포지역을 예로 들면 목포를 중심으로 500 km 이내를 지나는 태풍 중 기압강하량이 가장 큰 태풍은 MIREILLE(9119)로서 367.7 km 떨어진 최근접거리를 지날 때 940.5hPa을 기록하고 있으며 이는 목포지역에서 발생하기는 다소 비현실적인 수치이다. 따라서 본 연구에서는 이러한 비현실적인 태풍이 배제되도록 반경 300 km 이내 태풍 51개를 대상으로 하였다. 이렇게 선정된 태풍 경로를 Fig. 1에 제시하였는데 각 태풍별로 경로상에서 목포에 최근접한 위치를 기준으로 100 km 거리별, 15도 방향별 태풍수를 그림의 우하단에 함께 나타내었다. 대상 태풍 중 최근접거리가 정북쪽에서 형성된 경우는 전무하였고 가항반원인 동쪽을 통과한 태풍이 32개로 위험반원인 서쪽을 통과한 태풍수 19개보다 배 가까이 많은 것으로 나타나고 있다.
각 태풍의 해당지점 최근접시 태풍의 위경도, 중심기압, 최근접거리, Coriolis, 이동속도, 위치각 등의 매개변수는 RSMC자료를 이용하여 산정하였으며 목포지점에 대한 예를 Table 1에 제시하였다. 즉, 태풍의 위도와 경도는 목포 조위관측소와의 최근접시 좌표이며 이때 태풍의 중심과 해당지점과의 거리를 측정하여 최근접거리로 산정하였다. 중심기압 및 이동속도는 3~6시간 간격으로 발표되는 정보를 토대로 최근접거리에 위치하였을 때의 값을 내삽법으로 산정하였다. 또한 위치각은 최근접시 위치를 Fig. 1에 나타내었듯이 정동쪽을 0도로 하고 반시계방향의 각도로 설정하였다.
3. 몬테칼로 시뮬레이션
3.1 최대풍속 산정
태풍시 발생하는 풍속의 빈도를 산정하기 위해 몬테칼로 시뮬레이션을 적용하였다. 여기에는 임의로 발생되는 태풍 매개변수에 따라 풍속이 산정되는 과정이 포함되어 있는데, 최대풍속 산정을 위해 태풍의 바람장 모델인 Holland(1980) 모델을 이용하였다. 태풍의 눈에서 r만큼 떨어진 곳의 1분 평균 경고도 풍속은 다음 식 (1)과 같이 표현된다.
여기서 VT는 태풍 이동속도(translation velocity)(m/s), θ는 태풍 진행 방향을 기준으로 시계방향의 관심지점 사이의 각도(o), r0는 최대풍속반경(radius to maximum wind; RMW)(km), ∆p(=p∞–pc)는 기압차(pressure deficit)(hPa), p∞와 pc는 각각 태풍 영향권 밖의 기압(≒1013hPa)과 중심기압, f는 코리올리 파라메타, ρ는 공기밀도이다. B는 태풍 프로파일의 형상을 결정하는 파라메타로 대략 1<B<2.5의 범위에 있으며, 식 (2)와 같은 Vickery et al.(2000)이 제안한 식을 이용하여 산정하였다.
최대풍속반경 산정식은 Graham and Nunn(1959)이 제시한 식을 비롯하여 Vickery et al.(2000), Powell et al.(2005), Willoughby et al.(2006) 등 다양한 식이 제안되고 있다. 이러한 식들은 대부분 북대서양에서 발생한 허리케인에 대하여 유도된 식으로 중심기압과 위도 등의 함수로 최대풍속반경이 산정되고 있다. 이외에 국내에서 Kang et al.(2002)이 제안한 식은 다음 식 (3)과 같이 중심기압만의 함수로 제시되고 있다. 최대풍속반경은 태풍의 공간적 풍속분포를 결정하게 되므로 태풍 또는 해일 모의시 매우 중요한 매개변수이지만 본 연구의 주관심사가 태풍의 실제적 모의에 있지 않으므로 최대풍속반경이 얼마인지는 크게 중요하지 않게 된다. 오히려 식 (1)에서 볼 수 있는 바와 같이 태풍중심에서 관심지역 사이의 거리(r)가 최대풍속반경(r0)에 얼마나 근접한지가 훨씬 중요한 요소이므로 본 연구에서는 국내 환경이 반영된 식 (3)을 채택하였다.
한편 식 (1)을 사용하여 추정한 풍속은 경고도에서의 값이고 구조물 설계를 위해서는 해수면 10 m에서의 풍속 Vs,10으로 변환해야 한다. 본 연구에서는 Kwon and Lee(2008)가 채택한 방식과 동일하게 다음 식 (4)(Vickery and Twisdale, 1995)를 사용하였다. 이때 1분 평균과 10분 평균 풍속의 비율은 1.18을 사용(Batts et al., 1980)하였다.
3.2 매개변수 산정
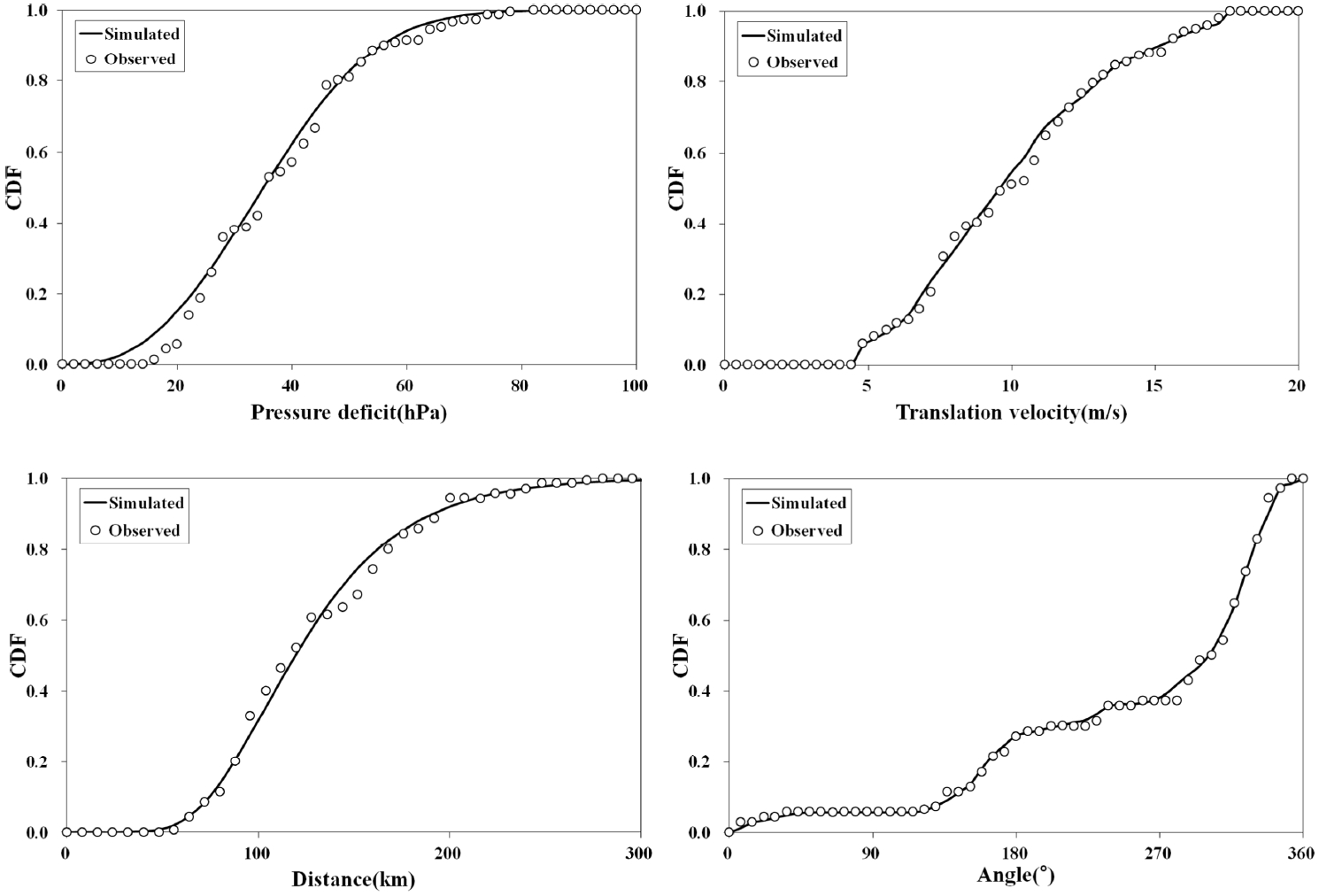
풍속 산정식인 식 (1)의 적용을 위해 태풍 매개변수가 산정되어야 하는데, 각 매개변수에 적합한 확률분포함수를 설정한 후 임의로 발생시킨 매개변수 세트가 구성된다. 매개변수별 확률분포함수는 Kwon and Lee(2008)에 정리되어 있는 유사 연구들을 참고하여 선정하였으며 Table 1을 토대로 매개변수가 산정된다. 선정된 확률분포함수 및 산정된 매개변수값과 함께 확률분포함수의 적합도 검정결과를 Table 2에 제시하였다. Chi-square검정을 비롯한 4가지 검정결과 5% 유의수준에서 모두 통과하고 있어 모든 매개변수에서 채택한 각 확률분포함수가 적합한 것으로 나타나고 있고 Fig. 2에 도시된 누가분포함수 역시 검정결과와 일맥상통하고 있음을 보이고 있다.
이와 같이 산정된 확률변수값을 이용하여 Monte-Carlo 시뮬레이션을 반복하여 설계풍속을 산정하였다. 시뮬레이션에 의하여 구한 풍속을 크기순으로 정렬하면 i번째 풍속(Vi)에 해당하는 재현기간(N)은 다음 식 (5)와 같이 산정된다(Kim et al., 2005; Kwon and Lee,2008).
여기서 m은 생성된 풍속의 총 개수이고 nrate는 연간 태풍 내습 횟수이다. Kwon and Lee(2008)에 따르면 적절한 반복횟수는 50,000회 이상으로 제안되고 있어 본 연구에서는 100,000회의 시뮬레이션을 시행하였다.
3.3 빈도별 풍속
식 (4)와 식 (5)로부터 재현기간별 최대풍속을 산정할 수 있으며 목포와 동일한 방법으로 인천, 군산, 그리고 제주지역까지 포함한 100년 빈도 풍속을 타연구결과와 함께 Table 3에 제시하였다. 여기서 Ko et al.(2014)의 결과는 목포와 군산 및 제주 등이 외해쪽으로 멀리 이격되어 있는 해상에 위치한 곳인 동시에 100 m 상공에서의 값으로 제시되어 있어 본 연구결과에 비해 상당히 크게 산정되는 것으로 파악되고 있다. 다른 두 연구결과와 비교해 보면 본 연구결과가 중간 정도의 값을 보이고 있어 전반적으로 잘 일치하고 있다고 평가된다. 특히 Kim and Ha(2004)를 제외하고 제주-목포-군산-인천 순(Fig. 1의 위치 참조)으로 풍속이 작게 산정되고 있음을 볼 수 있는데, 북쪽에 위치할수록 풍속이 약해지는 것으로 나타나는 것은 Table 1에 제시된 대상태풍의 최근접시 중심기압이 북쪽으로 갈수록 약화되는 것과 일맥상통한 결과로 해석된다. 이러한 경향은 함께 제시한 50년 빈도 및 200년 빈도 결과에서도 확인할 수 있다.
3.4 민감도 분석
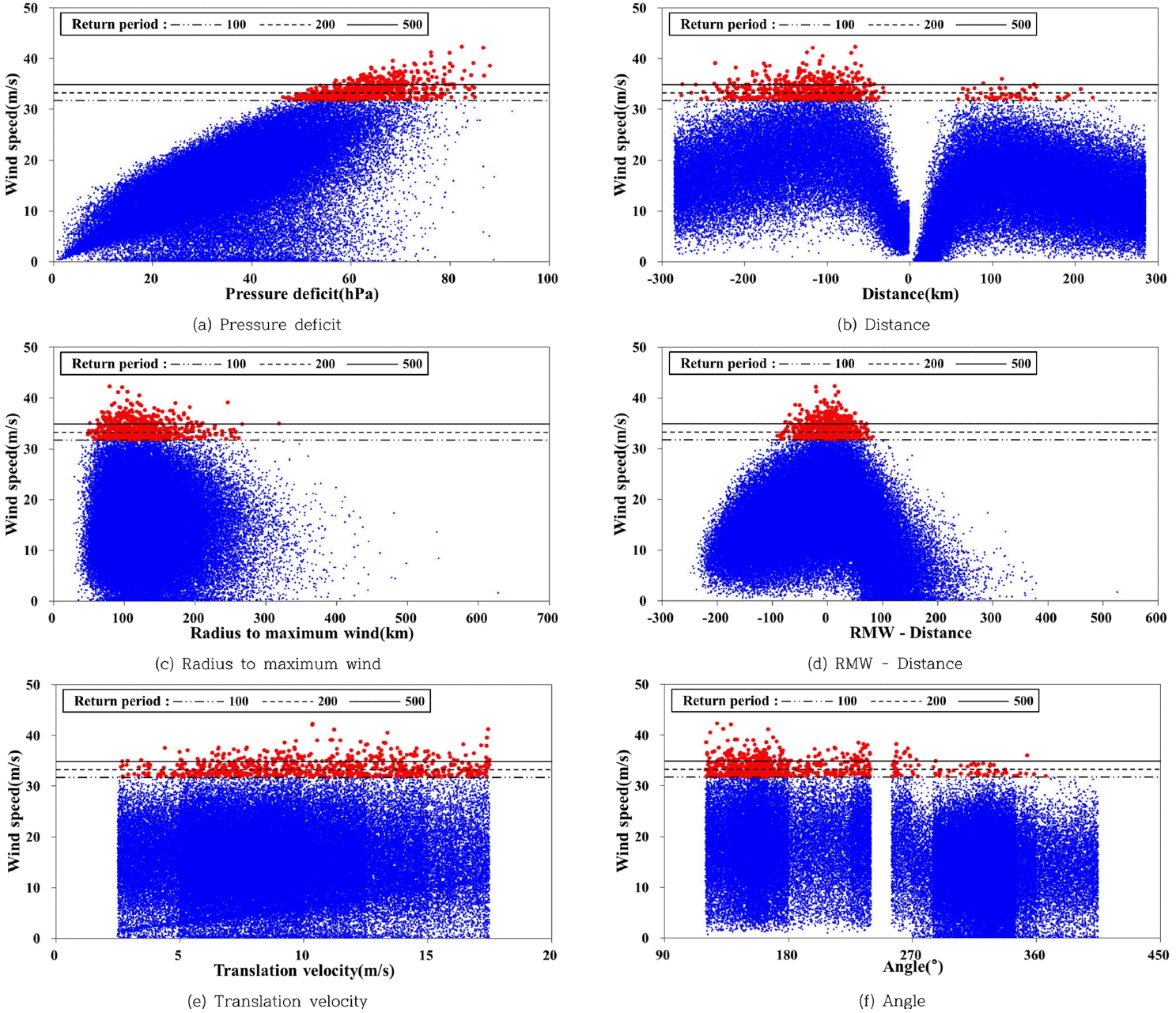
각 매개변수가 풍속에 미치는 영향성 분석을 위하여 목포지역의 매개변수에 따른 풍속의 분포를 Fig. 3에 도시하였다. Fig. 3(a)의 기압강하량이 커질수록 풍속이 크게 산정되는 경향을 보이고 있으며, Fig. 3(b)의 최근접거리(r)는 최대풍속반경(r0)이 위치한 지점 부근에서 빠른 풍속을 보이고 있는데 Fig. 1의 위치각에 따라 위험반원과 가항반원으로 구분되어 음(-)의 값으로 표시된 위험반원에서 더욱 큰 풍속을 보이고 있다. 식 (3)에 제시된 최대풍속반경에 의한 결과는 Fig. 3(c)와 같은데, 최대풍속반경 자체보다 Fig. 3(d)에 보인 바와 같이 태풍중심과의 거리(r)와 최대풍속반경(r0)과의 차이에 의한 풍속 영향성이 더욱 크게 나타나고 있다. Fig. 3(e)의 이동속도의 경우 식 (1)에 보인 바와 같이 이동속도가 빠를수록 최대풍속은 크게 나타나는 경향이 미미하게 나타나고 있다. Fig. 3(f)의 위치각에 의한 풍속 영향성은 270o를 전후로 설정되는 가항반원 및 위험반원 구분에 따른 영향은 크게 나타나고 있지만, 많은 모의가 이루어지는 구간에서 그에 비례하여 큰 풍속값이 많이 발생함을 감안하면 동일 반원에서 풍속 영향성은 크지 않은 것으로 평가된다.
표준태풍을 설정하기 위해서는 민감한 매개변수 순으로 먼저 결정되어야 하므로 매개변수별로 풍속에 미치는 상대적 영향성을 정량화하여야 하는데 대표적인 방법으로 매개변수 변화에 따른 풍속변화에 대한 상관계수를 산정하는 방법이 있다. Fig. 3(a)에 보인 기압강하량의 경우 상관계수가 0.64로 풍속과의 상관성이 선형적으로 뚜렷하게 보이고 있는 반면 여타 매개변수에서는 상관성이 옅거나 비선형적 상관성을 보이고 있다. 특히 Fig. 3(b)의 최근접거리는 Fig. 1의 위치각에 따라 위험반원과 가항반원으로 구분된 상태에서 풍속과의 비선형 상관성이 분명해 보이지만 상관계수로 정량화시키기에는 한계가 있다.
또 다른 방법으로 기준 매개변수 세트를 설정한 후 매개변수 변화에 따른 풍속의 변화를 정량적으로 산정하는 방법이 있다. 즉, 매개변수별 평균치를 기준매개변수 세트로 구성하여 풍속을 구한 후 평균치로부터 표준편차만큼 증감시킨 매개변수 값에 의한 풍속과의 비를 산정함으로써 민감도를 정량화할 수 있다. 정량화된 민감도분석 결과를 각 매개변수의 기준치인 평균과 표준편차, 그리고 기준 매개변수에 따른 풍속과 함께 Table 4에 제시하였다. 기압강하량의 민감도 비율이 1.25 및 0.71로 단연 민감한 매개변수로 나타나고 있음을 볼 수 있는 반면 최대풍반경과 최근접거리의 경우 기준 매개변수에서 표준편차만큼 증감된 경우 민감도 비율이 모두 1보다 작은 값을 보이고 있어 매개변수 변화에 따른 민감도를 정량화시키기에는 한계가 있음을 시사하고 있다.
따라서 본 연구에서는 Fig. 3의 각 매개변수별로 해당 매개변수가 풍속 크기에 민감한지 여부를 다음 식 (6)을 통해 정량적으로 비교 평가하였다. 즉, 식 (6)과 같이 분산의 비로 정의되는 집중도(C)라 명명한 값이 작을수록 해당 매개변수가 한정된 좁은 범위에서 큰 풍속을 유발하는 반면 1에 가까울수록 고빈도 풍속이 해당 매개변수에 둔감한 것으로 평가된다.
여기서
σ 2 σ t 2
집중도를 산정하기 위한 한계풍속으로 Fig.3에 보인 바와 같이 100년 빈도 풍속을 적용하여 100년 빈도 이상의 풍속자료는 진하게 나타내었다. 산정된 집중도를 Table 5에 제시하였는데, 최근접거리(0.31) 및 최대풍반경(0.70) 자체보다 그 차이값(0.11)이 가장 민감한 것으로 나타나고 있다. 위치각(0.33)은 위험반원과 가항반원의 구분에 기인하여 민감한 편으로 나타나고 있으며 기압강하량(0.35) 역시 민감하게 나타나고 있다. 이동속도(1.17)는 둔감한 매개변수로 나타나고 있지만 이 값이 커질수록 최대풍속이 크게 나타나는 경향이 미약하게 보이고 있다.
4. 표준태풍
4.1 매개변수 설정
본 연구에서 추구하는 목표는 임의의 지역에서 특정 재현 기간별 풍속 산정과 함께 해당 풍속을 발생시키는 평균적인 태풍을 설정하는 것이다. 이를 표준태풍이라 명명하였고 설정된 태풍에 대하여 해일모의를 통해 빈도별 해일고까지 산정할 수 있으며, 더 나아가 EST기법에 가상태풍으로 반영할 수 있게 된다. 이를 위해 우선 200년 빈도의 표준태풍에 대한 매개변수를 다음과 같이 민감한 매개변수 순으로 설정하였다.
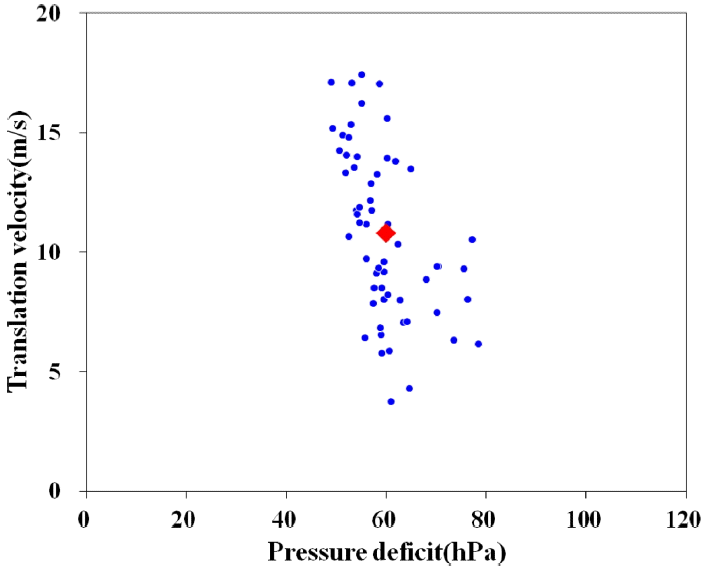
Table 5에 보인 바와 같이 최근접거리와 최대풍반경의 차이가 가장 민감하며 위치각과 중심기압차 순으로 민감한 매개변수로 나타나고 있는 반면 이동속도는 둔감한 것으로 나타나고 있다. 따라서 최근접거리와 최대풍반경의 관계를 먼저 설정한 후 여타 매개변수를 순차적으로 설정하여 표준태풍을 생성하고자 한다. 전술하였듯이 최근접거리는 최대풍반경에 근접할수록 풍속이 증가함은 자명한 사실이다. 본 연구의 목적이 예보에 있지 않으므로 우선 최근접거리가 최대풍반경과 일치할 경우를 표준태풍의 첫 번째 조건으로 선택하였다. 이때 위치각의 민감도를 반영하여 최근접거리는 위치각이 90도~270도 사이에 있는 위험반원에 해당하면서 최대풍반경과 일치하도록 선정한다. 10만번 모의된 태풍사상 중 200년 빈도 풍속에 근사(32.8~33.8 m/sec)하면서 위험반원에 해당하는 동시에 최근접거리와 최대풍반경과의 비율이 0.9~1.1범위에 해당하는 경우는 총 58번 발생하였으며 이들이 표준태풍의 압축된 후보군으로 선별된다. 이들로부터 민감도분석결과를 감안하여 기압강하량과 이동속도를 산정하여야 하는데 58개 사상별 기압강하량과 이동속도를 Fig. 4에 제시하였다. 기압강하량의 경우 50~80 hPa 사이에 집중적으로 분포하고 있으며 이동속도의 경우 전체 범위에 산재하고 있으며 양 매개변수는 미약하게 반비례하는 경향을 보이고 있다. 따라서 평균적인 200년 빈도 표준태풍은 Fig. 4에 나타낸 (◆)로 표시된 중앙부에 위치하는 매개변수 세트를 선택함으로써 Table 6과 같이 설정하였다. 목포(MP) 외에 인천(IC), 군산(GS), 제주(JJ), 이어도(IED) 역시 동일한 방법으로 설정할 수 있으며 200년 빈도 결과를 100년 빈도 결과와 함께 Table 6에 제시하였다.
4.2 경로 및 기압강하량 설정
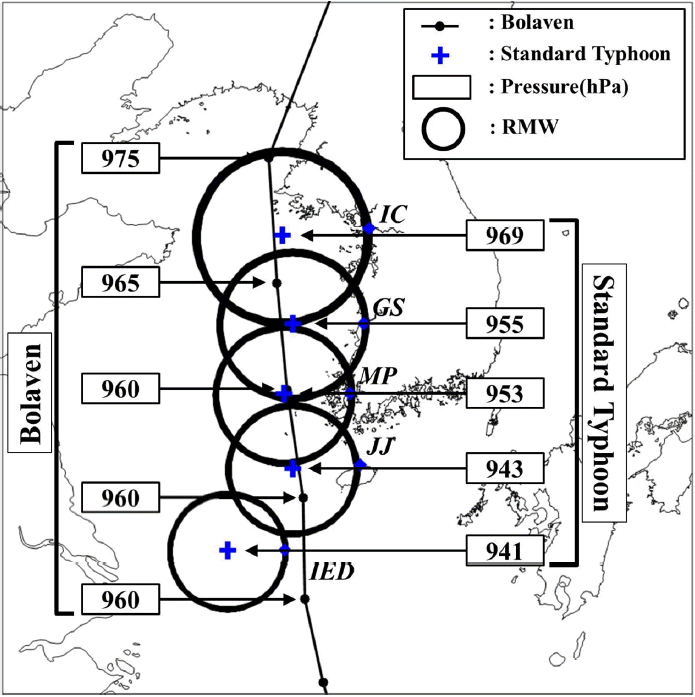
목포 지역에 해당하는 표준태풍 제원은 Table 6에 제시된 바와 같이 설정될 수 있는데, 이는 태풍경로상에서 목포에 최근접하는 1개 지점의 정보에 불과하므로 태풍에 의한 해일의 수치모의 등에 활용하기 위해서는 태풍경로상의 추가적인 조건이 요구된다. Table 6에 제시된 바와 같이 목포 뿐 아니라 인천, 군산, 제주 등지에서 태풍이 최근접하는 상황에 대한 정보, 즉 최대풍속, 최대풍반경, 기압강하량, 이동속도 등의 매개변수를 추가적으로 설정하였다. 이러한 정보를 태풍진행 방향으로 순차적으로 설정함으로써 표준태풍을 완성할 수 있는데, 제주 이남에서의 기압강하량을 산정하기 위하여 국내 최남단인 이어도에서의 분석을 추가하여 동일 위도의 표준태풍에 반영하였다. 이렇게 설정된 서해안을 통과하는 200년 빈도 표준태풍의 경로와 기압변화상을 Fig. 5에 도시하였다.
제시된 결과에 따르면 인천, 군산, 목포 등 서해안 주요도시에 대한 해석으로부터 설정된 표준태풍의 경로는 Fig. 5에 보인 바와 같이 태풍 Bolaven(1215)의 경로와 매우 유사하게 나타나고 있음을 보여주고 있다. 태풍 Bolaven(1215)에 비해 중심기압이 낮게 형성되고 있으며 북쪽에 위치한 지점일수록 태풍의 세력이 약화되어 Table 6에 제시된 바와 같이 기압강하량과 최대풍속이 감소하는 반면 최대풍반경은 증가하고 있음을 보이고 있다.
이러한 표준태풍에 대하여 해일모의를 수행함으로써 표준태풍으로 야기되는 빈도별 해일고 역시 산출할 수 있으며 이는 해당빈도 풍속과 일맥상통하는 의미를 갖게 된다. 더 나아가 극치해면고 산정과 관련된 EST기법에 있어 가상태풍의 빈도설정에도 활용될 수 있다.
4.3 가항반원
4.1절에 기술한 바와 같이 Fig. 3(b)의 왼쪽인 음(-)의 최근접거리인 경우는 태풍중심의 위치가 해당지점(목포)의 서측으로서 해당지점에서의 진행속도와 풍속이 동일 방향인 위험 반원인 경우이다. 반면 그림의 우측인 양(+)의 최근접거리인 경우는 태풍중심이 동측으로서 가항반원에 해당하는 경우이다. Fig. 1에 보인 바와 같이 목포의 경우 가항반원을 통과하는 태풍이 2배 가까이 많지만 위험반원의 최고풍속이 더욱 크게 산정되고 있음을 볼 수 있다. 한편 Kang(2015)이 지적했듯이 서해안 지점에서는 동측으로 통과하는 남해안 상륙 태풍의 경우 set-down에 의한 음의 해일고가 발생할 수 있다. 따라서 동측으로 통과하는 태풍만을 대상으로 동일한 해석을 통해 저극조위 산정의 기초로서 음의 해일고가 유발되는 최대풍속 산정 역시 가능하다.
5. 결론 및 제언
몬테칼로 시뮬레이션을 이용하여 서해안 4개 지점에서 빈도별 풍속을 산정한 결과 Kwon and Lee(2008) 등 타연구와 유사한 결과를 도출하였다. 또한 풍속에 미치는 상대적인 영향성을 파악하기 위하여 Holland(1980) 모델의 매개변수별 민감도 역시 분석하였다. 최근접거리가 최대풍반경에 얼마나 가까운지가 최대풍속 산정에 가장 민감한 매개변수임을 보이고 있고 기압강하량 역시 매우 민감한 것으로 나타나고 있는 반면 이동속도와 위치각은 둔감한 결과를 보이고 있다. 특히 위치각은 위험반원과 가항반원으로 구분된 상태에서 동일 반원에서는 최대풍속에 미치는 영향이 크지 않았다.
이를 토대로 빈도별 풍속을 야기하는 평균적인 태풍상황을 의미하는 표준태풍을 생성할 수 있었다. 즉, 위험반원에 해당하고 최근접거리가 최대풍반경에 근접한 상태의 빈도별 최대풍속을 초래하는 매개변수 세트 중에서 기압강하량과 이동속도의 평균값을 선정함으로써 특정지점에서 최근접한 상태의 표준태풍을 설정할 수 있다. 서해안에 연한 인천, 군산, 목포, 제주 등지에서 각각 이러한 해석을 동일하게 수행함으로써 표준태풍의 경로와 기압변화상 등을 확정지을 수 있다.
이렇게 만들어진 표준태풍을 태풍-해일 모의가 가능한 해수유동 수치모형에 적용하게 되면 풍속의 빈도와 일맥상통하는 해일고를 산정할 수 있게 되며 이는 EST 방법의 트레이닝세트의 가상태풍 설정에 활용될 수 있을 뿐 아니라 극치해면고 산정을 위한 설계태풍으로도 활용될 수 있다. 또한 가항반원에 해당하는 자료만을 대상으로 해석하게 되면 서해안 지역에서 음의 해일고를 유발하는 빈도별 최대풍속을 산정할 수 있으며, 해당 빈도의 표준태풍 역시 생성할 수 있다.
그러나 본 연구에서 채택한 방법 역시 1978년부터 30여년 자료로부터 산정된 결과이므로 고빈도 예측값을 산정하기에는 자료의 비정상성과 불확실성에 대한 담보는 부족한 상황이며, 특히 지구온난화 등에 기인한 미래 태풍의 강도변화는 간과되고 있는 실정이어서 기후변화 등에 따른 영향성이 보완되어야 하며 이는 추후 연구과제로 남겨둔다.