정상흐름 하에서 스포일러 부착형 해저파이프라인의 자가매설 기구에 관한 수치해석
요약
본 연구에서는 정상흐름 하에서 스포일러가 부착된 해저파이프라인의 자가매설 기구를 분석하기 위하여 유체역학적 특성을 고정도로 해석할 수 있는 Navier-Stokes Solver(LES-WASS-2D)를 이용하였다. 본 논문에서 적용하는 수치모형의 타당성 및 유효성을 확보하기 위하여 기존의 스포일러 유무에 따른 파이프라인 주변의 흐름특성을 나타낸 수리모형실험결과와 비교·분석하였다. 그리고 입사유속, 스포일러의 제원 및 배치에 따른 파이프라인 주변의 수리특성(유동, 와동, 압력)과 작용력 특성을 수치적으로 분석하였다. 그 결과 1차적으로 해저파이프에 스포일러가 부착된 경우에 투영면적이 증가함으로 인하여 배후로 빠져나가는 유속이 커지고, 동시에 배후에서 발생하는 후류에 기인한 강한 와동이 발생한다. 그리고 2차적으로는 스포일러의 영향으로 상하 비대칭적인 유동 및 와동장이 발생하고, 이로 인해 비대칭적인 압력장이 형성된다. 이것은 파이프에 작용하는 힘의 비대칭성을 증가시켜 하향의 유체력을 크게 발달시킨다. 이와 같은 두 가지의 큰 원인으로 인하여 스포일러 부착형 해저파이프라인이 자가매설 되는 것으로 이해된다.
핵심용어: 스포일러 부착형 해저파이프라인, 자가매설 기구, 정상흐름, 유체력, Navier-Stokes 방정식 모형
Abstract
This study used Navier-Stokes Solver(LES-WASS-2D) for analyzing hydrodynamic characteristics with high order in order to analyze self-burial mechanism of pipeline with spoiler under steady flow. For the validity and effectiveness of numerical model used, it was compared and analyzed with the experiment to show flow characteristics around the pipeline with and without the spoiler. And the hydraulic(flow, vortex, and pressure) and force characteristics were numerically analyzed around the pipeline according to the incident velocity, and shape and arrangement of spoiler. Primarily, if the spoiler is attached to the pipeline, the projected area is increased resulting in higher flow velocity toward the back and strong vortex caused by wake stream in the back. Secondly, the spoiler causes vertically asymmetric flow and vorticity fields and thus asymmetric pressure field. It increases the asymmetry of force on the pipe and thus develops large downward fluid force. Both of them are the causes of selfburying of the pipeline with spoiler.
Keywords: submarine pipeline with spoiler, self-burial mechanism, steady flow, fluid force, Navier-Stokes solver
1. 서 론
과거부터 여러 나라에서 해양자원에 대해 많은 관심을 가지고 있으나, 기술력 및 자본이 부족하여 쉽사리 개발에 나서지 못하고 있다. 일부에서는 선진국을 주축으로 이미 해양 자원을 개발하여 채굴하고 있으나, 대륙붕의 범위에서 주로 석유 또는 천연가스를 채굴하는데 그치고 있는 실정이다. 한편 머지않은 미래에 육지에 매장된 자원은 고갈될 것이고, 자원에 대한 가격폭등 하는 것은 누구나가 예견할 수 있는 일이다. 이에 세계 각국에서는 해양자원에 대한 관심을 가지고 있을 뿐만 아니라 실제 해양자원 개발에 나서는 나라들이 많아지고 있다.
해양자원의 개발이 활발해질 경우, 해양에서 채굴한 자원을 육지로 이송하는데 선박이용에는 한계가 있다. 따라서 저렴하면서도 안정적으로 자원을 운반할 수 있는 해저파이프라인의 이용이 증가할 것으로 예상된다. 이 해저파이프라인은 해양에서 생산되는 자원을 육지로 수송하거나, 필요로 하는 인접한 나라에 직접 수출할 수 있는 물류망으로 활용될 수 있다. 그리고 정보의 이동전달수단으로 이용되고 있는 국제적 네트워크가 거의 대부분 해저케이블로 연결되어 있으며, 이것 역시 하나의 해저파이프라인으로 볼 수 있다.
안정적으로 해저파이프라인의 기능을 수행하기 위해서는 파이프 자체가 구조적으로 안정해야 할 뿐만 아니라, 다양한 해양외력(파랑, 조류, 해류 등)으로부터 안전하게 보호되어야 한다. 특히 Fig. 1 (a)와 같이 파이프라인 저면에 세굴이 발생하게 되면, 파이프의 자중과 유체력에 의해 접지부분에서는 응력이 집중되고, 나머지 부분에서도 인장 또는 압축응력을 받게 되어 Fig. 2 (b), (c)와 같은 피해가 발생할 수 있다. 파이프라인 저면의 세굴을 방지하기 위한 여러 가지 세굴방지공법이 적용되고 있다. 대표적인 세굴방지공법은 크게 두 분류로 나누어질 수 있으며, 트렌칭백필링(trenching and backfilling)에 의한 매설방식 그리고 콘크리트 덮개나 보호블록을 이용하는 피복형인 비매설 방식이 있다. 일반적으로 이상과 같은 세굴방지공법을 적용하게 되면, 시간과 공간적 제약을 받을 뿐만 아니라, 추가적인 유지보수비용이 발생하게 된다. 한편 ( Hulsbergen(1984)에 의해서 추가적인 세굴방지공법의 적용 없이 파이프가 스스로 매설되는 스포일러 부착형 파이프라인을 고안하였다. 이것은 파이프라인 상단부에 물고기의 등지느러미 형상의 핀(fin)이 부착되는 구조로서 1989년 Submarine Pipeline Spoiler 사에 의해 북해에 처음으로 설치되었다( Hulsbergen and Bijiker, 1989). 최근 중국 항저우만에도 스포일러를 부착한 해저파이프라인이 설치되었다. 이 자가매설형 해저파이프라인은 상단에 스포일러를 부착하여 저면의 세굴현상을 촉진시켜, 단기간에 스스로 매설되어 파이프의 안정성을 확보하게 된다. 이 방식은 특별한 세굴방지공법이 필요하지 않으며, 유지보수도 거의 발생하지 않기 때문에 시간과 비용을 절약할 수 있는 장점이 있다. 하지만 해저 지반이 점성토 또는 사질토로 구성된 특정한 환경에만 자가매설 효과를 나타나는 단점을 가지고 있기도 하다. 스포일러 부착형 파이프라인이 개발/설치된 후에 대부분의 연구들은 스포일러에 의한 파이프 주변의 세굴 특성에 대해 논의하고 있다. 대표적인 예로서 Chiew (1993)는 수리모형실험을 통하여 파랑작용 하에서 스포일러 유무에 따른 파이프저면을 빠져나가는 흐름에 의한 국부세굴 특성을 조사하였으며, 스포일러에 영향으로 저면의 세굴이 심화되는 것을 확인하였다.
Zhao et al.(2009)는 FLUENT모형을 활용한 해석결과에서는 흐름장의 유속이 커질수록 해저면에 작용하는 전단응력이 증가하였으나, 스포일러 길이변화에 대한 전단응력은 큰 차이를 나타내지 않았다. Yang et al.(2012)는 실험적 연구를 통하여 레이놀즈수 및 스포일러 길이가 커질수록 세굴심이 증가한다고 보고하였으며, 이것을 토대로 세굴심에 관한 경험식을 제안하였다. Zhu et al.(2013)이 수행한 RANS모형의 계산결과는 스포일러 길이와 해저파이프가 바닥으로부터 떨어진 거리에 따라 파이프 주변의 유동장은 매우 민감하게 반응하고, 스포일러 길이가 길수록, 파이프가 바닥에 가까울수록 자가매설에 용이하다고 나타내었다. 유동/와동특성에 대해서는 Cheng and Chew(2003)가 Navier-Stokes 방정식 모형을 이용하여 전반적인 수리특성(유동장, 와동장, 압력장 등)을 검토하여 스포일러의 효과에 대하여 논의하였다. Oner(2010)은 PIV시스템을 적용한 수리모형실험을 통하여 레이놀즈수 변화에 따른 스포일러 부착형 해저파이프라인 주면의 흐름장을 면밀히 분석하였다. Han(2012)은 유연한 재질을 스포일러를 고려한 수리모형실험을 수행하였으며, 스포일러 길이가 길어질수록 세굴심이 증가함과 더불어 자가매설이 용의해진다고 보고하였다. 스포일러 부착형 파이프 주변의 압력장 및 작용하는 힘에 대해서는 Barendse(1988)는 실험적 연구를 통하여 다양한 해양외력조건(파랑, 흐름, 파랑-흐름 상호작용) 하에서 스포일러 부착형 해저파이프라인에 작용하는 유체력을 추정하기 위하여 항력계수에 대한 고찰을 수행하였다. Cheng and Chew(2003)는 스포일러 길이가 증가할수록 root mean square(RMS) 수직력이 크게 증가하여 파이프라인의 자가매설이 용이한 하강력이 발생한다고 수치적으로 분석하였다. Bakhtiary and Zeinali(2008)는 RANS모형을 활용하여 파이프에 작용하는 항력 및 양력을 산정하고, 입사유속과의 관계를 통하여 항력계수 및 양력계수를 추정하였다.
이상의 각각의 연구결과를 종합적으로 분석하면, 먼저 해저파이프에 스포일러를 부착할 경우에 유동/와동/압력장이 급격히 변화하게 된다. 그 영향으로 인하여 파이프 저면에서는 세굴이 가속화되고, 파이프라인에는 하강력이 작용하는 것으로 분석된다. 이 현상들이 복합적으로 작용하여 스포일러 부착형 해저파이프라인이 자가매설 되는 것으로 이해된다. 이 일련의 자가매설 과정 및 기구를 명확하게 분석한 결과는 찾아볼 수 없다.
본 연구에서는 스포일러가 부착된 파이프라인의 자가매설 원리를 분석하기 위하여 Navier-Stokes(N-S) solver를 이용한 고정도의 수치모의를 수행한다. 먼저 스포일러 유무에 따른 파이프라인 주변의 수리특성(유동장, 와동장, 압력장 등)을 분석한 후, 파이프라인에 직접적으로 작용하는 유체력을 산정한다. 이 수치해석결과를 토대로 스포일러 부착에 의한 해저파이프라인 주변의 수리특성을 분석하고, 자가매설 기구에 대하여 심도 깊게 논의한다. 나아가 스포일러에 제원 및 배치에 따른 수치시뮬레이션을 수행하여 자가매설이 용이한 스포일러의 제원 및 배치를 검토하는 것을 본 연구의 목적으로 하고 있다.
2. 수치모형의 개요
본 연구에서는 스포일러 부착형 해저파이프라인의 자가매설 기구를 분석하기 위하여 수치시뮬레이션을 실시한다. 이 수치시뮬레이션은 Hur et al.(2011)이 개발한 단면 2차원 유체역학적 모형 LES-WASS-2D를 적용한다. LES-WASS-2D는 porous body model(PBM) 기반의 단면 N-S solver로서 투수매체에 유체저항(관성, 난류, 층류)을 직접 계산하여 투수매체의 특성(입경, 공극, 형상 등)에 따른 에너지소산을 고려할 수 있다. 아격자 스케일의 난류현상까지 구현하기 위하여 large eddy simulation(LES)기법을 이용하고 있다. 한편 본 연구에서 이용하는 LES-WASS-2D는 유한차분법을 기반으로 이산화한 수치모형임으로 직각좌표체계를 가진다. 그러므로 원형 해저파이프를 구성하는 것에 있어서 계단식 격자처리로 인하여 왜곡현상이 발생하게 된다. 이 현상을 최대한 보완하기 위하여 Hur et al.(2008)이 제안한 경사면처리기법을 적용하여 원형에 가까운 다각형으로 해저파이프를 구성한다.
2.1 수치모형(LES-WASS-2D)
2.1.1 지배방정식
기초방정식은 단면 2차원 비압축성·점성유체에서 무반사로 흐름과 파랑을 발생시킬 수 있는 소스항이 포함된 연속방정식 (1) 그리고 다공질 내에서의 유체저항(관성/난류/층류)항을 도입하여 수정된 Navier-Stokes 운동량 방정식 (2)로 구성된다.
여기서 νi는 x, z방향의 유속, q∗는 소스의 유량밀도, γv는 체적 공극률, γi는 x, z방향의 면적 공극률, t는 시간, ρ는 유체의 밀도, p는 압력, νT는 유체의 동점성계수(ν)와 와동점성계수(νt)의 합이다. Dij=12∂vi∂Xj+∂vj∂Xi 는 변형률속도텐서, Si는 CSF모형을 기반의 표면장력항, Qi는 흐름 또는 파랑의 소스항, Ri는 투과성 매체에 의한 유체저항항, gi는 중력가속도항, Ei는 에너지 감쇠항이다.
VOF함수 F는 각 격자에서 유체가 차지하고 있는 체적비율로서 연속방정식 (1)에 비압축성 유체에 대한 가정과 PBM에 기초한 VOF함수를 적용하여 유체의 보존형식으로 나타내면 식 (3)과 같다.
2.1.2 흐름생성
LES-WASS-2D는 엇갈림 격자체계(staggered mesh system)로 구성되며, 식 (4)와 같이 흐름소스셀의 격자크기(Δxs)에 따른 유량밀도(q∗)를 지배방정식 (1)-(3)에 대입한다. 따라서 목표 흐름을 정확하게 생성할 수 있을 뿐만 아니라, 흐름소스에 의한 유동장의 교란을 배제할 수 있다.
여기서 Vc는 입사흐름의 유속, xs는 소스셀을 의미하며, 나머지 셀(x≠xs)에서는 유량밀도(q∗)가 0으로 주어진다.
2.1.3 안정조건
본 연구에서는 수치계산의 안정성을 확보하기 위하여 이류항으로부터 생기는 courant-friedrichs-lewy(CFL)조건과 확산항으로부터 생기는 확산불안정(diffusive time limit), DTL조건을 이용한다. 먼저 CFL조건은 식 (5)의 수가 만족되어야 한다.
여기서 vi는 x, z방향의 유속 그리고 Δxi는 x, z방향의 격자크기이다.
CFL수가 1보다 작을 경우에 수치계산의 안정성이 확보될 수 있다. 이것은 1회의 시간스텝 사이에 어떤 변수를 운반한 거리 viΔt
가 공간의 이산폭인 Δxi를 초과할 수 없다는 것을 의미한다. 즉 VOF함수 F값의 추정이 donor-acceptor법에 의해 결정되기 때문에 CFL<1 이어야 한다. 따라서 시간스텝의 간격 Δt는 식 (5)에 의해 식 (6)을 만족하여야 한다.
여기서 vmax,wmax 는 각각 x, z방향의 최대유속, κ는 가중계수로 본 수치계산에서는 0.9를 적용한다.
DTL조건에 대해서는 식 (7)의 DTL수가 만족되어야 한다.
DTL수가 0.5보다 작은 경우에 수치계산의 안정성이 확보될 수 있으므로 식 (7)에 의해 식 (8)을 만족하여야 한다.
본 수치계산에서는 초기의 계산시간간격을 임의로 지정하고, 그 이후는 CFL 조건식 (5) 및 DTL 조건식 (7)이 만족되도록 Δt를 매 계산스텝마다 조정한다.
2.2 LES-WASS-2D의 검증
본 연구에서 이용하는 수치모형 LES-WASS-2D의 유효성과 타당성을 확인하기 위하여 기수행된 Oner(2010)의 수리모형실험에서 측정한 파이프 저면의 평균 유속과 비교, 검토한다. Oner(2010)의 실험은 먼저 PIV 시스템을 이용하여 바닥으로부터의 이격거리( G)와 파이프 직경( D)과의 비( G⁄D)에 따른 파이프 주변의 유동장을 측정하였다. 측정된 유동장으로부터 파이프 주변의 유선 및 저면의 연직 유속특성을 분석하였다. 여기서는 바닥으로부터의 이격거리가 가장 큰 G⁄D= 0.3의 배치조건에 대한 검증을 수행한다.
Fig. 2는 LES-WASS-2D의 검증을 위하여 Oner(2010)의 실험조건을 기반으로 구성한 수치수조이다. 32 cm 수심의 해석영역에는 길이 1 cm의 스포일러가 부착된 직경 5 cm의 해저파이프를 설치하며, 바닥으로부터 떨어진 거리는 1.5 cm이다. 양쪽 경계에 의한 반사를 배제시키기 위하여 부가감쇠영역, 개경계조건(open boundary), 흐름소스를 적절히 배치한다. 따라서 소스에서는 일정하고, 안정적인 흐름을 생성할 수 있으며, 부가감쇠영역에서는 수직유속을 점진적으로 감소시켜 수조 밖으로 흐름에너지를 완전하게 방사할 수 있다. 검증에 적용한 입사유속( V0)은 19 cm/s이고, 수평 및 수직방향으로는 0.5 mm의 격자크기(Δ x, Δ z)를 구성하고, 초기 계산시간간격 1/2000 초이다.
Fig. 3은 수치모의결과와 Oner(2010)의 실험에서 측정한 유속을 비교하여 나타낸 것으로 입사유속( V0) 19 cm/s에 대하여 무차원하여 나타낸다. (a)는 스포일러가 없는 경우, (b)는 스포일러가 존재하는 경우이며, 유속의 측정단면은 Fig. 4에서 확인할 수 있다. 여기서 원(  )은 실험결과, 실선(  )은 계산결과이다.
Fig. 3으로부터 스포일러가 부착됨으로 인하여 파이프라인 저면으로 빠져나가는 유속이 증가하는 경향을 나타내고 있다. 시뮬레이션에서 측정한 유속이 Oner(2010)이 실험에서 측정한 유속을 조금 과대평가하고 있지만, 스포일러 유무에 따른 전체적으로 해저파이프 주변의 유속을 매우 잘 재현하고 있다. 또한 스포일러 설치 유무에 따라 측정단면에서 최대유속이 나타나는 지점을 본 연구의 시뮬레이션결과가 실험결과를 거의 정확하게 나타내고 있다. 제한적인 수리모형실험과의 검증이지만, 이용하는 LES-WASS-z2D의 타당성 및 유효성이 어느 정도 확보되었다고 할 수 있다.
따라서 본 연구에서는 LES-WASS-2D( Hur et al., 2011)를 이용하여 정상흐름 하에서 스포일러 부착형 파이프라인의 자가매설 기구를 수치적으로 분석한다.
2.3 수치수조 및 입사조건
스포일러 부착형 해저파이프라인의 자가매설 기구를 분석하기 위하여 해저파이프 주변의 수리특성을 분석한다. 수리특성 분석을 위한 수치시뮬레이션을 수행하기 위하여 Fig. 5과 같은 수치수조를 설치한다. 흐름에 의한 수치수조의 교란을 방지하기 위해 양쪽 경계에는 개경계조건, 전면에는 부가감쇠영역을 구성한다. 수심 30 cm의 해석영역에는 직경( D) 5 cm의 파이프라인을 수중에 배치한다. 수평과 수직방향으로는 2 mm의 격자크기(Δ x, Δ z)를 구성하고, 초기 계산시간간격(Δ t)은 1/1000 초로 설정한다.
Fig. 6은 해저파이프에 부착된 두께 2 mm의 스포일러 제원 및 배치를 나타내는 것으로 (a)는 스포일러 길이( SL), (b)는 스포일러의 배치각( αs)에 따른 구성도이다. Table 1은 스포일러의 제원과 배치 그리고 입사유속( Vc)에 따른 실험조건들을 나타내며, 각각의 조건들을 조합하여 총 13경우에 대해 시뮬레이션을 수행한다. Table 1에서 입사유속( Vc)은 15~60 cm/s, 파이프 직경과 스포일러 길이와의 비( SL ⁄ D)는 0~0.5, 스포일러의 배치각( αs)은 -30~+30o(-는 반시계 방향, +는 시계 방향), 해저파이프 직경에 대한 레이놀즈수( ReD)는 7430~29700이다.
3. 수치해석결과
3.1 파이프 주변의 유동 및 와동분포 특성
3.1.1 입사유속에 따른 특성
Fig. 7은 스포일러가 없는 경우 그리고 Fig. 8은 스포일러 길이( SL)가 2.5 cm의 SL ⁄ D=0.5, 배치각( αs)이 0 o이며, 입사유속( Vc)에 따른 평균 유동장 및 와동장을 나타낸다. 그리고 평균 유동 및 와동장은 정상흐름 하에서 반복되는 흐름 및 와동패턴을 평균한 것이다. Fig. 7과 8에서 (a)는 Vc=15 cm/s, (b)는 Vc=30 cm/s, (c)는 Vc=45 cm/s 그리고 (d)는 Vc=60 cm/s의 경우이고, 파이프 입경( D)에 대한 레이놀즈수( ReD)는 각각 7430, 14850, 22280, 29700이다. 여기서 파란색 계열은 시계방향의 와도로서 음(-)의 값, 붉은색 계열은 반시계 방향의 와도로서 양(+)의 값을 가진다.
Fig. 7과 8로부터 Vc와 ReD가 증가할수록 파이프 주변에 강한 와도가 발생하는 것을 확인할 수 있다. 그리고 스포일러가 없는 Fig. 7에서는 상하 대칭적인 평균 유동 및 와동장이 형성되는 반면에 Fig. 8과 같이 스포일러가 부착될 경우에는 스포일러의 영향으로 상하 비대칭적인 평균 유동 및 와동장이 나타난다. 이것은 스포일러가 부착될 경우 투영 면적이 증가하여 스포일러의 상단과 파이프의 아래로 빠져나가는 흐름이 커지기 때문에 나타나는 현상으로 이해될 수 있다. 이 영향으로 스포일러의 끝과 파이프 아래 부근에서 강한 와동이 발생하여 비대칭적인 구조를 가지며, Vc과 ReD가 증가할수록 뚜렷이 나타나며, 이와 같은 유동/와동현상은 파이프 주변의 압력장을 변화시켜 파이프에 작용하는 유체력에 큰 영향을 미칠 것으로 판단된다.
Fig. 9의 그래프는 Fig. 10과 같이 파이프라인 저면의 전면과 후면에서 시간평균 와도를 공간 평균하여 나타낸 것이다. 그래프의 횡축은 파이프 직경에 대한 레이놀즈수( ReD), 종축은 와도 크기이다. 속이 빈 원(  )과 삼각형(  )은 스포일러가 없는 경우, 속이 찬 원(  )과 삼각형(  )은 2.5 cm 길이의 스포일러가 부착된 경우이다. 그리고 원(  ,  )과 삼각형(  ,  )은 파이프라인 저면의 전면과 후면의 평균와도를 각각 나타낸다.
Fig. 9로부터 전체적으로 ReD가 증가할수록 파이프 저면의 와도가 강해지는 것을 확인할 수 있다. 후면의 평균와도는 크게 증가하는 반면에 전면의 평균와도는 증가가 미미하다. 이것은 ReD가 증가할수록 전면의 유동변화는 커지 않으나, 후류가 강하게 발생하기 때문에 배후의 와도가 증가되는 것으로 이해될 수 있다. 이와 같은 저면의 와도현상은 해저파이프라인이 저면에 설치될 경우, ReD가 증가할수록 강한 와도에 의해 세굴을 유발시킬 것으로 판단된다.
3.1.2 스포일러 길이에 따른 특성
Fig. 11은 스포일러 길이( SL) 변화에 따른 평균 유동 및 와동장이며, 정상흐름 하에서 반복되는 흐름 및 와동패턴을 평균하여 나타낸 것이다. Fig. 11 (a)는 스포일러가 없는 경우, Fig. 11 (b)는 SL가 1.25 cm로 SL ⁄ D = 0.25, Fig. 11 (c)는 SL가 2.5 cm로 SL ⁄ D=0.5의 경우이다. 여기서 입사흐름( Vc)은 45 cm/s, ReD=22280, 스포일러의 배치각( αs)은 0 o이며, 파란색 계열은 시계 방향의 -와도, 붉은색 계열은 반시계 방향의 +와도이다.
Fig. 11에서 전술한 바와 같이 스포일러가 존재함으로 인하여 파이프 상하의 유동 및 와동의 비대칭성이 커지는 것을 재확인할 수 있다. SL ⁄ D가 증가할수록 투영면적이 증가하기 때문에 흐름이 빠져나갈 수 있는 단면적이 작아져 파이프 저면과 스포일러 상단의 유속이 증가함과 동시에 강한 와도가 형성된다. 이와 같은 유동 및 와동현상은 파이프 주변의 압력장과 파이프에 작용하는 유체력에 영향을 미칠 것으로 생각된다.
Fig. 12는 Fig. 10에 나타낸 파이프라인 저면의 전면과 후면에서 측정한 공간 평균와도이며, 에 따라 나타낸다. 여기서 원(  )은 파이프 저면의 전면, 삼각형(  )은 파이프 저면의 후면의 평균와도이다.
Fig. 12에서 SL ⁄ D가 증가할수록 파이프 저면의 평균와도가 증가하는 경향을 보인다. 여기서 후면의 평균와도는 크게 증가하는 반면에 전면의 평균와도는 미미하게 증가한다. 이것은 앞서 논의한 것과 같이 SL ⁄ D가 증가할수록 투영면적이 증가하여 파이프를 빠져나가는 유속이 커진다. 이로 인하여 파이프 후면의 후류가 강해지게 된다.
이상의 유동 및 와동특성으로 인하여 해저파이프라인이 저면에 설치될 경우, SL ⁄D가 증가할수록 파이프 저면의 세굴 발생에 큰 영향을 미칠 것으로 판단된다.
3.1.3 스포일러의 배치각에 따른 특성
Fig. 13은 스포일러의 배치각( αs)에 따른 평균 유동 및 와동장이며, 정상흐름 하에서 흐름 및 와동의 반복패턴으로 평균하여 나타내며, (a)는 αs=-30º, (b)는 αs=-15º, (c)는 αs=0º, (d)는 αs=15º, (e)는 αs=30º의 경우이다. 수치모의의 입사/초기조건은 Vc=45 cm/s, ReD= 22280, SL ⁄ D= 0.5이다. 여기서 파란색 계열은 -값으로 시계 방향의 와도, 붉은색 계열은 +값으로 반시계 방향의 와도를 의미한다.
Fig. 13으로부터 스포일러의 배치각이 양의 값을 가지는 경우에서 스포일러의 끝이 흐름의 입사방향으로 향할수록 스포일러의 배후에서 강한 와도가 발생하는 것을 확인할 수 있다. 이것은 구조적으로 αs가 작을수록 흐름이 유연하게 유도될 뿐만 아니라, 배후의 차폐영역이 좁아지기 때문에 후류현상이 감소한다. 반면에 αs가 증가할수록 스포일러가 부착된 형상적으로 유체저항이 증가하고, 배후에서는 차폐영역이 넓어지게 때문에 후류에 의한 강한 와도가 발생한다. 그리고 파이프라인 아래에서는 αs가 증가할수록 파이프라인에 의한 유체저항이 커져 와도가 발달하다가 (e) αs= 30º에서는 다시 감소하는 경향을 나타낸다. 전술한 것과 같이 αs가 양의 값을 가지게 되면, 형상적으로 유체저항이 증가함과 동시에 투영 면적이 작아진다. 이것에 기인하여 파이프 아래로 빠져나가는 유속이 작아지기 때문에 나타나는 현상으로 이해된다.
Fig. 14는 스포일러의 배치각( αs)에 따른 평균와동특성을 나타내며, 원(  )은 파이프 저면의 전면, 삼각형(  )은 파이프 저면의 후면의 평균와도이다. 여기서 파이프라인 저면의 전면과 후면의 평균와도 측정영역은 Fig. 10과 같다.
Fig. 14로부터 전반적으로 αs가 증가할수록 파이프 저면의 평균와도가 증가하는 경향을 보이나, αs= 30º의 경우에는 도리어 감소한다. 앞서 언급한 것과 같이 αs가 커질수록 유체저항이 증가함으로 인하여 스포일러가 있는 상측보다는 저면으로 빠져나가는 흐름이 발달하기 때문으로 이해할 수 있다. 하지만 αs=30º의 경우에는 투영면적이 또한 작아지기 때문에 파이프 상하로 빠져나가는 전제적인 유속이 감소하여 발생하는 현상으로 생각된다.
이상의 유동 및 와동장의 분석결과를 종합하면, 스포일러 부착형 파이프라인이 해저면에 설치되면 흐름이 강할수록 저면의 강한 흐름/와도에 의해 세굴이 크게 발생하게 될 것이다. 스포일러 길이와 파이프 직경과의 비(SL ⁄D)가 증가할수록, 배치각(αs)이 15o에 근접할수록 자가매설에 유리한 세굴 현상이 더욱 심화될 것으로 판단된다.
3.2 파이프 주변의 압력분포 및 작용력 특성
3.2.1 입사유속에 따른 특성
Fig. 15는 해저파이프라인에 스포일러가 없는 경우, Fig. 16은 길이 2.5 cm의 스포일러가 부착된 경우( αs=0º, SL ⁄ D= 0.5)이며, 입사유속( Vc)에 따른 평균 동압력장을 나타낸다. 평균 동압력장은 정상상태의 흐름에서 반복되는 동압력장을 평균한 것이다. Fig. 15와 16에서 (a)는 Vc=15 cm/s, (b)는 Vc= 30 cm/s, (c)는 Vc=45 cm/s 그리고 (d)는 Vc=60 cm/s이고, 파이프 입경(D)에 대한 각각의 레이놀즈수( ReD)는 7430, 14850, 22280, 29700이다. 여기서 파란색 계열은 정수압보다 낮은 압력으로 음(-)의 값 그리고 붉은색 계열은 정수압보다 높은 압력으로 양(+)의 값을 가진다.
Fig. 15와 16으로부터 전반적인 특성을 Fig. 7과 8의 평균 패턴 와동 및 유동장과 함께 살펴볼 수 있다. Vc와 ReD가 증가할수록 전면에서는 흐름에 의한 동압력이 증가하는 반면에 후면에서는 와동이 강해지는 현상으로 인하여 동압력이 감소하는 경향이 나타난다. 스포일러가 부착됨으로 인하여 유체저항이 증가하기 때문에 파이프전면에 동압력이 그렇지 않은 경우에 비해 크게 증가한다. 또한 스포일러가 존재하지 않는 Fig. 15에서는 전술한 평균 유동/와동장과 같이 상하 대칭적인 평균 압력장이 형성된다. 하지만 Fig. 16에서는 스포일러의 영향으로 생성된 비대칭적 와동장의 형성으로 압력장 역시 비대칭적인 구조를 가진다. 스포일러 배후에서 발생한 강한 와도가 동압력이 떨어뜨리기 때문에 나타나는 현상으로 이해된다. 이와 같은 비대칭적 압력장은 해저파이프에 작용하는 힘에 큰 영향을 미칠 것으로 판단되며, Fig. 17에서 논의한다.
Fig. 17은 ReD에 따른 파이프라인에 직접적으로 작용하는 연직방향의 평균 유체력을 산정하여 나타낸 것이며, 수직력에 대해서만 논의하기로 한다. 여기서 원(  )은 스포일러가 설치되지 않은 경우, 삼각형(  )은 스포일러의 제원과 배치가 SL ⁄ D = 0.5, αs = 0º의 경우이다.
Fig. 17로부터 전술한 Fig. 16과 17의 논의에 따르면, 해저파이프에 스포일러가 설치됨으로 인하여 상하 비대칭적인 평균 동압력장이 형성된다. Vc 및 ReD가 커질수록 전면의 압력은 증가하고, 배후의 압력은 감소하게 된다. 따라서 스포일러가 설치되지 않은 경우에는 Vc 및 ReD에 따른 평균 동압력의 증감이 상하 대칭적으로 나타나기 때문에 수직으로 작용하는 힘에는 큰 영향을 미치지 못한다. 반면에 상하 비대칭적인 평균 압력장을 나타내는 스포일러를 부착한 경우에는 Vc 및 ReD가 커질수록 평균 압력장의 비대칭성이 심화되어 파이프에 작용하는 하강력이 커지는 것을 알 수 있다.
3.2.2 스포일러 길이에 따른 특성
Fig. 18은 스포일러 길이와 파이프 직경과의 비( SL ⁄ D)에 따른 평균 동압력장으로 정상흐름 안에서 반복되는 압력패턴을 평균하여 나타낸다. 여기서 입사흐름( Vc)은 45 cm/s, ReD = 22280, 스포일러의 배치각( αs)은 0º이다. 그리고 Fig. 18 (a)는 스포일러가 없는 경우, Fig. 18 (b)는 SL가 1.25 cm로 SL ⁄ D=0.25 그리고 Fig. 18 (c)는 SL가 2.5 cm로 SL ⁄ D=0.5의 경우이다. 파란색 계열은 정수압보다 낮은 압력으로 -값, 붉은색 계열은 정수압보다 높은 압력으로 +값이다.
Fig. 18로부터 스포일러가 없는 경우에는 (a)와 같이 상하 대칭적인 평균 동압력장이 형성되고, 그렇지 않은 (b)와 (c)에서의 평균 동압력장은 가 커질수록 전후면의 압력차가 증가할 뿐만 아니라, 비대칭성이 커지는 것을 알 수 있다. 이 같은 비대칭적 압력장은 한 방향으로 치우치는 힘이 파이프라인에 작용될 것으로 예상된다.
Fig. 19는 스포일러 길이와 파이프 직경과의 비( SL ⁄ D)에 따라 파이프라인에 작용하는 연직방향의 평균 유체력을 나타낸 것이다. 여기서 입사흐름( Vc) 45 cm/s, ReD = 22280, 스포일러의 배치각( αs)은 0º의 경우이다.
Fig. 19는 Fig. 18과 함께 살펴볼 필요가 있으며, Fig 18의 상하 비대칭의 평균패턴 동압력장으로 인하여 파이프라인에 작용하는 연직 평균 유체력이 SL ⁄ D가 증가할수록 증가하는 경향을 나타낸다. 스포일러 존재 유무에 따라서는 파이프에 작용하는 하강력은 큰 차이를 나타내지만, SL ⁄ D에 대해서는 큰 증가폭을 가지지 않은 것을 확인할 수 있다.
이와 같이 스포일러 부착형 파이프라인에 작용하는 평균 하강력이 SL ⁄D가 커질수록 증가하지만, 그 효과는 크지 않은 것을 확인하였다. 따라서 지반 및 해양외력의 특성을 고려하여 자가매설을 용이하게 하강력을 발생시킬 수 SL ⁄D 를 설정해야 할 것이며, 스포일러의 구조적 안정 또한 배제해서는 안된다. 적절한 SL ⁄D를 추정하기 위해서는 다각도(파이프의 제원, 해저질, 해양외력 등)의 검토가 필요할 것으로 판단된다.
3.2.1 입사유속에 따른 특성
Fig. 20은 스포일러의 배치각( αs)에 따른 평균 동압력장을 나타낸 것으로 (a)는 αs=-30º, (b)는 αs=-15º, (c)는 αs=0º, (d)는 αs=15º, (e)는 αs=30º의 경우이다. 계산의 입사 및 초기조건은 Vc=45 cm/s, ReD = 22280, SL ⁄ D = 0.5과 같다. 여기서 파란색 계열은 정수압보다 -압력 그리고 붉은색 계열은 정수압보다 +압력을 의미한다.
Fig. 20으로부터 모든 경우에서 상하 비대칭적인 평균 동압력장을 보이고 있다. 해저파이프에 부착된 스포일러의 배치각( αs)이 음의 값을 가지는 (a)와 (b)보다는 형상적으로 유체저항이 큰 (c)와 (d)에서는 파이프 전면의 평균 동압력이 증가하고, 후면에서는 -값을 나타내는 영역이 커지는 것을 확인할 수 있다. αs가 30º인 (e)에서는 (d) αs= 15º보다 파이프 전면의 +동압력은 감소하고, 후면의 −동압력은 증가하는 경향을 나타낸다. 이 현상은 유동 및 와동장에서 논의한 것처럼 αs가 증가할수록 투영면적이 작아지기 때문에 나타나는 현상으로 판단된다.
Fig. 21는 스포일러의 배치각( αs)에 따른 파이프에 작용하는 평균 수직력을 나타낸 것으로 입사흐름( Vc)이 45 cm/s, ReD = 22280, 스포일러 길이와 파이프 직경과의 비( SL ⁄ D)는 0.5의 경우이다.
Fig. 21로부터 전반적으로 αs가 증가할수록 파이프에 작용하는 하강력이 증가하는 경향을 나타내며, αs= 15º의 경우가 가장 큰 하강력을 받는 것을 알 수 있다. 이것은 앞서 논의한 유동/와동장 특성에서 확인한 바와 같이 αs가 증가할수록 유체저항이 증가하지만, αs = 30º의 경우에는 투영면적이 또한 작아지기 때문에 파이프에 작용하는 하강력이 약해지는 것으로 이해된다.
이상의 압력 및 작용력에 관한 결과들에 근거하여 스포일러 부착형 해저파이프라인 주변에서는 상하 비대칭적인 압력장이 발생하여 파이프에 직접적으로 작용하는 하강력이 발생하게 된다. 이 영향으로 인하여 스포일러 부착형 파이프라인의 자가매설이 용이하게 된다. 이상의 수치모의결과에 근거하여 이 하강력은 SL ⁄D가 증가할수록, αs가 15º에 근접할수록 크게 발생하였다.
본 연구에서 검토한 수치실험조건 내에서의 스포일러의 제원 및 배치에 따른 파이프라인 저면의 와동특성, 파이프에 작용하는 수직력을 Table 2에 나타낸다. 이것을 종합적으로 분석하면 SL ⁄ D =0.25, αs = 15º의 스포일러 부착형 해저파이프 라인이 자가매설에 가장 유리한 조건인 것을 알 수 있다.
4. 결론 및 고찰
본 연구에서는 스포일러가 부착된 파이프라인의 자가매설 원리를 분석하기 위하여 고정도의 수치모형인 2차원 N-S solver(LES-WASS-2D; Hur et al., 2011)를 이용하였다. 수치시뮬레이션을 통하여 스포일러 유무에 따른 파이프라인 주변의 수리특성(유동장, 와동장, 압력장)을 분석하였고, 이것을 토대로 파이프라인에 직접적으로 작용하는 유체력을 산정하였다. 이로서 스포일러 부착형 파이프라인의 자가매설 기구를 확인할 수 있었다. 나아가 자가매설이 용이한 스포일러의 제원 및 배치를 검토하였다. 본 연구에서 논의한 주요한 결과를 아래와 같이 기술한다. (1) 수치시뮬레이션에 적용하는 LES-WASS-2D를 검증하기 위하여 스포일러 유무에 따른 파이프 저면의 유속을 측정한 수리모형실험결과( Oner, 2010)와 비교·검토하여 수치모형의 타당성 및 유효성을 확인하였다. (2) 해저파이프에 스포일러를 부착할 경우, 상하 비대칭적인 평균 유동/와동구조를 나타내었으며, 저면에서는 강한 와도가 발생하였다. 이것은 파이프라인 저면의 세굴을 심화시켜 자가매설에 유리하게 작용할 것이다.
(3) 이상의 유동/와동 현상으로 인하여 해저파이프 주변에서는 상하 비대칭적인 평균 동압력장이 형성되어 파이프에 직접적인 하강력이 작용하는 것을 확인하였다. 이와 같이 하강력이 증가하면, 파이프라인이 자가매설되기에 용이해지게 된다.
(4) 이상의 현상들이 복합적으로 발생하여 해저파이프에 스포일러를 부착할 경우, 유체운동의 변화에 의해 세굴이 심화됨과 동시에 하강력이 작용하여 파이프를 스스로 매설시키는 것으로 이해될 수 있었다.
(5) 본 연구에서 검토한 한정적인 조건 안에서는 스포일러의 제원 및 배치가 SD ⁄ L=0.25, αs= 15º일 때 자가매설에 유리할 것으로 판단된다.
실제 스포일러 부착형 해저파이프라인을 설치하기 위해서는 대상지역의 지질 및 해양외력 특성에 관한 충분한 조사가 선행되어야 할 것이다. 얻어진 조사결과를 바탕으로 적절한 스포일러의 제원 및 배치를 결정하기 위해서는 수리모형실험을 비롯하여 본 연구와 같은 고정도의 수치해석을 통하여 수행하여야 할 것이다. 향후에는 지형변동모형을 결합하여 스포일러 부착형 파이프라인의 자가매설 과정을 면밀히 분석할 예정이다.
감사의 글
이 논문은 2016년 해양수산부 재원으로 한국해양과학기술진흥원의 지원을 받아 수행된 연구임(연안침식대응기술개발).
Fig. 1.
Damage cases of submarine pipeline. 
Fig. 2.
Definition sketch of numerical water tank based on Oner(2010)’s experiments for verification of numerical model. 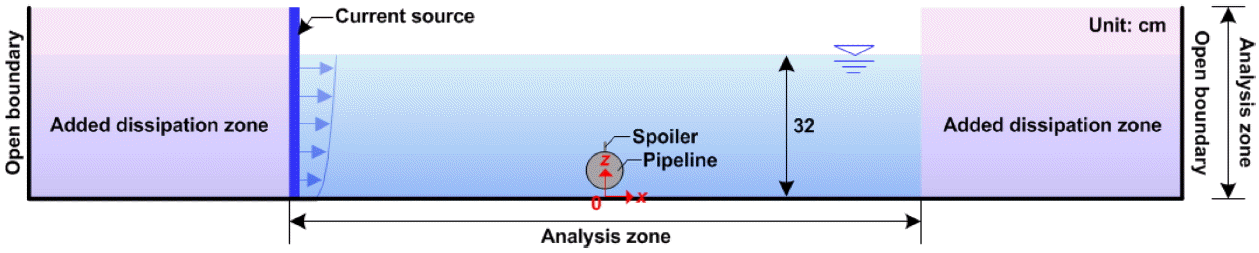
Fig. 3.
Comparison between measured( Oner, 2010) and calculated(LES-WASS-2D) time-averaged patterns of horizontal velocities. 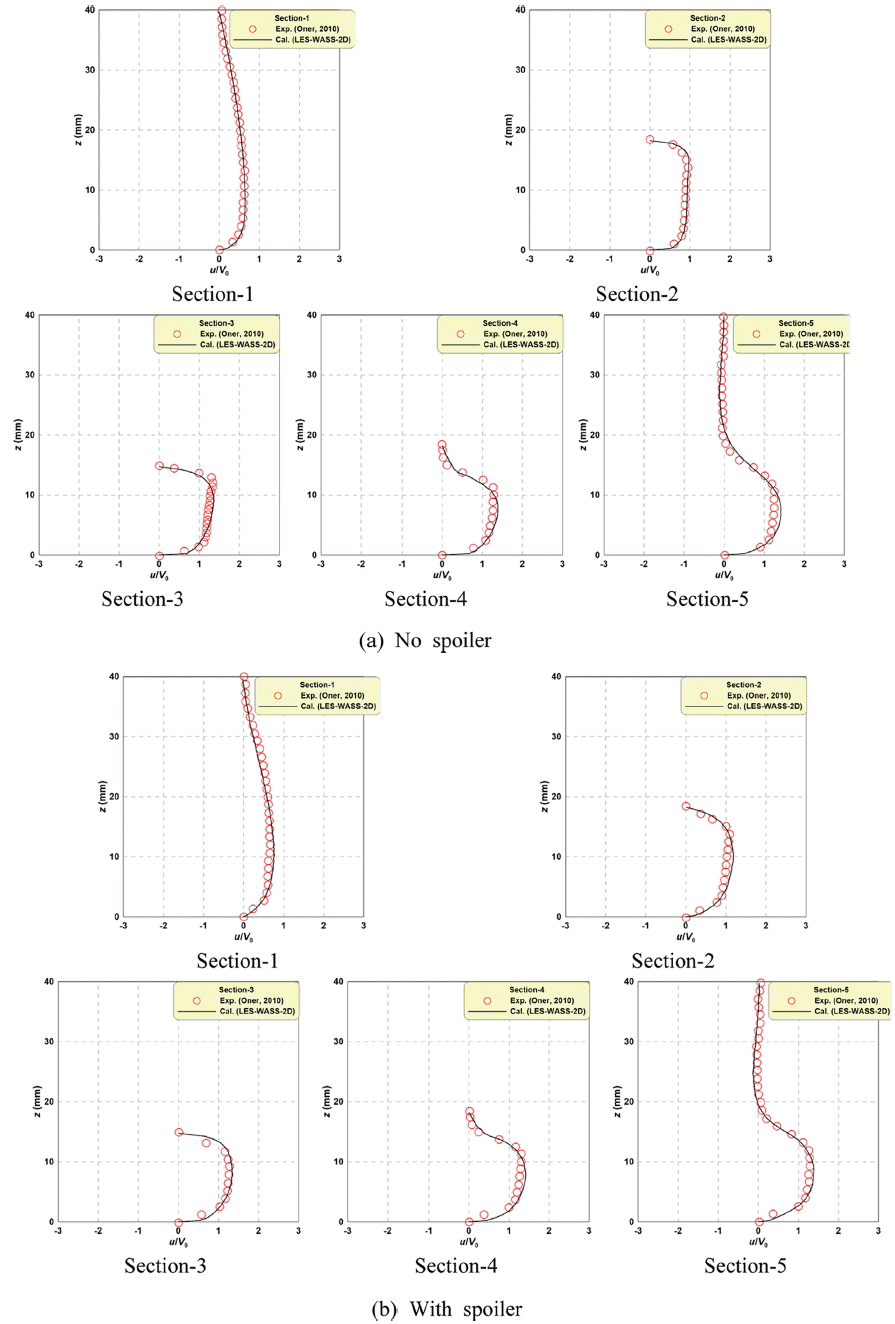
Fig. 4.
Measured sections of velocities under pipeline. 
Fig. 5.
Definition sketch of 2-D numerical water tank including pipeline. 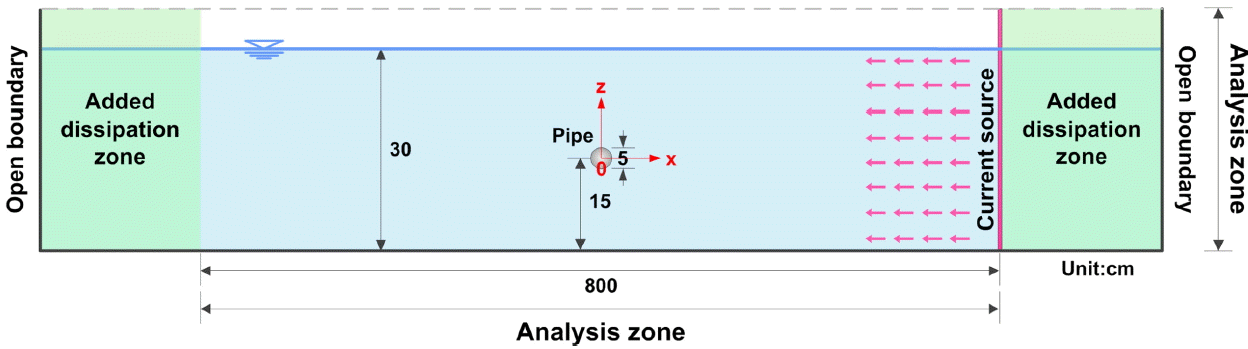
Fig. 6.
Shape and arrangement of spoilers on a pipeline. 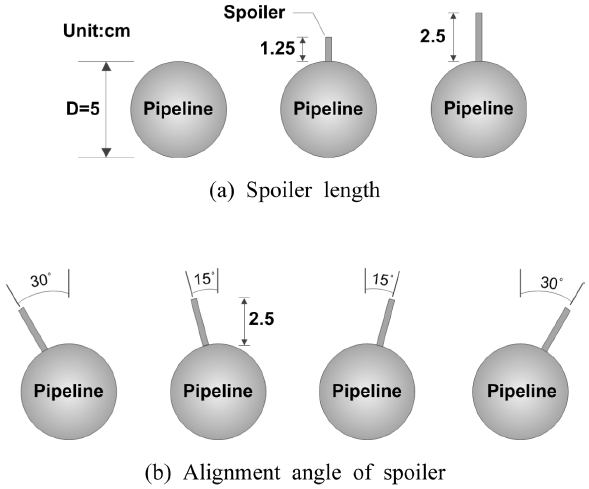
Fig. 7.
Time-averaged patterns of velocities and vorticities due to incident currents around pipeline without spoiler. 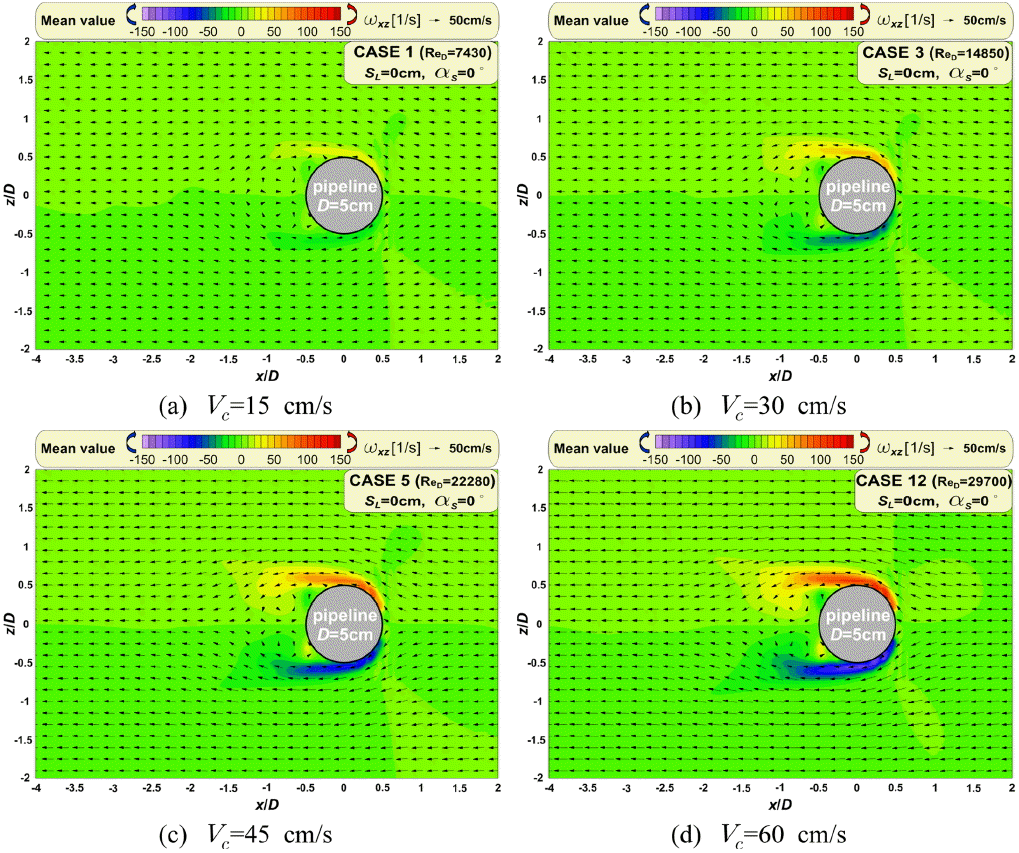
Fig. 8.
Time-averaged patterns of velocities and vorticities due to incident currents around pipeline with spoiler. 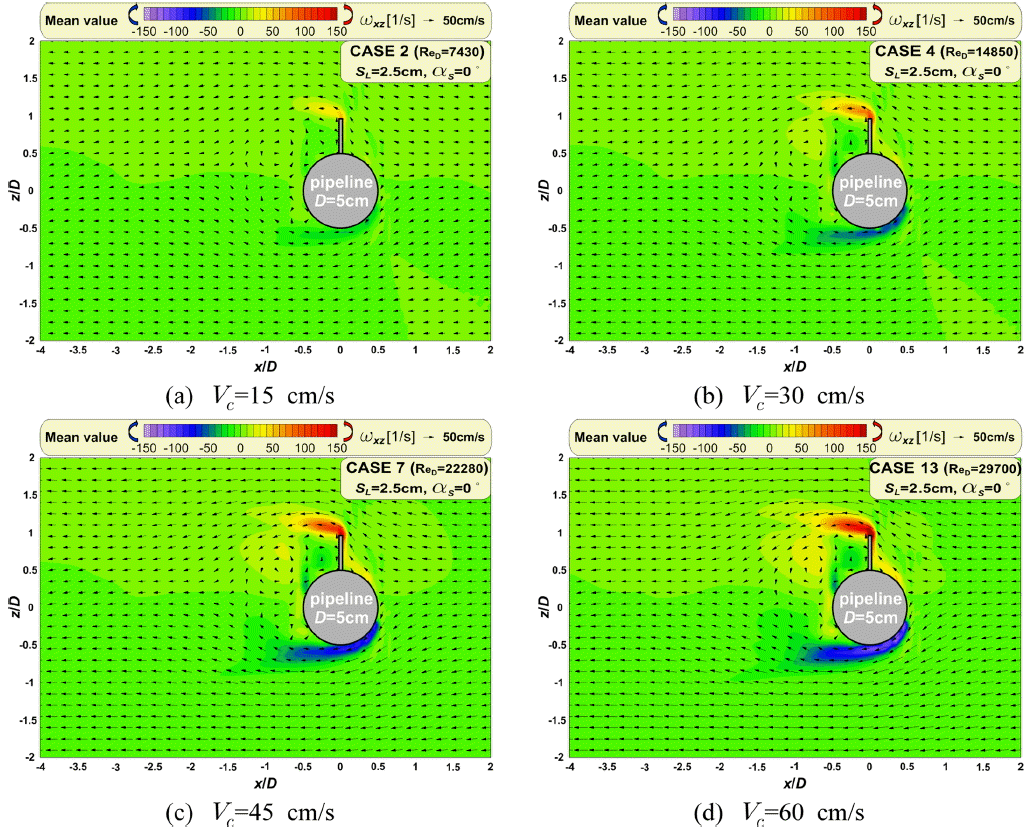
Fig. 9.
Distribution of mean vorticities due to in front and rear side under pipeline. 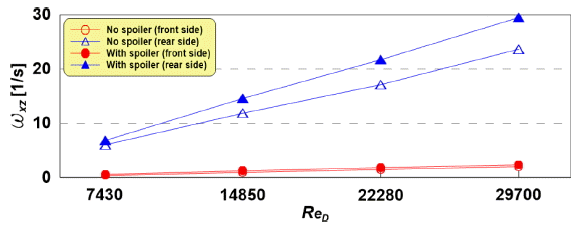
Fig. 10.
Estimated domains of vorticity under pipeline. 
Fig. 11.
Time-averaged patterns of velocities and vorticities due to spoiler lengths around pipeline. 
Fig. 12.
Distribution of mean vorticities due to in front and rear side under pipeline. 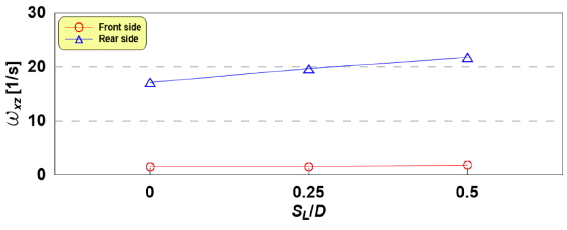
Fig. 13.
Time-averaged patterns of velocities and vorticities due to alignment angles of spoiler around pipeline. 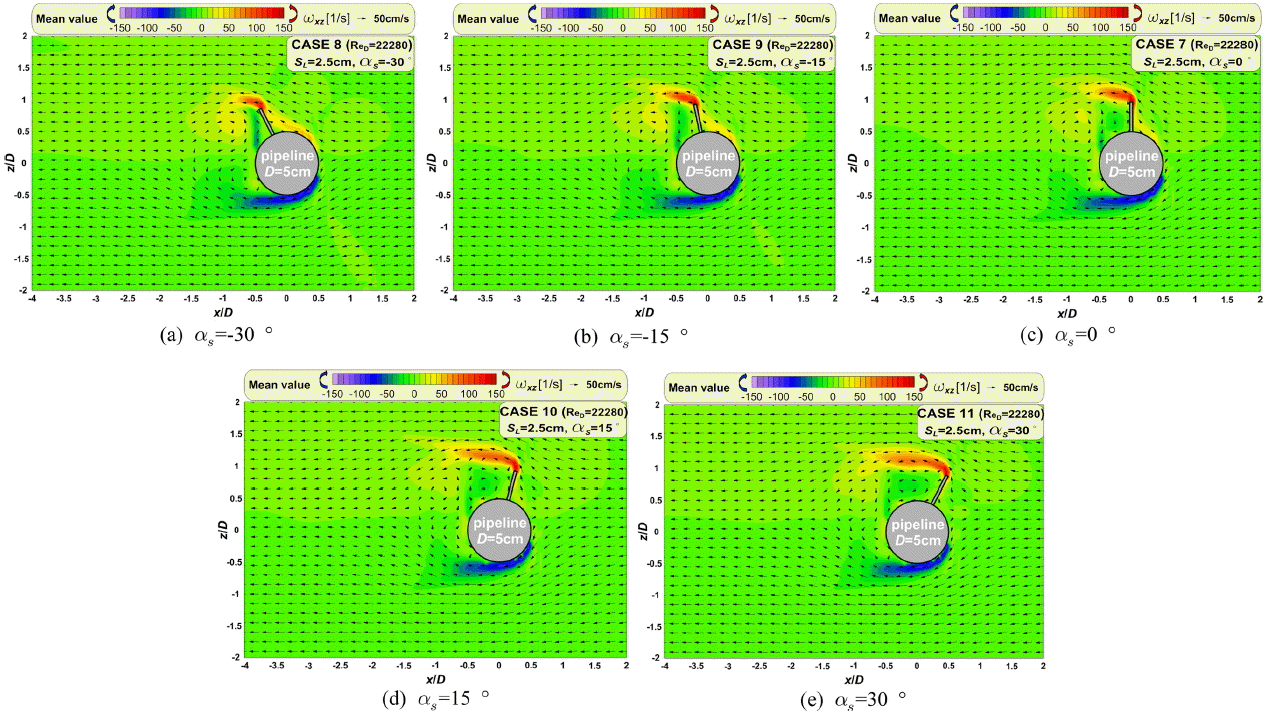
Fig. 14.
Distribution of mean vorticities due to in front and rear side under pipeline. 
Fig. 15.
Time-averaged patterns of dynamic pressures due to incident currents around pipeline without spoiler. 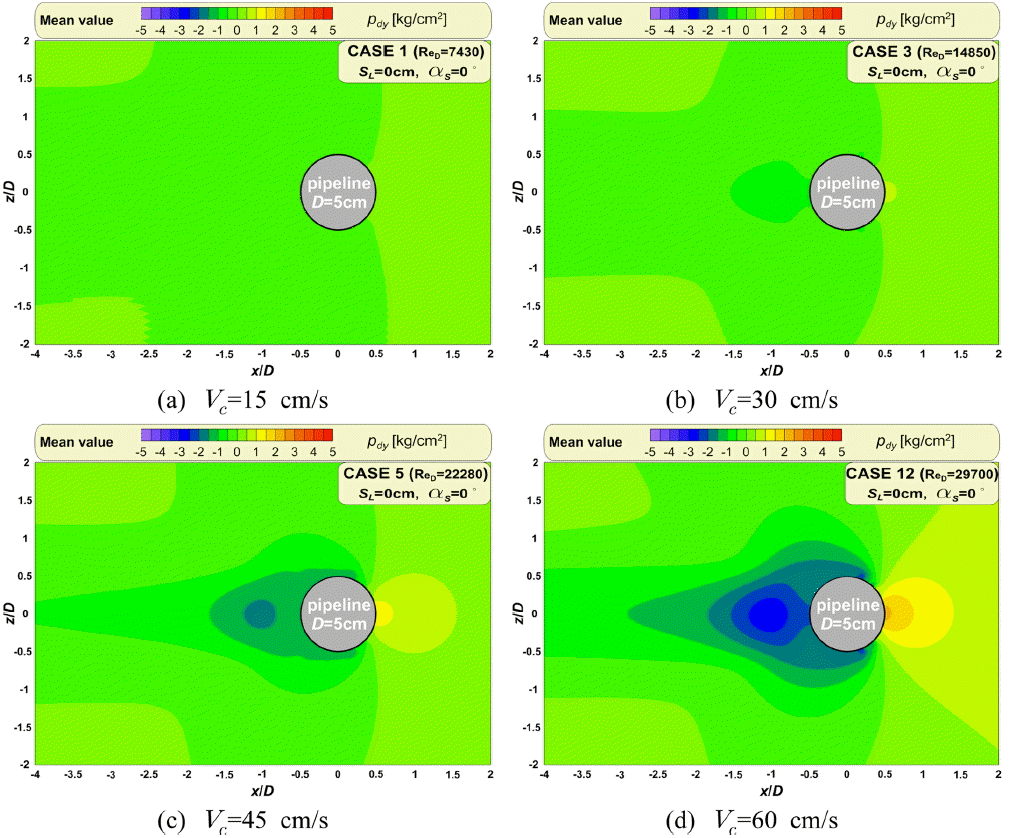
Fig. 16.
Time-averaged patterns of dynamic pressures due to incident currents around pipeline with spoiler. 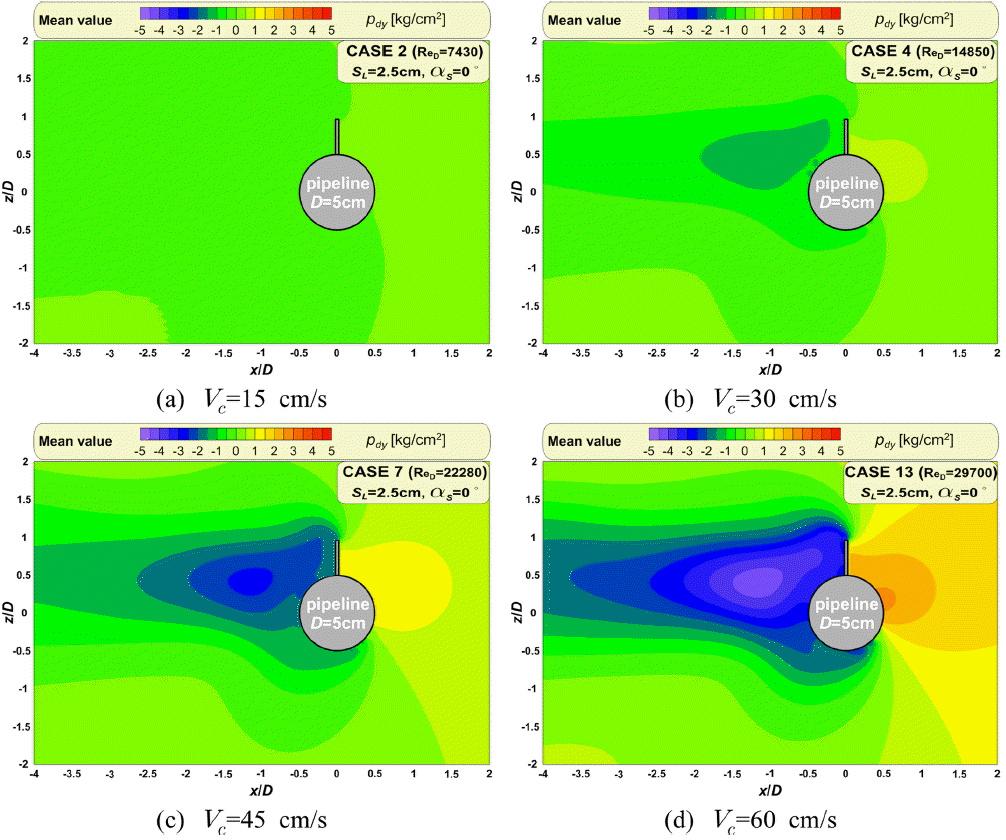
Fig. 17.
Comparisons of pattern-averaged vertical forces on pipeline according to presence or absence of spoiler. 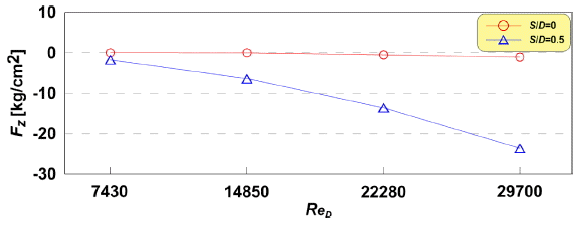
Fig. 18.
Time-averaged patterns of dynamic pressures due to spoiler lengths around pipeline. 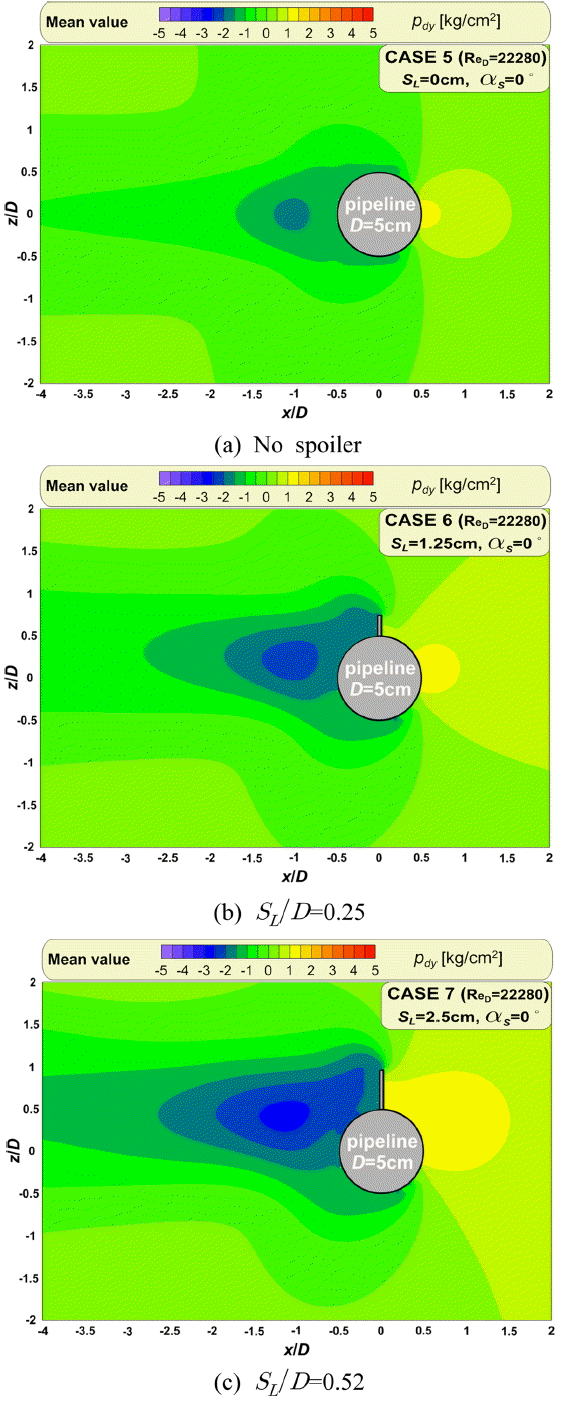
Fig. 19.
Distribution of pattern-averaged vertical forces on pipeline due to SL ⁄ D. 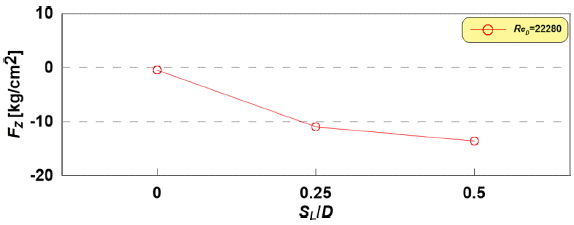
Fig. 20.
Time-averaged patterns of dynamic pressures due to alignment angles of spoiler around pipeline. 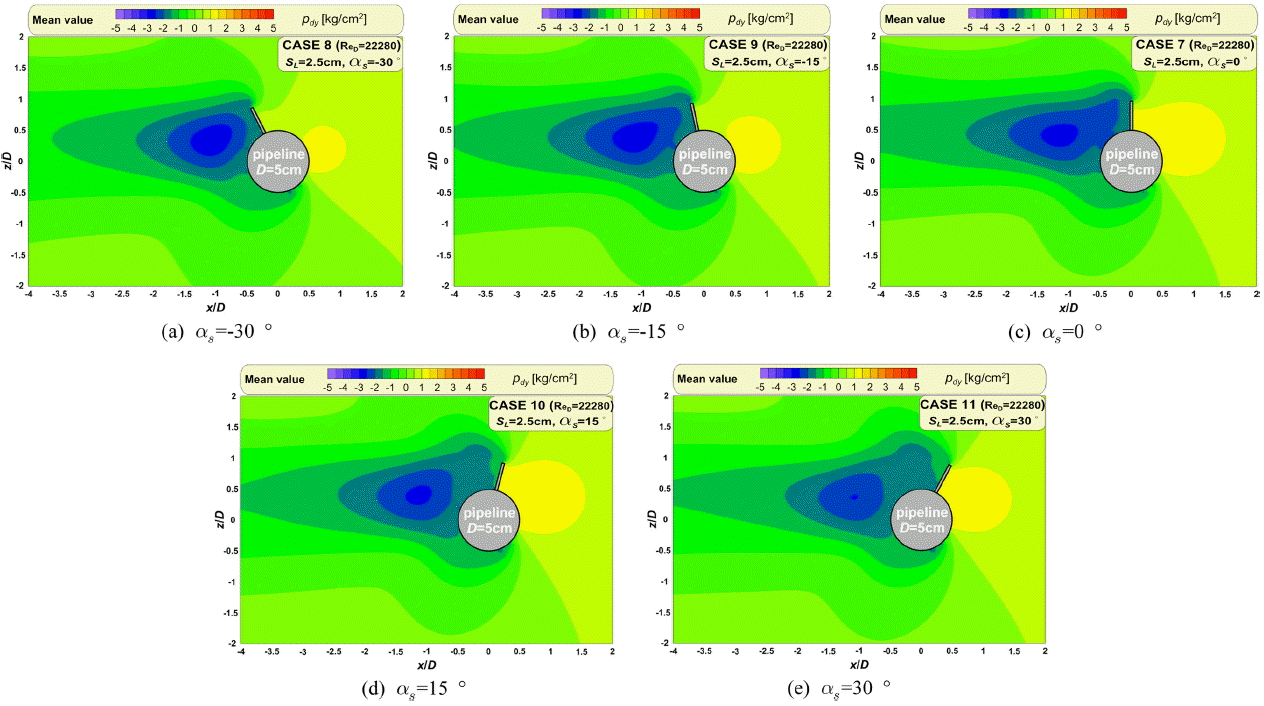
Fig. 21.
Distribution of pattern-averaged vertical forces on pipeline due to αs . 
Table 1.
Initial and incident conditions used in numerical simulations
CA
SE |
ReD
|
Vc [cm/s] |
SL/D
|
αs[o] |
|
1 |
7430 |
15 |
0 |
0 |
|
2 |
|
0.5 |
|
|
3 |
14850 |
30 |
0 |
0 |
|
4 |
|
0.5 |
|
|
5 |
22280 |
45 |
0 |
0 |
|
6 |
0.25 |
|
7 |
0.5 |
|
|
8 |
22280 |
45 |
0.5 |
−30 |
|
9 |
−15 |
|
10 |
15 |
|
11 |
30 |
|
|
12 |
29700 |
60 |
0 |
0 |
|
13 |
0.5 |
Table 2.
Mean vorticity and vertical force due to shape and arrangement of attaching spoiler to pipeline
CA
SE |
ReD
|
Vc [cm/s] |
SL/D
|
αs [o] |
Mean vorticity [1/s]
|
Fz [kg/cm2] |
|
rear |
front |
|
1 |
7430 |
15 |
0 |
0 |
6.01 |
0.39 |
0.01 |
|
2 |
0.5 |
6.82 |
0.59 |
−1.72 |
|
|
3 |
14850 |
30 |
0 |
0 |
11.84 |
0.94 |
−0.01 |
|
4 |
0.5 |
14.58 |
1.23 |
−7.36 |
|
|
5 |
22280 |
45 |
0 |
0 |
17.12 |
1.48 |
−0.48 |
|
6 |
0.25 |
19.68 |
1.52 |
−10.97 |
|
7 |
0.5 |
21.73 |
1.82 |
−13.61 |
|
|
8 |
22280 |
45 |
0.5 |
−30 |
16.23 |
1.36 |
−2.24 |
|
9 |
−15 |
17.22 |
1.41 |
−3.72 |
|
10 |
15 |
18.46 |
1.59 |
−7.21 |
|
11 |
30 |
13.43 |
1.21 |
−4.13 |
|
|
12 |
29700 |
60 |
0 |
|
23.66 |
2.01 |
−1.05 |
|
13 |
0.5 |
29.48 |
2.33 |
−23.61 |
References
Bakhtiary, AD, Zeinali, M (2008). Numerical simulation of hydrodynamic forces on submarine pipeline with a spoiler, International Conference on Coasts, Ports and Marine Structures(ICOPMAS), Ports and Marine Organization, 8, 1-12.
Barendse, CAM. (1988). Hydrodynamic forces on a near-bed offshore pipeline with spoiler during the selfburying process, TU Delft, Faculty of Civil Engineering.
Brackbill, JU, Kothe, DB, Zemach, C (1992). A continuum model for modeling surface tension, Journal of Computational Physics, 100, 335-354.  Cheng, L, Chew, L (2003). Modelling of flow around a nearbed pipeline with a spoiler, Ocean Engineering, 30, 1595-1611.  Chiew, Y (1993). Effect of spoilers on wave induced scour at submarine pipelines, J. Waterway, Port, Coastal, Ocean Engineering, 417, 417-428.  Ergun, S (1952). Fluid flow through packed columns, Chemical Engineering Progress, 48(2):89-94.
Germano, M, Piomelli, U, Moin, P, Cabot, WH (1991). A dynamic subgrid-scale eddy viscosity model, Physics of Fluids, 3, 1760-1765.  Han, Y (2012). Study on the submarine pipeline with flexible spoilers, Key Engineering Materials, 501, 431-435.  Hur, DS, Lee, KH, Choi, DS (2011). Effect of the slope gradient of submerged breakwaters on wave energy dissipation, Engineering Applications of Computational Fluid Mechanics, 5, 83-98.  Hur, DS, Lee, WD, Bae, KS (2008). On reasonable boundary condition for inclined seabed/structure in case of the numerical model with quadrilateral mesh system, Journal of Korean Society of Civil Engineers, KSCE, 28(5B):591-594 (in Korean).
Hulsbergen, CH. (1984). Stimulated self-burial of submarine pipelines, Proceedings of the 16th Offshore Technology Conference, OTC 4667. 171-177.  Hulsbergen, CH, Bijker, H. (1989). Effect of spoilers submarine pipeline stability, Proceedings of the 21st Offshore Technology Conference, OTC 6154. 337-350.  Lilly, DK (1992). A proposed modification of the Germano subgrid-scale closure method, Physics of Fluids, 4, 633-635.  Liu, S, Masliyah, JH (1999). Non-linear flows in porous media, Journal of Non-Newtonian Fluid Mechanics, 86, 229-252.  Oner, AA (2010). The flow around a pipeline with a spoiler, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering, 224(1):109-121.  Sakakiyama, T, Kajima, R. (1992). Numerical simulation of nonlinear wave interacting with permeable breakwater, Proceedings of 23rd International Conference on Coastal Engineering, ASCE. 1517-1530.  Smagorinsky, J (1963). General circulation experiments with the primitive equation, Monthly Weather Review, 91, 99-164.  Yang, L, Shi, B, Guo, Y, Wen, X (2012). “Calculation and experiment on scour depth for submarine pipeline with a spoiler.”, Ocean Engineering, 55, 191-198.  Zhao, J, Wang, X (2009). CFD numerical simulation of the submarine pipeline with a spoiler, Journal of Offshore Mechanics and Arctic Engineering, 131, 031601.  Zhu, H, Qi, X, Lin, P, Yang, Y (2013). Numerical simulation of flow around a submarine pipe with a spoiler and currentinduced scour beneath the pipe, Applied Ocean Research, 41, 87-100. 
|
|
 )은 실험결과, 실선(
)은 실험결과, 실선( )은 계산결과이다.
)은 계산결과이다. )과 삼각형(
)과 삼각형( )은 스포일러가 없는 경우, 속이 찬 원(
)은 스포일러가 없는 경우, 속이 찬 원( )과 삼각형(
)과 삼각형( )은 2.5 cm 길이의 스포일러가 부착된 경우이다. 그리고 원(
)은 2.5 cm 길이의 스포일러가 부착된 경우이다. 그리고 원( ,
,  )과 삼각형(
)과 삼각형( ,
,  )은 파이프라인 저면의 전면과 후면의 평균와도를 각각 나타낸다.
)은 파이프라인 저면의 전면과 후면의 평균와도를 각각 나타낸다. )은 파이프 저면의 전면, 삼각형(
)은 파이프 저면의 전면, 삼각형( )은 파이프 저면의 후면의 평균와도이다.
)은 파이프 저면의 후면의 평균와도이다. )은 파이프 저면의 전면, 삼각형(
)은 파이프 저면의 전면, 삼각형( )은 파이프 저면의 후면의 평균와도이다. 여기서 파이프라인 저면의 전면과 후면의 평균와도 측정영역은 Fig. 10과 같다.
)은 파이프 저면의 후면의 평균와도이다. 여기서 파이프라인 저면의 전면과 후면의 평균와도 측정영역은 Fig. 10과 같다. )은 스포일러가 설치되지 않은 경우, 삼각형(
)은 스포일러가 설치되지 않은 경우, 삼각형( )은 스포일러의 제원과 배치가 SL ⁄D = 0.5, αs = 0º의 경우이다.
)은 스포일러의 제원과 배치가 SL ⁄D = 0.5, αs = 0º의 경우이다.





























