Estimation of Entrainment Rate of Fluid Mud using Annular Flume

Dong-Ho Kim; Won-Kyu Kim; Kyu-Nam Hwang

doi:10.9765/KSCOE.2016.28.5.257

요약

본 연구에서는 머드유동층의 연행부상률 산정을 목적으로 국내 최초로 환형수조를 이용하여 고령토 머드유동층에 대한 연행부상 실험이 수행되었다. 고령토로 제작된 머드유동층의 초기농도를 변화시키면서 총 6회의 연행부상 실험이 수행되었으며, 머드유동층의 연행부상률이 정량적으로 산정되었다. 본 연구결과에 따르면, 머드유동층의 부상률과 반대방향으로 작용하는 토사의 침강의 영향으로 인하여, 경계면에서 난류 운동에너지의 부가 손실이 유발되고, 결과적으로 리차드슨 수가 높은 경우에 염수 성층 구조일 때 보다 상당히 감소된 부상률이 초래되는 것으로 나타났다. 또한, 과거 타 연구결과와의 비교·검토를 통하여 본 연구에서 사용된 환형수조는 성능 상에 문제가 없음이 간접적으로 확인되었으며, 연행부상 실험 방법 및 실험 결과의 타당성이 입증되었다.

핵심용어: 연행부상률, 머드유동층, 고령토, 리차드슨 수, 환형수조

Abstract

In this study, experiments for measurements of entrainment rate of fluid mud were carried out using annular flume domestically for the first time. Six entrainment tests using kaolinite sediments were conducted with different initial concentrations of fluid mud. It is shown that sediment settling counteracts the otherwise buoyancy dependent entrainment of fluid mud, and that the settling effect leads to a measurably decreased entrainment rate at higher Richardson numbers in comparison with entrainment of salt water, due to additional dissipation of turbulent kinetic energy in the interfacial layer. Through the comparison with previous other studies, the overall performance of the annular flume, the experimental procedure and the test results in simulating the entrainment of fluid mud are shown to be good enough to verify.

Keywords: entrainment rate, fluid mud, kaolinite, Richardson number, annular flume

1. 서 론

일반적으로 미세 점착성 퇴적물로 구성되어 있는 저면의 침식은 크게 표면침식, 붕괴침식, 머드유동층의 연행부상 및 파랑에 의한 머드유동층 발생의 4가지 형식으로 분류된다(Mehta, 2014). “연행부상”이라는 말은 더욱 광범위하게 연구된 염수-담수의 성층화된 흐름에서 염수가 담수 속으로 연행부상(entrainment)되는 작용으로부터 차용된 용어이다. 미세 점착성 퇴적물의 경우에 토사입자들은 함수비가 큰 토사덩어리의 형태로 머드유동층으로부터 분리되어 부상되기 때문에, 이 용어는 퇴적물 이송학적으로 침식을 의미한다.

한편, 우리나라 서·남해안에는 갯벌이 널리 분포하고 있는데, 이러한 해역에는 부분적으로 수층과 저면의 경계면에 수 센티미터에서 수 미터의 두께를 가지는 유동적인 점토층이라 할 수 있는 머드유동층이 존재한다(Kim, 2011). 이러한 머드유동층은 고농도의 미세 퇴적토의 수중 부유체로 약 20~320 g/L의 농도 값을 갖는데(Ross et al., 1987), 머드유동층의 발생은 퇴적(압밀되어 저면을 형성하기 전 단계) 혹은 저면 침식(액상화 후 연행부상 발생 전 단계)의 과도기 단계에서 일반적인 사항이라 할 수 있다(Nguyen et al., 2012). 보통 머드유동층은 소성유체(plastic fluid)의 거동 특성을 보이는데(Hamm and Migniot, 1993), 실질적으로 전단강도가 영의 값을 갖기 때문에, 흐름 발생 시에 상부 수층과의 경계면은 불안정한 상태가 된다. 또한 단단하게 압밀된 저면 퇴적토에 비해 상대적으로 느슨한 결합구조를 갖는 머드유동층은 작은 전단 흐름하에서도 상부 수층으로 쉽게 부상되며, 이러한 특성으로 인하여 수층 탁도의 급격한 증가가 초래될 수 있다. 따라서 머드유동층의 부상 특성에 대한 명확한 이해 없이 과거 통상적으로 사용되어 온 저면 퇴적토의 침식률 공식의 적용은 침식률의 과소평가를 초래할 수 있다(Odd and Cooper, 1989).

머드유동층의 연행부상에 대한 연구는 실험장치의 부재 및 실험방법의 어려움으로 인하여 국내외적으로 그다지 많지 않은 상태이다. 해외에서의 대표적인 연구 사례로는 Mehta and Srinivas(1993)와 Winterwerp and Kranenburg(1997)을 들 수 있는데, Mehta and Srinivas(1993)는 특수 제작된 디스크 펌프가 부착된 경주로형 순환수조를 이용하여 고령토 머드유동층의 연행부상률을 측정하였으며, Winterwerp and Kranenburg (1997)는 Delft 수리 연구소의 환형수조를 이용하여 Caland 수로 머드유동층의 연행부상률을 측정하였다. 반면, 국내의 경우 실험장치 및 전문연구인력의 부족으로 인하여 머드유동층의 연행부상에 대한 연구는 완전히 전무한 실정이다.

이에 본 연구에서는 머드유동층의 연행부상 특성 해석을 위한 기초연구로써, 현장 퇴적물에 대한 실험에 앞서 고령토 시료를 이용한 실험이 수행되었다. 연행부상 실험은 국내 최초로 제작된 전북대 환형수조와 2차원 전자유속계를 이용하여 수행되었으며, 이를 통하여 머드유동층의 연행부상률이 정량적으로 산정되었다. 연행부상 측정을 위한 실험 방법은 Mehta and Srinivas(1993)와 Winterwerp and Kranenburg(1997)의 연구들을 참조하여 정립되었으며, 도출된 연행부상률 산정 결과는 과거 연구결과와의 비교·분석을 통하여 그 타당성이 검토되었다.

2. 이론적 배경

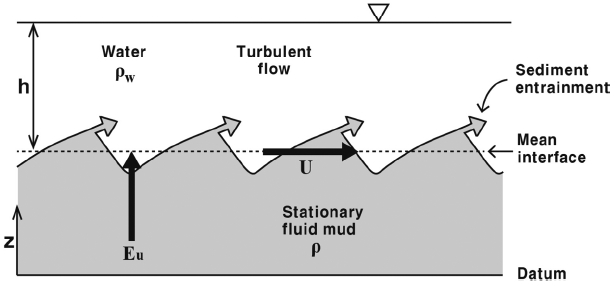
머드유동층의 연행부상은 흐름에 의한 난류 운동에너지의 생성과 퇴적물을 연행부상 시키기 위해 필요한 부력 에너지 및 점성에 의한 에너지 소산간의 평형을 나타내는 항들로 표현된다. Fig. 1에 주어진 바와 같이 밀도가 ρ인 머드유동층이 높이가 h이고 밀도가 ρ_w인 수층 아래에 놓여 있는 2개 층으로 된 밀도 성층 구조에서의 연행부상은 머드유동층의 경계면이 상승하는 속도인 연행부상률(E_u)의 항으로 표현된다. 또한 머드유동층과 수층 사이의 경계층에서의 평균 유속은 U이며, 이 흐름은 하부의 머드유동층을 상승시키기 위해 필요한 에너지를 공급한다.

이러한 시스템의 경우, 단순한 형태에서의 머드유동층 위의 수평적으로 균일한 경계층에 대한 부정상 난류에너지에 대한 평형식은 다음과 같이 표현 될 수 있다.

(1)

∂ek∂t=−u′w′¯∂U∂z−gρρ′w′¯+εt

여기서 e_k는 단위질량당 난류 운동에너지이며, u′은 종방향 유속의 순간 난류 변동치, w′은 연직(z)방향에서의 유속 변동치이고, ρ′은 ρ의 변동치, ε_t는 단위 질량 당 에너지 소산율, 그리고 g는 중력가속도이다. 한편, 난류전단의 생성항( -u′w′∂U⁄∂z)과 점성에 의한 에너지 소산항(ε_t)은 U³에 비례한다고 할 수 있으므로 A_EU³⁄h로 표현될 수 있으며, 난류운동에너지 e_k는 U²에 비례하므로 B_EU²⁄(h⁄E_u)로 표현 될 수 있다(Mehta, 2014). 따라서 식(1)은 다음과 같이 된다.

(2)

BEU2h/Eu=AEU3h−gρρ′w′¯

여기서 A_E는 비례계수, B_E는 축척을 나타내는 상수이며 (Zilitinkevich, 1975), h⁄E_u는 연행부상의 시간과 관련된 특성인자이다. 한편, 부력 에너지항인 −gρ′w′¯/ρ는 식(3)과 같이 부력 연행부상 플럭스(E_e), 침강 및 점착성과 관련된 부력 플럭스(E_s), 분자확산에 의한 부력 플럭스(E_d)의 합으로 주어지며, 각각의 항은 식(4)와 같이 표현된다(Moore and Long, 1971; Mehta and Srinivas, 1993).

(3)

−gρ′w′¯/ρ=Ee+Es+Ed

(4a)

Ee=−g′Eu

(4b)

Es=−g′ws=−CEg′hU

(4c)

Ed=DEg′DbUh

여기서 g′은 부력차(혹은 축소된 중력가속도)로 g(ρ–ρ_w)⁄ρ로 정의되며, C_E는 침강계수, D_E는 비례상수, D_b는 분자 확산계수이다. 한편, 분자확산에 의한 부력 플럭스(E_d)는 머드유동층의 연행 부상을 유발시키는 난류 조건 하에서는 그 값이 상대적으로 미미하기 때문에, 영으로 간주 될 수 있다. 따라서, 분자확산에 의한 부력 플럭스를 제외한 나머지 플럭스들을 부력 에너지항에 대입하고, 무차원 연행부상률( E˜u=Eu/U)에 대해 리차드슨 수(R_i)의 함수로 정리하면, 식(5)의 결과가 도출된다.

(5)

E˜u=EuU=AE−CERi2BE+Ri

여기서 g′h⁄U²으로 정의되는 R_i는 관성력에 대한 부력의 비를 나타내는데, 성층유체의 불안정성 해석시 사용되는 인자이며 프루드 수의 제곱근의 역수 형태를 취한다. 한편, 국부적으로 평형상태 즉, ∂(e_k)⁄∂_t = 0인 경우에, B_E는 영이 되므로, 식(5)는 다음과 같이 간단하게 된다.

(6)

E˜=AERi−CERi

결과적으로, R_i의 함수로 주어지는 E˜u의 산정식은 난류 전단과 점성에 의한 에너지의 영향을 받는 비례계수 A_E와 침강과 관련된 계수 C_E의 값으로 주어지며, 이 계수 값들은 실험을 통하여 산정되어야만 한다.

3. 연행부상 실험

3.1 실험장비

본 연구에서는 전북대 환형수조(Fig. 2)와 2차원 전자 유속계를 이용하여 머드유동층에 대한 연행부상 실험이 수행되었다. 본 연행부상 실험에 사용된 전북대 환형수조의 구조적 특성과 수동학적 특성에 대한 자세한 설명은 Hwang et al.(2005)에 주어진다. 한편, 앞서 식(6)에서 제시된 바와 같이 연행부상률은 리차드슨 수(R_i)의 함수로 표현되며, R_i는 머드유동층과 수층 사이의 경계층에서의 유속과 밀도의 함수로 주어진다. 따라서, 연행부상 실험시 밀도와 유속의 측정은 필수적인 사항이다.

본 연행부상 실험에서는 Alec사의 2차원 전자유속계(모델명 ACM2-RS)를 이용하여 머드유동층과 수층을 모두 포함하는 전체 단면에서의 유속이 총 9개 높이(2.5, 4.0, 5.5, 7.0, 8.5, 10.0, 11.5, 13.0, 14.0 cm)에서 측정되었다. ACM2-RS 유속계는 센서부의 직경이 6 mm로 상용 유속계 중에서 센서부의 크기가 가장 작다. 본 실험에서는 총 3개의 유속계가 동시에 적용되었는데, 유속 측정시 유속 센서에 의한 흐름 교란을 최소화시키기 위하여 각 유속계는 환형수조 원주 길이의 3등분되는 위치에 각각 거치되었으며, 3개의 각기 다른 높이에서 거의 준 동시에 유속이 측정되었다.

본 실험에서는 유속 측정의 효율성 및 정밀도 향상을 위하여, 인터페이스 및 PC로 연결된 통합 유속 측정 시스템이 구축되었다. Fig. 3에 제시된 바와 같이, 3개의 유속계는 인터페이스를 통하여 한 개의 PC로 통합 운용되었다. 한편, 각각의 유속계는 측정 높이의 조절기능을 갖춘 특수 제작된 거치대를 이용하여 환형수조에 장착되었다(Kim, 2011). 일반적으로 개수로에서는 수로 상부에 유속계가 거치되나, 환형수조에서는 흐름 생성을 위해 상부 링이 회전되므로, 본 거치대는 수조 바닥에 장착될 수 있도록 특수 제작되었다. 한편, 부유사 농도의 측정을 위해서는 전체 수심에 대해 거의 준 동시에 부유사 농도가 측정될 수 있도록 총 13개의 채수 밸브가 3~5개씩 분리 되어 각기 다른 높이(2.0, 2.5, 4.0, 4.5, 5.5, 6.0, 7.0, 7.5, 8.5, 10.0, 11.5, 13.0, 14.0 cm)로 환형수조 외벽에 부착되었다.

3.2 표본시료의 기본 특성

본 연구에서는 머드유동층의 연행부상률 실험을 위한 퇴적물 시료로 상용 고령토(kaolinite)가 사용되었다. 고령토는 점착성 퇴적물의 침식, 침강 등의 이송특성 해석을 위한 실내 실험 시에 가장 널리 사용되는 점토 중의 하나로써, 상용화 되어 있어 구입이 용이하다는 장점을 갖는다. 본 실험에서 사용된 고령토의 입경분포는 한국화학시험연구원에 의해 분석되었는데, 그 결과는 Fig. 4에 주어지며, 또한 광물학적 성분은 Table 1에 주어진다.

3.3 실험방법 및 실험조건

머드유동층의 연행부상 실험시 우선적으로 하부 머드유동층과 상부 수층으로 구성되는 2층 밀도성층(Fig. 1 참조)의 조성은 필수적 사항이다. 이를 위하여 본 연구에서는 환형수조 내에 물을 6 cm 높이로 채운 후, 바닥으로부터 약 2 m의 높이에 있는 저장탱크로부터, 수두차의 원리를 이용하여, 충분히 혼합된 동일 밀도의 머드유동층을 환형수조 바닥을 통하여 10 cm 두께로 주입하였다. 머드유동층-수층의 2층 밀도성층이 성공적으로 조성되는 즉시, 머드유동층을 포함하는 전체 깊이(총 16 cm)에 걸쳐 연직방향에서의 순간 농도분포를 측정하기 위해 환형수조 외벽의 총 13개 채수 밸브로부터 거의 준 동시에 탁수가 채취되었다. 초기 순간 농도의 측정이 완료되면, 환형수조 상부 링의 회전속도 조정을 통하여 단계별로 각기 다른 흐름을 발생시켰다. 각 단계별 흐름 발생 동안, 수조 내 전체 깊이에 걸쳐 유속 및 농도 측정이 거의 준 동시에 이루어졌다. 순간 연직 유속 분포의 측정은 통합 유속측정 시스템을 이용하여 기 설정된 총 9개 높이에서 거의 준 동시에 이루어졌으며, 각 단계별 순간 농도분포의 측정은 앞서 초기 순간 연직 농도분포 측정시 사용된 방법과 동일한 방법으로 수행되었다. 실험 방법에 대한 자세한 사항은 Kim(2011)에 주어진다.

본 연구에서는 고령토 머드유동층의 초기농도를 변화시키면서 총 6회의 실험이 수행되었다. 각 실험별 초기조건은 Table 2에 주어진다. 머드유동층은 고령토와 담수(수돗물)를 혼합하여 제작되었으며, 상부 수층 또한 담수로 조성되었다. 각 실험별로 초기 머드유동층의 농도(C_o)는 52 g/L에서부터 108 g/L까지 변화되었는데, 여기서 C_o는 2층 밀도성층 조성을 위하여 수조 바닥을 통하여 주입된 머드유동층의 평균 농도로써, 1 단계 흐름 발생 바로 전 시간, 즉 t=0에서의 머드유동층의 농도를 나타낸다. 또한, Table 2에는 수층의 초기 수온 값이 주어지는데, 모든 실험에서 상부 수층의 수온은 19.5~20.0°C로 거의 동일하게 유지되었음을 알 수 있다.

4. 실험결과

4.1 농도단면도

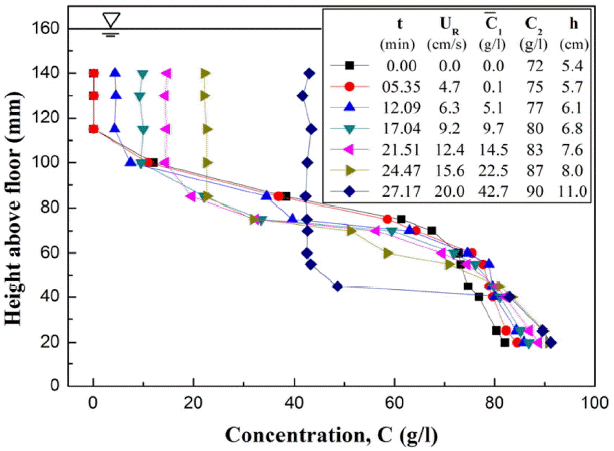
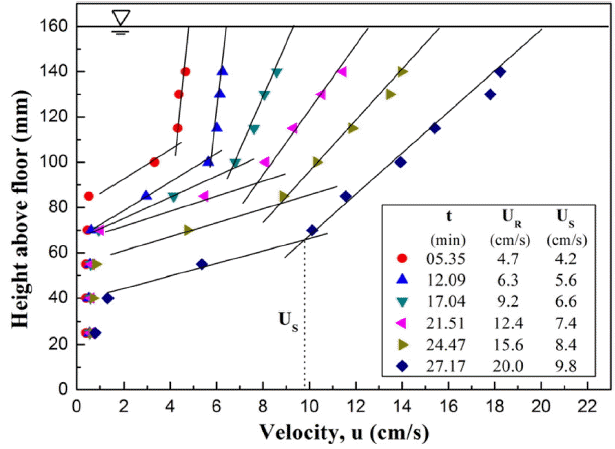
연행부상 실험시 측정된 결과 중 유속 증가에 따른 연직 농도단면 변화의 대표적인 예로 Test #3에 대한 결과가 Fig. 5에 주어지는데, 여기서 U_R은 환형수조 상부 링과 접합된 수면에서의 유속(cm/s)을 나타내며, t는 누적시간(min)이다. 그림으로부터, 2층 밀도성층 흐름에서의 농도단면도는 전형적으로 하부의 고농도 머드유동층과 상부의 저농도 수층으로 구분되고, 또한 두 층 사이에는 급격한 밀도경사를 갖는 밀도 경계층이 존재함을 알 수 있다. 또한, 상부 수층의 부유 농도가 연직방향에서 상당히 균등한 값을 가지며, 유속이 커짐에 따라 증가됨을 알 수 있다. 상부 수층의 농도가 균일한 이유는 환형수조 상부 링의 회전에 의해 생성된 상부 수층에서의 강한 난류 흐름에 의한 혼합현상 때문이다.

일반적으로 상부 수층의 농도 증가율은 밀도경계층에서의 유속(U_s), 부력차(g′) 및 상부 수층의 두께(h)에 따라 변화된다. 하부 머드유동층의 연행부상은 밀도경계층에서의 부력차가 난류 운동에너지보다 충분히 더 커질 때까지 지속된다(Kim, 2011). 연행부상이 지속됨에 따라 상부 수층 농도는 증가되고, 이로 인하여 밀도경계층에서의 난류 운동에너지는 감소되는 반면에, 상부 수층에서의 위치에너지는 증가되며, 결과적으로 연행부상은 현저히 감소하게 된다.

그림을 자세히 보면, 수층 아래로 매우 가파른 밀도경사(lutocline)를 갖는 밀도경계층이 존재함을 또한 알 수 있다. 이론적으로 이 경계층은 무한한 밀도경사 값을 가지나, 실질적으로는 가파른 유한의 밀도경사 값을 갖는다.

당초 연행부상 실험시 머드유동층의 초기농도는 연직방향에서 균일한 값을 갖도록 설정되었으나, 관측된 결과는 깊이에 따른 농도경사가 존재하고 바닥으로 갈수록 농도가 증가함을 보여준다. 또한 바닥 근처에서 머드유동층의 농도는 시이 지남에 따라 항상 증가되는 것으로 나타났는데, 이러한 결과는 고농도 부유토사(즉, 머드유동층)의 간섭침강에 의해 비롯된 것으로 여겨진다.

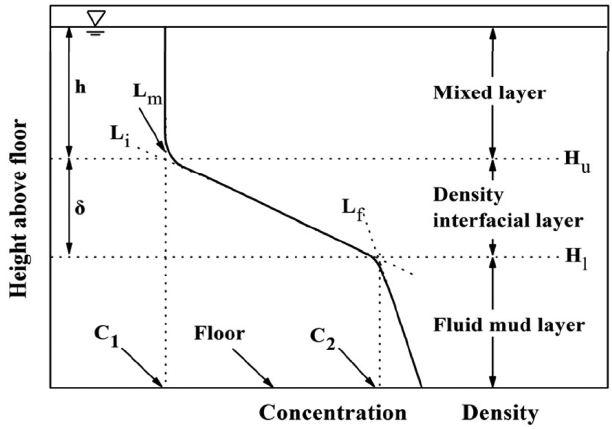
한편, 하부 머드유동층과 상부 수층으로 구성되는 2층 밀도성층 구조에서 전단 흐름에 의해 발달되는 밀도경계층 및 관련 인자들에 대한 정의는 Fig. 6의 모식도에 주어진다. Fig. 6의 모식도에서 밀도경계층의 상단과 하단 높이는 각각 H_u와 H_l로 정의된다. 여기서, 상단 높이 H_u는 밀도경계층의 농도 경사선 L_i와 수층의 농도 경사선 L_m의 교차점으로 정의되며, 하단 높이 H_l은 밀도경계층의 농도 경사선 L_i와 머드유동층의 농도 경사선 L_f의 교차점으로 제시된다. 한편, 이러한 정의는 과거 Narimousa and Fernando (1987) 및 Mehta and Srinivas(1993)가 사용한 정의와 일치한다. 이러한 정의에 입각하여, 본 연구에서는 각 실험별 농도단면도로부터 각 시간 단계별로 상부 수층의 수심 h 및 수심평균 농도 C1과 머드유동층의 상단(즉, 밀도경계층의 하단)에서의 농도 C₂가 각각 산정되었다(Fig. 5 참조).

4.2 유속단면도

연행부상 실험시 측정된 결과 중 흐름 단계별 유속단면 변화의 대표적인 예로 Test #3에 대한 결과가 Fig. 7에 주어진다. 그림으로부터, 상부 수층에서의 유속이 시간에 따라 증가됨을 알 수 있는데, 이는 연행부상 실험시 각 시간 단계별로 환형수조 상부 링의 회전속도를 증가시켜, 환형수조 내에서 발생되는 흐름력을 증대시켰기 때문이다.

상부 수층의 경우에, 유속의 연직방향 변화가 비교적 선형적임을 알 수 있는데, 이는 환형수조 상부 링의 회전에 의해 발생되는 흐름이 코엣류(couette flow)와 유사하기 때문이다. 또한 그림으로부터 상부 수층에서의 유속구배(ΔU⁄Δz)가 시간 단계가 커짐에 따라 함께 증가됨을 알 수 있는데, 이 또한 환형수조 내의 흐름이 코엣류와 유사하기 때문이다. 코엣류에서 유속구배는 상대속도에 비례하고 두 평판간의 거리에 반비례한다. 따라서 Fig. 7에서 시간 단계별 상부 수층 유속구배의 증가는 상부 링으로부터 밀도경계층까지의 거리, 즉 상부 수층 수심의 증가율보다 환형수조 상부 링 회전속도의 증가율이 상대적으로 더 크다는 것을 나타낸다.

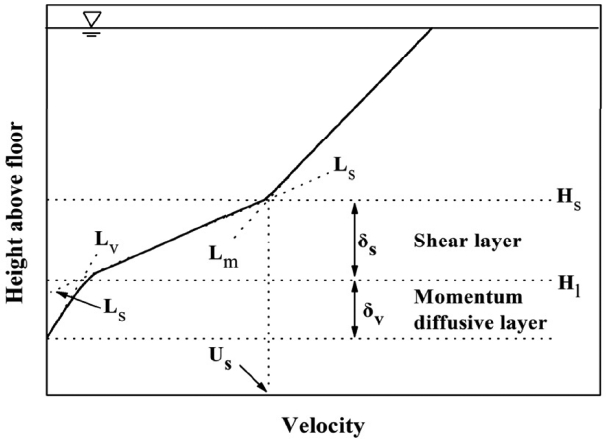
상부 수층 아래로는 매우 가파른 유속구배를 갖는 얇은 전단층(shear layer)이 존재함을 알 수 있다. 전단층은 머드유동층과 수층의 2층 밀도성층 시스템에서 두 층사이의 정역학적 안정성 및 혼합 등급을 지배하는 인자이기 때문에, 머드유동층의 연행부상 과정에서 이 층은 매우 중요한 역할을 한다. 전단층 아래로는 매우 얇은 운동량 확산층이 존재한다. 이 층에서의 유속구배는 상부 전단층에서의 유속구배보다 작아지며, 유속은 실질적으로 영이 된다. 운동량 확산층은 머드유동층의 연행부상과 직접적인 관련이 없으므로, 이에 대한 자세한 설명은 생략된다.

본 분석에서는 Narimousa and Fernando(1987) 및 Mehta and Srinivas(1993)의 방법과 유사한 방법으로 전단층이 정의되었다. 전단층의 정의를 나타내는 모식도는 Fig. 8에 주어진다. 그림에서 알 수 있는 바와 같이, 전단층의 상부경계 높이(H_s)는 전단층의 유속경사선 L_s와 상부수층의 유속경사선이 만나는 점으로 정의되었으며, 전단층의 하부 경계 높이 H_l은 L_s와 운동량 확산층의 유속경사선 L_v의 교차점으로 정의되었다. 한편, L_v의 산정을 위한 유속 데이터가 충분치 않으므로, 본 분석에서 전단층의 하부경계 높이(H_l)는 농도단면도에서 밀도경계층의 하부경계 높이와 같다고 가정하여 분석하였다.

본 연구에서 머드유동층의 연행부상은 실질적으로 전단층의 상부 경계 높이에서 발생한다고 가정되었다. 따라서 연행 부상률 공식 산정시 유속 매개변수로 전단층 상부 경계 높이에서의 유속 U_s가 적용되었다. 본 연구에서는 Fig. 8에 제시된 전단층의 정의에 대한 모식도에 근거하여 각 실험별 유속 단면도로부터 각 단계별 유속 U_s가 각각 산정되었다.

4.3 리차드슨 수 및 연행부상률의 산정

본 연구에서는 앞서 설명한 바와 같이 밀도성층 경계층에서의 유속 U로 전단층 상부 경계 높이에서의 유속 U_s가 적용되었는데, 리차드슨 수(R_i)와 무차원 연행부상률( E˜u)은 각각 다음과 같이 정의된다.

(7)

Ri=g′hUs2

(8)

E˜u=EuUs=Eeg′Us

여기서 g′는 부력차(buoyancy jump), h는 상부 수층의 수심이다. 참고로, 식(8)에서 연행부상률 E_u는 식(4a)에 의해 부력 연행부상 플럭스 E_e로 환산되었다. 한편, 본 연구에서는 g′ 계산시 ρ 값으로 ρ₂, ρ_w 값으로 ρ1값이 적용되었으며, 부력 연행부상 플럭스(E_e)는 Moore and Long(1971)에 의해 제시된 정의가 사용되었는데, 이 식들은 각각 다음과 같다.

(9)

g′=gρ2−ρ1¯ρ1¯

(10)

Ee=gρ1¯dmdt

여기서 ρ1는 상부 수층의 수심평균 밀도, ρ₂는 경계면에서의 머드유동층의 밀도, dm⁄dt는 머드유동층으로부터 상부 수층으로 이송되는 질량 플럭스이다. 한편, 식(10)에서 dt의 시간변화 동안 머드유동층으로부터 상부 수층으로 이송된 질량(dm)은 아래 주어진 식과 같이 상부 수층의 평균 농도( C1)와 상부 수층 수심의 곱의 시간 단계별 차로부터 산정되었다.

(11)

dm=C1¯h|t+dt−C1¯h|t

여기서 t와 t + dt는 각각 C1 및 h가 측정된 시간 단계의 전후를 나타낸다. 또한 ρ1과 ρ₂는 각각 C1과 C₂에 해당하는 부피밀도 값들인데, 농도 C의 부피밀도 ρ로의 환산은 다음의 식을 이용하여 이뤄질 수 있다.

(12)

ρ=ρw+C(1−ρwρs)

여기서 ρ_w와 ρ_s는 각각 물과 토사 입자의 밀도이다.

본 연구에서는 총 6회의 연행부상실험을 통하여 도출된 농도 및 유속단면도 데이터들에 식(7)~식(12)의 식들을 적용하여 각각의 R_i 값들 및 이에 대응하는 E˜u값들이 산정되었다.

4.4 연행부상률 산정 결과

고령토 머드유동층에 대한 무차원 연행부상률 E˜u 및 리차드슨 수 R_i의 산정결과는 최소자승접합법으로 산정된 연행부상률 곡선과 함께 Fig. 9에 도식된다. 비록 데이터가 다소 분산되어 있기는 하나, R_i가 증가함에 따라 E˜u이 감소함을 명확히 보여주고 있다. 특히 R_i가 비교적 큰 구간에서 E˜u이 급격히 감소하고, 작은 R_i 구간에서는 느리게 감소하는 비선형적인 형태를 보인다. R_i는 두 밀도 경계층에서의 전단유속(U_s)에 대한 부력차(g′)의 비로 정의되므로, U_s가 작을수록 그리고 g′가 클수록 R_i는 증가하게 된다. 한편, 일반적으로 U_s이 작다는 것은 흐름력이 작음을 의미하며, g′가 크다는 것은 하부 머드유동층의 밀도가 상대적으로 더 크고 주어진 흐름력에 대한 머드유동층의 저항력이 더 큼을 의미하기 때문에, R_i가 증가할수록 E˜u은 감소하게 된다.

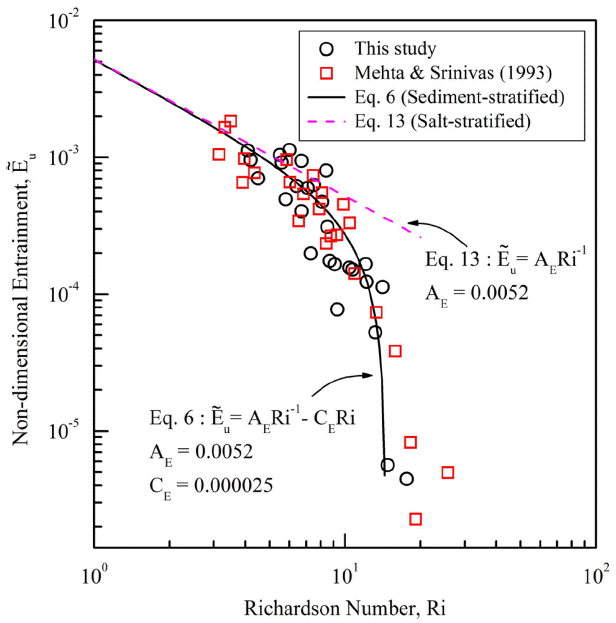
한편, 머드유동층의 연행부상률 산정식은 리차드슨 수의 함수로 주어지는데, 앞서 식(6)에서 설명된 바와 같이, 계수 A_E와 C_E는 실험을 통하여 산정되어야만 하는 실험적 계수이다. 따라서, 본 실험을 통하여 도출된 고령토 머드유동층에 대한 연행부상률 측정 데이터들에 식(6)을 적용하여, 최소자승접합법으로 산정한 실험적 계수 A_E와 C_E 값들은 그림에 도식된 것처럼 각각 0.0052 및 0.000025인 것으로 나타났다.

본 실험을 통하여 도출된 머드유동층의 연행부상률 산정 결과의 타당성 검증 및 특성 분석을 위하여, 본 연구 결과와 타연구 결과와의 비교·분석이 수행되었다. 과거, 염수 성층 시스템에서의 염수의 연행부상에 대한 연구는 상당히 많이 수행되었다(Ellison and Turner, 1959; Lofquist, 1960; Kato and Phillips, 1969; Narimousa et al., 1986). 반면 토사 성층 시스템에서 수행한 머드유동층의 연행부상에 대한 연구는 몇몇 사례 밖에 없는 상태로, 가장 대표적인 예는 Mehta and Srinivas(1993)의 연구라 할 수 있다. 본 연구를 통하여 도출된 Fig. 9의 결과와 함께 Mehta and Srinivas(1993)의 실험 결과 및 염수 성층 시스템에서의 연행부상 산정식이 Fig. 10에 도식된다.

그림에서 점선은 염수와 담수의 2층 성층 구조에서의 염수의 무차원 연행부상률( E˜u)을 나타내는데, 이에 대한 표현식은 다음과 같다.

(13)

E˜u=AERi−1

여기서 A_E 값은 Fig. 9의 결과와 동일하게 0.0052이다. 한편, 이 식은 염수 성층 시스템에서의 염수의 연행부상률을 나타내는 가장 타당성 있는 식(Narimousa et al., 1986)으로, 염수의 연행부상률은 R_i가 증가함에 따라 선형적으로 감소하며, 결과적으로 단지 1개의 비례계수 A_E의 함수로 표현된다는 것을 나타낸다. 또한 Fig. 10으로부터, 염수 성층 구조에서 보다 토사에 의한 밀도 성층 구조에서 R_i의 증가에 따른 E˜u의 감소가 훨씬 더 빠른 것을 알 수 있다. 염수 성층 구조과 토사 성층 구조 사이에서의 연행부상률의 차이는 부유 토사 입자(혹은 플록)의 침강 효과로 인하여 비롯된 것으로 알려지고 있다(Mehta and Srinivas, 1993). 염수나 수온 성층의 시스템과 달리, 이러한 토사의 침강은 입자의 연직방향 플럭스에 영향을 미치는 가장 중요한 작용 요소임을 알 수 있다.

한편, 그림에서 가장 주목할 만한 사항은 본 연구 결과와 과거 수행된 Mehta and Srinivas(1993)의 연구가 대체적으로 유사한 값을 갖는다는 것이다. 환형수조가 아닌 경주로형 수로를 사용한 실험에도 불과하고, 고령토 머드유동층의 연행부상률 산정 결과가 거의 유사한 것으로 나타났다는 것은 상당히 흥미로운 결과라고 할 수 있다. 이는 실험장치나 실험방법에 다소 차이가 있더라도 실험에 사용된 재료의 특성이 거의 동일하면 유사한 결과가 도출되어야만 하는 기본적인 관점에 비추어, 본 실험을 통하여 산정된 고령토 머드유동층의 연행부상률 측정값들은 타당성 있는 값들이라고 할 수 있다. 결론적으로 본 연구에 사용된 전북대 환형수조가 연행부상률 산정을 위한 실험시 성능적으로 문제가 없는 것으로 판단되며, 머드유동층-수층의 2층 밀도 성층의 제작 과정을 포함하는 연행부상 실험방법 및 연행부상률 산정 결과에 대해 타당성을 갖는다고 할 수 있다.

5. 결 론

본 연구에서는 국내 최초로 머드유동층에 대한 연행부상 실험이 전북대 환형수조를 이용하여 수행되었다. 연행부상 실험은 고령토 머드유동층의 초기농도를 변화시키면서 총 6회 수행되었으며, 각 실험별 농도 및 유속 단면도의 시간적 변화 측정 결과들로부터 머드유동층의 연행부상률이 정량적으로 산정되었다.

실험 결과에 따르면, 리차드슨 수가 증가함에 따라 머드유동층의 연행부상률은 명확히 감소하는 것으로 나타났다. 특히, 리차드슨 수가 비교적 큰 구간에서 연행부상률이 급격히 감소하고, 작은 리차드슨 수 구간에서는 느리게 감소하는 비선형적인 형태를 보였다. 이는 염수 성층 구조에서 보다 토사에 의한 밀도 성층 구조에서 리차드슨 수가 증가할수록 연행부상률이 훨씬 더 빠르게 감소한다는 것을 나타낸다. 염수성층 구조와 토사 성층 구조 사이에서의 연행부상률의 이러한 차이는 부유 토사 입자(혹은 플록)의 침강 효과로 인하여 비롯된 것으로, 염수나 수온 성층의 구조에서와는 달리, 토사의 경우 침강은 입자의 연직방향 플럭스에 영향을 미치는 가장 중요한 작용 요소임을 의미한다.

한편, 과거 동일한 시료에 대해 수행된 Mehta and Srinivas (1993)의 연구 결과와의 비교·분석을 통해 본 연구 결과는 매우 타당한 결과임이 확인되었다. 특히, 서로 다른 실험 장치를 사용했음에도 불과하고, 본 연구 결과와 과거 수행된 Mehta and Srinivas(1993)의 연구 결과가 거의 동일한 범위의 값을 갖는다는 것은 매우 고무적이다. 결론적으로 이러한 사실들은 본 연구를 통하여 사용된 전북대 환형수조가 그 성능상에 문제가 없으며, 연행부상 실험 결과 역시 정량적·정성적으로 타당성을 갖는다는 것을 간접적으로 입증한다고 할 수 있다.

환형수조를 이용한 머드유동층의 연행부상률 산정