1. 서 론
근래, 세계적으로 지진의 발생빈도가 급증함에 따라 지진에 의한 피해가 다수 보고되고 있고, 뿐만 아니라 해저지진이나 해저지반의 활동 혹은 해저화산 등에 의해 수 분에서 수 시간의 주기를 갖는 지진해일이 빈번히 발생한다. 이러한 지진해일은 일반적으로 연안에 가까워짐에 따라 천수, 굴절, 회절 및 쇄파 등에 의해 변형되고, 해안에 접근하는 동안 응축된 에너지에 의해 파고가 증가되며, 동시에 파장이 감소되는 현상이 동반된다. 대표적인 예로 2004년 12월 26일 발생한 규모 M9.1의 지진에 의한 인도양지진해일과 2010년 2월 27일 칠레에서 발생한 규모 M8.8의 지진에 의한 지진해일, 가장 최근의 예로 2011년 3월 11일 일본에서 발생한 규모 M9.0의 동일본대지진에 의한 지진해일 등의 경우를 들 수 있다.
한편, 지진해일은 경우에 따라 막대한 인명피해 뿐만 아니라 저지대의 침수·범람에 따른 가옥의 파괴, 항만, 도로 및 철도와 같은 사회간접자본의 치명적인 붕괴 등 연안역에 엄청난 피해를 발생시킨다. 여기서, 연안역에서 도로와 철도의 일부 구간은 교량으로 구성된 경우가 많고, 인도양지진해일과 동일본지진해일 시에 해안가와 하천에 가설된 연안교량들이 유실된 수 많은 사례가 보고되어 있다. 이러한 연안교량의 파괴는 긴급한 피해복구를 포함한 사회·경제활동에도 심각한 지장을 초래한다. Photo 1에 동일본대지진에 의한 지진해일로 연안교량이 피해를 입는 당시의 상황을 예로 나타낸다.
국내에서는 지진해일에 의한 교량의 피해사례가 보고된 바는 없지만 Kim et al.(2015)은 해외에서 발생된 지진해일에 의한 교량의 피해유형을 검토하고, 지진해일이 내습할 가능성이 높은 동해연안에 가설된 연안교량에 대해 교량의 형태와 교각높이 등을 조사하여 다음의 Table 1과 같은 결과를 제시하고 있다. 이에 따르면 전체 15 m 이하의 교량 중에 5 m이하의 교량이 57%로 가장 많은 부분을 포함하고 있다. 이로부터 1983년 동해안의 임원항에 내습한 중부지진해일의 경우 처오름고가 5 m 정도이었다는 것(Kim et al., 2007)을 감안하면 중부지진해일급 이상의 지진해일이 내습하는 상황에서는 지진해일에 의한 연안교량의 피해가 충분히 예상될 수 있다.
지진해일은 지형적인 요소와 결부되면서 수심이 깊은 경우에는 고립파로, 수심이 얕은 경우는 단파로 연안에 도달하기 때문에 지진해일과 연안교량으로 대표되는 구조물과의 상호작용해석에서는 단파 혹은 고립파로 근사될 수 있다(Ramsden, 1993). 여기서, 연안교량에 작용하는 지진해일파력에 대한 연구는 2004년 인도양지진해일 시에 다수의 교량이 유실되는 피해를 입은 이후 본격적으로 수행되기 시작하였다. 예로, Iemura et al.(2005), Shoji and Moriyama(2007) 등은 당시 교량의 피해정도 및 교량의 안정성에 대해, Araki(2010a; 2010b) 등은 실험에 기초하여 교량에 작용하는 지진해일파력에 대해, Shoji et al.(2009)은 지진해일파력의 분류에 대해, Shigihara et al.(2010)은 지진해일파력과 교량의 안전율에 대해 각각 연구를 수행하였다. 특히, Shoji et al.(2010)은 쇄파단파의 작용 하에 교량에 작용하는 수평 및 연직방향의 지진해일파력의 연구를 수행하였다. 한편, 지진해일파력의 수치해석에서는 대부분이 고정도의 수치해석법으로 알려진 Navier-Stokes운동방정식과 VOF(Hirt and Nichols, 1981)법을 병용하는 수법 혹은 SPH(Smoothed-Particle Hydrodynamics)법 등을 적용하고 있다. 이에 대한 연구사례로 Arikawa et al.(2005), Xiao and Huang(2008), Shigihara et al.(2010), Nakamura et al.(2013), Tanabe et al.(2013), Yim and Azadbakht(2013), Bricker and Nakayama(2014) 및 Xu(2015) 등의 다수를 들 수 있다. 이들의 대부분은 수치결과를 실험결과와 비교하여 수치해석의 유용성을 확인하고 있다. 또한, 지진해일파력의 수치해석에 Navier-Stokes solver에 기초한 혼상류해석법으로부터 지진해일과 교량의 상호작용에서 특히 공기의 역할을 규명하고 있는 연구사례도 있으며, 이에 대해서는 항력과 관성력을 고려한 Morison식으로부터 고립파에 의한 지진해일파력을 추정한 Kim et al.(2016), 단파의 전파과정에서 발생하는 공기의 혼입이 파력에 미치는 영향을 검토한 Hartana et al.(2013) 및 교량에 작용하는 단파에 의한 파력의 분류에 대한 Lau et al.(2011) 등을 들 수 있다.
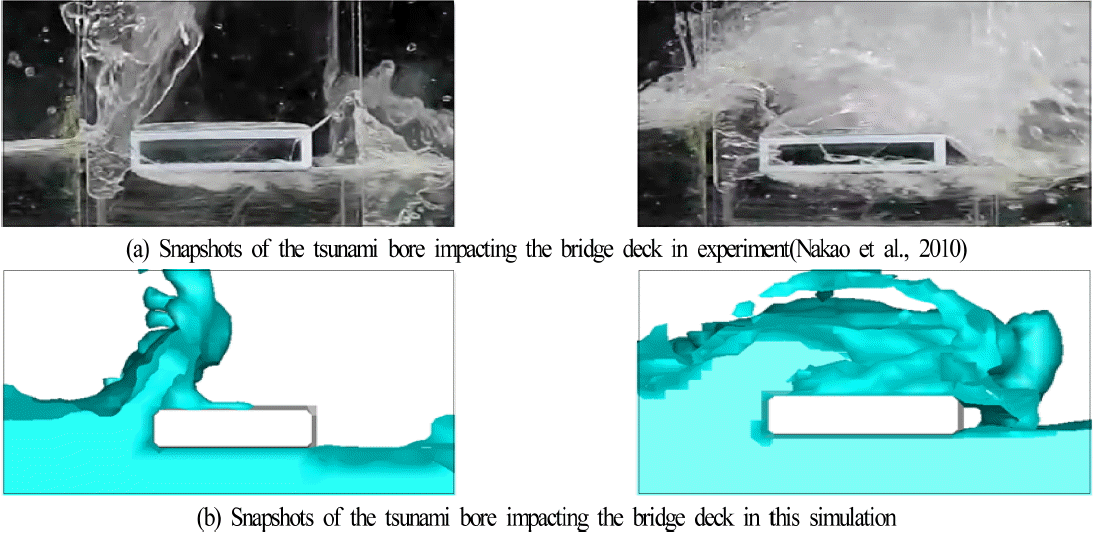
본 연구에서는 지진해일을 단파로 가정하여 지진해일과 연안교량과의 상호작용해석을 수치적으로 수행한다. 수치해석기법으로는 연안교량에 작용하는 지진해일파력을 고정도로 해석할 수 있고, 또한 유용성이 충분히 검증된 3차원혼상류해석법인 TWOPM-3D(3D one-field model for immiscible two-phase flows)를 적용한다(Lee et al., 2011). 동시에, TWOPM-3D에 의한 수치해석결과의 검증은 Nakao et al.(2010)에 의한 수조실험결과와의 비교·분석으로부터 검토된다. 이와 같은 타당성을 근거로 2004년 인도양지진해일 시에 피해를 입은 인도네시아 Lueng Ie Bridge(Shoji et al., 2009)를 중심으로 단파강도, 수심, 연안교량의 형상 및 거더(girder) 수 등을 변화시켜 연안교량에 작용하는 작용파력의 변화특성을 검토·분석한다.
2. 수치해석이론
본 연구의 수치해석에서 단파는 고수위와 저수위의 각 저수조(storage water tank)를 분리하는 중간의 게이트를 순간적으로 제거함으로써 수위차로 조파된다. 이 때, 수치해석에서는 게이트의 두께와 게이트가 개방되는데 소요되는 시간은 무시되었다. 한편, 단파는 전파과정에서 다량의 공기가 혼입되어 매우 복잡한 수면거동을 나타내는 것으로 알려져 있다(Arnason, 2005; Lee et al., 2008b). 따라서, 본 연구에서는 이러한 단파의 동역학적 거동을 상세히 검토하기 위하여 비선형, 비정수압 및 점성을 동시에 고려할 수 있는 기존의 fully nonlinear Navier-Stokes방정식에 상층부의 공기의 영향 및 수중으로 연행되는 공기의 영향을 고려할 수 있도록 수정된 two-phases fully nonlinear Navier-Stokes방정식을 기초방정식으로 적용하여 유한차분법으로 수치해석을 수행하였다(Lee et al., 2008a). 또한, 난류의 영향을 고려하기 위하여 LES(Large Eddy Simulation)모델(Smagorinsky, 1963)을, 수면형의 추적에는 VOF법(Hirt and Nichols, 1981)을 적용하였다. 기초방정식의 이류항에는 1차원 CIP법을 방향분리법(directional splitting method)을 사용하여 3차원으로 확장하는 MCIP법(Multidimensional Cubic Interpolated Pseudo Particle)법(Nakamura and Yabe, 1999)을 채용하여 수치확산을 최소화하였고, 비이류항에 대해서는 유한차분법에 기초하여 계산하였다. 여기서, 서로 혼합되지 않는 혼상(multi-phase)의 점성 및 비압축성 유체를 고려하면 각각의 유체는 서로 다른 상의 유체와 명확한 경계면으로 식별될 수 있다. 즉, 혼상유체의 흐름운동에서 경계면의 추적이 가능할 경우 서로 혼합되지 않는 혼상유체의 운동에 대해서 단일유체모델(one-field model for immiscible two-phase fluid)을 적용할 수 있다. 단일유체모델은 각 상의 유체가 국소질량중심과 함께 이동하는 것으로 가정하여 식(1) 및 식(2)~(4)와 같이 단일의 연속방정식(1)과 각 방향의 Navier-Stokes운동방정식(2)~(4)에 의해 기술될 수 있다.
(2)
(3)
(4)
여기서, t는 시간, u, v, w는 x, y, z방향에 대한 각 유속성분, p는 압력, g는 중력가속도, τij는 SGS(Sub-Grid Scale)에서 난류응력, Dij는 변위-응력에 대한 GS(Grid Scale)성분, Fs는 표면장력에 의한 체적력, λ는 부가감쇠영역에서의 감쇠계수, ρ ^ v ^
3. 본 수치해석의 타당성 검토
3.1 Nakao et al.(2010)에 의한 수리실험의 개요
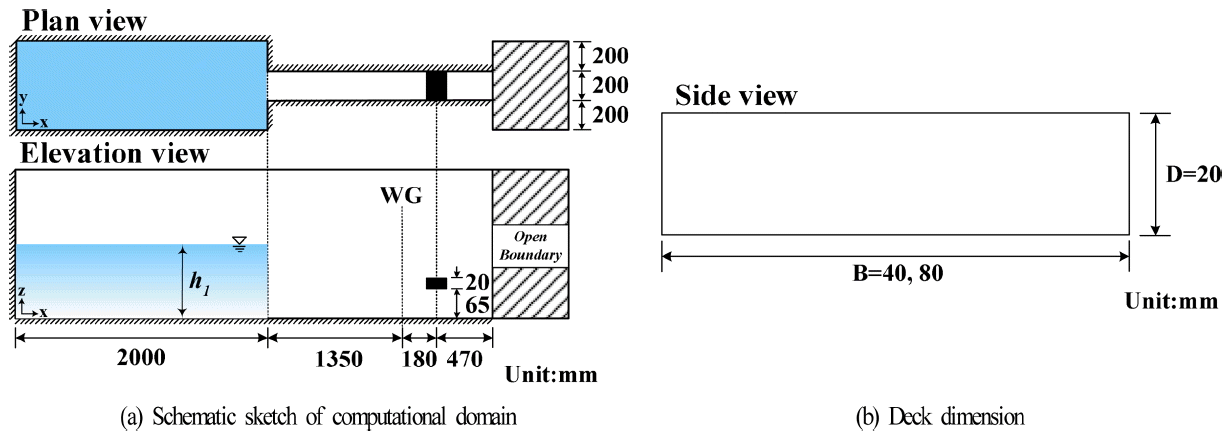
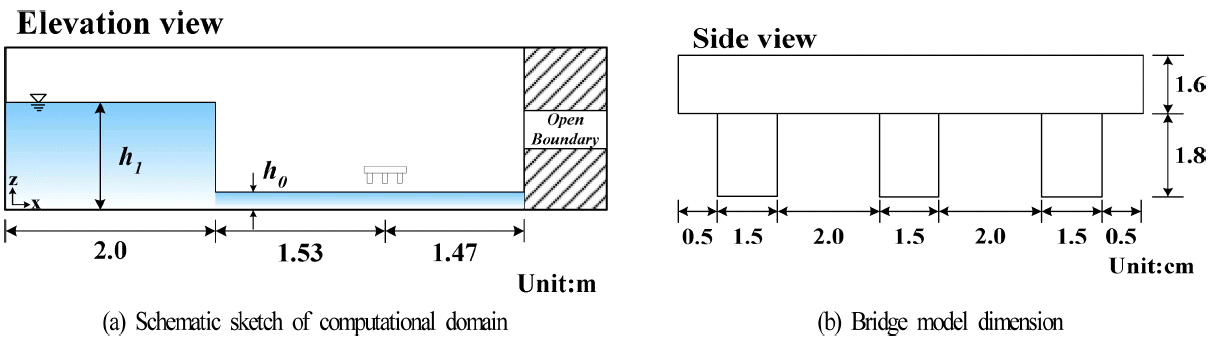
Nakao et al.(2010)은 상·하류측에 큰 수위차를 갖는 수조 내 게이트를 급속히 개방하여 이 때 발생하는 단파가 하류측의 교량에 작용하는 파력을 측정하였다. 본 연구의 수치해석의 검증에 적용되는 모델교량의 형상 및 제원은 Nakao et al.(2010)에서의 실험조건과 동일하게 Fig. 1과 같이 구성되었으며, 여기서 수조의 크기는 길이 4 m(상류측 : 길이 2 m, 폭 0.6 m; 하류측 : 길이 2 m, 폭 0.2 m)로, 단파를 발생시키기 위하여 상류측에서 하류측으로 2 m의 지점에 게이트를 설치하였다. 실험과 수치해석 모두 게이트의 상류수심 h1을 20, 23, 25 cm로 각각 변화시켜 교량에 작용하는 수평 및 연직파력을 측정하였다. 격자는 교량의 주변 영역에서 Δx = 0.5 cm, Δy = 1 cm, Δz = 0.5 cm로 구성되었고, 수조 끝단은 개경계(open boundary)를 적용하여 반사파가 발생하지 않도록 하였고, 모델교량으로 폭 B와 높이 D의 비 B/D가 2(40 mm/20 mm), 4(80 mm/20 mm)인 직사각형단면을 사용하였으며, 이는 거더가 없는 RC 슬래브(slab)교에 해당한다.
3.2 수치해석의 결과
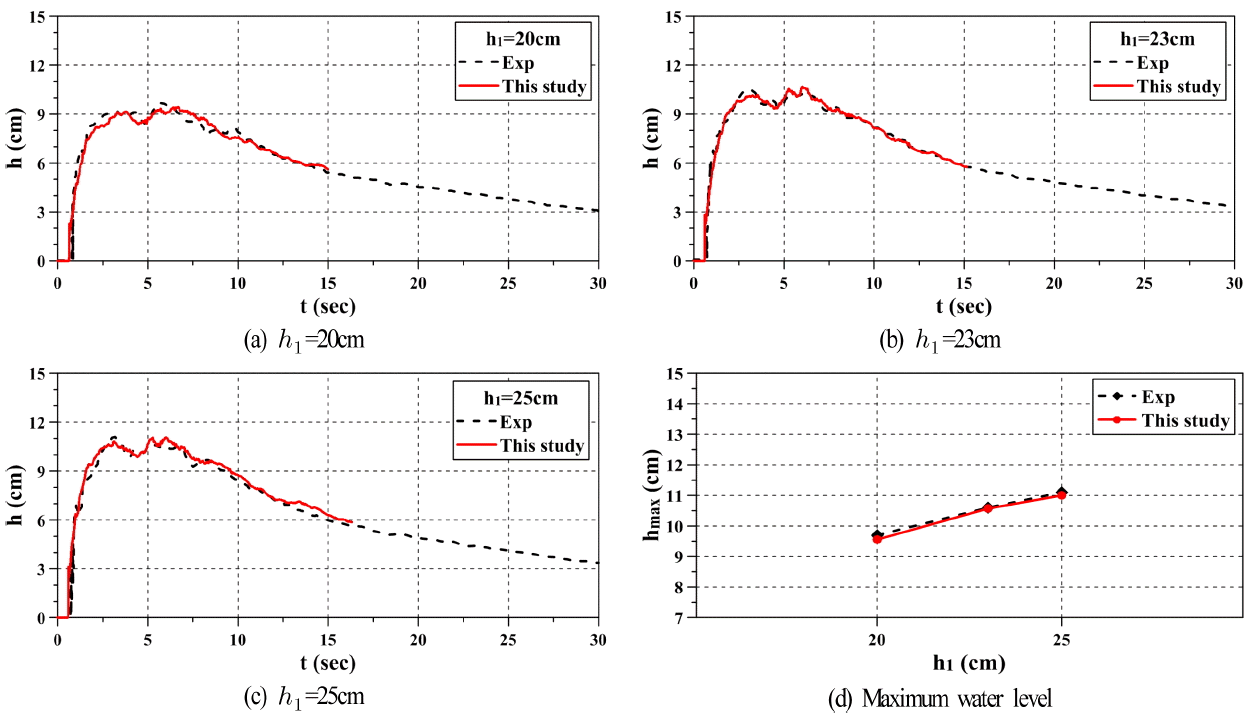
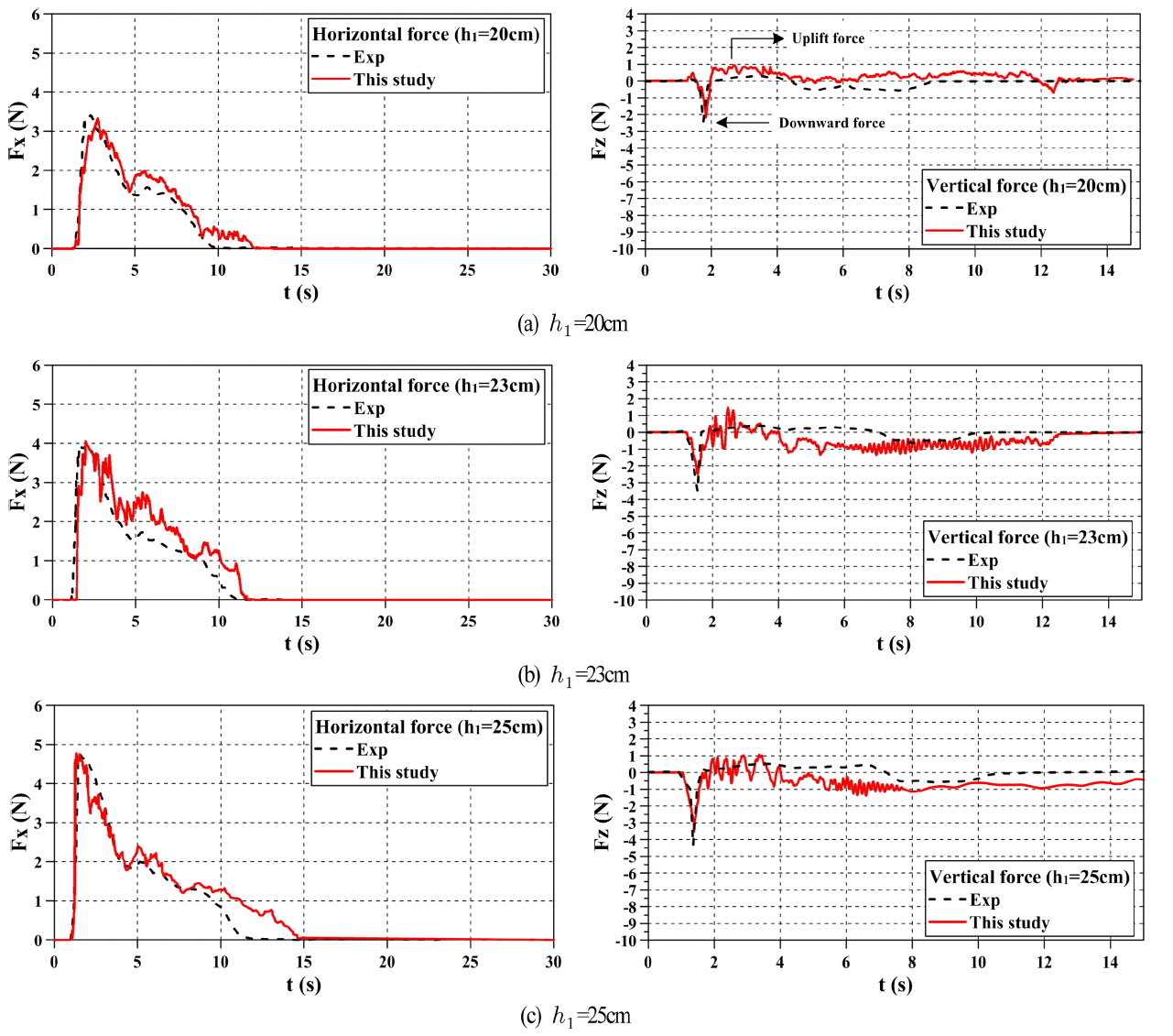
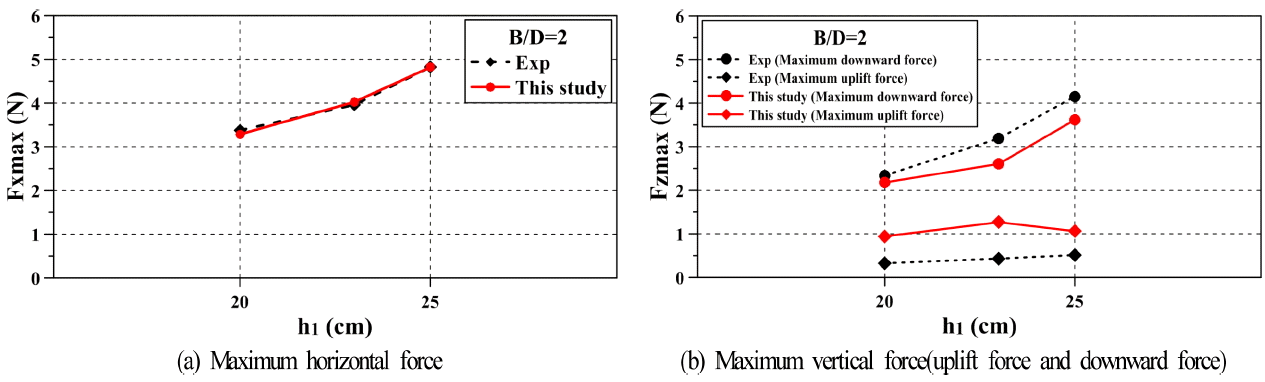
Fig. 2는 모델교량이 설치되지 않은 경우에 모델교량의 위치에서 상류수심이 h1= 20, 23, 25 cm일 때 단파의 수위변동에 따른 수치해석결과와 실험결과를 비교한 것이고, Figs. 3과 4는 B/D = 2인 모델교량의 데크(deck)에 작용하는 단파에 의한 수평(horizontal) 및 연직(vertical)파력의 시계열과 최대 파력을 각각 비교한 결과이다. 여기서, 연직상방의 최대파력을 최대연직상방파력(maximum uplift force), 그 연직하방의 최대파력을 최대연직하방파력(maximum downward force)으로 각각 정의한다.
상류수심 h1의 변화에 따른 단파의 수위변동 h에 관한 Fig. 2의 실험치와 해석치를 비교하면 단파가 도달하는 시간과 시간의 경과에 따른 수위의 변동형상 및 t = 5 s 전후에서 발생하는 높은 수위에 관하여 모두 좋은 대응성을 나타내고 있으며, 최대수위를 제시한 Fig. 2(d)로부터도 실험치와 해석치가 잘 일치한다는 것을 확인할 수 있다. 다음으로, 모델교량에 작용하는 Fig. 3의 파력을 살펴보면 적용된 B/D = 2에서 수평파력 Fx는 두 결과에서 최대치의 발생시간 전후에서 약간의 위상차가 발생하지만 시간의 변화에 따른 파력의 변동과정, 즉 단파의 도달과 더불어 급격히 파력이 상승한 다음에 최대파력이 나타나고, 이어서 파력이 저감되는 일련의 과정이 잘 일치하는 것을 알 수 있고, 특히 Fig. 4(a)에서 최대수평파력 Fx max에서도 두 결과가 거의 동일한 값을 나타내는 것을 알 수 있다. 한편, 연직파력 Fz의 경우를 살펴보면 모델교량에 단파가 도달하는 즉시 하향의 연직파력이 발생하고, 시간의 경과에 따라 상향의 연직파력(양력)이 발생하지만 경우에 따라서는 하향과 상향의 연직파력이 반복되는 상황이 일어나기도 한다. 여기서, 연직파력의 경우에 최대치 Fx max는 단파가 모델교량을 월류하기 때문에 하향으로 나타나고, 시간적으로는 단파가 도달한 즉시 발생된다. 하지만, 단파가 교량을 월류하지 않는 경우에는 하향연직파력은 발생되지 않을 것이다. 연직파력의 경우 상향력이 하향력보다 두 결과에서 오차가 상대적으로 크며, 상향력의 수치해석결과에서는 진동성분이 크게 포함되어 나타난다. 이러한 결과는 Nakamura et al.(2013)이 지적하고 있는 바와 같이 데크의 하부에 형성되는 와의 형성에 대한 실험결과와 수치결과에서의 차이에 기인하는 것으로, 와의 형성이 수치적으로는 정확하게 재현되지 않기 때문인 것으로 판단된다. 본 수치해석결과와 Nakamura et al.(2013)에 의한 수치해석결과를 비교하면 본 연구의 경우가 진동성분이 훨씬 작게 나타나는 것을 알 수 있다. 연직파력에서 최대하향력과 최대상향력을 제시한 Fig. 4(b)를 보면 최대상향력에서 데크 하부에서 와 발생에 대한 재현성 때문에 두 결과의 차이가 약간 크게 나타나지만 전반적으로 시간의 경과에 따른 연직파력의 변동양상이 잘 일치하는 것으로 판단된다.
Fig. 5는 Fig. 1에서 제시된 경우와 동일한 조건에서 B = 80 mm(B/D = 4)인 경우에 h1= 25 cm에서 단파가 데크에 도달하여 최대처오름고가 발생하는 순간과 그 직후의 수위의 변동상황을 나타낸 것으로, Nakao et al.(2010)에 의한 실험과 본 수치해석으로부터 얻어진 결과이다. 수치해석결과에서 단파가 데크에 작용한 직후의 처오름현상과 최대처오름고가 발생한 이후 교량을 월류하는 상황 등을 잘 재현하고 있는 것을 알 수 있다. 반면, 단파가 데크에 도달하는 순간 데크 배후에서의 수위상승이 수리실험에서는 나타나지만 수치결과에서는 데크 배후면에서 보다 이격된 거리에서 보다 작게 나타나는 것을 알 수 있으며, 이는 수치해석에서 고려되지 않은 데크에서 표면마찰 등의 영향으로 판단된다.
4. 수치해석
4.1 계산조건
교량에 작용하는 단파에 의한 지진해일파력의 수치해석은 2004년 인도양지진해일시 인도네시아에서 실제로 약 4 m가량 이동된 Lueng Ie Bridge(Shoji et al., 2012)를 대상으로 하였다. 본 연구에서는 Fig. 6과 같이 총 길이 5 m, 폭 0.2 m의 3차원수치파동수조를 적용하였으며, 단파를 발생시키기 위하여 상류측에서 하류측으로 2 m인 지점에 게이트를 설치하였다. 그림에서 나타내는 바와 같이 하류측 수심은 h0= 3 cm로 일정하며, 상류측 수심은 h1= 10, 12, 14, 16, 18 cm로, 단파강도를 변화시켜 연안교량에 작용하는 수평 및 연직파력을 산정·분석하였다. 여기서, 단파강도는 게이트의 상류측과 하류측의 수심차
h1-h0로 정의된다. 격자구성은 교량의 주변영역에서 Δx = 0.5 cm, Δy = 1 cm, Δz = 0.2 cm로 구성하였고, 수조의 끝단을 개경계로 설정하여 흐름에 미치는 반사류의 영향이 없도록 하였다. 적용된 모델교량은 실제 교량의 크기를 1:108로 축척된 값이며, 하류측 수면상의 1 cm에 설치되었다.
4.2 단파강도의 변화에 따른 작용파력의 변화
4.2.1 수위변동
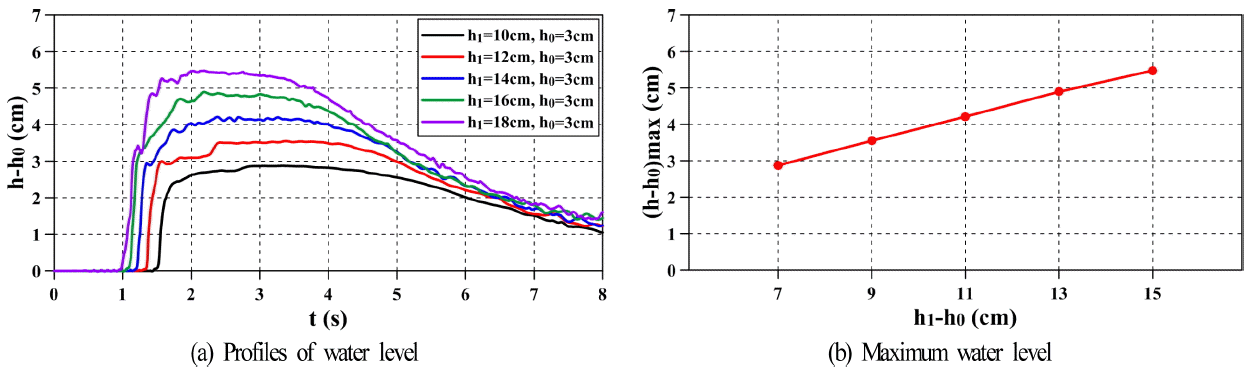
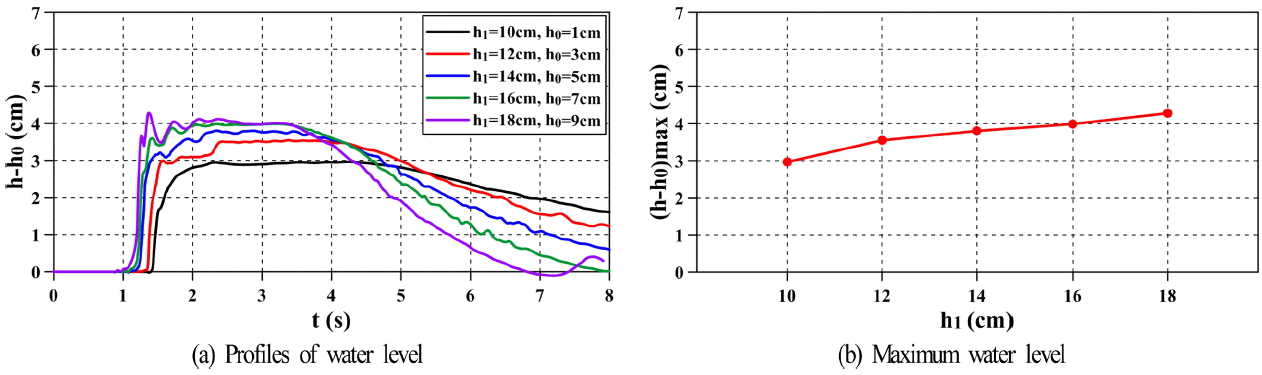
Fig. 7(a)는 Fig. 6(a)에서 제시된 수로에서 교량이 존재하지 않는 경우 상류측 수심 h1= 10, 12, 14, 16, 18 cm 및 하류측 수심 h0= 3 cm로 일정할 때 모델교량이 놓이는 위치의 중앙에서 수위의 시간변동을 나타내고, Fig. 7(b)는 각 경우에 최고수위를 나타낸다. 결과를 살펴보면 단파강도가 강할수록 상류측의 수심이 깊어지기 때문에 단파의 전파속도가 빨라지고 초기 불연속면에서 형성되는 큰 수위변화 및 빠른 유속으로 인한 표면에서 국부적인 쇄파로 불안정한 수위(파상단파; Lee et al., 2008b)가 나타나는 것을 알 수 있다. 그리고, 상류측 수심이 일정한 간격으로 증가함에 따라 최고수위는 거의 선형적으로 증가하는 현상을 확인할 수 있으며, 단파강도의 변화에 따른 이러한 결과는 Lee et al.(2008b)과 일치한다.
4.2.2 작용파력
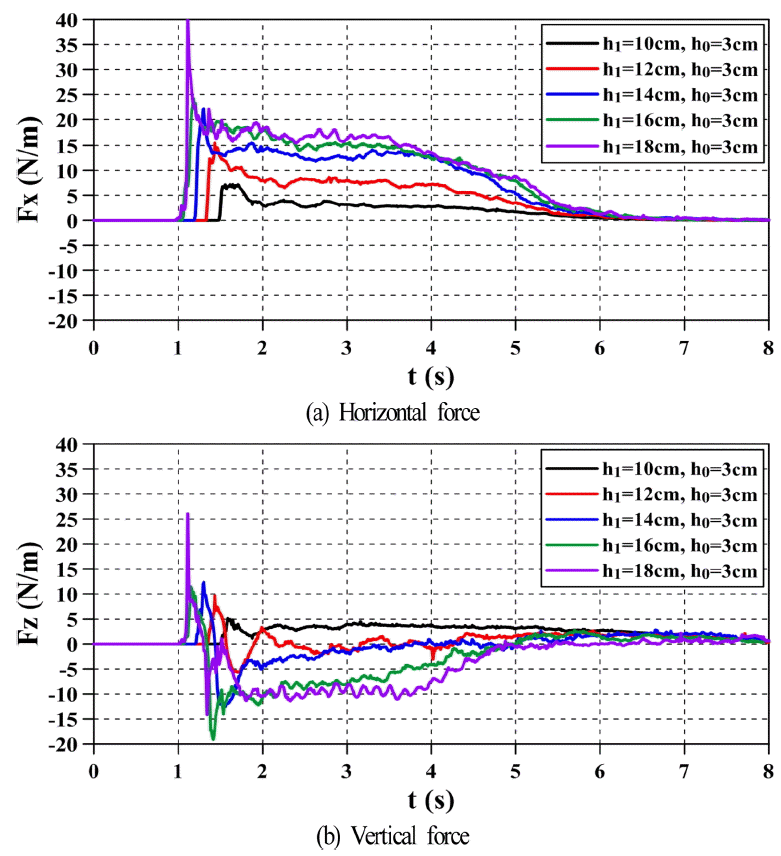
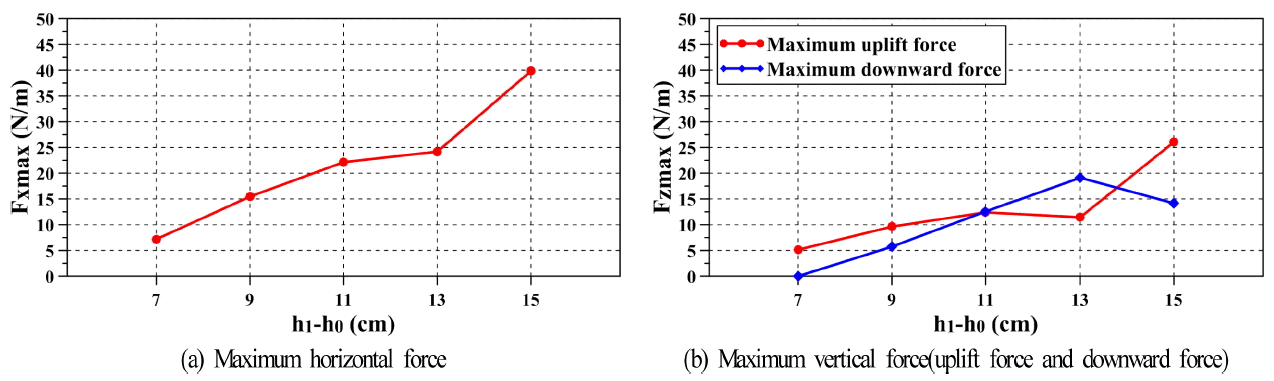
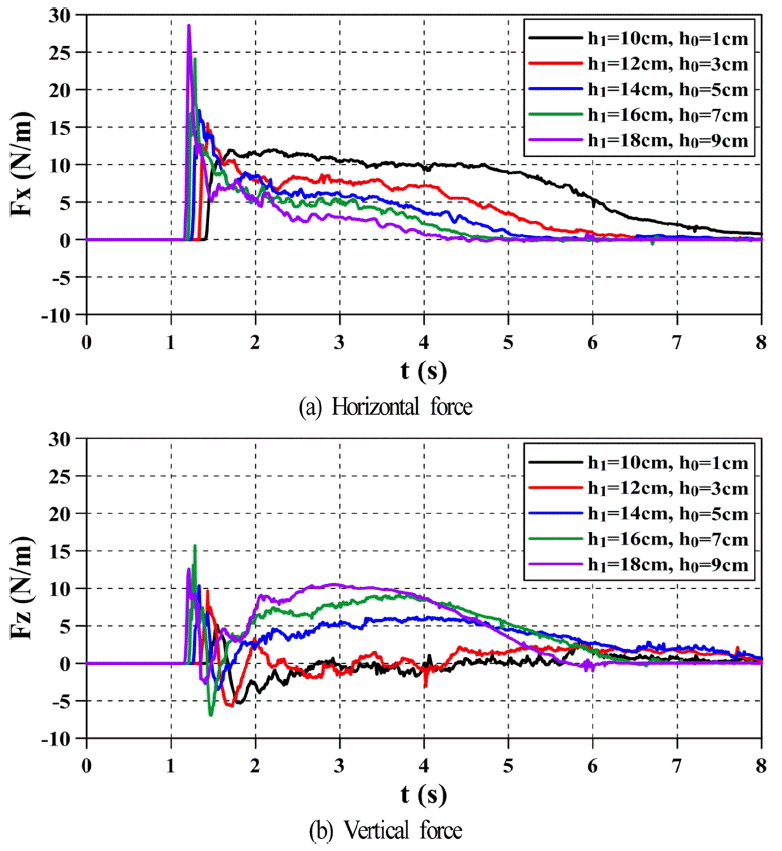
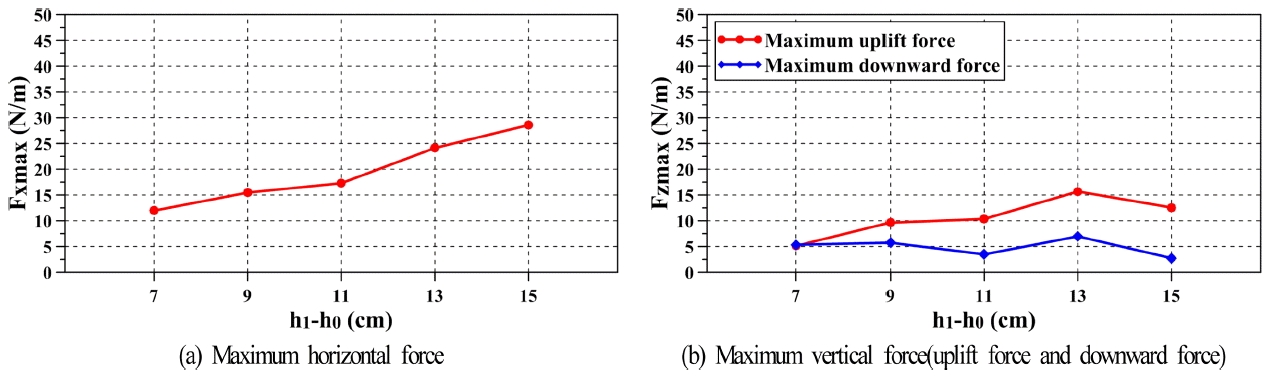
Fig. 8은 교량에 작용하는 단파에 의한 수평 및 연직파력의 시계열을 나타내고, Fig. 9는 수평 및 연직파력의 최대치를 나타낸다. 먼저, Fig. 8을 살펴보면 단파강도가 커질수록 파력의 작용시점이 빨라지고, 또한 충격적인 타격으로 인한 충격파력과 같은 급격한 수평파력의 상승을 나타내며, 이후에는 완만하게 감소되는 수위변동에 의해 완만하게 감소되지만 단파강도가 클수록 전체의 작용시간에 걸쳐 보다 큰 수평파력을 나타내는 것을 알 수 있다. 이것은 단파강도가 클수록 단파 전면의 불연속면의 높이가 커지고, 수심의 증가에 따라 그의 전파속도가 빨라지기 때문이다. 수평파력의 최대치는 단파의 불연속면이 교량에 작용하는 시점, 즉 수평파력이 급격히 증가하는 시간대에 발생한다. 연직파력의 시계열을 살펴보면 단파강도가 커질수록 연직상방파력(양력으로 상향력)과 연직하방파력(하향력) 모두 증가하는 경향을 보이고, 단파의 불연속면이 모델교량에 도달하는 순간에 연직상방파력이 발생되고, 이후의 시간대에서 연직하방파력이 나타나지만 단파강도가 가장 작은 h1= 10 cm, h0= 3 cm의 경우는 연직하방파력은 거의 발생되지 않는다. 이러한 결과는 연직하방파력이 작용되는 Fig. 3에서의 결과와는 달리 연직상방파력이 초기에 작용하고, 이와 거의 동시에 전술한 수평파력의 최대치가 작용하므로 교량의 안정성 측면에서 양력과 수평력이 동시에 작용하는 것으로 되기 때문에 매우 불리한 경우에 해당한다.
Fig. 8에서 제시된 결과 중에 각각의 최대치만을 제시한 결과가 Fig. 9이다. 그림으로부터 h1-h0=7~11 cm까지 최대수평파력과 최대연직상방파력의 증가경향 및 최대연직하방파력과 최대연직상방파력의 변동과정이 유사하지만 h1-h0=13, 15 cm에서 최대연직하방파력과 최대연직상방파력의 변화는 서로 반대의 경향을 나타낸다. 최대연직하방파력은 지속적으로 증가하다가 h1-h0=15 cm에서 감소하고, 최대연직상방파력은 =13 cm에서 감소하다가 다시 h1-h0=15 cm에서 증가하는 결과를 나타낸다. 여기서, =15 cm에서 두 연직파력이 반대 경향을 나타내는 것은 다음과 같이 설명될 수 있다.
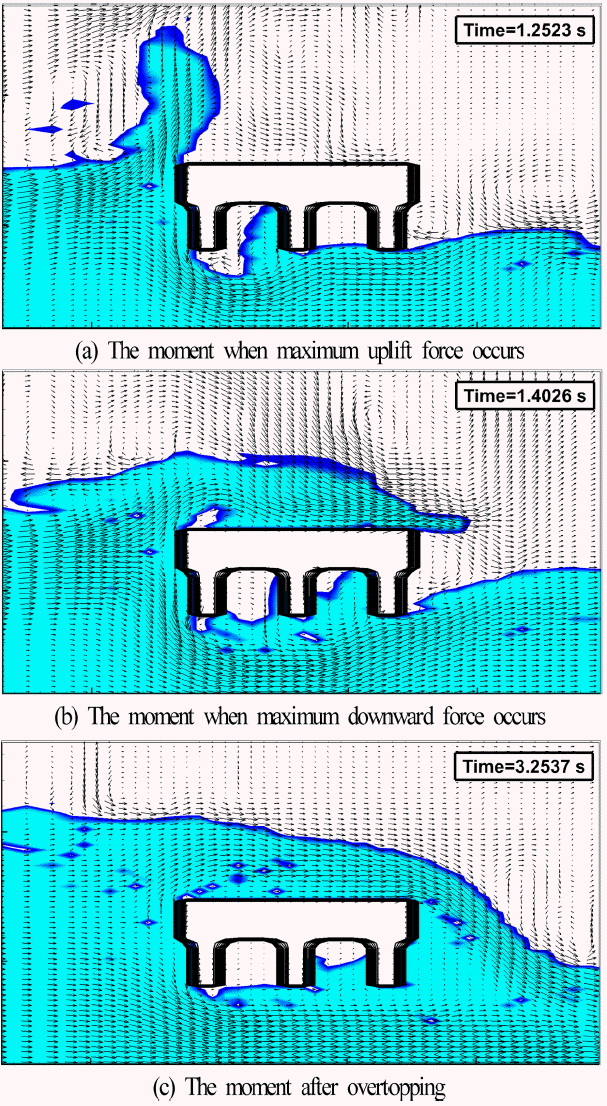
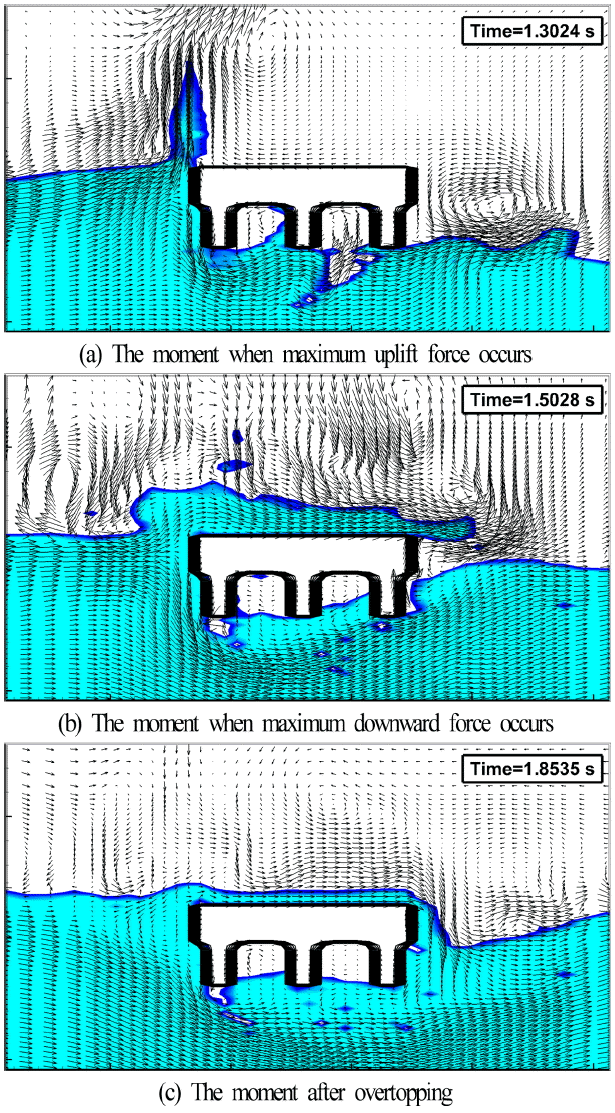
Figs. 10과 11은 h1= 16, 18 cm일 때 단파가 모델교량에 전파되어 최대연직상방파력과 최대연직하방파력 및 이후의 월류 상황에 대한 시·공간분포를 나타낸다. Fig. 10의 h1= 16 cm일때와 Fig. 11의 h1= 18 cm일 때를 비교하면 h1= 16 cm일 때 첫 번째 거더의 저면 및 두 번째 거더의 일부 저면에서는 연직상방파력이 작용하지 않고, 또한 첫 번째 거더와 두 번째 거더 사이의 데크 저면의 일부 및 두 번째 거더와 세 번째 거더 사이의 데크 저면에 연직상방파력이 작용하지 않는 것을 볼 수 있다. 반면, h1= 18 cm일 때는 모델교량에 단파가 충돌한 직후 h1= 16 cm의 경우보다 더 높은 처오름고가 발생하면서(Fig. 9(a)에서 h1= 18 cm의 경우가 h1= 16 cm보다 더 큰 수평파력이 발생되는 원인) 3개 거더의 저면 모두에 연직상방파력이 작용하는 것을 Figs. 10(a)와 11(a)의 비교로부터 확인할 수 있다. 다음으로, 연직하방파력에 대한 Figs. 10(b)와 11(b)의 경우를 검토한다. h1= 16 cm의 Fig. 10(b)에서는 대부분의 월류량이 모델교량의 데크 상부에 놓이고, 이로부터 연직하방으로 누르는 힘(연직하방파력)이 크게 작용하는 반면, h1= 18 cm의 Fig. 11(b)에서는 월류한 일부의 유량만이 모델교량의 데크 상부 끝단에 작용하게 되므로 상대적으로 h1= 16 cm의 경우보다 최대연직하방파력이 작게 나타나는 것으로 판단된다. 최대연직하방파력이 발생한 시간 이후에는 다량의 공기가 연행되고, 모델교량의 하부 및 배후 근방에서 와가 형성된다. 특히, 이러한 현상은 h1= 18 cm의 경우가 보다 현저히 나타나며, 모델교량의 배후에 반시계방향의 와가 형성되고, 모델교량의 상부 및 전후에서 보다 높은 수위가 나타난다.
4.3 수심의 변화에 따른 작용파력의 변화
4.3.1 수위변동
Fig. 12는 모델교량이 존재하지 않는 경우 Fig. 6(a)에 정의된 바와 같이 상류측 수심을 h1= 10, 12, 14, 16, 18 cm로, 하류측 수심을 h0 = 1, 3, 5, 7, 9 cm로 변화시키면서 수심차 h1-h0가 9 cm로 일정한 단파강도의 경우에 대한 결과이다. Fig. 12(a)는 모델교량이 놓이는 위치의 중앙에서 수위 h의 시간변동에 하류측 초기수위 h0를 뺀 수위변동 h-h0를, Fig. 12(b)는 각각에서 도출되는 최고수위 (h-h0)max를 나타낸 것이다. 여기서, 수위변동에서 하류측의 초기수위를 뺀 것은 초기수위가 없는 육상에 단파가 소상하는 경우와 비교하면서 단파강도의 개념을 적용하고자 한 것이고, 하류측에 초기수위를 적용한 것은 육상부에 존재하는 감조하천을 횡단하는 연안교량을 상정한 것이다. 결과를 살펴보면 상·하류측에서 단파강도가 일정하지만 상류측의 수심 h1과 하류측 수심 h0가 같이 깊어질수록 단파의 전파속도가 빨라지고 최고수위는 거의 선형적으로 증가하지만 전술한 Fig. 7(b)의 경우보다 동일한 상류측 수심에 대해 상대적으로 작은 최고수위를 나타내므로 동일한 상류측 수심 h1에 대해 점차적으로 증가하는 단파강도에서의 경우보다 동일한 단파강도의 경우가 최대수위의 변동기울기가 상대적으로 작게 나타난다. 그리고, 전술한 Fig. 7(a)의 경우와 비교하면 동일한 상류측 수심임에도 상류측 수심의 변화에 따른 전파속도의 변화율은 하류측 수심이 존재하는 Fig. 12(a)의 경우가 작으며, 이러한 결과로부터 하류측 수심이 단파의 전파속도에 큰 영향을 미치게 된다는 것을 알 수 있다. 또한, 불연속면 전후에서 각각의 수심이 상이하지만 동일한 단파강도의 경우는 수위의 하강속도가 상대적으로 빨라지는 것을 확인할 수 있다. 이상으로부터 수위변동에서 전파속도, 크기 및 수위의 변화율 등에 하류측의 수심 h0가 큰 영향을 미친다는 것을 알 수 있다. 한편, 상류측의 수심 h1이 깊을수록 Lee et al.(2008)이 지적하고 있는 바와 같이 불연속면에 파상단파가 형성되는 것을 알 수 있다.
4.3.2 작용파력
Fig. 13은 모델교량에 작용하는 단파에 의한 수평 및 연직 파력의 시계열을 나타내며, Fig. 14는 시계열 중에서 수평 및 연직파력의 최대치를 나타낸다. 전술한 수위변동에서 언급된 바와 같이 상·하류측 수심이 깊을수록 단파의 전파속도가 빠르기 때문에 파력의 감지 시간이 빨리 나타나며, 모델교량에 불연속면의 급격한 타격으로 불연속면의 도달시간에 파력의 급격한 상승이 발생된다. 특히, 불연속면의 전후에서 수위가 큰 h1= 16 cm, h0= 7 cm와 h1= 18 cm, h0= 9 cm의 경우에는 전술한 Fig. 8에서와 같이 충격적인 타격으로 인한 충격파력이 나타나고, 이후에 감소되는 현상은 동일하지만 같은 단파강도
h1-h0=9cm에 대해 h1이 클수록 수평파력이 완만하게 감소되는 구간에서 수평파력은 보다 작아지는 것을 확인할 수 있다. 그리고, Fig. 8의 경우와 비교하면 수평파력의 최대치는 유사한 경향으로 수심의 증가에 따른 상승을 나타내지만 전반적인 변화율은 보다 작다(얕은 수심에서 큰 값을, 깊은 수심에서는 작은 값을 나타낸다)는 것을 알 수 있다.
연직파력의 시계열을 살펴보면 시간의 경과에 따라 초기에는 연직상방의 파력이, 다음에는 연직하방의 연직파력이, 이후에는 교차적으로 나타지만 수심이 깊을수록 t > 2.5 s의 시간대에서 연직상방의 파력이 점차로 증가하는 경향을 나타낸다. 또한, 수심이 깊을수록 연직상방의 파력이 연직하방의 연직파력의 크기보다 커지는 것이 일반적인 경향으로 판단된다. 그리고, 불연속면 전후에서 수심이 깊을수록 최대연직상방파력의 발생시간과 최대수평파력의 발생시간이 일치하고, 그의 값도 크게 되므로 교량의 안정성에서는 불리한 측면으로 된다. 전술한 Fig. 8의 경우와 비교하면 전체적으로 연직하방의 파력에서 그의 지속시간이 짧고(Fig. 13의 h1= 18 cm, h0= 9 cm에서는 연직하방의 파력이 거의 나타나지 않는다), 또한 최대치가 작은 특성을 갖는다. 수평 및 연직파력에서 주어진 이러한 특징으로부터 하류측 수심이 파력의 특성에 미치는 영향이 크며, 특히 연직파력에 큰 영향을 미친다는 것을 확인할 수 있다.
Fig. 14을 살펴보면 최대수평파력은 수심이 깊을수록 증가하고, 최대연직상방파력도
h1-h0=7~13 cm까지는 수심이 깊어질수록 증가하며,
h1-h0=15 cm에서 감소한다. 반면, 최대연직하방파력은 수심의 변화에 일정한 경향의 변화를 나타내지 않지만 최대연직상방파력과 최대연직하방파력의 차이는 수심의 증가에 비례하여 증가하는 경향을 나타낸다. 이러한 최대연직파력의 변화양상은 전술한 Fig. 9(b)와는 큰 차이를 나타낸다는 것을 알 수 있다.
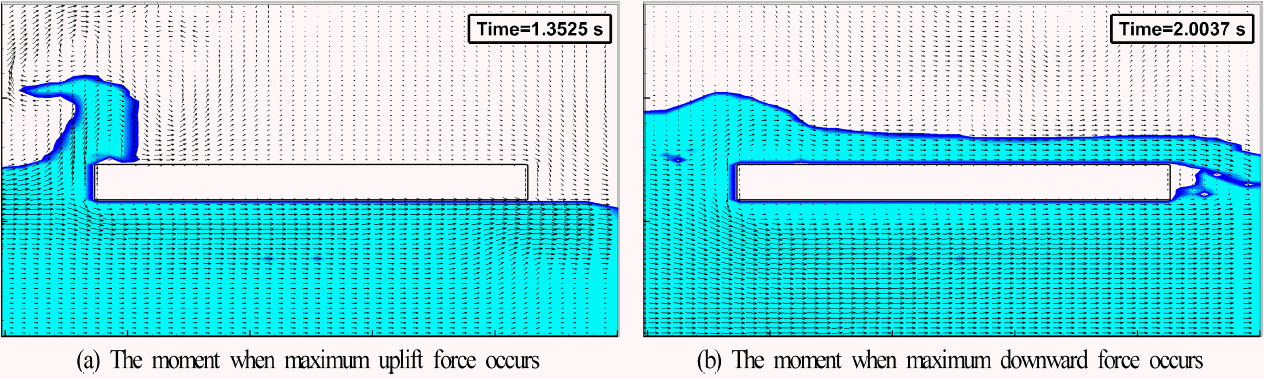
Figs. 15와 16은 각각 h1= 16 cm, h0= 7 cm; h1= 18 cm, h0= 9 cm일 때 단파에 의한 최대파력이 모델교량에 작용되는 순간에 포착된 교량 주변에서 수위변동과 공기를 포함한 유체 내에서 유속분포 등을 나타낸 결과로, 각 그림에서 (a)가 최대연직상방파력이, (b)가 최대연직하방파력이 작용되는 순간에 대한, 그리고 (c)가 이후의 월류 상황에 대한 시·공간분포이다. 최대연직상방파력의 경우를 보면 h1= 16 cm, h0= 7 cm의 경우보다 h1= 18 cm, h0= 9 cm에서는 모델교량 전면에 유속벡터의 수평성분이 상대적으로 강하게 나타나지만(따라서, 최대 수평파력이 상대적으로 크게 나타난다) h1= 18 cm, h0= 9 cm에서는 거더의 저면에 작용하는 상향의 연직파력(최대연직상방파력)이 공기의 연행으로 작게 나타나는 것(특히, 두 번째 거더 저면에서)으로 판단된다. 반면, 최대연직하방파력이 작용될 때의 두 경우를 비교·검토하면 h1= 16 cm, h0= 7 cm의 경우가 월류된 유량이 데크의 상부면 전체에 분포하고, 월류된 유량이 데크의 상부면 일부에 분포하는 h1= 18 cm, h0= 9 cm에 비해 하향으로 작용하는 연직하방파력이 상대적으로 크게 된다. 다음으로, 이후의 월파 상황을 살펴보면 h1= 18 cm, h0= 9 cm의 경우가 데크의 상부면에서 더 높은 수위를 가지고 월류되는 것을 파악할 수 있다.
4.4 연안교량의 형태 및 거더 수에 따른 작용파력의 변화
4.4.1 연안교량의 형태
Fig. 17은 거더가 없는 모델 RC 슬래브교(여기서는 거더 수가 0개인 교량으로 고려된다)와 2개 및 6개의 거더를 갖는 모델 거더교의 형상 및 제원을 각각 나타낸다. 수치파동수로와 격자구성은 전술한 경우와 동일하고, 적용한 수심은 상·하류측에서 각각 h1= 16 cm, h0= 3 cm이며, 모델교량은 하류측 수면상 1 cm의 위치에 거치된다.
4.4.2 작용파력
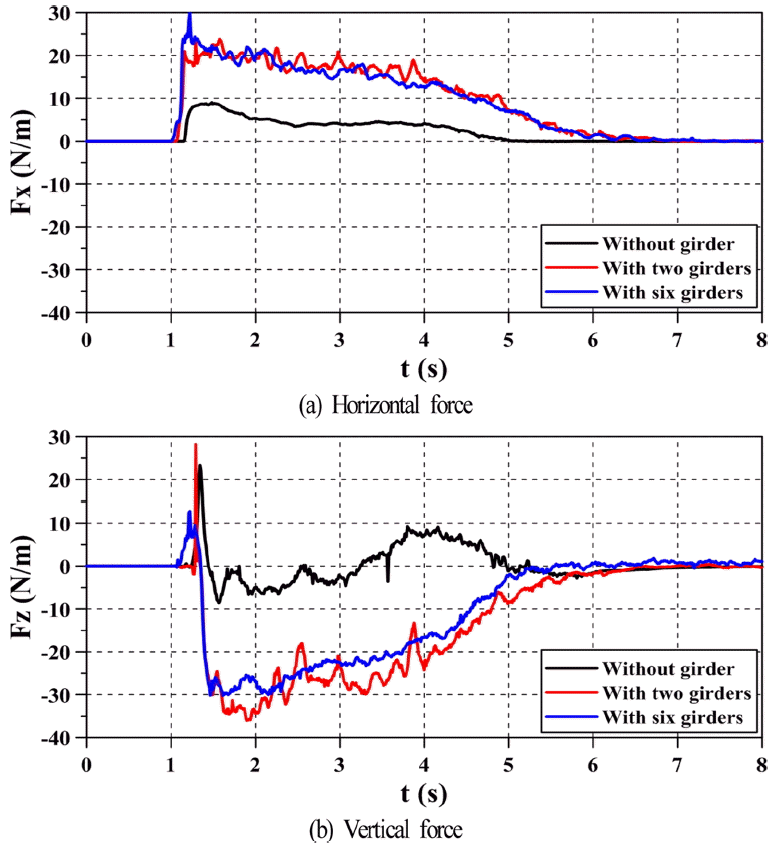
Fig. 18은 적용한 상·하류측의 수심 h1= 16 cm, h0= 3 cm에 의해 형성되는 단파에 의해 3개의 모델교량에 작용하는 수평 및 연직파력의 시계열을 나타낸 것이고, Fig. 19는 여기서 수평 및 연직파력의 최대치를 나타낸 것이다. 그리고, Figs. 20~22도 h1= 16 cm, h0= 3 cm일 때 단파가 모델교량에 전파되어 최대연직상방파력이 작용하는 순간과 최대연직하방파력이 작용하는 순간에 수위와 유속에 대한 시·공간분포를 나타낸다. 먼저, 작용파력의 시계열에 대한 Fig. 18에서 수평파력을 살펴보면 거더가 있는 경우가 큰 값을 갖고, 또한 급격한 수평파력의 증가를 나타내며, 모델 거더교에서 거더 수가 많는 경우가 급격한 수평파력이 약간 증가하는 결과를 나타내지만 크기에서 차는 그다지 크지 않다는 것을 알 수 있다. 거더교에서 거더의 유무에 따른 차이는 기본적으로 단파가 작용하는 연직면적이 상이하기 때문이며, 또한 거더 수가 많은 경우에는 거더가 갖는 연직면이 많지만 수평방향으로의 투영면적은 차이가 없기 때문에 거더 수의 변화에 따른 수평파력의 차이는 크게 나타나지 않는 것으로 판단된다.
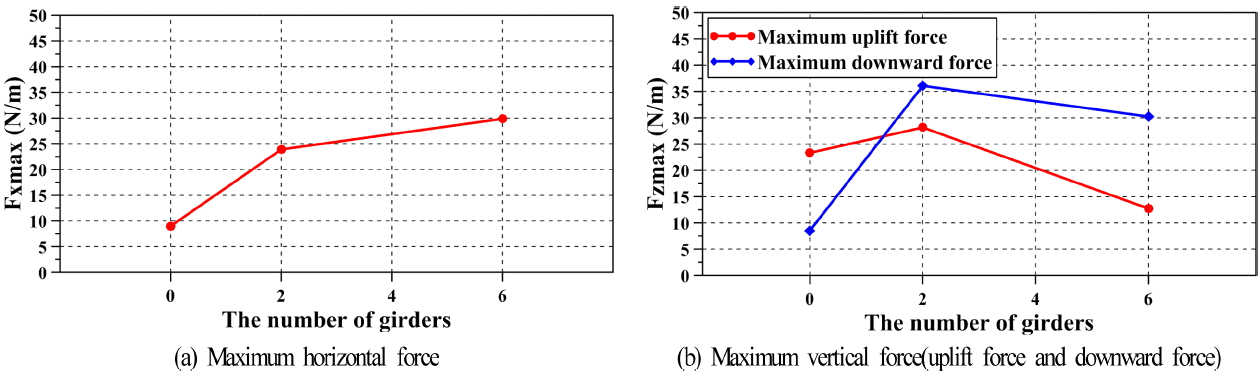
다음으로, 연직파력의 경우를 살펴보면 최대수평파력이 작용한 직후 0.2~0.3 s 지난 후에 최대연직상방파력이 작용하는 것을 알 수 있다. 거더의 유무에 따른 차이로는 연직하방파력에서 큰 차이를 나타내며, 거더가 존재하는 경우가 큰 연직하방파력을 나타낸다. 그리고, 거더가 존재할 때는 연직하방으로 작용하는 연직하방파력의 지속시간이 길어지는 반면, 거더가 없는 경우에는 작용하는 지속시간이 짧고, 약 3.2 s 이후에는 연직상방파력이 작용하는 것을 알 수 있다. 그리고, 연직상방파력에서는 거더 수가 많은 경우가 가장 작은 값을 나타내며, 연직하방파력에서는 전술한 바와 같이 거더가 있는 경우가 큰 값을 나타내지만 거더 수가 많을수록 큰 값을 나타내지 않고, 오히려 거더 2개의 경우가 6개보다 값의 차이는 크지 않지만 더 큰 값을 나타내는 것을 확인할 수 있다. 이러한 결과들은 모델 거더교의 거더 사이에 연행되는 공기가 큰 영향을 미치는 것으로 판단되며, 이에 대해서는 후술한다. 한편, 전술한 바와 같이 각각의 최대치를 거더 수의 함수로 나타낸 결과가 Fig. 19이며, 그림으로부터 최대수평파력은 거더 수에 비례하지만 최대연직상방파력과 최대연직하방파력은 거더 수의 변화에 일률적인 경향을 나타내지 않으며, 본 연구에서는 거더 수가 2개인 경우가 가장 큰 최대연직상방파력과 최대연직하방파력을 나타낸다.
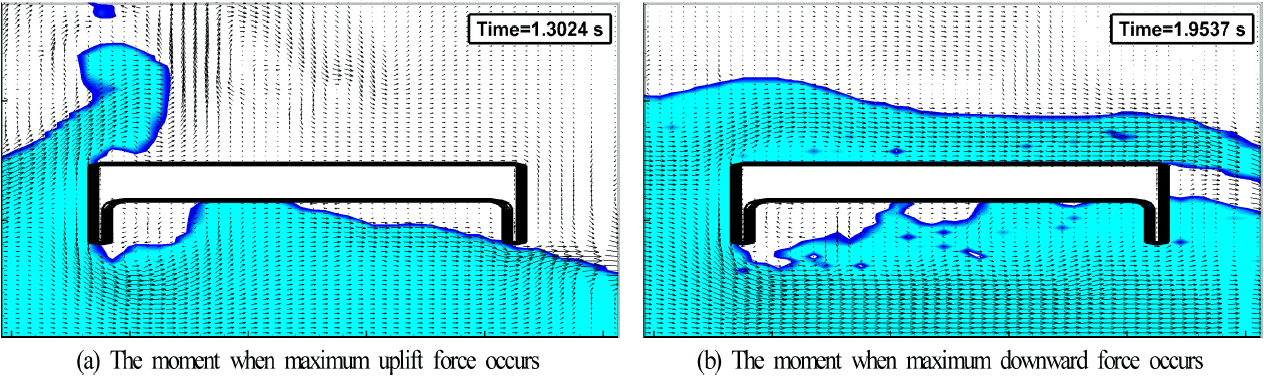
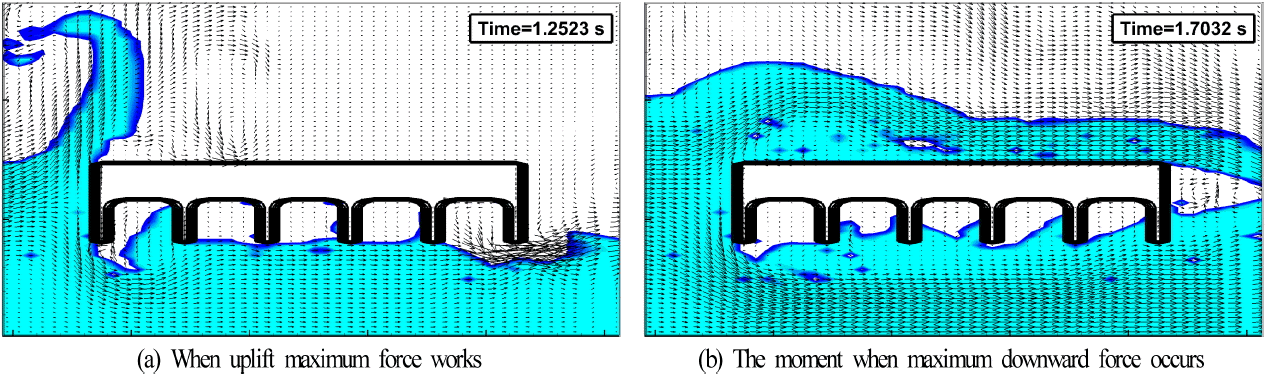
Figs. 20~22에서 각 그림의 (a)를 살펴보면 Fig. 20(a)는 거더가 없는 RC 슬래브교로 데크 하부의 전면적이 유체와 접하고 있으므로 최대연직상방파력이 Fig. 21(a)보다 큰 것으로 보이지만 처오름고가 Fig. 21(a)에서보다 작기 때문에 데크 하부에서 유체와 접촉 면적이 작지만 압력강도가 크기 때문에 Figs. 21(a)의 경우가 더 큰 최대연직상방파력을 나타낸다. 다음으로, Figs. 21(a)와 22(a)를 비교하면 처오름고는 Fig. 22(a)가 훨씬 큰 값을 나타내지만 데크 하부는 거의 전부 공기가 포함되어 있고, 6개의 거더 저면에 작용하는 연직상방파력도 작기 때문에 최대연직상방파력은 거더가 2개인 Fig. 21(a)에서 발생되는 것으로 판단된다.
한편, 거더가 6개인 경우보다 거더가 2개인 경우가 최대연직하방파력이 더 크게 나타나는 것은 거더가 6개인 Fig. 22(b)에서는 6개의 거더 저면에 연직상방의 파력이 작용하는 반면에 거더가 2개인 Fig. 21(b)에서는 거더 저면에 연직상방의 파력이 작용되지 않기 때문에 거더가 2개인 Fig. 21(b)에서 상하방향으로 합력으로 산정되는 최대연직하방파력이 더 크게 도출되게 된다. 여기서, 거더 수의 변화에 따른 최대파력의 일반적인 특징을 도출하기 위해서는 더 많은 케이스의 수치시뮬레이션이 요구되고, 교량 주변에서 압력의 변화, 와의 형성 및 난류강도 등에 대한 더 세밀한 검토가 필요한 것으로 판단된다.
5. 맺음말
본 연구에서는 연안교량에 작용하는 단파에 의한 지진해일 파력을 난류해석이 포함된 3차원혼상류해석법인 TWOPM-3D를 적용하여 검토하였다. 더불어, Nakao et al.(2010)에 의한 실험결과와 비교·검토하여 본 수치해석법의 타당성을 검증하였고, 2004년 인도양지진해일 시 인도네시아에서 실제로 피해를 입은 Lueng Ie Bridge를 축척한 모델교량에 대해 단파 강도, 수심 및 거더의 개수 등을 변화시켜 작용파력의 특성을 면밀히 분석하였다. 이로부터 얻어진 본 연구의 주요한 사항을 아래에 기술한다.
(1) 상류측 수심의 변화에 따른 수위변동에 대해 본 수치해석치와 실험치를 비교한 경우, 단파의 전파시간, 시간의 경과에 따른 수위변동 및 최대수위 모두가 수리실험결과와 높은 대응성을 나타내었다. 또한, 거더가 존재하지 않는 RC 슬래브교에 대해 수치해석결과와 실험결과를 비교·검토한 경우, 수평파력은 매우 잘 일치하는 것을 알 수 있었고, 연직상방파력 및 연직하방파력에서 약간의 차이가 나타나지만 좋은 대응성을 나타내며, 시간이력에서도 잘 일치하는 것을 알 수 있었다. 이러한 비교·검토로부터 본 연구의 TWOPM-3D에 대한 타당성을 충분히 확인할 수 있었고, 교량에 작용하는 단파에 의한 파력을 수치시뮬레이션으로 충분히 재현할 수 있는 것으로 판단된다.
(2) 단파강도의 변화에 따라 연안교량(거더교)에 작용하는 단파에 의한 파력에서, 단파강도가 커질수록 최대수평파력이 증가하고, 연직파력의 경우 연직상방파력은 증가하는 경향이 나타나지만 연직하방파력은 감소하는 경우도 나타난다.
(3) 수심 변화에 따라 연안교량(거더교)에 작용하는 단파에 의한 파력에서, 동일한 단파강도에서 상·하류측의 수심이 증가할수록 최대수평파력은 증가하는 반면, 연직파력은 증가 혹은 감소하는 일률적인 경향을 나타내지 않는다. 또한, 상·하류측의 수심이 증가할수록 최대수평파력과 최대연직상방파력이 작용하는 시간은 거의 동일하며, 최대연직상방파력과 최대연직하방파력의 차이가 증가한다.
(4) 거더가 많을수록 수평파력이 증가하고, 급격한 수평파력의 작용시간 직후 0.2~0.3 s 후에 연직상방파력이 작용하는 것을 알 수 있었다. 또한, 거더가 많을수록 단파가 교량에 작용하는 순간 거더와 거더 사이에 있는 공기의 완충효과로 인하여 연직상방파력이 작게 산정된다.