1. 서 론
전 세계적으로 기후변화에 따른 기상이변이 속출하고 예기치 못한 대형급 태풍으로 사회 기반시설물의 피해 규모는 증가하고 있는 추세이다. 지난 2003년 태풍 매미의 내습으로 부산항을 비롯한 부산지역 항만시설의 방파제 상치콘크리트 및 테트라포드(TTP)의 유실, 컨테이너 및 크레인의 전도 등 항만시설에 대한 막대한 피해가 발생하였다(Seo, 2004). 특히, 항만시설의 경우 바람에 직접적으로 노출되어 있어 태풍이 내습하는 경우 막대한 피해를 입을 수 있고, 항만 시설이 일부 마비됨으로써 물류 손실 등의 2차 피해도 발생할 수 있기 때문에 항만시설물에 대한 내풍 안전성의 확보는 매우 중요하다. 또한 컨테이너 크레인 및 선박 운송용 컨테이너와 같은 경량구조물은 바람에 취약하기 때문에 풍하중을 우선적으로 검토해야 한다. 컨테이너 크레인에 관한 내풍 안정성에 관한 연구는 풍동실험 및 수치해석 등을 통하여 수행된 바 있다(An et al., 2008; Kim et al., 2005; Kim and Lee, 2010; Lee et al., 2009; Lee et al., 2005). 그러나 선박 운송용 컨테이너에 대한 내풍 안전성에 대한 연구는 매우 제한적으로 수행된 바 있다(Wu et al., 2011). 따라서 본 연구에서는 풍동실험을 통해 선박 운송용 컨테이너의 풍력특성을 조사하고, 그 결과를 토대로 컨테이너의 중량별 피해발생풍속을 평가하고자 한다.
2. 풍동실험
2.1 자연풍의 모사
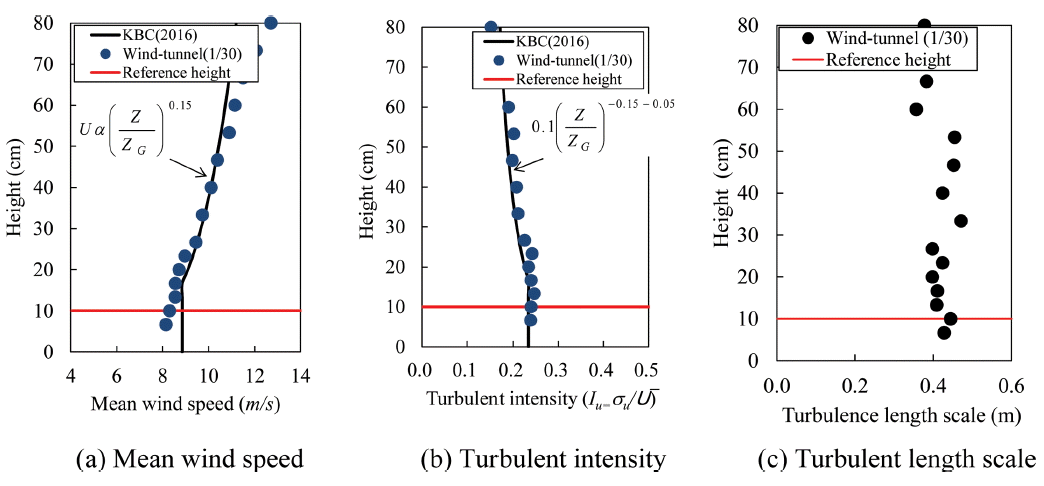
풍동을 이용한 풍력실험(high-frequency force balance test)은 일본 동경공예대학의 풍공학연구센터에 소재한 폭 2.2 m, 높이 1.8 m의 대형경계층풍동(boundary layer wind tunnel)에서 수행되었다. 풍속의 고도분포지수관련 기준은 국외의 경우 IEC 61400-3, American Society of Civil Engineers(ASCE 7-10), National Building Code of Canada(NBCC 2010), Architectural Institute of Japan(AIJ 2004) 등이 있으며, 위의 기준에서의 고도분포계수는 각각 0.14, 0.1, 0.16과 0.1이다(Ko et al., 2012, 2013). 우리나라의 경우 건축구조기준 및 해설(KBC 2016)이 있으며, 평탄지 조건의 고도분포계수는 0.15로 제시되어 있다. 본 연구에서는 국외 기준과 크게 다르지 않은 KBC 2016의 지표면조도(지표면조도분포, 0.15)의 평균풍속(mean wind speed) 및 난류강도(turbulent intensity)를 풍동에서 재현하였다. 풍동 내 기류는 스파이어(spire), 조도블럭(roughness block) 등을 이용하여 고도분포지수(exponential power law of roughness)를 재현하였으며, 이때 사용된 장비는 I형 열선풍속계(I-type hot-wire anemometer)로, tungsten wire 길이 5 μm, 센서 길이 5 mm이다. Fig. 1은 풍동 내에서 재현된 평균풍속, 난류강도 및 난류적분스케일(turbulent length scale)의 연직분포를 나타낸 것이다. 난류적분스케일(Lu)은 계측된 변동풍속의 자기상관함수와 평균풍속의 관계로 식(1)로 구할 수 있다(Liu, 1991).
여기서, R(τ)는 자기상관함수, U ¯
Fig. 1과 같이 평균풍속 및 난류강도의 연직분포는 KBC(2016)에서 제시하는 것과 유사한 분포를 보였다. 또한 일반적으로 난류적분스케일은 실험모형의 높이(이 실험의 경우 10 cm)보다 크게 평가되어야 하기 때문에 풍동 내에서 자연풍은 적절하게 모사되었다고 볼 수 있다.
2.2 실험모형 및 실험절차
우리나라 해운회사들은 국제적으로 표준화되어 있는 ISO 규격의 20ft, 30ft, 40ft 컨테이너 등을 주로 사용하고 있으며, 철도 운송용 컨테이너는 일본철도(JR화물)에서 사용하는 12ft, 19.7ft, 30.3ft 등을 주로 사용하고 있다. 본 연구에서는 선박 및 철도 운송용 컨테이너의 피해 발생풍속을 평가하기 위해 Table 1에 제시한 바와 같이 12ft, 20ft, 40ft, 40ft high cube의 컨테이너를 대상으로 풍력실험을 수행하였다.
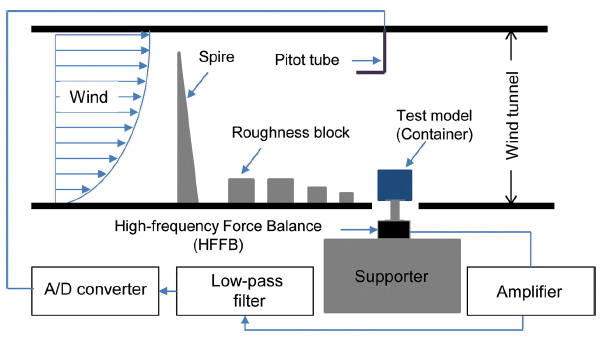
풍력실험은 상사법칙을 이용하여 모형스케일(Lmodel/Lfull), 풍속스케일(Umodel/Ufull), 시간스케일((Tmodel/Tfull= (Lmodel/Lfull) × (Ufull/Umodel))은 각각 1/30, 1/6, 1/5로 설정하였으며, 컨테이너에 작용하는 풍력은 6분력계(6-components high-frequency force balance)를 이용하여 측정하였다. 6분력계는 LMC-6566A-50N (Nissho Electric Works Co., Ltd.)로 허용하중(Fx, Fy, Fz)은 각각 ± 50 N, ± 50 N, ± 50 N이며, 허용모멘트(Mx, My, Mz)는 각각 ± 5Nm, ± 5Nm, ± 5Nm이다. 실험시 계측주파수는 100 Hz이었으며, 실험풍향은 컨테이너의 정면을 중심으로 0o에서 90o까지 10o 간격으로 고려하였다. Fig. 2는 풍력실험에 대한 계측 시스템을 도식적으로 나타낸 것이며, Fig. 3은 풍동 내에 설치된 모형 사진을 나타낸 것이다.
2.3 해석절차
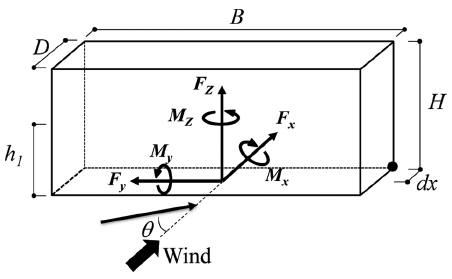
풍력실험에 의해 측정된 성분별 풍력 및 모멘트는 식(2)와 식(3)과 같이 무차원화 시킨 평균 풍력계수 및 전도모멘트계수로 나타내었으며, 컨테이너에 작용하는 하중 및 풍향각은 Fig. 4에 나타내었다.
여기서, C F i C M i F i M i
여기서, ρa는 공기밀도(= 1.22 kg/m3), UH는 대상구조물 높이에서의 설계풍속이다. 설계풍속은 기상청에서 제공하는 기상연보의 부산의 42년간(1972년~2014년) 계측된 연최대풍속 자료를 이용하여 50년 재현주기 기대풍속(33.8 m/s)을 산정하였고, 이 기대풍속을 이용하여 설계풍속으로 환산하였다.
3. 실험결과 및 고찰
3.1 풍력계수의 특성
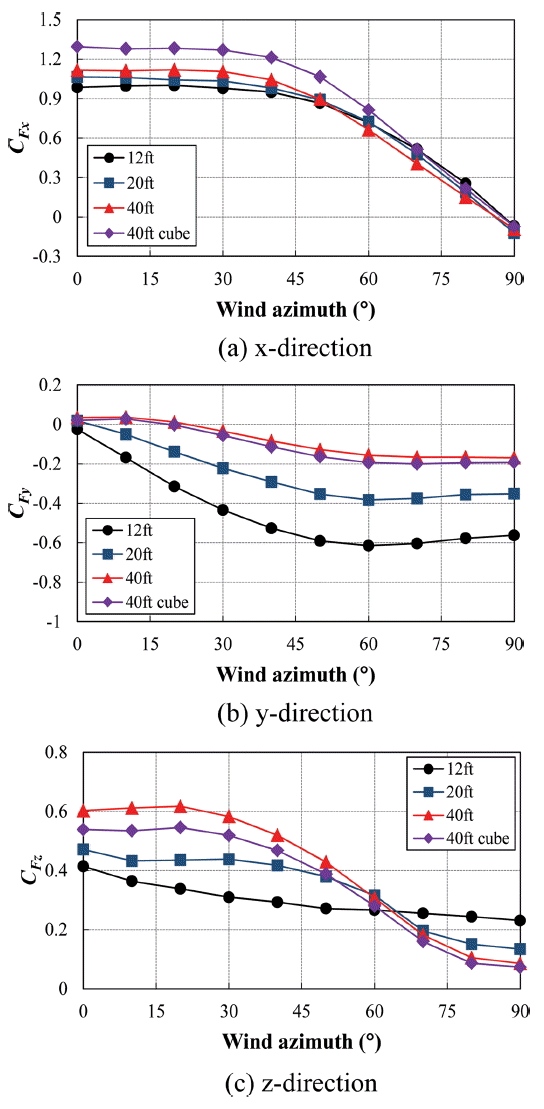
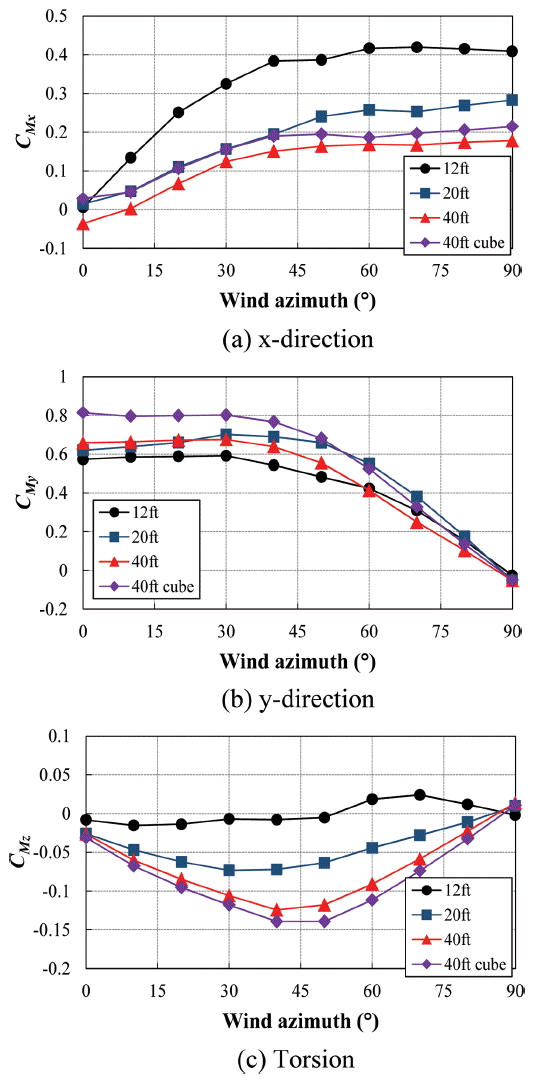
Fig. 5와 6은 축방향별 컨테이너에 작용하는 평균 풍력계수 및 전도모멘트계수의 특성을 나타낸 것이다. Fig. 5(a)의 x 방향에 대한 컨테이너에 작용하는 평균 풍력계수의 특성을 살펴보면, 전반적으로 풍향이 커짐에 따라 x 방향에 대한 평균 풍력계수는 감소하며, 풍향 0o일 때의 평균 풍력계수는 12ft, 20ft, 40ft, 40ft high cube 순으로 증가하는 것으로 나타났다. 그러나 y 방향의 경우에는 풍향이 증가함에 따라 컨테이너의 평균 풍력계수는 증가하며, 풍향 90o일 때의 평균 풍력계수는 40ft high cube, 40ft, 20ft, 12ft 순으로 증가하는 것으로 나타났다(Fig. 5(b) 참조). 이와 같은 특성은 풍향이 증가하면서 컨테이너의 풍상면(windward surface)의 모서리에서 박리되는 난류의 전단층(shear layer)이 다시 컨테이너의 측면(side surface) 부근에서 재부착(reattachment) 되면서 y 방향의 평균 풍력계수가 감소하게 되는데(Laneville et al., 1975), 변장비(D/B)가 작을수록 재부착이 측면의 풍상측에 가까운 쪽에서 발생하기 때문에, 40ft 컨테이너에 작용하는 y 방향의 평균 풍력계수가 감소되는 것으로 판단된다. Fig. 5(c)의 z 방향에 대한 평균 풍력계수를 살펴보면 12ft의 평균 풍력계수의 분포는 다른 컨테이너의 비해 변동의 폭이 작게 나타났다. 특히 풍향이 60° 이하인 경우, 평균 풍력계수는 12ft, 20ft, 40ft, 40ft high cube 순으로 증가하는 것으로 나타났지만, 풍향이 60°를 초과하면서 반대 효과가 나타나는 경향을 보였다. 이러한 이유는 y 방향의 평균 풍력계수의 특성과 유사하게 난류의 전단층이 컨테이너의 측면에 재부착 되면서 평균 풍력계수가 감소하는 것으로 보인다. 즉, 변장비가 작아질수록 z 방향에 대한 평균 풍력계수 또한 감소하는 것을 의미한다.
Fig. 6(a)와 (b)의 x, y의 평균 전도모멘트계수(CMx, CMy)의 분포는 y, x 방향의 평균 풍력계수에 상응하는 것으로 나타났다. 이것은 정형적인 정방형 구조물에 작용하는 풍력계수와 전도모멘트 특성과도 잘 부합하는 것을 알 수 있다(Kim et al., 2015). 반면에 컨테이너에 작용하는 평균 비틀림 모멘트계수(CMz)는 40ft high cube, 40ft, 20ft, 12ft 순으로 증가하는 것으로 나타났다(Fig. 6(c)). 그러나 최대 평균 비틀림 모멘트계수는 12ft를 제외하고 풍향 45o 부근에서 발생하는 것으로 나타났다.
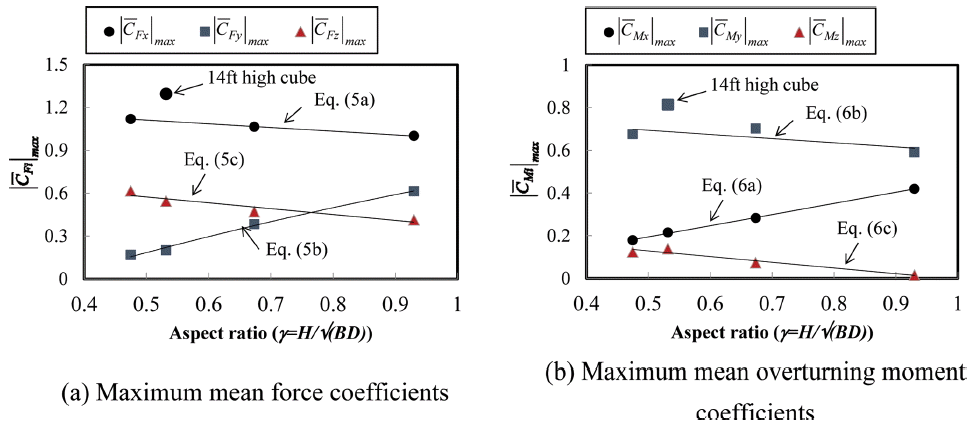
컨테이너의 형상비에 따른 최대 평균 풍력계수 및 모멘트계수의 특성을 Fig. 7에 나타내었다. 또한 그 결과를 토대로 컨테이너에 작용하는 최대 평균 풍력계수 및 모멘트계수는 형상비(γ = H / B D
3.2 활동 및 전도발생 풍속의 평가
선박 운송용 컨테이너의 피해발생 풍속은 활동발생 풍속과 전도발생 풍속으로 구분할 수 있다. 활동발생 풍속은 횡방향 풍하중과 컨테이너의 자중 및 마찰계수의 관계로 식(7)을 이용하여 평가할 수 있다.
여기서, WF는 컨테이너에 작용하는 횡방향 풍하중으로 WFx와 WFy의 합성으로 나타낼 수 있으며, W'C는 컨테이너의 자중과 연직방향의 풍하중을 이용하여 구할 수 있다. μ는 컨테이너의 마찰계수(화물적재고박 등에 관한 기준(2015)에 의해 0.3(강재와 목재 또는 강재와 고무사이)을 적용)이다. 따라서 횡방향 풍하중과 컨테이너의 자중과 관계는 식(8)과 같다.
여기서, WFx, WFy, WFZ는 각각 x, y, z에 작용하는 등가정적 풍하중(N)으로써, 식(9)과 같이 나타낼 수 있다.
여기서, qH, C ¯ F i
한편, 전도발생 풍속은 풍방향 및 연직방향 모멘트의 합과 컨테이너 자중에 따른 모멘트의 관계로 식(11)을 이용하여 평가할 수 있다.
여기서, WFx, WFz는 x, z 방향에 작용하는 풍하중, WC는 컨테이너의 자중, h1은 지표면에서 WFx의 작용점까지의 높이(h1 = (CMy/CFx) × H), dx는 컨테이너의 중심에서 모멘트의 끝단까지 거리(= D/2)이다(Fig. 4 참조).
3.3 컨테이너 중량 및 풍향에 따른 피해발생 풍속의 특성
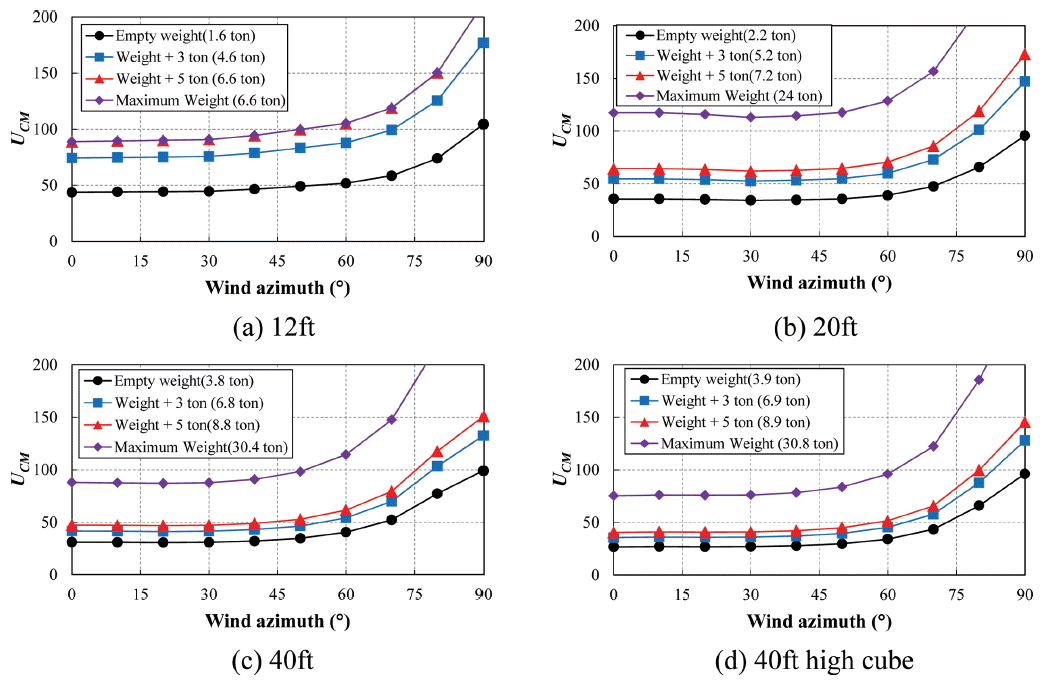
컨테이너의 중량 및 풍향에 따른 활동발생 풍속과 전도발생 풍속은 Fig. 8과 9에 나타내었다. Fig. 8의 활동발생 풍속의 특성을 살펴보면, 컨테이너의 자중만을 고려했을 때, 활동발생 풍속은 40ft high cube, 40ft, 20ft, 12ft 순으로 각각 20.4 m/s, 22.9 m/s, 25.2 m/s, 29.4 m/s로 평가되었다. 즉, 활동발생 풍속은 컨테이너의 자중 보다는 유효수압면적(effective projected area)에 의존됨을 알 수 있으며, 유효수압면적이 클수록 활동발생이 일어날 가능성이 높다는 것을 의미한다. 한편, 컨테이너의 중량별 활동발생 풍속을 살펴보면, 풍향 0°~40° 내에서 활동발생 풍속은 컨테이너의 중량 및 규모 그리고 풍향에 상관없이 거의 유사한분포를 보이지만, 풍향 40°를 초과하면서 활동발생 풍속이 점차 증가하는 경향을 보였다. 위의 결과는 Fig. 5(a)의 x 방향 평균 풍력계수의 특성과도 잘 부합하는 것을 알 수 있다.
한편, Fig. 9의 전도발생 풍속의 특성을 살펴보면, 전도발생 풍속은 활동발생 풍속에 비해 전반적으로 높게 평가되었지만, 풍향 0°~40° 내에서 전도발생 풍속의 분포는 활동발생 풍속의 분포와 유사한 경향을 보였다. 또한 전도발생 풍속은 활동발생 풍속과 유사하게 40ft high cube(26.8 m/s), 40ft(30.8 m/s), 20ft(34.2 m/s), 12ft(43.8 m/s) 순으로 높게 평가되었다. 그러나 풍향 40°를 초과하면서 전도발생 풍속은 활동발생 풍속의 분포와 유사한 형태로 급격히 증가하는 경향을 보였으며, 이는 곧 컨테이너가 활동발생 및 전도발생이 일어날 가능성이 낮다는 것을 의미한다. 이러한 이유는 활동발생 및 전도발생 풍속을 평가할 때 적용한 x 방향의 평균 풍력계수의 급격한 감소 때문인 것으로 판단된다.
Table 2는 전 풍향에서 컨테이너의 중량에 따른 활동발생 풍속 및 전도발생 풍속이 가장 낮게 평가된 값들을 정리한 것이다. Table 2에 나타낸 것과 같이, 피해발생 풍속은 컨테이너의 전도보다는 활동이 일어날 확률이 상대적으로 높은 것을 알 수 있다. 특히 바람에 의한 활동 및 전도가 발생할 확률이 가장 높은 컨테이너는 40ft high cube가 비어 있을 때이다. 이때 활동발생 풍속은 20.4 m/s이며, 전도발생 풍속은 26.8 m/s으로 평가되었다. 반면, 최대 중량에 따른 40ft high cube 컨테이너의 최대 활동발생 풍속은 57.3 m/s이며, 전도발생 풍속은 75.3 m/s으로 평가되었다.
3.4 컨테이너의 중량과 피해발생 풍속의 상관
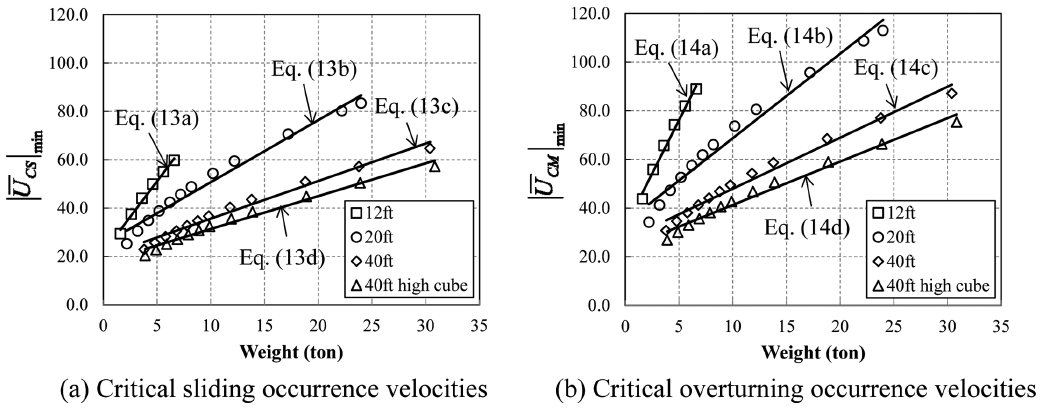
Fig. 10은 컨테이너의 중량에 따른 활동발생 및 전도발생 풍속의 관계를 나타낸 것이다. 그림에서와 같이 활동발생 및 전도발생 풍속은 중량에 비례하여 선형적으로 증가하는 것을 알 수 있다. 특히, 12ft 컨테이너의 경우, 중량이 증가할수록 활동발생 및 전도발생 풍속이 급격히 증가하는 경향을 보였다. 이러한 이유는 활동발생 및 전도발생 풍속에 크게 영향을 미치는 x, z 방향의 풍력계수와 유효수압면적이 다른 컨테이너에 비해 상대적으로 작기 때문에 컨테이너의 중량이 증가할수록 활동발생 풍속 및 전도발생 풍속이 크게 증가하는 것으로 판단된다. 또한 컨테이너의 활동발생 및 전도발생 풍속은 12ft, 20ft, 40ft, 40ft high cube 순으로 컨테이너의 중량에 따라 완만하게 증가하는 경향을 보였다. 위의 결과를 토대로 컨테이너의 중량에 따른 활동발생 및 전도발생 풍속의 평가식을 식(13)과 식(14)과 같이 제안하였다. 식(13)과 식(14)의 평가식을 적용한다면 ISO 규격의 선박 운송용 컨테이너의 중량에 따른 피해발생 풍속을 사전에 예측할 수 있을 뿐 아니라, 선박 운송용 컨테이너의 고박 등의 설치를 위한 구조설계 기준 정립시 유용하게 활용할 수 있을 것으로 판단된다.
4. 결 론
본 연구에서는 풍동실험을 이용하여 선박 운송용 컨테이너의 풍력특성을 조사하였고, 그 결과를 토대로 컨테이너의 중량에 따른 활동발생 및 전도발생 풍속을 평가하였다. 실험결과를 요약하면 다음과 같다.
(1) 실험결과 선박 운송용 컨테이너의 활동발생 및 전도발생 풍속은 x 방향의 평균 풍력계수가 증가할수록 작게 평가되는 것을 알 수 있었다. 이때, x 방향에 대한 평균 풍력계수는 12ft, 20ft, 40ft, 40ft high cube 순으로 증가하는 것으로 나타났다.
(2) 반면, y방향의 평균 풍력계수는 40ft high cube, 40ft, 20ft, 12ft 순으로 증가하는 것으로 나타났으며, 이러한 이유는 컨테이너의 풍상면의 모서리에서 박리된 난류의 전단층이 다시 컨테이너의 측면에 재부착 되면서 y 방향에 작용하는 풍력계수가 감소한 것으로 판단된다.
(3) 전 풍향에서 컨테이너의 중량에 따른 피해발생 풍속을 평가한 결과, 컨테이너의 전도보다는 활동이 일어날 확률이 상대적으로 높은 것으로 나타났으며, 가장 불리한 컨테이너는 40ft high cube이며, 이때의 활동발생 풍속은 20.4 m/s으로 평가되었다.
(4) 마지막으로 컨테이너의 중량과 피해발생 풍속의 상관을 토대로 컨테이너의 중량에 따른 활동발생 및 전도발생풍속을 평가할 수 있는 평가식을 제안하였다.
본 실험결과는 강풍시 선박 운송용뿐만 아니라 화물적재용 컨테이너의 고박 등의 구조설계 기준 정립에 있어서 유용하게 활용될 것으로 판단된다. 그러나 일반적으로 선박 운송용 컨테이너는 단독으로 있는 경우보다, 혼합적재, 세트적재 및 단일적재 등 다양하게 적재되고 있기 때문에 적재 방법에 따른 피해발생 풍속의 평가에 대한 추가적인 연구가 필요할 것으로 판단된다.