오일러형 해빈류 모형의 3차원 파랑응력을 소개하기에 앞 서, 이의 지배방정식을 식 (1)~(4)에 나타내었다.

여기서, x, y : 해안선 법선 및 평행 방향

U, V : x 및 y 방향의 3차원 유속

Ω : 가 연직속도(pseudo vertical velocity)

M_x, M_y : x 및 y 방향의 파랑질량흐름

η : 평균 해수면

h : 정수위(still water depth)

D : 전체수심, D= η +h

v_{t, h}, v_{t ,v} : 수평 및 연직 방향 난류점성계수

F_x, F_y : x 및 y 방향의 파랑응력

앞서 언급한 바와 같이, 오일러형 해빈류 모형의 계산 질량흐름은 파랑질량흐름과 분리되어 있어, 식 (1)의 평균 해수면은 질량흐름 및 파랑질량흐름의 경사에 의해 계산된다. Xie(2011)는 Xia et al.(2004)의 3차원 해빈류 모형을 오일러형 해빈류 모형으로 분류하였지만, Xia et al.(2004)의 모형에서는 질량흐름과 파랑질량흐름이 구분되지 않아, 라그랑지형 해빈류 모형이라고 보는 것이 타당하다. 이 외에 Xia et al. (2004)의 파랑응력은 실제 물리적 현상을 잘 반영하지 않는 경우가 있어 해빈류 계산에 적합하지 않는 부분이 있는데, 이를 부록에 기술하였다.

평균 해수면(σ = 0) 및 해저면(σ = − 1)에서의 U, V, Ω의 경계조건을 식 (5)와 식 (6)에 나타내었다.

여기서, τη, x와 τη, y는 x 및 y 방향의 평균 해수면 응력을 나타내며, τb, x와 τb, y는 x 및 y 방향의 바닥응력을 나타낸다.

Newberger and Allen(2007)는 천수 선형파랑을 가정한 다음, 척도분석(scaling analysis)을 통해 파랑응력을 유도하였다. Newberger and Allen(2007)의 파랑응력은 평균 해수면 응력 및 운동방정식의 체적력(body force) 으로 주어지는데, 이를 식 (7)~(10)에 각각 나타내었다.

여기서, k_x, k_y : x 및 y 방향의 파수

ω_r : 상대 각주파수(relative angular frequency)

E : 파랑 에너지

D_br : 쇄파 에너지

U₀, V₀ : 평균 해수면에서의 유속

식 (7), (8)은 평균 해수면 응력을 나타내며, 파랑질량흐름 이동방정식과 평균 해수면에서 파랑주기 평균화된 Navier-Stokes 방정식으로부터 이들을 각각 유도하였다. 식 (7), (8)은 파의 쇄파 에너지항으로 만 구성 되어 있기 때문에 쇄파대내에서 파랑 진행 방향과 동일한 방향으로 작용하는 특성이 있다. 이를 바꾸어 말하자면, 쇄파대 외에서는 파랑에 의한 평균 해수면 응력은 작용하지 않음을 의미한다. 즉, Newberger and Allen(2007)의 모형에서는 쇄파대 외에서의 평균해수면 응력이 0이기 때문에 평균 해수면 근처에서의 유속의 연직 경사는 0이라고 할 수 있다. 한편, y 방향의 평균 해수면 응력인 식 (8)은 해저면이 해안선에 대해 수평일 경우, 이를 잉여응력으로 나타낼 수 있다. 먼저, 해저면이 해안선에 대해서 수평일 경우, 에너지 평형 방정식을 다음과 같이 쓸 수 있다.

여기서, c_{g, x}는 x 방향의 군속도를 나타낸다. 식 (11)의 양변에 k_y/ω_r을 곱하면, 다음과 같은 식을 얻을 수 있다.

해저면이 해안선에 대해서 평행할 경우에는 Snell의 법칙, ∂k_y/∂x = 0가 성립하므로, 식 (12)을 다음과 같이 쓸 수 있다.

식 (13)에서 (Ec_g,xk_y)/ω_r은 잉여응력 S_xy과 같다. 따라서 해저면이 해안선에 대해서 수평일 경우에는 쇄파대 내에서 잉여응력과 동일한 평균 해수면 응력이 작용한다고 볼 수 있다.

Chun(2012)의 해빈류 모형 역시, 평균 해수면 응력과 체적력에 파랑응력이 포함되어 있다. 먼저 평균 해수면 응력을 다음에 나타내었다.

여기서 w0~ : 평균해수면에서의 연직방향에 대한 파랑 물입자 속도

<> : 파랑 주기에 대한 평균 연산자

S_xx, S_xy, S_yy : 잉여응력

식 (14), (15)는 식 (7), (8)과 마찬가지로 파랑질량흐름 이동방정식과 평균 해수면에서의 파랑 평균된 Navier-Stokes 방정식에서 유도되었다. 그러나 Chun(2012)의 해빈류 모형에서는 Wave-induced Reynolds stress가 0이 아니라고 보기 때문에 식 (14), (15)와 식 (7), (8)은 그 형태가 서로 다르다. 여기서 Wave-induced Reynolds stress는 Garcez Faria et al.(2000)에 의해 처음 제안되었으며 < u~w~ >, < v~w~ >와 같이 표시하는데, 이의 형태가 Reynolds stress와 유사하여 Wave-induced Reynolds stress라고 부른다. 이 항의 수식은 연구자들마다 서로 다른데, 본 연구의 해빈류 모형에서는 Chun(2012)의 식을 사용하였다. 이의 자세한 유도과정은 Chun(2012), Chun and Suh(2016)에 기술되어 있어 본 논문에서는 이에 대한 기술을 생략한다. 식 (7), (8)과 식 (14), (15)는 형태 뿐만 아니라 물리적으로도 서로 다르게 작용하는데, 대표적으로 식 (7), (8)이 쇄파대 외에서는 0이 되는 반면에 식 (14), (15)는 쇄파대외에서 0이 아니다. 특히 쇄파대외에서 식 (15)가 0이 아니기 때문에 본 연구의 수치모형은 포물선형 연직분포를 가지는 연안류를 재현할 수 있다(Chun and Suh, 2017). 연안류의 포물선형 연직분포는 Garcez Faria et al. (1998)가 DUCK94 현장실험으로부터 처음 제시하였는데, Chun and Suh(2017)이 수치모의 실험에서 이를 성공적으로 재현한 바 있다. 특히 해저면이 해안선에 평행할 때, 이 현상을 명확하게 볼 수 있는데, 해저면이 해안선에 대해서 평행할 경우에는 ∂/∂y = 0와 같이 쓸 수 있다. 이를 식 (15)에 대입해 정리하면, 다음과 같다.

식 (16)의 M_x의 작용방향은 해안선에 법선방향이므로 항상 M_x의 > 0을 만족한다. 따라서 식 (16)는 연안류가 해안선 방향으로 증가할 때에는 연안류의 반대 방향으로 평균 해수면 응력이 작용함을 의미한다. 한편 0이 아닌 해안선 평행 방향의 평균 해수면 응력으로 인해 평균 해수면에서의 연안류의 법선방향 경사는 0이 아니다. 이 외에 천해역 파랑이 해안선에 대해서 법선방향으로 입사할 경우, 식 (16)은 다음과 같은 식으로 쓸 수 있다.

또한, Wave-induced Reynolds stress항은 평균 해수면 응력 외에 체적력에도 포함되어 있는데, Chun(2012)의 파랑응력은 다음과 같은 형태로 최종 정리된다(Chun and Suh, 2017).

여기서 u~, v~, w~ 는 x, y, z 방향의 파랑 물입자 속도를 나타낸다. 식 (18)과 식 (19)를 연직 방향에 대해서 적분하면 다음과 같은 식을 얻을 수 있다.

여기서, θ는 파향을 나타내며, 파랑 진행 방향에 대해 반시계 방향을 기준으로 하였다. n은 군속도와 파속의 비를 나타낸다. 식 (14), (15)에서 식 (20), (21)을 각각 빼면 Smith(2006) 해빈류 모형과 동일한 파랑응력을 얻을 수 있다(Chun and Suh, 2016). 천해역 파랑이 해안선에 법선 방향으로 입사할 때, 식 (20)은 식 (22)와 같은 형태로 쓸 수 있다.

여기서 수심의 경사도 크기를 무시할 수 있을 정도로 작다고 가정한 다음, 식 (17), (22)을 Newberger and Allen(2007)의 파랑응력인 식 (7), (9)와 비교하면, Chun(2012)의 평균 해수면 응력은 1/2∂E/∂x 만큼 더 큰 반면에, 체적력의 파랑응력은 반대로 1/2∂E/∂x 만큼 작다. 그러나, 쇄파대 내에서는 파랑에너지가 감소하기 때문에 Chun(2012)의 해안선 법선방향으로의 평균 해수면 크기는 실제로 1/2∂E/∂x 만큼 작은 반면에, 체적력의 파랑응력 크기는 1/2∂E/∂x 만큼 더 크다.

Hamilton et al.(2001)의 LSTF(Large-scale Sediment Transport Facility) 수리모형 실험은 파랑 조건에 따른 해저지형 변동에 관한 수리모의 실험으로, 본 수리모형 실험이 해저 지형 변동에 초점이 맞춰져 있었지만, 수리모형 실험 당시 파랑 및 해빈류도 관측되었다. 이 때의 파랑 빛 해빈류 관측 자료는 해저지형 변동을 고려하지 않는 3차원 해빈류 모형의 검증 자료로도 활용된 바 있다(Johnson, 2003; Svendsen et al., 2003). 이에 따라 본 연구에서도 해저 지형 변동을 고려하지 않고 3차원 해빈류 계산을 수행하였다. 여기서 Chun(2012) 및 Newberger and Allen(2007)의 파랑응력을 Chun(2012)의 해빈류 모형에 적용하여, 각각의 파랑응력에 따른 해빈류 계산결과를 비교하였다. LSTF 수리모형 실험에서는 다양한 파랑 조건을 가진 수리모형 실험이 수행되었으나, 본 연구에서는 불규칙파 조건을 적용한 Case 1, Case 3, Case 8에 대해서만 해빈류 계산을 수행하였다. 각 수리모형 실험의 입사파 조건으로 단방향 TMA(TEXEL, MARSEN, ARSLOE) 파랑 스펙트럼이 사용되었다. 여기서 입사파 파랑 스펙트럼 형상은 동일하지만, 실험 조건에 따라 유의파고 및 첨두주기는 서로 다르다. Case 1, Case 3, Case 8의 입사파 유의파고는 0.25 m, 0.23 m, 0.225 m이다. 그리고 각각에 대한 입사파의 첨두주기는 1.5 s, 3 s, 2.5 s이다. 반면에 입사파 파향은 10°로 동일하다. 이 외에 모든 실험 조건에서 모래 입자의 크기로 D₅₀ = 0.15mm가 사용됨에 따라, 본 연구의 수치모의실험에서도 바닥 마찰계수 계산 시에 이를 적용하였다. 그러나 Case 1과 Case 3가 이동상(moveable bed) 조건에서 수리실험이 수행되었기 때문에 이들 수리모형 실험의 해저면에서는 파랑 및 유동 조건에 따라 잔물결(ripple)이 관측 된다. 일반적으로 해저면에서의 잔물결은 바닥응력을 강화시키는 효과를 보이는데, 본 연구에서는 Wikramanayake and Madsen(1994)의 모형을 본 수치모형에 이용하여 바닥 조도 계수(bottom roughness height)를 산정하였다. 이 외에 고정상(non-moveable bed) 조건에서 수행된 Case 8에 대한 수치모의 실험에서는 바닥 잔물결을 고려하지 않았다. 그러나, Case 1 및 Case 3에서와 마찬가지로 겉보기 조도높이(apparent roughness height)를 고려하여 계산을 수행하였다. Chun(2012)의 수치모형에서는 Madsen(1994)의 모형을 이용하여 겉보기 조도높이를 산정하였다. 이 외에 본 연구의 수치모의 실험에서 해안선에 평행 및 법선방향의 계산 격자 크기로 각각 1.0 m, 0.2 m를 사용하였으며, 시간 격자 간격은 0.3초를 사용하였다. 또한 수면변위 계산에서 외해 경계 조건으로 관측값을 사용한 반면에, 해안선 평행 및 법선방향의 유량 조건으로 Neunmann 형의 경계 조건을 사용하였다. 또한 본 연구의 수치모의 실험에서 사용된 Chun(2012)의 해빈류 모형은 동적결합형 파랑-해빈류 모형으로 평균 해수면, 연안류, 이안류 외에 유의파고가 계산결과로 주어진다. 여기서의 파랑모형에 대한 기술은 Chun(2012)에서 제시되고 있어, 본 논문에서는 파랑 모형 부분에 대한 기술은 생략한다. 수치모의 실험 이후, 계산 결과의 정확도를 bias, RMSE, SI, r 등의 통계량을 이용하여 정량적으로 나타내고 이를 비교하였다. 각각의 정의는 Chun et al.(2014)에 기술되어 있어 본 논문에서는 이를 별도로 제시하지 않았다. 해빈류 계산 결과의 정확도를 이와 같은 통계량으로 나타내는 사례가 많지 않지만, 본 연구 외에 Rusu and Guedes Soares(2010)와 Xie(2011) 등도 이들 통계량으로 해빈류 계산결과의 정확도를 나타낸 바 있다.

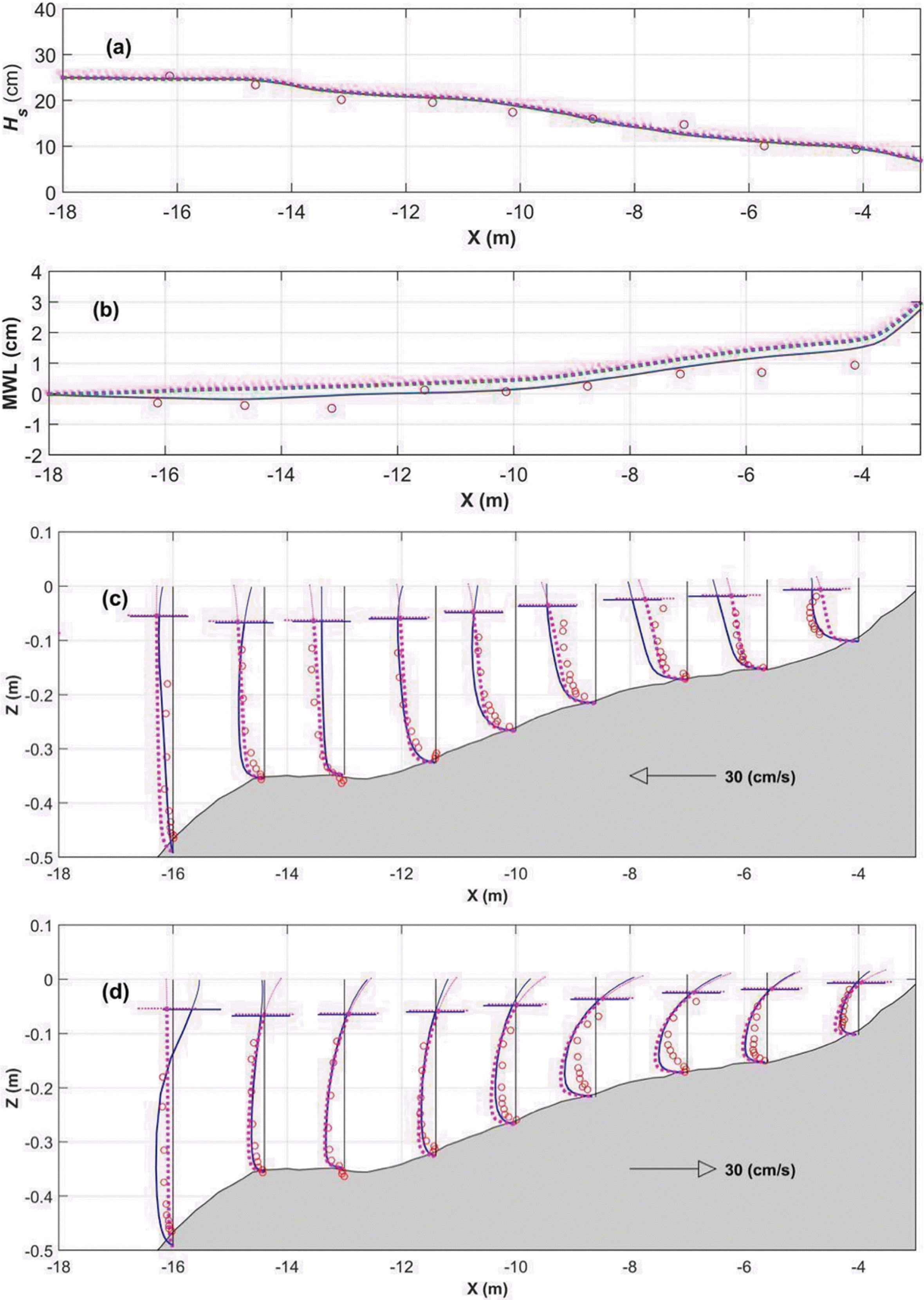
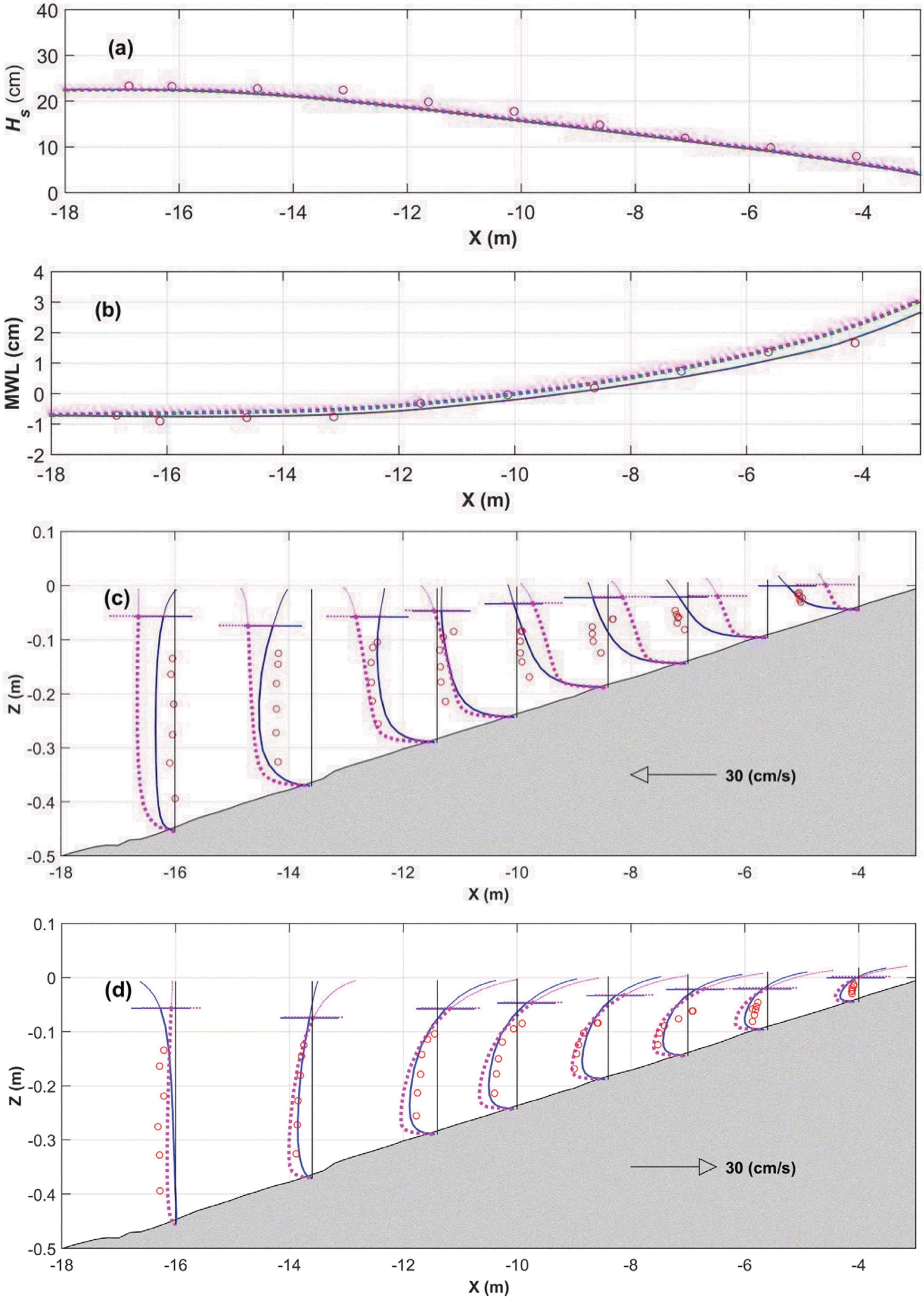
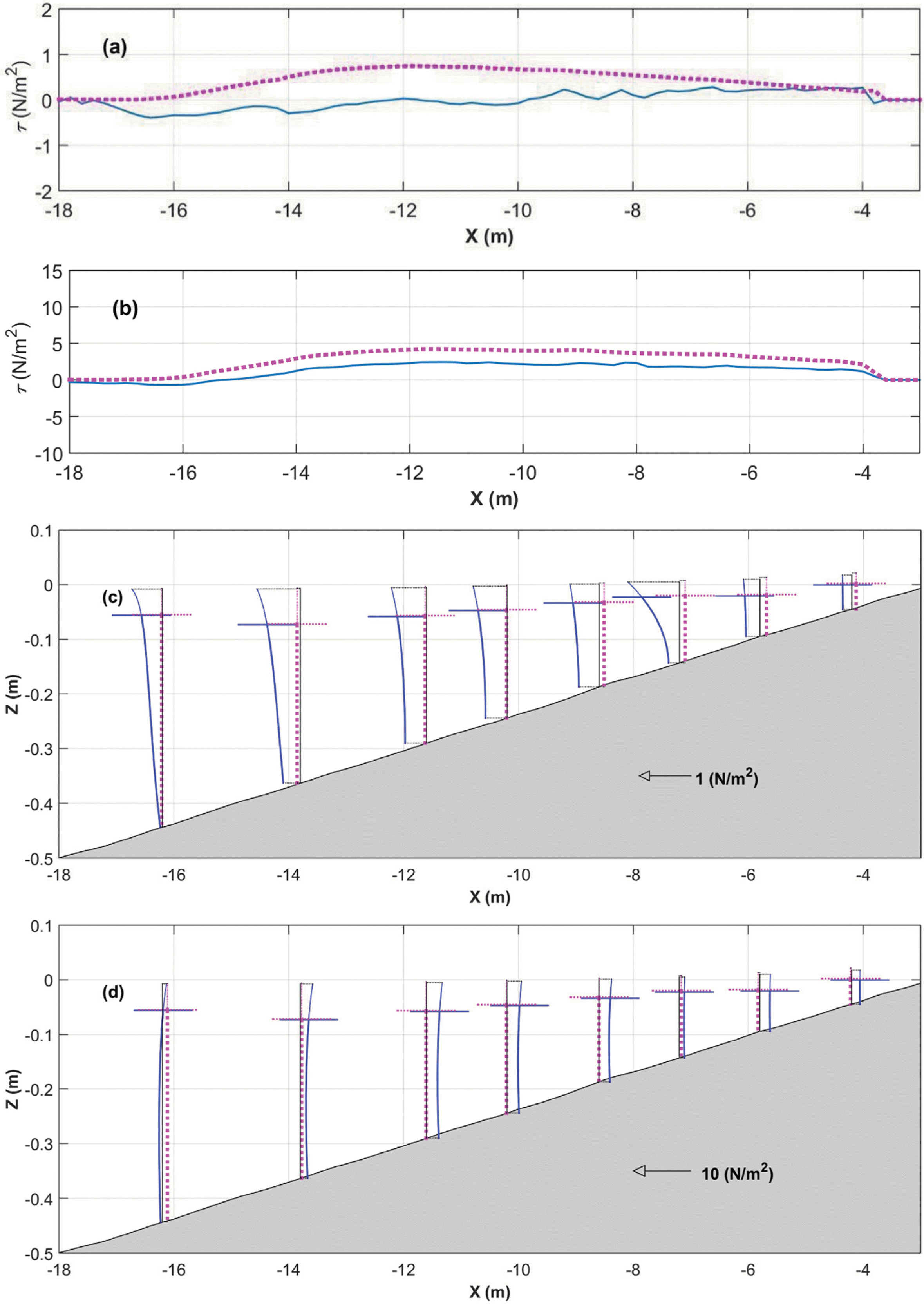
Case 1에 대한 3차원 해빈류 계산결과와 이의 정확도를 Fig. 1과 Table 1에 각각 나타내었다. Fig. 1(a)에 의하면, 유의파고 계산결과는 파랑응력 모형에 관계없이 대체로 유사한 것으로 나타나고 있다. 그러나 Table 1에 의하면, Chun(2012)의 유의파고에서 수치오차(numerical error)가 0.6 mm정도 더 큰 것으로 파악되고 있다. 반면에 Fig. 1(b)를 보면, 파랑응력 모형에 따라 평균 해수면 계산 결과가 확연하게 다른 것으로 나타나고 있다. 특히, Newberger and Allen(2007)의 계산결과에서는 wave set-down이 잘 나타나지 않으며, Newberger and Allen(2007)의 평균 해수면이 과대 계산되는 경향이 있다. 실제로 Table 1을 보면, Newberger and Allen(2007)의 평균 해수면 계산 결과의 수치오차가 Chun(2012)의 경우보다 2.6 mm 정도 더 큰 것으로 나타나고 있다. Newberger and Allen(2007)의 모형에서 평균 해수면이 과대산정된 것은 앞에서 예측한 바와 같이 평균 해수면 응력이 상대적으로 크기 때문인데, Chun(2012)와 Newberger and Allen(2007)의 해안선의 법선방향의 평균 해수면 응력은 Fig. 2(b)에 제시되어 있다. 또한 Fig. 1(c)를 보면, 평균 해수면과 달리 연안류는 거의 차이가 없는 것으로 확인된다. 이러한 특징으로 인해 Table 1의 Pearson 상관 계수는 서로 동일한 것으로 나타나고 있다. 다만, Chun(2012)의 해안선 평행 방향의 파랑응력의 크기가 상대적으로 더 큰 탓에, Chun(2012)의 파랑 계산 결과의 수치오차가 0.33 cm/s 정도 더 큰 것으로 파악되고 있다.

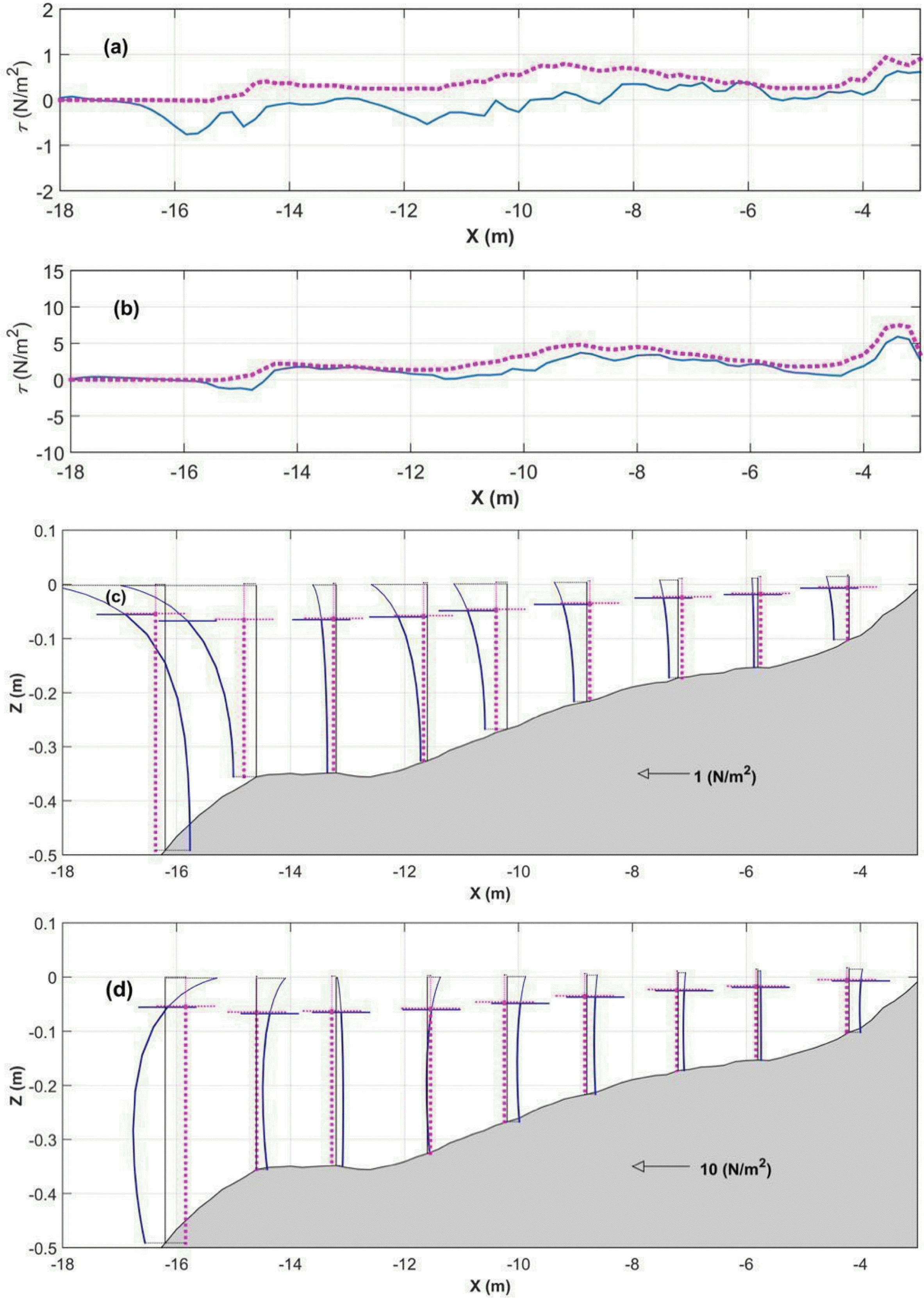
Fig. 1(c)를 보면, Chun(2012)의 해안선 평행 방향의 평균해수면 응력이 연안류 반대 방향으로 작용한 결과, Chun(2012)의 연안류 계산 결과에서 포물선형 연직분포를 성공적으로 재현되고 있다. 이러한 해안선 방향의 평균 해수면 응력의 방향은 식 (16)에서도 보여진 바 있다. 이와 달리 Newberger and Allen(2007)의 연안류 계산결과에서는 로그형 연직분포를 보이고 있다. 이는 해안선 평행 방향의 평균 해수면의 응력이 연안류와 같은 방향으로 작용되어 나타나는 결과이다. 이와 같은 평균해수면 응력의 방향 차이는 Fig. 2(a)에서 확인되는데, Chun(2012)과 Newberger and Allen(2007)의 해안선 평행 방향의 평균 해수면 응력이 서로 반대 방향으로 작용하고 있다. 한편 파랑응력의 차이는 해향저류 계산 결과에서도 차이를 나타내는데, 해향저류와 해안선의 법선방향의 파랑응력의 차이는 Fig. 1(d)와 Fig. 2(d)에서 볼 수 있다. Fig. 1(d)를 보면 최외해 지점에서의 해향저류가 매우 다르게 나타나는 경향이 있는데, 이는 해당 지점에서의 파랑응력 차이로 보여진다. 해당 지점에서의 파랑응력 차이는 Fig. 2(d)에서 확인된다. 이 외에 해향저류 계산 결과에서는 Chun(2012)의 계산 결과의 수치 오차가 0.66 cm/s 더 작은 탓에 Pearson 상관 계수도 더 높은 것으로 나타나고 있다.

Fig. 2(c)와 Fig. 2(d)를 보면, Newberger and Allen(2007)의 파랑응력은 천해역 파랑을 가정한 탓에 수심에 따라 일정하게 분포하고 있다. 반면에 Chun(2012)의 파랑응력은 수심에 따라 다르게 분포하고 있는데, Chun(2012)의 Wave-induced Reynolds stress의 영향으로 수심에 따른 영향이 크게 나타나고 있다. 그리고 파랑응력의 크기 또한 더욱 크게 나타나고 있다. 특히 해안선에 대해서 법선방향으로 작용하는 파랑응력인 Fig. 2(d)를 보면 이러한 경향이 더욱 두드러지는데, 이는 식 (9), (22)의 비교로도 뒷받침된다. 이 외에 Chun(2012)에서 Wave-induced Reynolds stress를 고려한 탓에 평균해수면 근처에서의 파랑응력 경사가 큰 편이다.

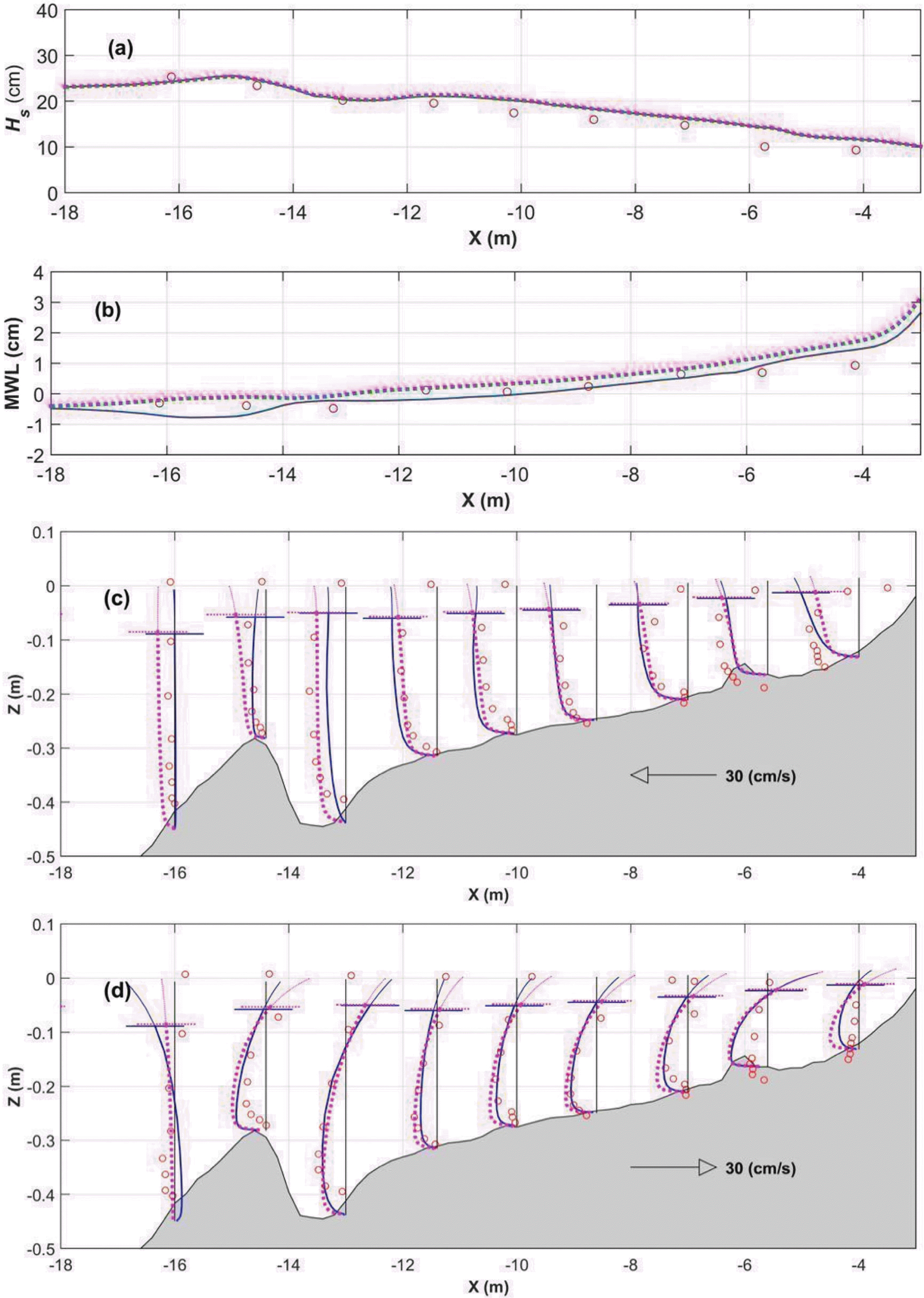
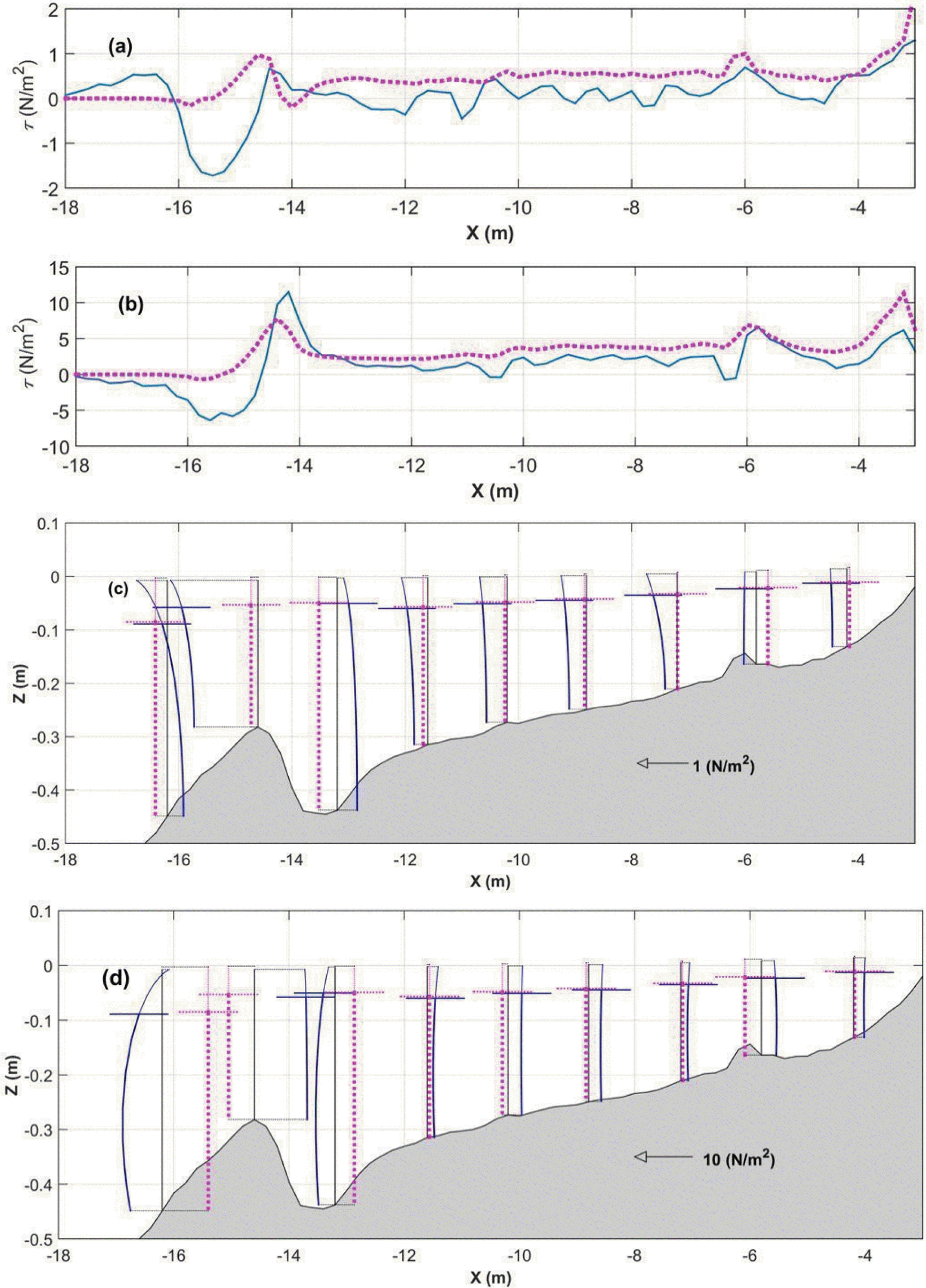
Case 3에 대한 계산결과 및 이의 정확도를 Fig. 3와 Table 2에 정리하여 나타내었다. Fig. 3(a)를 보면 Chun(2012)과 Newberger and Allen(2007)의 유의파고 계산 결과는 서로 유사한 것으로 확인된다. 다만 Chun(2012)의 파랑응력을 포함한 경우, 유의파고의 수치 오차가 0.3 mm 정도 더욱 큰 편이며, 이로 인해 Chun(2012)의 유의파고의 Pearson 상관계수가 상대적으로 더 낮게 나타나고 있다. 한편, Fig. 3(b)를 보면, Fig. 1(b)와 마찬가지로 Newberger and Allen(2007)의 평균 해수면이 과대 산정되는 경향이 있다. 그러나, Newberger and Allen(2007)의 파랑응력에 의한 평균해수면의 정확도가 더 높은 것으로 나타나고 있다. 이는 Chun (2012)의 해빈류 계산 결과, 쇄파 지점 인근에서 평균해수면 응력이 외해역 방향으로 다소 과대 산정되어, wave set-down이 관측치보다 낮게 계산되어 나타난 결과로 보인다. 실제로 Chun(2012)의 평균해수면 수치오차가 0.6 mm 정도 더 크게 계산되었으며, 이로 인해 Pearson 상관계수 역시 낮게 나타나고 있다. 연안류 역시 Chun(2012)의 경우에서 수치오차가 0.17 cm/s 정도 더 크게 나타나, Pearson 상관계수 역시 더 낮은 것으로 나타났다. 이 외에 Case 1과 마찬가지로 Case 3에서도 연안류 반대 방향으로 평균 해수면 응력이 작용해 포물선형 연직분포를 가지는 연안류 가 나타나 있는 것을 볼 수 있다. 그러나 지역적인 수심 경사의 영향으로 Case 1보다 포물선형 분포를 가지는 연안류가 더 적게 나타나는 경향이 있다. 또한, 연안류 계산 결과와 달리 해향저류 계산 결과에서는, Chun(2012)의 파랑응력을 적용한 해향저류 계산 결과의 정확도가 더 높다. Table 2에 따르면, Chun(2012)의 파랑응력을 도입한 경우의 해향저류의 수치오차가 더 작은데, 이는 Newberger and Allen(2007)의 평균 해수면 응력이 상대적으로 크게 작용한 결과로 평균 해수면 인근에서의 해향저류가 크게 계산되어 수치오차가 크게 나타나고 있는 것으로 파악된다. 한편 Newberger and Allen(2007)의 해향저류의 Pearson 상관 계수가 매우 낮은데, 관측치 및 계산치 사이의 선형적인 관계 정도가 낮아 나타나는 결과로 보여진다. 이에 본 연구에서는 Newberger and Allen(2007)의 해향저류 계산결과에 대해 two-sample t-test를 수행하였는데, 이에 따르면 유의수준 0.05에서 Newberger and Allen(2007)의 해향저류 계산결과가 관측치와 일치하는 것으로 파악되었다. 한편, Chun(2012) 및 Newberger and Allen(2007)의 파랑응력을 비교하여 Fig. 4에 나타내었다. Fig. 2와 마찬가지로 Chun(2012)과 Newberger and Allen(2007)의 파랑응력은 확연히 다른 연직분포 경향을 가지고 있다. 여기서, Chun (2012)의 파랑응력은 수심에 따라 파랑응력이 다르지만, 파랑 특성때문에 수심 약 0.2 m 이하인 경우에는 수심에 따라 파랑응력이 거의 일정한 것으로 나타나고 있다.

Case 8 수리모형 실험은 Case 1과 Case 3와 달리 일정한 경사를 가지며, 고정상에서 수행되었다. 그러나 Case 8에 대한 수치모의 실험 결과는 연안류를 제외하고, Case 1 및 Case 3에 대한 수치모의 실험 결과와 대체로 유사한 것으로 나타나고 있다. 우선 Table 3와 Fig. 5(a)를 보면, 이전 결과들과 동일하게 Chun(2012)의 유의파고의 수치 오차가 0.8mm 정도 더 큰 편이나, 유의파고 계산 결과는 대체로 유사하다. 이 외에 Fig. 5(b)의 평균 해수면 계산결과를 보면, Newberger and Allen(2007)의 wave set-down이 잘 나타나지 않으며, 평균해수면은 과대 산정되었다. 이로 인해 수치오차는 0.4 mm 더 크게 나타나고 있다.

이 역시 Newberger and Allen(2007)의 해안선의 법선방향의 평균 해수면 응력이 더욱 크게 나타난 결과로, Chun(2012)과 Newberger and Allen(2007)의 해안선 방향의 평균해수면 응력 크기는 Fig. 6(b)에서 볼 수 있다. 하지만, Case 8의 연안류 계산 결과는 Case 1 또는 Case 3와 달리 파랑응력 모형에 따라 확연한 차이를 보이고 있다. 특히, Newberger and Allen(2007)의 연안류 계산결과가 관측치와 크게 차이나는데, Fig. 5(c)를 보면 해안선 근처에서는 연안류가 과소산정하고 있는 반면에 외해역에서는 과대산정되고 있다. 이는 연안류 운동 방정식에 포함되어 있는 대류항이 외해역 방향으로 연안류를 이송시키는 역할을 수행하고 있는 반면에, Newberger and Allen(2007)의 파랑응력이 상대적으로 작아 나타난 결과로 파악된다. 이로 인해 Newberger and Allen(2007)의 연안류 계산 결과의 정확도 역시 낮은 것으로 나타나고 있다. 반면에 Chun(2012)의 연안류 계산 결과는 상대적으로 관측치와 잘 일치하고 있다. 그리고 Case 8 역시 외해역을 중심으로 포물선형의 연직분포를 잘 재현하고 있다. 한편 해향저류 계산 결과는 파랑응력 모형에 관계없이 대체로 유사한 편인데, Chun(2012)의 파랑응력 모형을 적용한 경우의 수치 오차가 0.62 cm/s 더 큰 탓에 이의 Pearson 상관 계수 역시 다소 낮은 편이다.

Fig. 6의 파랑응력은 이전 수리모형실험 조건들에 비해서 상대적으로 작은데, 이는 파랑응력이 파랑 에너지의 크기보다는 파랑에너지의 경사에 결정되는데, 앞서의 경우에 비해서 Case 8의 수심 경사가 완만해, 파랑 에너지의 경사 역시 완만해 나타나는 결과로 파악된다. 이는 Fig. 5(a)의 유의파고 분포도에서도 확인된다.

한편, Fig. 6의 파랑응력을 보면, 파랑응력의 크기가 전체적으로 작은 가운데, Newberger and Allen(2007)의 파랑응력이 Chun(2012)의 파랑응력보다 더욱 작은 것으로 나타나고 있다. 이러한 경향은 Case 1 및 Case 3에서 동일하게 나타나고 있다.