Block and Extraction of Wave Energy Using a Rolling Porous Pendulum Plate

Il-Hyoung Cho

doi:10.9765/KSCOE.2018.30.4.180

요약

파랑 중 횡 방향으로 운동하는 투과성 진자판을 파랑에너지를 차단과 추출을 동시에 하는 복합 시스템으로 활용하는 기초 연구를 수행하였다. Porter and Evans(1995)가 제안한 Galerkin 방법을 사용하여 투과성 진자판에 대한 회절과 방사 문제를 풀어 반사율과 투과율, 운동변위, 그리고 추출파워를 구하였다. Galerkin 방법은 고유함수전개법 보다 수렴성이 좋기 때문에 짧은 계산시간에도 불구하고 정확한 해를 주었다. 투과성 진자판이 불투과성 진자판 보다 파랑에너지 추출과 차단 측면에서 모두 효과적이라고 말할 수는 없지만 파랑 하중을 줄일 수 있고 해수 교환이 가능하다는 장점은 지니고 있다.

핵심용어: 투과성 진자판, 파랑에너지 추출, 파 차단, 갈라킨 법, 공극률 계수

Abstract

The preliminary study was carried out to utilize the rolling porous pendulum plate as a hybrid system combining blocking and extracting of wave energy. The Galerkin method suggested by Porter and Evans (1995) was used to solve the diffraction and radiation problems to obtain reflection and transmission coefficient, roll displacement, extracted power. The Galerkin method provides better convergence than the matched eigenfunction expansion method (MEEM), which improves the accuracy of the analytical solution even if the CPU time is shorter. The porous plate can not be said to be more effective than the impermeable plate in terms of wave energy extraction and wave blocking, but it has the advantage of reducing the wave load and exchanging seawater.

Keywords: porous pendulum plate, wave energy extraction, wave block, Galerkin method, porosity-effect parameter

1. 서 론

산업 안정기를 지나면서 해양에 대한 이용 관점 및 욕구도 다양해져서 환경과 조화를 이루는 지속 가능한 해양/연안 구조물로 패러다임이 바뀌기 시작하였다. 이에 따라 해양외력 및 생태환경 특성을 고려하여 안전하고, 쾌적하며, 생산성 높은 해역 이용이 가능할 수 있도록 해양/연안 구조물을 개발하여야 한다.

파랑중 진자판의 횡 방향 운동으로부터 에너지를 추출하는 진자형 파력발전장치(oscillating surge wave energy converter)는 가동물체형 파랑에너지 변환장치의 한 종류이다. 진자형 파력발전장치는 현재 상용화 단계에 와 있는 발전장치로 대표적인 장치로는 Oyster(Whittaker and Folley, 2012)와 WaveRoller(Lucas et al., 2012)가 있다. 국내에서는 선박해양플랜트연구소(KRISO)에서 개발한 부유식 진자형 파력발전장치에 대한 실물 제작이 완료되어 현재 파력발전 실해역 시험장(제주도 차귀도)에 설치되어 시험평가에 들어갔다. 진자형 파력발전장치는 1차 변환과정을 통하여 파랑에너지를 진자판의 운동에너지로 바꾸고, 진자판의 운동에너지는 2차 변환장치인 유압모터를 작동시켜 전기에너지를 생산한다. 진자형 파력발전장치는 진자판의 회전축이 해저면 가까이 위치한 몰수형(submerged type)과 수면위에 놓인 관통형(surface-piercing type)으로 분류된다. 두 종류 모두 수심 10 m에서 20 m 사이의 연안에 설치되는 천수역 발전장치이다. 이러한 진자형 파력발전장치는 진자판이 운동을 하는 것을 제외하면 파 차단제(wave barrier)와 형태가 유사하다. 이런 구조적 특징으로 파랑에너지의 추출과 차단 기능을 결합한 복합 기능 시스템을 제안하게 되었다. 이러한 복합 시스템은 하나의 지지 구조물을 공통으로 사용하므로 제작, 설치, 유지/보수에 관한 비용 절감 효과뿐만 아니라 파와 흐름을 부분적으로 허용하므로 환경 친화적인 구조물이다.

직립 판을 파 차단제로 활용하는 연구는 연안 공학 분야에서 오랜 관심 주제였다. Ursell(1947)은 깊은 수심에서 두께가 얇은 직립 판에 의한 파의 회절 문제(diffraction problem)에 대한 초기 연구를 수행하였다. Evans(1970)는 선형포텐셜 이론을 기반으로 수면 아래 잠긴 직립 판에 작용하는 1차 및 2차 파랑 하중과 모멘트를 구하였다. Losada et al.(1992)와 Abul-Azm(1993)은 직립 판이 서로 다른 배치 형상을 갖고 수중에 놓여 있을 때의 경사파의 회절 문제를 고유함수전개법(matched eigenfunction expansion method)을 사용하여 풀었다. Porter and Evans(1995)는 직립 판에 의한 경사파의 회절 문제를 Galerkin 방법을 사용하여 풀어 보다 높은 정확도를 갖는 반사율과 투과율을 얻었다. Martins-Rivas and Mei(2009)와 Chang et al.(2012)는 3차원 직립 판에 의한 회절 문제에 Porter and Evans(1995)가 제안한 Galerkin 방법을 적용하였다. Galerkin 방법의 장점은 판 끝단 근처에서 특이 거동을 보이는 유속을 정확하게 모델링 할 수 있다. 따라서 얇은 판의 끝단이 수중에 놓여 있는 모델에 관해서는 고유함수전개법보다 수렴성이 우수하여 짧은 계산시간에도 불구하고 매우 정확한 결과를 준다. Cho et al.(2017a, b)는 고유함수전개법을 사용하여 횡 방향으로 운동하는 불투과성 진자판의 회전축이 수면위에 놓인 경우와 해저면 바닥에 놓인 경우에 대하여 추출파워와 효율을 고유함수전개법을 사용하여 구하고 WAMIT 상용프로그램을 이용한 수치해석 결과와 비교하였다.

투과성 구조물이 지닌 여러 장점들로 인해 투과성 판과 파와의 상호작용 문제는 연안 공학 분야에서 매우 흥미로운 주제로 지금까지 많은 연구가 진행되고 있다. Macaskill(1979)은 깊은 수심에 놓인 투과성 직립 판에 의한 파의 회절에 대한 Tuck(1975)의 연구 결과를 유한 수심으로 확장하여 투과성 직립 판과 입사파의 상호 작용 연구를 수행하였다. Sahoo(1998)는 깊은 수심에서 투과성 판에 의한 파의 회절 문제를 섭동법(perturbation method)을 사용하여 해석하였다. Isaacson et al.(1998)는 수면 아래 일부분 잠긴 투과성 직립 벽과 입사파의 상호 작용에 대한 해를 구하기 위하여 고유함수전개법을 사용하였고, 모형실험을 통하여 해석해를 검증하였다. Karmakar and Guedes Soares(2014)는 고유함수전개법을 이용한 다층 투과성 벽에 의한 파의 전달에 대한 해석 기법을 개발하였다. Gayen and Mondal(2014)은 제 2종 적분방정식을 풀어 수면 아래 놓인 경사진 투과성 판에 의한 반사율과 투과율을 구하였다.

본 연구에서는 파랑에너지의 일부분을 차단하여 배후 해역의 정온도를 확보하고 동시에 파랑에너지로부터 전기를 추출하는 횡 방향으로 운동하는 투과성 진자판을 다루었다. 이러한 복합 기능 시스템의 장점은 제작, 설치, 유지/보수에 관한 비용을 크게 줄일 수 있으며, 같은 지지 구조물을 사용하기 때문에 해양 환경에 미치는 부정적인 영향을 최소화할 수 있다. 투과성 진자판이 갖는 복합 시스템의 실현 가능성을 살펴보기 위해 여러 설계 변수(입사의 주파수, 진자판의 높이와 공극률)의 변화에 따른 파랑에너지 차단과 추출 성능을 살펴보았다. 파랑에너지 차단 성능의 지표로 반사율과 투과율을, 파랑에너지 추출 성능의 지표로 추출파워와 효율을 잡았다. 2장에서는 Porter and Evans(1995)가 제안한 Galerkin 방법을 적용하여 회절과 방사 문제를 푸는 과정을 소개하였다. 3장에서는 투과성 진자판의 횡 방향 운동방정식을 유도하고, 이를 풀어 운동 변위, 추출파워, 그리고 효율을 구하였다. 또한 진자판의 횡 운동에 따른 방사파를 고려한 전체 반사율과 투과율을 살펴보았다. 4장에서는 투과성 진자판의 여러 설계변수가 파의 차단과 추출 성능에 미치는 영향을 살펴보고 복합 기능 시스템의 활용 가능성에 관하여 논하였다. 끝으로 본 논문의 중요한 결론들을 5장에서 언급하였다.

2. 문제의 정식화

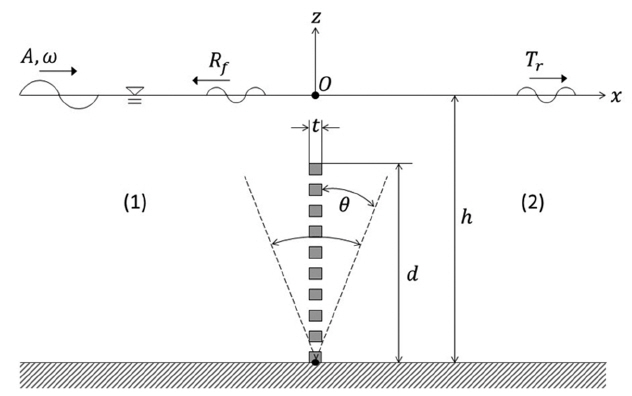
파랑중 횡 방향으로 운동하는 투과성 진자판을 해석 모델로 잡았다(Fig. 1 참조). 진자판은 투과성 재질로 높이는 d이며 두께는 t이다. 진자판의 길이는 무한히 길다고 가정하여 2차원 문제로 다루었다. 수심은 h로 일정하며, 진폭(A), 주파수(ω)를 갖는 규칙파가 x축의 양의 방향으로 진행한다고 가정하였다. 비압축성, 비점성 유체로 가정하고, 유동을 비회전성이라 하면 속도포텐셜을 도입할 수 있다.

입사파가 주파수 ω를 갖고 조화운동을 하므로 속도포텐셜, 진자판에서의 유속, 진자판의 운동 변위를 시간과 공간 함수로 분리하여 아래와 같이 쓸 수 있다.

(1)

Φ(x,z,t)=Re{ϕ(x,z)e−iωt},U(z,t)=Re{u(z)e−iωt},θ(t)=Re{θoe−iωt},

여기서 θo은 횡 방향 운동변위의 복소진폭이다.

공간의 함수인 속도포텐셜 φ(x, z)를 선형 이론에 따라 아래와 같이 회절 포텐셜(φ_D)과 진자판의 횡 방향 운동에 따른 방사 포텐셜(φ_R)의 합으로 표현할 수 있다.

(2)

ϕ(x,z)=−igωAϕD(x,z)−iωθoϕR(x,z),

여기서 회절 포텐셜(φ_D)은 입사 포텐셜(φ_I)과 산란 포텐셜(φ_S)의 합으로 표현할 수 있으며, 입사 포텐셜(φ_I)는 다음과 같다.

(3)

ϕ1(x,z)=coshk(z+h)coshkheikx.

여기서 k는 파수(wave number)이다.

진자판에서의 경계조건식을 제외하면 회절 포텐셜(φ_D)과 방사 포텐셜(φ_R)는 아래 주어진 경계치 문제를 만족한다.

(4)

{∇2ϕR,D=0,∂ϕR,D∂z−ω2gϕR,D=0 at z=0,∂ϕR,D∂z=0 atz=−h,limx→±∞(∂ϕR,S∂x∓ikϕR,S)=0,

파장에 비하여 진자판의 두께가 작다는 가정 아래에서 진자판에서의 경계조건식을 x = 0에서 적용한다. 진자판(x = 0)에서의 경계조건식은 아래와 같다.

(5a, b)

∂ϕR,D−∂x=∂ϕR,D+∂x=0,−h≤z≤0{ϕR,D−=ϕR,D+,[uR,D*]+−=ikG(ϕR,D−−ϕR,D+,−(h−d)≤z≤0−h≤z≤−(h−d)

윗 식에서 위첨자 ±는 각각 투과성 진자판의 전 후면을 의미한다. u*R, D는 진자판에서의 수평방향 유속 ∂ϕR,D∂χ과 진자판의 수평 속도간의 상대 속도를 나타낸다. 따라서 uD*=∂ϕD∂χ, uR*=∂ϕR∂χ-z+h이다. 식(5a)는 연속방정식을 나타내며, 식(5b)는 진자판이 없는 경계면에서는 압력값은 서로 같고, 투과성 진자판이 놓인 경계면에서는 수평방향의 상대 속도는 투과성 판 전 후면의 압력 차와 선형적으로 비례한다는 Darcy의 법칙을 뜻한다. 이때 비례상수 G = P/[kt(f − is)]를 공극률 계수(porosity-effect parameter)라 부르며 투과성 판의 공극률과 국부형상(local shape)에 밀접한 관련이 있다(Yu, 1995). 여기서 P, f, s는 각각 투과성 판의 공극률과 저항 계수(resistance coefficient) 그리고 관성력 계수(inertial coefficient)를 나타낸다. G(= G_r + iG_i)의 실수부Gr = Pfktf2+χ2와 허수부Gi = Psktf2+χ2는 각각 파가 투과성 판을 통과할 때 일어나는 에너지 손실과 위상차를 나타내는 항이며, 각 항은 저항력과 관성력에 밀접한 관련이 있다. Cho and Kim(2008)은 작은 구멍들이 일정한 간격을 갖고 균일하게 배열된 투과성 판에 대한 체계적인 모형실험을 수행하여, 그 결과를 해석결과와 비교하여 실제 공극률 P와 공극률 계수 Gr 사이에는 선형 관계가 있음을 밝혔다(Gr = (57.63P − 0.9717)/2π, Gi = 0). 즉, 공극률이 증가하면 공극률 계수도 선형적으로 증가한다. G→0는 불투과성 판을 의미하며, G→∞는 입사파에 전혀 영향을 주지 않는 가상의 판이 놓여 있는 경우이다.

2.1 회절 문제(Diffraction Problem)

이 절에서는 진자판이 수직으로 고정되어 있을 때 입사파에 의한 회절 문제를 다루었다. 먼저 유체영역을 진자판이 놓인 x = 0을 기준으로 2개의 영역(영역(1), 영역(2))으로 나눈다. 먼저 식(4)을 만족하는 영역(1), (2)에서의 회절 포텐셜은 다음과 같다.

(6)

ϕD(1)(x,z)=∑n=0∞[e−knxδno+aneknx]fn(z), x≤0,ϕD(2)(x,z)=∑n=0∞bne−knxfn(z), x≥0,

여기서 n = 0일 때를 진행파 모드(propagating mode)라 부르며, n이 0보다 클 때를 비진행파 모드(evanescent modes)로 진자판으로부터 멀어짐에 따라 사라지는 항이다. 자유표면 경계조건식과 바닥 경계조건식을 만족하는 식(6)의 고유함수 fn(z)와 분산식(dispersion relation)은 다음과 같다.

(7)

fn(z)=coskn(z+h)cosknh, n=0,1,2,3…

(8)

ω2=−gkntanknh.

여기서 진행파 모드에 대한 고유치는 k₀= − ik이다. 따라서 진행파에 대한 분산식은 ω² = gktanhkh이다.

식(7)의 고유함수는 아래의 직교성을 만족한다.

(9)

∫−h0fm(z)fn(z)dz=Nnδmn

여기서 Nn = 1cos2knhh2+sin2knh4kn이다. 식(9)의 δmn는 m = n일 때 1이고, m ≠ n일 때 0의 값을 갖는 Kronecker-Delta 함수이다.

x = 0에서의 수평방향 유속은 서로 같으며, 유속 u_D(z)을 고유함수(f_n(z))의 전개식으로 나타내면 다음과 같다.

(10)

∂ϕD(1)(0,z)∂x=∂ϕD(2)(0,z)∂x=uD(z)=∑n=0∞udnfn(z)

식(6)을 식(10)에 대입하여 a_n, b_n을 u_dn으로 나타내면 각 영역에서의 속도포텐셜은 다음과 같다.

(11)

ϕD(1)(x,z)=(eikx+e−ikx)f0(z)+∑n=0∞udnkneknxfn(z), x≤0,ϕD(2)(x,z)=−∑n=0∞udnkne−knxfn(z), x≥0.

회절 문제에 대한 x = 0에서의 경계조건식(5b)를 다시 쓰면 다음과 같다.

(12)

ϕD(1)−ϕD(2)={0,−(h−d)≤z≤01ikG∂ϕD∂x,−h≤z≤−(h−d)

Porter and Evans(1995)의 방법에 따라 진자판 전후의 속도포텐셜의 차를 아래와 같이 Chebychev의 다항식을 포함한 기저함수(basis function)로 전개시킨다.

(13)

ϕD(1)−ϕD(2)={0,−(h−d)≤z≤0∑p=0∞apχp(z),−h≤z≤−(h−d)

식(13)의 a_p는 전개식의 계수로 미지수이다. 기저함수 χ_p(z)는 아래와 같이 정의된다.

(14)

χp(z)=2(−1)pd2−(h+z)2π(2p+1)dhU2p(h+zd),

여기서 U_n(x)는 n차 Chebychev의 다항식으로 Unx=sinn+1θsinθ,x=cosθ이다. 식(14)는 바닥 경계조건식을 만족하고, 진자판 끝단에서의 제곱근(√)의 특이성을 나타낸다.

식(11)을 식(13)에 대입한 후 양변에 fm(z), (m = 0, 1, 2, …)를 곱한 뒤, − h부터 0까지 z에 대하여 적분하면 아래의 관계식을 유도할 수 있다.

(15)

R=1+iud0k=(2N0)−1∑p=0∞apFp0,udmkm=(2Nm)−1∑p=0∞apFpm, m=1,2, …,

여기서

(16)

Fpm{∫−h−(h−d)χp(z)f0(z)dz=(−1)pI2p+1(kd)khcoshkh, m=0∫−h−(h−d)χp(z)fm(z)dz=J2p+1(kmd)kmhcoskmh, m=1,2,…

여기서 J_2p+1, I_2p+1는 (2p + 1)차 Bessel 함수와 modified Bessel 함수를 나타낸다.

식(15)를 이용하여 식(11)을 다시 쓰면 다음과 같다.

(17)

ϕD(1)(x,z)=(eikx+Re−ikx)f0(z)+∑n=1∞1(2Nn)∑p=0∞apFpneknxfn(z), x≤0,ϕD(2)(x,z)=Teikxf0(z)−∑n=1∞1(2Nn)∑p=0∞apFpne−knxfn(z), x≥0,

여기서 R=12N0∑p=0∞apFp0, T = 1 − R는 각각 고정된 진자판에 의한 반사율과 투과율을 나타내며 투과성 진자판을 통과하면서 소멸되는 에너지 손실률은 ε(= 1 − R2 − T2)이다.

식(17)을 식(12)에 대입한 후 양변에 p_m(z), (m = 0, 1, 2, …)를 곱하고 − h부터 − (h − d)까지 z에 대하여 적분하면 아래와 같은 대수방정식을 유도할 수 있다. 이때 기저함수의 개수(p, m = 0, 1, 2, …, M)와 고유함수의 개수(n = 0, 1, 2, …, N)는 유한개를 취한다.

(18)

∑p=0Map{∑n=0N1Nn(2G−knik)FpnFmn}=2Fm0.

식(18)에 주어진 대수방정식을 풀어 미지수 ap(p= 0, 1, 2, …, M)을 구하고 식(17)에 대입하여 각 영역에서 완전한 해를 구한다.

진자판에 작용하는 횡 방향의 파기진력(F_E(t) = ARe{fEe^−iωt})은 회절파의 동압력을 투과성 진자판을 따라 적분하여 얻어진다. 이때 투과성 진자판의 공극률에 따른 면적의 손실분은 무시하였다.

(19)

fE(ω)=ρg∫−h−(h−d)(z+h)[ϕD(1)(0,z)−ϕD(2)(0,z)]dz,=ρg∑n=0N1N∑p=0MapFpn∫−h−(h−d)(z+h)fn(z)dz.

2.2 방사 문제(Radiation Problem)

이 절에서는 투과성 진자판의 횡 방향 운동에 의한 방사 문제를 다루었다. 회절 문제와 동일한 방법으로 유체영역을 진자판을 기준으로 2개의 영역으로 나누고, 식(4)을 만족하는 영역(1), (2)에서의 방사 포텐셜을 쓰면 다음과 같다.

(20)

ϕR(1)(x,z)=∑n=0∞Aneknxfn(z), x≤0,ϕR(2)(x,z)=∑n=0∞Bne−knxfn(z), x≥0.

진자판에서의 유속을 고유함수의 전개식uRz=∑urnn=0∞fnz으로 표현한 후, 연속방정식(5a)에 대입하면 A_n = − B_n = u_rn/k_n이다. 식(20)을 다시 쓰면 다음과 같다.

(21)

ϕR(1)(x,z)=∑n=0∞urnkneknxfn(z), x≤0,ϕR(2)(x,z)=−∑n=0∞urnkne−knxfn(z), x≥0.

회절 문제와 동일한 방법으로 진자판 전후의 압력 차이를 기저함수의 전개식으로 나타내고 투과성 진자판에서의 경계조건식을 적용하면 영역(1), (2)에서의 방사 포텐셜은 다음과 같다.

(22)

ϕR(1)(x,z)=∑n=0∞1(2Nn)∑p=0∞ap*Fpneknxfn(z), x≤0,ϕR(2)(x,z)=∑n=1∞1(2Nn)∑p=0∞ap*Fpne−knxfn(z), x≥0.

방사 문제에 대한 경계조건식에서 진자판에서의 수평방향 유속은 진자판의 수평 속도를 고려한 상대 속도로 표현된다.

(23)

ϕR(1)−ϕR(2)={0,−(h−d)≤z≤01ikG(∂ϕR∂x−(z+h)),−h≤z≤−(h−d)

식(22)를 식(23)에 대입하기에 앞서 (z + h)를 고유함수 fn(z)의 전개식으로 표현하면 다음과 같다.

(24)

z+h=∑n=0∞γ^nfn(z),

여기서 전개식의 계수 γ^n는 고유함수 fn(z)의 직교성을 이용하면 γˆn = 나타낼 수 있다.

식(22)와 식(24)를 식(23)에 대입한 뒤 양변에 pm(z), (m = 0, 1, 2, …, M)를 곱하고 − h부터 0까지 z에 대하여 적분하면 아래와 같은 대수방정식을 얻을 수 있다.

(25)

∑p=0Map*{∑n=0N1Nn(2G−knik)FpnFmn}=2ik∑n=0Nγ^nFmn,

대수방정식(25)를 풀어 구한 미지수 ap*를 식(22)에 대입하면 방사 포텐셜에 대한 완전한 해를 얻을 수 있다.

투과성 진자판의 횡 방향 운동에 의한 동유체력(F_R(t) = Re{f_Re^−iωt})는 다음과 같다. 이때 투과성 판의 면적 손실의 영향은 무시하였다.

(26)

fR=ρω2θ0∫−h−(h−d)(z+h)[ϕR(1)(0,z)−ϕR(2)(0,z)]dz,=ρω2θ0∑n=0N1Nn∑p=0Map*Fpn∫−h−(h−d)(z+h)fn(z)dz.

동유체력(fR)은 부가질량(added mass)와 방사감쇠계수(radiation damping coefficient)의 합으로 아래와 같이 표현된다.

(27)

fR=(ω2+a33+iωg33)θ0.

3. 운동방정식과 추출파워

진자판의 횡 방향 운동변위를 구하기 위해 아래 주어진 횡방향 운동방정식을 풀어야 한다.

(28)

Jθ¨(t)=FE(t)+FR(t)+Fv(t)+FS(t)+FPTO(t),

여기서 J는 회전축(z = − h) 중심에서의 진자판의 관성모멘트, F_S(= − K_Sθ(t))는 진자판의 부력과 중력의 차로 생기는 복원력, F_PTO(= − b_PTOθ ·(t))는 PTO(Power Take-off) 장치 설치에 따른 PTO 감쇠력, Fv(= − bvθ ·(t))는 점성 감쇠력을 뜻한다. 본 논문은 포텐셜 이론에 기반을 두고 있어 점성 감쇠력은 고려하지 않았다. 일반적으로 자유감쇠실험(free-decay test)이나 점성수치(CFD) 코드를 이용하여 점성 감쇠력을 고려한다.

진자판의 두께가 진자판의 폭과 높이에 비하여 작고, 진자판의 질량이 균일하게 분포되어 있다고 가정하면 진자판의 단위 폭 당 관성모멘트와 복원력 계수는 다음과 같다. d ≤ h인 경우, 진자판의 무게중심(z_g)과 부력중심(z_b)은 d/2이다.

(29)

J≈13ρtd3,KS≈12ρgtd2(1−ρfρ),

여기서 ρf는 진자판의 밀도이다. 관성모멘트와 복원력을 계산할 때 투과성 진자판의 공극률의 효과는 고려하지 않았다.

식(28)의 우변의 외력들을 F_{E, R, S, PTO} = Re{f_{E, R, S, PTO} e^−iωt}라 놓고 식(28)에 대입하여 횡 방향 운동변위를 구하면 다음과 같다.

(30)

θ0=AfE(ω)−ω2(J+a33)−iω(b33+bPTO)+KS.

PTO 감쇠계수 bPTO와 진자판의 횡 방향 운동속도의 제곱에 비례하는 단위 폭 당 시간평균 추출파워는 아래와 같다.

(31)

P¯(ω)=12ω2bPTO|θ0|2,=12ω2bPTOA2|fE(ω)|2{−ω2(J+a33)+KS}2+ω2(b33+bPTO)2.

최적의 PTO 감쇠계수 (b~PTO)는 시간평균 파워가 최대값을 가질 때이다. 따라서 최적의 PTO 감쇠계수를 얻기 위한 조건식은 ∂P¯/∂bPTO=0이다. 이로부터 구한 최적의 PTO 감쇠계수는 다음과 같다.

(32)

b˜PTO=(ωN2−ω2)2(J+a33)2+(ωh33)2ω.

여기서 ωN는 횡 방향 운동의 비감쇠 고유주파수(undamped natural frequency)로 아래와 같다.

(33)

ωN=KSJ+a33(ωN).

식(33)에서 ω_N는 초기값 ωN1=KS/J을 가지고 주파수별로 미리 구해 놓은 부가질량 a33(ω)을 가지고 축차법(iteration method)을 이용하여 계산된다.

식(32)을 식(30)에 대입하면 PTO 장치를 연결한 상태를 의미하는 PTO-on 상태에서의 진자판의 횡 방향 운동변위를 구할 수 있으며, 식(31)에 대입하면 최적의 시간평균 추출파워를 얻을 수 있다. 최적의 시간평균 추출파워를 단위 폭 당 입사파의 평균 파워로 나누면 아래와 같이 최적조건에서의 효율을 구할 수 있다.

(34)

ηopt(ω)=Popt(ω)12ρgA2Cg,

여기서 Cg=12ωk1+2khsinh2kh는 파랑에너지의 전파 속도(group velocity)이다.

투과성 진자판의 횡 방향 운동에 따른 방사파를 포함한 반사율과 투과율과 그리고 전체 에너지 손실률은 다음식과 같다.

(35)

Rf=R+ω22gN0∑p=o∞ap*Fp0(θ0A),Tr=T−ω22gN0∑p=o∞ap*Fp0(θ0A),εT=1−Rf2−Tr2.

4. 계산결과 및 고찰

Table 1은 수심(h) 10 m에서 높이(d) 8 m인 불투과성 진자판(G = 0)이 수직으로 고정되어 있을 때 Galerkin방법과 고유함수전개법(MEEM)을 사용하여 얻은 반사율(R)과 투과율(|T|)의 수렴도를 정리한 표이다. 전개식의 개수 M이 작다는 것은 최종적으로 풀어야 할 대수방정식의 크기가 줄어들어 계산시간이 단축됨을 의미한다. Galerkin 방법인 경우, M(= 1, 2, …, 10)을 증가시키면서 반사율과 투과율의 수렴도를 살펴본 결과, M = 3 이상이면 소숫점 이하 4자리까지 일치하는 결과를 주었다. 그러나 고유함수전개법을 사용한 경우, M = 100일 때는 소숫점 이하 2자리까지는 Galerkin의 결과와 일치하지만 나머지 자리수의 값에서 약간의 차이를 보였다. 이를 줄이고자 M = 500까지 늘려보았지만 계산 결과는 크게 개선되지 않았다. 이와 같이 Galerkin 방법이 MEEM보다 수렴도가 우수한 이유는 진자판의 끝단에서 나타나는 유속의 제곱근 특이성을 전개식(14) 안에 포함시켰기 때문이다. 이후의 모든 계산에서는 정확도가 확실히 보장된 M = 8을 사용하였다.

공극률 계수가 실수값을 가질 때 G의 변화에 따른 반사율과 투과율을 Fig. 2에 그렸다. x축은 무차원화된 주파수 ωh/g로 잡았다. 여기서 선은 Galerkin 방법을 사용한 결과이며, 기호는 고유함수전개법(M = 100)을 사용한 결과이다(Cho, 2017a). 두 해석결과는 서로 잘 일치함을 보여준다. 여기서 G = 0은 불투과성 진자판을 뜻한다. Cho and Kim(2008)의 연구결과에 따르면 에너지 손실과 관련 있는 G의 실수부는 공극률과 서로 선형 비례관계를 갖는다. Fig. 2a를 살펴보면 예상대로 G가 증가할수록 다시 말하여 공극률이 증가함에 따라 반사율이 일정하게 줄어드는 경향을 보여주고 있다. 반면에 투과율은 G = 0인 불투과성 진자판을 제외하곤 G가 증가할수록 진자판을 통과하여 빠져나가는 파랑에너지의 증가로 다소 커지는 경향을 보여주고 있다. G의 변화에 따른 에너지 손실률(ε)은 Fig. 2b에 그렸다. 에너지 손실률이 크다는 것은 투과성 진자판을 통과하면서 소멸되는 에너지의 양이 많음을 의미한다. G = 0.5, 1.0은 G = 2.0보다는 에너지 손실률이 크다. 또한 G = 0.5와 G = 1.0을 비교하면 G = 0.5는 고주파수 영역에서 상대적으로 큰 에너지 손실률을 나타낸다. 즉, 에너지 손실률은 G에 따라 달라지며 입사파의 주파수에 따라 최적의 G가 존재함을 알 수 있다. Fig. 2c에서는 투과성 진자판에 작용하는 무차원화된 횡 방향의 파기진력을 G의 변화에 따라 그렸다. 반사율 곡선과 유사하게 G가 증가할수록 파기진력은 줄어든다.

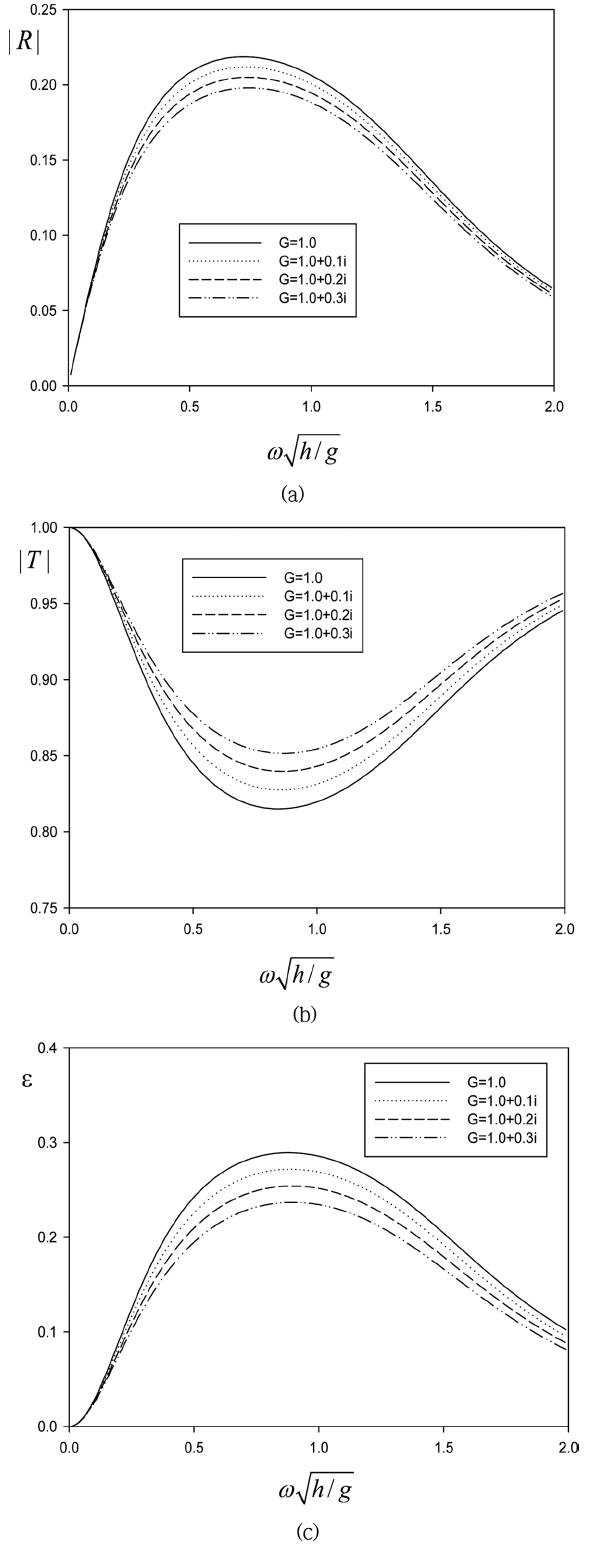
Fig. 3은 Fig. 2와 동일한 계산조건 하에서 복소수 G의 실수부는 일정한 값(Gr = 1.0)을 갖고 허수부(Gi)를 변화시켰을 때의 반사율과 투과율을 보여주고 있다. Gr과 Gi는 각각 저항력과 관성력에 밀접한 관련이 있는 항이다. 실제로 파가 투과성 진자판을 통과하면서 발생하는 에너지 손실은 저항력에 따라 달라지지만 관성력도 Gr의 크기에 영향을 주므로 에너지 손실에 부분적으로 관여한다. 또한 관성력의 효과로 G=Geiθ는 복소수가 되므로 파가 투과성 판을 통과할 때 위상 변화가 일어난다. Gi가 증가함에 따라 반사율은 줄어들며 투과율은 증가하는 특징을 보여주고 있다. Fig. 3c에 나타난 에너지 손실률은 Gi가 증가함에 따라 약간 줄어드는 특징을 보여주고 있다.

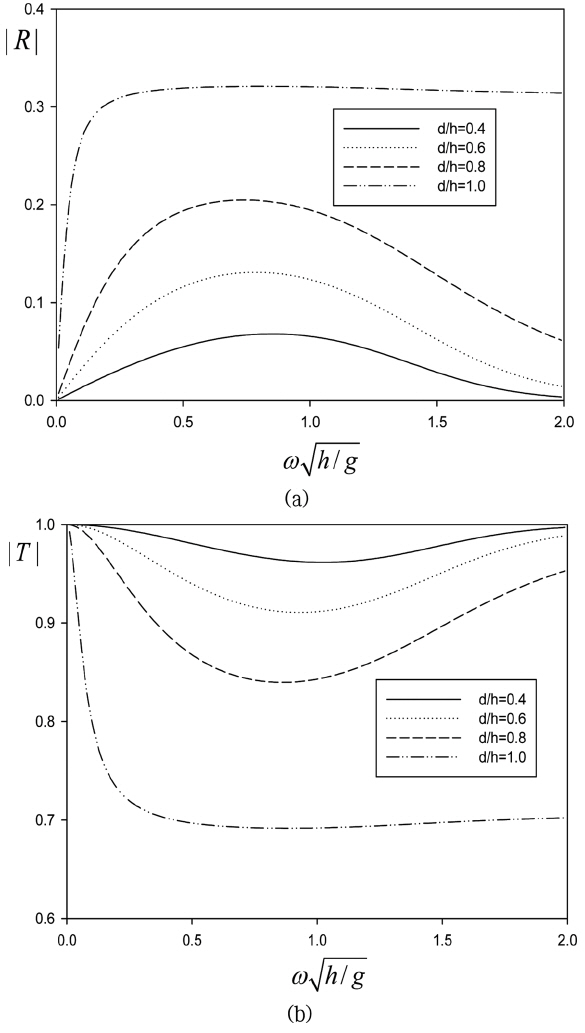
Fig. 4에서는 고정된 투과성 진자판에 의한 반사율과 투과율을 진자판의 높이 변화(d/h)에 따라 살펴보았다. 공극률 계수를 G = 1.0 + 0.2i로 고정시키고 4개의 무차원화된 진자판의 높이(d/h = 0.4, 0.6, 0.8, 1.0)에 대하여 살펴보았다. 예상대로 진자판의 높이가 커질수록 파 차단 효과가 커져 반사율은 커지고 투과율은 줄어드는 특징을 보이고 있다. 특히, 진자판의 높이가 수심과 같은 d/h = 1.0일 때 저주파수 영역에서는 주파수에 따라 급격한 변화를 보이다가 ωh/g=0.3 이후 반사율(= 0.3)과 투과율(= 0.7)은 일정한 값을 갖는다.

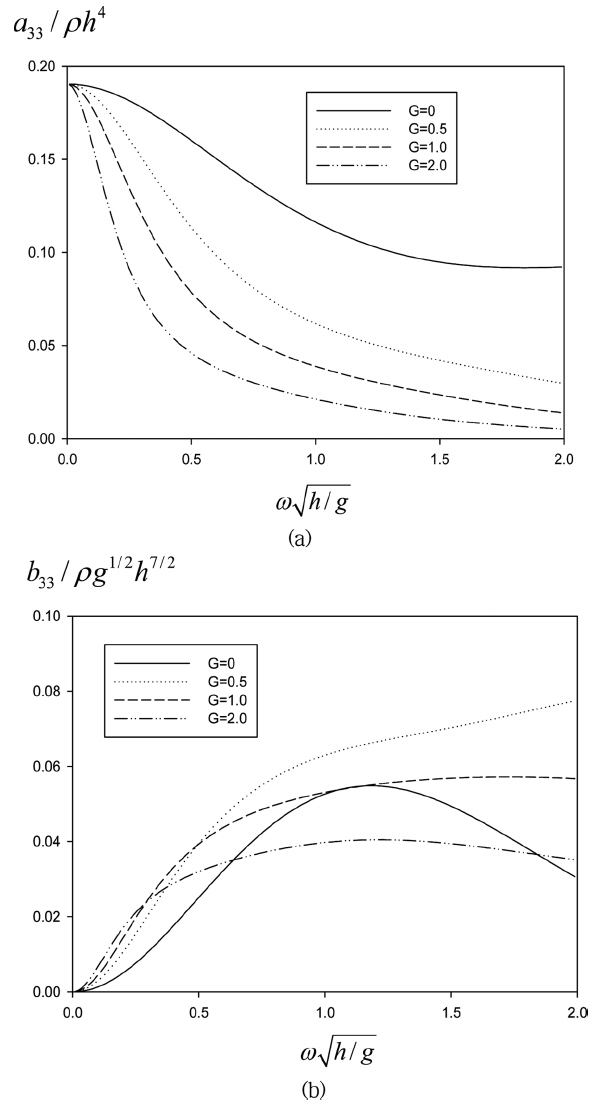
Fig. 5는 부가질량과 방사감쇠계수를 실수값을 갖는 G의 변화에 따라 살펴보았다. 예상대로 G가 증가할수록 다시 말하여 공극률이 증가할수록 진자판의 횡 방향 운동이 주변의 유체를 교란하는 정도가 약하기 때문에 부가질량은 줄어들며 방사파의 에너지와 관련 있는 방사감쇠계수도 불투과성 진자판의 결과를 제외하곤 G가 증가함에 따라 감소하고 있는 것을 알 수 있다.

Fig. 6은 PTO 장치를 설치하지 않은 상태(PTO-off)와 설치한 상태(PTO-on)에서 입사파의 진폭으로 나눈 진자판의 횡방향 운동의 RAO(|θo/A|, Response Amplitude Operator)을 ωh/g에 따라 그린 그림이다. PTO-on일 때, 식(32)에 주어진 추출파워가 최대가 되는 최적의 PTO 감쇠계수 (b~PTO)을 사용하였다. 무차원화된 진자판의 높이와 두께는 각각 d/h = 0.8, t/h = 0.1이고, 진자판의 밀도는 해수의 밀도보다 가벼운 ρf/ρ = 0.25이다. 횡 방향 운동 RAO 곡선에서의 피크값은 식(33)의 횡 운동 고유주파수(ωN)에서 발생한다. 고유주파수(ωh/g= 0.354)에서 공진으로 큰 횡 방향 운동변위를 보여주고 있다. 실수값을 갖는 공극률 계수 G가 증가할수록 에너지 감쇠 효과로 공진주파수에서의 피크값이 줄어드는 것을 볼 수 있다. 또한 PTO 감쇠력이 추가로 발생하여 설치하지 않았을 때(PTO-off)와 비교하여 공진주파수에서의 횡 방향 운동변위가 크게 줄어든 것을 알 수 있다.

Fig. 7에서는 Fig. 6과 같은 계산조건 하에서 최적의 시간 평균 추출파워와 효율을 무차원화된 주파수 ωh/g에 따라 살펴보았다. PTO-on 상태에서 추출파워와 효율의 피크값은 공진주파수에서 발생하였다. G = 0인 불투과성 진자판을 설치하였을 때의 추출파워와 비교하여 공극률 계수 G가 증가할수록 에너지 감쇠효과로 추출파워와 효율 모두 전 주파수에 걸쳐 크게 줄어들었다. 이는 투과성 진자판은 파랑에너지 추출 측면에서 효과적이지 못함을 의미한다. 그럼에도 불구하고 투과성 진자판의 강점은 파랑에너지의 일부분을 소멸시킬 수 있어 진자판에 작용하는 파랑 하중을 크게 줄일 수 있고, 투과성 진자판을 통하여 해수 교환이 가능하므로 환경 친화적이라는 점이다.

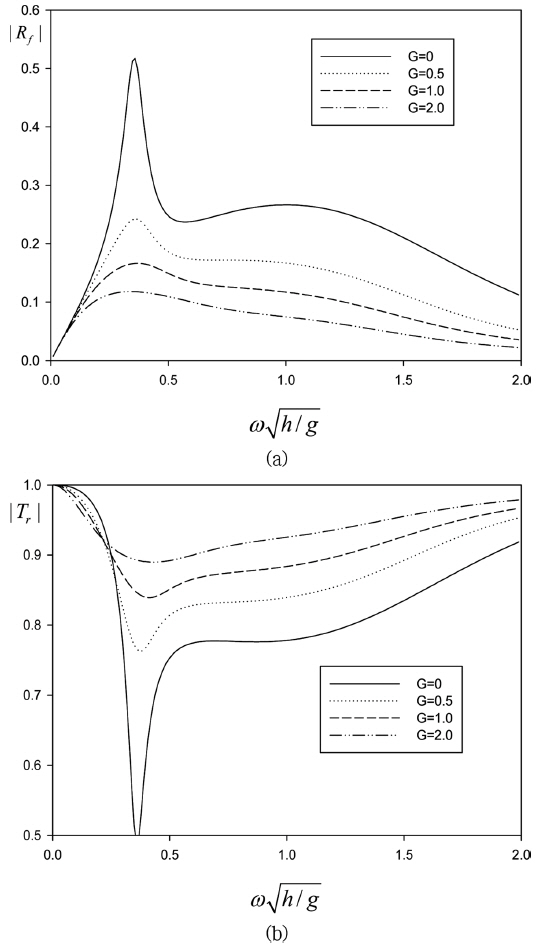
Fig. 8에서는 PTO-on 상태에서 회절파와 투과성 진자판의 운동에 의한 방사파 모두를 고려한 전체 반사율과 투과율을 실수값을 갖는 G의 변화에 따라 살펴보았다. 투과성 진자판은 불투과성 진자판(G = 0)보다 전 주파수에 걸쳐 투과율은 커지고 반사율은 줄어든다. 또한 G가 증가함에 따라 투과율은 점차 증가하고 반사율은 감소하는 경향을 보여주고 있다. 특히, 진자판의 횡 방향 운동변위가 크게 일어나는 공진주파수에서 반사율은 크게 증가하며 투과율은 크게 감소하는 특징을 보여준다.

끝으로 진자판의 횡 방향 운동에 따른 방사파를 포함한 전체 에너지 손실률을 PTO-off와 PTO-on 상태로 구분하여 Fig. 9에 그렸다. PTO-on 상태에서는 PTO 감쇠력이 추가로 발생하여 불투과성 진자판(G = 0)을 설치하였음에도 불구하고 에너지 손실률이 크게 발생하였다. PTO-off 상태에서 공진주파수에서의 에너지 손실률이 PTO-on과 비교하여 다소 크게 나타났지만 ωh/g=0.5보다 큰 고주파수영역에서는 PTO-on 상태에서의 에너지 손실률이 전반적으로 크게 나타났다.

5. 결 론

본 해석에서 사용한 Galerkin 방법은 고유함수전개법과 비교하여 계산시간을 단축시켰고 해의 정확도를 크게 향상시켰다. 공극률 계수가 실수값을 가질 때 G가 증가함에 따라 반사율과 횡 방향의 파기진력은 줄어들고 투과율은 커지는 경향을 보여주었다. 이는 G와 실제 투과성 판의 공극률 사이에는 선형 비례관계가 성립하기 때문이다. 또한 투과성 진자판을 통과하면서 발생하는 에너지 손실률이 최대가 되는 적절한 G(또는 공극률)이 존재함을 확인하였다. 투과성 판에 작용하는 관성력 효과를 나타내는 G의 허수부를 증가시켰을 때 반사율은 줄어들고 투과율은 증가하는 경향이 나타났다.

진자판의 높이가 증가할수록 반사율은 커지고 투과율은 줄어드는 경향을 보였다. 특히, 진자판의 높이가 수심과 같은 d/h = 1.0일 때 ωh/g=0.3 이후 주파수에서 반사율과 투과율은 일정한 값을 유지하였다.

공극률 계수의 실수값을 가질 때 G가 증가함에 따라 투과성 진자판을 통과하면서 발생하는 에너지 손실효과로 공진주파수에서 크게 증폭된 횡 방향 운동변위는 줄어드는 경향이 나타났다. 또한 2차 변환장치인 PTO 장치의 설치(PTO-on)로 PTO 감쇠력이 추가로 발생하여 PTO-off 상태와 비교하여 공진주파수에서의 횡 방향 운동변위가 크게 줄어들었다. 횡 방향 운동변위와 동일하게 추출파워도 공진주파수에서 가장 큰 값을 갖는다. 동일한 계산조건에서 불투과성 진자판(G = 0)보다 투과성 진자판을 설치하였을 때 추출파워와 효율이 전 주파수에 걸쳐 낮게 나타났다. 또한 진자판의 횡 방향 운동에 의한 방사파를 포함한 전체 반사율과 투과율 곡선을 살펴보면, 투과성 진자판은 불투과성 진자판보다 투과율은 증가하고 반사율은 감소하는 경향을 보인다. 결과적으로 투과성 진자판이 불투과성 진자판과 비교하여 파랑에너지 추출과 차단 측면에서 효과적이라고 말할 수는 없다. 그러나 투과성 진자판은 파랑 하중을 크게 줄일 수 있고 해수 교환이 가능하므로 친환경적이라는 장점은 지니고 있다.

횡 방향으로 운동하는 투과성 진자판을 이용한 파랑에너지 차단과 추출