1. 서 론
불규칙한 파랑에너지를 전력으로 변환하려는 장치인 파력 발전장치(WEC; Wave Energy Converter)는 설치 구조 형식에 따라 부유식과 착저식으로 크게 구분할 수 있다. 해양의 부유식 구조물은 강풍, 폭풍파 등의 가혹한 외력 환경에 노출되어 있으므로 사용성을 위해서 작용하중에 대한 안전성(safety)과 안정성(stability)을 동시에 확보하는 것이 중요하다. 계류형 해양구조물도 일반적인 구조물처럼 사용성과 밀접한 관계를 가지지만 안전성 문제가 전체 구조물의 목적성에 결정적인 영향을 미치는 경우가 많다. 부유식 구조물의 경우 계류 시스템의 파손은 부유체의 위치 이탈을 야기하므로 시스템의 해체 뿐만 아니라 항행 선박과의 충돌 등과 같은 이차적인 피해가 예상된다. 따라서 부유식 구조물의 경우에 있어서 안전성 확보를 위한 합리적인 외력 산출은 가장 중요한 문제 중 하나라고 할 수 있다. 한편 부유식 파력발전장치는 통상적으로 상시파랑조건에서 파랑에너지 추출 효과를 극대화할 수 있도록 설계되므로 평상시의 파랑 특성을 파악하는 것이 매우 중요하다.
국내의 경우 해양에너지 개발연구와 관련하여 파랑에너지는 조력과 더불어 그 관련 연구 성과들이 매우 풍부하다(홍 등, 2004; 신 등, 2005; 경 등, 2006; 류 등, 2007; 홍 등, 2007; 남 등, 2011; 박 등, 2011). 그러나 파력발전장치의 종류가 다양하고 관심을 두는 성능평가 부분이 서로 다를 뿐만 아니라 해역의 파랑환경 또한 다르기 때문에 이들의 연구성과 수준을 직접적으로 비교하기는 곤란한 측면이 있다. 그러나 파력발전장치의 가장 기본적인 입력정보에 해당하는 해역의 파랑정보 분석 수준은 비교가 가능하다. 실질적으로 연안의 파랑특성은 제어 가능한 인자가 아니라 주어진 환경으로 인식하여야 하기 때문에 파력발전장치 설계를 위해서는 주어진 대표적인 파랑 환경 조건과 변동성에 대한 분석이 선행되고, 그 특성을 입력정보로 하여 최적으로 반응할 수 있는 장치 설계가 수행되어야 한다.
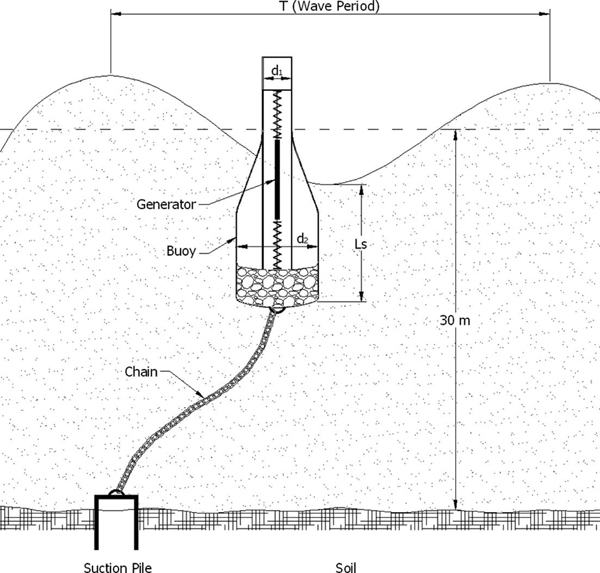
공진형 파동에너지 추출시스템은 파력발전장치의 일종으로서 우리나라와 같이 비교적 파랑에너지가 작은 해역에서 에너지 흡수효율을 높이기 위하여 고안된 전력생산부이(power buoy) 등으로 구성되어 있다(Fig. 1 참조). 조와 권(2011)은 선형발전기가 탑재된 원형 기둥을 이용하여 파랑에너지를 추출하는 방법에 대하여 제안한 바 있다. 이 시스템은 부이가 파랑에 의해 가진되면 내장된 직렬발전기의 운동자와의 상대 속도로 전력을 생산할 수 있다. 일반적으로 해양 구조물의 안정성 검토를 위하여 재현빈도별 설계파를 사용하지만, 본 시스템은 평상시에 전력생산을 하여야 하므로 상시파랑의 특성을 파악하는 것이 필요하다. 주된 외력인자인 파랑의 파악은 파력에너지 분포특성, 내장형 발전기 기본설계 조건 파악, 계류시스템 구조해석 등을 위하여 필수불가결하다. 외력산정 결과는 공진형 부이 설계, 구동부 및 발전기 용량 설계, 파력부이 전력생산 추정, 계류시스템의 피로파괴 검토 등에 활용된다.
하지만, 우리나라는 부유식 파력생산부이의 설계를 위하여 대상 해역에서 직접 관측한 파랑자료를 분석한 사례가 거의 없는 실정이다. 대부분의 기존 연구들은 수치모형 결과를 이용하거나 개략적인 파랑조건을 이용하여 장비 및 시설, 시스템의 성능평가를 수행하는데 국한되었으며(류 등, 2004; 류 등, 2009; 유 등, 2009; 홍 등, 2010) 파랑조건의 변동성에 따른 성능평가를 수행한 경우는 미미한 실정이다. 송 등(2004), Kim et al.(2012)은 후측 파랑자료(hindcast wave data)를 분석하여 우리나라 해역의 파랑 에너지 부존량을 제시한 바 있다. 그리고 정 등(2007)은 속초항, 후포항 및 울산항 해역에서의 관측자료를 이용하여 동해 연안의 파랑에너지 부존량을 추정한 바 있다.
본 연구는 실해역 관측자료로부터 부유식 파력에너지 추출시스템에 요구되는 상시파랑의 특성을 파악하여 공진형 전력생산부이와 발전기 설계를 위한 입력 자료를 검토한다. 또한 전력생산부이의 성능평가에 중요한 입력자료에 해당하는 평균 스펙트럼을 추정하여 기존의 스펙트럼의 한계와 새로운 형식의 스펙트럼 추정함수를 제안하였다.
2. 파랑 관측
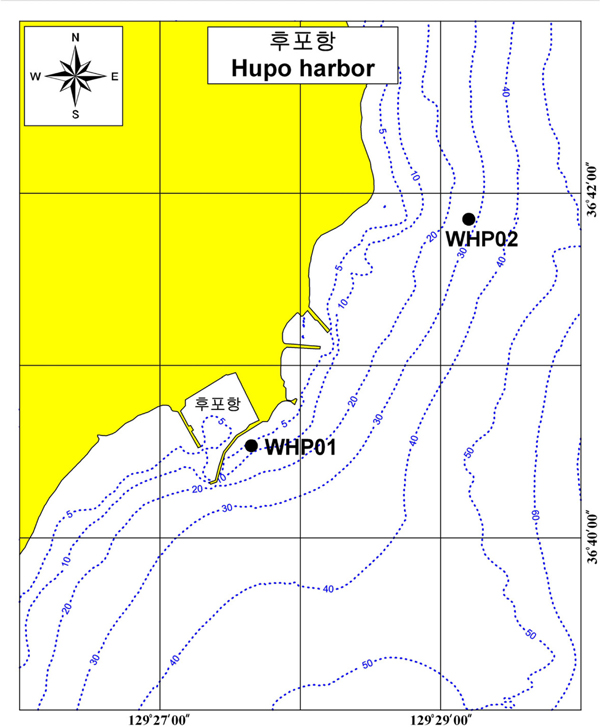
본 연구는 경상북도 울진군 소재 후포항의 동측 및 북측 해안 부근(Fig. 2 참조)에서 수압식 파고계(WTG; Wave and Tide Gauge)로 취득한 파랑자료를 분석대상으로 한다. 후포항에서의 파랑관측은 해수교환시설의 최적설계를 위한 파랑조건 검토를 위해 2002년 4월 26일부터 정점 WHP01(129o27'40''E, 36o40'35''N, 수심 =약 10 m)에서 시작되었으며 2005년 5월부터는 정점 WHP02(수심 =약 18.5 m)로 위치를 변경하고 현재까지 관측이 계속되고 있다. 본 연구에서는 전력생산부이의 현장 성능시험 평가를 위한 위치 및 수심 조건이 유사한 정점 WHP01 지점에서 2002년 5월~2005년 3월까지 취득된 약 3년간의 자료를 분석하였다.
자료 해석 시에는 먼저 0.5초 간격으로 연속적으로 계측된 압력자료를 30분마다 2,048개씩 선정하고 FFT 기법을 사용하여 압력 스펙트럼을 구하였다. 그 다음에 선형파 이론에서 구해진 주파수별 파압-파고 스펙트럼 전달함수를 적용하여 압력 스펙트럼을 파랑에너지 스펙트럼으로 변환하고 이를 사용하여 유의파고 Hs, 첨두주기 Tp , 평균주기 Tz 등의 파랑특성 계수들을 산출하였다. 이때, 0.5초 간격으로 계측된 자료의 파랑에너지 스펙트럼은 5/128~64/128 Hz 사이의 1/128 Hz 간격의 60개 성분으로 제시되었다.
후포 연안의 파랑특성 분석은 이 등(1984)에 의하여 수행된 바가 있으나 결측율이 상당히 높고 또 설치수심에도 큰 차이가 나서 상세한 비교는 생략하였다. 조 등(2012)에 따르면 기본적인 파랑정보는 1년 이상의 자료를 사용하는 경우, 파랑 모수 추정오차는 크게 감소하며, 3년 정도의 자료를 사용하는 경우 평균 파고 추정오차는 10% 이내, 평균 주기 추정오차는 0.5초 정도로 제시되었다. 따라서 보다 장기간의 자료를 이용한 검증이 필요하기도 하지만 본 연구에서 사용한 후포 연안의 3년간의 자료는 후포 연안의 평상조건에서의 파랑정보를 대표할 수 있는 자료로 간주할 수 있다.
3. 파랑특성계수와 파력의 월별 변화
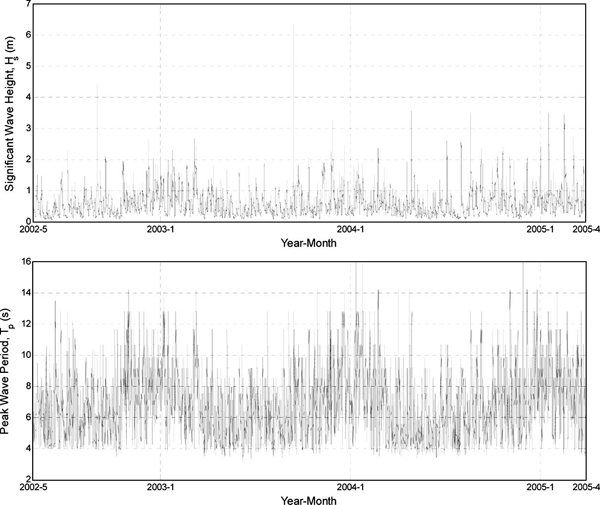
파력발전 부이의 최적설계를 위해서는 시간에 따른 주기변화에 대한 정보를 파악해야 한다. 파랑 인자는 1개월 이내의 짧은 기간 중에도 큰 변화를 보이고 있으나, 본 연구에서는 월별 대표 주기 및 파고 변화를 중점적으로 분석하였다. 정점 WHP01에서 관측된 자료의 유의파고와 첨두주기 시계열 자료의 시간 도시(time plot)는 Fig. 3과 같다.
Fig. 3에 제시된 것처럼 유의파고 Hs는 계절적 변화가 비교적 확연하게 나타난다. 2002년 9월 1일과 2003년 9월 13일에 태풍 루사와 매미에 의하여 각각 4.4 m와 6.3 m의 유의파고들이 관측된 것을 제외하면 큰 파가 겨울철에 발생한 경우가 많고 대체로 11월 이후부터 약간씩 커지는 경향을 보인다. 첨두 주기 Tp는 계절 변화가 매우 뚜렷하게 보이며 겨울철에 길어 졌다가 여름철에 짧아지는 경향을 보인다. 이를 통하여 유의 파고와 첨두 주기의 크기가 대체로 상관관계가 있는 것처럼 파악되었다. Suh et al.(2010)은 실측자료를 바탕으로 우리나라 해역의 유의파고 Hs와 유의파주기 T1/3 의 관계가 비례함을 보인 바 있다. 이 때, 파고가 커지면 커질수록 파고-주기 상관관계도 높아진다. 본 연구는 월별 파고와 주기의 분포 특성을 파악하고자 하며, 이러한 파랑특성계수의 변화는 파력부이의 최적설계와 파력발전단지(WEF; Wave Energy Farm) 조성을 위한 부이의 최적 흘수심 조정을 위한 입력정보로 활용될수 있다.
3.1 월별 주기 변화
공진형 파동에너지 추출시스템은 파력발전단지를 형성하여 인근 지역에 안정적인 전력을 공급하고자 하는 것이 목표이다. 따라서 계절별 부존 파력과 공급의 불균형을 해소하기 위해서는 우선 부존파력의 계절적 변화특성을 파악해야 한다. Table 1은 후포항 북방파제 전면 해역의 월별 파고 및 주기분포를 보인 것이다. 첨두주기 Tp는 월별 평균 스펙트럼에 의한 분석 결과이며 평균 주기의 산술평균은 평균주기 Tz와 달리 관측된 파의 주기 전체의 평균값에 해당한다. 그리고 월별 파고분포와 주기분포는 각각 표에 보인 바와 같이 산술평균, 자승평균 rms, 최빈값 mode로 정리할 수 있다.
후포항의 월별 주기변화는 대체로 최대발생빈도 주기 mode값과 자승평균인 rms값이 일치하지 않음을 보이고 있다. 특히, 첨두주기 Tp의 mode값은 4, 5, 6, 8월에 작게 나타나며 다른 달의 값들과 차이가 상당히 크다. 하지만, 산술평균주기 Tz의 변화는 비교적 연중 안정된 것으로 보인다. 이러한 월별 주기변화는 다수의 부이를 운영할 경우에 있어서 연중 파력에너지 생산목표를 만족할 수 있는 부이의 배치 및 개수 결정을 위한 자료로 활용할 수 있다. 연중 각 달의 Tp가 rms값으로 최대 8.89초에서 최소 5.75초까지 변화하며 그 차이는 3.14초에 달한다.
Table 1
Representative information of monthly changed wave characteristics and power
3.2 월별 파력 변화
파력부이 내에 탑재된 발전기는 파력의 일부분을 전기에너지로 변환하는 장치이며 그 용량 설계는 파력으로부터 추정이 가능하다. 즉, 일반적인 발전기의 효율(<1)을 설정하여 이를 적용하면 추정용량을 산정할 수 있다.
송 등(2004)과 Kim et al.(2010)은 후측 파랑자료를 사용하여 우리나라 근해의 파랑에너지 분포를 분석하였다. 송 등(2004)은 우리나라의 평균파력에너지 부존량이 단위파봉장당 대략 3 kW/m이며 계절별 변화가 뚜렷한 것으로 제시하였다. 본 연구에서는 송 등(2004)의 연구에서 제시한 다음의 식 (1)을 사용하여 불규칙파의 평균파력을 산정하였다.

여기서, ρ = 1,030 kg/m3이고 Ksm는 Tz의 rms값과 수심 h=9.8m에 상응하는 천수계수이며, 다음의 식 (2)로부터 계산된다. 식(2)의 L은 파장으로 분산관계식 (3)으로부터 계산된다.
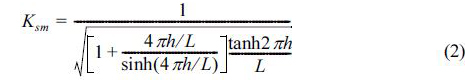
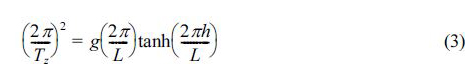
식 (1)의 Hs와 TZ값으로는 각각 Table 1에서 rms값을 이용하였으며 이렇게 추정된 후포항 북방파제 전면 해역에 부존하는 단위파봉장당 평균파력의 월별 변화량을 Table 1에 제시하였다. 파력에너지는 동계인 11, 12, 1, 2월이 상대적으로 크고 5, 6, 7월이 작게 나타난다. 최대파력인 1월의 2.92 kW/m와 최소인 6월의 0.65 kW/m는 2.27 kW/m의 차이가 있으며 연평균 파력은 1.73 kW/m이다. 따라서 후포연안의 평균 파력부존량 1.73 kW/m에 대하여 약 20% 전력 추출효율을 가정하면, rms값으로 0.3~0.4 kW급 발전기 규모가 적절하다고 판단된다.
4. 연중 주기의 변화분석
정점 WHP01에서 관측된 자료는 매 30분마다의 스펙트럼으로부터 유의파고, 첨두주기, 평균주기 등의 파랑특성계수들로 환산된다. 이러한 자료들을 바탕으로 연중 특성값을 분석해야 하며 여기서는 평균주기의 최빈값과 유의파고와 첨두주기의 상시파랑 스펙트럼을 각각 분석하고자 한다. 즉, 스펙트럼 정보는 진폭의 증폭과 관계되므로 부이의 설계에 이용하고, 발전기 운동자는 부이와 위상차를 발생시켜야 하므로 부이의 설계주기와는 다른 평균주기의 정보가 필요하다. 단, 상시파랑의 스펙트럼은 어느 정도 큰 풍파를 표시할 수 있는 표준 스펙트럼으로는 표현이 불가능하므로 새로운 수학식을 제안하고자 한다.
4.1 평균주기의 최빈 발생빈도 및 파고의 발생확률
본 연구는 Tz의 최빈값을 얻기 위하여 다음과 같은 수순과 방법으로 분석하였다.
1) 최빈 평균주기는 확률분포함수로부터 첨두 지점에 해당하는 주기를 추출
2) 최빈 주기의 ±0.1초 영역에 위치하고 있는 파고 정보를 추출
3) 추출된 파고 정보를 이용하여 확률밀도함수를 도시
Fig. 4는 파고-주기 산포도에 의한 최빈 주기값과 최빈주기에 해당하는 파고의 분포를 발생확률밀도로 보인 것이다. 파고-주기 산포도에는 일반적인 유의파고와 유의주기의 관계식(Goda 공식, SPM 공식; 서 등(2008))을 도시하였으며, 산포도에 사용한 유의파주기 자료는 평균주기에 1.2를 곱하여 산정하였다(Goda, 2000). 한편, 도시한 최빈주기에 해당하는 파고는 부이 설계 시에 목표 공진주파수일 경우 내장된 직렬발전기의 행정길이(stroke) 판단을 위하여 주요한 정보가 될 수 있다.
유의파고의 누적발생 빈도를 분석한 결과, 약 1.0 m 이하가 전체의 95% 정도로 대부분을 차지하고, 유의파주기로 환산한 주기는 Fig. 4에서 볼 수 있는 바와 같이 4.0-12.0초 범위에서 대부분이 발생한다. 분석한 평균주기의 최빈값 (Tz)mode은 5.31초이며, 최빈주기 ±10% 영역의 평균파고는 0.45 m로 파악되었다. 이번의 분석에서 (Tz)mode=5.31초와 평균주기의 산술평균 값 (Tz)AA= 5.75초는 식 (4)와 같은 관계를 가진다.

식 (4)의 관계로부터 평균주기의 최빈값이 산술평균값보다 작게 나타남을 알 수 있다.
4.2 첨두주기에 의한 에너지 스펙트럼 분석
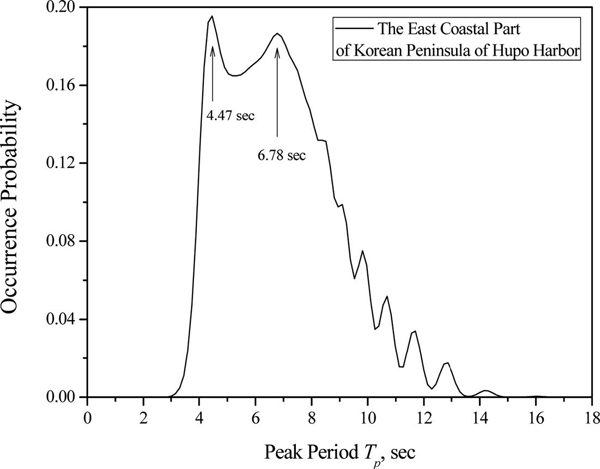
스펙트럼 분석을 하기 전에 우선 첨두주기의 발생빈도 분포를 파악할 필요가 있다. 일반적으로 스펙트럼 분석에서 첨두주기는 이론적으로 최대 발생빈도 주기와 일치하지만 실측 자료의 경우 확인이 필요한 것으로 사료된다. 첨두주기 Tp는 분포곡선이 일산형(single peak)이 아니고 이산형(double peak) 이상일 경우도 있다. Fig. 5는 본 연구에서 관측된 첨두주기의 발생빈도 분포를 보인 것이다.
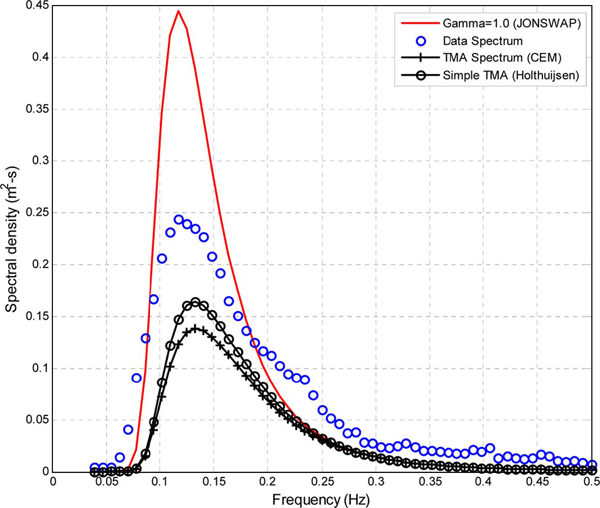
Fig. 5에 제시된 첨두주기의 발생확률을 보면 첨두주기가 4.47초와 6.78초에서 각각 나타나고 있다. 평균 스펙트럼이 표준 스펙트럼형으로 설명이 가능하지 여부를 알기 위하여 JONSWAP 스펙트럼 및 천해 효과를 고려한 TMA 스펙트럼과 비교하였다. JONSWAP 스펙트럼을 TMA 스펙트럼으로 변환하는 방법은 Suh et al.(2010) 및 US Army Corps of Engineers에서 발간한 CEM manual(2008)을 참조하였다. 또한 Holthusijen(2007)이 제안한 간략 환산계수 공식도 이용하여 그 차이를 비교하였다.
Fig. 6은 표준 스펙트럼과 상시파랑 관측자료에 의한 평균 스펙트럼의 주파수별 에너지밀도 분포를 비교한 것이다. 비교에 사용된 표준 스펙트럼은 실측 스펙트럼에 비하여 첨두주파수 fp에서의 에너지 밀도가 크게 나타난다. 하지만, 본 연구에서 분석한 파랑은 이상파랑만을 대상으로 한 것이 아니며 연중 계속적으로 관측된 자료이다. 따라서 주로 이상파랑처럼 첨두주파수의 에너지밀도가 탁월한 표준 스펙트럼형보다는 에너지가 비교적 평활화되어 있다고 할 수 있다.
평균 스펙트럼으로부터 산출한 Tp= 8.53초는 평균주기의 최빈값 Tmode= 5.31초보다 상당히 주기가 긴 파에 해당한다. 즉, 에너지 밀도가 가장 큰 8.53초 주기대의 파는 자주 발생한 파보다 빈도는 낮으나 비교적 파고가 큰 파가 내습한 것으로 판단할 수 있다.
Fig. 6에 보인 바와 같이 연간 평균에너지 밀도분포는 JONSWAP 스펙트럼의 형태로 표현하기가 어렵다. 본 연구는 상시파랑의 평균에너지밀도를 다음의 식 (5)에 보이는 누적함수 분포형태를 보이는 GEV(Generalized Extreme Value) 분포로 추적하고자 한다.

여기서, μ는 위치 파라메터, σ >0는 축척 파라메터, ξ는 형상 파라메터이다. 식 (5)에 보인 누적형태함수를 밀도함수로 변환하면 다음의 식 (6)과 같이 되며 이는 일산형 밀도함수이다.
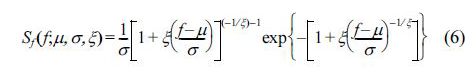
본 연구는 주파수별로 동일한 환산자를 선택하기 위하여 다음의 식 (7)와 같은 관계식을 도입하였다.

여기서, 첨자 obs는 관측치를 말하며, n은 스펙트럼 면적계산을 위한 주파수 등분수를 말하며 여기서는 60으로 하였다. df는 0.0078125(=1/128)로 계산하였다. 따라서 평상시 연속적으로 관측된 파랑의 평균 스펙트럼의 표현식은 다음의 식 (8)과 같이 표현할 수 있다.

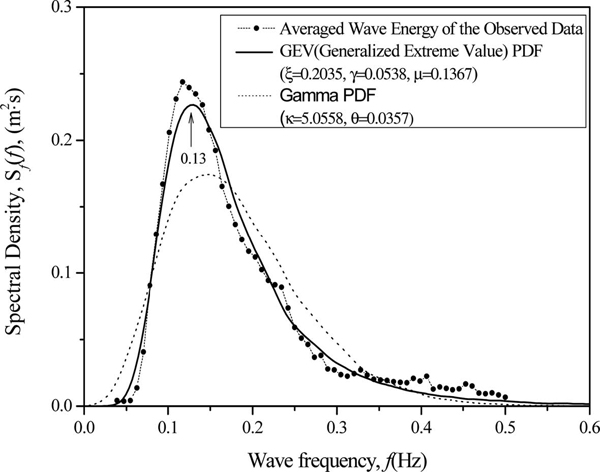
여기서, 스펙트럼 면적 환산자 k는 관측 스펙트럼의 면적에 해당하며 그 크기는 0.0329이다. 다음의 Fig. 7에 보인 자료에 대하여 식 (6)의 모수를 최우도법(maximum likelihood method)으로 추정하면 각각 ξ = 0.23035, σ = 0.0538, μ =0.1367로 된다.
한편, Gamma 확률밀도 함수는 식 (9)와 같으며 2개의 매개함수로 표현된다.
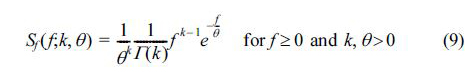
식 (9)도 확률밀도함수이므로 전체면적이 1로 된다. 따라서 관측 스펙트럼을 표현하기 위해서는 환산계수가 필요하다. 식 (9)의 모수 추정값은 각각 k = 5.0558, θ = 0.0357이며, 환산계수는 0.0329로 GEV함수의 경우와 동일하다.
Fig. 7은 관측자료로부터 분석된 평균 스펙트럼을 GEV와 감마확률함수로 추적하여 비교한 것이다. 이 그림에서 보인 바와 같이 평균 스펙트럼의 형상은 GEV로 비교적 유사한 형상을 추적할 수 있음을 알았다. 첨두주파수에 상당하는 에너지밀도는 약간 작게 나타나지만 전체 주파수 영역에서 비교적 유사한 추적이 가능함을 알 수 있다. 상시파랑의 평균 스펙트럼 형상은 각 주파수별 확률밀도함수값에 동일한 환산자를 곱하여 표현이 가능함을 알 수 있다. 이 때, 환산자는 관측 스펙트럼의 면적으로 계산이 가능하다. 감마밀도함수는 첨두주파수 영역에서 에너지밀도가 작게 평가되므로 이를 적용 하기는 곤란함을 알 수 있다.
본 분석에서 보인 바와 같이 목표 공진주파수의 추정은 파랑에너지 밀도의 크기에 의해 정할 수 있으나 주기에 의한 발생빈도 분포가 이산형을 나타내기 때문에 선택의 문제가 발생한다. 따라서 목표 공진주파수를 최빈주파수로 할 것인지 첨두주파수로 할 것인지의 여부는 공진형 파동에너지 추출시스템의 전체적인 전력생산의 효율에 관한 것이므로 이를 평가하는 시스템은 별도로 구성되어야 할 것으로 생각된다.
6. 결 론
본 연구에서는 지점흡수식 파력변환장치의 공진형 부이와 직렬발전기의 운동자 설계를 위한 실해역 관측자료를 분석하였다. 후포해역에서 구해진 관측자료의 분석 결과를 통해 구해진 주요 결론 및 토의사항은 다음에 정리하였다.
- 후포항 북방파제 전면해역에서 취득한 3년간의 실해역 관측자료에 대한 스펙트럼 분석을 통하여 유의파고, 첨두주기, 평균주기 등의 파랑특성계수들을 산출하였다.
- 첨두주기는 계절적 변화가 뚜렷하게 나타나서 여름철에 길고 겨울철에 짧은 특성을 보였으며 유의파고도 유사한 경향을 나타내어 유의파고와 첨두주기의 상관성이 뚜렷하지는않으나 어느 정도(상관계수 = 0.625)의 상관관계를 보이는 것으로 확인되었다.
- 월별 주기변화는 대체로 최대발생빈도 주기 mode값과 자승평균인 rms값이 일치하지 않는 것으로 나타났으나 산술평균주기 TZ의 변화는 비교적 연중 안정된 것으로 나타났다.
- 파력에너지는 11~2월에 상대적으로 크고 5~7월에 작게 나타난다. 파력이 최대인 1월에는 2.92 kW/m, 최소인 6월에는 0.65 kW/m로 나타났으며 연평균 파력은 1.73 kW/m이다. 평균 파력부존량 1.73 kW/m에 대하여 약 20% 전력 추출효율을 가정하면 0.3~0.4 kW급 발전기 규모가 적절하다고 판단된다.
- 파고-주기 산포도에 의한 최빈 주기값과 최빈주기에 해당하는 파고의 분포를 분석한 결과 평균주기의 최빈값은 5.31초이며, 최빈주기 ±10% 영역에 포함되는 유의파고의 평균은 0.45 m로 나타났다.
- 평균 스펙트럼과 표준 스펙트럼형의 합치성을 판별하기 위하여 JONSWAP 스펙트럼 및 TMA 스펙트럼과 비교한 결과 상당한 차이를 나타냈다.
- 상시파랑의 평균에너지밀도를 누적함수 분포형태의 GEV분포로 추적하여 첨두주파수에 상당하는 에너지밀도는 약간 작게 나타나지만 전체 주파수 영역에서는 비교적 유사한 결과를 제시하는 새로운 상시파랑의 스펙트럼 표현식을 제안하였다.