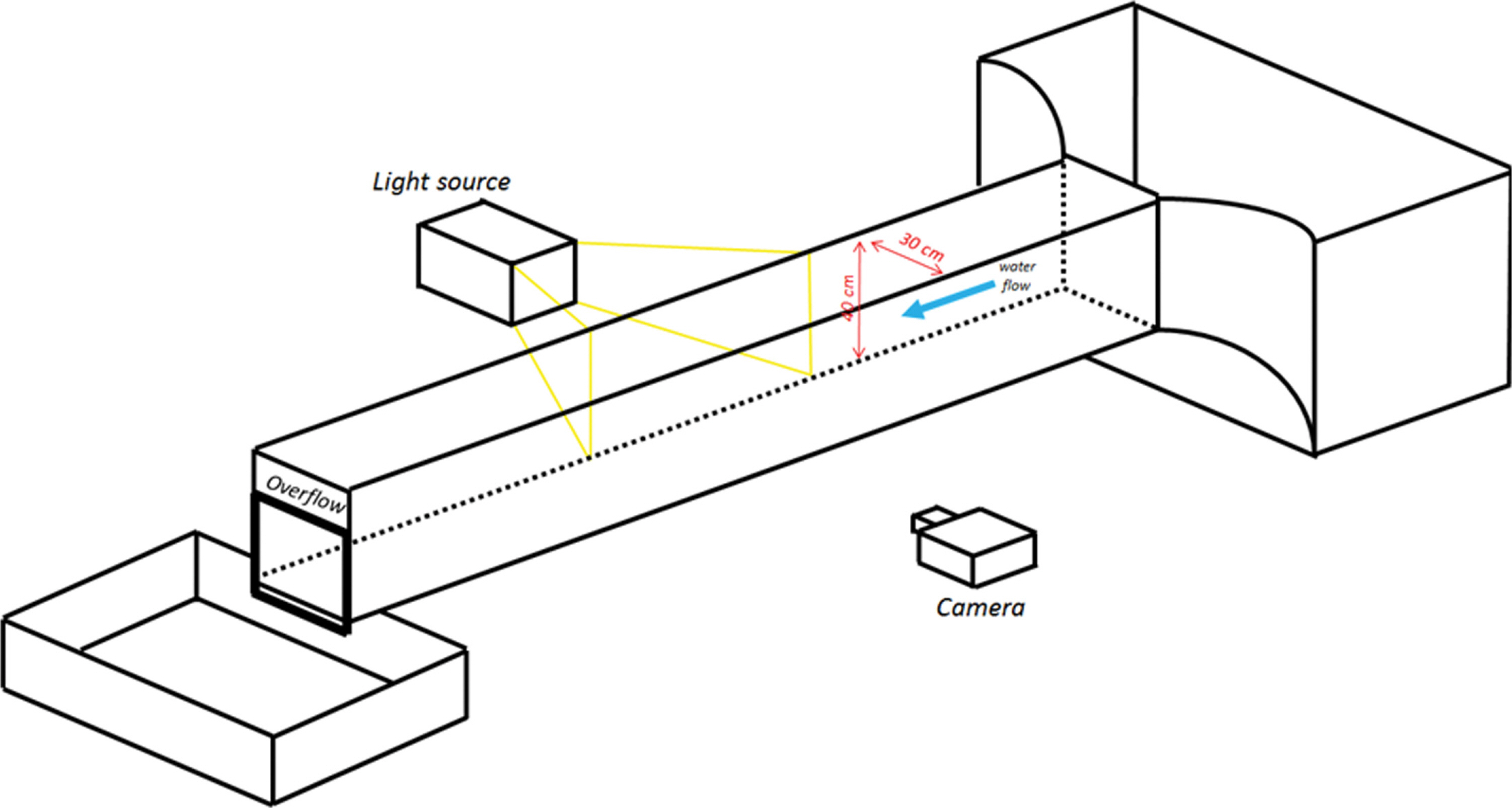
본 연구의 수리실험은 길이 10 m, 폭 0.3 m, 높이 0.4 m의 크기를 갖는 개수로에서 수행되었다. 3면에서 광학적 측정이 가능하도록 수로의 양면과 바닥면이 강화 유리로 제작되었다. 수로의 유량공급은 순환식으로 이루어지고 이를 위해 상류에 유량공급수조와 하류에 유출수조를 설치하였다. 펌프를 이용한 수로 순환의 최대 가동 유량은 0.007 m³/s이며, 수위는 하류의 월류형 수문으로 조절된다(Fig. 1).

도수 흐름은 상류에 보를 설치하여 흐름이 월류하며 발생하도록 하였다. 월류 후 발생한 도수의 직선흐름구간의 유속(U₁)과 수심(d₁)으로부터 산정된 Froude 수(=U1/gd1)는 7.3이었으며 하류 수문을 조절하여 하류 수위가 일정하게 상승하도록 하였다. 본 연구의 Froude 수는 조석단파 조건에 비해 다소 큰 편이나 롤러의 거동을 명확히 확인하기 위해 큰 Froude 수를 대상으로 하였다. 하류수위가 상승하면서 도수의 위치는 하류에서 상류 쪽으로 점진적으로 이동하였으며, 하류 수위를 일정하게 고정한 후 도수가 일정한 구간에서 거동한 이후 측정하였다. 하류 조건은 총 5개로 변화하였으며 각 하류 조건에 대한 롤러의 수위를 측정하였다. 실험조건은 Table 1에 제시되었다.

본 연구는 도수의 롤러를 측정하기 위해 그림자기법을 적용한 영상측정기법을 적용하였다. 본 기법은 유동장 정보를 눈으로 볼 수 있게 하는 유동 가시화(flow visualization) 기술의 하나로서 유체의 이동현상(transport phenomena)을 이해하기 위한 효율적인 기법이다. 유동 가시화는 현유체 현상을 순간적으로 제시하고자하기 때문에 영상 혹은 공간적인 분포의 형태로 보여지며, 따라서 광학적 특성의 이해가 가시화의 질을 결정한다. 가시화는 일반적으로 정성적인 방식으로 고려되어왔으나, 영상측정의 정도가 향상되고 가시화 방안이 유동 인자의 특성을 적절히 반영할 경우 영상정보로부터 정량적인 결과를 도출할 수 있게 되었다. 다상흐름의 경우 물과 공기의 다상차에서오는 중간 경계(interface) 및 각 위상의 밀도 및 특성 차이로 인해 접촉식 혹은 영상측정에 있어 제약이 많다. 유동가시화를 이용하여 유속을 측정하는 대표적인 기법인 PIV(particle image velocimetry) 기법 또한 이러한 제약으로 인해 다상흐름 측정에 많은 문제점을 갖는다. 본 연구에서 적용하는 그림자기법은 영상기법 시 사용되는 광원을 측정 대상의 후면에서 노출시키는 방식으로서 전면에서 비추는 광원에 빛 산란(light scattering) 혹은 포화(saturation)를 유발하는 다상의 경계차를 그림자형상으로 나타내는 기법이다. Fig. 2는 그림자기법을 이용한 영상측정 기법의 개요도이다. Fig. 2에서 D는 피사체 심도(depth of field)로서 카메라 조리개에 조절에 따른 선명한 영상이 측정되는 구간을 의미하며, S와 R은 피사체 심도의 시작지점 및 끝지점을 나타낸다. 피사체 심도는 원근 효과가 측정될 수 있는 화상 측정에서 피사체의 정확한 위치 정보를 얻기 위해 필요한 개념으로서 기포의 밀도에 따라 조절한다. 자세한 내용은 Ryu et al. (2005)에 제시되어 있다.

영상기법을 위한 시스템은 화상을 취득하기 위한 CCD 카메라와 기포 및 중간경계를 가시화하기 위한 후면 면광으로 구성된다. 본 실험에 사용된 CCD 카메라는 1028 × 1024 픽셀의 해상도와 8 bit의 분해능을 가지고 있으며 고속카메라 기능을 포함하고 있다. 영상기법은 PIV 기법과 같이 유속측정으로도 사용이 가능하여 일반적으로 고속카메라 기능으로 측정되나 본 연구에서 대상으로하는 수위 변동성은 초당 100장 이하의 데이터로 충분하여 고속측정 기능을 사용하지 않고 50장의 취득률로 측정하였다. 다만, 화상에 저장된 흐름의 잔상을 최소화하여 선명한 수위를 얻기 위하여 카메라의 노출속도를 조절하였으며, 광원 세기와 상호적으로 조절하여 잔상을 최소화하고 충분한 밝기를 갖는 화상을 취득하도록 하였다. 면광은 일정한 세기의 LED 칩으로 패널에 등간격으로 배열하였으며, 면광을 균등하게 발생시키기 위해 전면에 흰색 불투명 아크릴판을 위치시켰다. 광원 신호의 입출력이 가능하도록 동기화 시스템을 설치하여 조도를 조절할 수 있도록 하였다. 이 연구에 사용된 LED는 점멸신호에 대한 발광의 반응이 빨라 짧은 시간에 두화상을 녹화해야하는 영상유속기법에 적합하며 LED 기술의 발달로 빛의 세기가 강해져 기포밀도가 높은 다상흐름에도 적용이 가능하다. Fig. 3(a)는 영상측정기법을 이용한 측정 모습이며, Fig. 3(b)는 기법을 적용하여 측정된 도수의 화상이다.

측정된 화상을 Digitalizing하여 모든 픽셀의 밝기를 수치화하여 이를 바탕으로 수위를 결정하였다. 영상으로부터 수위를 결정하는 방안은 수로 벽면의 유체가 대부분 측정이 되지만 수위의 경우 Wall effect는 미미한 것으로 확인되었다. 화상에서 수위를 측정하는 기준은 화상 전체의 평균밝기와 기포영역의 밝기를 상대적으로 확인하여 수위를 찾아내었는데 Eq. (1)과 같이 수면 위 공간의 색밝기의 평균보다 큰 경우를 수위로 결정하였으며 실험안 별 화상 특성을 고려한 계수 α를 반영하여 수위를 결정하였다.

여기서, I는 색밝기, x는 종방향 좌표, z는 연직방향 좌표, η는 수위이다. Fig. 4는 도수 화상에 본 기법을 적용하여 얻은 수위를 도시하여 나타내었다. 이와 같은 방법으로 그림자기법을 적용하여 얻은 화상으로부터 각 픽셀에 해당하는 위치정보를 반영하여 수위를 결정하였다.

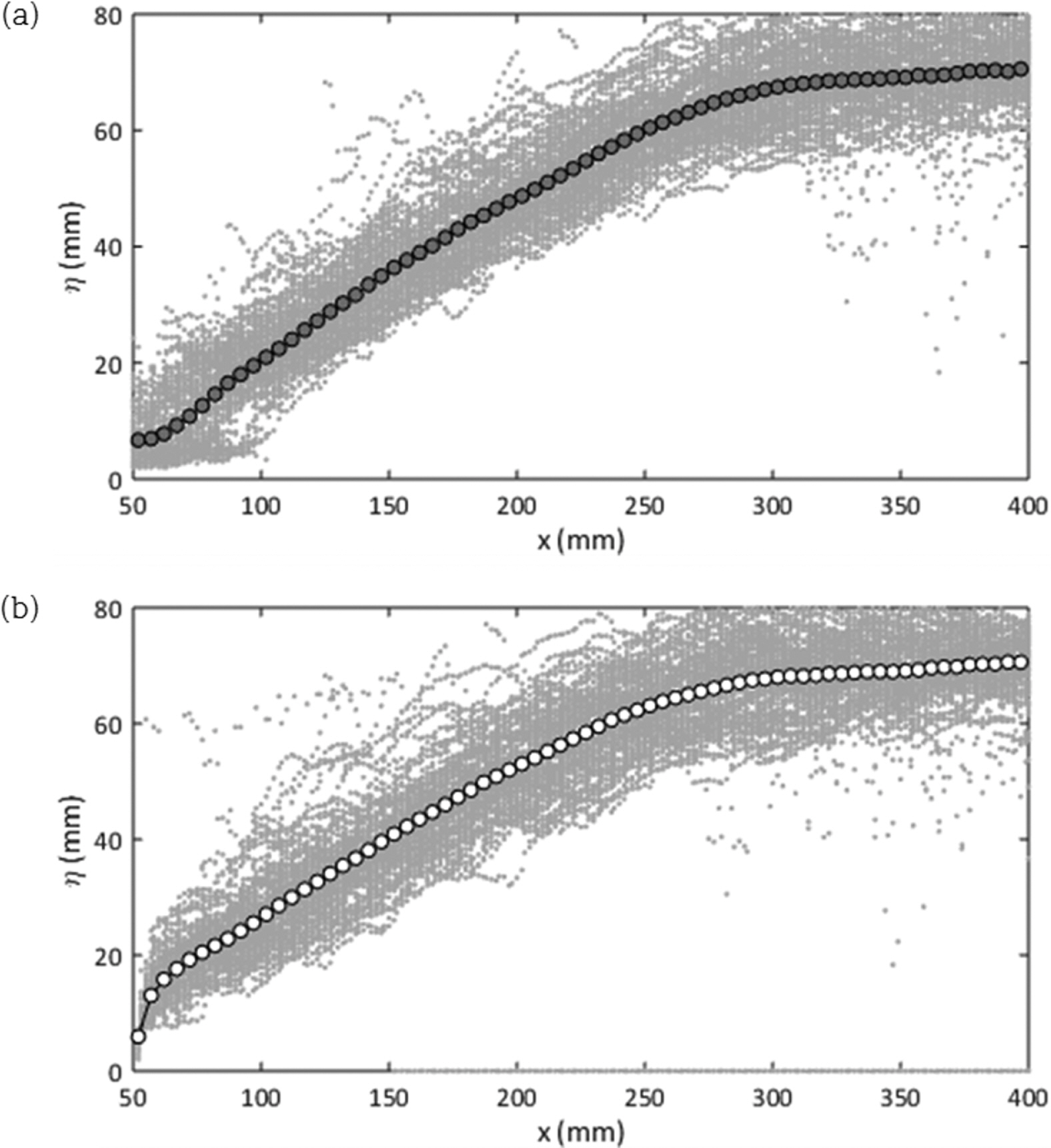
본 연구에서는 하류심 상승에 따른 도수 롤러 주변의 수위 변화를 측정하여 그 특성을 분석하였다. 도수는 난류성이 큰 흐름으로서 변동성이 심한 거동 특성을 보여주는데 특히 도수에서 가장 큰 난류도를 나타내는 롤러가 자유수면 근처에 위치하므로 수면 변동성은 더욱 심해지는 양상을 보인다. Fig. 5는 Case 1(d₂ = 0.077m)의 순간 수면결과로부터 평균값을 나타내고 있는데 다른 방식을 적용하여 다른 평균 수면을 도출하였다. 그림에서 x축은 수평흐름이 시작하는 지점인 월류보 끝단을 원점으로 지정하였다. η는 자유수면으로서 바닥저면으로부터 높이로 산정하였다. 또한, Figs. 3과 4에 나타난 바와 같이 실험에서 도수는 우측에서 좌측으로 방류되었으나 x축에 맞게 도시하기 위하여 방향을 바꾸었다. Fig. 5(a)에 제시된 평균 분포는 가장 일반적인 시간평균 기법을 적용하여 얻은 결과이다. 흐름을 준정상류로 판단하고 순간 분포를 고정된 자리에서 평균한 것이다. Fig. 5(a)의 평균은 일반적인 기법이지만 도수가 종방향으로 진동이 심하여 도수 수위의 평균값이 완만해지는 경향을 보인다. 단파의 경우, 전면의 경사 또한 중요한 의미를 갖기 때문에 도수시작점을 기준으로 평균하는 방법으로 얻은 결과를 Fig. 5(b)에 제시하였다. 이는 일종의 앙상블평균(ensemble averaging)의 개념으로서 정상류로 해석되는 도수의 시간에 따른 변화가 상대적으로 크다는 것으로부터 본 연구에 적용되었다. 각 평균 공식은 Eqs. (2)와 (3)에 제시되었다. 그림에서 회색으로 표시된 순간 수위분포는 다른 지점에서 유사한 크기의 편차를 보인다는 것을 알 수 있으나, 도수시작점을 일치시켰기 때문에 도수 전면(x = 50 mm 근처)에서 편차가 상대적으로 작게 나타난다. 따라서 도수의 전반적인 수위 분포는 유사해 보이나 전면부의 수위 분포는 차이를 보인다.

여기서, x1는 평균 도수시작점, x₁는 순간 도수시작점, n은 순간시작점의 개수이다.

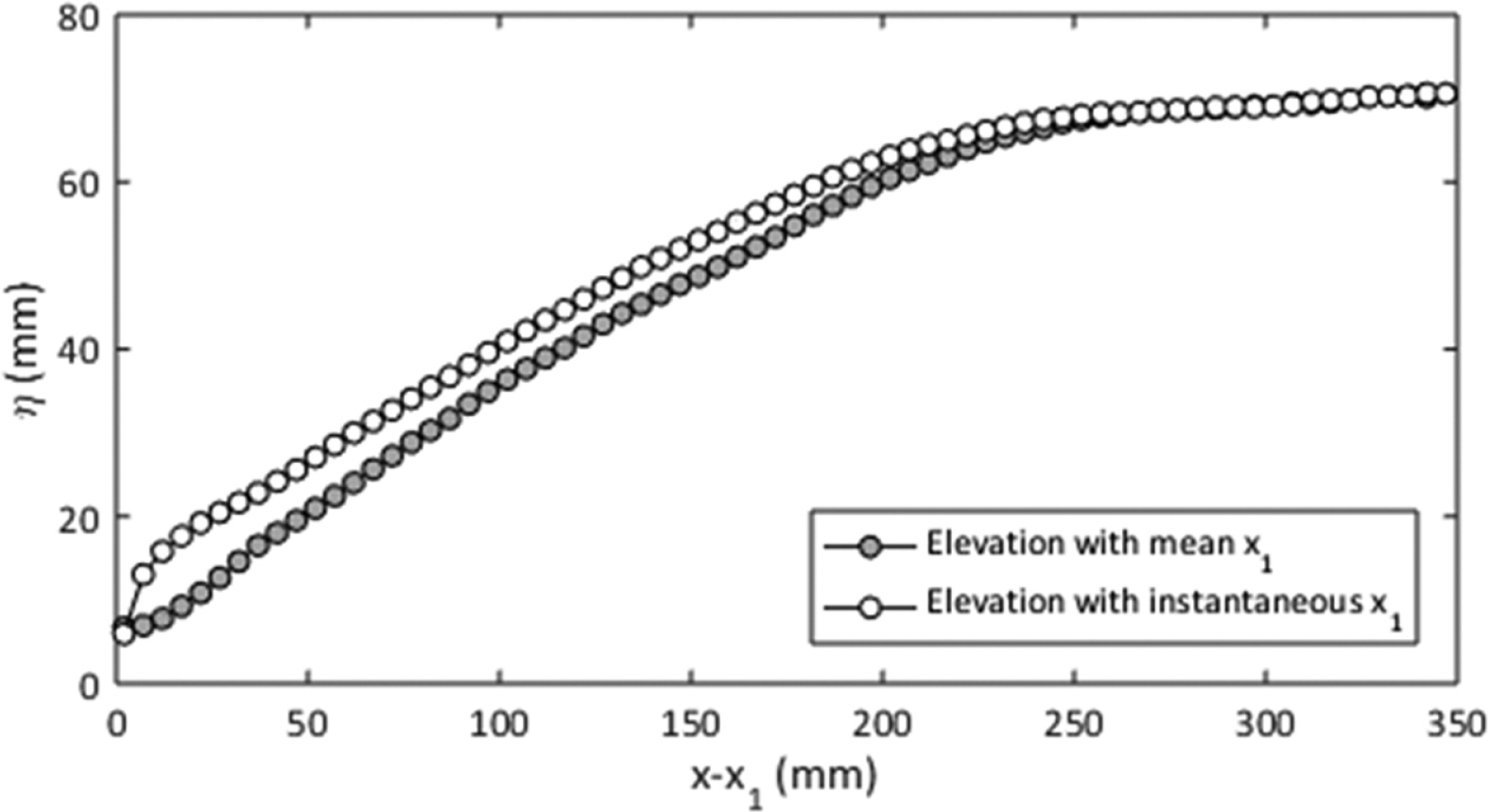
Fig. 6은 Fig. 5에서 제시된 두 가지 평균 방식으로 얻은 평균 수위 결과를 비교하였다. 두 평균 방식으로 얻어진 분포는 하류로 가면서 서로 수렴하지만 전면부의 수위 분포는 차이를 나타낸다. 특히, 도수시작점을 일치시켜 앙상블평균으로 얻은 평균 수위의 경우 일반적인 방식의 평균 수위 분포에 비해 전면 경사가 큰 것으로 나타난다. 즉, 평균을 구하는 방식에 따라 평균 분포가 다르다는 것으로서 본 연구에서는 진동성이 큰 도수의 전면부, 롤러가 위치하는 구간에서 상대적으로 진동이 크다는 것을 알 수 있으며, 평균 성분을 구하는데 이와 같은 위상(phase)을 고려한 해석의 필요성을 보여준다. 단파(bore)의 특성은 해수면이 상승하며 도수와 같이 단파 전면부가 하천 방향으로 전진하기 때문에 단파의 전면부 특성은 일반 도수에 비해 중요한 의미를 갖는다. 따라서, 조석단파(tidal bore) 해석시 Fig. 5(b)에 제시된 앙상블평균방식이 상대적으로 유의미한 결과를 제시할 수 있다.

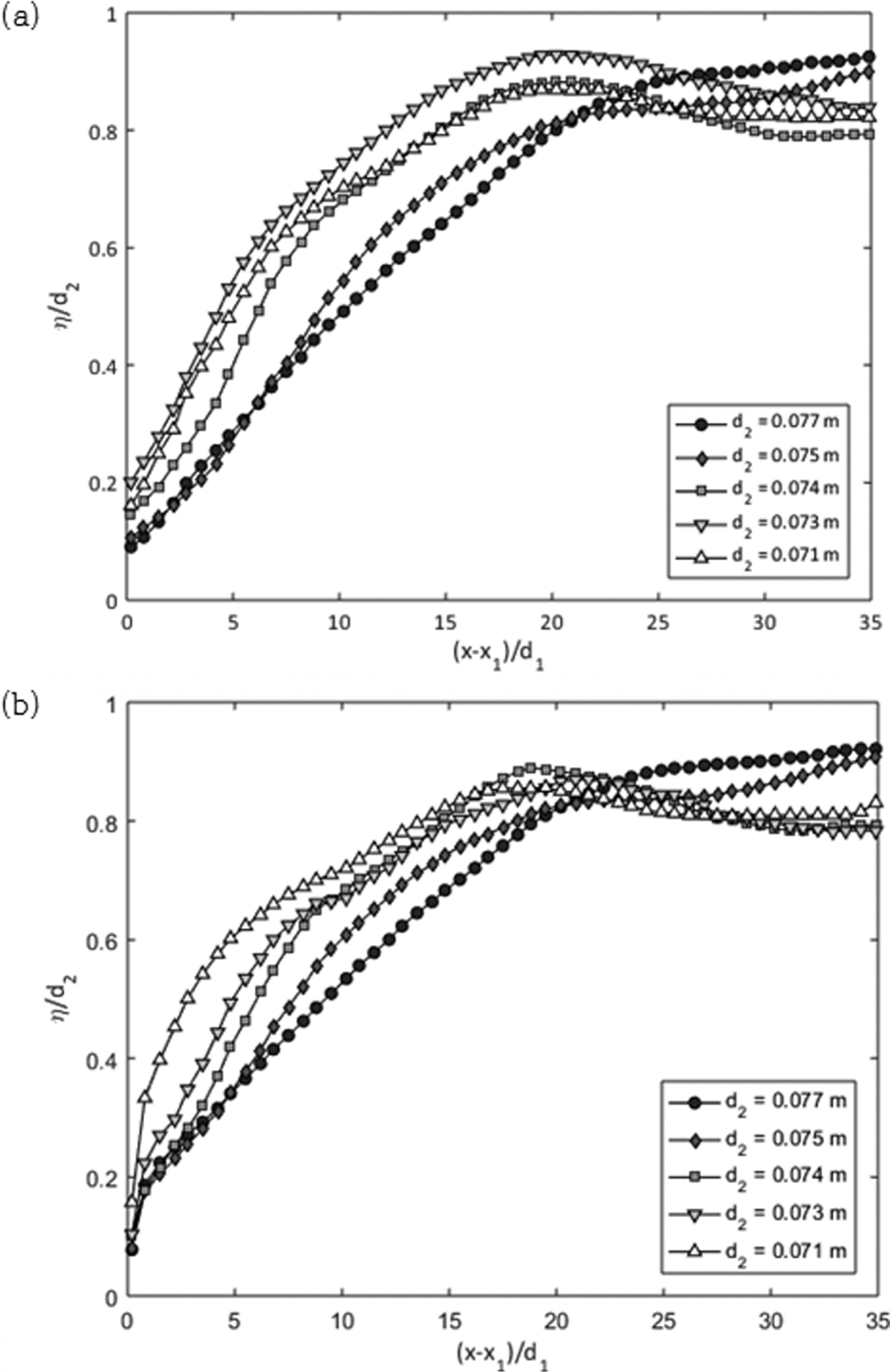
Fig. 6에서 비교된 평균 수위 파형을 모든 실험안에 대하여 적용하고 전반적인 분포 비교를 Fig. 7에 제시하였다. Fig. 7(a)는 정상류로 가정하고 얻은 시간평균 분포이며 Fig. 7(b)는 앙상블평균으로 얻어진 결과를 제시하였다. Fig. 6에서 제시한 Case 1과 같이 앙상블평균으로 얻어진 평균 분포가 전반적으로 경사가 큰 파형을 나타내었다. Fig. 6에서 제시된 실험안은 하류심이 d₂ = 0.077m이 경우로서 전체 실험안 중 파형이 상대적으로 완만한 결과를 보여준다. 즉, 앙상블 평균에 의한 결과와 시간 평균에 얻어진 결과의 차이는 다른 실험안에서 더욱 두드러진다는 것을 의미한다. Fig. 7(a)에 제시된 결과는 모든 실험안에서 logarithmic한 분포를 보여주지만 도수시작점 근처에서는 exponential한 분포 양상을 나타내기도 한다. 반면, Fig. 7(b)에서는 전면부 또한 logarithmic한 분포를 보여주며 일반적으로 인지되는 단파의 전면 형상을 나타내고 있다. 전면부를 제외한 영역의 경우 다소 차이를 보여주지만 일정한 경향을 보여주지 않으며 진동하는 분포를 보여주기 때문에 전면부를 제외한 해석의 경우 시간 평균 또한 적용이 가능하다.

Fig. 7(b)의 결과로부터 전면부 파형의 변화를 하류심의 변화에 따라 검토하면, 하류심이 낮을 때 상대적으로 전면 파형의 경사가 심하다는 것을 알 수 있다. 즉, 하류심이 커지며 점진적으로 상류 방향으로 접근하는 도수 전면부는 더욱 완만해 지는 양상을 보인다. 조석단파의 경우로 해석해 볼 때 하천에서 유출 유량이 일정할 경우 흐름의 운동량은 상류에 가까울수록 바닥 경사를 포함한 에너지 소산 인자로부터 상대적으로 적은 영향을 받기 때문에 그 세기가 크다. 즉 도수가 상류 흐름에 가까울수록 도수 롤러는 큰 운동량의 상류 흐름과 상호작용을 하게 된다고 볼 수 있는데 이 경우 전면 파형이 완만해지는 양상을 나타낸다고 볼 수 있다. 특이한 점은 상대적으로 감소한 상류흐름과 상호작용이 예상되는 작은 하류심의 경우에서 롤러의 중간 및 후반 영역의 파형이 공간적으로 변동성이 크다는 것이다. 난류도 상대적으로 변동성과 상응하는 것으로 알려져 있는 바 Reynolds 수가 상대적으로 작을 것으로 예상되는 작은 하류심의 경우에서 공간적 변동성이 크다는 것은 다른 인자의 영향, 혹은 공간적으로 일정한 파형을 갖을 수 있음을 의미한다. 이는 개수로에서 sill에 의해 발생하는 wave type flow처럼 수심에 따라 일정한 공간적 분포의 파형을 갖는 경우가 있으므로 이에 대한 추가적인 분석이 필요하다.

Fig. 7(b)로부터 logarithmic한 분포 양상은 (x − x₁)/d₁ 값이 20까지 나타나는 것을 확인하였다. (x − x₁)/d₁ < 20의 구간은 전면파형이 거의 형성되는 구간으로 볼 수 있기 때문에 이 구간에 해당하는 파형을 무차원변수 관계로부터 유도하였다. Fig. 8은 Fig. 7(b)에 제시된 무차원변수의 관계로부터 Similarity를 유도한 결과이다. Fig. 8의 실선은 선형회귀분석한 결과이며 높은 상호관계를 갖는다. 본 Similarity로부터 얻어진 공식은 Eq. (4)와 같다. 공식에서 도수를 기준으로 직선흐름구간 수심과 하류심 간의 관계로 나타낼 수 있다. 공식에서 α(= 0.06)와 β(= 1.0)는 회귀분석에서 얻는 계수로서 향후 다양한 Froude 수에 대한 실험 결과를 추가할 경우 이를 상수에서 조건에 부합하는 계수를 얻을 수 있을 것이다.

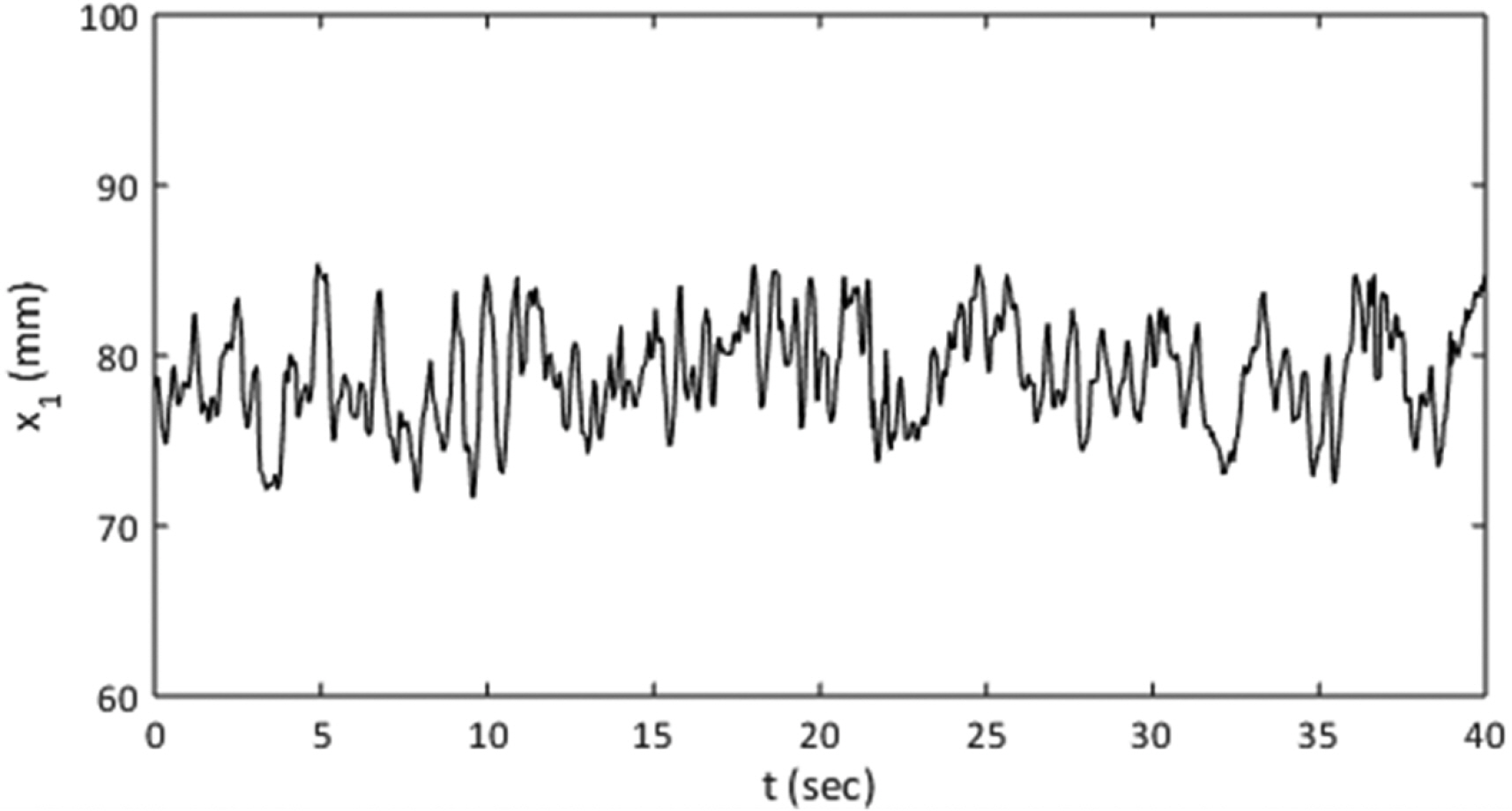
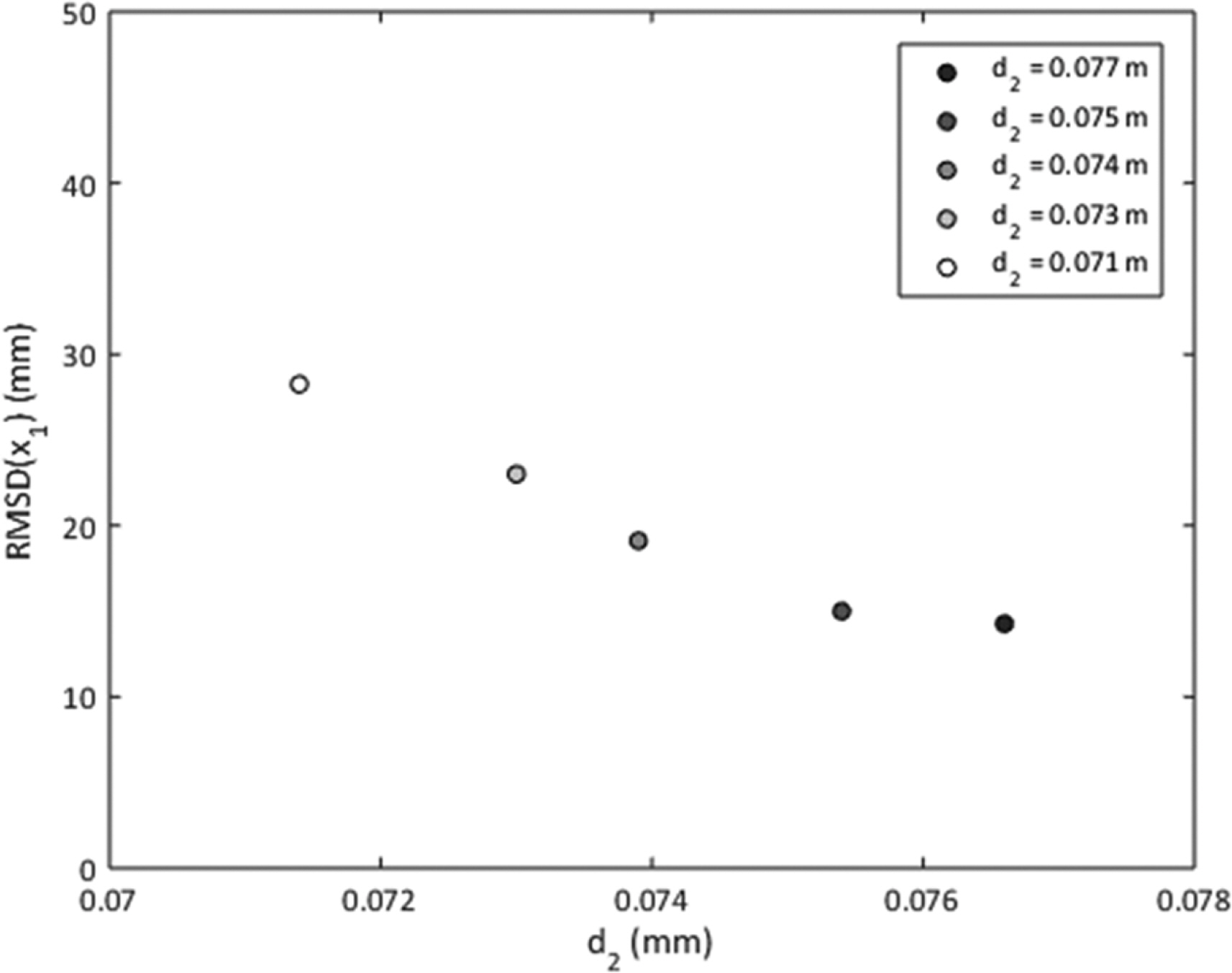
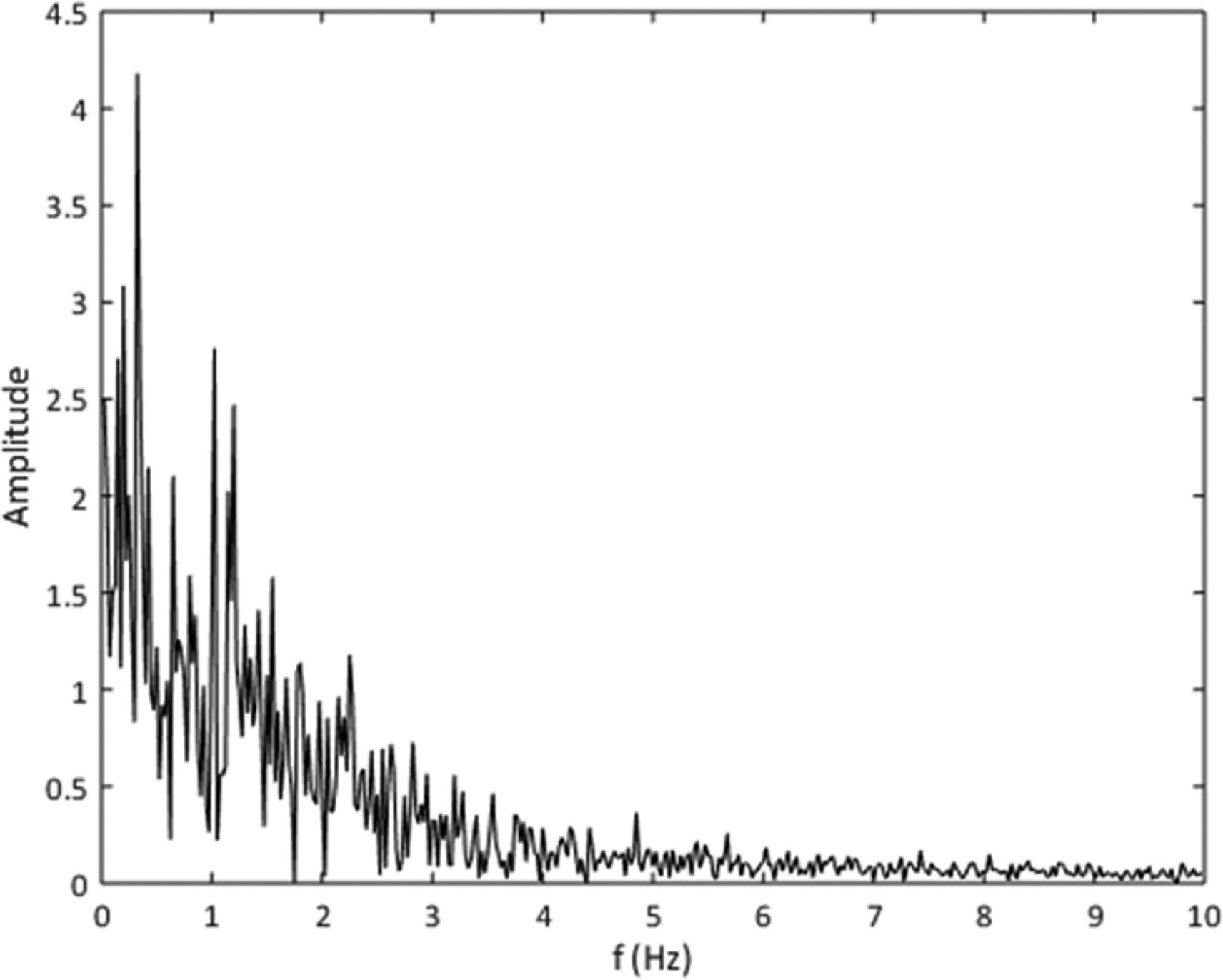
본 연구에서는 앙상블 평균 방식으로 수위 파형을 유도하였기 때문에 이 때 근거로 사용된 순간 파형에서 도수의 시작점을 시계열 변화를 분석하였다. Fig. 9는 Fig. 5(b)에 상응하는 조건에서 순간 도수시작점(x₁)의 시간에 따른 변화를 나타내었다. 도수시작점의 시간적 분포는 그림에 제시된 바와 같이 어느 정도 일정한 크기의 진동 폭을 나타낸다. 평균 지점의 경우 본 연구에서는 의도적으로 하류심을 조절하여 얻었기 때문에 본 장에서는 시작점의 변동성 확인을 위한 편차를 검토하였다. Fig. 10은 Fig. 9에 제시된 시계열의 시작점 분포를 시간평균 개념을 바탕으로 한 평균제곱근편차(root mean square error, RMSE)를 계산하여 나타내었다. Fig. 10에 제시된 결과는 도수시작점의 진동이 하류심이 낮은 경우 상대적으로 크고 하류심이 클 경우 상대적으로 작다는 것을 보여준다. 즉 도수의 전면부 롤러의 거동은 하류심이 낮은 경우 상대적으로 불안정하다는 것을 알 수 있다. 이는 조석단파로 해석할 때 해수면이 낮은 경우에 전면부의 큰 이동폭으로 인해 바닥저면에 큰 영향을 줄 수 있다는 것을 예상할 수 있다. 유속이 작은 경우에도 큰 유속 변화는 상대적으로 큰 충격량을 유발 할 수 있기 때문에 유사이동 및 에너지 소산에 중요한 요소가 될 수 있다. 본 연구에서는 도수시작점의 변동 성분으로부터 시계열을 갖는 도수시작점 분포가 특정 주기를 갖는 변동성이 있는지를 검토하기 위해 스펙트럼 분석을 수행하였다. Fig. 11은 FFT(fast fourier transform)으로 얻어진 Fig. 9의 시계열의 스펙트럼 분포 결과이다. 약 0.4 Hz 주파수 대에서 가장 큰 에너지를 보였으나 noise가 크고 두 번째 크기의 에너지와 큰 차이가 없어 유의미한 특정 주파수를 얻을 수 없었다. 다른 실험안에서도 스펙트럼 분석의 결과가 유사하여 특징적인 주파수대의 주기적 변동성을 보여주지 않았다. 다만, 스펙트럼 분석을 위한 실험 표본수가 부족했을 수 있으므로 측정시간을 확대한 결과로부터 추가적인 분석이 필요하다.