1. 서 론
바람 강도의 지역적인 차이로 인해 풍속, 취송거리, 지속시간에 따라 변하는 파랑에너지도 지역적인 편차가 크게 나타난다. 특히, 파랑에너지로부터 전기에너지를 생산하는 파력발전장치의 경우, 설치 해역의 파랑에너지 밀도가 전력생산에 큰 영향을 미친다. 파랑에너지 밀도가 높은 몇몇 유럽 국가들을 제외하고 바다를 접한 우리나라를 포함한 대부분 국가들은 파랑에너지 밀도가 낮아 파력발전의 적지로 평가받지 못하고 있다. 그러나 미래의 에너지 수요와 화력, 원자력 발전으로 유발되는 환경문제를 고려한다면 이를 극복하기 위한 연구가 요구된다.
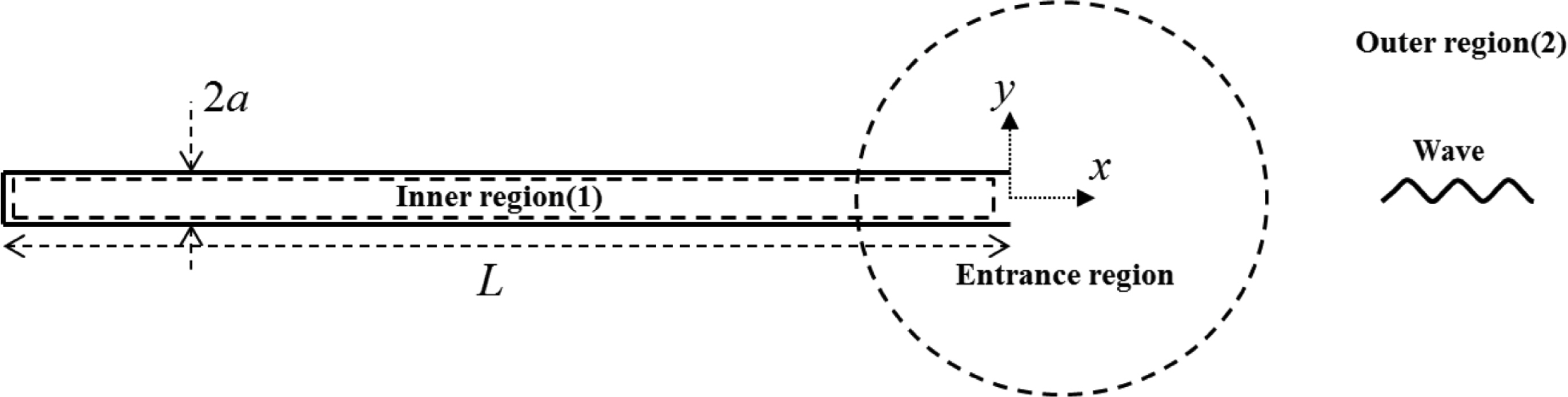
본 연구에서는 파랑에너지 밀도가 낮은 해역에서 파랑에너지를 전기 생산이 가능한 기준 이상으로 증폭시키는 ‘Y’자 수로형 공명구조물을 제안하였고, 공명구조물내 내부유체의 공진을 이용한 파랑에너지 증폭 효과를 살펴보았다. Fig. 1에 나타낸 수로형 공명구조물은 길이가 폭에 비해 매우 긴 수로 형태로 파가 들어오는 입구는 열려있고, 수로 끝단은 막혀 있다. 수로내부로 파랑에너지 집중을 높이고자 입구에 부채꼴 모양의 유도판(wave guider)을 두고 있다. 이러한 수로형 공명구조물은 두 가지 원리로 수로내의 파랑에너지를 높인다. ① 수로입구에 설치된 부채꼴 형태의 유도판은 넓은 폭의 입사파 파랑에너지를 수로 안쪽으로 모아주는 기능을 가지고 있다. ② 수로형 공명구조물은 항만과 유사한 닫혀진 내부유체영역을 갖는다. 이러한 구조는 입사파 주기와 수로 길이에 따라 형성되는 내부유체의 여러 고유주기가 일치하는 공진조건이 만족되면 항만공진과 같이 수로내의 수면운동은 정지파 형태로 크게 증폭한다. 수로형 공명구조물내의 파도응답은 항만내 파도응답과 유사하며 연안공학분야에서 이론 및 실험적인 방법으로 지속적인 연구가 수행되어 왔다. 이 분야의 선구적인 연구로 Miles and Munk(1961)는 사각형 항만에 대한 항만공진 문제를 다루었다. Ippen and Goda(1963)는 사각형 항만내의 파도응답에 대한 해석해를 구하고 수리모형실험 결과와 비교하였다. 또한 Lee(1970)는 체계적인 모형실험을 수행하여 이론해와 실험 결과를 서로 비교하여 이들이 서로 잘 일치함을 보였다. Hwang and Tuck(1970)은 적분방정식을 풀어 수심이 일정한 해역내에 임의의 형상을 갖는 항만내 파도응답 문제를 해석하였다. Üntüata and Mei(1975)는 입사파의 파장이 항만입구의 폭보다 아주 길다는 가정하에 섭동법(perturbation)의 일종인 정합점근전개법을 이용하여 사각형 항만에 대한 해석해를 구하였다. 이때 항만입구에서 발생하는 박리에 의한 에너지 손실에 대한 모델을 함께 고려하였다. Rogers and Mei(1978)는 폭이 좁은 직사각형 항만 공진을 비선형 Boussinesq 방정식을 풀어 해석하였다. 한편 Lepelletier(1981)은 수리모형실험과 비선형 수치모형을 이용하여 항만입구에서 일어나는 에너지 손실계수에 관한 경험식을 제공하였다. Cho(1991)는 사각형 항만내에 계류된 선박을 세장체로 가정하여 항만내 파도응답과 그 안에 계류된 선박의 운동응답에 대한 해석이론을 발표하였다. Isaacson and Qu(1990)와 Chou and Han(1993)은 항만내 안벽에서의 부분 반사를 포함한 개방경계조건식을 도입하여 항만내 파도응답을 경계요소법을 사용하여 해석하였다. Jeong et al.(1999)는 Chen(1986)이 제시한 유한요소법 수치모형에 항만 입구의 에너지 손실을 고려하여 감천항에 적용하였다. Bellotti et al. (2012)는 항만과 같이 부분 차단된 영역내의 고유값과 고유함수를 구하는 새로운 해석 기법을 제안하였다.
본 논문에서는 ‘Y’자 수로형 공명구조물내 파도응답 특성을 체계적으로 살펴보기 위하여 먼저, 유도판이 없는 단순한 사각형태의 수로형 공명구조물을 고려하였고 근사해법인 정합점근전개법(matched asymptotic expansion method: MAEM)을 이용하여 살펴보았다. 한편 수로입구에 유도판이 놓인 문제에는 수치해법인 경계요소법(boundary element method: BEM)을 사용하여 파도응답을 계산하였다. 이론적으로 구한 해석해와 수치해는 제주대학교 2차원 조파수조에서 수행한 모형실험 결과와 비교하여 검증하였다. 모형실험에서는 입사파의 주기를 바꿔가며 수로내 수면운동 특성을 살펴보았다. 수로내 유체공진이 만족되는 조건에서 파도응답은 급격히 증가하였으며, 최대파고는 공진조건을 만족함과 동시에 입사파의 주기에 따라 위치를 달리하는 파복(anti-node)에서 발생하였다. 수로내의 파도응답을 높이기 위하여 설치한 유도판의 길이와 설치각도를 바꿔가며 증폭비(amplification factor)를 살펴보았다. 수로내 파도응답은 내부유체의 공진과 유도판 설치를 통해 넓은 주기대역에서 높은 증폭비를 얻을 수 있었다. 제안된 수로형 공명구조물은 파력발전기의 에너지 추출 효율을 높이거나 파력발전장치 개발에 유용하게 활용될 수 있을 것으로 사료된다.
2. 해석기법
2.1 정합점근전개법
유도판이 없는 폭 2a, 길이 L인 사각형 공명구조물이 수심 h인 바닥면에 놓여 있을 때 입사파가 공명구조물을 향하여 진행한다고 가정한다. 공명구조물의 폭이 입사파의 파장(λ)에 비해 작고, 파와 공명구조물간의 마찰 및 수로 입구에서의 박리에 의한 에너지 손실은 무시하였다. 선형포텐셜 이론을 가정하여 속도포텐셜을 도입하고 유동은 주파수 ω를 갖고 시간에 따라 조화운동을 한다고 가정하면, 속도포텐셜은 식(1)과 같이 쓸 수 있다.
복소함수인 수면 변위 η(x, y)와 φ(x, y)의 관계는 다음과 같다.
여기서 A는 입사파의 진폭이다.
수면 변위 η(x, y)는 식(3)에 주어진 2차원 헬름홀쯔(Helmholtz) 방정식을 만족한다. 주파수 ω는 선형분산식(ω2 = gktanhkh)을 만족한다.
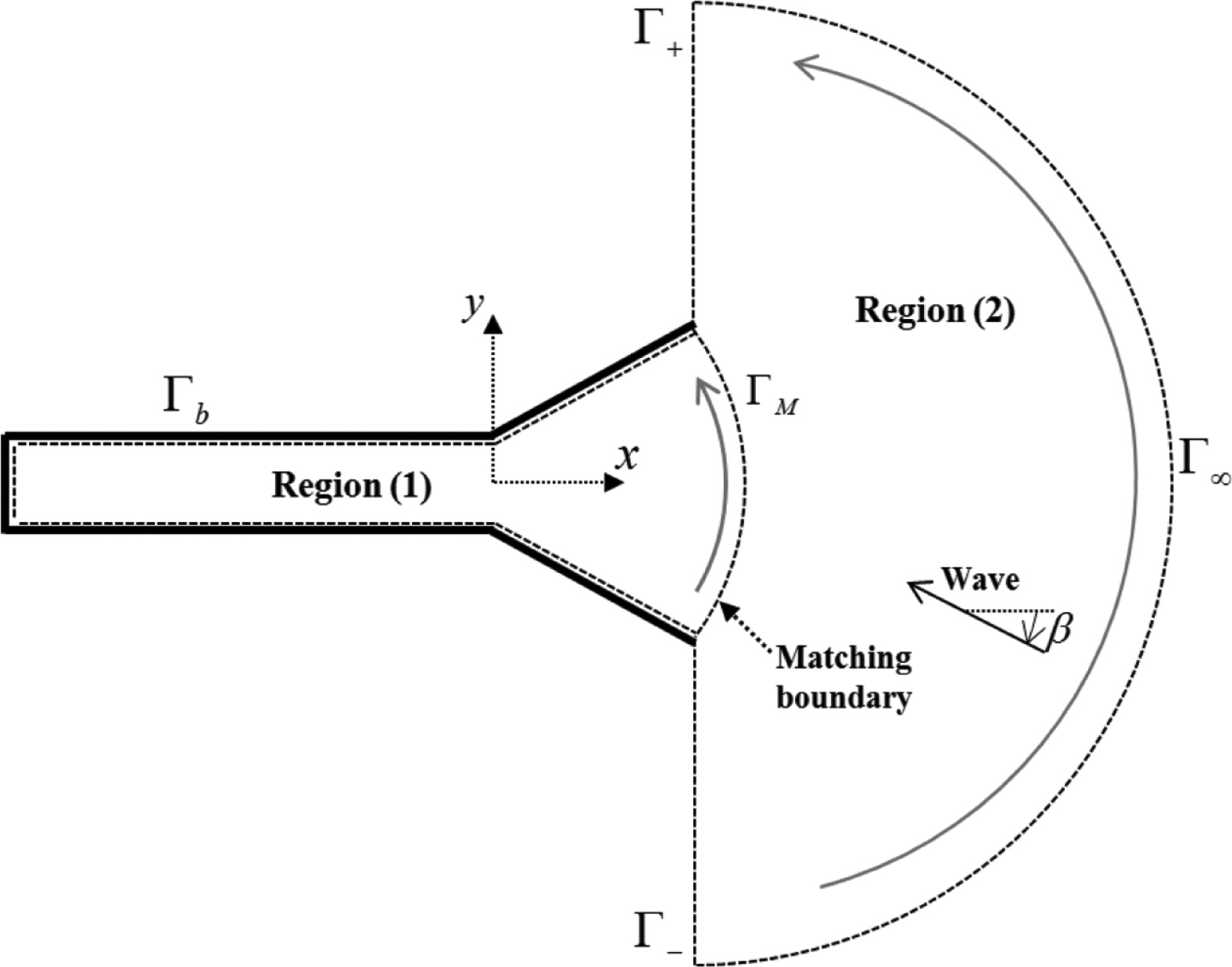
정합점근전개법을 적용하기 위해서 Fig. 2에 나타낸 것과 같이 유체영역을 내부영역(1)과 입구영역 그리고 외부영역(2)으로 나누어 각 영역에서 경계치 문제를 독립적으로 풀고, 부족한 경계조건식으로부터 생기는 미지수는 인접한 영역의 해와 정합(matching)시켜 해를 구한다.
2.1.1 외부영역
사각형 공명구조물 입구로부터 멀리 떨어진 외부영역에 대한 전체 파계(η(2))는 입사파(η0)와 수로입구로부터의 산란파(ηS)의 합으로 식(4)와 같이 표현할 수 있다. 수로 입구로부터 외부영역으로 빠져나가는 산란파를 나타내기 위하여 원점에 특이점(singular point)인 소스(source)를 놓아 표현하였다.
여기서 H 0 ( 1 )
수로 입구영역의 해와 정합하기 위하여, kr→0 일 때, η(2)에 대한 근사해를 구해 최저차항만을 취하면 식(5)와 같이 나타낼 수 있다.
여기서 lnγ(= 0.5772157…)은 Euler 상수이다.
2.1.2 입구영역
수로 입구의 폭이 입사파의 파장에 비하여 작다고 가정하면, 입구영역에서의 지배방정식은 헬름홀쯔 방정식에서 2차원 라플라스(Laplace) 방정식으로 바뀌게 되어 파동문제는 2차원 수로내의 흐름문제로 바뀐다. 2차원 수로내의 흐름문제의 해를 Schwarz-Christoffel 형태의 등각사상(conformal mapping)을 통하여 구할 수 있다(Newman, 1974; Liu, 1975). 입구영역의 해를 외부영역과 내부영역으로 외부전개(outer expansion)시키면 식(6)과 식(7)과 같다.
2.1.3 내부영역
수로의 폭이 길이에 비하여 작다는 가정으로부터 수로 내부영역에서의 해는 1차원 파형으로 식(8)과 같이 나타낼 수 있다. 입구영역의 해와 정합시키기 위해 kx→0로 내부전개(inner expansion) 시키면 식(9)와 같다.
한편, 2차원 조파수조에서 수행한 모형실험 결과와 비교하기 위하여 폭 2b를 갖는 조파수조의 벽면효과를 고려하여야 한다. 이 경우 수로 내부영역과 입구영역의 해는 전과 동일하나 외부영역의 산란파에 대한 해는 조파수조 벽면에서의 경계조건식을 만족해야 하므로 특이점을 원점뿐만 아니라 간격 2b를 갖고 폭 방향으로 무한개 분포시킨다. 이때 산란파의 해는 식(13)과 같이 바뀐다(Monkewitz, 1985).
입구영역의 해와 정합을 수행하기 위하여 kr→0 일 때, η(2)에 대한 근사해를 구하면 아래와 같다.
2.2 경계요소법
부채꼴 모양의 유도판이 포함된 ‘Y’자 수로형 공명구조물 내 파도응답은 경계요소법을 사용하여 구하였다. 유체영역내의 속도포텐셜은 식(3)에 주어진 헬름홀쯔 방정식과 수로 벽면 그리고 무한 원방에서의 방사 경계조건식을 만족한다. 2차원 헬름홀쯔 방정식과 방사 경계조건식을 만족하는 Green 함수는 다음과 같다.
여기서 X0 = (x0, y0)는 특이점의 위치를 나타낸다.
위에 주어진 Green 함수와 속도포텐셜 φ(X)를 Green 정리에 적용하여 X = (x, y)가 경계면 위에 놓여 있을 때 아래와 같은 적분 방정식을 만족한다.
여기서 밑첨자 n은 경계면에서의 법선 방향의 미분을 뜻한다.
적분 방정식(17)을 수치적으로 풀기 위하여 경계면(Γ)을 여러 개의 요소(∂Γj)로 분할하고 각 요소내에서 속도포텐셜(φj)과 법선방향 속도 벡터(φnj)가 일정하다고 가정하면 식(17)을 아래식과 같이 쓸 수 있다.
여기서 N은 요소 분할 개수이다. 윗식에서 각 요소내에서 수행된 적분값을 아래와 같이 정의한다.
위에 정의된 식(19)을 이용하여 식(18)을 다시 쓰면, 아래 식(20)과 같다.
식(20)을 행렬식으로 표현하면 다음과 같다.
행렬식(22)을 풀어 경계면에서의 속도포텐셜 또는 법선방향 속도를 구한다. 경계면에서의 값들을 가지고 유체영역내의 임의의 지점 X = (x, y)에서의 속도포텐셜을 구하기 위해 다음 식을 사용한다.
경계요소법을 적용하기 위하여 Fig. 3과 같이 유체영역을 편의상 내부영역(1)과 외부영역(2)으로 나눈다. 두 영역이 만나는 경계면을 정합 경계면이라 부르고 ΓM로 나타내었다. 각 영역에서의 속도포텐셜은 윗첨자 (1), (2)를 사용하여 구분하였고 정합 경계면에서의 속도포텐셜을 윗막대 –를 사용하여 나타내었다.
먼저 내부영역(1)에서의 속도포텐셜을 내벽(Γb) 경계면과 정합(ΓM) 경계면으로 구분하여 행렬식으로 나타내면 다음과 같다.
φ(1), φn(1)는 내벽(Γb) 경계면에서의 속도포텐셜과 법선방향 속도값이다. 그리고 ϕ ( 1 ) ϕ n ( 1 )
한편 외부영역(2)에서의 속도포텐셜은 입사파 포텐셜과 내부영역으로부터 산란된 포텐셜의 합으로 쓸 수 있다.
여기서 β를 x축과 이루는 입사각이라 할 때 입사파 포텐셜은 다음과 같다.
내부영역에서 발생하는 산란파 포텐셜은 무한 경계면(Γ∞)에서 방사 경계조건식을 만족한다.
외부영역의 경계면(Γ±)에서 산란파의 영향이 작다고 가정하면 외부영역의 산란파 적분방정식은 아래와 같이 정합 경계면에서의 기여분만 남는다.
여기서 ϕ S ϕ S n
내부영역과 외부영역이 만나는 정합 경계면에서의 정합조건식은 다음과 같다.
정합조건식(29)를 식(24)와 식(28)에 적용하면 아래와 같다.
행렬식(32)를 풀어 내부영역(1)의 내벽 경계면에서의 속도포텐셜(φ(1))과 정합 경계면에서의 속도포텐셜(ϕ
내부영역내의 임의의 지점에서의 증폭비는 다음과 같이 정의된다.
2.3 모형 실험
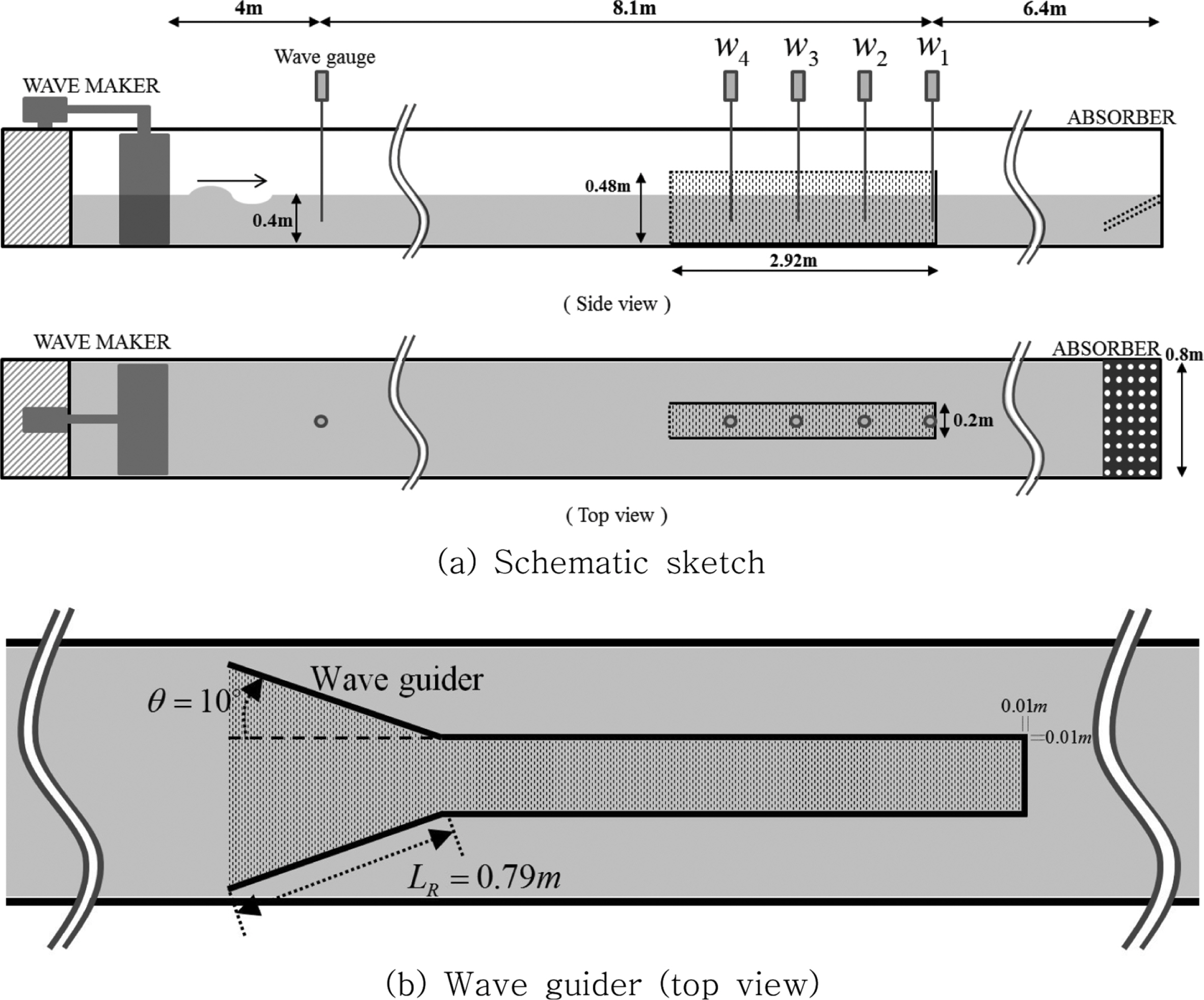
정합점근전개법으로부터 얻은 해석해와 경계요소법으로부터 구한 수치해의 검증을 위해 길이 20 m, 폭 0.8 m, 깊이 1.0 m인 제주대학교 2차원 조파수조를 이용하여 모형실험을 실시하였다. 아크릴로 제작된 실험모형은 수심이 0.4 m인 수조 바닥면에 고정하였다. 실험모형의 전체 제원과 실험 구성은 Fig. 4에 나타내었다. 수로의 길이와 폭은 각각 2.92 m, 0.2 m이며, 유도판의 길이는 0.79 m이고 설치 각도는 10도이다. 입사파의 진폭은 조파장치로부터 4 m 떨어진 지점에 설치된 파고계로 측정한 값을 사용하였다. 수로 길이에 따른 파도응답 특성을 살펴보고자 수로내에 4개의 파고계를 일정 간격을 갖는 고정된 위치에서 놓고 실시한 실험과 입사파의 주기에 따라 변하는 수로내 파복위치에 파고계를 설치하여 실험을 실시하였다. 먼저 파고계를 고정한 실험에서의 파고계의 위치는 수로 끝단(ω1)에 1개, 나머지 3개(w2, w3, w4)는 0.73 m씩 간격을 두고 설치하였다. 반면에 입사파의 주기에 따라 파고계의 위치를 바꾸는 실험에서는 4개의 파고계가 수로벽면으로부터 형성된 정지파의 파복위치에 순서대로 놓이도록 하였다.
입사파의 주기변화에 따른 파도응답 특성을 파악하기 위하여 0.8 s부터 1.6 s까지 0.05 s 간격으로 주기를 선택하였고, 부분적으로 더 분할된 주기에 대한 실험도 추가하였다. 모든 주기에 대하여 조파기에 입력한 파고는 0.01 m로 고정하였다. 파의 생성시간은 총 60 s이며, 공명구조물과 조파장치간의 거리를 에너지 전파속도(group velocity)로 나누어 수로내에 정지파가 형성되는 시점으로부터 조파판으로부터 재반사파가 파고계에 도달하기 전까지의 유효한 데이터를 추출하여 각 파고계 위치에서의 평균 파고를 구하였다. 데이터 취득에서 사용된 샘플링 주파수는 100 Hz이다. Fig. 5는 조파수조에 설치된 두 실험모형 사진을 나타내었다.
3. 계산결과 및 고찰
수로형 공명구조물내 파도응답의 결과는 측정 위치(wi, i = 1, 2, 3, 4)에서의 파 진폭(η i = η i / A A m i
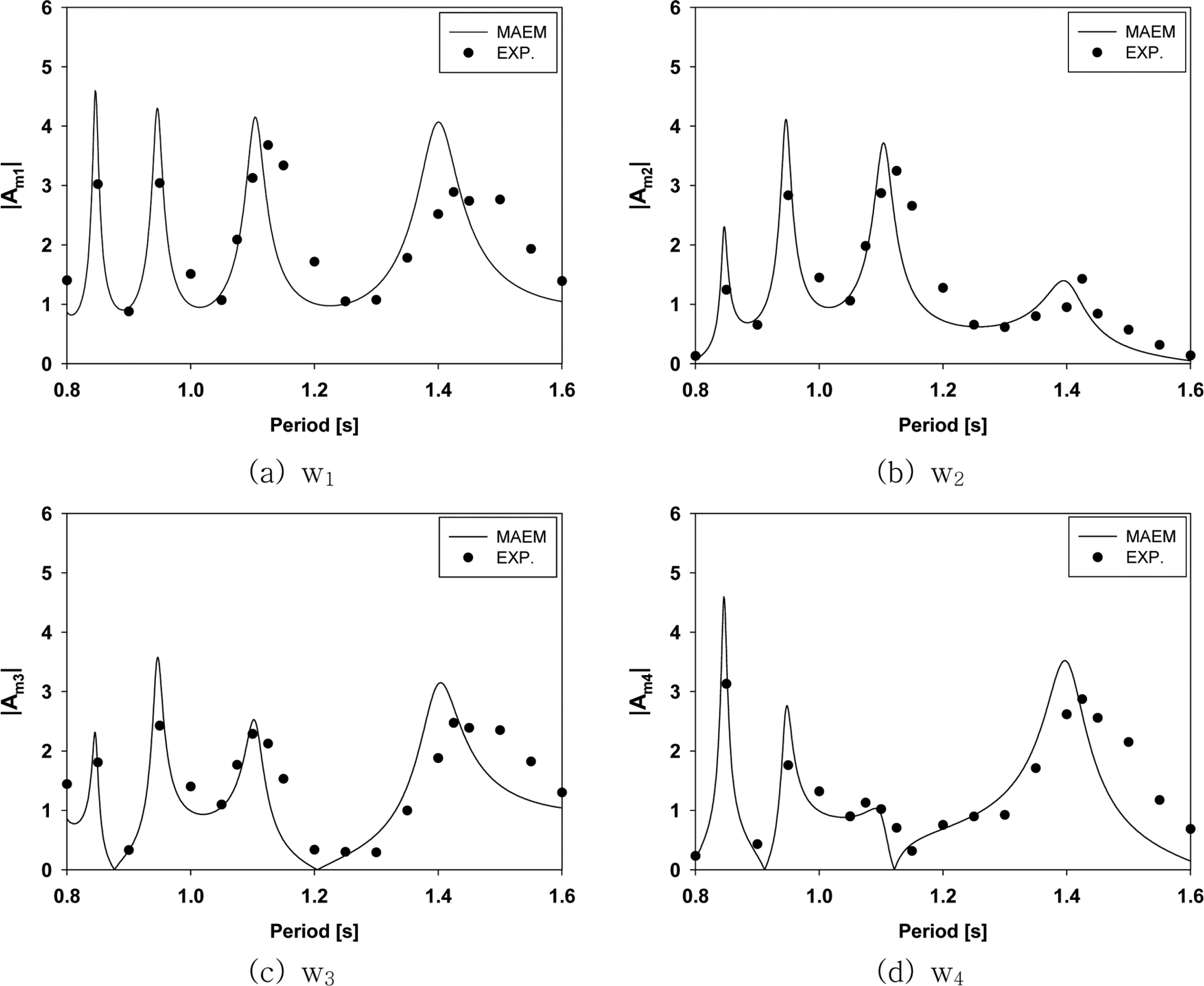
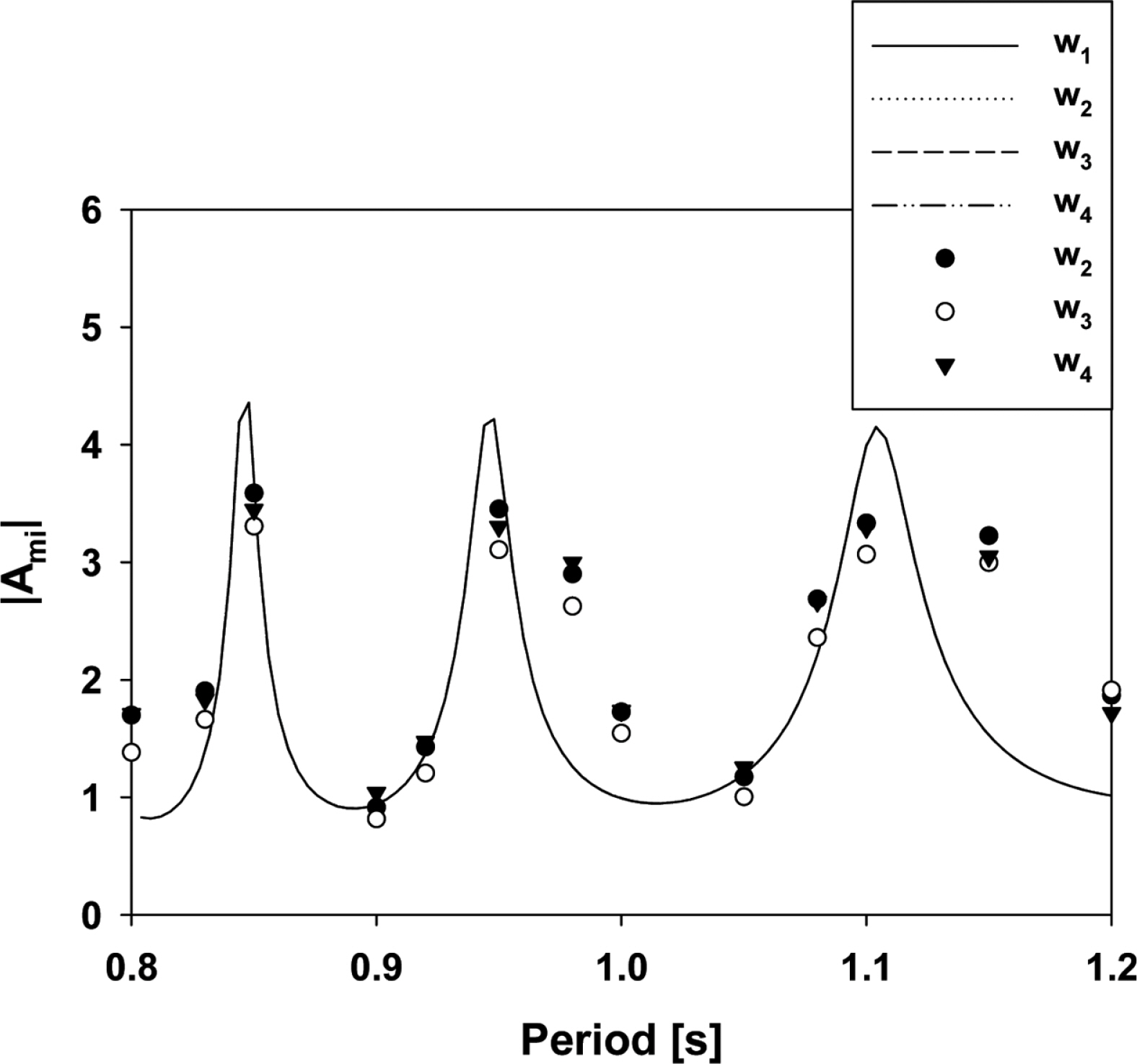
Fig. 6(a)는 파복이 형성되는 수로 끝단(w1)에서의 증폭비를 비교한 그림이다. 주기 범위내에서 총 4개의 내부유체 공진주기가 존재함을 볼 수 있다. 각 유체 공진주기에서 수로 내 수면운동은 크게 발생하여 약 3 이상의 높은 증폭비를 보여주고 있다. 그러나 유체 공진주기를 벗어난 주기에서의 증폭비는 약 1 근처의 값으로 수면운동 증폭 효과는 사라졌다. Fig. 6(b), (c), (d)는 수로 끝단에서 0.73 m씩 떨어진 두번째(w2), 세 번째(w3), 네 번째(w4) 파고계 위치에서의 증폭비를 보여주고 있다. 항상 파복이 형성되는 수로 끝단에서의 결과와 다른 경향을 보인다. 두 번째 파고계 위치에서의 증폭비 곡선을 보면 4개의 피크 값을 보이지만, 단주기(T = 0.83 s)와 장주기(T = 1.4 s) 쪽에 위치한 두 공진모드에서의 피크값은 수로 끝단(w1)에서의 증폭비보다 크게 낮아짐을 볼 수 있다. 특히, 주기 0.8 s와 1.6 s에서는 증폭비가 거의 0에 가까운 값을 보여 이 위치에서 파절(node)이 형성됨을 알 수 있었다. 즉, 수로내 완전반사로 수로내의 파형은 정지파의 형태로 나타나기 때문에 파복을 벗어난 위치에서는 파랑에너지 증폭 효과를 기대할 수 없다. 동일 간격으로 배치된 세 번째와 네 번째 파고계 위치에서의 증폭비 또한 주기에 따라 증폭비가 커질 수도 작아질 수도 있다. 결론적으로 수로내의 내부유체 공진을 이용하면 수면운동을 크게 증폭시킬 수 있다. 그러나 파력발전장치의 최적 설치지점을 선정하기 위해서는 내부유체의 공진주기를 파악하는 것 외에 증폭비가 최대가 되는 파복위치를 정확히 파악하는 것이 중요하다.
Fig. 7은 4개의 파고계를 수로내 파복위치에 놓고 수행한 실험결과를 해석결과와 함께 나타내었다. 각 파복위치에서의 해석결과는 동일하며, 실험결과를 정성적으로 잘 따라가고 있다. 수로내 정지파의 형태로 나타나는 수면운동에서 파복은 반 파장 간격으로 형성되기 때문에 3지점에서의 증폭비 곡선은 거의 비슷한 경향을 보여주고 있다. 앞의 결과와 동일하게 내부유체 공진에 따라 파복에서는 높은 파도응답을 보인다. 또한 수로내의 길이 방향으로 형성하는 내부유체의 여러 공진모드 중에서 장주기 영역으로 이동할수록 공진대역이 점점 넓어지는 경향을 보였다.
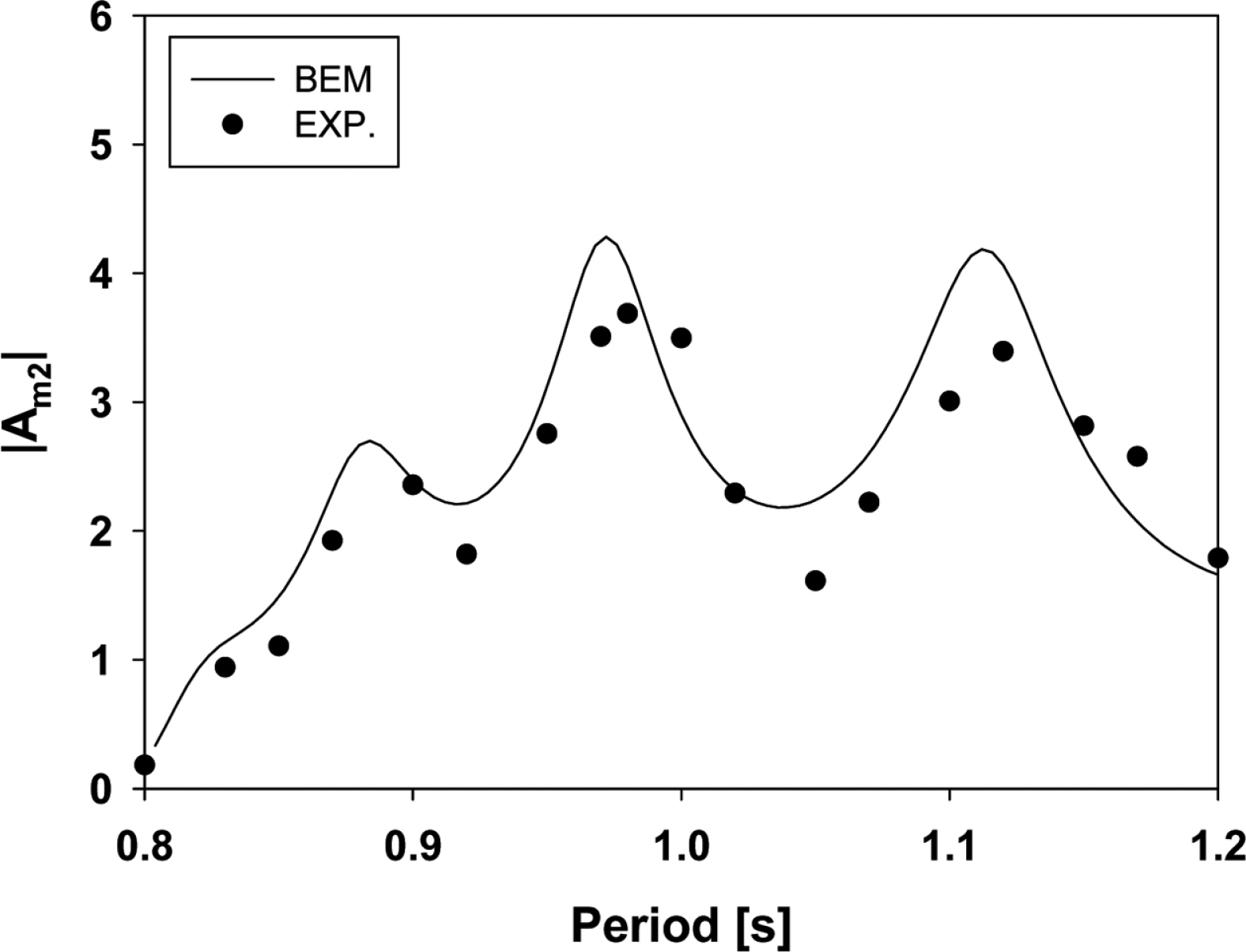
다음은 수로형 공명구조물 입구에 유도판을 설치한 경우를 살펴보았다. 실험에 사용된 유도판의 형상과 제원은 Fig. 4(b)에 나타내었다. 경계요소법으로 구한 수치해의 검증을 위해 수로 끝단으로부터 0.73 m 떨어진 위치(w2)에서의 증폭비를 측정하여 그 결과를 Fig. 8에 BEM 수치해와 함께 그렸다. 두 결과는 정성적으로 잘 일치함을 볼 수 있으며, 정량적인 값 차이는 수로 입구에서의 박리에 의한 에너지 손실과 수로벽과 바닥에서의 마찰에 의한 에너지 손실에 기인한다. 유도판의 없는 Fig. 6b와 비교하면 공진주기의 이동과 증폭비의 값 차이가 나타남을 볼 수 있다. 이는 유도판의 설치로 수로 내부유체의 공진주기 변화와 점성에 의한 감쇠력의 차이를 유발하였기 때문으로 사료된다.
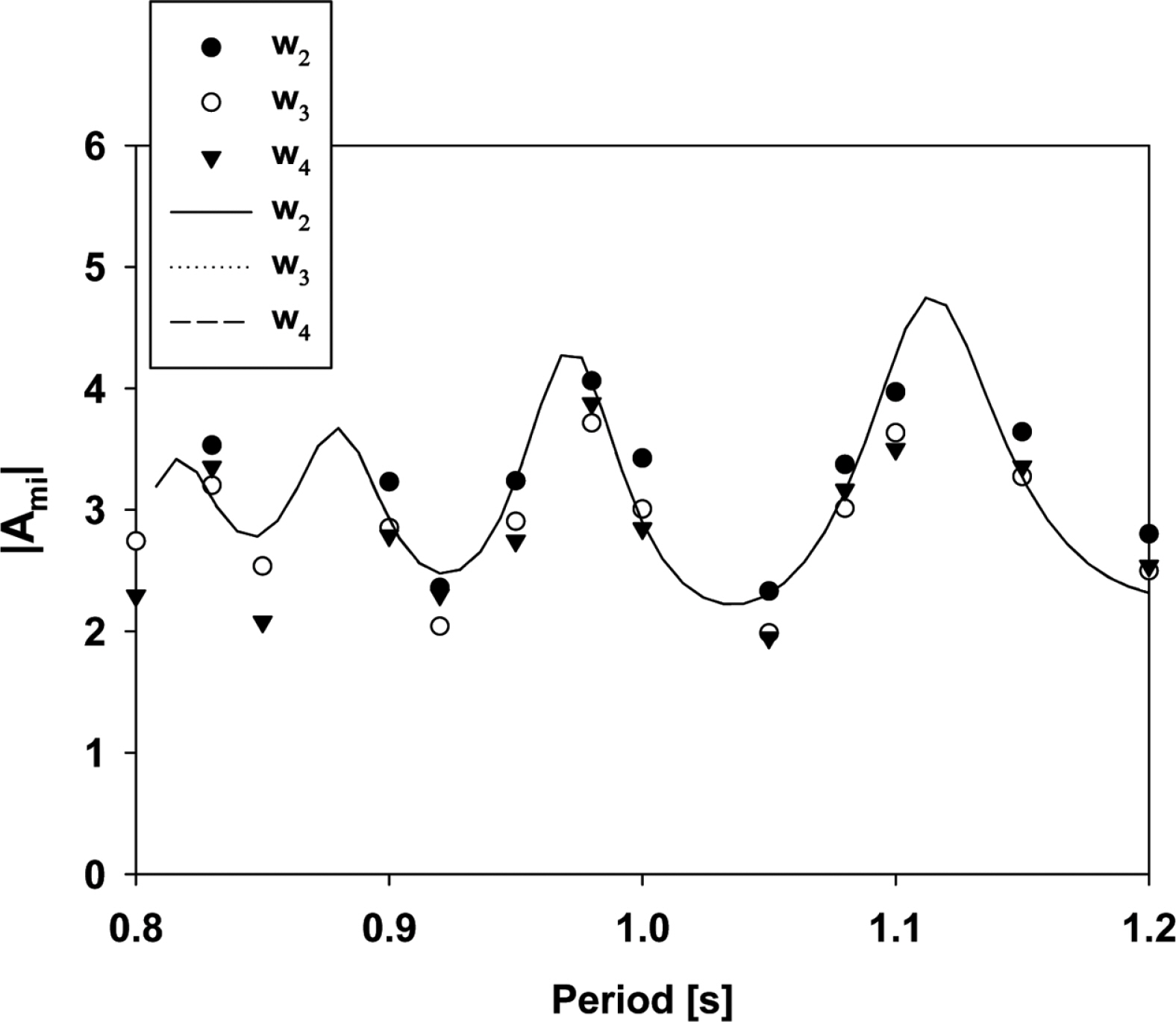
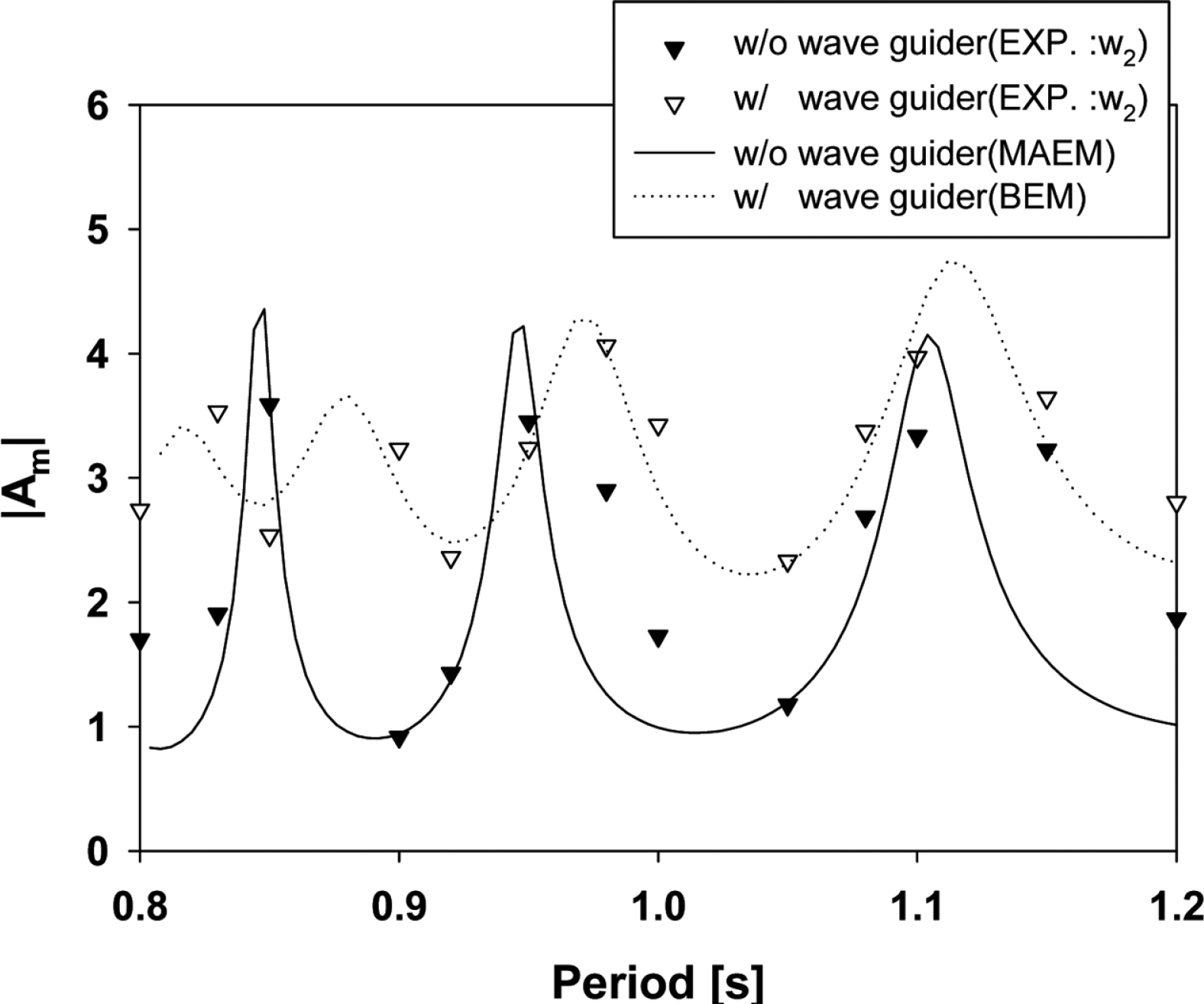
Fig. 9는 유도판을 설치한 상태에서 벽면을 제외한 3개의 파고계(w2, w3, w4)를 수로내 파복에 위치시켰을 때 모형실험과 수치계산 결과를 보여주고 있다. 각 파복위치에서의 수치해는 같은 값을 주며, 모형실험 결과와 서로 잘 일치하고 있다. 두 결과 모두 실험주기 범위내에서 최소 2 이상의 높은 증폭비를 나타내었고, 해석범위 내에서 주기가 짧은 쪽을 단주기 영역, 긴 쪽을 장주기 영역으로 구분할 때, 장주기 영역에 속한 공진주기에서의 증폭비가 약 4에 가까운 매우 높은 파도응답을 보였다. 이러한 결과는 내부유체의 공진주기에서 벗어난 주기대역에서 증폭비가 떨어지는 단점을 유도판을 이용해 개선시킬 수 있음을 보였고, 또한 내부유체의 공진주기에서의 증폭비도 더욱 높일 수 있음을 보여주었다. 설치된 유도판이 수로내 수면운동에 미치는 영향을 확인하고자 유도판 유무에 따른 증폭비 계산 결과와 w2 지점에서의 실험결과를 함께 Fig. 10에 따로 그렸다. 유도판이 있을 때는 유도판이 없을 때와 비교하여 대부분의 주기대역에서 높은 증폭비를 보였다. 앞서 언급하였듯이, 내부유체의 공진이 발생하지 않는 주기대역에서 증폭비가 약 2배 가까이 증가된 것을 볼 수 있다. 이는 공명구조물 전면에 설치된 부채꼴 형상의 유도판의 설치로 입사파의 에너지를 2배로 증가시켰기 때문이다. 만약 최적화된 길이와 설치 각도를 갖는 유도판을 적용한다면 수로내 더욱 높은 증폭비를 얻을 수 있을 것으로 기대된다.
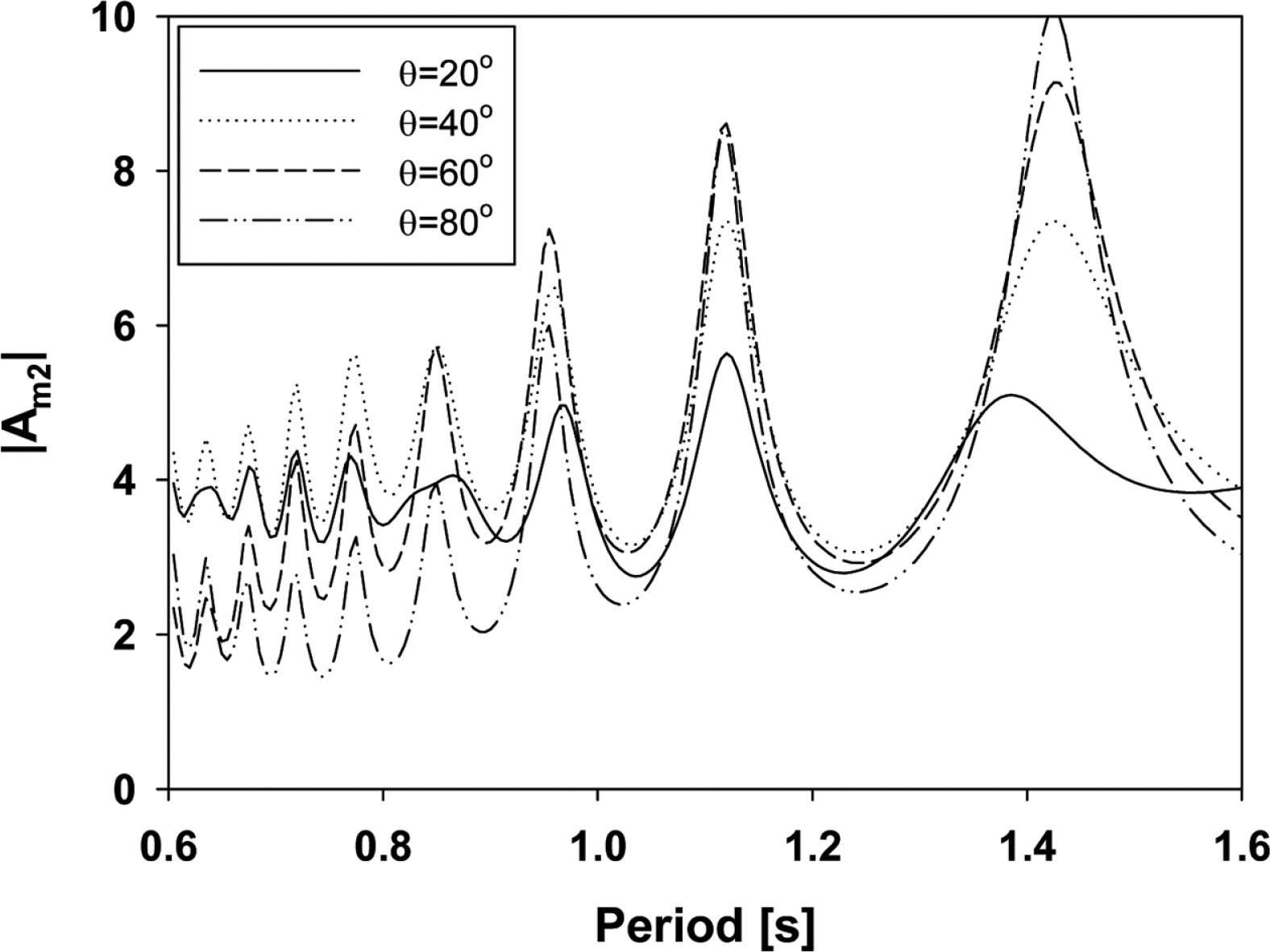
유도판의 효과를 극대화하기 위하여 유도판의 길이와 설치각도를 변경하며 수로내 파도응답 특성을 살펴보았다. 여기서 증폭비는 수로 끝단으로부터 두번째 파복(w2)에서 계산된 값이다. Fig. 11은 유도판의 길이(LR = 0.79m)를 고정하고 설치각도(θ)를 20도부터 80도까지 20도 간격으로 바꿔가면서 계산된 증폭비를 나타내었다. 그래프의 경향을 살펴보면, 설치각도 변화에 따른 내부유체의 공진주기 변화는 작은 반면에 공진주기에서의 증폭비 차이는 크게 나타남을 확인할 수 있다. 주기 0.6 s부터 시작하는 단주기 영역에서는 상대적으로 설치각도 40도가 높은 파도응답을 보였고, 주기 0.93 s 이후부터는 설치각도 60도에서 증폭비가 급격히 증가하여 장주기 영역까지 높은 값을 유지하고 있다. 설치각도에 따라 일정한 경향이 나타나지 않지만, 유도판의 각도가 증가할수록 장주기 영역에서 높은 증폭비를 보여주고 있다. 수로형 공명구조물은 수로내부의 파도응답을 극대화시키는 것이 본 연구의 주된 목적이라고 생각할 때, 유도판의 최적 설치각도의 범위는 40도와 60도가 적절한 것으로 판단된다.
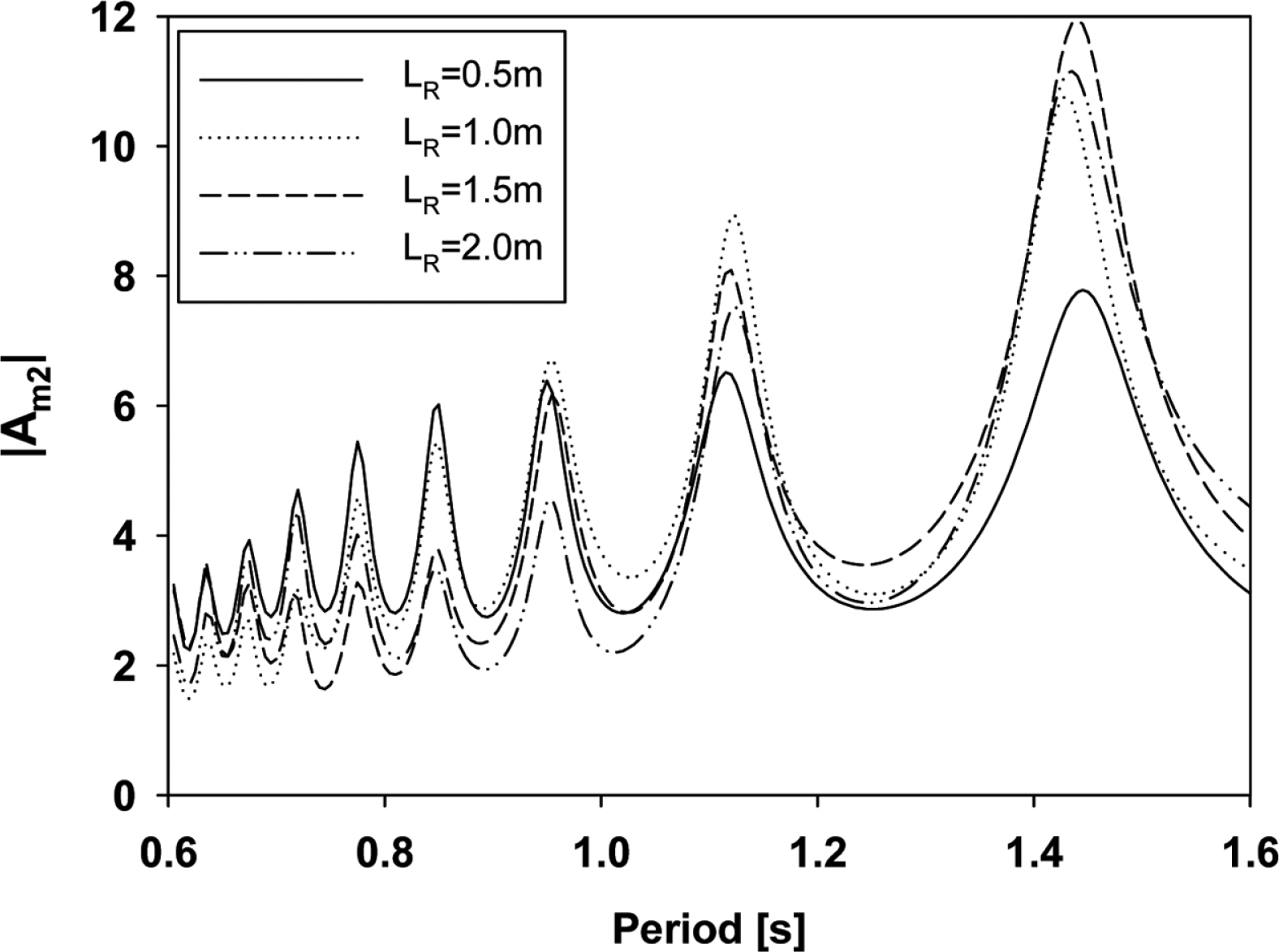
Fig. 12는 유도판의 각도를 60도로 고정시키고 유도판의 길이를 0.5 m부터 2.0 m까지 0.5 m 간격으로 증가시키면서 길이 변화에 따른 두번째 파복(w2)에서의 증폭비를 나타내었다. 증폭비 곡선을 살펴보면, 내부유체의 공진주기는 유도판의 길이 변화에 크게 영향을 받지 않는 반면, 증폭비의 차이는 다소 크게 나타나고 있다. 여기서 주목할만한 점은 특정한 주기에 대해 최대 증폭비를 나타내는 최적의 유도판 길이가 존재한다는 것이다. 이러한 결과는 설계관점으로 볼 때, 설치해역의 파랑특성을 미리 파악하여 반사면 길이에 대한 최적 설계가 이뤄져야 한다. 그래프를 살펴보면, 유도판의 길이가 0.5 m인 경우에는 주기 0.6-0.88 s에서 가장 높은 증폭비를 보이고 있으며, 주기 0.88s-1.17 s에서는 유도판 길이 1 m가 높은 증폭비를 나타내고 있다. 이후 장주기 영역까지 살펴보면, 유도판의 길이가 길수록 장주기 영역에서 높은 증폭비를 보임을 알 수 있다. 즉, 본 해석범위내에서는 길이가 짧은 유도판이 단주기 특성을 갖는 파랑조건에서 유리하며, 긴 유도판은 장주기 영역에서 효과적임을 알 수 있다. 현재의 수치해는 마찰 및 점성에 의한 감쇠효과가 고려되지 않아 다소 과장된 결과를 보인다고 하더라도 내부유체의 공진으로 매우 높은 증폭비를 주었고 공진에서 벗어난 주기범위에서도 증폭비가 2 이상으로 유도판의 효과는 매우 긍정적으로 나타남을 확인할 수 있었다. 유도판의 길이는 구조물의 구조적 안전성과 제작 및 설치 비용과 직접적인 관련이 있기 때문에 가급적 짧으면서도 높은 증폭비를 유지할 수 있도록 설계하는 것이 바람직하다. 따라서, 설치해역의 파랑특성을 고려하여 유도판의 길이와 각도를 적절히 선정해야 한다.
4. 결 론
파랑에너지 밀도가 낮은 해역에서 파랑에너지를 높이기 위해 고안된 ‘Y’자 수로형 공명구조물의 에너지 증폭효과를 이론적 방법과 실험적 방법을 통해 살펴보았다. 먼저, 유도판이 없는 사각형 공명구조물에 대한 수로내 파도응답 해석방법으로 정합점근전개법을 사용하였고, 조파수조를 이용한 모형실험을 통해 해석해를 검증하였다. 해석결과와 모형실험 결과는 잘 일치하였다. 실험주기 범위내에서 여러 개의 유체 공진주기가 나타나는 것으로 보아 수로내에는 여러 공진모드가 존재함을 알 수 있었다. 내부유체의 공진으로 인해 크게 증폭된 수로내 수면운동의 최대값은 파복에서 발생하며 파절에서는 최소값이 일어남을 확인하였다. 한편, 수로입구에 부채꼴 모양의 유도판을 설치한 ‘Y’자 수로형 공명구조물내의 파도응답은 경계요소법을 사용하여 수치해를 구하고 모형실험결과와 비교하였다. 두 결과는 서로 잘 일치하였다. 외해의 파랑에너지를 수로내로 모아주는 유도판은 특히, 내부유체 공진주기에서 벗어난 주기대역에서 증폭비를 높이는데 효과적임을 수치적, 실험적 방법을 통하여 밝혔다. 최적의 유도판의 형상을 찾기 위하여 유도판의 길이와 설치각도를 바꿔가며 수로내의 파도응답을 살펴보았다. 수로내 파도응답에 큰 영향을 미치는 내부유체의 공진주기는 유도판의 설치각도 및 길이에 따라 변화가 거의 없었으며, 유도판의 설치각도는 40도와 60도에서 높은 증폭비가 넓은 주기범위에서 잘 나타나 해석 범위내에서는 최적값으로 판단하였다. 그리고 유도판의 길이 변화에 따른 계산 결과로부터 특정 주기대역에서 최대 증폭비를 주는 최적의 유도판의 길이가 존재함을 확인하였다. 유도판은 설치비용뿐만 아니라 구조적인 문제를 동반하므로 설계에 있어 단순히 최대 증폭비를 얻기 위해 과도한 설계안을 도출하기 보다는 설치해역의 파랑특성을 고려하여 적절한 각도와 길이를 선택하는 것이 중요하다. 유도판을 포함한 수로형 공명구조물은 낮은 에너지 밀도를 가진 파랑에너지를 크게 높이는 데 효과적임을 밝혔으며, 향후 파력발전장치와 같은 에너지 추출 시스템에 효과적으로 활용될 수 있을 것으로 기대된다.