Spatial Variation of Diffracting Wave Amplitudes on the Front and Lee Sides of the Semi-Infinite Breakwater

Jae-Sang Jung; Changhoon Lee

doi:10.9765/KSCOE.2020.32.4.203

요약

반무한방파제 전면 및 후면에서 회절파 진폭의 공간적인 변화에 대해 Penney and Price(1952)의 해석해를 활용하여 분석하였다. 방파제 전면에 회절파의 영향으로 입사파와 반사파를 합친 중복파의 파력보다 더 큰 파력이 발생한다. 좀 자세히 알아보면, 회절파는 방파제의 선단 (x, y) = (0, 0)을 기존으로 동심원 형태로 위상 변화가 발생하는 반면 입사파와 반사파는 평면 형태로 위상 변화가 발생한다. 따라서, 입사파(또는 반사파)와 회절파가 중첩에 의한 파의 진폭은 에너지 불연속선에서부터 떨어진 곳에서는 항상 요동치게 된다. 방파제 전면 및 후면 (x, y) = (0, y) 지점은 회절파 파봉선을 따라 에너지 불연속선 지점에서부터 y(π/2 - β) 만큼 떨어져 있다. 회절파 에너지의 감쇠의 정도는 회절파 파봉선을 따라 에너지 불연속선 지점에서 떨어진 거리에 비례한다. 따라서, 방파제 전면 및 후면 (x, y) = (0, y) 지점에서의 회절파의 진폭은 y(π/2 - β)의 제곱근에 반비례한다.

핵심용어: 반무한방파제, 회절파, 해석해, 이론적인 해석

Abstract

Spatial variation of diffracting wave amplitudes along a semi-infinite breakwater is investigated using the analytical solution of Penney and Price (1952) for wave diffraction. On the front side of the breakwater, the fluctuation of wave amplitudes due to diffracting waves would cause a wave force greater than that of superposed incident and reflected waves. The diffracting wave phase varies in circular shape from the breakwater tip of (x, y) = (0, 0) whereas the incident and reflected wave phases vary in planar shape. So, the total wave amplitude of the incident (or reflected) waves and the diffracting waves would fluctuate at a position away from the energy discontinuity line. The position (x, y) = (0, y) on the front and lee sides of the breakwater is at a distance y(π/2 - β) of the point on the energy discontinuity line along the diffracting wave crest line. The degree of reduction of the diffraction wave energy is proportional to the distance from the point on the energy discontinuity line along the diffracting wave crest line. Therefore, the diffracting wave amplitudes on the front and lee sides of the breakwater would be inversely proportional to the square root of y(π/2 - β) .

Keywords: semi-infinite breakwater, diffracting wave, analytical solution, theoretical investigation

1. 서 론

최근 지구온난화에 따른 해수면 상승과 태풍의 대형화에 따른 고파랑의 발생으로 국내외 직립방파제에 활동피해가 발생한 사례가 다수 보고되었다. 직립방파제에서의 활동피해는 뱀이 기어가는 형태를 보이므로 사행피해(meandering damage)로 칭하였으며, 많은 학자들이 그 원인을 회절파(diffracting wave)로 보고 있다(Ito and Tanimoto, 1971; Jung et al., 2016; Choi et al., 2020). 일본에서는 이러한 직립방파제의 사행피해 사례가 Hattori et al.(1984) 및 Miyai et al.(1993)에 의해 다수 보고 되었으며, 국내에서는 2018년 10월 남해안에 내습한 제25호 태풍 콩레이에 의해 부산항 외곽방파제에 활동피해가 발생한 사례가 있다(Choi et al., 2020).

일반적으로 방파제 주변에서의 회절은 입사파가 진행함에 따라 방파제 배후에서 나타나는 Shadow zone에서 입사파의 에너지 이동에 의해 발생하고, 방파제 전면에서 중복파가 발생함에 따라 중복파 영역에서 입사파만 존재하는 영역으로 에너지가 이동하여 또한 발생한다. 방파제 주변에 발생하는 중력파의 회절현상에 대해서는 Lamb(1945)가 Sommerfeld (1896)에 의해 제시된 빛의 회절이론으로부터 반무한방파제(semi-infinite breakwater)에 수직으로 입사하는 규칙파에 대한 해석해를 제시하였다. 이후 Penney and Price(1952)는 Lamb의 연구를 확장하여 반무한방파제 및 양익방파제(breakwater gap)에 비스듬히 입사하는 규칙파에 대한 회절의 해석해를 제시하였다. Goda et al.(1978)은 다방향불규칙파의 회절에 대해 수리모형실험, 현장관측 및 해석해를 이용하여 연구하였으며, Dalrymple et al.(1984)은 완경사방정식(mild-slope equation)을 이용하여 수직 실린더 주변에서의 회절에 대해 연구하였다. Yu(1995)는 투수성 반무한방파제에 수직으로 입사하는 규칙파의 회절에 대한 해석해를 제시하였으며, McIver (1999)는 Yu의 연구를 확장하여 투수성 반무한방파제에 비스듬히 입사하는 규칙파의 회절에 대한 해석해를 제시하였다. Lee and Kim(2006)은 다방향 불규칙파랑을 대상으로 반무한방파제 주변의 회절에 대해 수치적으로 검토하였다. Suh and Kim(2008)은 방파제 전면에서 부분반사가 발생하는 경우에 대해 반무한방파제에 수직으로 입사하는 규칙파에 대한 회절의 해석해를 제시하였으며, Kim et al.(2011)은 Suh and Kim의 연구를 확장하여 전면에 부분반사가 발생하는 반무한방파제 및 양익방파제에 비스듬히 입사하는 규칙파의 회절에 대한 해석해를 제시하였다. Jung et al.(2015)은 반무한방파제 형식의 장대구조물(long structure)에 작용하는 파력에 대해 회절 효과를 고려하여 검토하였으며, Jung et al.(2016)은 반무한방파제 주변에 회절에 의한 파력의 공간적인 분포에 대해 연구하였고 방파제 전, 후면에서 회절의 영향를 고려하면 최대 34%의 파력이 증가함을 보였다. Choi et al.(2020)은 3차원 전산유체역학 모델인 olaFlow를 적용하여 사석마운드 위에 놓인 케이슨 방파제 주변의 회절에 대해 검토하였다.

과거 회절현상에 대해 매우 다양한 연구가 수행되었으나 회절에 따른 파력의 공간적인 분포에 대해서는 거의 연구된 사례가 없다. 또한, 기존의 연구에서 제시한 회절의 해석해는 매우 복잡한 적분식을 포함하고 있어서 현장의 기술자들이 직접 활용하기에는 한계가 있었다. 따라서, 본 연구에서는 Kim et al.(2011)이 제시한 해석해를 활용하여 반무한방파제 주변에서 발생하는 규칙파의 회절에 대해 물리적으로 설명하고, 반무한방파제 배후의 회절파에 대한 근사식을 제시하였다. 그리고, 새로운 무차원 변수를 도입하여 반무한방파제에 작용하는 상대 파력에 대한 그래프를 제시함으로써 항만 설계 및 시공 관련 실무자들이 쉽게 활용할 수 있도록 하였다.

2. 반무한방파제 주변의 회절

2.1 방파제 전면에 부분반사가 있는 경우 회절의 해석해

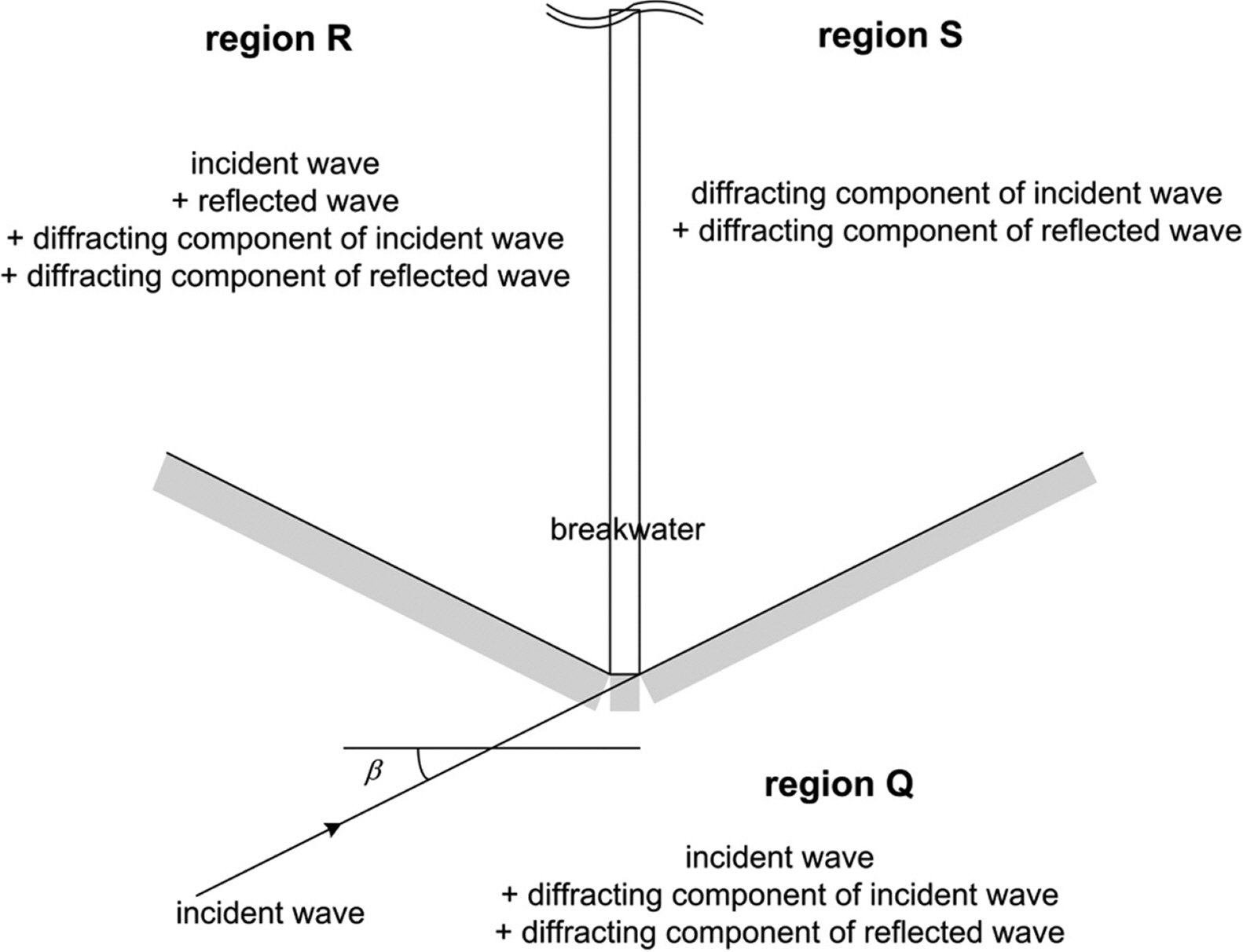
반무한방파제 전면에 부분반사가 있는 경우 회절의 해석해는 Kim et al.(2011)에 의해 유도되었다. 각 변수에 대한 설명은 Fig. 1과 같으며, 여기서 L은 파장(wavelength), d는 방파제의 폭, β는 방파제 전면에 수직인 선과 파향선의 교각, 그리고 η는 자유수면변위를 뜻한다.

반무한방파제 주변에서의 각 파랑성분이 분포하는 영역은 Fig. 2와 같다. Fig. 2에서 반무한방파제 전면의 Region R에는 입사파, 반사파, 입사파의 회절성분 및 반사파의 회절성분이 모두 존재한다. 반면, Region Q에는 방파제가 존재하지 않는 영역이므로 입사파, 입사파의 회절성분 및 반사파의 회절 성분이 존재한다. 방파제 배후의 Shadow zone인 Region S에는 입사파 및 반사파의 회절성분만이 존재한다.

반무한방파제 주변의 회절을 해석하기 위해 선형의 동역학적 자유수면 경계, 운동학적 자유수면 경계 및 바닥 경계조건을 이용하여 연속방정식을 풀면 다음 식과 같은 속도포텐셜이 유도된다.

(1)

φ(x,y,z,t)=igωcoshk(z+h)coshkhaiF(x,y)eiωt

여기서, ϕ는 속도포텐셜, g는 중력가속도, ω는 각진동수(angular frequency), a_i는 입사파의 진폭을 나타낸다. 식(1)을 방파제에서의 부분반사 경계조건을 활용하고 포물선 좌표계 및 극좌표로 변환하여 해석하면 다음과 같은 식을 구할 수 있다(Kim et al., 2011).

(2)

F(r,θ)=e-ikrsin(θ+β)f(ψ)+Kreikrsin(θ-β)f(ψ′) inetion S

(3)

F(r,θ)=e-ikrsin(θ+β)-e-ikrsin(θ+β)f(-ψ)+Kreikrsin(θ-β)f(ψ′) in Region Q

(4)

F(r,θ)=e-ikrsin(θ+β)+Kreikrsin(θ-β)-e-ikrsin(θ+β)f(-ψ)+Kreikrsin(θ-β)f(-ψ′) in Region R

(5)

f(ψ)=12(1+i)∫-∞ψe-π2iu2du

(6)

ψ2=4krπsin212(θ-π2+β),ψ′2=4krπsin212(θ+π2-β)

(7)

r=x2+y2

여기서, K_r은 방파제 전면에서의 반사율, θ는 극좌표에서 각도, k는 파수(wave number)를 각각 나타낸다. 식(2)는 Region S에서의 회절을 나타내며, 첫번째 항은 입사파의 회절성분, 두번째 항은 반사파의 회절성분이다. 식(3)은 Region Q에서의 해이며, 첫번째 항은 입사파, 두번째 항은 입사파의 회절성분 그리고 세번째 항은 반사파의 회절성분이다. 식(4)는 방파제 전면의 Region R에 대한 해이며, 첫번째 항은 입사파, 두번째 항은 반사파, 세번째 항은 입사파의 회절성분 그리고 네번째 항은 반사파의 회절성분을 각각 나타낸다. 입사파와 반사파의 회절성분은 식(5)와 같은 Fresnel 적분식을 포함한다.

2.2 반무한방파제 주변의 회절 특성

반무한방파제 주변에서 회절특성에 대해 검토하기 위해 식 (2)~(7)을 이용하였다. 입사파랑은 규칙파이며, 입사각 β는 30도, 수심 10 m, 파고 1 m, 주기는 10초이다. 방파제 전면의 반사율은 1.0을 적용하였으며, 해석 결과는 Figs. 3~7과 같다.

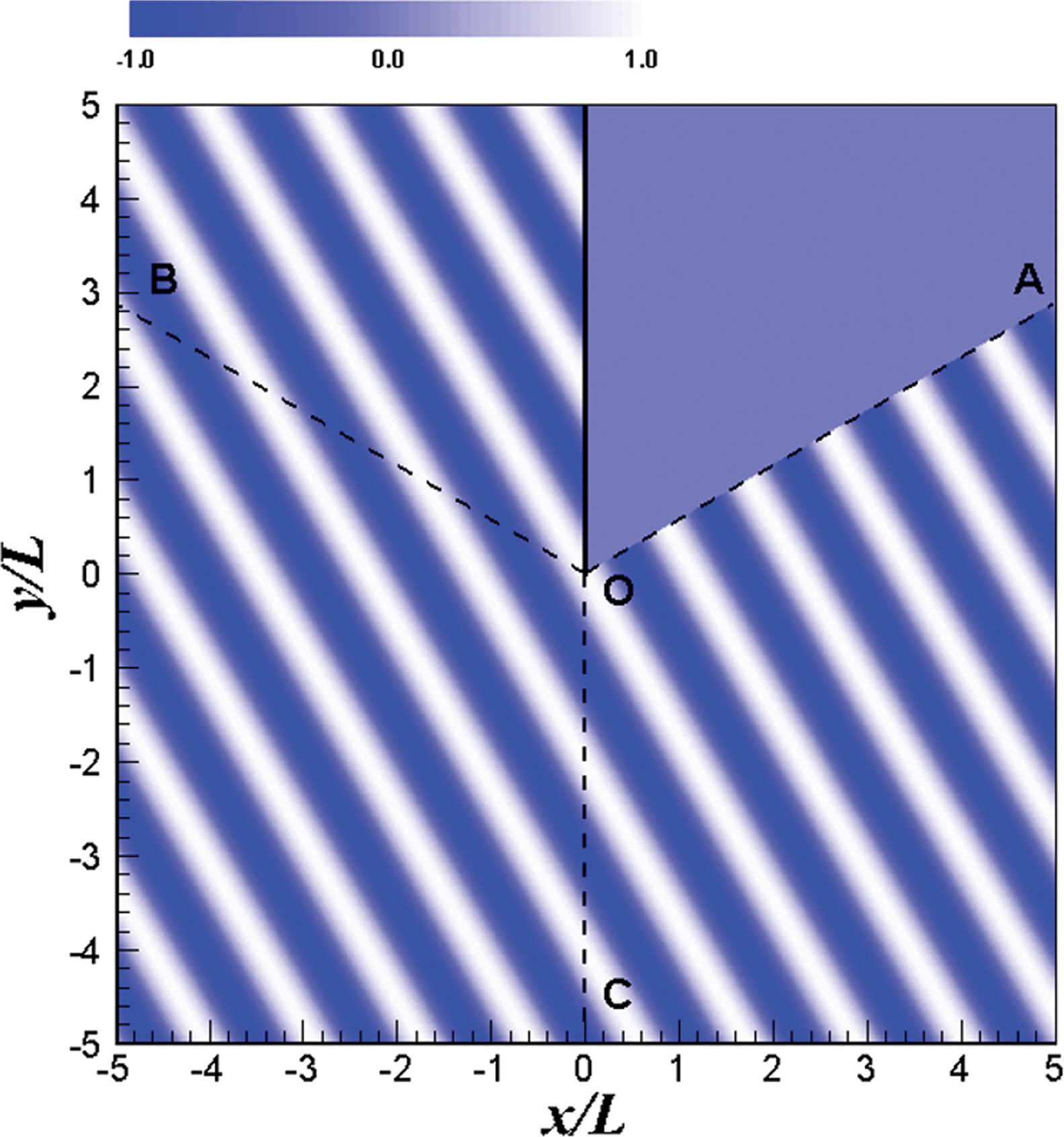
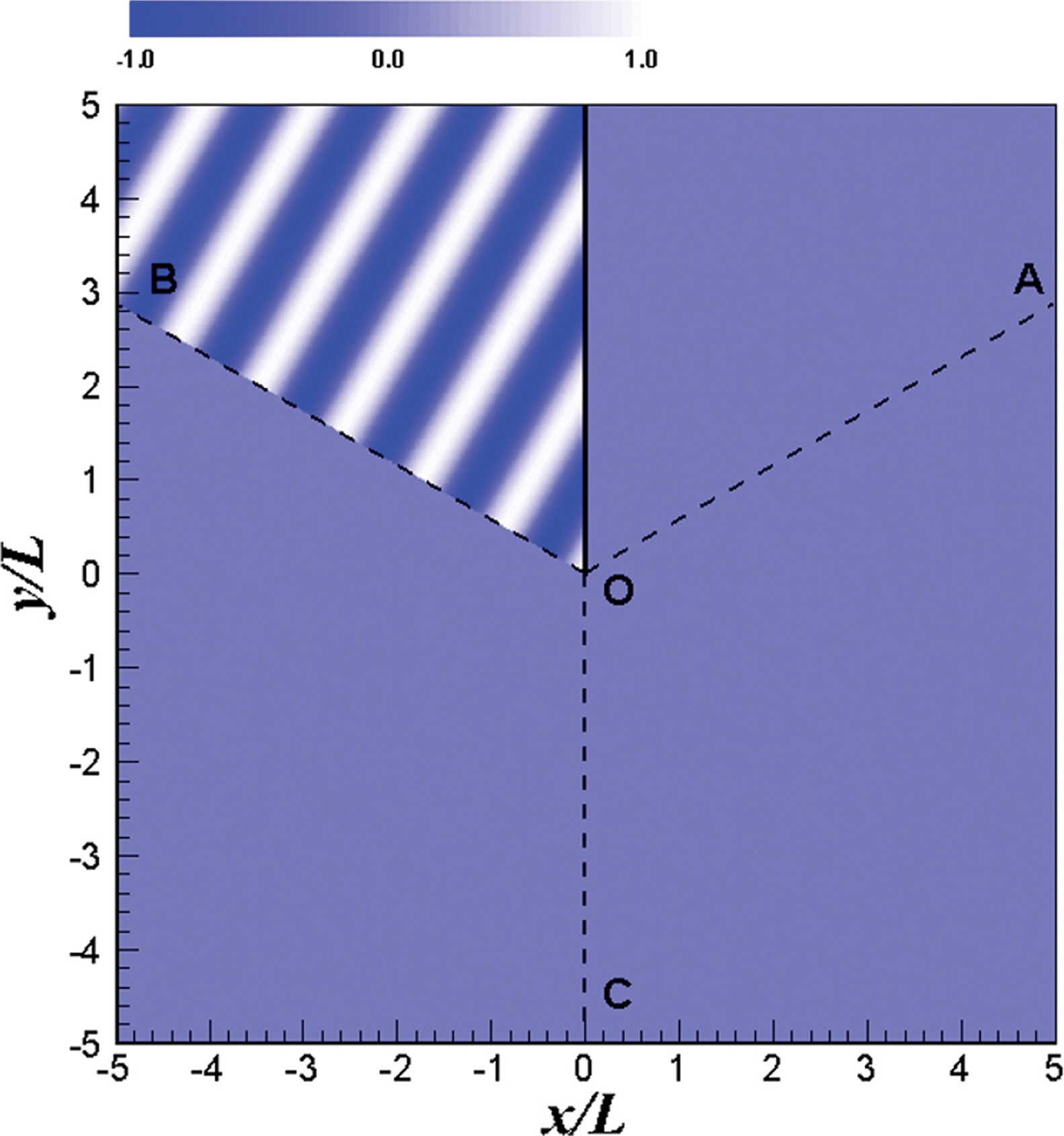
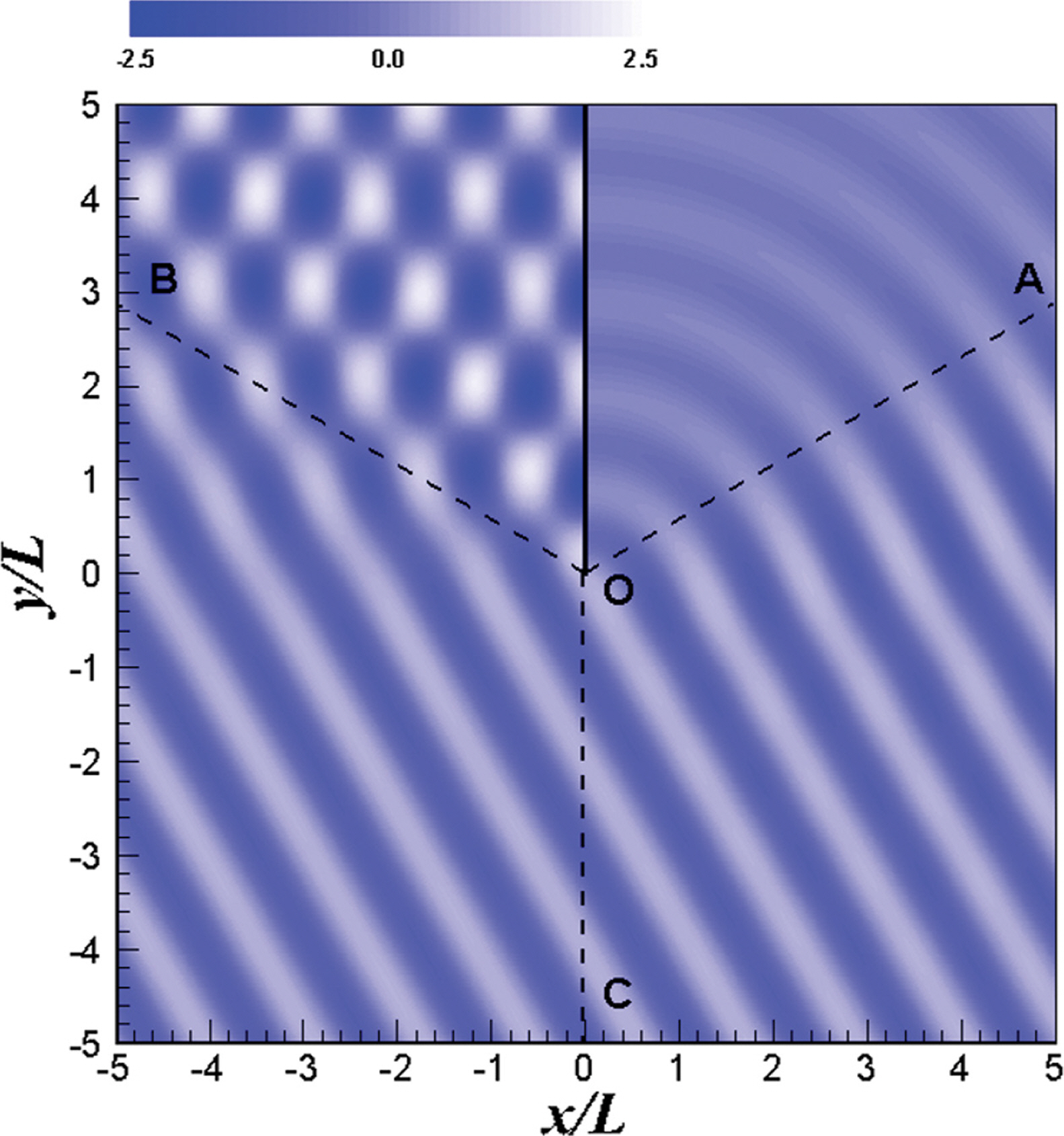
Fig. 3은 입사파의 자유수면변위이며, Fig. 4는 반사파의 자유수면변위, Fig. 5는 회절파의 자유수면변위 그리고 Fig. 6는 입사파, 반사파 및 회절파를 모두 포함하는 자유수면변위를 나타낸 그림이다. Fig. 3에서 입사파의 에너지 불연속 선은 O-A 이며, Fig. 4에서 반사파의 에너지 불연속 선은 O-B 이다. Fig. 5에서 회절파의 자유수면변위는 방파제 두부(O)를 기준으로 동심원상으로 전파하는 것을 볼 수 있다. Fig. 5의 O-A와 O-B에서 회절파 위상이 서로 반대인 것을 볼 수 있다. Fig. 3에서 O-A 아래쪽(Region Q)의 입사파 파봉(wave crest)에서는 O-A 위쪽 Region S로 에너지가 전파하여 회절파의 파봉이 형성된다. 입사파의 파곡에서는 반대로 O-A 위쪽 Region S의 수위가 Region Q의 파곡(wave trough) 보다 높으므로 Region Q로 회절파가 전파하여 파봉이 형성된다. 즉, O-A를 기준으로 Region S와 Region Q에서 회절파의 위상이 반대가 된다. 마찬가지로 Fig. 4에서 O-B 위쪽(Region R)과 아래쪽(Region Q)에서 반사파의 회절파가 형성되며, 역시 위상은 반대가 된다. 이와 같은 매커니즘으로 회절파가 방파제 주변 전체 영역에서 형성되는데, 방파제 전, 후면에서도 회절파 위상차이가 180도가 나며, 방파제의 연장선인 O-C의 양측에서도 회절파의 위상은 180도 차이가 난다. 이와 같은 현상은 Jung et al.(2016)도 언급한 바 있다. 반무한방파제 전면과 후면에서 회절파의 위상이 180도 차이가 난다는 것은 방파제 전면의 회절파 성분의 파봉이 위치하면, 방파제 후면에서는 반드시 파곡이 위치함을 뜻한다. 즉 회절파의 영향이 방파제 전면만 고려한 경우보다 후면까지 고려하면 2배가 됨을 알 수 있다.

반무한방파제 주변에서 무차원화된 진폭의 분포는 Fig. 7에 나타내었다. 특히 방파제 전면에서 입사파와 반사파의 중복파가 발생함으로 무차원화된 진폭은 약 2.0으로 계산되었다. 반면 회절성분의 영향에 의해 무차원화된 진폭은 방파제 전면에서 2.0을 중심으로 진동하는 경향을 보였다.

2.3 반무한방파제 배후에서 회절파의 근사화

파랑의 에너지는 회절에 의해 에너지 불연속면(O-A, O-B)으로부터 전파된다. 회절파의 파랑 에너지 감소는 에너지 불연속면으로부터 회절파 파봉을 따르는 원호의 길이에 의존한다. 에너지 불연속면으로부터 회절파의 파봉을 따르는 원호는 방파제 두부((x, y) = (0, 0))를 중심으로 하는 원호 형상이며, 이는 Fig. 8과 같다. 따라서, 다음과 같은 회절파 진폭의 관계식을 구할 수 있다.

(8)

ad2l=ad2r(π2-β)=constant

여기서, a_d는 회절파의 진폭, l은 에너지 불연속면으로부터 회절파 파봉을 따르는 원호의 길이를 나타내며, r은 방파제 두부로부터 떨어진 직선 거리를 나타낸다. 따라서, 회절파의 진폭은 다음 식과 같이 근사화할 수 있다.

(9)

ad=Cr(π2-β)

식(9)를 무차원화 하면 다음 식과 같다.

(10)

adai=CrL(π2-β)

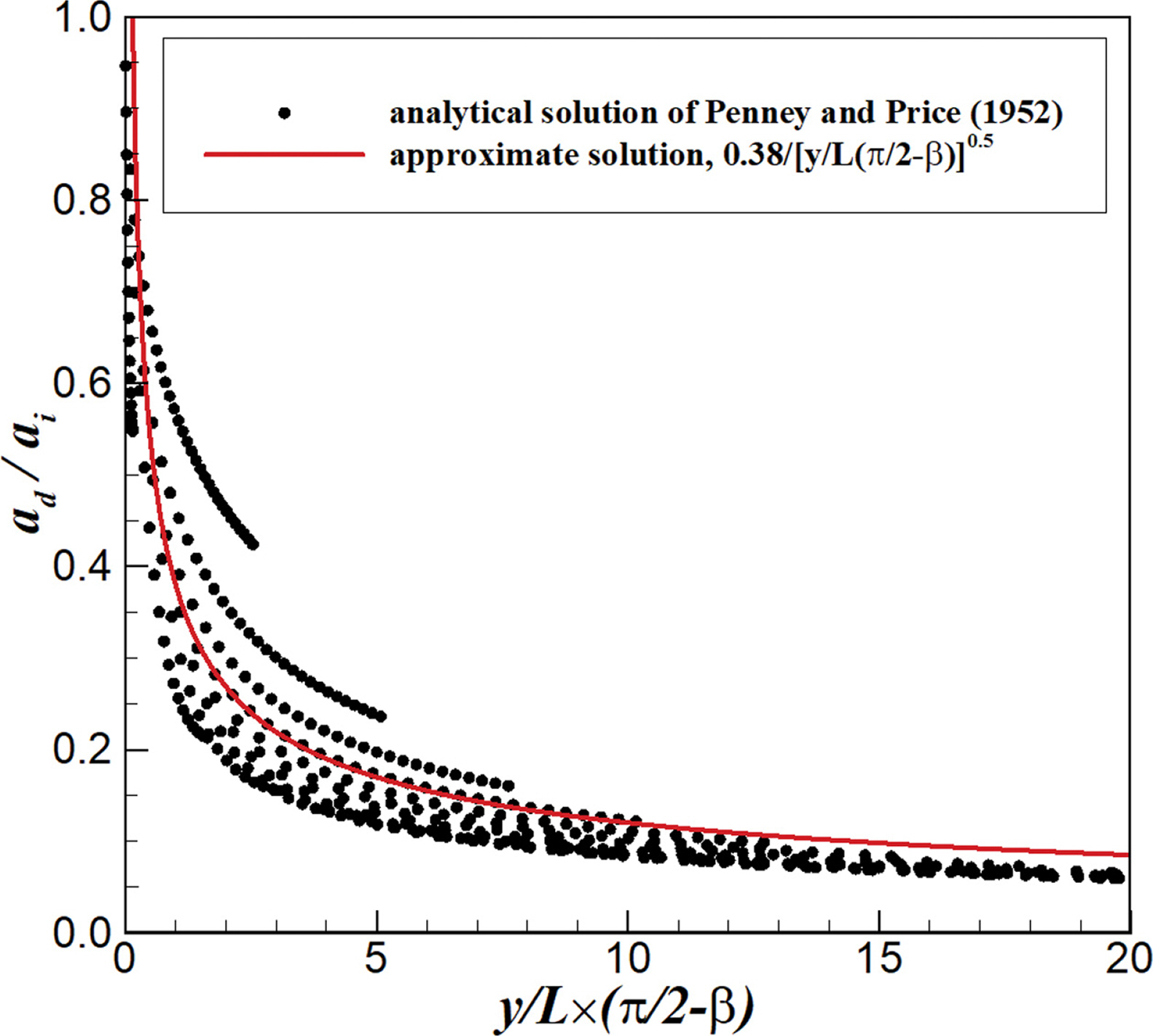
여기서, a_i는 입사파의 진폭, L은 입사파의 파장 그리고 C는 상수이다. Fig. 9는 무차원 변수 y/L(π/2 - β)에 따른 무차원화된 회절파 진폭(a_d/a_i)의 변화를 나타낸 그림이다. 그림에서 symbol은 식(2)를 이용하여 계산한 방파제 배후에서의 회절파 진폭을 나타낸다. 실선은 C/[r/L(π/2 - β)]^0.5 형태의 근사해로 평균제곱근오차가 최소가 되도록 best-fit한 결과이다. 근사식을 유도하기 위해 y/L = 1~15, ∆(y/L) = 0.05, β = -80° ~ +80° 및 ∆β = 10°인 조건에서 검토하였다. 평균제곱근오차가 최소가 되는 경우 상수 C는 0.38로 검토되었으며, 이 때 평균제곱근오차는 0.0028이다. 즉, 식(10)으로 주어진 회절파의 근사해는 방파제 배후에서 해석해와 매우 유사한 값을 가짐을 알 수 있다.

요약하면, 방파제 전면과 후면에서 파고(진폭)의 공간적인 진동은 회절에 의해 발생한다. 방파제 전면에서 회절파에 의한 파고의 공간적인 진동은 입사파 및 반사파의 중복파에 의한 파력보다 더욱 큰 파력을 야기할 수 있다. 다시 말해서, 회절파는 방파제 두부((x, y) = (0, 0))를 중심으로 동심원상으로 위상이 변화하며, 입사파 및 반사파는 평면상에서 직선적인 파향을 따라 위상이 변화한다. 따라서, 입사파, 반사파 및 회절파의 총 진폭은 에너지 불연속면으로부터 떨어진 거리에 따라 진동하게 된다. 방파제의 전면과 후면에서 회절파의 진폭은 에너지 불연속면으로부터 회절파 파봉을 따라 y(π/2 - β) 만큼 떨어진 방파제 법선을 따라 변화한다. 회절파의 에너지 감소 정도는 에너지 불연속면으로부터 회절파 파봉을 따라 떨어진 거리에 비례한다. 따라서, 방파제 전,후면에서 회절파의 진폭은 y(π/2 - β)^0.5에 반비례한다.

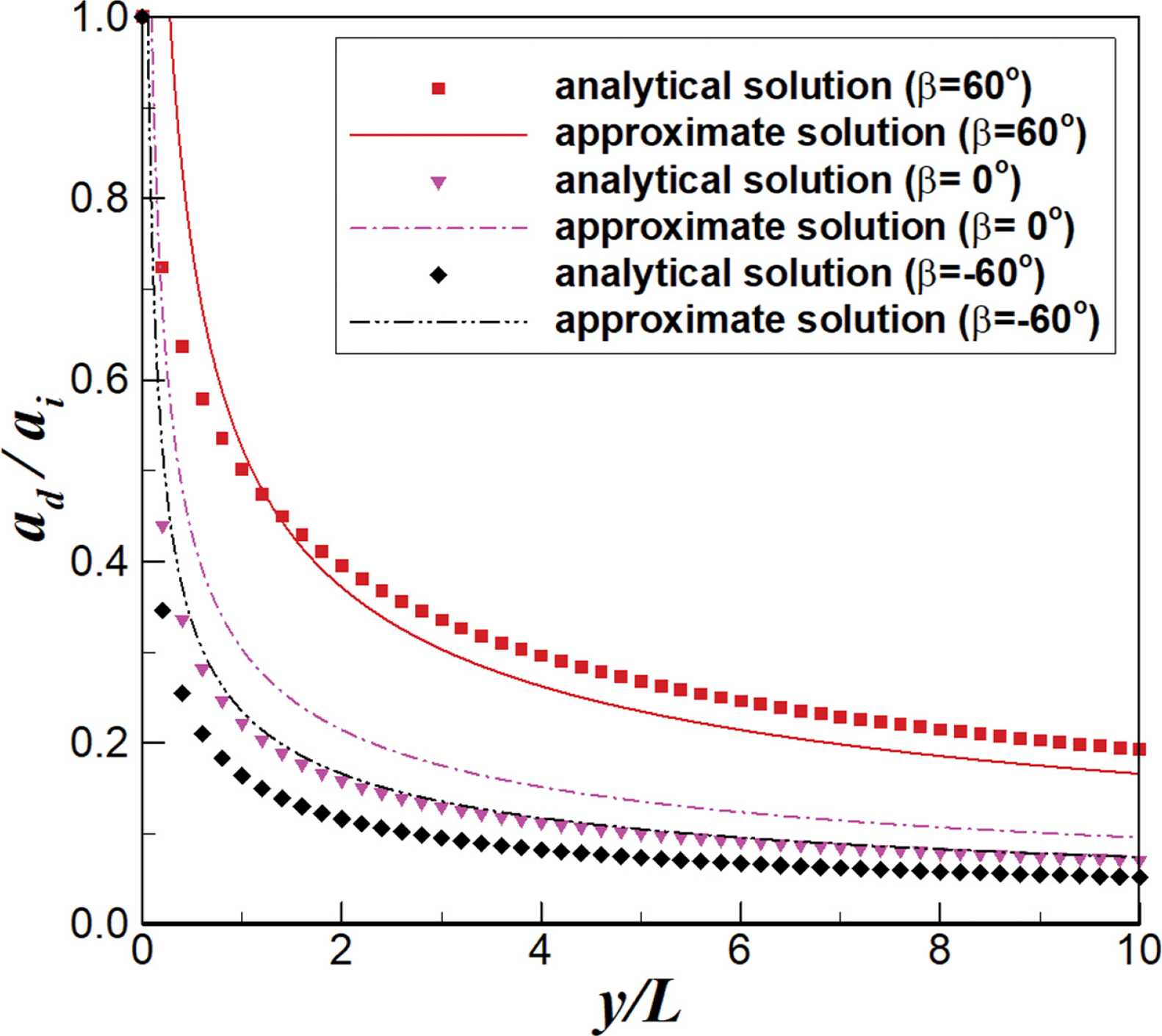
방파제 배후에서의 상대 위치(y/L)를 고정하고 입사파의 입사각(β)에 따른 회절파의 무차원화된 진폭을 Fig. 10에 나타내었고, 입사파의 입사각(β)을 고정하고 방파제 배후에서의 상대 위치(y/L)에 따른 회절파의 무차원화된 진폭은 Fig. 11에 나타내었다. Fig. 10에서 입사파의 파향이 양수인 경우 방파제 배후의 Shadow zone의 폭이 좁으므로 회절파의 진폭은 크게 나타났고, 입사파의 파향이 음수인 경우에는 Shadow zone의 폭이 넓어 회절파의 진폭은 감소하였다. Fig. 10에서 본 연구에서 제시한 근사해는 방파제 배후에서의 상대 위치(y/L)가 3.0인 경우가 다른 경우에 비해 해석해와 비교적 일치하는 경향을 보였다. 그리고 입사각(β)이 0.9~1.0(50~60도) 근처에서 해석해와 근사해는 특히 일치하였다. Fig. 11에서 입사각(β)이 60도인 경우 근사해와 해석해는 비교적 일치하는 경향을 보였다. 전반적으로 방파제 배후에서의 상대 위치(y/L)가 증가할수록 근사해와 해석해는 더욱 일치하였다.

3. 회절에 따른 반무한방파제 주변 파력의 공간적인 변화

3.1 회절에 따른 반무한방파제에 작용하는 파력

회절에 의한 방파제 전, 후면의 파력차를 고려하여 반무한 방파제에 작용하는 파력은 선형파 이론을 사용하여 Jung et al.(2016)에 의해 유도되었다. 방파제의 폭이 0인 경우 방파제 전, 후면의 파력차를 고려한 파력 및 무차원 파력은 다음 식과 같다(Jung et al., 2016).

(11)

Pt=Pf-Pl=ρghtanhkhkhai(1+Kr)(1-2ℱ)ei(ωt-kysinβ)

(12)

Pr,t=|1-2ℱ|

(13)

Pr,f=|1-ℱ|

(14)

Pr,l=|ℱ|

여기서,

(15)

ℱ=f(ψ)=12(1+i)∫-∞ψe-π2iu2du

(16)

ψ=2kyπsin2[12(β-π2)]

식(11)~(16)에서, P_t는 회절에 따른 방파제 전, 후면의 파력차를 고려한 파력, P_{r, t}는 회절에 따른 방파제 전, 후면의 파력차를 고려한 무차원 파력, P_{r, f}는 회절을 고려한 방파제 전면의 무차원 파력 그리고 P_{r, l}은 방파제 후면에 작용하는 회절파의 무차원 파력을 각각 나타낸다.

3.2 반무한방파제 주변 파력의 공간적인 변화

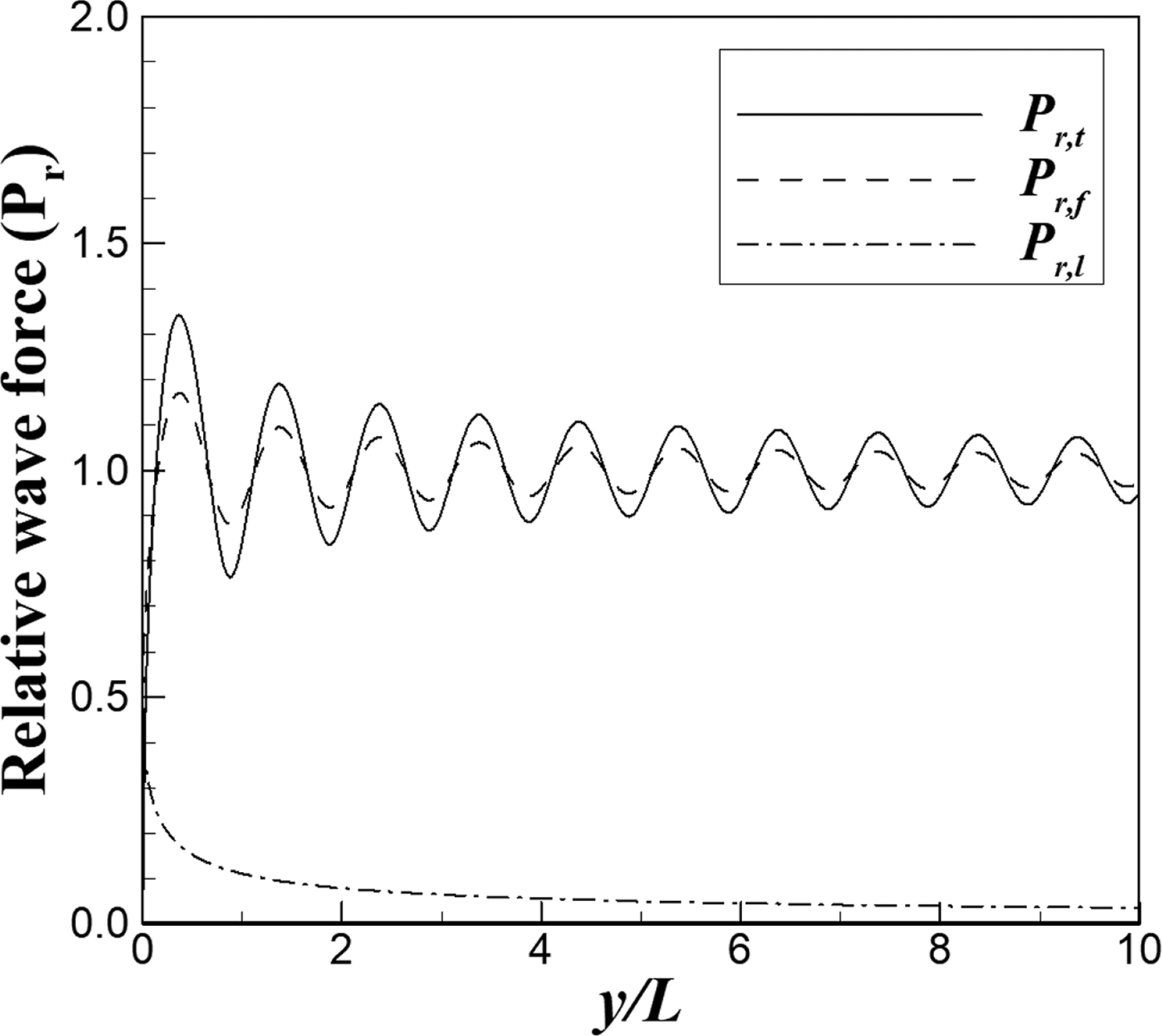
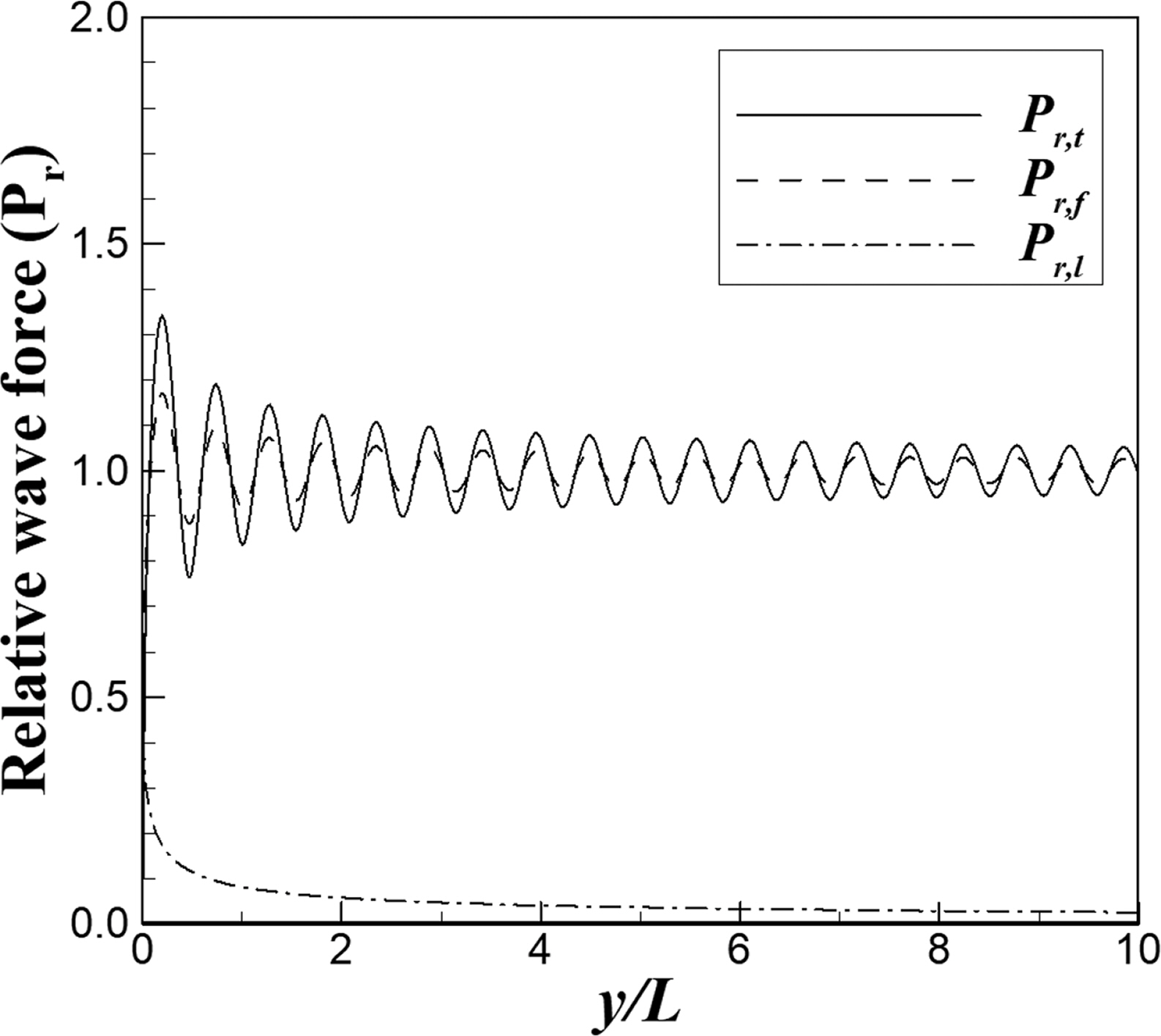
회절에 따른 반무한방파제 주변에 작용하는 파력의 공간적인 변화를 식(12)~(16)을 이용하여 계산하였다. 수치해석을 위한 입사파랑의 파고는 1.0 m, 주기 10초, 수심 10 m 이며, 방파제 전면 및 후면의 y 방향 공간격자 크기는 ∆y = 0.02L이다. 방파제 전면에서의 반사율(K_r)은 완전반사 조건인 1.0을 적용하였다. 방파제에 작용하는 무차원 파력의 계산 결과는 Figs. 12~14와 같다. Fig. 12는 입사각(β)이 60도인 경우이고, Fig. 13은 입사각이 0도 그리고 Fig. 14는 입사각이 -60도인 경우에 파력분포를 나타낸 그림이다. 각 그림에서 실선은 전, 후면 파력차를 고려한 무차원파력(P_{r, t}), 파선은 전면에 작용하는 무차원 파력(P_{r, f}) 그리고 일점쇄선은 후면에 작용하는 무차원 파력(P_{r, l})을 각각 나타낸다. Jung et al.(2016)의 결과와 마찬가지로 Figs. 12~14에서 입사각이 클수록 전, 후면 파력차를 고려한 무차원파력(P_{r, t})과 전면에 작용하는 무차원 파력(P_{r, f})의 진동하는 파장은 더욱 길게 나타났다. 방파 후면에 작용하는 무차원 파력(P_{r, l})은 입사각이 클수록 더욱 상대적으로 크게 검토되었다.

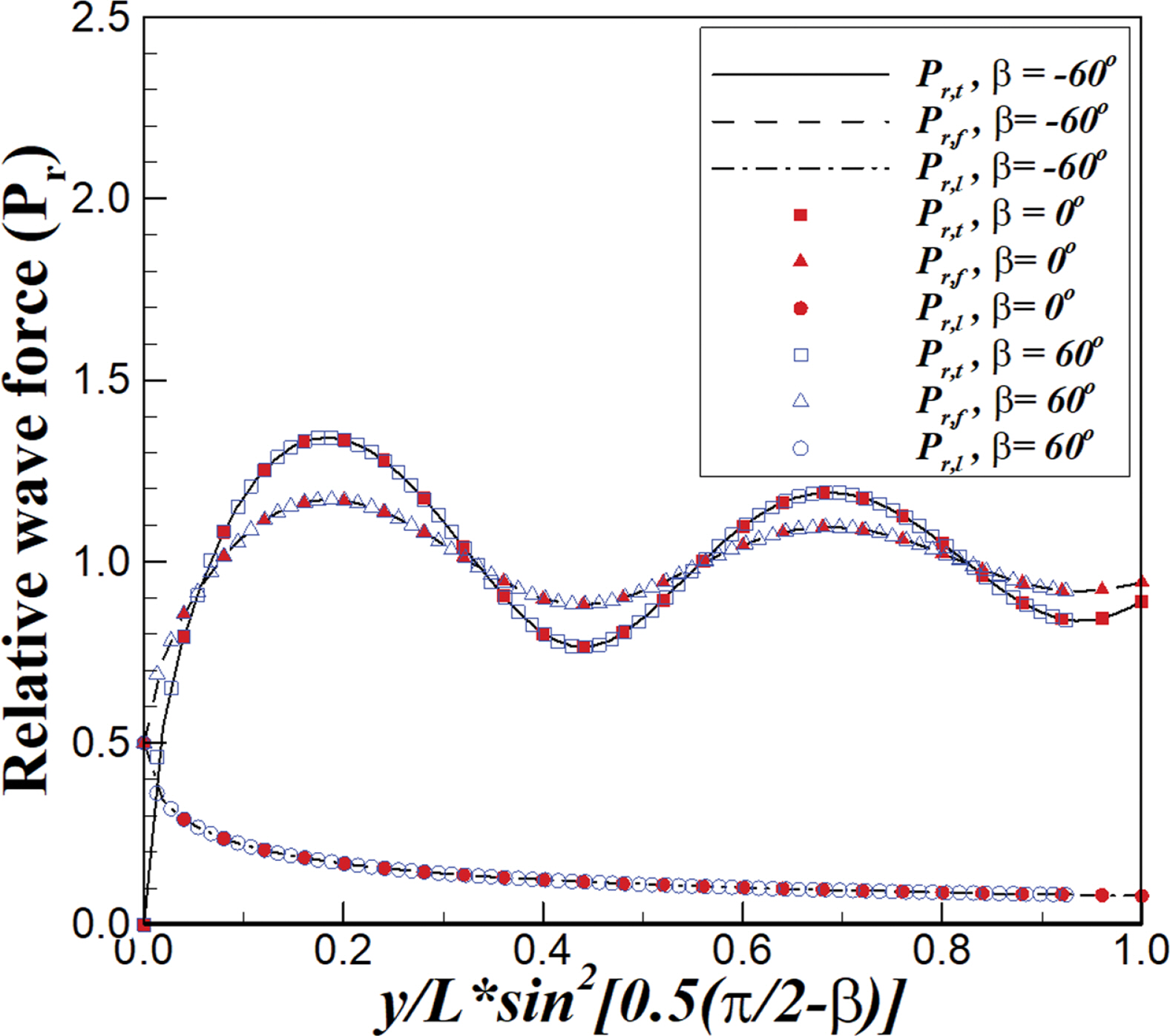
새로운 무차원 변수를 이용하여 회절에 따른 반무한방파제에 작용하는 파력의 공간분포를 검토하였다. 식(12)~(14)에서 방파제 전, 후면 파력차를 고려한 무차원 파력, 방파제 전면 및 후면에서의 무차원 파력은 모두 함수 F로 표현된다. 그리고, 식(15) 및 (16)에서 함수 F는 yLsin2[12(β-π2)]의 함수임을 알 수 있다. 따라서, 본 연구에서는 두가지 변수, 즉 방파제 두부로부터 상대위치(y/L) 및 입사파랑의 입사각(β)을 이용한 무차원 변수에 대한 상대파력을 검토하였으며, 이를 Fig. 15에 나타내었다. Fig. 15에서 무차원 변수 yLsin2[12(β-π2)]에 대한 상대파력은 입사각(β)에 관계없이 모두 동일하게 나타남을 볼 수 있다. 즉, 항만 관련 실무자들이 반무한방파제에서 무차원 변수 yLsin2[12(β-π2)]만 알고 있으면 Fig. 15를 이용하여 방파제에 작용하는 상대파력을 매우 쉽게 찾아낼 수 있다.

4. 결 론

본 연구에서는 새로운 무차원 변수를 도입하여 반무한방파제에 작용하는 전, 후면 파력차를 고려한 무차원 파력(P_{r, t}), 전면에 작용하는 무차원 파력(P_{r, f}) 및 후면에 작용하는 무차원 파력(P_{r, l})에 대해 검토하였다. 방파제에 내습하는 입사파랑의 입사각(β)이 클수록 전, 후면 파력차를 고려한 무차원 파력(P_{r, t})과 전면에 작용하는 무차원 파력(P_{r, f})의 진동하는 파장은 더욱 길게 나타났으며, 방파제 후면에 작용하는 무차원 파력(P_{r, l})은 입사각이 클수록 더욱 상대적으로 크게 검토되었다. 무차원 변수에 대한 상대파력은 입사각(β)에 관계없이 모두 동일하게 나타났으며, 본 무차원 변수를 실무자들이 이용할 경우 매우 쉽게 반무한 방파제에 작용하는 파력에 대해 검토가 가능할 것으로 생각된다.

반무한방파제 전면과 후면에서 회절파의 공간적인 변화