1. 서 론
지각 내부에서 발생하는 단층파괴 현상은 파열속도 및 승강속도를 이용하여 동적 거동 특성을 나타낼 수 있다. 파열속도는 단층파괴가 한 지점에서 발생하여 이웃하는 단층으로 전파하는 속도를 나타내며, 승강속도는 파괴면을 따라 단층이 올라가거나 내려가는 속도를 의미한다. 이러한 단층파괴의 동적거동은 해저면의 변화에도 영향을 미치며, 지진해일의 초기파형 형성을 거쳐 최종적으로 연안에서의 최대 처오름 높이에 큰 변화를 준다.
단층파괴와 관련된 연구는 단층의 파괴현상 자체에 초점을 둔 연구와 단층의 파괴현상으로 인해 발생한 지진해일의 생성 및 전파에 관한 연구로 구분된다. Ammon et al.(2005) 및 Ishii et al.(2005)은 다양한 관측자료를 바탕으로 2004년 Sumatra-Andaman 지진 발생시 다양한 단층파괴 특성을 분석하였으며 Fujii and Satake(2007) 및 Rhie et al.(2007)은 동일한 지진에 대해 조위계 및 위성관측 자료를 이용하여 단층의 파열속도 및 매개변수와 관련된 연구를 수행하였다. Maercklin et al.(2012)은 2011 Tohoku 지진 발생시 가속도계에서 측정된 자료에 backprojection 기법을 적용하여 단층 파괴 양상을 분석하였으며 Satake et al.(2013)은 다수의 소단층을 이용하여 동일한 지진에 대해 단층의 미끄럼 값을 파악하였다.
단층의 파괴는 해저 지면에 영향을 주어 수심변화를 야기시키며 이러한 수심변화는 바로 위에 있는 수체에 영향을 주어 지진해일의 초기파형을 형성한다. 이와 관련된 기존의 연구는 대부분 수동적 발생(passive generation)을 가정하여, 해저 지형의 변화와 자유 수면의 변화가 동일하다고 놓고 지진 해일의 전파를 해석하였으나 이는 경우에 따라 많은 오차를 유발하기도 한다. Hammack(1973)은 선형파 이론에 Fourier 및 Laplace 변환을 적용하여 바닥의 변화가 자유수면에 미치는 영향을 이론적으로 해석하였다. 그의 해석해를 활용하면 바닥의 상승 속도(또는 단층의 상승속도)가 느린 경우에는 바닥의 변화 양상과 자유 수면의 변화 양상이 매우 다르다는 것을 확인할 수 있다. Dutykh et al.(2006), Dutykh and Dias (2007), Kervella et al.(2007), Dutykh et al.(2013), Gal et al.(2017), Jung and Son(2018) 및 Gal et al.(2018) 등은 Hammack의 해석해를 확장하여 단층의 파열속도 및 증강속도가 지진해일 초기파형의 생성 및 전파에 미치는 영향을 검토하였다.
해석해를 이용한 연구는 단순화된 지형 조건에서 수행된 반면 실제 지진해일 사례에 대해서는 주로 수치 모델을 활용한 연구가 활발히 진행되었다. Ohmachi et al.(2001)은 단층파괴에 대한 해석해와 수체운동에 관한 수치해를 결합하여 단층의 동적 거동이 지진해일의 생성 및 전파에 미치는 영향을 검토하였으며, Grilli et al.(2007)은 다양한 단층의 매개변수 및 파열속도에 대해 Boussinesq 수치모형의 결과와 관측치를 비교하여 매개변수 및 파열속도를 설정한 후 상세 수치모의를 수행하였다. Suppasri et al.(2010)은 2004년 인도네시아 지진에 대해 단층의 파열속도를 고려한 수치모의를 수행하여 파열속도가 지진해일의 처오름 높이 및 도달시간에 미치는 영향을 검토하였으며 Imai et al.(2010)은 2011년 동일본 지진에 대하여 수치모의를 통해 시간차를 지닌 단층파괴가 해안에서의 지진해일의 처오름 높이에 미치는 영향을 분석하였다.
단층의 동적 거동에 대한 분석이나 이러한 동적 거동이 지진해일의 생성 및 전파에 미치는 영향이 국외에서는 다양하게 시도되었으나 국내에서는 아직 제대로 된 연구가 수행되지 않았다. Jung and Son(2020)은 최초로 1993년 홋카이도 지진해일에 대해 시간차를 지닌 단층파괴가 동해안의 처오름 높이에 미치는 영향을 분석하였으나 이 때 사용한 소단층의 매개변수가 모두 다르기 때문에 시간차에 의한 단층파괴가 지진해일에 미치는 영향에 대한 분석이 체계적으로 이루어지지 않았다. 따라서, 본 연구에서는 Jung and Son(2020)의 연구에 대한 보완으로 단층의 배치를 남북 및 동서인 경우로 구분하고 소단층의 매개변수도 모두 동일하게 하여 단층의 동적 거동과 배열이 지진해일의 전파에 미치는 영향을 분석하였다.
2. 수치 모의
2.1 수치모형
지진해일은 수심에 비해 파장이 매우 크기 때문에 장파의 가정이 유효하다. 따라서 대부분의 지진해일 전파모형은 천수방정식을 지배방정식으로 하고 있으며 대표적으로는 NOAA (The National Oceanic & Atmospheric Administration)에서 개발한 MOST(Method Of Splitting Tsunami)모형과 Cornell 대학에서 개발한 COMCOT(COrnell Multi-grid COupled Tsunami model)이 있다. 본 연구에서는 현재 국내에서 가장 활발하게 사용되고 있는 COMCOT 모형을 이용하여 수치모의를 수행하였다. COMCOT 모형은 구형 좌표계 및 직교 좌표계 모두에 대해 선형 또는 비선형 천수방정식을 이용하여 해석이 가능하다. 일반적으로 심해에서 발생하여 전파하는 지진해일의 경우에는 구형좌표계에서 선형 천수방정식을 주로 사용하며 국부지역에서의 파랑해석은 직교좌표계에서 비선형 천수방정식을 많이 사용한다. 각각에 대한 지배방정식은 다음과 같이 나타낼 수 있다.
선형천수방정식(구형좌표계):
비선형천수방정식(직교좌표계):
위의 지배방정식으로부터 수치해를 구하기 위해 교호격자체계에 Explicit leap-frog 유한차분법을 적용하였으며 자세한 내용은 Wang(2009) 및 Wang and Power(2011)의 보고서에 기술되어 있다.
2.2 격자구성 및 단층정보
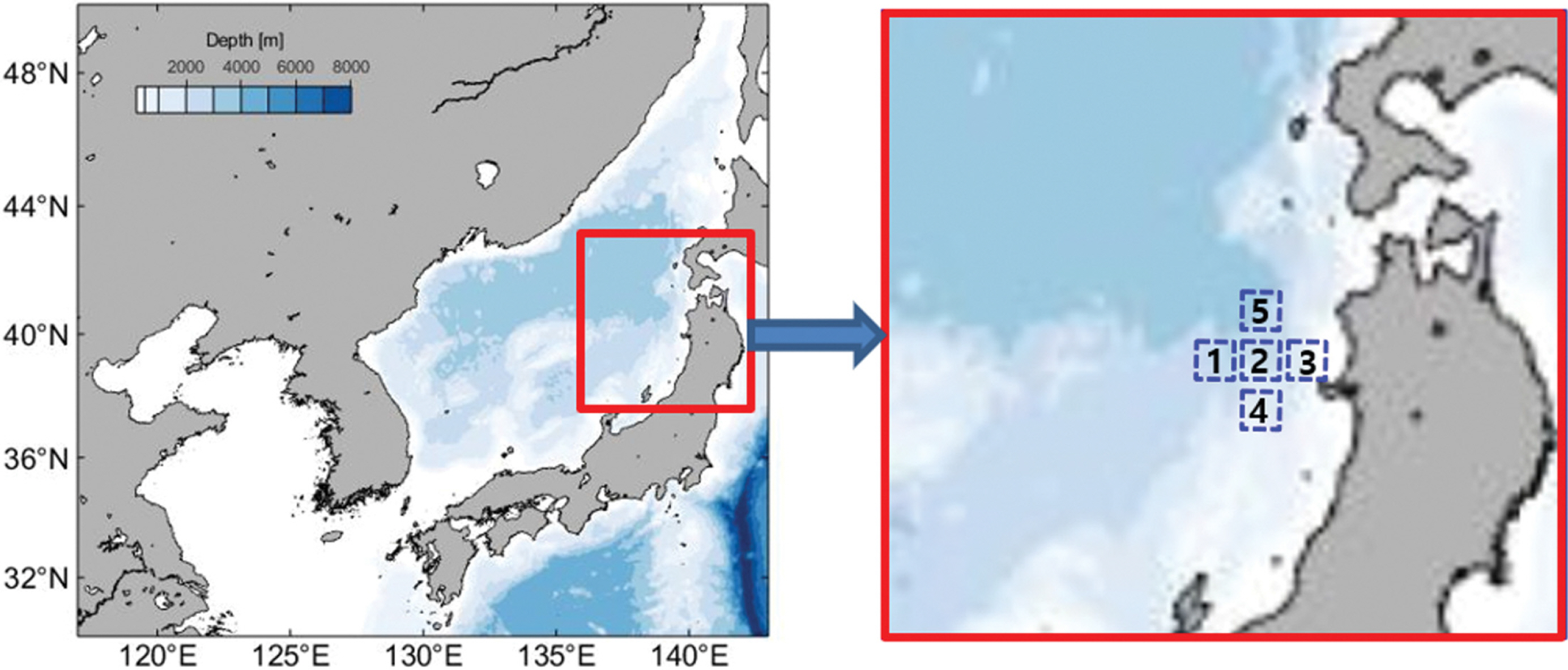
지진해일파의 생성, 전파 및 연안에서의 처오름을 모두 고려하기 위하여 4단계의 격자체계가 사용되었다. Layer1은 Fig. 1의 왼쪽 영역을 의미하며, 그림에서 보는 바와 같이 동해안과 지진발생지점을 모두 포함하는 광역이다. Layer2, 3 및 4의 격자 크기는 상위 격자의 1/4 크기로 구성하였으며 모든 격자의 위치 및 크기는 Table 1에 나타나있다. 격자망을 구성하는데 필요한 수심자료는 NOAA(National Oceanic and Atmospheric Administration)에서 제공하는 ETOPO2를 사용하였다.
Fig. 1의 오른쪽에 있는 그림은 각각의 소단층 위치를 나타낸다. 남북방향 및 동서방향으로 진행되는 단층파괴를 모의하기 위하여 총 5개의 소단층을 사용하였으며 지진을 모의하기 위한 소단층의 매개변수는 Table 2와 같이 모두 동일하게 고정한 후에 소단층의 위경도 좌표만 변경하여 5개를 구성하였다. 단층 파괴에 의한 해저 지형의 변화는 Okada (1985) 모형을 사용하여 계산하였으며, 해저 지형의 변화에 의한 지진해일의 초기 파형은 Passive 가정을 사용하여 해저 지형의 변화와 동일하다고 가정하였다.
2.3 처오름 높이 계산
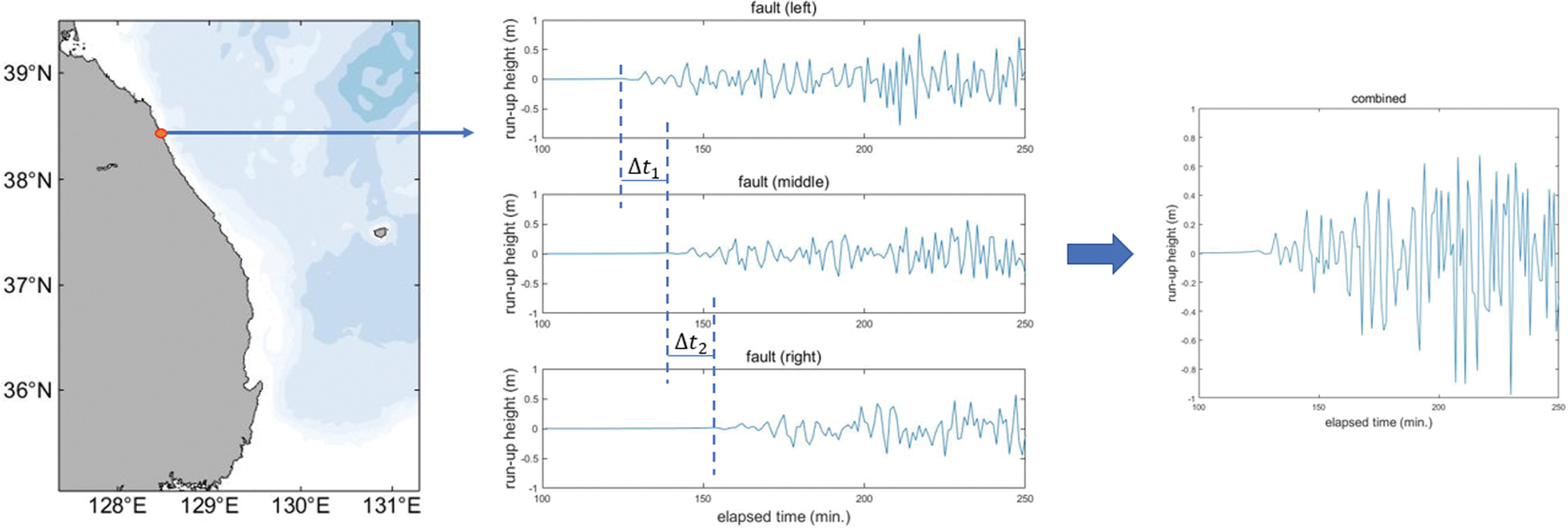
3개의 소단층을 이용하여 시간차를 지닌 단층 파괴 활동을 고려하였다. 이웃한 단층파괴활동 간의 시간차는 1분간격으로 0분부터 60분까지 고려하여 하나의 단층파괴 시나리오에 대하여 총 3,721개의 경우가 있으며 단층파괴 진행방향 시나리오는 서에서 동, 동에서 서, 남에서 북 및 북에서 남으로 총 4가지가 있다. 따라서 총 경우의 수는 14,884로 설정된다. 모든 경우에 대하여 수치모의를 수행하기에는 제약이 있어 본 연구에서는 선형 중첩방법(Imai et al., 2010)을 이용함으로써 효율성을 높였다. 각각의 소단층을 이용하여 지진해일파를 생성하고 연안에서의 처오름을 계산한 뒤에 시간차를 두면서 선형중첩하여 최종적인 처오름 높이를 계산하였다. Fig. 2는 동서방향으로 단층 파괴가 발생하는 경우에 동해안의 한 지점에서 처오름 높이를 계산하는 과정을 나타낸 그림이다. ∆t1 및 ∆t2는 각각 첫번째 소단층파괴와 두번째 소단층파괴, 그리고 두번째 소단측파괴와 마지막 소단층파괴 사이의 시간차를 의미한다. 이를 중첩하면 Fig. 2의 우측 그림과 같이 최종적인 처오름 높이에 관한 시계열 자료를 구할 수 있으며 이를 이용하여 해당 지점에서의 최대 처오름 높이를 구할 수 있다. 동해안 연안을 따라 총 6507 지점에 대해 위와 같은 방법을 사용하여 최대 처오름 높이를 구하였으며 다음과 같이 정의되는 기하평균값을 이용하여 정량화하였다.
여기서, Hmax, i는 i번째 해안지점에의 최대 처오름 높이를 의미하며, N은 측정 지점의 총 개수를 의미한다.
3. 결과 분석
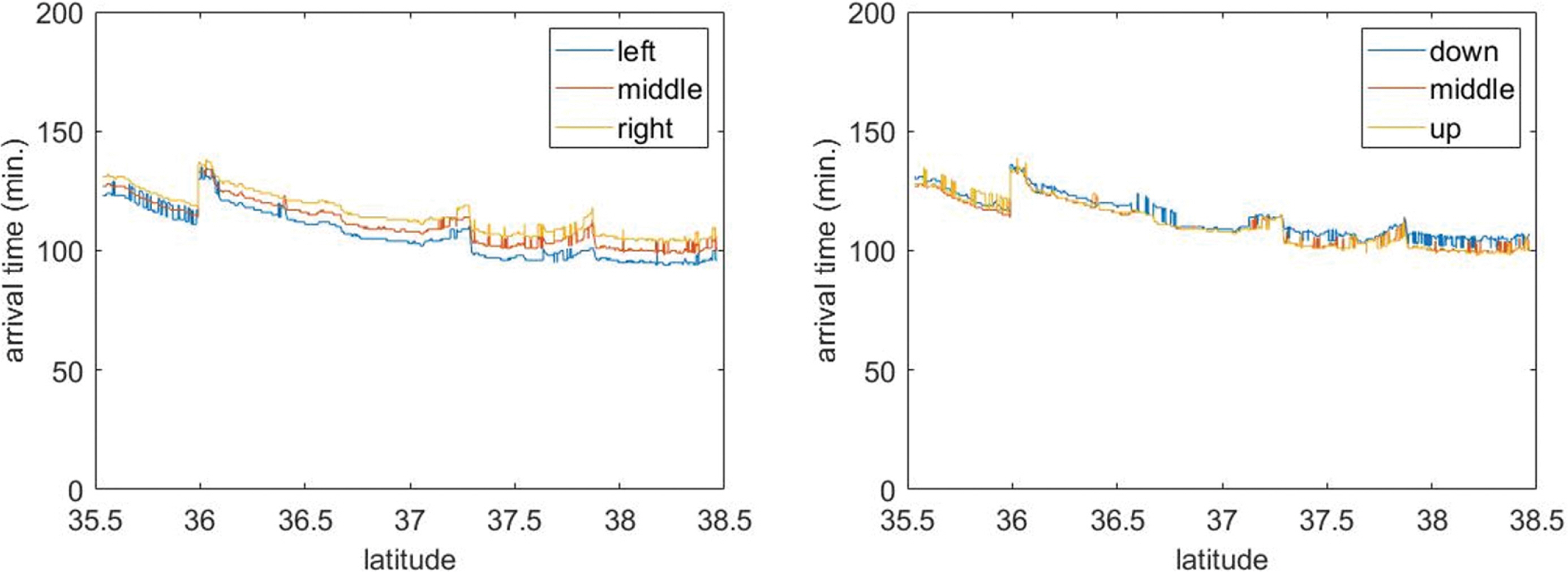
단층 위치에 따른 연안에서의 지진해일 도달시간 및 최대 처오름 높이를 그림으로 나타내보면, Fig. 3(a) 및 4(a)는 동서로 위치한 경우에 대한 결과이며, Fig. 3(b) 및 4(b)는 남북으로 위치한 경우에 대한 결과이다. 단층이 동서로 위치한 경우에는 위치에 따라 도달시간의 차이는 있었으나 처오름 높이는 별다른 차이를 보이지 않았으며 남북으로 위치한 경우에는 반대로 도달시간에는 큰 차이를 보이지 않았으나 처오름 높이는 위치에 따라 차이가 났다. 동서로 위치한 경우 동쪽에 위치한 소단층에서 발생한 지진해일이 해안으로부터 가까워 가장 빨리 도달하였으며 서쪽에 위치한 소단층에서 발생한 지진해일이 가장 늦게 도달하였다. 남북으로 위치한 경우에는 남쪽에 위치한 소단층에서 발생한 지진해일이 상대적으로 큰 처오름 높이를 보였다. 모든 경우에 대해 위도 37도와 37.5도 사이의 지점에서 최대 처오름 높이를 보였으며, 이는 지진 발생지점과 동해안 사이의 지형적인 특성에 의한 영향으로 유추될 수 있다. 고위도에서 저위도로 갈수록 진앙에서 멀어져 도달시간이 증가하였으나 위도 36도 부근에서는 돌출 지형의 영향으로 갑작스럽게 감소한 후에 다시 증가하였다.
한편, Fig. 5는 이웃한 단층파괴 사이에 시간차를 두면서 기하평균값을 계산한 결과이다. Fig. 5(a) 및 (b)는 각각 서쪽에서 동쪽으로, 동쪽에서 서쪽으로 단층파괴가 발생하는 경우이며 Fig. 5(c) 및 (d)는 각각 남쪽에서 북쪽으로, 북쪽에서 남쪽으로 단층파괴가 발생하는 경우에 대한 결과이다. 소단층파괴간 시간차가 작은 경우에는 중첩 효과로 인하여 최대 처오름 높이의 기하평균값이 크게 나왔으나 시간차가 큰 경우에는 중첩의 효과가 거의 발생하지 않아 전체적으로 작은 값이 나왔다. Fig. 5(b)의 경우에는 다른 결과와는 다르게 ∆t1 = 5 min 또는 ∆t2 = 5 min을 기준으로 큰 기하평균값이 발생하였다. Fig. 1을 보면 단층이 위치한 지점에서의 수심값은 대략적으로 3,000 m되며, 이 때의 지진해일파 전파속도는 171 m/s가 된다. 따라서 이웃한 단층까지 도달하는데 대략적으로 5분 정도가 된다. 처오름 높이 관측지점(동해안)이 지진해일 발생지점을 기준으로 서쪽에 위치하고 있기 때문에 동쪽에 위치한 단층에서 발생한 지진해일이 서쪽으로 진행하면서 가운데에 위치한 단층에 의한 지진해일파와 중복이 발생한 경우와 가운데에 위치한 단층에 의한 지진해일파가 서쪽에 위치한 단층에 의해 발생한 지진해일파와 중복이 발생한 경우로 해석할 수 있다. 이러한 특징은 서쪽에서 동쪽으로 단층파괴가 발생하는 경우나 남북으로 단층파괴가 발생하는 경우에는 두드러지게 발생하지 않았다.
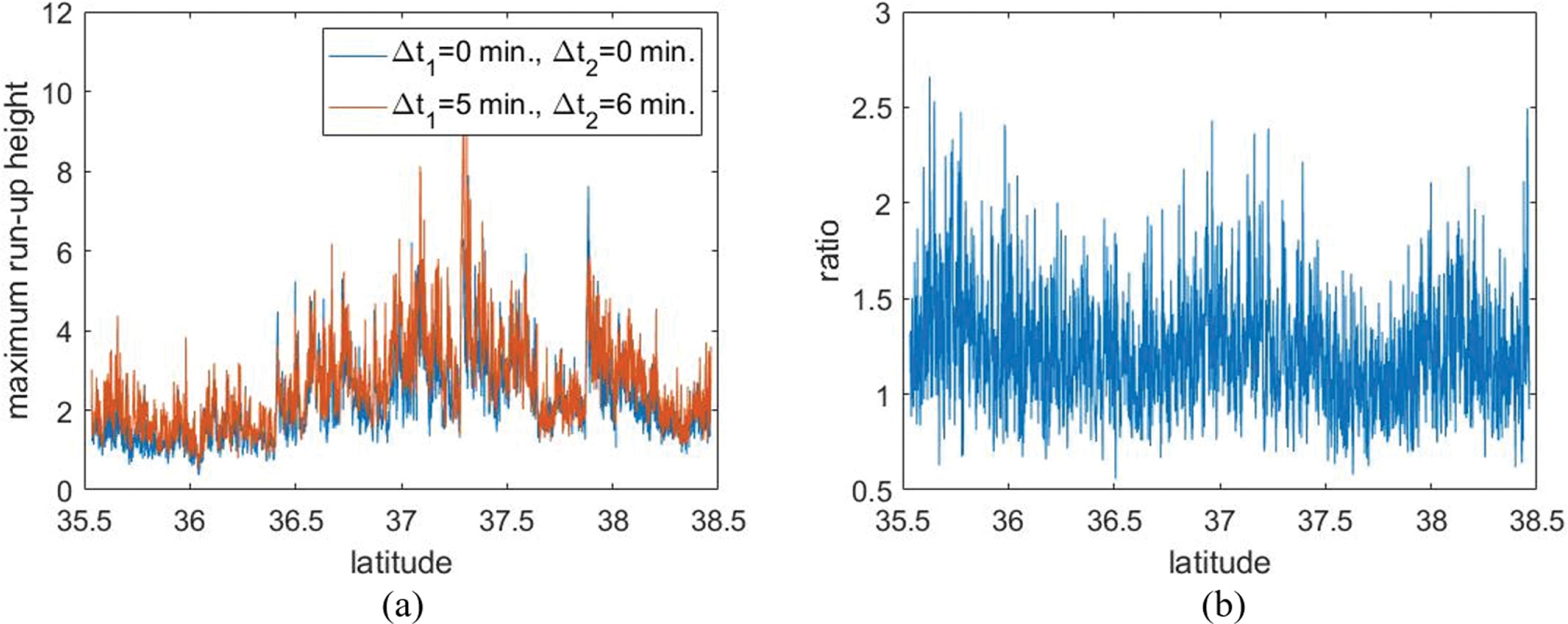
Fig. 5의 결과에서 가장 큰 값을 보여주는 경우(∆t1 = 5 min, ∆t2 = 6 min)에 대하여 최대 처오름 높이를 구한 후 시간차를 고려하지 않은 경우(∆t1 = ∆t2 = 0 min)의 결과와 비교해보았다. Fig. 6(a)는 최대 처오름 높이를 계산한 결과이며 Fig. 6(b)는 두 경우의 비를 그린 결과이다. 지진해일파 사이의 중첩이 크게 발생한 경우에는 전 위도에 걸쳐 처오름 높이가 증가하였으며 대부분의 경우에 시간차를 두지 않은 경우에 비하여 1.5배 이상 증가하였으며 지역에 따라서는 2.5배 이상 증가하기도 하였다.
4. 토의 및 결론
시간차를 지니고 단층파괴가 발생하는 경우에 대하여 단층파괴의 동적거동이 연안에서의 처오름 높이에 미치는 영향을 검토하였다. 다수의 단층을 동서 및 남북방향으로 배치하여 동에서 서, 서에서 동, 남에서 북 및 북에서 남으로의 단층파괴 진행방향을 고려하였으며 이웃한 단층간에 발생하는 단층파괴 시간차는 1분간격으로 0분에서 60분까지 고려하였다. 과도한 수치계산을 줄이기 위하여 개개의 단층파괴로 인해 발생하는 지진해일파에 대해 연안에서의 처오름 높이를 계산하고, 시간차를 두면서 중첩하여 최종적인 처오름 높이를 계산하였다. 개개의 단층에 의해 발생한 지진해일파의 전파특성을 보면, 단층들이 동에서 서로 위치한 경우에는 해안에서 가까울수록 지진해일의 도착시간이 짧아지는 것이 확연하게 드러났으나 남북으로 위치한 경우에는 대부분 비슷한 시간에 도달하였다. 해안선을 따라서 저위도 갈수록 진원에서 멀어져 도달시간이 증가하였으나 위도 36도 부근에서는 돌출 지형으로 인해 도달시간이 갑작스럽게 감소한 후에 다시 증가하였다. 시간차에 의한 효과를 정량화하여 분석하기 위해 해안선에서의 최대 처오름 높이를 이용하여 기하평균값을 구하여 비교하였다. 전체적으로 시간차가 큰 경우에는 개개의 단층에 의해 발생한 지진해일파 사이의 중첩효과가 크지 않아 기하 평균값이 작게 나왔으며 시간차가 작은 경우에는 반대로 크게 발생하였다. 서에서 동쪽으로 단층파괴가 발생하는 경우에는 특정 조건에서 먼저 발생한 지진해일파와 후에 발생한 지진해일파 사이의 중복이 발생하여 최대 처오름높이 기하평균값의 증가가 두드러지게 발생하였다. 시간차에 의한 단층 파괴는 하나의 단층에서 주방향(strike direction)으로 파괴가 발생하는 경우와 별개의 이웃한 단층이 시간차를 가지면서 파괴가 발생하는 경우로 구분할 수 있다. 두 과정은 발생 메커니즘이 다르기 때문에 정확한 구분이 필요하나 본 연구에서는 이를 고려하지 않고 하나의 단층 파괴과정으로 가정하여 연구를 수행하였다. 향후 이와 관련된 추가적인 연구가 필요하며 아울러, 다양한 단층 매개변수에 대한 수치모의도 필요할 것으로 판단된다.