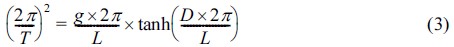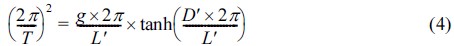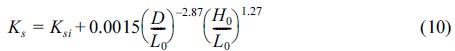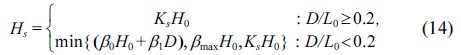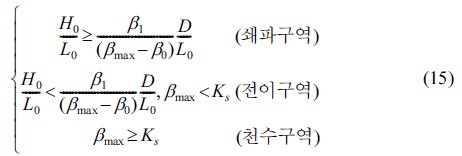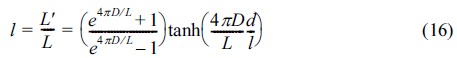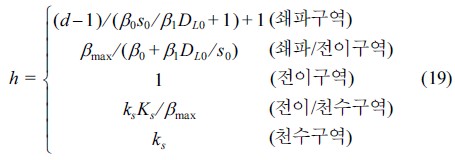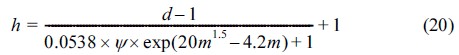1. 서 론
지난 30년 동안, IPCC (Intergovernmental Panel on Climate Change)를 주축으로 한 국제 사회는 온실가스 배출량과 그에 따른 기후변화를 예측하기 위한 연구를 지속적으로 수행해오고 있다(Houghton et al., 1996; Marchetti, 1977; Marland et al., 2003; Schneider and Chen, 1980; Stern, 2006). 그 결과 IPCC에서는 주기적으로 온실가스 배출 시나리오를 발표해오고 있다. 지금까지 발표된 온실가스 배출 시나리오는 각각 다른 가정을 기반으로 하고 있으며 그 변화 추이도 서로 다르다. 하지만 온실가스 배출량 증가로 인한 지구 평균기온의 상승과 이에 따른 해수면 상승은 IPCC가 제안한 모든 온실가스 배출 시나리오에서 예측되고 있다. 즉 미래의 해수면 상승은 발생이 불가피한 것으로 간주되고 있다. 따라서 해수면 상승에 대한 정량적인 예측과 해수면 상승에 따른 다양한 영향의 예측은 IPCC의 온실가스배출 시나리오가 발표된 이래로 지속적인 연구의 대상이 되고 있다.
해안 구조물은 해수면 상승의 영향을 가장 직접적으로 받게 된다. 해수면 상승에 따른 수심 증가와 파랑특성의 변화가 해안 구조물 안정성에 미치는 영향을 예측하고 이를 활용해 구조물의 적절한 안정성 확보를 위한 설계변수의 변화와 구조물 보강에 대한 연구가 다각적으로 수행되고 있다(Chini and Stansby, 2012; Klein et al., 1998; Okayasu and Sakai, 2006; Reeve, 2010; Stern, 2006; Suh et al., 2012; Sutherland and Wolf, 2002; Takagi et al., 2011; Torresan et al., 2008; Wigley, 2009). 그러나 이 연구들은 대부분 특정 온실가스 배출 시나리오를 바탕으로 적용 대상지역이 국소 지역으로 제한되어 있어 이를 해안 구조물 설계에 직접적으로 적용하기에는 제약이 있다(Burgess and Townend, 2004; Townend, 1994a,b; Townend and Burgess, 2004).
Townend(1994b)는 해수면 상승을 해수면 상승 전·후의 수심변화율로 표현하고 이를 이용하여 수심변화율에 따른 파랑특성(파고, 파장, 천수계수, 굴절계수 등)의 변화율을 식과 그래프의 형태로 제안하였다. 또한 제안된 파랑특성의 변화율을 이용하여 수심변화율에 따른 월파량의 변화, 마루높이의 변화, 해안구조물 저단부 표고의 하강율 등 구조물의 설계변화를 식과 그래프의 형태로 제안하였다.
그러나 Townend(1994b)의 방법은 규칙파를 기본으로 제안된 것으로 불규칙파가 지배적인 실제 해역에 적용하기에는 부적절 하다(Lee et al., 2013). 따라서 본 연구에서는 해수면 상승에 따른 파랑의 특성변화를 고찰하기 위해 Townend(1994b)의 방법을 불규칙파에 적용 가능하도록 확장하고 이를 식과 그래프로 제시하였다.
단, 여기서부터 편의상 Townend의 방법은 Townend(1994b)에서 제안한 파랑특성 변화율 산정 방법을 의미한다.
2. 연구방법
2.1 연구방법 개요
해수면 상승이 파랑에 미치는 영향을 산정하기 위해 Townend가 제안한 방법과 같이 해수면 상승을 해수면 상승 전·후의 수심변화율로 표현하였다. 본 연구에서는 바닥경사가 일정한 해안에 대해 수심변화율에 따른 파랑 특성(파고, 주기, 천수계수, 굴절계수 등)의 변화율을 산정하였으며 Townend의 방법을 불규칙파로 확장하기 위해 불규칙파에 적용 가능한 파랑변형식과 천수계수식을 사용하였다. 또한 적용의 편의를 위해 각 파랑 특성 변화율 계산식을 상대수심(수심과 심해파장의 비)과 심해 파형경사(심해파고와 심해파장의 비)의 함수로 나타내었다.
2.2 용어 정의
D=수심 [m] H=파고[m]
H0=심해파고 [m] Hs=유의파고 [m]
L=파장 [m] L0=심해파장 [m]
C=파속 [m/s] C0=심해파속 [m/s]
m=바닥경사 Ks=불규칙파 천수계수
Ksi=규칙파 천수계수 Kr=굴절계수
T=파 주기 [s] Ts=유의파 주기 [s]
α0=심해파향 [Deg] α=대상지역 파향 [Deg]
s0=H0/L0 (심해파형경사) g=중력가속도=9.81 [m/s2]
'=변수의 오른쪽 상단에 더하여 수심변화 이후의 변수를 의미함
“대문자 변수의 소문자 형태”=수심변화 전·후의 변수비를 나타냄. 예를 들면, h는 해수면 상승 이전의 파고(H)와 해수면 상승 이후의 파고(H')의 비를 의미하며 이를 수식으로 나타내면 식 (1)과 같음.
2.3 연구 절차
수심변화율(또는 해수면 상승)에 따른 불규칙파의 변화를 산정하기 위해 파장, 굴절계수, 천수계수, 파고 등의 변화율을 고찰하였으며 각각의 연구방법은 아래에 자세히 기술하였다.
2.3.1 해수면 상승에 따른 파장의 변화
해수면 상승 전 수심을 D, 해수면 상승 후 수심을 D'이라 하면 수심변화율(d)은 식 (2)와 같다.
Townend는 분산관계식(식 3)을 이용하여 해수면 상승에 따른 파장의 변화율을 규칙파에 대해 제안하였다.
본 연구에서는 식 (3)에서 규칙파 주기를 유의파 주기로 대체하여 수심변화율에 따른 불규칙파의 파장 변화율을 산정하였다.
식 (4)는 해수면 상승 후의 주기와 파장과의 관계를 나타내며 식 (3)과 (4)로부터 L과 L'을 계산하여 수심변화율에 따른 불규칙파의 파장 변화율을 산정하였다.
2.3.2 해수면 상승에 따른 굴절계수의 변화
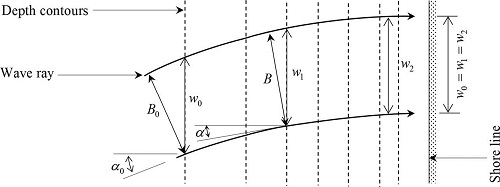
수심변화율에 따른 굴절계수의 변화율을 산정하는 방법은 Townend가 수행한 과정과 동일하며 본 과정을 수행하기 위해 바닥의 등심선이 해안선과 평행한 지역에 사각으로 입사하는 파랑을 Fig. 1과 같이 가정하였다.
Fig. 1과 같은 조건에서 굴절계수는 식 (6)를 이용하여 계산할 수 있으며 해수면 상승 이후 굴절계수는 식 (7)과 같다. 다방향 불규칙파의 경우 α는 주파향으로 간주하고, Snell의 법칙(식 5)과 식 (6), (7)을 이용하여 해수면 상승에 따른 굴절계수의 변화를 산정하였다.
2.3.3 해수면 상승에 따른 천수계수의 변화
Townend는 규칙파의 천수계수식(식 8)을 이용하여 해수면 상승에 따른 천수계수의 변화를 식 (9)와 같이 제안하였다.
본 연구에서는 해수면 상승에 따른 불규칙파 천수계수의 변화를 산정하기 위해 불규칙파에 적용이 가능한 천수계수식(Kweon and Goda, 1996)을 이용하였으며 식 (10)과 같다. 식 (10)은 Iwagaki 등(1982)이 제안한 천수계수식의 형태를 고정하고 계수를 조정하여 Goda(1975a)가 제안한 천수계수 그래프를 근사적으로 표현한 식으로 비선형 불규칙 파랑에 적용 가능하다.
2.3.4 해수면 상승에 따른 파고의 변화
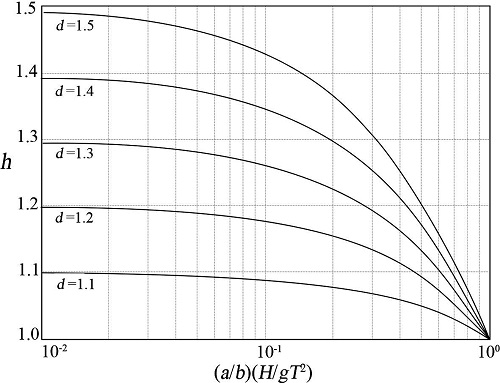
Townend는 쇄파대 내의 파고 변화를 산정하기 위해 Weggel(1972)이 제안한 식 (11)을 사용하여 해수면 상승에 따른 파고 변화를 식 (12)와 같이 제안하였으며 쇄파대 밖의 파랑에 대해서는 식 (13)과 같이 제안하였다.
여기서, a = 43.75(1.0−e−19m), b = 1.56(1.0+e−19.5m)−1이다.
본 연구에서는 불규칙파의 파고를 대표하는 값으로 유의파고(Hs)를 사용하였다. 해수면 상승 이전의 유의파고를 Hs, 해수면 상승 후의 유의파고를 H's이라 하면 유의파고의 변화율hs은 로 표현할 수 있다. 단, 여기서부터 편의를 위해 hs을 h로 대체해 표기하였다.
해수면 상승에 따른 불규칙파의 파고 변화를 산정하기 위해 Goda(1975b)가 제안한 식 (14)을 사용하였다.
여기서, βmax=max{0.92,0.32 s0−0.29e2.4m}, β0=0.028s0−0.38e20m1.5, β1 =0.52e4.2m, 이다.
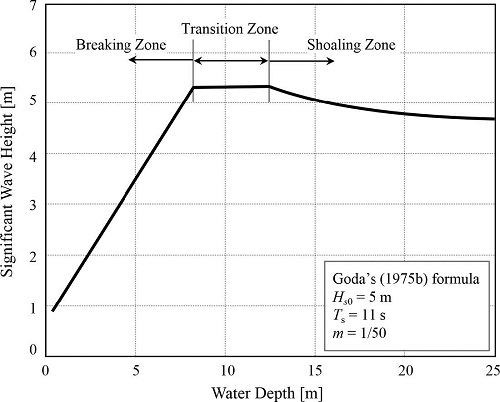
식(14)는 바닥경사가 일정하다는 가정 하에 H0/L0, D/L0, m값을 이용하여 쇄파대 내에서 수심에 따른 유의파고 값을 산정하기 위해 제안된 식이다. 그러나 식 (14)에서 상대수심이 0.2 보다 크거나 같은 경우 파는 쇄파대에 밖에서 천수 효과의 영향을 받게 된다. 따라서 식 (14)에서 불규칙파에 적용 가능한 천수계수를 사용할 경우 식의 적용 범위를 쇄파대보다 깊은 수심으로 확장이 가능하다.
식 (14)를 이용해 불규칙파(Hs0=5 m, Ts=11 s)가 해안(등심선이 해안선과 평행하고 바닥경사가 1/50)에 직각으로 입사할 때 수심의 변화에 따른 유의파고를 계산하면 Fig. 2와 같다. 본 연구에서는 Fig.2에서 파고 변화의 형태적 특성을 이용해 파랑의 상태를 천수구역, 전이구역, 그리고 쇄파구역으로 나누었다. 여기서 전이구역은 파랑이 심해에서 천해로 전파되어 가는 과정에서 본격적인 쇄파가 일어나기에 앞서 수심이 얕아져도 파고가 커지거나 작아지지 않고 일정한 값을 가지며 전파되는 구역을 의미한다. 실제로는 이 구역에서 파고가 완만하게 변화하지만 일정한 값으로 근사한 것이며 몇 퍼센트 이내의 작은 오차를 보인다. 식(14)에서 상대수심(D/L0)이 0.2 보다 크거나 같을 경우에는 천수구역으로 분류할 수 있으며 상대수심이 0.2 보다 작을 경우에는 식 (14)와 Fig. 2를 이용하여 각 구역의 조건식을 심해 파형경사와 상대수심을 사용해 식 (15)와 같이 나타내었다.
여기서, β0, β1, 그리고 βmax는 식 (14)에 정의된 것과 동일하다.
식 (14)와 (15)를 사용하여 각 구역의 파고를 계산할 수 있으며 이를 이용하여 해수면 상승에 의한 파고 변화를 산정하였다.
3. 연구 결과 및 토의
3.1 해수면 상승에 따른 파장의 변화
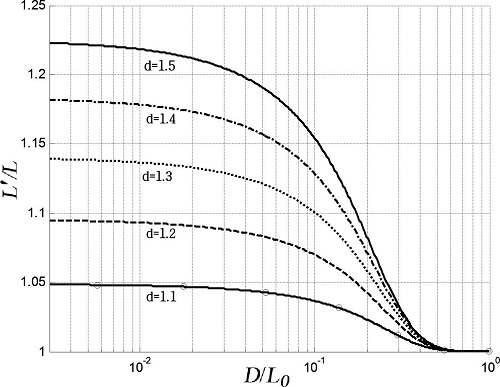
Townend는 해수면 상승에 따른 파장의 변화를 식 (16)과 같이 음함수의 형태로 제안하였으며 수심변화율과 상대수심(D/L)을 이용한 그래프를 제안하였다. 본 연구에서는 분산관계식(식 3)에 입력되는 주기 값으로 유의주기(Ts)를 사용하였으며 적용의 편의를 위해 상대수심에서 파장을 심해 파장으로 대체하여 그래프로 나타내었다(Fig. 3).
Fig. 3로부터 상대수심(D/L0) 값이 작을수록 그리고 수심변화율이 클수록 파장의 변화율이 커짐을 알 수 있다. 수심변화율을 1.5로 가정할 경우에는 상대수심이 0.1보다 작은 구역에서 파장의 변화율이 최고 약 22%로 나타난다. 반면 상대수심이 0.3보다 큰 천수구역의 경우 파장의 변화율이 5% 미만으로 그 영향이 매우 작음을 알 수 있다.
3.2 해수면 상승에 따른 굴절계수의 변화
해수면 상승에 따른 굴절계수의 변화는 식 (5)~(7)을 이용하여 산정되었으며 식 (17)과 같다.
여기서, A = tanh2(2πD/L)×sin2(α0), 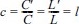 이다.
이다.
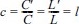 이다.
이다.
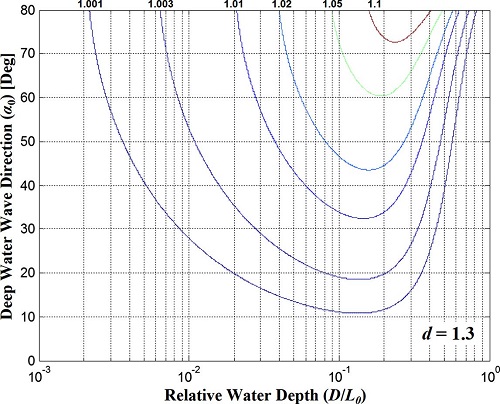
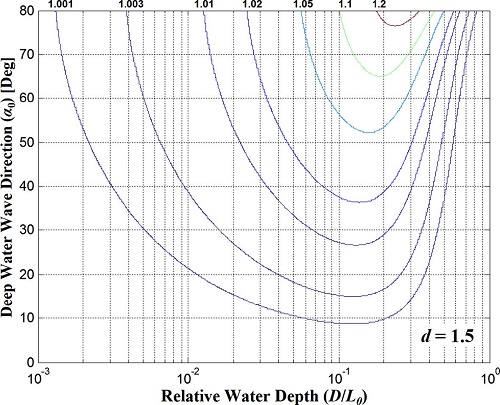
Fig. 4~6은 수심변화율이 1.1, 1.3, 1.5일 때 심해파향과 상대수심에 따른 굴절계수의 변화율을 각각 나타낸다. Fig. 4~6에 의하면 d = 1.1일 경우 굴절계수의 최고 변화율이 5%로 매우 작은 반면 d = 1.5일 경우 굴절계수의 최고 변화율이 약 20%로 상대적으로 큰 값을 가진다. 즉, 해수면 상승률이 커질수록 굴절계수의 변화율이 커짐을 알 수 있다.
Fig. 4~6에 제안된 1.1, 1.3, 1.5 이외의 수심변화율 조건에서 굴절계수의 변화율은 수심변화율이 1.1 미만일 경우에는 상대수심과 심해파향 값으로부터 d = 1일 경우(Kr= 1)와 d = 1.1일 때의 굴절계수의 변화율 값을 이용한 보간법을 통해 굴절계수의 변화율을 산정한다. d = 1.1~1.3 그리고 d = 1.3~1.5 인 경우에도 Fig. 4~6, 그리고 보간법을 이용해 수심변화율에 따른 굴절계수의 변화율을 산정할 수 있다.
3.3 해수면 상승에 따른 천수계수의 변화
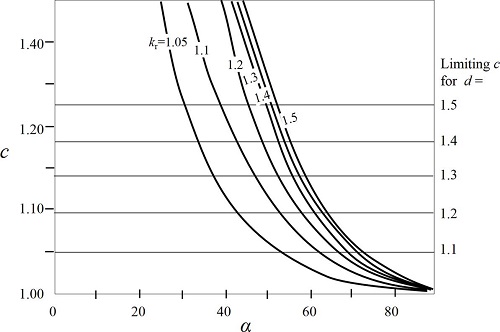
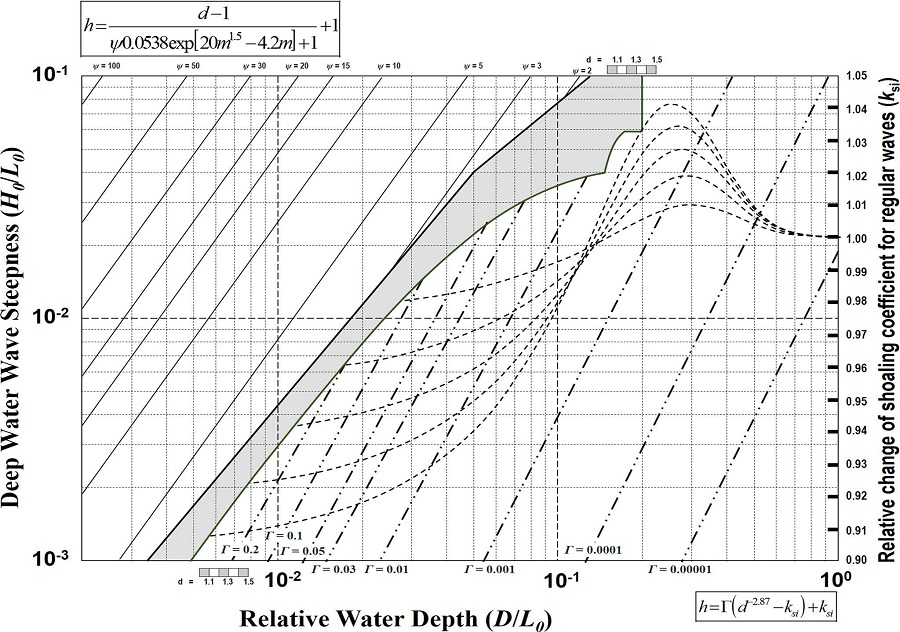
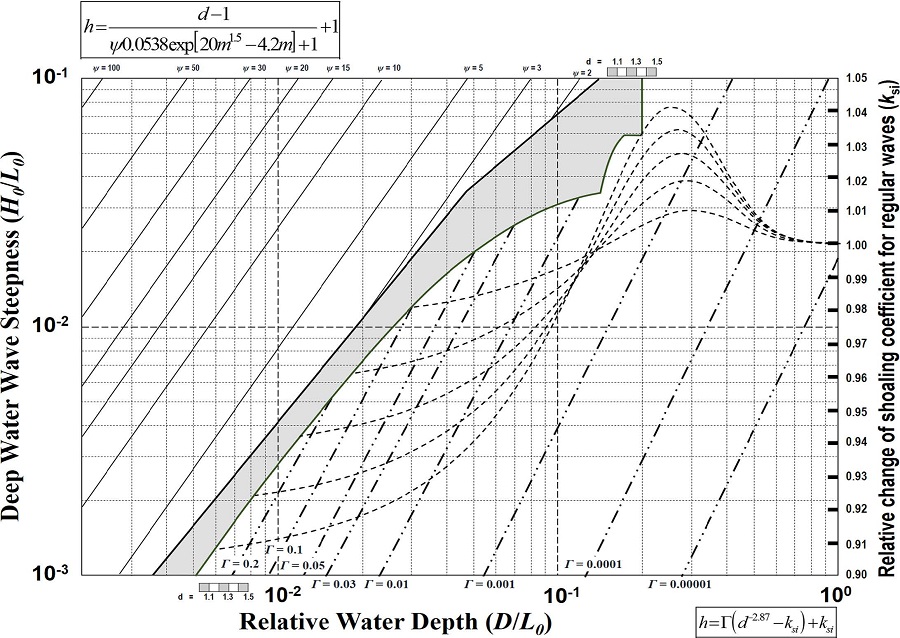
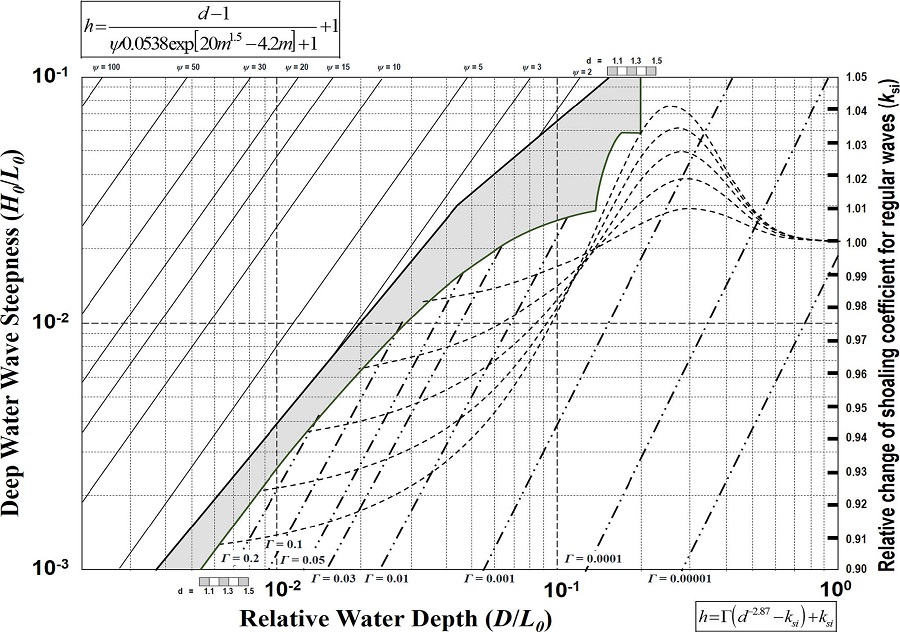
해수면 상승에 의한 천수계수의 변화는 식 (8)~(10)을 이용하여 산정되었으며 식 (18) 그리고 Fig. 8와 같다.
여기서, Γ = 0.0015×Ks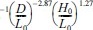 이다.
이다.
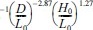 이다.
이다.식 (18)과 Fig. 8을 이용하여 수심변화율에 따른 천수계수의 변화율을 얻기 위해서는 수심변화율에 따른 규칙파의 천수계수 변화율(ksi)과 Γ의 값이 필요하다. 규칙파의 천수계수 변화율은 수심변화율(d), 상대수심(D/L0), 그리고 Fig. 8에 점선으로 그려진 그래프를 오른쪽 세로축 눈금 값으로 읽어 결정할 수 있다. 또한 심해 파형경사 및 상대수심에 대하여 비스듬히 그어진 실선 값을 읽어 Γ의 값을 결정할 수 있다. 식 (18)을 직접 이용하여 천수계수를 산정하기 위해서는 Townend가 규칙파에 대해서 제안한 천수계수식(식 9)을 사용하여 ksi를 계산하고 상대수심과 심해 파형경사로부터 Γ를 직접 계산하는 방법이 있다. 그러나 불규칙파 조건에서의 천수계수의 변화율이 크지 않고 식을 적용하는데 비교적 많은 양의 계산이 필요함으로 Fig. 8을 이용하여 천수계수의 변화량을 산정하는 것이 보다 간단하다.
Fig. 8에 따르면 상대수심이 작아질수록 그리고 심해 파형경사가 커질수록 수심변화율에 따른 천수계수의 변화율이 커지는 것을 알 수 있다. 다만 상대수심이 작아질 경우에는 파랑이 쇄파되기 때문에 천수계수가 의미를 가지지 않게 됨으로 쇄파 이전까지의 범위에서만 해수면 상승에 따른 천수계수의 변화율을 산정한다.
3.4 해수면 상승에 따른 파고의 변화
식 (14), (15)를 이용하여 수심변화율에 따른 파고의 변화율을 각 구역별로 산정하면 식 (19)와 같다.
여기서 DL0 = D/L0이고, 쇄파/전이구역은 해수면 상승 전에는 쇄파구역에 속해 있다가 해수면 상승 후에는 전이 구역에 속하게 되는 경우를 의미하며, 마찬가지로 전이/천수구역은 해수면 상승 전에는 전이구역에 속해 있다가 해수면 상승 후에는 천수구역에 속하게 되는 경우를 의미한다.
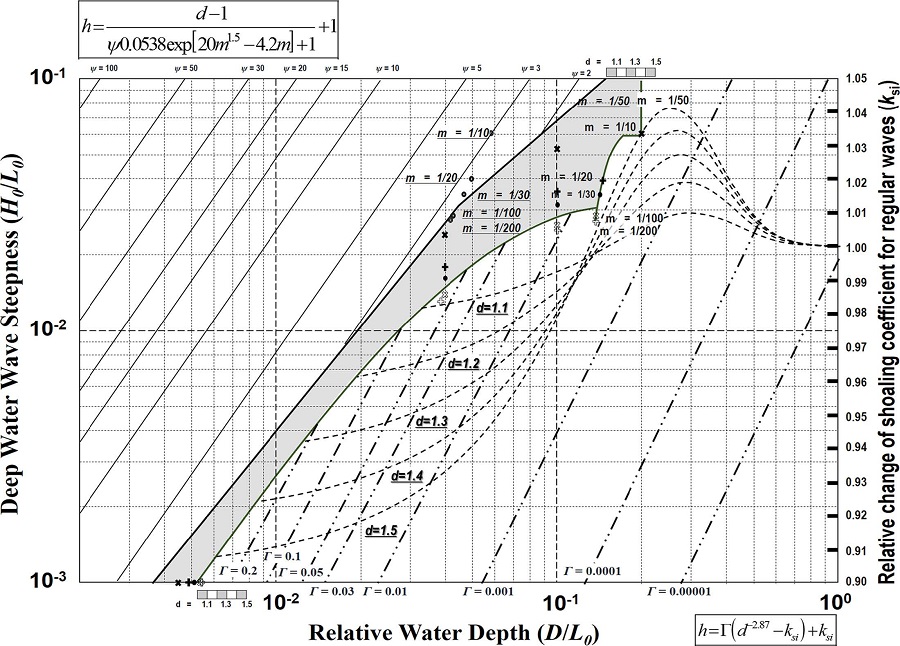
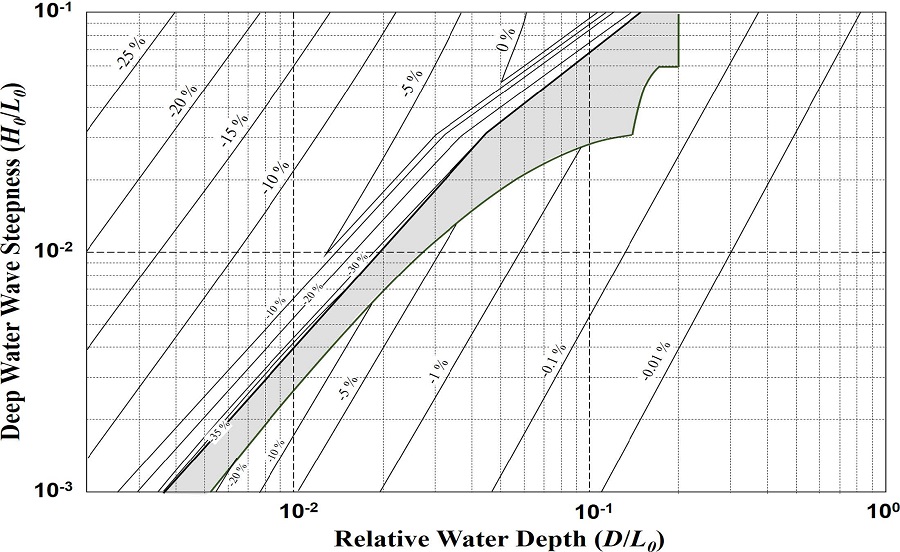
식(15)와 (19)를 이용하여 해수면 상승에 따른 파고의 변화율을 나타내면 Fig. 9와 같다.
Fig. 9에서 음영으로 표현된 구역이 전이구역을 나타내며 전이구역을 중심으로 좌측이 쇄파구역 우측이 천수구역으로 각각 나누어진다. Fig. 9에서 음영으로 표시된 전이구역은 1/50 바닥경사에 대한 경계이며, 그 밖의 바닥경사에 대한 경계를 산정하기 위해서는 Fig. 9를 이용하거나 식 (15)를 이용할 수 있다. Fig. 9를 이용하여 경계를 추정하기 위해서는 그림 내에 여러 바닥 경사에 대하여 표시된 점들과 1/50 경사에 대한 경계를 활용한다. 그림에 주어진 m값은 바닥경사를 의미하며, 이탤릭체로 아래에 밑줄이 쳐진 m값이 쇄파구역과 전이구역을 구분하기 위한 바닥경사를 의미하고 ‘°’로 각 지점을 표시하였다. 보통 글꼴의 m 값은 전이구역과 천수구역을 구분하기 위한 바닥경사를 의미하며 각각 다른 점(x:m = 1/10; +:m = 1/20; •:m = 1/30; x:m = 1/100; +:m = 1/200)으로 표현되었다. 쇄파구역과 전이구역의 경계는 그림에 주어진 바닥경사 점을 중심으로 1/50 경사에 대한 경계와 평행하다. 전이구역과 천수구역을 나누는 경계의 경우 직선이 아닌 곡선으로 표현되며 주어진 바닥경사 점들을 부드럽게 연결하여 경계를 결정한다. 단 점으로 주어지지 않은 바닥경사에 대한 경계는 보간법을 이용하여 결정한다. 대상 지역의 파랑 조건이 식 (19)의 쇄파/전이구역과 전이/천수구역에 포함되는지 여부를 판단하기 위해 전이구역의 상단과 하단에 수심변화율을 표현하는 축척을 두었다. 즉, 각 경계는 해수면 상승에 의해 축척에 나타난 만큼 우측으로 평행이동하게 되며 경계의 이동으로 인해 파랑의 구역이 변하게 될 경우에는 쇄파/전이구역 혹은 전이/천수구역에 속하게 된다.
Fig. 9를 이용하여 수심변화율에 따른 파고의 변화율을 산정하기 위해서 우선 상대수심, 심해 파형경사, 바닥경사, 그리고 수심변화율을 이용하여 파랑이 속해 있는 구역을 결정한다. 파랑이 쇄파구역에 속한 경우에는 상대수심과 심해 파형경사에 해당되는 값을 읽는다. 그 다음 바닥경사(m), ψ, 그리고 수심변화율(d) 값을 식 (20)에 대입하여 파고의 변화율을 계산한다. 파랑이 천수구역에 속해 있을 경우에는 수심변화율에 따른 천수계수의 변화율이 파고의 변화율과 동일하므로 천수계수의 변화율을 구하는 방법(식 18)을 그대로 적용할 수 있다. 파랑이 전이구역에 속할 경우에는 해수면 상승에 따른 파고의 변화율은 1로 산정된다. 파랑이 쇄파/전이구역 또는 전이/천수구역에 속할 경우에는 Fig. 9를 사용해 파고의 변화율을 산정하지 않고 식 (19)를 사용해 수심변화율에 따른 파고의 변화율을 산정한다.
여기서, ψ = s00.62/(D/L0)이다.
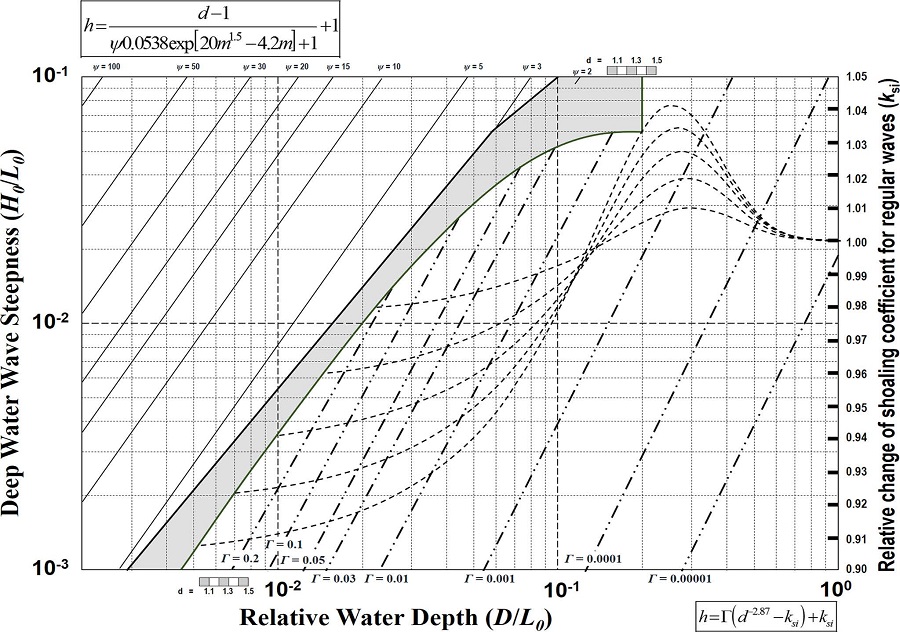
위에서 바닥경사가 1/50이 아닌 경우 Fig. 9를 사용하는 방법에 대하여 설명하였지만, 너무 복잡하여 사용이 어려울 수가 있기 때문에, 사용자의 편의를 위해 바닥 경사 1/10, 1/20, 1/30, 1/100일 때의 수심변화율에 따른 파고 변화율을 Fig. 10~13에 각각 나타내었다.
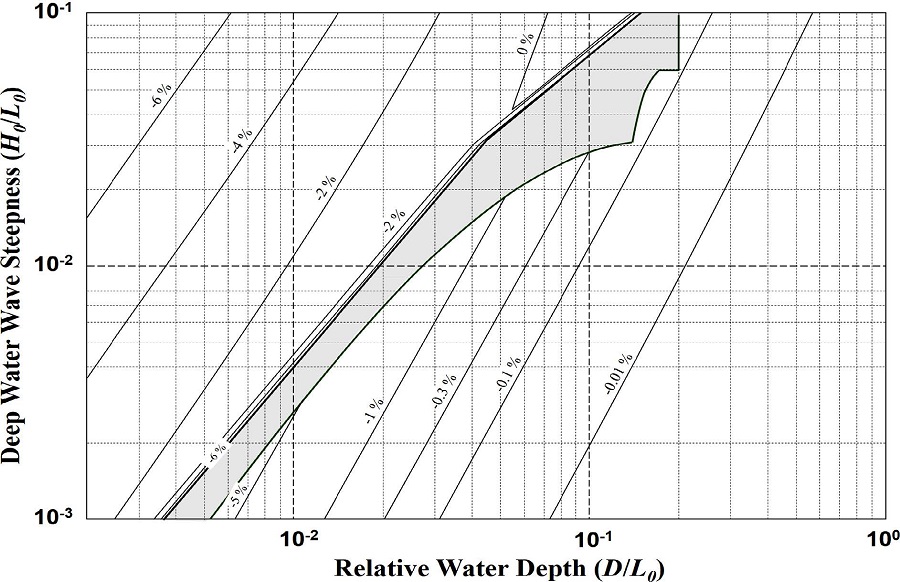
본 연구에서 제안된 수심변화율에 따른 파고의 변화율을 Townend에 의해 제안된 파고의 변화율과 비교하기 위해 바닥경사를 1/50으로 고정하고 수심변화율이 1.1과 1.5인 경우를 각각 가정하였다. 전이구역 주변의 경우 수심변화율이 1.1일 때, 쇄파대 내에서 해안선 주변일 경우 수심변화율이 1.5일 때 각각 실제 해수면 상승에 따른 수심변화율과 가깝게 된다. 가정된 값을 본 연구의 방법과 Townend의 방법에 각각 적용해 산정한 파고의 변화율을 비교하여 두 방법 간의 차이를 식 (21)을 이용하여 백분율(e%)로 나타내었으며 Fig. 14 ~15에 그 결과를 도시하였다.
여기서, h =본 연구에서 제안한 파고의 변화율, hT= Townend가 제안한 파고의 변화율을 나타낸다.
Fig. 14~15에서 Townend가 제안한 파고의 변화율과 본 연구에서 제안한 파고의 변화율 사이의 차이는 쇄파구역과 전이구역을 나누는 경계에서 가장 크게 계산되며, 전체적으로 Townend의 방법에 의해 제안된 파고의 변화율이 더 크게 산정되었다. 쇄파대 내에서는 상대수심이 같을 경우에는 심해파형경사가 클수록 차이가 커지며, 쇄파구역과 전이구역을 나누는 경계로부터 상대수심이 작아질수록 차이가 점점 감소하다가 다시 증가하는 양상을 보인다. 수심변화율이 1.5일 때 해안선 방향으로 최고 약 25%의 차이가 발생하며 쇄파구역과 전이구역의 경계부근에서 최고 약 35%의 차이가 발생한다. 수심변화율이 1.1일 경우에는 해안선 방향으로 최고 약 6%의 차이가 발생하며 쇄파구역과 전이구역의 경계부에서 최고 약 6%의 차이가 발생한다. 상대수심이 0.1 보다 크고 천수구역일 경우에는 각 수심변화율 모두에서 차이가 1% 미만으로 거의 같다고 할 수 있다. 전이구역과 천수구역의 경계부 주변의 경우 심해 파형경사가 클수록, 그리고 경계에 가까울수록 차이가 증가하는 양상을 보인다. 전이구역과 천수구역의 경계부에서 수심변화율이 1.5일 때 최고 약 20%의 차이가 발생하며, 수심변화율이 1.1일 때 최고 약 6%의 차이가 발생한다.
Fig. 14~15에서 살펴본 바에 따르면 규칙파 공식을 바탕으로 제안된 Townend의 결과와 불규칙파 공식을 바탕으로 제안된 본 연구의 결과 사이에는 최고 약 35%의 차이가 발생함을 알 수 있다. 그러나 실제 해수면 상승에 의한 수심변화율을 고려해 볼 때 쇄파구역과 전이구역의 경계부근에서 수심변화율 1.5일 때 발생된 차이의 값은 과대 산정되었다고 할 수 있다. 실제 해수면 상승을 고려한 최대 차이는 해안선 주변 지역에서 수심변화율이 1.5일 때 발생되며, 최고 약 25%로 계산되었다. 쇄파구역과 전이구역의 경계부의 경우 수심변화율이 1.1일 때 최고 약 6%의 차이가 계산되었다.
실제 해수면 상승을 고려할 때 최대 약 25%의 차이가 발생하며, 각 수심변화율에서의 최대 차이 값이 쇄파구역과 전이구역의 경계부에서 발생하고 있어 파랑을 쇄파와 비쇄파로 나누어 각각의 파고 변화율을 제안한 Townend의 방법(비쇄파시: Fig. 8의 ksi; 쇄파시: Fig. 16)을 실제 해역 전체에 적용하는 것은 바람직하지 않은 것으로 생각된다.
따라서 불규칙파의 특성을 보이는 실제 해역에서 해수면 상승에 따른 파고의 변화율을 산정할 때 규칙파 공식을 이용하여 제안된 Townend의 방법을 이용하는 것보다 불규칙파 공식을 토대로 본 연구에서 제안된 식과 그래프를 활용하는 것이 바람직할 것으로 생각된다.
4. 결 론
본 연구에서는 해수면 상승이 연안 지역의 파랑특성에 미치는 영향을 산정하기 위해 Townend가 제안한 방법을 불규칙파랑에 대해서 확장하였다. 고찰한 파랑특성은 파장, 굴절계수, 천수계수, 그리고 파고로 한정하였으며, 파장, 굴절계수의 경우 규칙파 주기를 유의주기로 대체하고 파향은 주파향으로 간주하여 Townend의 방법을 그대로 적용하였다. 단, 파장과 굴절계수에 대해 Townend가 제안한 식과 그래프를 보다 적용하기 쉬운 형태로 수정하여 제안하였다(Fig. 4~7, 그리고 식 17). 수심변화율에 따른 불규칙파의 천수계수와 파고의 변화율을 산정하기 위해 불규칙파에 적용 가능한 천수계수 공식(Kweon and Goda, 1996)과 파랑변형공식(Goda, 1975b)을 사용하였으며 이를 이용해 불규칙파에 적용 가능한 천수계수의 변화율과 파고의 변화율을 식과 그래프의 형태로 제안하였다(Fig. 8~13 그리고 식 18~20). 제안된 식은 모두 상대수심(D/L0)을 이용하여 그래프로 나타내었으며 천수계수와 파고의 경우 심해 파형경사와 상대수심의 함수로 나타내었다.
특히 파고의 경우 본 연구에서 제안한 방법과 Townend의방법 사이의 차이를 백분율로 계산하여 Fig. 14~15에 나타내었다. Fig. 14~15에 따르면 Townend의 방법과 본 연구에서 제안한 방법 사이에 실제 해수면 상승을 고려할 때 최대 약 25%의 차이가 존재하며, 각 수심변화율에서의 최대 차이 값이 쇄파구역과 전이구역의 경계부에서 발생하고 있어 파랑을 쇄파와 비쇄파로 나누어 각각의 파고 변화율을 제안한 Townend의 방법을 사용해 파고의 변화율을 산정하는 것은 적절하지 않다.
따라서 실제 해역에서 해수면 상승이 파랑에 미치는 영향을 산정하기 위해 Townend의 방법을 적용하는 것보다 본 연구에서 제안한 식과 그래프를 사용하는 것이 바람직하다.