1. 서 론
갯벌과 여울은 하구와 내만역에서 발달되는 조간대로 하천을 통해 운반되는 모래, 진흙 및 유기물이 퇴적되어 조성된다. 특히 갯벌은 생물의 다양성 보전, 수질정화, 철새도래지 등과 같은 다양한 환경학적 기능뿐만 아니라 해양생태계의 학습 및 여가활동의 장소로도 사람들과 밀접한 관계를 갖는 해역이다(Hanawa, 2006). 최근 들어, 갯벌의 이러한 다원적 기능이 다시 주목받기 시작함에 따라 갯벌재생은 물론이거니와 일본에서는 해역의 준설토사를 유용한 인공갯벌의 조성이 시도되고 있다(Mang and Hong, 2008; Kim and Jeon, 2015). 인공갯벌은 생물이 자연스럽게 정착하여 수질정화 및 생태보호와 같은 자연갯벌과 동일한 기능을 발휘하는 것으로 보고되고 있다(Imamura et al., 1993; Kimura et al., 2002). 갯벌의 저질조건은 저생생물의 결정적인 서식 환경적 요소이며, 자갈과 모래만으로 구성된 갯벌에 비해 약 5-30% 범위의 진흙성분을 포함한 저질에서 저생생물의 종류와 개체수가 최대가 되는 것으로 알려져 있다(Takayama et al., 2008). 또한, 갯벌에서 형성되는 둑(berm)에 의해 지형변화가 크게 발생하여 표고가 평균 수위와 만조 시의 수위를 초과하는 경우는 저생생물의 서식환경 악화로 개체밀도가 크게 감소하는 것으로 알려져 있다(Kuwae, 2005). 따라서, 인공갯벌에 있어서 저질의 입도변화와 침하, 퇴적을 포함한 지형변화와 같은 물리적 안정성을 확보하는 것은 갯벌의 순기능을 유지하기 위한 중요한 과제중의 하나이다. 인공갯벌은 주로 모래와 진흙(점토 + 실트)으로 구성되어 있으며, 이러한 혼합토사의 특성은 진흙의 함유율, 종류, 건조체적밀도(dry bulk density) 등에 따라 복잡하게 변화한다. 또한, 혼합토사는 진흙의 함량에 따라 토사에 포함된 모래 입자의 구조가 변화되며 이에 따른 토사의 이동특성도 변화하게 된다. 진흙 함유량이 적은 경우(15-30% 이하) 모래 입자 사이의 구조는 진흙이 포함되지 않은 경우와 유사하게 서로 접촉하고 있는 네트워크를 형성하지만, 모래 입자 사이에 존재하는 진흙의 응집효과에 의해 모래 입자의 이동한계는 증가할 수 있다. 그러나 이러한 진흙의 응집 효과의 영향은 비교적 작다. 반면, 진흙 함유량이 큰 경우(15-30% 이상)는 모래 입자가 진흙에 의해 완전히 포위되고, 이로 인해 모래 입자에 작용하는 진흙의 응집효과가 증가한다. Mitchener and Torfs(1996)는 응집성 퇴적물(진흙)과 비응집성 퇴적물(모래)로 이루어진 혼합토사의 이동특성을 조사하기 위해 수리실험을 수행하였으며, 진흙 함량이 5-15%의 범위에서 혼합토사는 비응집성 거동(non-cohesive behavior)에서 응집성 거동(cohesive behavior)으로 전환되고, 혼합토사가 균일하게 혼합된 경우의 최대 이동한계전단응력(critical bed-shear stress)은 진흙 함량이 50-70%의 범위에 존재함을 확인하였다. Panagiotopoulos et al.(1997)은 실험을 통해 진흙 함유율이 30%를 초과할 때 비응집성 거동에서 응집성 거동으로 전환되는 천이영역이 나타남을 밝혔다. 이러한 응집성과 비응집성 거동의 경계는 실험에 사용된 모래와 진흙의 종류, 실해역에 있어서는 혼합토사에 포함된 유기물의 함량에 따라 변화하기 때문에 실험조건에 의존하는 경향이 있다. 한편, Ashida et al.(1982)는 산지 유역의 침식 메커니즘과 하도 변동성의 감소를 목적으로 모래와 진흙으로 이루어진 혼합토사에 주목하여 진흙의 점착력(cohesive force)이 혼합토사에서 모래 입자의 이동한계에 미치는 영향을 고찰하기 위한 실험을 실시하였다. 실험 결과, 혼합토사에 있어서 모래 입자의 이동은 진흙의 함수비, 진흙 고유의 점착력, 진흙의 함유율과 같은 3개의 매개변수에 의해 지배되는 것을 확인하였으며, 혼합토사의 기하학적 구조 특성을 활용하여 진흙의 함수비, 진흙 고유의 점착력, 진흙의 함유율을 고려한 혼합토사에서의 모래 입자에 대한 이동한계식을 제안하였다. Van Rijn(2020)와 Wu et al.(2020)는 혼합토사의 이동 특성은 진흙의 함유량 외에도 혼합토사의 압밀정도를 나타내는 건조체적밀도에 의존하는 것을 밝혔으며, 실험자료를 바탕으로 건조체적밀도를 적용한 혼합토사의 이동 한계 전단응력식을 제안하였다. 또한 Van Rijn and Barth(2019)는 혼합토사의 압밀과 건조체적밀도의 변화를 조사한 수리실험을 통해 혼합토사의 건조체적밀도를 산출하는 간단한 실험식을 제안하였다. Kumagai et al.(2012)는 수리실험을 통해 모래 성분이 50%인 혼합토사의 저면에서 생성되는 균열에 의해 저면 내부의 진흙이 유출되는 현상과, 강한 파랑 조건하에서 저면의 표면으로부터 진흙이 유실되는 특성이 있음을 보였다. Rafati et al.(2020)은 다양한 입경으로 구성된 혼합모래의 판류(sheet flow) 이동에 있어서 저질의 피복효과(armoring effect)와 노출효과(exposure effect)를 규명하기 위해 Cheng et al.(2017)이 제안한 Eulerian-Lagrangian 난류 평균 모델을 이용하여 수치모의를 실시하였다. 그 결과, 흐름장의 유속 크기가 작고 가속도가 증가할 수록 표층에서 입경이 거칠어지는 역 분류(inverse grading)에 의해 표사이동량이 감소하는 저질의 피복 효과가 지배적이며, 이와 반대인 경우는 노출효과가 우세함을 확인하였다. 한편, 수리실험과 현지조사를 통해 혼합토사의 이동특성을 규명하고 그에 따른 혼합토사의 표사이동식이 제안되어 왔으나 파랑장에서 혼합토사 모델에 대한 연구는 극히 제한적이다. Nakamura et al.(2013)과 Cho et al.(2019)은 Ashida et al.(1982)가 제안한 혼합토사에서 진흙의 점착력에 기인하는 모래 입자의 이동한계전단 응력의 변화를 고려하여 혼합토사 유송모델을 구축하고 파랑장 조건하에서 혼합토사 표층에서 발생하는 진흙 유출에 따른 진흙 함유량의 공간적 변화를 모의하였다. 하지만, Ashida et al.(1982)에 의해 제안된 모래입자의 이동한계응력은 포함된 주요 파라미터들의 정의가 모호하며, 혼합토사의 이동특성에 있어서 중요한 건조체적 밀도의 영향과 혼합토사에서의 진흙의 이동한계는 고려되어 있지 않다. 또한, 낮은 진흙 함유량에 중심을 둔 모래입자 중심의 지형변화와 진흙의 침식, 퇴적에 대한 검토는 수행되지 않았기 때문에 혼합토사 모델의 개량이 요구된다. 갯벌에 있어서 저질의 진흙 함유량은 그 기능을 충분히 발휘할 수 있는지에 대한 중요한 지표가 되기 때문에, 혼합토사로 이루어진 저질에 대한 진흙의 동적 특성을 파악하기 위해서는 보다 고정도의 모의가 가능한 혼합토사의 수치모델 개발이 필요하다.
본 연구에서는, 혼합토사의 이동특성에 영향을 미치는 진흙의 함유량과 건조체적밀도를 고려한 혼합토사의 수치계산 모델을 위하여 토사의 기하학적 구조에 기초한 격자법에서 서로 다른 토사의 재현방법을 제안하고 이를 바탕으로 수치모델을 구축하였다. 구축한 모델의 평가를 위해 사면 붕괴에 대한 계산을 수행하고, 초기 혼합토사의 진흙 함유량 변화에 따른 모델의 혼합토사 이동계산에 대한 안정성을 평가하였다.
2. 혼합토사 모델의 Framework
2.1 혼합토사의 이동특성
모래와 진흙(점토 d50 < 0.008 mm, 실트 d50 < 0.063 mm)으로 구성된 혼합토사에 있어 모래 입자의 이동한계는 모래를 둘러싼 진흙에 의한 응집성(cohesive)과 결합성(binding)의 영향을 받는다. 이러한 효과는 혼합토사의 건조체적밀도와, 진흙과 진흙에 포함된 점토의 비율을 고려한 수정계수(correction factor)를 도입함으로써 고려될 수 있다(Van Rijn, 2020). 또한, 혼합토사에서의 진흙의 이동특성은 진흙의 전기 화학적 성질과 진흙에 포함된 유기물의 영향, 점토의 점착력 및 진흙의 압밀정도 등의 영향을 받는다. 혼합토사에 있어서 진흙의 이동한계는 모래 입자의 이동한계를 계산하는 방법과 유사하게 점토의 점착력과 혼합토사의 건조체적밀도를 고려한 수정계수와 중앙입경 d50 = 63 μm를 가지는 실트의 한계전단응력으로부터 구할 수 있다(Van Rijn, 2020). 혼합토사의 모래와 진흙의 이동한계전단응력식을 식(1)과 식(2)에 각각 나타낸다.
여기서, τcm, sand는 혼합토사에서 모래 입자의 한계전단응력, ϕc는 보정계수, τc0, sand는 모래의 한계전단응력, τcm, fines는 혼합토사에서 진흙의 한계전단응력, τc0, fines는 진흙의 한계전단응력이다. 보정 계수 ϕc와 계수 β는 각각 다음 식으로부터 산정할 수 있다.
여기서, pfines는 진흙의 함유율(= Wfines/(Wfines + Wsand)), Wfines는 진흙의 중량(= Wclay + Wsilt), Wsand는 모래의 중량, pclay는 점토의 함유율(= Wclay/(Wfines + Wsand)), Wclay는 점토의 중량, ρdry, m은 혼합토사의 건조체적밀도, ρdry, max는 혼합토사의 최대 건조체적밀도(≈ 1,600 kg/m3), α1과 α2는 경험계수(empirical coefficient)이다. α1과 α2는 수리실험을 통해 모래의 경우 각각 2.0, 1.5, 진흙의 경우 2.0, 2.0이 사용된다. 혼합토사의 건조체적밀도는 모래, 점토, 실트의 함유율에 의존한다. Van Rijn and Barth(2019)는 수리실험 및 현지조사를 통해 모래와 점토로 구성된 혼합토사의 건조체적밀도를 모래, 점토, 실트의 함유율과 유기물의 영향을 고려한 다음의 식을 제안하였다.
여기서, porg는 유기물의 함유율이다. 식(5)로부터 유기물이 혼합토사에 함유되면 혼합토사의 건조체적밀도는 감소하는 특징이 있다. 하지만, 유기물의 영향에 대해서는 아직까지도 명확하게 규명되어 있지 않고, 본 연구에서는 진흙과 모래만으로 구성된 혼합토사를 대상으로 하고 있으므로 유기물의 영향은 고려하지 않았다(porg = 0.0). 식(5)에서 모래의 건조체적밀도를 나타내는 1,600의 계수에 주목하면, 모래만 존재하는 경우, 건조체적밀도는 1,600 kg/m3가 되며, 이는 통상 모래의 밀도가 2,650 kg/m3임을 고려할 때 모래만으로 이루어진 저질의 공극률이 약 0.4(≈ 0.3962)가 된다. 또한, 혼합토사의 최대 건조체적밀도가 1,600 kg/m3로 여겨지고 있으므로, 혼합토사의 최대 건조체적밀도는 단일 모래로 구성된 경우와 같아지며, 이는 혼합 토사의 공극률이 약 0.4로 유지된다고 고려될 수 있다. 점토 및 실트의 밀도가 모래와 같다고 하면, 점토와 실트가 각각 단일 토사로만 존재할 경우, 점토의 공극률은 약 0.85, 실트의 공극률은 약 0.70가 된다. 여기서, 모래와 마찬가지로 점토와 실트에도 0.4의 공극률이 존재한다고 가정하면 점토의 경우 0.45, 실트의 경우 0.3의 여분의 공극이 존재한다. 이러한 특성은 토사의 물리적 성질로 잘 알려진 바와 같이 토사의 입경이 작을수록 함수율이 증가하며, 결과적으로 토사의 체적이 증가하는 효과이다. 위의 식에서 점토와 실트에 사용된 계수에 착안하면, 토사가 물을 흡수하는 성질에 의해 팽창한 체적률이 점토의 경우 0.45, 실트의 경우 0.3에 상당하다고 볼 수 있으며, 이러한 특징은 실제 사용하는 진흙의 건조체적밀도 실험을 통해 구할 수 있다.
여기서, D*는 무차원 토사입경(= d50[(s-1)g/ν2]1/3), d50은 토사의 중앙입경, s는 토사의 상대밀도(= ρsoil/ρw), ρsoil는 토사의 밀도(모래, 카오린의 경우 2,650 kg/m3), ρw는 물의 밀도(= 997 kg/m3), g는 중력 가속도(= 9.81 m/s2), ν는 물의 동점성 계수(= 0.000000893 m2/s)이다. τc0, fines의 경우 상술한 바와 같이 d50 = 63 μm를 가지는 실트의 한계전단응력(≈ 0.12 N/m2)을 사용한다.
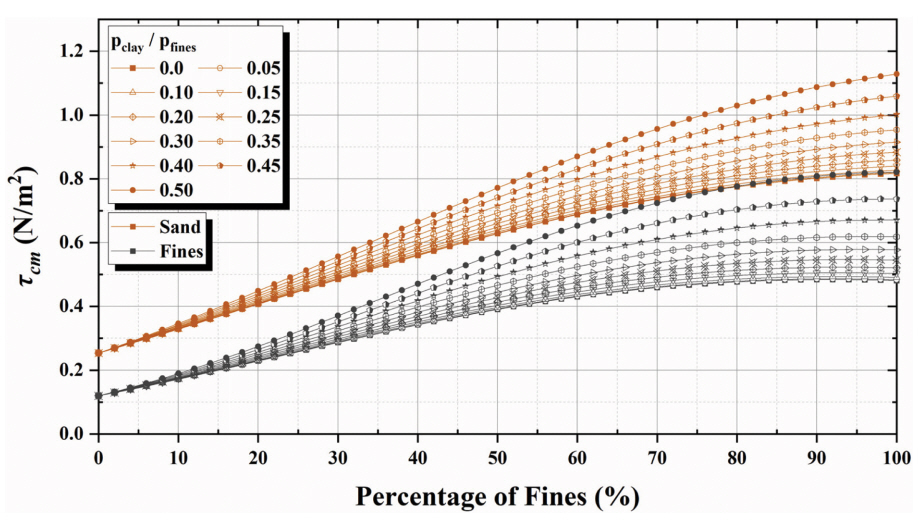
모래의 중앙입경이 0.439 mm(D* = 11.1)의 경우, 진흙 함유율의 변화에 따른 혼합 토사에서의 식(1), (2)로부터 산정한 모래와 진흙의 한계전단응력의 변화를 Fig. 1에 보인다.
Fig. 1에서의 심볼은 진흙 함유율에 있어서의 점토의 비 pclay/pfines를 갈색 실선은 혼합 토사에서의 모래의 한계전단응력, 검은 실선은 혼합토사에서의 진흙의 한계전단응력을 나타낸다. 진흙 함유율에 의한 한계전단 응력은 모래의 경우 0.25~1.13 N/m2, 진흙의 경우 0.12~0.82 N/m2의 범위에서 증가하는 것을 알 수 있다. 또한, 진흙 함유율 증가에 따른 모래와 진흙의 한계전단응력의 증가율은, 진흙 속의 점토의 비율이 높을수록 커지는 것을 알 수 있다. 하지만, 진흙에서의 점토의 비가 0.5 이하의 경우, Fig. 1에 나타낸 것과 같이 같은 점토 함유율에 있어서 진흙의 한계전단응력이 모래보다 작다. 이는 혼합토사로 이루어진 저질에 있어서, 우선적으로 저질의 표층에서의 진흙이 모래보다 이동하기 쉬운 것을 의미하며, 표층으로부터 진흙이 이동하게 되면, 표층의 진흙 함유율이 변화하여 모래의 한계전단응력도 변화(저하)하게 된다. 예를 들어, 파랑에 의한 전단 응력이 0.4 N/m2, 초기 진흙 함유율이 30%(pfines = 0.3)이라고 가정하면, 혼합토사에 의한 토사의 이동은 진흙에서부터 발생한다. 시간 경과에 따른 표층에서의 진흙의 이동은, 진흙 함유율을 감소시킴과 동시에 초기 진흙 함유율에서의 이동량보다 증가하게 되고 이는 진흙의 유실을 가속화 한다. 이에 따라, 진흙 함유량이 약 15%까지 감소하게 되면, 모래 입자도 이동하게 된다. 이와 같이 혼합토사에서 토사의 이동은, 초기 이동한계전단응력의 측면에서뿐만 아니라 시간 경과에 따라 진흙의 유실부터 모래의 이동까지의 일련의 과정을 통한 이동 메커니즘도 중요하기 때문에, 혼합토사로 구성된 진흙과 모래의 이동에 따라 변화하는 저질에서의 진흙과 모래의 양, 그에 따른 진흙 함유율의 변화를 고려할 수 있는 모델이 필요하다.
2.2 혼합 토사 모델의 개요
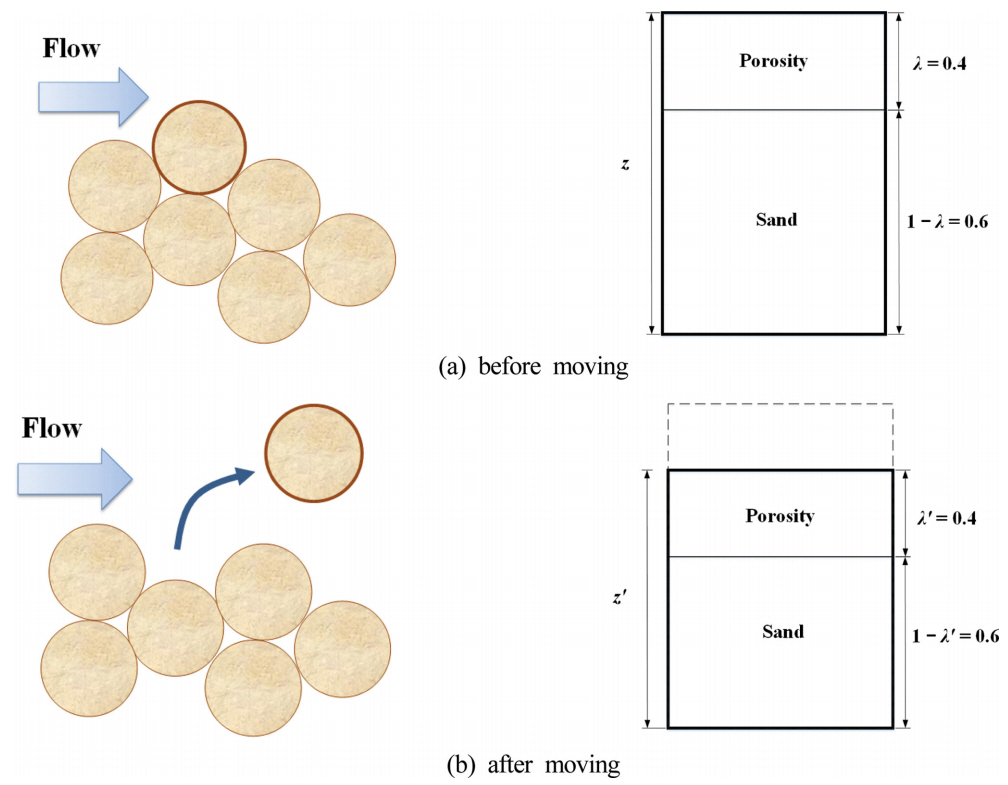
기존의 격자법에서는 토사로 구성된 흙 구조물의 지형이 격자 내에 존재한 중앙입경 d50으로 대표되는 토사(비응집성 토사:모래, 자갈)와 그에 따른 공극의 크기로 표현되었다. 이 경우, 토사량은 격자 크기와의 체적률로 표현된다. 예를 들어 높이 10 mm의 격자를 공극률 λ = 0.4의 토사가 전부 채우고 있다면 토사는 격자 내에서 단위폭당 6 mm, 공극은 4 mm를 점유하게 된다. Fig. 2에 격자법에 있어서 표사이동계산의 개념을 예시한다.
Fig. 2(a)에 보인 바와 같이, 격자 내부와 체적률 1 - λ의 모래와 공극률 λ로 나타내어 진다. 그 후 Fig. 2(b)와 같이, 흐름에 의해 모래가 이동하게 되면 Fig. 2(b)의 우측 그림과 같이, 모래의 체적률은 이동한 모래의 체적률 만큼 감소한 1 - λ'가 되고, 공극률은 변화한 모래의 체적률에 의해 λ'로 변화한다. 이때의 지형은 모래의 체적률 뿐만 아니라 모래에 의해 형성되는 공극률 λ'를 포함한 체적의 높이 z'가 된다. 모래의 이동 전후의 공극률 λ, λ'는 초기 설정의 공극률 0.4를 가지지만, 그 체적은 각각의 지형을 나타내는 높이 z, z'에 대한 체적률을 의미하므로 실제 체적과는 일치하지 않는다. 이처럼 격자법에서의 표사의 계산방법은 토질역학에서 널리 사용되는 토립자의 시상도와 유사하다. Ashida et al.(1982)는 전술한 바와 같이 토립자의 시상도에 기초하여 진흙의 점착력을 고려한 혼합토사에 있어서의 모래 입자의 한계전단응력에 대한 산정식을 제안하고 있다. 반면, Ashida et al.(1982)의 제안식은 혼합토사를 구성하는 모래의 공극을 진흙이 전부 채우고 있다고 가정하기 때문에, 진흙 함유율의 증가에 따른 혼합토사 내의 진흙과 모래의 분포, 공극률의 처리 등과 같은 수치모델화에 있어서 많은 어려움이 존재한다. 한편, Van Rijn(2020)이 제안한 건조체적밀도를 고려한 실험식은 혼합 토사의 공극이 일정한 값으로 유지된다고 볼 수 있으며, 그 크기는 간단한 실험을 통해서 얻을 수 있다. 또한, 혼합토사의 건조체적밀도가 점토, 실트, 모래의 함유율로부터 정의되므로 혼합토사 내부를 차지하는 각각의 토사들의 분포를 간접적으로 파악할 수 있다. 따라서, Ashida et al.(1982)이 전개했던 혼합토사의 시상도를 바탕으로 혼합토사의 건조체적밀도를 고려한 Van Rijn(2020)의 실험식의 기하학적 해석을 통해 혼합토사 모델을 구축하였다.
수중에서의 모래와 진흙(점토 + 실트)으로 구성된 혼합토사의 시상도를 Fig. 3에 나타낸다. Fig. 3(a)에 도시된 바와 같이 혼합토사의 공극은 물로 채워져 있으므로 공극에 존재하는 물의 체적을 Vw, 물의 밀도를 ρw, 진흙의 중량을 Wm, 진흙의 체적을 Vm, 진흙의 밀도를 ρm, 진흙에 의해 함수된 물의 중량을 Wmw, 물의 체적을 Vmw, 모래의 중량을 Ws, 모래의 체적을 Vs, 모래의 밀도를 ρs(= ρm)로 한다. 또한, 모래의 공극률을 λsand, 모래의 체적률을 1 - λsand, 혼합 토사의 공극률을 λmix, 혼합 토사의 체적률을 1 - λmix로 하고, 진흙의 체적률을 λmud, 진흙에 함수된 물의 체적률을 λmw로 한다. 진흙의 중량에 의한 함유율 pfm는 Mm/(Mm + Ms)로 정의된다. 반면, 진흙의 함유율에 의한 체적률의 표현을 간편화하기 위해, 중량에 의한 함유율 대신에 체적에 의한 함유율 pfv = Vm/(Vm + Vs)을 도입하였다. pfm와 pfv의 관계는 식(7)과 같다.
여기서, sm는 진흙의 상대 밀도(= ρm/ρw), ω는 진흙에 의해 함수된 물과 진흙의 중량비이다. 혼합 토사의 전체 체적을 Vt =Vw + Vm + Vmw + Vs라고 하면 Vs는 Vt (1 - λsand)가 되고, Fig. 3(a)의 기하학적 관계로 부터, 모래의 공극률 λsand은 식 (8)이 된다.
따라서 모래의 체적률은,
가 된다. 이와 유사하게 진흙에 의해 함수된 물을 포함한 진흙의 체적률은, Fig. 3(a)로부터 λsand - λmix의 관계를 가지므로 식(10)과 같이 나타내지며, 1 - λsand 대신에 식(9)를 대입하면 λsand - λmix는 식(11)로 부터, 함수된 물을 포함한 진흙의 공극률 λfines는 식(12)로부터 구할 수 있다.
계속해서, Fig. 3(b)에 나타낸 진흙이 포함하고 있는 물의 체적률 λmud는 식(11)에서 λsand - λmix= (Vm + Vmw)/Vt의 관계로부터 Vm에 Vmw/(smω)를 대입하면 진흙이 함수한 물의 체적률 λmw은 다음의 식으로 표현된다.
또한, 진흙의 체적률 λmud는 λsand - λmix - λmw의 관계로부터 식(14)에 의해 계산할 수 있다.
따라서, 혼합토사의 공극률 λmix과 진흙의 함유율 pfm을 안다면, 식(7)-(14)를 통해 혼합 토사에서의 모래, 진흙의 체적을 계산할 수 있다. 또한, 본 연구에서 도입한 함수비 ω는 토사의 물리적 성질을 반영하는 것보다 진흙의 건조체적밀도의 재현에 초점을 맞추고 있으며 진흙의 체적변화 이외의 특성은 고려하지 않는다. 그렇기 때문에, 함수비 ω는 식(5)와 같이, 진흙의 건조체적밀도의 계수(400, 800)에 의해 변화하며, 진흙의 건조체적밀도계수를 Cf라고 하면, Cf는 Fig. 3(a)에 있어서 진흙과 진흙에 포함된 물만으로 혼합토사를 구성할 경우, Cf = λmud× ρm가 되고 이하의 식으로부터 함수비 ω를 구할 수 있다.
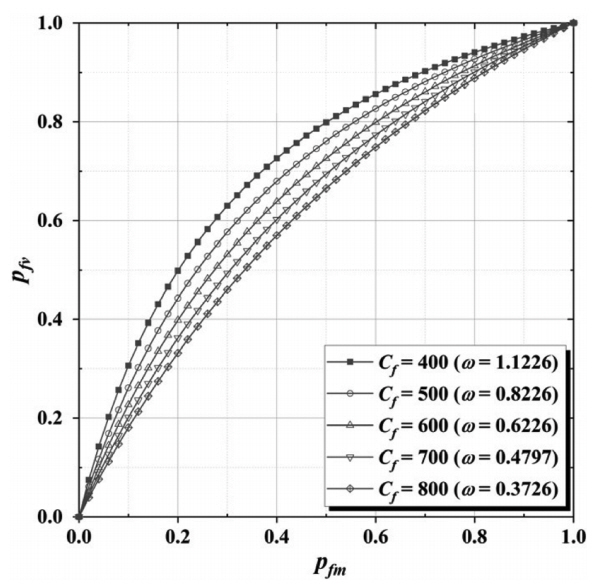
건조체적밀도계수 Cf의 변화에 따른 진흙의 중량에 의한 함유율 pfm과 체적에 의한 함유율 pfv의 관계를 Fig. 4에 나타낸다.
Fig. 4에서 확인되는 바와 같이 Cf가 작을수록 pfv는 pfm보다 더 큰 것을 알 수 있다. 이는 Cf가 작을수록 함수비가 커지게 되고, 그로 인해 진흙의 체적률과 진흙이 포함한 물의 체적률의 합으로 정의된 pfv는 진흙이 흡수한 물의 양이 증가할수록 물을 포함한 진흙의 체적률이 증가하기 때문이다. 이러한 pfv의 증가율은 비교적 진흙 함유율이 작은 영역에서 커지는 경향을 보인다.
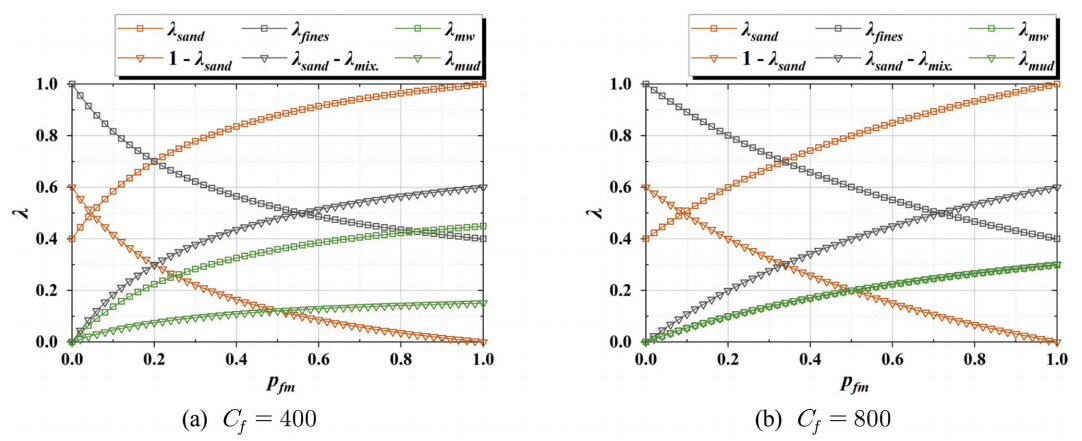
Fig. 5에 Fig. 4와 동일한 파라미터를 이용하여 식(7)-(15)로부터 산출한 Cf = 400, 800의 경우의 진흙 함유량 변화에 따른 각각의 체적률 변화를 보인다. Fig. 5(a)로부터 물의 흡수가 큰 Cf = 400에서는 진흙 함유율이 클수록 모래의 체적률(역삼각형의 갈색선)이 크게 감소하지만, 물을 포함한 진흙의 체적률(역삼각형의 검은색선)과 진흙이 포함한 물의 체적률(사각형의 녹색선)은 크게 증가한다. 또한, 진흙이 포함한 물의 체적률과 진흙의 체적률(역삼각형의 녹색선)의 차이는 진흙 함유율이 클수록 커진다. 한편, 상대적으로 물의 함수 비율이 작은 Cf = 800에서는 진흙 함유율의 증가에 따라 모래의 체적률의 감소율과 물을 포함한 진흙의 체적률의 증가율이 비교적 작은 진흙 점유율에서 조금 크게 나타나지만 Cf = 400와 비교를 하면 그 크기는 미소하다. Cf = 800의 경우, ω = 0.3726이며 진흙의 체적과 진흙이 함유한 물의 체적 비 Vmw/Vm로 환산하면 0.99로 진흙의 체적과 함수된 물의 체적이 거의 같다는 것을 알 수 있다. 그렇기 때문에, 진흙 함유율의 증가에 따라 진흙의 체적률과 물의 체적률이 동률적으로 증가하므로 진흙이 함수한 물의 영향은 크지 않고, 이로 인해 진흙 함유율에 의한 모래와 진흙의 증감률은 크지 않은 것으로 판단된다. 또한, 도시된 그림과 같이 진흙 함유율에 따라 모래와 진흙의 체적률, 그리고 각각의 공극률의 변화가 적절히 표현되어지는 것을 확인할 수 있다. 따라서, 모래와 진흙으로 구성된 혼합 토사 모델을 Nakamura and Mizutani (2010, 2016)가 개발한 3차원 유체, 구조, 지형변화, 지반연성 수치계산모델(Three-Dimensional Coupled Fluid-Structure-Sediment-Seabed Interaction Model; FS3M)에 적용하여 건조체적밀도를 고려한 혼합토사의 표사계산 수치모델을 구축하였다.
3. 건조체적밀도를 고려한 혼합토사 수치모델
3.1 FS3M의 개요
FS3M은 유체, 구조물, 지형변화, 지반연성의 4자간의 상호작용을 해석할 수 있는 수치모델로써 메인 솔버(solver)와 4개의 모듈(module)로 구성된다. 메인 솔버에는 기체와 액체의 경계면을 추적하는 Volume of Fluid(VOF) 법을 개량한 Multi Interface Advection and Reconstructions Solver (MARS)에 기초한 VOF 모듈, 유체와 구조물의 연성 해석(Fluid Structure Interaction, FSI)을 수행하는 Immersed Boundary (IB) 법에 기초한 IB 모듈, 와류와 침투삼출류, 간극 수압의 효과를 고려하며 소류사와 부유사의 유송에 동반되는 이동상의 지형변화 계산과 부유사의 부유, 이류 확산, 침강의 각 유송 과정을 고려한 부유사 농도 분포를 해석하는 Sediment Trnasport(ST) 모듈, u-p 형식의 Biot 식을 유한 요소법(Finite Element Method, FEM)에 의해 해석함으로써 지반의 물과 흙의 연성 해석을 수행하는 FEM 모듈로 구성되어 있다. 메인 솔버와 VOF 모듈의 지배 방정식은 다음과 같다.
(17)
여기서, xi는 위치 벡터(= [xyz]T), t는 시간, p ¯ ρ ^ μ ^ f i S f i o b D i j ¯ τ i j a
3.2 혼합 토사를 고려한 ST 모듈
ST 모듈은 Roulund et al.(2005)를 참조하여 구축한 소류사량을 소류사 유송 모델과 지형변화의 계산 후에 사면의 붕괴를 계산하는 사면 붕괴 모델, 저질의 부유와 침강에 의한 부유사 유송 플럭스를 계산함과 동시에 부유사의 부유, 이류, 확산, 침강의 유송 과정을 고려한 부유 유송 모델, 이동상의 지형변화를 계산하는 저질의 질량 보존식으로 구성되어 있다. 본 연구에서 제안한 혼합 토사 모델을 적용한 FS3M의 ST 모듈은 다음과 같다.
우선, 저질의 질량 보존식은 다음과 같이 주어진다.
여기서, zs는 기준면으로 부터의 이동상 표면의 높이, qx, qy는 각각 x, y 축 방향의 소류사량, PN, s과 PN, f는 모래와 진흙의 부유 함수, q z b , s S q z b , f S
3.3 혼합 토사를 고려한 사면 붕괴 모델
사면의 경사각 β가 저질 입자의 안식각 θr보다 미소각 θr+ 만큼 초과하는 경우 사면은 붕괴를 시작하고 θr보다 미소각 θ- 만큼 작아질 때까지 붕괴가 지속되기 때문에 Roulund et al.(2005)를 참조하여 사면의 경사각 β가 θr+ θ+를 초과할 때, 저질 입자 전체가 정수 상태에서 일정 속도 vb로 사면의 아랫 방향으로 붕괴한다고 가정한다. 또한, 사면 붕괴 시, 토사에 작용하는 양력의 영향은 충분히 작다고 가정하고, 사면 붕괴에 의해 동반되는 저질 입자의 유송 속도 ν b s l i d e
여기서, ε는 차폐계수, CD1는 비선형 저항력 계수(= 0.45), s는 상대 밀도, β는 사면 경사각, μd는 저질의 동마찰계수(= tanθd), θd는 동마찰각이다(= 32.0°). 이때의 사면 경사각 β는 θd와 θr - θr-보다 크고, θs와 θr+ θr+보다 작은 범위가 된다. 사면 붕괴에 동반되는 소류사량 q i s l i d e
여기에서, Cslide는 사면 붕괴에 관한 무차원 파라미터이다(= 290). 사면의 붕괴에 동반되는 저질의 질량 보존식은 q i s l i d e q x s l i d e q y s l i d e q x = q x s l i d e q y = q y s l i d e q x s l i d e q y s l i d e q x s l i d e = q x , s s l i d e + q x , f s l i d e , q y s l i d e = q y , s s l i d e + q y , f s l i d e P N , s = P N , f = 0 , q z b , s S = q z b , f S = 0
4. 혼합 토사로 이루어진 저질의 사면 붕괴
4.1 계산 영역
본 연구에서 제안한 건조체적밀도를 고려한 혼합토사 모델의 수치적 안정성을 평가하기 위해 혼합토사로 이루어진 토사 구조물을 붕괴시켜 그에 따른 혼합토사의 소류이동과 그에 따른 진흙과 모래의 양이 일정하게 유지되는 지를 검토하였다. 본 연구에서는 실제 혼합토사의 사면 붕괴에 관한 재현 계산이 아니므로 정량적 검토보다는 정성적 검토에 초점을 맞췄다. 수치실험에 사용된 계산영역을 Fig. 6에 나타낸다.
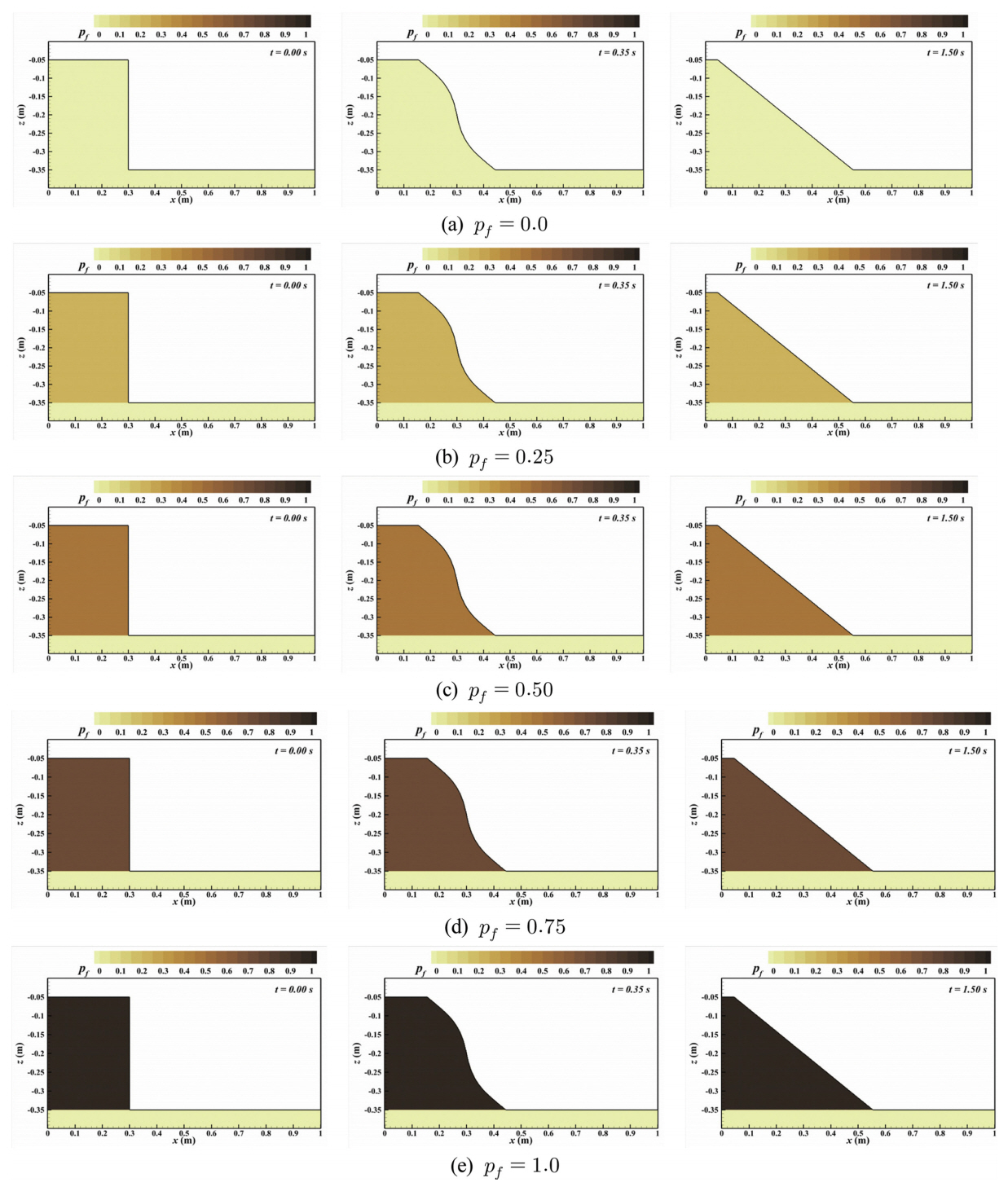
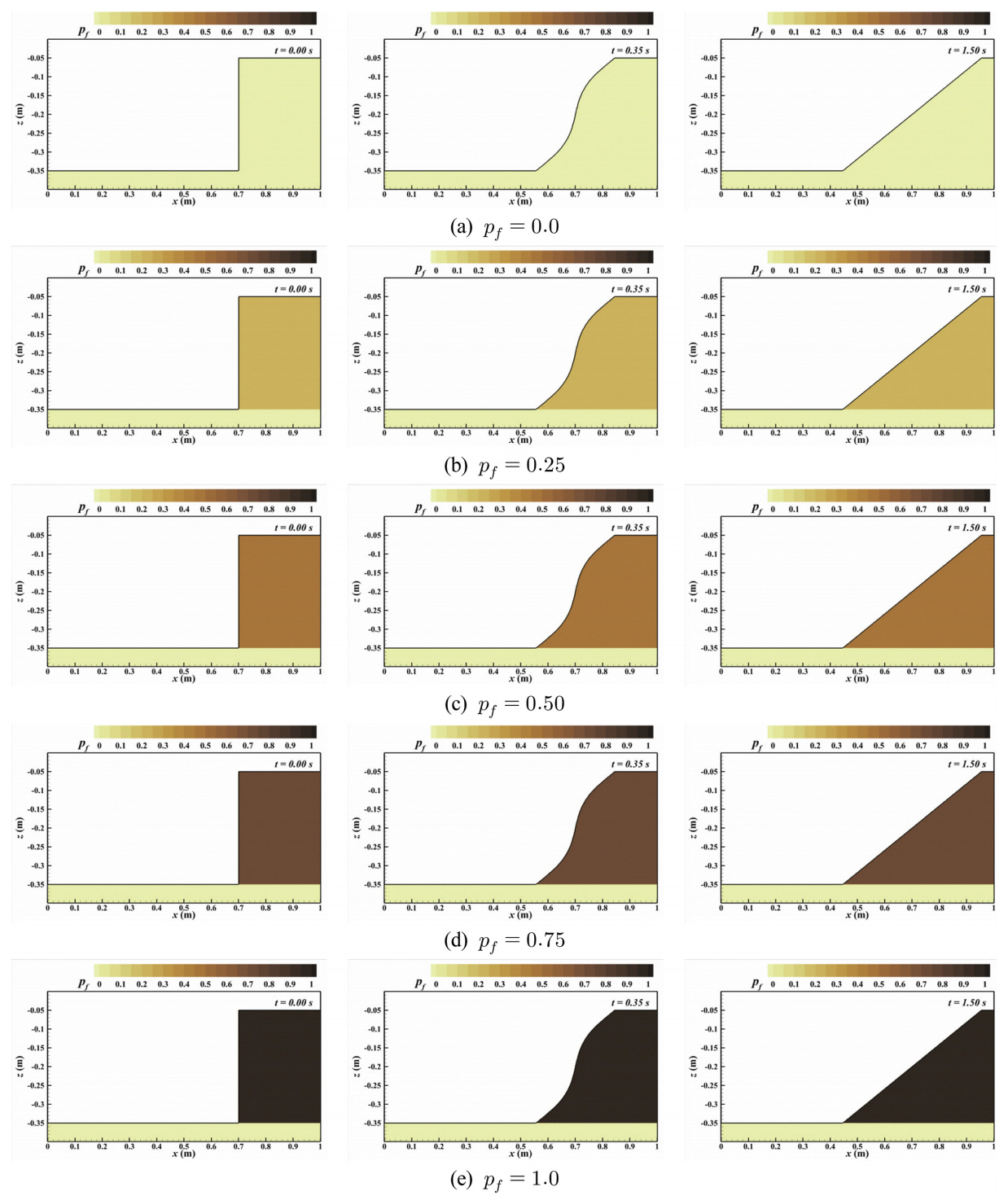
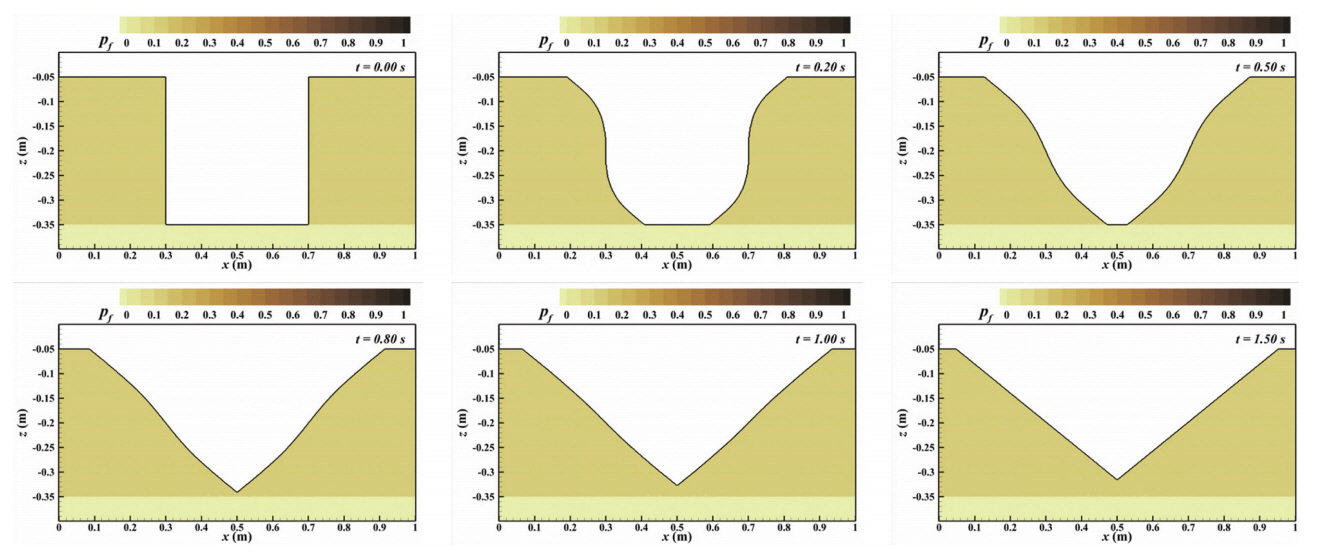
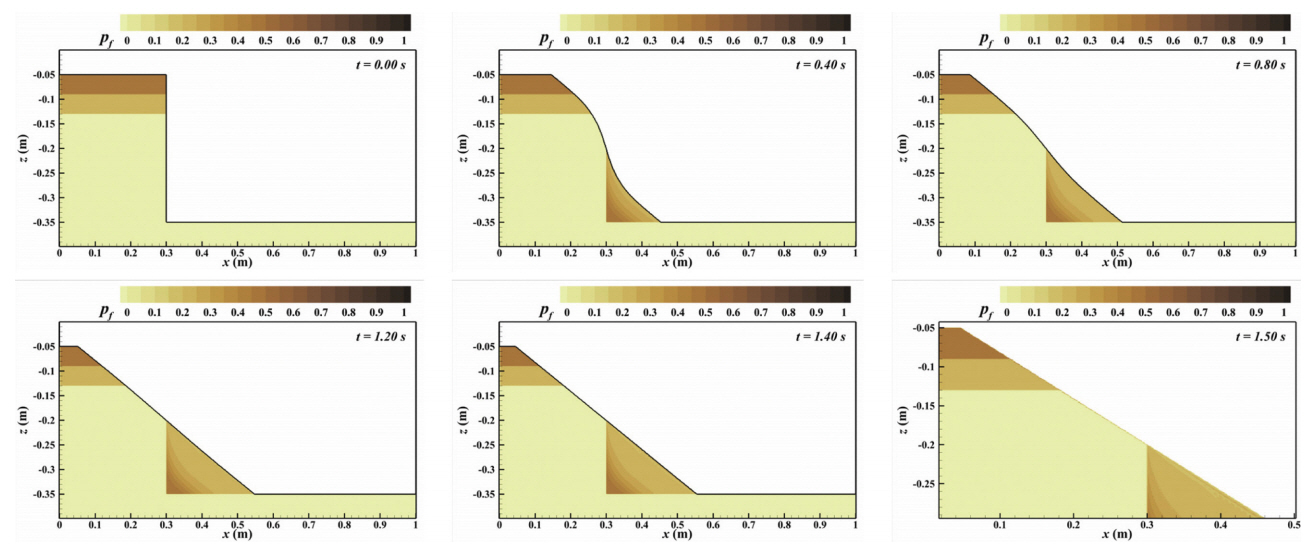
수치계산은 가로 1.004 m(x-방향), 세로 0.4 m(z-방향)의 2차원 해석을 수행하였으며 x 방향 격자 크기는 dx = 0.002 m, z 방향 격자 크기는 dz = 0.001 m로 설정하였다. 혼합토사로 이루어진 흙 구조물은 가로 0.3 m, 세로 0.3 m의 정방형 구조이다. 혼합토사의 사면 붕괴 계산에 있어서 서로 다른 진흙 함유율을 가진 토사 간의 경계에서 수치적 불안정성이 확인되었기 때문에, 사면 붕괴가 일어나는 흙 구조물의 저면에는 0.05 m 두께의 순수 모래(d50 = 0.4 mm)를 설치하여 모래층 위로 퇴적하는 혼합토사의 계산 양상을 검토하였다. 혼합 토사의 진흙 함유율에 따른 안정성을 평가하기 위해 좌측과 우측으로 붕괴하는 혼합 토사에 있어 중량에 의한 진흙 함유율 pf = 0.0, 0.25, 0.5, 0.75, 1.0의 5종류에 대해 계산을 실시하였다. 또한, Fig. 6(c), (d)와 같이 양방향에서 붕괴하는 동일 진흙 함유율의 혼합토사 모의와, 서로 다른 진흙 함유율의 층을 가진 혼합토사에 대해서도 검토하였다. 수치모의 시간은 사면 붕괴가 종료되는 1.5 s로 설정하였다.
4.2 계산 결과
혼합토사의 사면 붕괴 계산에 따른 모래와 진흙의 공간적 분포를 나타내는 혼합토사 구조물의 진흙 함유율 결과를 Figs. 7~10에 나타낸다. Figs. 7, 8에 보인 바와 같이 좌측에서 우측으로, 우측에서 좌측으로의 사면 붕괴에 있어 사면 붕괴가 종료될 때까지 초기 진흙 함유율을 유지한 채 소류이동을 하는 것을 확인할 수 있다. 또한, 진흙 함유율이 서로 다른 저면(순수 모래) 위에서의 퇴적도 수치적 오류 없이 재현되는 것이 확인되었다. 사면 붕괴에 의한 지형변화에 있어서도, 기존 모래만의(pf = 0.0) 사면 붕괴와 동일한 지형변화를 보이며 소류이동에 있어서 안정적으로 계산되는 것이 확인되었다.
Fig. 9에 보인 양방향에서의 사면 붕괴 계산에 있어서도, 사면 붕괴에 의해 교차하는 x = 0.5 m의 경계에서 진흙과 모래의 양이 균일하게 유지되며 사면 붕괴가 발생하는 것을 확인하였다. 서로 다른 진흙 함유율을 가진 혼합토사 구조물에서의 사면 붕괴 양상은 Fig. 10에 도시된 바와 같이 최상단의 진흙 함유율이 높은 층부터 붕괴가 발생하여 저면에 퇴적되고, 그 이후 상대적으로 저 함유율 층이 이동하며 퇴적이 발생하는 초기 토사 구조물의 우측에서 곡선의 굴곡을 가진 진흙 함유율이 변화하는 것이 관찰된다. 또한, 시간 경과에 따라 상층부의 고 함유율보다 그 밑의 저 함유율 층의 붕괴량이 많아지면서 우측 저면에 퇴적되는 혼합토사의 진흙 함유율은 위로 갈수록 저하되는 것이 확인되었다. 하층부에 있는 순수 모래층도 붕괴를 하면서 계산 종료 시에는 순수 모래층의 상단에 얇은 진흙 함유율을 가진 막이 형성되는 것을 확인할 수 있다. 이를 통해, 본 연구에서 제안한 건조체적밀도를 고려한 혼합토사 모델의 수치적 모델 안정성이 확인되었으며, 본 모델을 바탕으로 실제 파랑장에서의 표사유동모델을 구축함으로써 혼합토사 모델의 활용 가능성이 확인되었다.
5. 결 론
본 연구는 혼합토사의 이동한계에 있어서 중요한 요소인 진흙의 함유율과 혼합토사에 있어서의 진흙과 모래의 건조체적밀도를 고려한 혼합토사 계산모델을 혼합토사의 기하학적 구조를 나타내는 토립자의 시상도를 바탕으로 구축하였다. 건조체적밀도의 특성을 고려하기 위해 혼합토사의 시상도에서 진흙이 함유하는 물의 함량을 나타내는 함수비를 도입함으로써 실험을 통해 얻어지는 진흙의 건조체적밀도를 재현할 수 있게 되었다. 이를 통해, 일정하게 유지되는 혼합토사의 공극률과 그 층에서의 진흙 함유율이 확인되면 혼합토사를 구성하는 모래, 진흙, 진흙이 함유하는 물의 체적율을 계산할 수 있다. 이는 역으로 혼합토사의 수치계산에 있어서 파랑 혹은 흐름에 의한 혼합토사 내의 모래와 진흙의 부피 변화가 확인된다면 변화된 체적율과 혼합토사의 공극률을 바탕으로 혼합토사의 함유율을 유추할 수 있다. 건조체적밀도를 고려한 혼합토사 수치모델을 통해 혼합토사의 사면 붕괴 계산에 있어서 수치적 안정성을 검토하였고, 사면 붕괴 방향 및 혼합토사를 구성하는 서로 다른 진흙 함유층에 있어서의 소류계산에서 안정적으로 수치모의가 가능한 것이 확인되었다. 이를 바탕으로 실제 파랑장 조건하에서 혼합토사의 이동 특성을 계산할 수 있는 표사모듈의 구축이 가능하며 효율적인 인공 갯벌의 유지 관리와 저질의 동적 특성을 해석할 수 있는 가능성이 시사되었다.
본 연구는 개발된 수치모델의 수치적 안정성을 검토하기 위해 혼합토사의 이동 및 공간적 분포특성을 고려한 사면붕괴 문제로 적용범위를 한정하였다. 향후, 실제 파랑 작용 하에서 혼합토사로 이루어진 저면에서의 진흙의 유출특성을 검토한 실험에 대해 수치모의를 실시하여 재현정도를 정량적으로 평가할 계획이다.