Numerical Analysis of Modified Seabed Topography Due to the Presence of Breakwaters of Varying Reflection Characteristics using Physics-based Morphology Model [SeoulFoam]

Yong Jun Cho

doi:10.9765/KSCOE.2021.33.4.168

Journal of Korean Society of Coastal and Ocean Engineers > Volume 33(4); 2021 > Article

방파제 형식에 따른 반사율 변화가 해저지형에 미치는 영향 수치해석: 물리기반 지형모형 SeoulFoam을 중심으로

Article

J Korean Soc Coast Ocean Eng 2021; 33(4): 168-178.

Published online: August 31, 2021

DOI: https://doi.org/10.9765/KSCOE.2021.33.4.168

방파제 형식에 따른 반사율 변화가 해저지형에 미치는 영향 수치해석: 물리기반 지형모형 SeoulFoam을 중심으로

조용준^*

^*서울시립대학교 토목공학과 교수

Numerical Analysis of Modified Seabed Topography Due to the Presence of Breakwaters of Varying Reflection Characteristics using Physics-based Morphology Model [SeoulFoam]

Yong Jun Cho^*

^*Professor, Department of Civil Engineering, University of Seoul 163 Seoulsiripdaero, Dongdaemun-gu, Seoul 02504 Korea

Corresponding author: Professor, Department of Civil Engineering, University of Seoul 163 Seoulsiripdaero, Dongdaemun-gu, Seoul 02504 Korea, Tel: +82-2-6490-2427, Fax: +82-2-6490-2424, young@uos.ac.kr

Received August 13, 2021 Accepted August 23, 2021

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

요약

방파제 형식에 따른 반사율 변화가 해저지형에 미치는 영향을 살펴보기 위한 수치 모의를 수행하였다. 수치 모형은 OpenFoam 기반 tool box인 OlaFlow와 물리기반 지형모형[SeoulFoam]으로 구성하였으며, 이 과정에서 침·퇴적으로 인해 변형을 겪는 해저지형과 내습하는 파랑 간의 상호작용은 Dynamic Mesh를 활용하여 기술하였다. 다양한 반사 특성을 보이는 사석 경사제, 직립제, 곡면 슬릿 케이슨 방파제는 서로 다른 정상파를 결과하였으며, 이는 해저지형에 상당한 영향을 미치는 것을 확인하였다. 이러한 결과는 저면 유속이 상대적으로 큰 정상파 마디[node]에서 연행된 모래가 경계층 drift에 의해 배[antinode]로 이송된다는 Nielsen(1993)의 연구 결과와도 일치한다. 이렇게 재배치되는 모래로 정상파의 배[antinode]에는 sand wave의 마루, 마디[antinode] 인근에는 sand wave의 곡이 형성되었으며, sand wave 진폭은 반사계수가 우월한 곡면 슬릿 케이슨에서 가장 크게 관측되었다. 이러한 현상은 반사계수가 큰 경우 마디에서의 저면 유속 증가로 상대적으로 많은 모래가 연행되어 발생하는 것으로 판단된다.

핵심용어: 물리기반 지형모형, 사석 방파제, 기부 침식, Dynamic Mesh, SeoulFoam, 연흔

Abstract

Numerical simulations were implemented to look into the modified seabed topography due to the presence of breakwaters of varying reflection characteristics. The numerical model was composed of OlaFlow, an OpenFoam-based tool box, and a physics-based morphology model [Seoul Foam]. In doing so, the interaction between the seabed, which undergoes deformation due to siltation and scouring, and the incoming waves was described using Dynamic Mesh. The rubble-mound, vertical, and curved slit caisson breakwaters with varying reflection characteristics resulted in standing waves that differ from each other, shown to have a significant influence on the seabed topography. These results are in line with Nielsen’s study (1993) that sands saltated under the surface nodes of standing waves, where the near-bed velocities are most substantial, convected toward the surface antinodes by boundary-layer drift. Moreover, the crest of sand waves was formed under the surface antinodes of standing waves, and the trough of sand waves was formed under the surface antinodes. In addition, sand wave amplitude reaches its peak in the curved slit caisson with a significant reflection coefficient, and the saltation of many grains of sand would cause this phenomenon due to the increased near-bed velocity under the nodes when the reflection coefficient is getting large.

Keywords: physics-based morphology model, rubble-mound breakwater, toe scouring, Dynamic Mesh, SeoulFoam, sand waves

1. 서 론

거친 해양환경으로부터 자유로운 수역을 얻기 위해 거치되는 방파제는 해양환경에 따라 다양한 형태를 지닌다. 초기에는 주로 거친 해양환경에서 발생하는 충격 쇄파압에 대해 충분한 내구성을 담보할 수 있도록 설계되어 조밀한 사석으로 제체를 조성하고 표층을 피복석과 상치 콘크리트로 마감하는 형태가 주류를 이루며 이러한 형식의 방파제는 사석 경사식 방파제[rubble-mound breakwater]로 분류된다. 최근에는 선박대형화로 인해 방파제는 수심이 20 m 내외인 해역에 거치되며 이 경우 소요되는 대규모 사석 확보가 어려워 직립식 케이슨 방파제가 선호되나, 파랑에너지 소산이라는 관점에서 보면 사석 경사제에는 미치지 못한다(Cho, 2020b). 전술한 직립식 케이슨 방파제는 사석 경사제에 견줄만한 파랑에너지 소산 효과를 얻기 위해 유수실과 슬릿이 추가로 장착되는 등 진화과정을 거치며 수리 특성을 규명하기 위해 수행된 다양한 노력으로 현재 연구성과가 상당하다(Cho, 2021a). 그러나 직립식 케이슨 방파제와 관련된 연구의 대부분은 유수실 수리특성, 충격 쇄파압 위주로 진행되어, 방파제 거치에 따른 수환경 변화가 해저지형에 미치는 영향을 체계적으로 다루려는 노력은 상당히 부족해 보인다.

이러한 추론의 근거는 방파제 기부 침식을 방지하기 위한 구조물 대부분은 여전히 하천 수리학에서 이야기하는 평형 하상[Equilibrium regime](Sumer and Fredsoe, 2002) 혹은 최대세굴 깊이(Sumer and Fredsoe, 2002) 등의 개념에 준거해사석을 다층 혹은 하나의 층으로 쌓아 보호하는 방법이 주류를 이룬다는 사실에서 찾을 수 있다(Cho, 2021a). 전술한 방법은 잔류수압으로 인한 액상화현상으로 인해 사석 밑에 있던 모래가 용출되는 등의 한계를 지니며 이는 사석 침하로 이어진다. 이와 더불어 해저지형은 내습하는 파랑에 대응하여 쉼 없이 그 모양이 바뀐다는 사실에 준거하면 쇄굴이 일정량 진행되면 더는 진행되지 않는다는 Equilibrium regime 혹은 최대 쇄굴심 등의 개념은 그 물리적 근거가 희박하다는 사실 이 해안공학계에서 끊임없이 제기되고 있어, 전술한 기부 보호공은 한계를 지니는 것으로 판단된다(Cho, 2021a; Cho, 2020a; Cho and Kim, 2019; Chang and Cho, 2019; Cho et al., 2019).

이러한 시각에서 최근 Cho(2021a)는 평형 하상 혹은 최대 쇄굴심의 물리적 근거를 확인하기 위해 물리 기반 지형모형인 SeoulFoam을 활용하여 사석 방파제 기부에서의 세굴을 수치 해석하였다. 이 연구에서 Cho(2021a)는 정상파에 노출되는 시간이 증가함에 따라 연흔의 진폭도 같이 증가하며, 방파제 기부 인근 수역에서의 세굴심도 깊어지는 것을 확인하는 등의 성과를 거둔 것으로 보인다. 전술한 Cho(2021a)의 연구 결과는 침·퇴적으로 인해 변형을 겪는 해저지형이 내습하는 파랑에 미치는 영향을 설명하지는 못했다는 점에서 개선의 여지는 있으나, 평형 하상과는 각을 이루는 것으로 사석 적층에 준거한 현재의 기부 침식 방지 공을 재평가하는 작업이 필요하다는 것을 함의한다.

이러한 인식에 기초하여 본 연구에서는 방파제 기부 침식 대응 방안을 마련하기 위한 기초연구의 일부로 방파제 형식에 따른 반사율 변화가 해저지형에 미치는 영향을 수치 해석하였다. 이 과정에서 침·퇴적으로 인해 변형을 겪는 해저지형과 내습하는 파랑 간의 상호작용은 물리기반 지형모형[Seoul Foam]의 해석 결과를 활용하여 수치 모의 단계별로 계산 격자망을 수정하는 Dynamic Mesh를 활용하여 기술하였다(Cho, 2021b).

2. 수치 모형

수치 모의는 동수역학 모형으로는 OpenFoam 기반 tool box인 OlaFlow와 물리 기반 지형모형인 SeoulFoam을 활용하여 수행하였으며, 이해를 돕기 위해 2.2.1절과 2.2.2절에는 OlaFlow와 물리 기반 지형모형인 SeoulFoam, 2.3절에는 Dynamic Mesh를 각각 정리하였다.

2.1 OlaFlow

OlaFlow에서 파랑 모형은 RANS[Reynolds Averaged Navier-Stokes equation]와 질량 보존식으로 구성되며, 자유수면은 VOF[Volume of Fraction] 법을 활용하여 추적된다. 난류 모형으로는 k-ε 모형을 사용하였다(Pope, 2004).

OlaFlow(Higuera et al., 2013a; Higuera et al., 2013b; Cho and Bae, 2019)에서 사용되는 파랑 모형인 RANS, 연속 방정식을 기술하면 다음과 같다.

(1)

▽·U = 0

(2)

∂ρU∂t+▽·(ρUU)-▽·(μeff▽U)=-▽p*-g·X▽ρ+▽U·▽μeff

식(1), (2)에서 U는 속도벡터, g는 중력가속도벡터, X는 위치벡터를 각각 나타낸다. μ_eff는 μ + ρν_turb로 정의되는 동점성 계수, p^*는 유사 동압력을 각각 나타낸다.

이상 유체를 해석하기 위한 VOF 식을 기술하면 다음과 같으며,

(3)

∂γ∂t+▽·Uγ+▽·Ucγ(1-γ)=0

여기서 γ는 VOF 법에서 자유수면을 추적하기 위해 도입된 지표로, 1에 가까울수록 액체 상태, 0에 가까울수록 기체상태를 나타내며 본 논문에서는 자유수면의 위치를 γ = 0.5로 정의하였다.

2.2 물리기반 지형모형[SeoulFoam]

물리기반 지형모형 SeoulFoam은 부유사 해석을 위한 이송확산 방정식과 표사수지로부터 유도된 Exner 식으로 구성된다(Cho, 2020a; Jacobsen et al., 2014). 전술한 Exner 식의 유도과정에는 소류사와 바닥으로 회귀하는 부유사를 고려하였으며, 표사 초기이송, 부유사 농도 저면 경계치, 소류사 이송률 산출과정에는 Shields Diagram, 삼차원 수치 모의된 유동계 정보로부터 직접 산출된 저면 전단응력이 활용된다(Cho, 2020a; Jacobsen et al., 2014).

2.2.1 이송확산 방정식

이송확산 방정식은 다음과 같이 기술할 수 있으며,

(4)

∂c∂t+▽·[(γu+wf)c]=▽·[γ(ν+νt)▽c]

여기서 c는 단위 체적당 부유사 농도, w_f와 u는 각각 모래침강속도와 유속 벡터를 나타내며, ν와 ν_t는 각각 동점성계수와 와동점성계수를 나타낸다.

SeoulFoam에서는 식(4)로 정의되는 초기·경계치 문제를 완결하는 데 필요한 바닥에서의 순간 체적 표사 농도 c_b는 다음과 같이 산출되며(Cho, 2020a; Jacobsen et al., 2014),

(5)

cb=co(1+1λb)3

여기서 c_o는 최대 부유사 농도를 나타내며 본 논문에서는 0.35의 값을 취하였으며, λ_b는 바닥에서의 순간 선형 표사 농도를 나타내며 다음과 같이 기술될 수 있다(Bagnold, 1954; Einstein, 1950).

(6)

λb2=κ2α120.013sθ'(θ'-θc'-π6μdpEF)

식(6)에서 θ'는 Shields parameter를 나타내며 이를 기술하면 다음과 같으며,

(7)

θ'=τbρ(s-1)gd

여기서 τ_b는 저면 전단응력, s는 모래 비중, ρ는 해수 밀도, d는 모래 지름을 각각 나타낸다. 식(6)에서 pEF는 모래가 움직일 수 있는 확률을 나타내며 다음과 같이 기술할 수 있다.

(8)

pEF=[1+(16πμdθ'-θc')]-1/4

식(8)에서 μ_d는 동적 마찰계수를 나타낸다.

2.2.2 물리기반 지형모형 SeoulFoam

물리기반 지형모형 Exner 식은 다음과 같이 기술할 수 있으며(Cho, 2020a; Jacobsen et al., 2014),

(9)

∂h∂t=-11-ed[▽·qb+E+D]

여기서 e_d는 공극률을 나타내며, 침식률을 나타내는 E는 다음과 같이 산출될 수 있다.

(10)

E=-(ν+νt)∂c∂n|N|

식(10)에서 n은 저면에서의 단위 외향 법선벡터를 나타내며, 따라서 외향 법선벡터 N은 다음과 같이 정의되며,

(11)

N=|N|n

여기서 |N|은 경계 인근 육면체로 구성된 셀에서 바닥과 접하는 면의 면적을 나타낸다. 식(9)에서 중력에 의해 바닥으로 회귀하는 모래를 나타내는 D는 침강속도 w_f와 유속 u의 합을 저면 법선벡터 N에 투영하여 산출되며 이를 내적을 활용하는 경우 다음과 같이 기술될 수 있다.

(12)

D=cb|(wf+u)·N|

여기서 c_b는 바닥에서의 순간 체적 표사농도를 나타내며 식 (5)에 이미 정의한 바 있다.

식(9)에서 q_b는 소류사 이송률을 나타내며 다음과 같이 기술할 수 있으며,

(13)

qb=16πdpEFub

여기서 소류사 이송속도 u_b는 다음과 같이 정의되는 평형방정식으로부터 산출된다(Cho, 2020a; Cho, 2019; Jacobsen et al., 2014).

(14)

wτ+ff+fD=0

표사에 작용하는 중력 w은 다음과 같이 기술될 수 있으며,

(15)

w=π6ρ(s-1)d3g

바닥과 나란한 방향으로 작용하는 접선방향 성분 w_τ은 외적을 활용하는 경우 다음과 같이 기술될 수 있다.

(16)

wτ=1|N|2[N×(w×N)]

표사가 u_b라는 속도로 움직이는 경우 생성되는 마찰력 f_f은 운동마찰계수와 수직반력으로 기술하면 다음과 같다.

(17)

ff=-1|N||w·N|μdub|ub|

모래 입자에 작용하는 항력 f_D는 다음과 같이 기술될 수 있으며,

(18)

fD=12ρcsπ4d2|uτ|uτ

여기서 상대속도 u_t은 u_nw,t,-u_b로 정의되며, c_s는 항력과 물에 잠긴 모래 입자의 부력에 의한 중량감소를 설명해 주는 계수로 Luque(1974)의 실험 결과에 준거하면 다음과 같이 기술될 수 있다.

(19)

cs=4μd3a212θc'

2.3 Dynamic Mesh

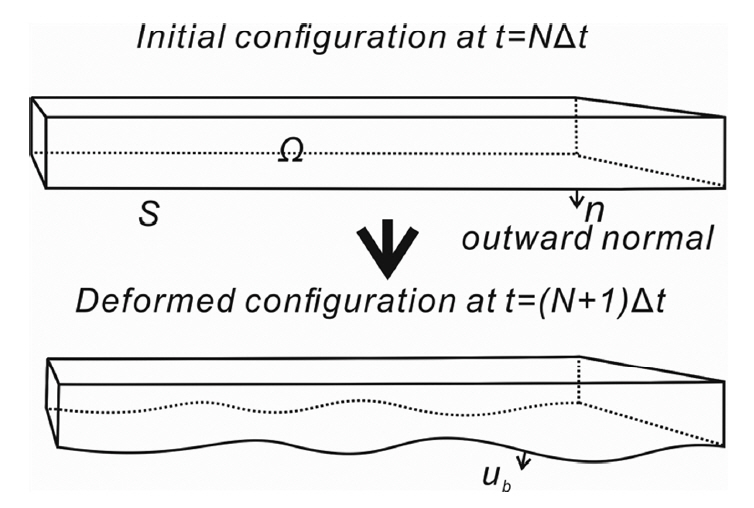
침·퇴적으로 인해 해저지형은 끊임없이 변하며 이렇게 변형된 해저지형은 파랑 전파과정에도 상당한 영향을 미친다. 전술한 해저지형과 파랑 사이의 상호작용은 Dynamic Mesh 기법을 활용하여 기술하였으며, 침·퇴적으로 인해 임의의 형상을 띄는 통제용적의 경우 질량 보존식은 다음과 같이 기술될 수 있다(Tukovic and Jasak, 2008) [Fig. 1 참조].

(20)

∂∂t∫ΩρϕΩ+∫sρn·(u-ub)ϕ∂s= ∫sρεϕn·▽ϕ∂s

상기 식에서 n은 외향 법선벡터, u는 유속, u_b는 침·퇴적으로 인해 바닥이 변형되는 속도, ε_ϕ는 확산계수를 각각 나타내며 통제용적의 체적변화율과 u_b는 다음과 같이 정의되는 공간 보존식을 충족한다.

(21)

∂∂t∫Ω∂Ω-∫sn·nb∂s=0

O(△t²)의 정도로 이산화하는 경우 식(20)은 다음과 같이 기술될 수 있으며,

(22)

3ρN+1ϕN+1ΩN+1-4ρNϕNΩN+ρN-1ϕN-1ΩN-12△t+∑f(m˙N-ρNV˙N)ϕN=∑f(ρεϕ)NSNnN·(▽ϕ)N

여기서 위첨자는 time step을 나타내며, m˙과 V˙은 각각 다음과 같이 정의된다.

(23)

m˙=n·uS

(24)

V˙=n·ubS

해저지형 변화가 점진적으로 진행되는 경우 식(20)에서 오른쪽 첫 번째 항은 미미하며, 이 경우 계산 격자망의 변형은 큰 변형을 겪는 구조물과 유사하게 다음과 같이 기술되는 Laplace 식을 충족한다(Tukovic and Jasak, 2008).

(25)

▽·(ε▽u)=0

식(9)에 기술된 Exner 식을 해석하여 얻은 해저지형 변형 혹은 속도 u_b는 전술한 Laplace 식의 외력 혹은 경계조건으로 활용되며, 각 격자점의 위치 X_NEW는 다음과 같이 갱신되며,

(26)

XNEW=XOLD+u△t

식(20), (25)의 확산계수 ε는 침·퇴적이 진행되는 바닥으로부터의 떨어진 거리에 반비례하는 것으로 취한다.

3. 수치 모의

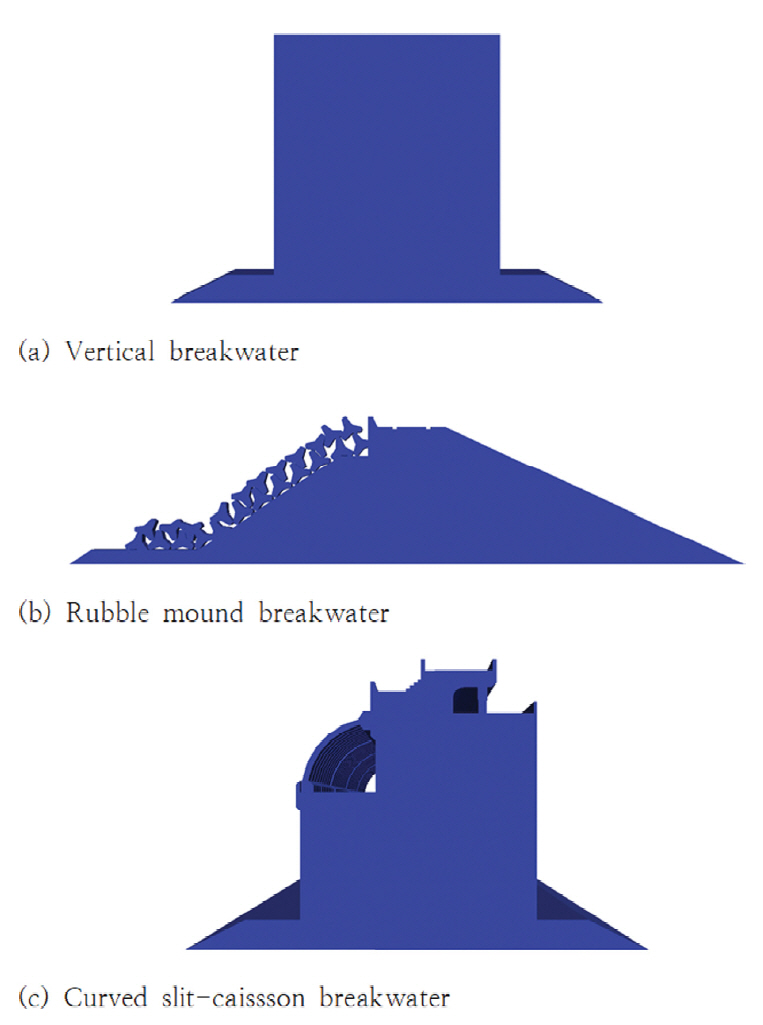
방파제 기부 침식 대응 방안을 마련하기 위한 기초연구의 일부로 방파제 형식에 따른 반사율 변화가 해저지형에 미치는 영향을 살펴보기 위한 수치 모의를 사석 경사제, 직립제, 곡면 슬릿 케이슨 방파제를 대상으로 수행하였다[Fig. 2 참조]. 식(9)에 정의된 Exner 식 형태의 물리기반 지형모형은 FAM(Finite Area Method)을 활용하여 수치해석 하였으며, 해저면은 동수역학 모형인 RANS 해석을 위해 사용된 격자망과 같은 해상도로 이산화하였다. Mesh는 과다한 계산을 피하고 보다 효율적인 수치 모의를 위해 0.25 s 간격으로 수정하였다. 이해를 돕기 위해 Fig. 3에는 수치 수조를 도시하였으며, 도시된 계산영역은 162,500(1625 × 1 × 100) 개의 절점을 사용하여 이산화하였다.

수심은 해안선으로부터 60~80 m 떨어진 지점까지 경사가 1/10 내외인 급경사의 전빈이 포진하며 이후 수심이 8 m 내외인 간조 단구[low tide terrace]가 넓게 포진하는 동해안 지형특성을 고려하여 8 m로 취하였으나(Cho, 2019; Chang and Cho, 2019, Cho and Kim, 2019, Cho et al., 2019), 최종수치 모의는 과다한 계산량을 피하가 위해 1/7로 축소된 시공간에서 수행하였다. 파형은 간조 단구에서의 수심을 고려하여 유한 수심에서의 대표적 비선형파랑 모형으로 알려진 Cnoidal wave로 취하였으며(Cho, 2019; Dean and Dalrymple, 2002), 모래는 동해안에 분포하는 모래 특성을 고려하여 d₅₀ = 0.6 mm를 사용하였다(Cho, 2019; Chang and Cho, 2019; Cho and Kim, 2019; Cho et al., 2019). Table 1에는 수치모의에 사용된 파랑 제원을 정리하여 수록하였다.

4. 수치 결과

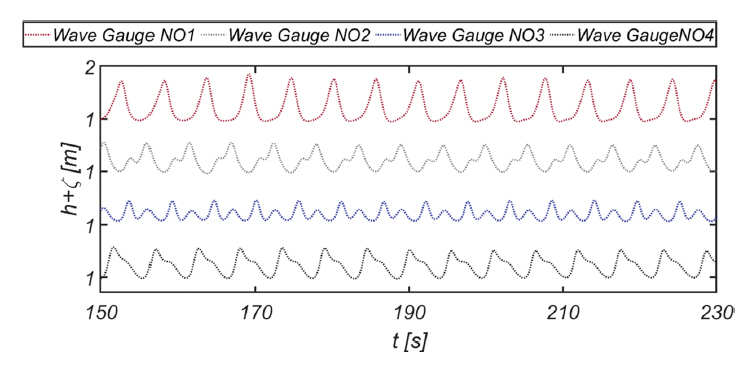
Fig. 4에는 RUN 4에서 관측되는 파동계를 정리하였으며, Fig. 5에는 Wave Gauge NO 1, 2, 3, 4[Fig. 3 참조]에서 관측된 자유수면 시계열자료를 도시하였다[RUN 1]. 목표했던 파랑이 정확히 조파되어 사석 경사제를 향해 정연하게 진행하며, 방파제 경사면을 따라서 진행되는 처오름과 처오름에 의해 결과되는 월파가 정확하게 모의 되는 것을 확인할 수 있다[Fig. 4 참조]. Wave Gauge NO 2, 3의 경우 사석 경사제로부터 시작되어 먼바다를 향해 진행하는 반사파로 인해 상당히 불규칙한 파랑이 관측된다. 진폭 크기로 미루어 보면 Wave Gauge NO 3 인근에는 정상파의 마디[node], Wave Gauge NO 4 인근에는 정상파의 배[anti-node]가 형성되는 것으로 보인다.

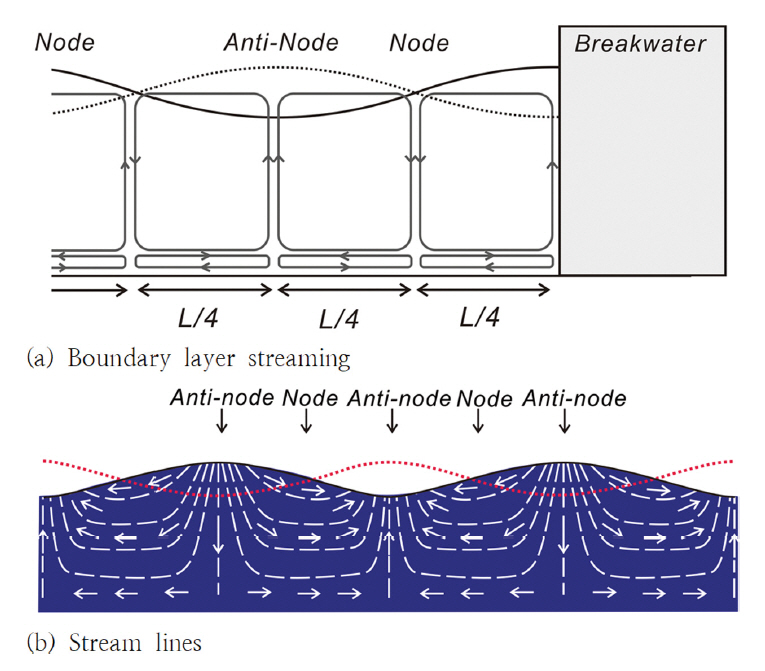
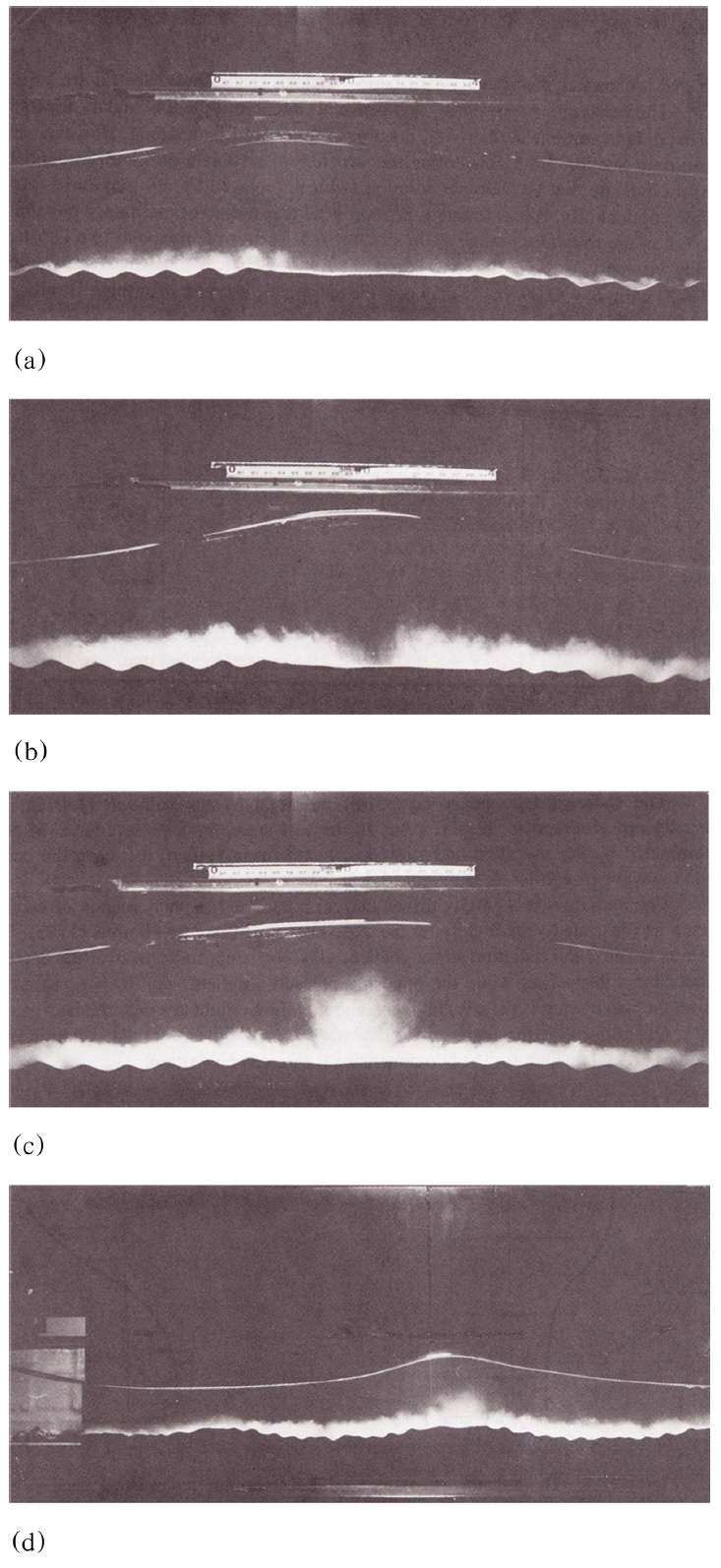
Nielsen(1993)의 연구성과에 따르면 저면 유속이 상대적으로 큰 정상파의 마디[node]에서 연행된 모래가 경계층 boundary layer streaming에 의해 배[antinode]로 이송되며, 이렇게 이송된 모래로 정상파의 배[antinode] 인근에는 sand wave의 마루, 마디[antinode] 인근에는 sand wave의 곡이 형성된다[Fig. 6, 7 참조]. 따라서 전술한 정상파의 마디[node]와 배[antinode] 바닥에서 형성되는 sand wave의 형상은 본 연구에서 제시한 Dynamic Mesh 기반 물리기반 지형모형[Seoul Foam]의 강건성을 가늠할 수 있는 검증자료로 활용될 수 있을 것으로 판단된다.

Fig. 8, 9, 10, 11에는 Dynamic mesh가 만들어내는 차이를 예시하기 위해 계산영역의 진화과정을 정리하였다. 파랑에 노출되는 시간이 증가함에 따라 방파제 전면해역에 형성되는 정상파와 전술한 정상파에서의 모래이송으로 인해 사주로 상징되는 해저지형 변화가 상당한 정도로 모의 되는 것을 확인할 수 있다.

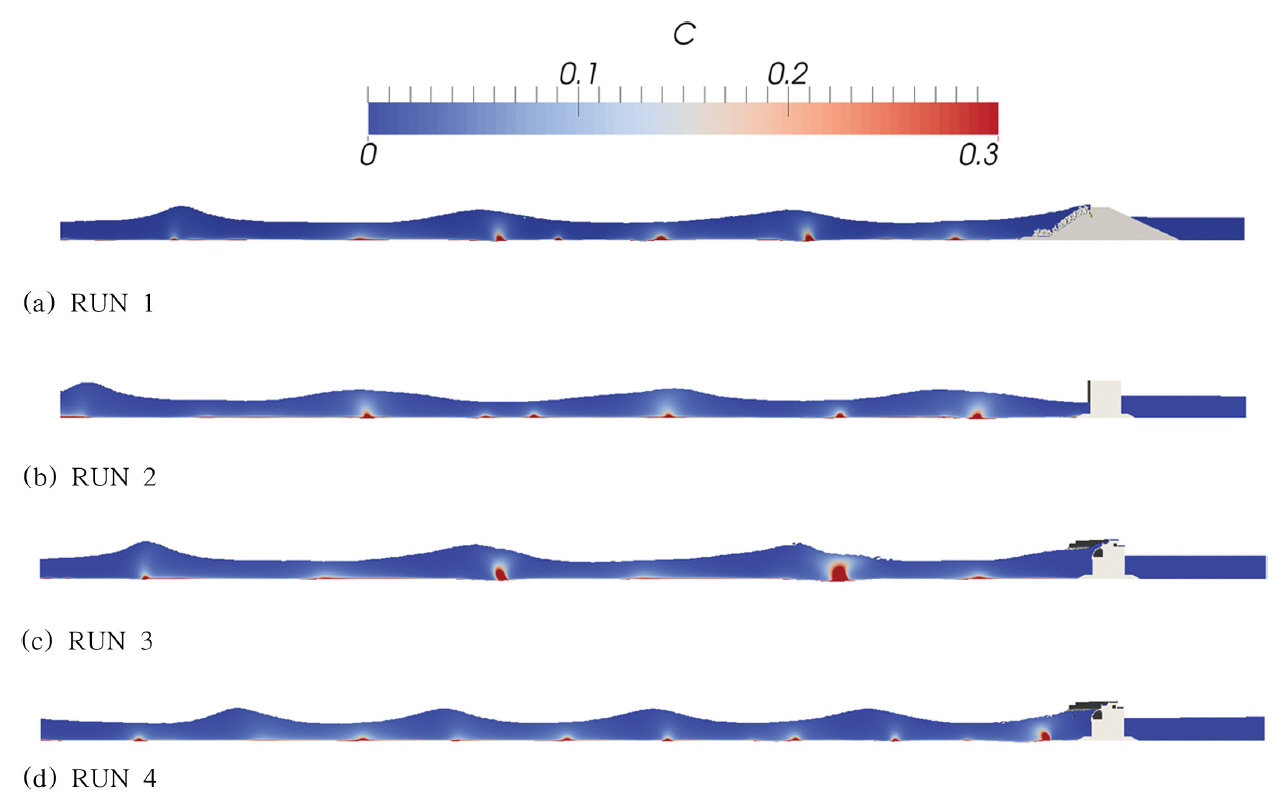
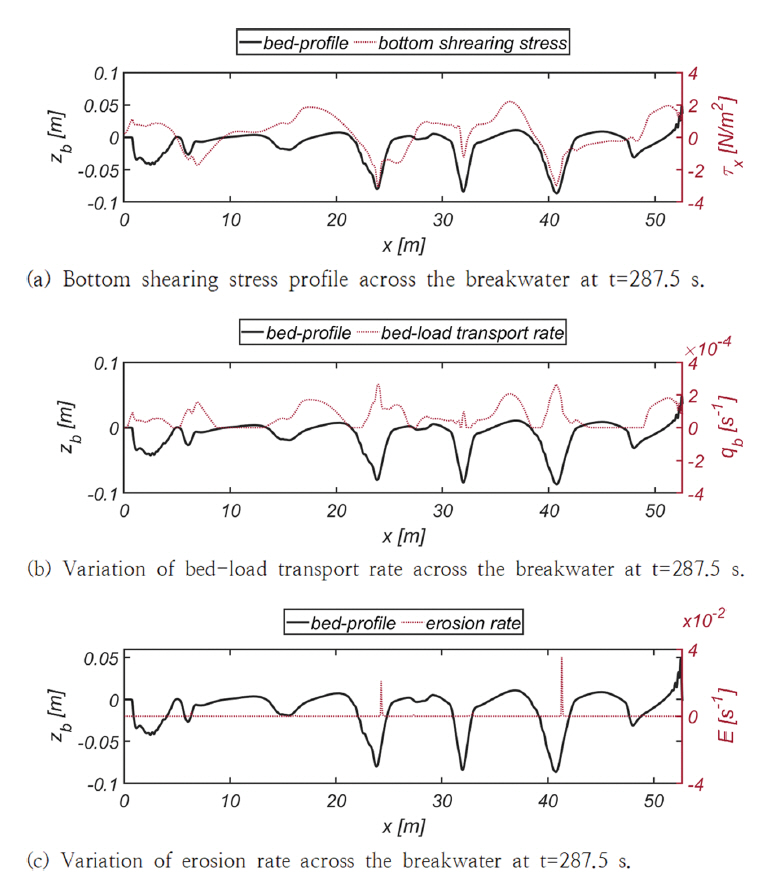
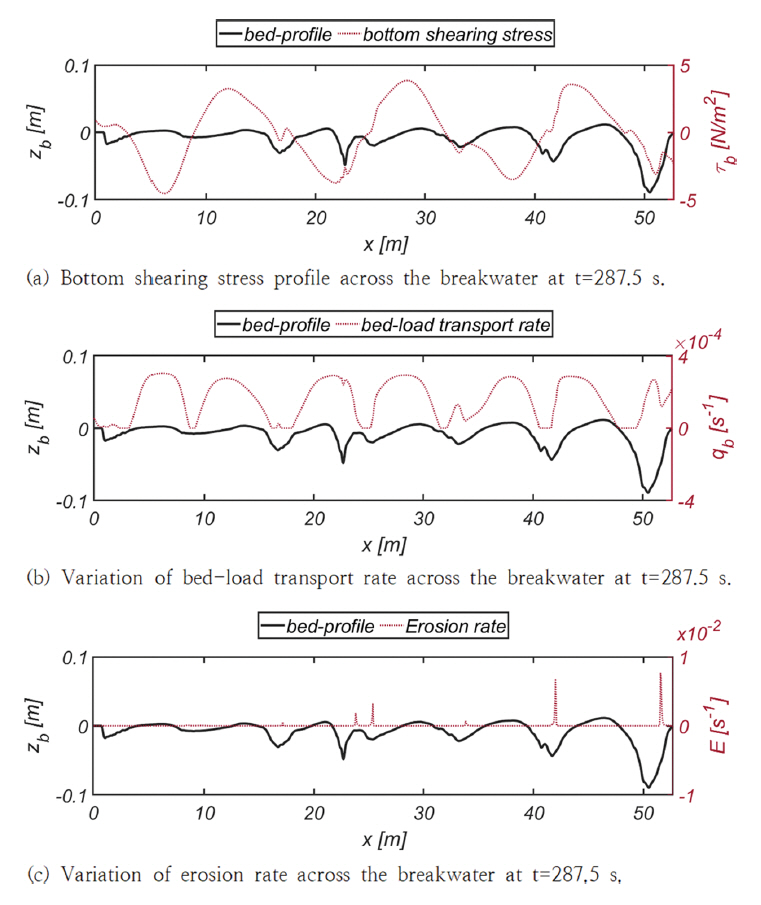
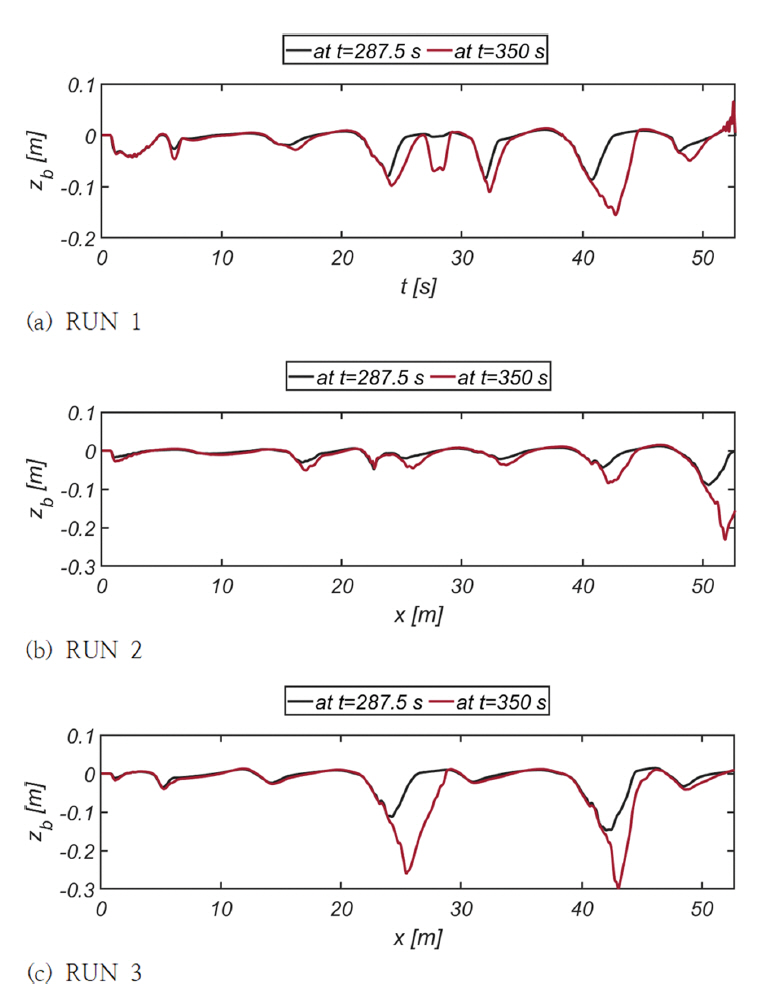
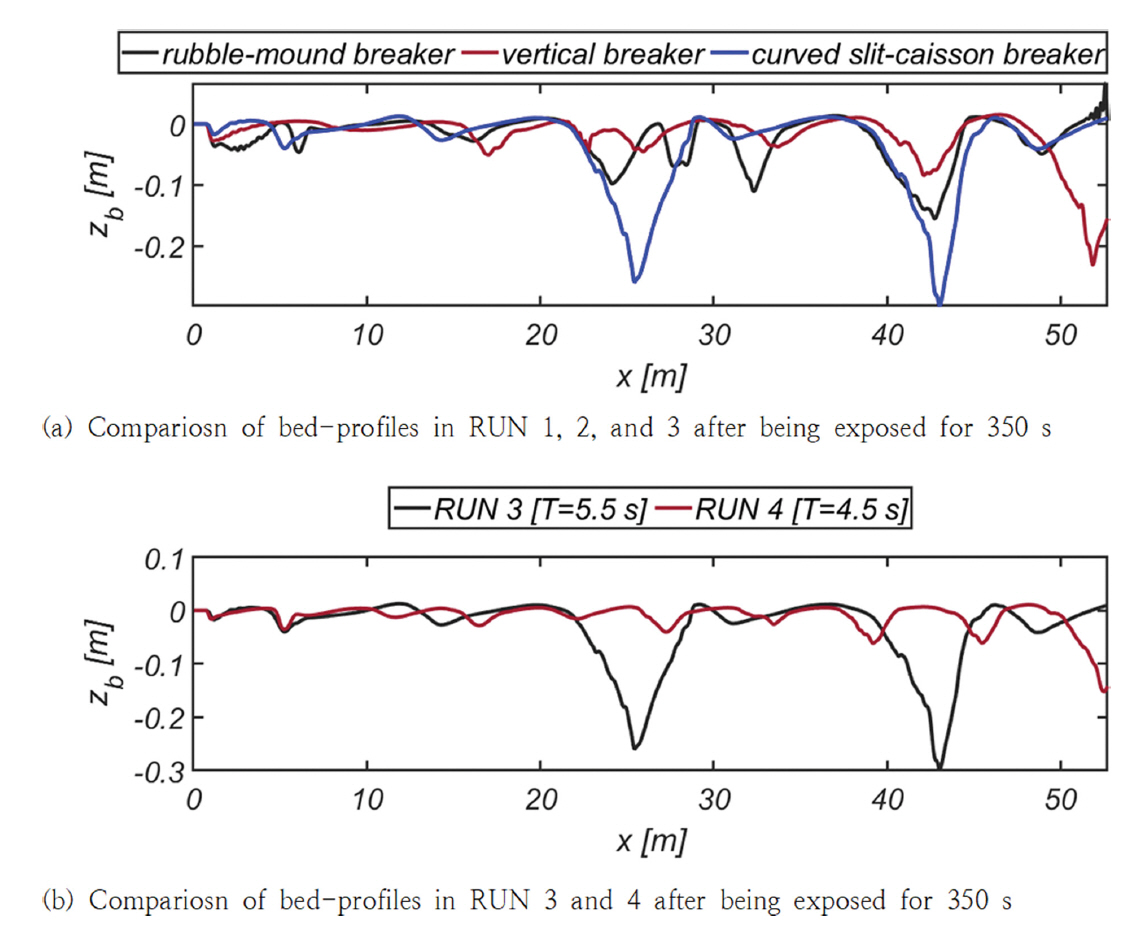
Fig. 12에는 287.5초 경과 후 RUN 1, 2, 3, 4에서 관측되는 부유사 농도분포를 정리하였다. Fig. 13, 14에는 RUN 1, 2에서 관측되는 저면 전단응력, 소류사 이송률, 침식률 분포를 각각 도시하였으며, Fig. 15에는 파랑에 노출되는 시간 증가에 따른 저면 형상이 진화하는 양상을 수록하였다[RUN 1, 2, 3]. Fig. 16(a)에는 350초 경과 후 RUN 1, 2, 3에서 관측되는 저면 형상을 비교하였으며, 내습하는 파랑의 주기가 저면 형상에 미치는 영향을 살펴보기 위해 Fig. 16(b)에는 RUN 3, 4에서 관측되는 저면 형상을 비교하였다.

내습하는 파랑의 성격이 RUN 1, 2, 3의 경우 같다는 사실을 상기하면 방파제 형식에 따른 반사파 변화가 상당히 다른 정상파를 결과하는 것을 알 수 있다[Fig. 12 참조]. 이러한 차이는 파랑에너지 소산 효과가 가장 우월한 사석 경사제[RUN 1]의 경우 쉽게 예상해 볼 수 있으나, 파랑에너지 소산 효과가 비슷한 것으로 추정되는 직립제[RUN 2]와 곡면 슬릿 케이슨[RUN3]의 경우 예상과는 달리 서로 다른 결과가 만들어져 논의가 필요해 보이며 눈에 띄는 수리 현상을 정리하면 다음과 같다:

I. 정상파 배에서의 진폭이 곡면 슬릿 케이슨에서 더 크게 관측되며[Fig. 12 참조]

II. 정상파 배와 마디가 형성되는 위치에도 미세한 차이가 발생하며

II. 곡면 슬릿 케이슨의 기부에서는 퇴적이, 직립제 기부에서는 쇄굴이 우월하며[Fig. 16(a) 참조]

IV. 연흔 진폭은 곡면 슬릿 케이슨에서 가장 크게 관측되며

V. 연흔의 파장과 진폭은 내습하는 주기에 비례하여 증가하였다.

전술한 차이 대부분은 직립제의 경우 벽면을 타고 바로 상승하는 처오름으로 인해 월류되는 양이 상당하여 발생하는 것으로 보인다. 월류되는 양의 증가로 인해 반사율은 감소하며 이는 정상파 마디에서의 유속 감소, 연흔[mega ripple, sand waves] 진폭감소로 이어진다. 이러한 추론은 연흔 파곡의 위치는 비슷하게 유지된다는 사실에서 찾을 수 있다[Fig. 16 참조]. 직립제 기부에서 쇄굴이 우월한 현상은 수위 하강 시 벽면을 타고 내려오는 흐름에 중력이 더해져 하강류의 세기가 증가하여 발생하는 것으로 보이며, 전술한 하강류에 의한 국부세굴은 해상 풍력 발전체 하부 구조물인 monoplie을 다룬 Cho(2020c)의 연구에서도 찾아볼 수 있다. 연흔 진폭이 곡면 슬릿 케이슨에서 가장 크게 관측되는 현상은 곡면 슬릿 케이슨의 반사계수가 가장 우월한 사실을 상기하면 수용 가능해 보인다. 반사계수가 우월한 경우, 마디에서의 저면 유속은 증가하며, 이는 상대적으로 많은 모래의 연행, 경계층 boundary layer drift에 의해 배[antinode]로 이송되는 모래의 증가로 이어져 큰 진폭의 연흔을 결과한다. 전술한 거동 특성은 Fig. 15에서 관측할 수 있다는 사실에 기초하면 본 연구에서 제시한 Dynamic Mesh 기반 물리기반 지형모형[Seoul Foam]의 강건성은 부분적으로 확인된 것으로 판단된다. Fig. 17에는 292.5초 경과 후 정상파에서의 속도벡터와 부유사 분포를 도시하였다. 바닥으로부터 연행된 모래로 연흔 곡이 형성된 곳에서의 수주가 자유수면 인근까지 상당히 혼탁해지는 것을 확인할 수 있다.

5. 결 론

거친 해양환경으로부터 자유로운 수역을 얻기 위해 거치되는 방파제는 해양환경에 따라 다양한 형태를 지닌다. 초기에는 조밀한 사석으로 제체를 조성하고 표층을 피복석과 상치 콘크리트로 마감하는 형태가 주류를 이룬다. 최근에는 대규모 사석 확보가 어려워 직립식 케이슨 방파제가 선호되나, 파랑에너지 소산이라는 관점에서 보면 사석 경사제에는 미치지 못한다. 전술한 직립식 케이슨 방파제는 사석 경사제에 견줄만한 파랑에너지 소산 효과를 얻기 위해 유수실과 슬릿이 추가로 장착되는 등 진화과정을 거치면서 다양한 노력이 이루어져 현재 완성도가 상당한 것으로 보인다. 그러나 직립식 케이슨 방파제와 관련된 연구의 대부분은 유수실 수리 특성, 충격 쇄파압 위주로 진행되어, 방파제 거치에 따른 수환경 변화가 해저지형에 미치는 영향을 체계적으로 다루려는 노력은 상당히 부족해 보인다.

이러한 추론의 근거는 방파제 기부 침식을 방지하기 위한 구조물 대부분은 여전히 하천 수리학에서 이야기하는 평형 하상[Equilibrium regime](Sumer and Fredsoe, 2002) 혹은 최대세굴 깊이(Sumer and Fredsoe, 2002) 등의 개념에 준거해 사석을 다층 혹은 하나의 층으로 쌓아 보호하는 방법이 주류를 이룬다는 사실에서 찾을 수 있다. 전술한 방법은 잔류수압으로 인한 액상화현상으로 인해 방지공 밑에 있던 모래가 용출되는 등의 한계를 지니며 이는 방지공의 침하로 이어진다. 이와 더불어 해저지형은 내습하는 파랑에 대응하여 쉼 없이 그 모양이 바뀐다는 사실에 준거하면 쇄굴이 일정량 진행되면 더는 진행되지 않는다는 Equilibrium regime 혹은 최대 쇄굴심 등의 개념은 그 물리적 근거를 찾을 수 없다는 사실이 해안공학계에서 끊임없이 제기되고 있어, 전술한 기부 보호공은 한계를 지니는 것을 알 수 있다(Cho and Kim, 2019; Chang and Cho, 2019; Cho et al., 2019).

이러한 인식에 기초하여 본 연구에서는 방파제 기부 침식 대응 방안을 마련하기 위한 기초연구의 일부로 방파제 형식에 따른 반사율 변화가 해저지형에 미치는 영향을 살펴보기 위한 수치 모의를 사석 경사제, 직립제, 곡면 슬릿 케이슨 방파제를 대상으로 수행하였다. 수치 모형은 OpenFoam 기반 tool box인 OlaFlow와 물리기반 지형모형[Seoul Foam]으로 구성하였으며, 이 과정에서 침·퇴적으로 인해 변형을 겪는 해저지형과 내습하는 파랑 간의 상호작용은 Dynamic Mesh를 활용하여 기술하였다(Cho, 2021b). 다양한 반사 특성을 보이는 사석 경사제, 직립제, 곡면 슬릿 케이슨 방파제는 서로 다른 정상파를 결과하였으며, 이는 해저지형에 상당한 영향을 미치는 것으로 모의 되었다. 이러한 결과는 저면 유속이 상대적으로 큰 정상파의 마디[node]에서 연행된 모래가 경계층 boundary layer streaming에 의해 배[antinode]로 이송된다는 Nielsen(1993)의 연구성과와 일치한다. 또한 전술한 모래 재배치로 정상파의 배[antinode]에는 sand wave의 마루, 마디[antinode] 인근에는 sand wave의 곡이 형성되는 것을 확인하였다. Sand wave 진폭은 반사계수가 우월한 곡면 슬릿 케이슨에서 가장 크게 관측되었으며, 이러한 현상은 반사계수가 큰 경우 마디에서의 저면 유속 증가로 많은 모래가 연행되어 발생하는 것으로 보이며 전술한 Nielsen(1993)의 연구성과에서도 찾아볼 수 있다. 이러한 사실에 준거하면 본 연구에서 제시한 Dynamic Mesh 기반 물리기반 지형모형[Seoul Foam]의 강건성은 확인된 것으로 판단된다.

감사의 글

본 연구는 해양수산부의 “연안 침식 저감기술 개발” 성과 중 일부분으로, 지원에 감사드립니다.

Figure 1.

Schematic sketch of mesh deformation problem.

Figure 2.

Layout of simple vertical type, rubble mound, and curved slit-caissson breakwater.

Figure 3.

Definition sketch of numerical wave flume.

Figure 4.

Sequential snapshots of numerically simulated wave field in RUN 4.

Figure 5.

Time series of numerically simulated water surface displacement in RUN 1.

Figure 6.

The pattern of steady boundary layer streaming in the vertical plane and stream lines under standing waves [reproduced from Sumer and Fredsoe (2002)].

Figure 7.

Sequential snapshots of sand bars under the surface antinodes due to the settlement of sediments, which was salated under the surface nodes where the near-bed velocities are strongest, convected toward the surface antinode by the boundary layer drift [reproduced from Nielsen (1993)].

Figure 8.

Evolution of computational mesh as the exposure time to incoming waves grows [RUN 1].

Figure 9.

Evolution of computational mesh as the exposure time to incoming waves grows [RUN 2].

Figure 10.

Evolution of computational mesh as the exposure time to incoming waves grows [RUN 3].

Figure 11.

Evolution of computational mesh as the exposure time to incoming waves grows [RUN 4].

Figure 12.

Contour plot of suspended-load volume concentration after being exposed to incoming waves for 287.5 s.

Figure 13.

RUN 1.

Figure 14.

RUN 2.

Figure 15.

Evolution of bed-profiles in RUN 1, 2, and 3 as the exposure time to incoming waves grows.

Figure 16.

Compariosn of bed-profiles in RUN 1, 2, and 3 after being exposed for 350 s.

Figure 17.

Vector plot of flow-velocities under standing waves and contour plot of a suspended load volume concentration after being exposed for 292.5 s.

Table 1.

List of wave conditions used in the numerical simulations

Cases	H [m]	T [s]	h_o [m]	d₅₀ [mm]	Breaker Type
RUN 1	0.6	5.5	1.2	0.6	Rubble-mound
RUN 2	0.6	5.5	1.2	0.6	Vertical type
RUN 3	0.6	5.5	1.2	0.6	Curved slit caisson
RUN 4	0.6	4.5	1.2	0.6	Curved slit caisson

References

Bagnold, R.A.. (1954). Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences 1954. 225(1160):49-63.

Cho, Y.J.. (2021a). Numerical analysis of modified bed-profiles due to the presence of a rubble mound breakwater using physicsbased morphology model [SeoulFoam], Journal of Coastal Disater Prevention, 8(3):151-163.

Cho, Y.J.. (2021b). Development of physics-based morphology model with an emphasis on the interaction of incoming waves with transient bed profile due to scouring and accretion using dynamic mesh, Journal of Coastal Disater Prevention (submitted).

Cho, Y.J.. (2020a). Development of the physics-based morphology model as the platform for the optimal design of beach nourishment project: a numerical study, J. Mar. Sci. Eng, 8, 828.

Cho, Y.J.. (2020b). Numerical Analysis of the changes in sea wave conditions by the presence of LCB [Low Crested Breaker]: centered on rip current formed at the open Inlet between LCB, Journal of Coastal Disaster Prevention, 7(4):181-193.

Cho, Y.J.. (2020c). Scour controlling effect of hybrid mono-pile as a substructure of offshore wind turbine, J. Mar. Sci. Eng, 2020(8.

Cho, Y.J.. (2019). Numerical analysis of the beach stabilization effect of an asymmetric ripple mat, Journal of Korean Society of Coastal and Ocean Engineers, 31(4):28-39.

Cho, Y.J., Bae, J.H.. (2019). On the feasibility of freak waves formation within the harbor due to the presence of Infra-gravity waves of bound mode underlying the ever-present swells, Journal of Korean Society of Coastal and Ocean Engineers, 31(1):17-27.

Chang, P.S., Cho, Y.J.. (2019). Preliminary study on the development of a platform for the optimization of beach stabilization measures against beach erosion III - centering on the effects of random Waves occurring during the unit observation period, and infra-gravity waves of bound mode, and boundary layer streaming on the sediment transport, Journal of Korean Society of Coastal and Ocean Engineers, 31(6):434-449.

Cho, Y.J., Kim, I.H.. (2019). Preliminary study on the development of platform for the selection of an optimal beach stabilization measures against the beach erosion-centering on the yearly sediment budget of the Mang-Bang beach, Journal of Korean Society of Coastal and Ocean Engineers, 31(1):28-39.

Cho, Y.J., Kim, I.H., Cho, Y.J.. (2019). Numerical analysis of the grand circulation process of Mang-Bang beach- centered on the shoreline change from 2017. 4. 26 to 2018. 4. 20, Journal of Korean Society of Coastal and Ocean Engineers, 31(3):101-114.

Dean, R.G., Dalrymple, R.A.. (2002). Coastal Processes with Engineering Applications. Cambridge University Press, New York, NY.

Einstein, H.A.. (1950). The bed-load function for sediment transportation in open channel flow. Tech. Bull. 1950, No. 1026. U.S. Dept. of Agriculture, Washington, DC.

Higuera, P., Lara, J.L., Losada, I.J.. (2013a). Realistic wave generation and active wave absorption for Navier-Stokes models: application to OpenFOAM, Coast. Eng, 71, 102-118.

Higuera, P., Lara, J.L., Losada, I.J.. (2013b). Simulating coastal engineering processes with OpenFOAM, Coast. Eng, 71, 119-134.

Jacobsen, N.G., Fredsoe, J., Jensen, J.H.. (2014). Formation and development of a breaker bar under regular waves. Part 1: Model description and hydrodynamics, Coastal Engineering, 88, 182-193.

Luque, R.F. (1974. Erosion and transport of bed-load sediment, Delft University of Technology; P.h. D. Dissertation.

Nielsen, P.. (1993). Coastal Bottom Boundary Layers and Sediment Transport. World Scientific Publishing Co.

Pope, S.B.. (2004). Ten equations concerning the large-eddy simulation of turbulent flows, New Journal of Physics, 6(35):1-24.

Sumer, B.M., Fredsoe, J.. (2002). The mechanics of scour in the marine environment. World Scientific.

Tukovic, V., Jasak, H.. (2008). Simulation of Free-Rising Bubble with Soluble Surfactant using Moving Mesh Finite Volume/Area Method, (2008). Simulation of Free-Rising Bubble with Soluble Surfactant using Moving Mesh Finite Volume/Area Method, 6th International Conference on CFD in Oil & Gas, Metallurgical and Process Industries, SINTEF/NTNU. June 2008.