1. 서론
월파는 파랑의 수면변위가 해안 제방, 호안, 방파제 등과 같은 해안구조물의 마루높이 보다 높을 때 해수가 구조물 내측으로 전달되는 현상으로 태풍이나 저기압, 쓰나미가 작용할때 발생한다. 최근 우리나라를 내습하는 태풍의 강도가 커지고 빈도가 증가하면서 월파로 인한 피해가 늘어나고 있다. 월파 대책에 대한 연구를 위해서는 넓은 해역의 월파를 경제적으로 해석할 수 있고 동시에 비선형 불규칙파의 파랑변형을 정도 높게 모의할 수 있는 수치모형이 필요하다.
월파 해석을 위한 수치모형은 기본적으로 Non-linear shallow water equation model(NLSW)과 Navier-Stokes equation model(NS)의 두 범주로 나눌 수 있다. NLSW모형은 Navier-Stokes equation의 단순화된 형태로서 시간과 공간상에서 수심과 수평 흐름 속도를 구하여 수평에 가까운 수심적분된 자유표면 흐름을 해석하는 정수압 모델(Tuan and Oumeraci, 2010)과 dispersive non-linear shallow water equation을 기본 식으로 사용하여 흐름의 연직구조와 비정수압을 해석할 수있는 SWASH 모형이 있다(Zijlema et al., 2011). 그러나 이 모형은 계산시간과 계산량을 많이 소모하여 구조물로부터 멀리 떨어진 곳에 외해 경계조건을 설정하기 어렵다.
Full Navier-Stokes 방정식은 시간과 공간상에서 3개의 속도성분과 압력, 난류를 해석함으로써 흐름을 가장 모의할 수 있는 모형이다. NS 모형은 난류흐름을 재현하고 정확성을 높이기 위해서 난류모형을 확장시키고 VOF 법으로 자유표면 흐름을 해석하는 방법이 개발되어 파랑과 투과구조물의 상호작용을 해석할 수 있는 모형들이 개발되었다(COBRAS; IHFOAM; CADMAS-SURF; OpenFOAM; FLOW-3D). 그러나 NS 모형은 주로 구조물 세부영역의 유체거동을 해석하며 NLSW 모형 보다 더 많은 계산시간과 계산량을 필요로 한다.
최근에 Boussinesq 방정식 모형들이 월파 연구에 널리 사용되고 있다. 이 모형의 장점은 NLSW 모형이나 NS 모형에 비하여 파랑을 중간수심 해역까지 더 넓은 영역을 해석할 수있다는 점이다. 이 모형은 구조물로부터 더욱 멀리 떨어진 곳에 외해 경계조건을 설정할 수 있고 쇄파의 시작을 파악할 수 있어서 전빈으로부터의 파랑전파와 쇄파 과정을 더 잘 표현할 수 있다(Stansby, 2003; Lynett et al., 2010; McCabe et al., 2013; Tonelli and Petti, 2013). 국내에서는 Boussinesq 모델을 이용하여 파랑의 스펙트럼 형상에 따른 월파와 처오름 현상을 분석한 연구가 있으며(Park et al., 2014), 투과성 구조물에서 파랑의 전달 파고를 해석한 연구가 있다(Huynh et al., 2017; 2019).
한편, Wei et al.(1995)은 Nowgu(1993)의 확장 Boussinesq 방정식처럼 특정 수심에서 유속을 변수로 선택하고 자유표면 경계조건의 비선형성을 그대로 유지하여 fully nonlinear Boussinesq equation을 유도하였다. Kirby et al.(1998)은 Wei 등이 유도한 fully nonlinear Boussinesq equation을 기본 식으로 사용하여 FUNWAVE 모델을 개발하고 많은 동수 역학 문제에 적용하였다. Chen(2006)은 Wei et al.(1995) 과 같은 방법을 사용하고 수직와도 항을 추가하여 파랑의 운동량을 더욱 잘 재현할 수 있는 fully nonlinear Boussinesq equation을 유도하였다. 그리고 Shi et al.(2012)은 쓰나미에 의한 해안의 침수현상을 해석하기 위해서 Chen(2006)의 식을 기본 식으로 하고 flux항을 TVD기법으로 푸는 FUNWAVETVD 모델을 수립하였다. 국내에서는 FUNWAVE 모델을 이용하여 쇄파 및 천수현상의 비선형 효과를 분석한 연구가 있으며(Yoon and Kim, 2001; Park and Yoon, 2004), FUNWAVE-TVD 모델의 기본 식 유도과정에서 수직와도 항의 부호를 수정하고 수중 천퇴를 천파하는 파랑의 쇄파 및 흐름을 해석한 연구가 있다(Choi and Seo, 2015; 2018).
월파 대책의 연구를 위해서는 진폭이 큰 폭풍파가 천해 역으로 전파해 올 때 진폭 수심 비가 커지면서 파랑의 비선형이 커지므로 강비선형 파랑모델이 필요하고, 넓은 해역의 월파를 동시에 해석할 수 있는 평면 파랑모델이 필요하다. 이에 본 연구에서는 강비선형 Boussinesq 모델인 FUNWAVETVD 모델을 이용하여 비선형 불규칙파의 전파를 모의하고 넓은 해역에서 해안구조물의 월파량을 산정할 수 있는 수치 모형을 수립하였다. 본 모형은 많은 실험 및 현지관측 자료로부터 얻어진 EurOtop(2018)의 월파량 산정 식들과 Goda (2009)의 경험식을 코딩하여 기존 FUNWAVE-TVD 모델의 서브루틴으로 추가하고 월파 유량을 산정할 수 있는 모형을 수립하였다. 모형의 검증은 직립구조물에 대한 불규칙파의 월파량을 수치계산하고 EurOtop(2018)에 제시된 실험결과와 비교하여 수행하였다.
2. 수치모형
2.1 지배방정식
FUNWAVE-TVD 모델은 Chen(2006)이 유도한 fully nonlinear Boussinesq equation을 지배방정식으로 사용하고 미분방정식의 이산화 기법인 MUSCL-TVD 법과 이동경계조건을 해석하는 HLL 기법을 사용하여 flux 항을 계산한다. 지배방정식은 보존식 형태의 Boussinesq 방정식으로 표시하면 다음과 같다.
여기서 Ψ와 Θ(Ψ)는 보존변수의 백터 성분과 flux 백터 함수로서 각각 다음과 같이 주어진다.
여기서
H는 H = h + η이고 H는 정수 면까지의 수심, η는 수면변위를 나타낸다. u, v는 zα = (α - 1)h + αη, α = 0.47 위치에서의 유속이고, 식(5), (6)의 첨자 x, y, t는 각각 공간과 시간에 대한 미분을 의미한다. 그리고 U'1, V'1, U''1, V''1, U2, V2, U4, V4는 분산항을 의미하고 U3, V3는 수직 와도 항을 나타낸다. R로 표시한 항은 바닥마찰, subgrid lateral turbulent mixing, 쇄파, 바람효과 등의 확산과 소실 항을 나타낸다.
공간의 이산화는 유한체적법과 유한차분법을 혼합하여 적용하고 있다. Flux항과 1차 미분 항들은 high-order 및 loworder MUSCL-TVD(Monotonic Upstream-centered Scheme for Conservation Laws-Total Variation Diminishing) 기법을 사용하는데 high-order 기법에는 Erduran et al.(2005)의 fourthorder MUSCL-TVD 기법이 적용된다. 그리고 시간 스텝은 비선형 공간 이산화에 대해서 third-order Strong Stability-Preserving(SSP) Runge-Kutta 기법을 사용한다(Shi et al., 2012; Choi and Seo, 2018).
2.2 월파량 산정방법
본 모형에서는 FUNWAVE-TVD 모델의 계산시간에 영향을 주지 않고 빠른 시간에 넓은 해역의 월파량을 산정하기 위하여 많은 실험 자료로부터 구해진 EurOtop(2018)의 월파량 식들과 Goda(2009)의 경험식을 코딩하고 수치계산에서 얻어진 비선형 불규칙파의 스펙트럼 유의파고(Hmo)와 스펙트럼 주기(Tm)를 이용하여 각 계산 cell에서 월파량을 산정하도록 서브루틴을 구성하였다.
월파량 산정 식은 파랑이 구조물 전면에서 쇄파가 발생하지 않고 월파하는 조건을 non-impulsive condition, 쇄파가 발생하는 조건을 impulsive condition으로 구분하여 다르게 적용한다. 비쇄파 조건의 월파는 파랑의 수면변위가 구조물의 마루높이보다 높은 상태로 다량의 유량을 월류시키는 반면 쇄파 조건은 구조물 전면에서 쇄파가 일어나고 벽면에 충격파가 반사되어 높이 처오름현상이 발생하면서 물안개를 일으키지만 월파 유량은 많지 않다. 월파량 산정 서브루틴에 사용된 식(9)는 직립제와 혼성제의 비쇄파 조건 시 평균월파량 산정 식이고, 식(10), (11)은 직립제의 경우 쇄파 시 평균월 파량 산정식이며, 식(12), (13)은 혼성제의 경우 쇄파 시 평균월파량 산정식이다. 또한 월파량 산정 서브루틴에는 식(14), (15), (16)과 같이 Goda(2009)가 제시한 경험식을 추가하였다. 경험식은 CLASH 자료를 분석하고 해저 면과 구조물이 이루는 각도 및 파랑의 입사각도에 대한 영향 등을 반영하여 계수를 결정한 식이다.
월파량 산정 식들은 주요 변수가 구조물 전면의 스펙트럼 유의파고 Hmo인 것을 알 수 있으며 월파량을 정확히 산정하기 위해서는 비선형 불규칙파의 유의파고를 정밀하게 수치계산하는 것이 중요하다.
- non-impulsive conditions (EurOtop, 2018)
- impulsive conditions (EurOtop, 2018)
- 경험식(Goda, 2009)
여기서 Hmo는 스펙트럼 유의파고(= 4.004 m o
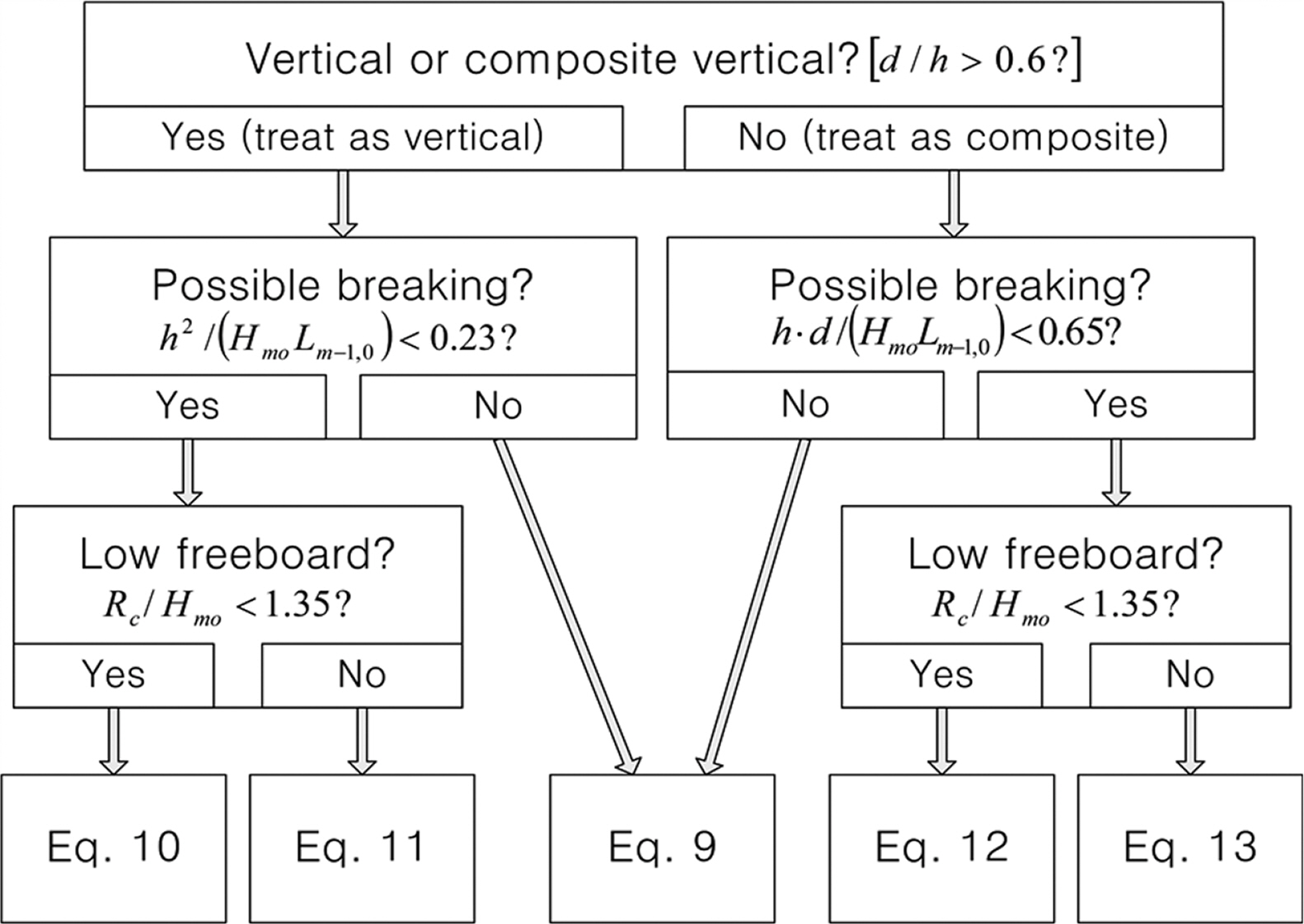
월파량 산정을 위한 서브루틴은 Fig. 1과 같이 EurOtop (2018)의 월파량 산정 식 decision chart를 참고하여 코딩을 하였다. 적절한 월파량 산정 식을 결정하기 위한 절차는 먼저 마운드 수심과 해저 수심의 관계로부터 마운드의 영향이없는 경우를 직립제(d/h > 0.6), 영향이 있는 경우를 혼성제로(d/h < 0.6) 구분한다. 다음은 구조물 전면에서 쇄파가 발생하는지 검토한다. 이때 직립제는 구조물 전면의 수심과 유의파고, 파장의 관계로부터 h2/(HmoLm-1, o) < 0.23이면 쇄파조건, 아니면 비쇄파조건으로 판단한다. 비쇄파 조건의 경우는 월파량 산정 식(9)를 사용하고, 쇄파조건의 경우는 상대여유고가 1.35보다 작으면(Rc/Hmo < 1.35) 월파량 산정 식(10), 크면 (Rc/Hmo > 1.35) 식(11)을 사용한다. 혼성제의 경우는 구조물 전면의 마운드 수심과 해저면 수심, 유의파고와 파장의 관계로부터 h·d(HmoLm-1, o) < 0.65이면 쇄파조건, 아니면 비쇄파조건으로 판단한다. 혼성제의 비쇄파조건 월파량은 식(9)로 산정하고 쇄파조건은 다시 상대여유고가 1.35보다 작으면 식(12), 크면 식(13)을 적용하여 월파량을 산정한다. 월파량은 구조물 전면에서 계산영역의 각 격자 cell마다 단위 폭당 유량 q로 산정된다. 따라서 실제 수역의 경우는 계산 격자 cell마다 임의수심 조건을 반영하여 Fig. 1의 decision chart 흐름에 따라 각각 월파 산정 식이 결정된다.
3. 모형의 검증
3.1 검증 계산
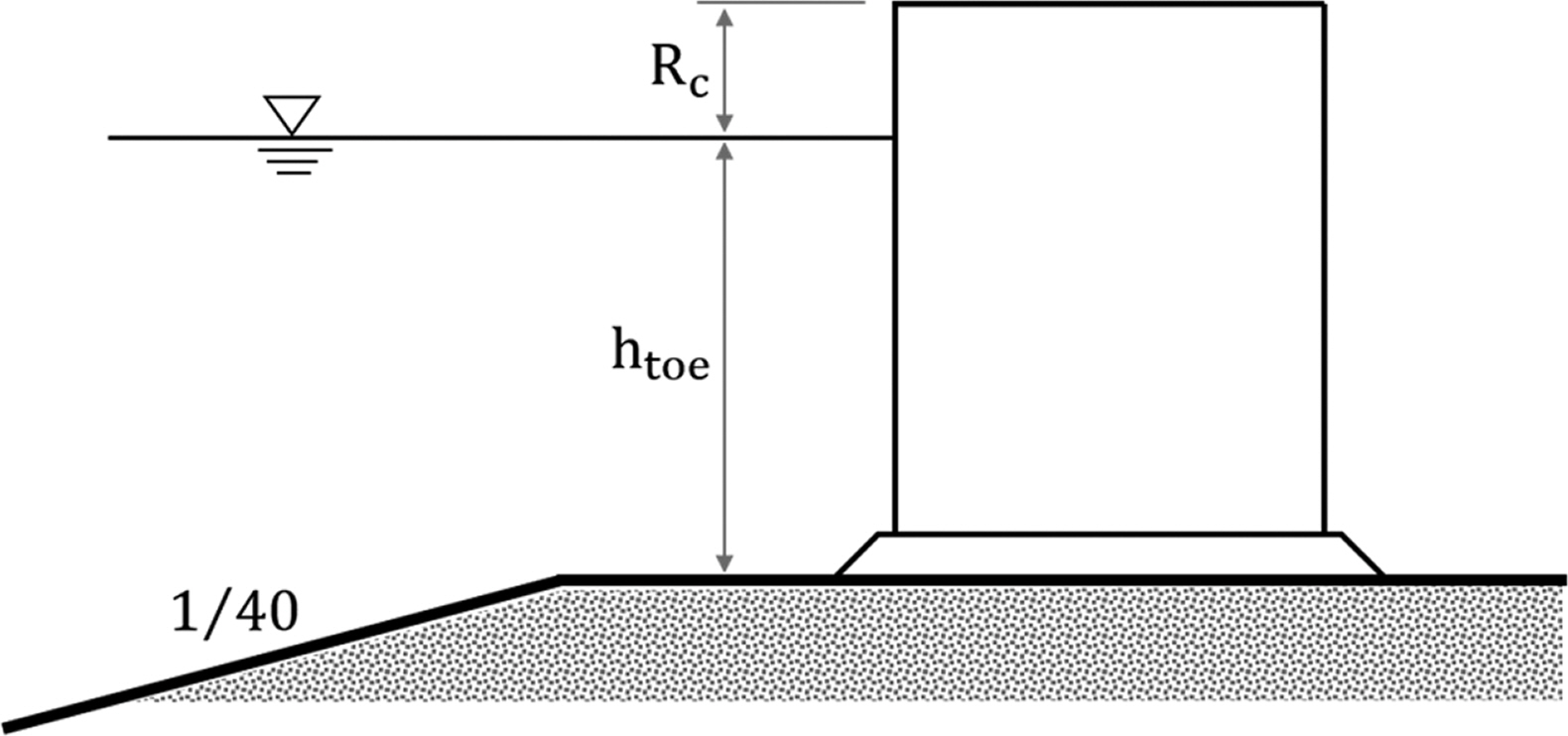
FUNWAVE-TVD 모델을 이용한 월파량 산정 수치모형의 검증은 직립구조물에 대한 불규칙파의 월파량을 수치계산하고 EurOtop(2018)의 실험 결과와 비교하여 수행하였다. 직립 구조물에 대한 검증계산 조건은 구조물 전면의 저면 경사가 1/40으로 변하는 수심 조건에서 직립구조물에 대한 월파 수리실험을 수행한 Kim and Lee(2015)의 실험 조건을 참조하였다(Fig. 2). 본 연구의 검증계산 조건은 centimeter 단위의 수리실험 조건을 scale factor 1:36으로 Froude 상사법칙을 적용하여 현지 스케일로 환산하였다.
수심조건은 구조물 전면의 수심이 10.8, 14.4, 18.0 m의 3 cases로서 외해 측으로 갈수록 저면경사 1/40의 비교적 급경사로 수심이 증가하여 내부 입사 경계의 수심은 30.8, 34.4, 38.0 m이다. 그리고 여유고 Rc와 내부 조파의 입사파고는 각각 1.8~7.2 m까지 0.9 m 간격으로 7 cases이다. 따라서 검증 계산은 수심조건과 여유고 및 입사파고 조건을 조합하여 총 147 cases를 수행하였다(Table 1).
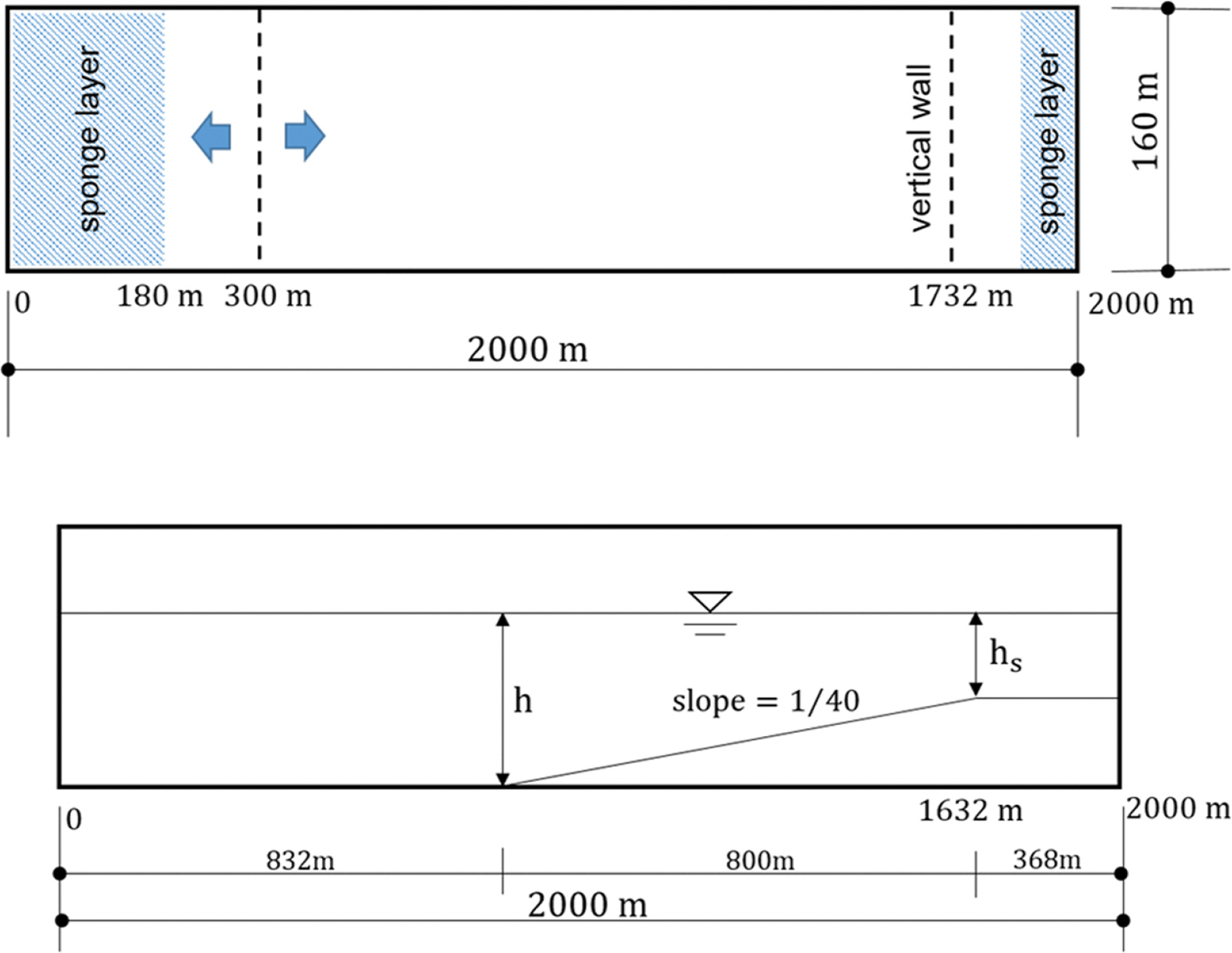
검증계산을 위한 계산영역은 2000 × 160 m의 2차원 조파 수조 형상으로 구성하였고 격자간격은 △x, △y를 동일하게 2 m로 설정하여 총 1001 × 81개의 격자망으로 구성하였다. 그리고 내부 조파 경계조건은 입사역 300 m 지점에 설정하였고 TMA 스펙트럼을 사용하여 불규칙파를 재현하였다. 계산 시간은 1 case 당 600 sec로 하였다. 샘플 계산 case에 대해서 3600 sec를 계산하고 월파량을 비교하였으나 600 sec의 계산 결과와 차이가 없어서 모든 case를 600 sec로 계산하였다. 그리고 외해 측에 폭 180 m, 해안 측에 폭 100 m의 스폰지 경계를 설정하여 양측으로부터의 반사파를 제어하였다. 계산 영역의 측면경계는 periodic boundary condition을 적용하여 측면으로부터의 반사를 제어하였다(Fig. 3).
한편, EurOtop의 실험식에 사용되는 구조물 전면의 유의파고는 구조물에 의한 반사파를 포함하지 않는 입사파의 파고 이다. 수리모형실험은 구조물 전면에서 중복파가 발생하여도 분할 판을 이용한 통과파 계측을 통하여 입사 파고를 추출할 수 있다. 그러나 수치계산의 경우는 중복파로부터 입반사파 분리가 어려우므로 중복파가 발생하지 않도록 수치모의하는 방법을 검토하였다. 검증계산에서는 진행파만을 재현하기 위하여 계산영역의 1732 m 지점에 구조물 경계조건을 설정하지 않고 입사 파랑이 통과하도록 하였다. 그리고 구조물 위치의 각 cell에 월파 계산을 위한 경계조건을 부여하여 주어진 월파 조건과 진행파의 유의파고로 월파량을 계산하였다.
월파량 계산을 위한 구조물 표면의 조도 영향계수 γf 는 1.0 (concrete wall), 경사 입사 영향계수 γα 는 1.0(normal incident)으로 하였다.
3.2 결과 비교
본 연구에서는 FUNWAVE-TVD 모델을 이용하여 비선형 불규칙파의 직립구조물에 대한 월파량을 산정하고 EurOtop (2018)의 실험 결과와 비교하였다. 월파량은 비쇄파조건(nonimpulsive conditions)와 쇄파조건(impulsive conditions)으로 구분하여 비교하였다.
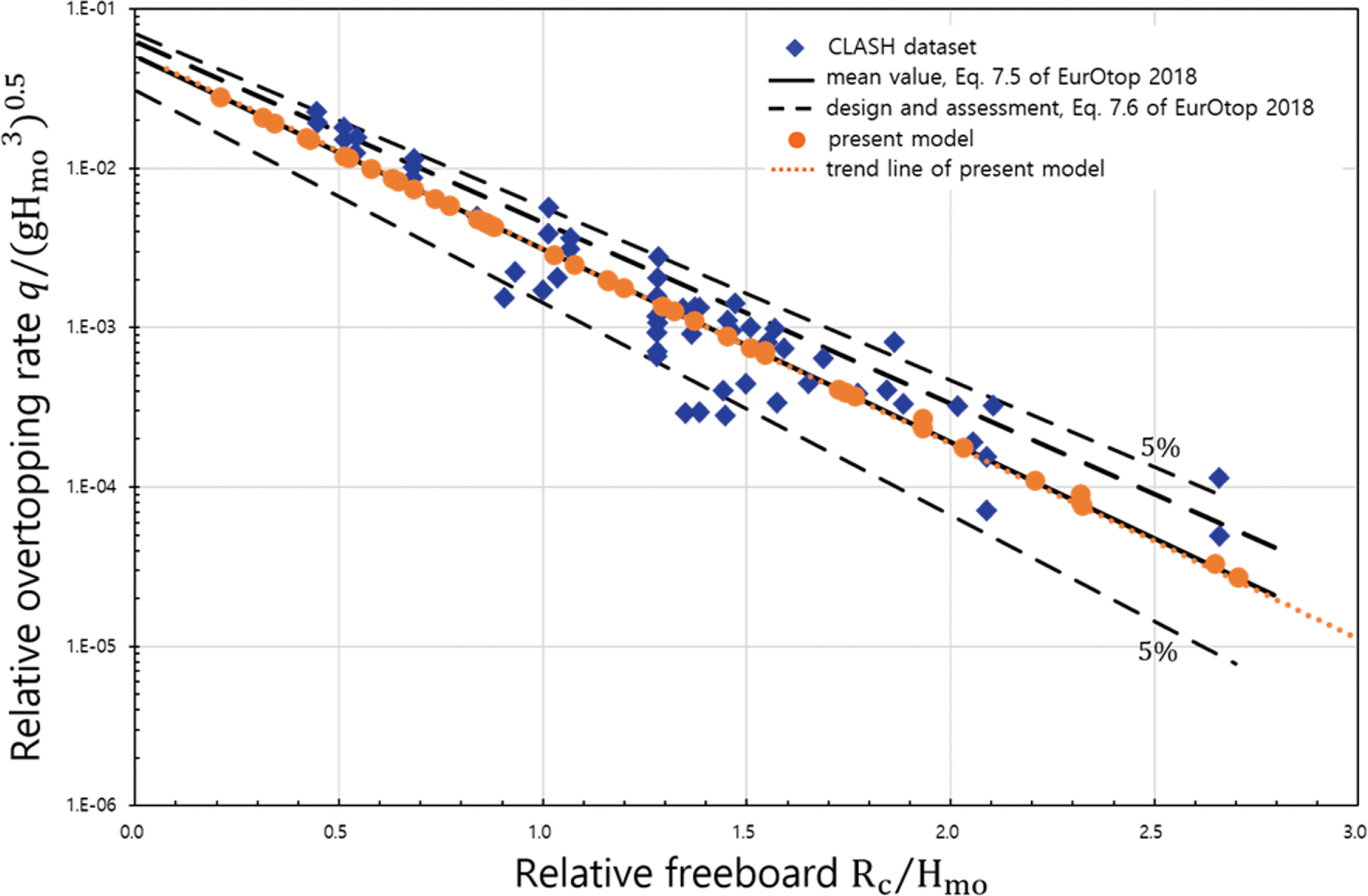
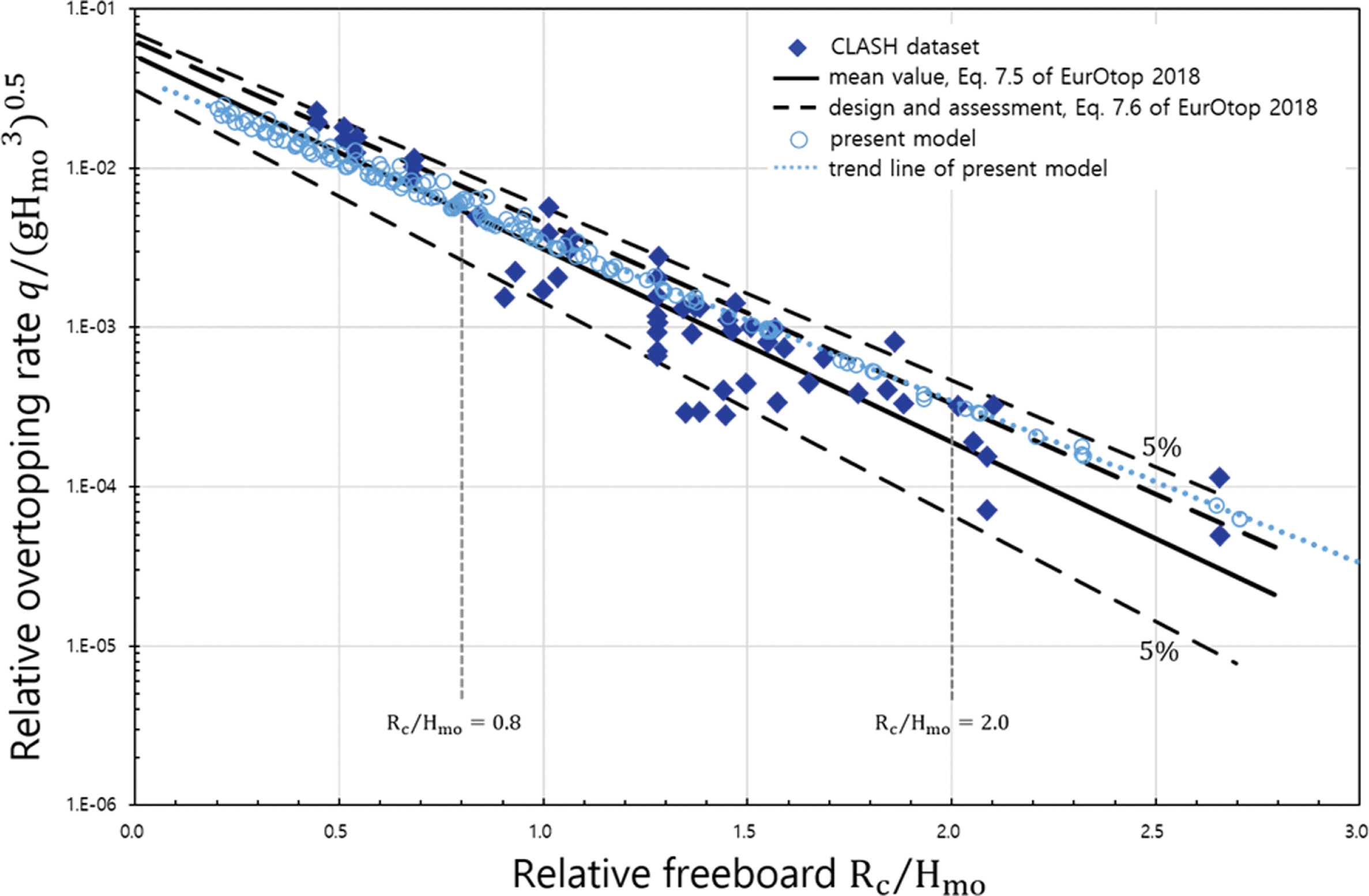
Fig. 4는 비쇄파조건의 월파량 결과를 비교한 것으로 그림의 수평축은 무차원 상대여유고를 나타내며 좌측으로 갈수록 여유고가 낮은 경우로서 월파량이 많아지고 우측으로 갈수록 여유고가 높은 경우로서 월파량이 적어진다. 연직축은 무차원 월파량을 나타낸다. 그림에서 마름모 심볼은 CLASH dataset을 의미하고 검정 굵은 실선은 EurOtop(2018)의 평균 월파량을 나타내며 굵은 파선은 설계월파량을 의미한다. 그리고 상하 5% 파선은 실험결과 중에서 상위 및 하위 5% 경계값을 의미하고 그 사이의 실험 결과는 90% 신뢰구간에 속한다. 본 모형의 결과는 비쇄파조건의 평균월파량 산정 식(9)를 적용하여 수치계산한 월파량으로서 오렌지색 원형 심볼로 표시였고 그 추세선을 오렌지색 점선으로 표시하였다. 본 모형의 월파량 산정 결과는 상대여유고가 작은 값에서부터 큰 값에 이르기까지 모든 구간에서 실험 결과와 매우 잘 일치함을 알 수 있다. 특히 수치계산 월파량의 추세선은 CLASH dataset으로부터 얻어진 EurOtop(2018)의 평균월파량 선과 잘 일치함을 확인할 수 있다. 본 모형이 EurOtop(2018)의 평균 월파량 식을 사용하였기 때문에 두 결과가 일치하는 것은 당연하다고 생각할 수 있으나 월파량 산정 식의 주요 변수가 구조물 전면의 유의파고 Hmo인 것을 감안하면 FUNWAVE-TVD 모델이 비선형 불규칙파의 파랑변형을 잘 수치모의 하였음을 알 수 있다.
Fig. 5는 Goda(2009)의 경험식을 적용하여 수치계산한 비쇄파조건의 월파량을 비교한 것이다. 실험 결과는 Fig. 4에서 설명한 자료와 같다. 수치계산 결과는 원형 심볼로 표시하였고, 그 추세선은 점선으로 표시하였다. 경험식에 의한 월파량 결과는 상대여유고가 Rc/Hmo < 0.8인 구간에서는 EurOtop(2018) 의 평균월파량보다 과소평가 되었으며Rc/Hmo > 0.8인 구간 에서는 여유고가 작을수록 EurOtop(2018)의 평균월파량 보다 커지며 Rc/Hmo > 2.0 구간에서는 설계월파량을 초과하는 것을 알 수 있다. 그러나 경험식에 의한 월파량은 상대여유고의 모든 구간에서 실험 결과의 90% 신뢰구간 내에 속하는 것을 알 수 있다.
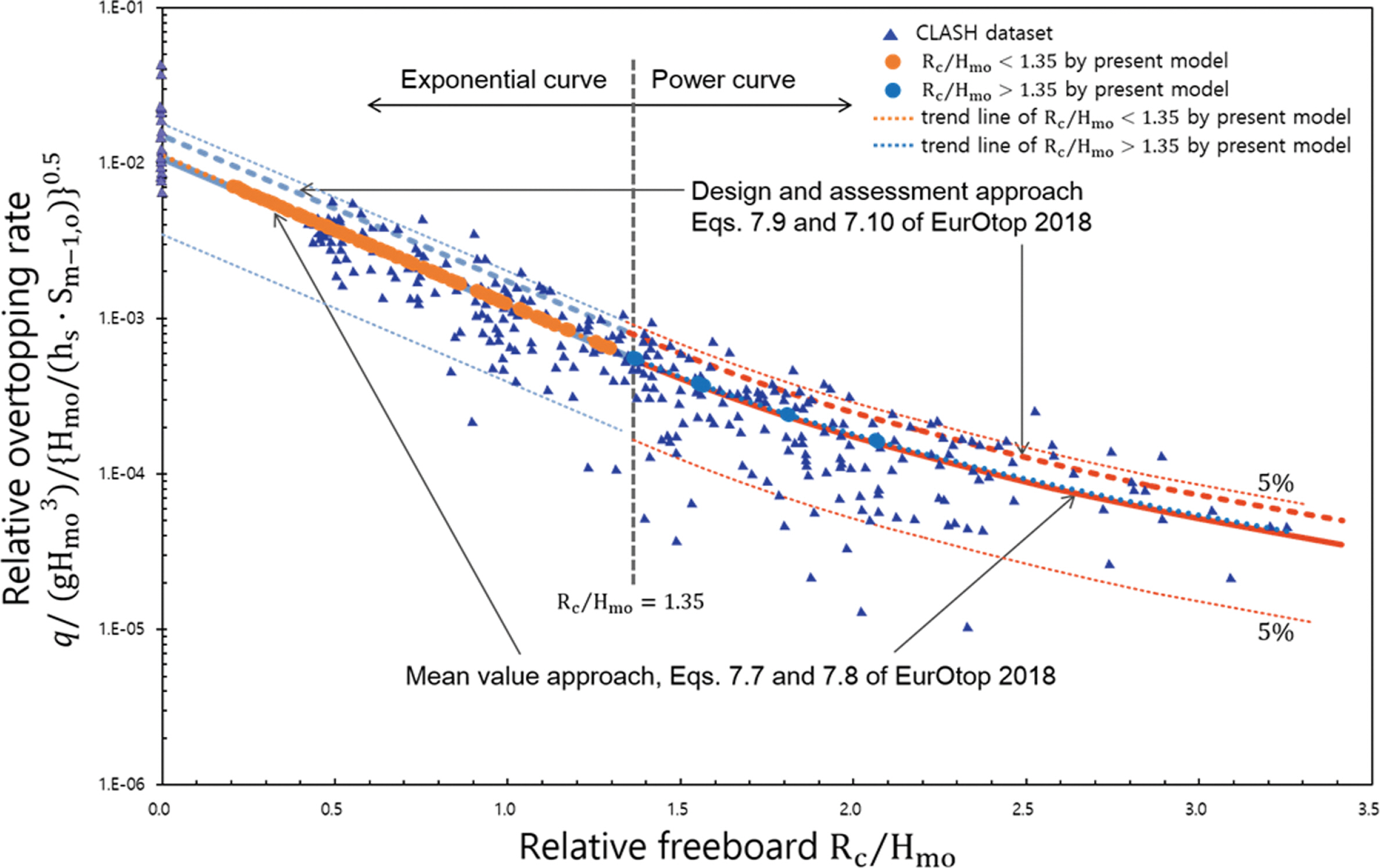
Fig. 6은 쇄파조건의 월파량을 비교한 것으로서 수평축은 상대여유고를 나타내고 연직축은 구조물 전면의 유의파고, 수심, 파형경사를 사용하여 무차원화한 월파량이다. 그림에서 상대여유고 Rc/Hmo = 1.35를 기준으로 Rc/Hmo < 1.35 구간은 exponential curve를 나타내고 Rc/Hmo > 1.35 구간은 power curve를 나타낸다. 그림에서 삼각형 심볼은 CLASH dataset 을 나타내며, 굵은 실선은 평균월파량을 의미하고 굵은 파선은 설계월파량을 의미한다. 그리고 상하 5% 점선은 실험 결과의 상하 5% 경계값을 나타낸다. 수치계산 결과는 exponential curve 구간의 월파량을 오렌지색 원형 심볼, power curve 구간의 결과를 파랑색 원형 심볼로 나타냈으며 그 추세선을 점선으로 표시하였다. 쇄파조건의 평균월파량 식(10), (11)을 적용하여 수치계산한 본 모형의 결과는 상대여유고 모든 구간에서 실험의 평균월파량 결과와 잘 일치함을 알 수 있고 수치계산의 월파량 추세선은 실험으로부터 얻어진 평균월파량 곡선과 매우 잘 일치함을 볼 수 있다.
4. 결론
본 연구는 완전비선형 Boussinesq 방정식을 사용한 FUNWAVE-TVD 모델에 EurOtop(2018)의 월파량 산정 식과 Goda(2009)의 경험식을 코딩하여 서브루틴으로 추가하고 2차원 평면 파랑장에서 비선형 불규칙파의 월파량을 추산할 수 있는 수치모형을 수립한 것이다. 모형의 검증은 비쇄파 및 쇄파조건에서 직립구조물에 대한 불규칙파의 평균월파량을 수치계산하고 EurOtop(2018)의 실험 결과와 비교하여 수행하였다. EurOtop(2018)의 식을 사용한 수치계산 결과는 비쇄파 조건 및 쇄파 조건 모두 상대여유고의 모든 구간에서 실험 결과와 매우 잘 일치하는 결과를 나타내었다. 특히 수치계산으로부터 구해진 월파량의 추세선은 실험결과로부터 얻어진 월파량의 곡선과 잘 일치함을 확인하였다. 경험식으로부터 구해진 수치계산 결과는 높은 여유고에서는 실험 결과보다 과소평가 되었고 낮은 여유고에서는 실험 결과보다 과대평가 되었다. 한편, 월파량 산정 식들의 주요 변수가 구조물 전면의 스펙트럼 유의파고 Hmo인 점을 감안하면 본 모형은 급경사 해저 면을 전파하는 비선형 불규칙파의 변형을 매우 정도 높게 해석하는 것을 검증 결과로부터 알 수 있었다. 따라서 본모형은 넓은 해역의 해안구조물에 대한 비선형 불규칙파의 월파 해석이 가능하므로 향후 월파 대책을 위한 연구에 유용하게 사용될 수 있을 것으로 생각한다.