1. 서 론
기후변화에 따른 해양환경은 점점 더 불확실해지고 항만 구조물의 노후화는 빠르게 진행되고 있다. 국내 항만의 노후 비율은 현재 대략 20%대 이지만 10년 후에는 거의 50%에 도달할 것으로 전망되고 있다. 따라서 항만 구조물의 성능, 특히 안전성과 기능성이 잘 발휘되도록 하기 위해서는 체계적으로 유지관리되어야 한다. 노후화를 유발하는 피해의 규모를 시간의 함수로 정확히 예측하여 사용기간 동안 안전성이 갑자기 위협받는 파괴가 발생되지 않도록 해야 하고, 또한 기능성이 일정하게 만족 되도록 해야 한다. 최소의 비용으로 최대의 성능을 확보하면서 항만 구조물의 장수명화를 도모하기 위해서는 언제 어떤 예방적 유지관리 조치 또는 행위들이 수행되어야 하는지를 알아야 한다. 이를 위해서는 불확실성을 고려하여 미래 시간에 대한 피해의 진행 과정과 그 크기를 정확히 예측할 수 있어야 하고, 또한 항만 구조물의 재령에 따른 잔류수명(Residual/Remaining Useful Lifetime: RUL)을 확률론적으로 올바로 추정해야 한다(Lee, 2016, 2019).
구조물이 그 기능을 수행하기 시작하는 최초 시점에서부터 파괴시까지의 시간 간격으로 정의되는 내구수명(lifetime)과 다르게, 잔류수명은 일정 재령이 경과한 기준시점에서부터 미래 파괴가 발생되는 시점까지의 시간 간격으로 정의된다. 따라서 잔류수명을 올바로 추정하기 위해서는 먼저 기준시점에서의 피해상태가 올바로 파악되어야 하고, 다음으로 미래의 피해 진행 과정이 정확히 예측되어야 한다. 기준시점 뿐만 아니라 그 이전의 과거 피해 상태에 대한 관측자료를 기반으로 접근되어야 한다(Cui et al., 2004; Wang, 2007; Pecht and Jaai, 2010; Gasperin et al., 2011; Ahmad and Kamaruddin, 2012). 이는 과거의 관측자료 속에 내포된 피해의 거동특성과 미래 시간의 경과에 따른 불확실성을 올바로 고려하기 위함이다. Si et al.(2012), Ye et al.(2012), Wang et al.(2014), 그리고 Li et al.(2019) 등의 연구에 의하면 현재까지 시간의 함수로 불확실성을 올바로 고려하면서 피해의 진행 과정을 예측하는데 가장 적합한 확률모형이 추계학적 확률과정(stochastic process)이다. Lee(2019, 2020)는 모형실험에서 얻어진 시간에 따른 누적 피해이력 자료를 활용하여 감마 확률과정(Gamma Process: GP)과 위너 확률과정(Wiener Process: WP)을 방파제의 대표적인 형식인 경사제에 적용하였다. 경사제의 시간에 따른 피해경로를 수치적으로 모의하고, 잔류수명에 대한 확률론적 해석을 수행하였다. 그러나 수리모형실험에서 얻어지는 아주 제한된 조건에서의 몇몇 자료를 제외하고는 실제 항만 구조물에서 피해와 관련된 하중조건이나 피해규모 등에 대한 시간 이력을 확보하기가 어렵다. 이는 항만 구조물과 같은 대부분의 중요 시설물의 경우 피해 사건이 아주 드물게 발생하고 피해 상태에 대한 점검이 어렵기 때문이다. 따라서 본 연구에서는 이와 같은 피해 이력 자료가 부족하거나 거의 없는 경우에 관련 분야 전문가의 경험을 활용할 수 있는 간편한 방법을 제시하고자 한다. 시간 의존 확률모형과 내구수명에 대한 분포함수를 이용하여 항만 구조물의 재령에 따른 평균 잔류수명(Mean Residual Life: MRL)을 추정할 수 있는 방법이다.
본 논문의 구성은 다음과 같다. 먼저 제 2절에는 시간 의존 확률모형을 이용하여 MRL을 추정할 수 있는 수학적 모형을 수립하였다. 또한 제 3절과 제 4절에서는 수립된 모형을 전면이 TTP로 피복된 경사제에 적용하여, 각각의 절에서 발생 가능한 모든 피해 유형에 대하여 내구수명의 분포함수를 산정, 검증하였고 또한 재령에 따른 평균 잔류수명을 추정하였다. 또한 동일한 조건에 대하여 WP 기반의 추계학적 확률모형도 함께 적용하였는데, 이는 본 연구에서 제시한 간편법을 검증하기 위함이다. 마지막으로 제 5절에 결론을 제시하였다.
2. 수학적 모형의 수립
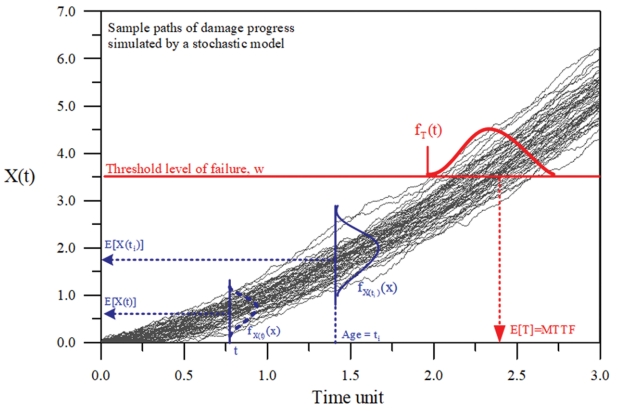
시간의 진행에 따른 항만 구조물의 누적피해를 X(t)라 정의하면 Fig. 1에서 볼 수 있듯이 피해에 영향을 주는 하중 및 저항과 관련된 많은 확률변수들에 의하여 다양한 피해의 진행경로가 나타날 수 있다. 따라서 누적피해 X(t)를 임의 분포함수 fX(t)(x)를 따르는 시간 의존 확률변수로 고려해야 한다. 이는 누적피해의 불확실성이 시간의 함수로 나타나기 때문이다.
먼저 임의의 시간 t에서 누적피해, X(t)가 파괴한계, w에 도달하지 않을 확률, 신뢰도(reliability), R(t)는 다음 식(1)과 같이 정의된다.
따라서 시간에 따른 항만 구조물의 신뢰도를 계산하기 위해서는 시간에 의존하여 불확실하게 거동하는 누적피해의 분포함수, fX(t)(x)를 정확히 알아야 한다. 이를 위해서는 누적피해에 대한 많은 시간 이력 자료와 관련 모수 추정 등 상당히 복잡한 과정을 거쳐야 한다(Lee, 2015, 2019, 2020). 추계학적 확률모형은 태풍 내습 때마다 점검과 진단(inspection & diagnosis)을 통해 얻어지는 시간 이력 피해자료를 기반으로 하기 때문이다. 그러므로 시간 이력 피해자료가 없는 경우에는 식(1)을 사용하여 시간에 따른 항만 구조물의 신뢰도를 계산할 수 없다.
따라서 본 연구에서는 식(1)을 사용하는 대신 내구수명의 분포함수를 이용하여 시간의 함수로 항만 구조물의 안전성을 확률론적으로 해석하고자 한다. 이는 누적피해, X(t)가 확률변수이기 때문에 최초 시점에서부터 파괴한계, w에 도달하는 시간 간격으로 정의되는 내구수명, T도 임의의 분포함수, fT(t)를 따르는 확률변수로 고려되어야 하기 때문이다. 그러므로 누적피해, X(t) = w가 되는 시간이 내구수명, t = T로 정의되고, 식(1)은 다음 식(2)와 같이 내구수명의 분포함수, FT(t) = P[T ≤ t]로 변환된다.
본 연구에서는 내구수명의 분포함수로 정의된 식(2)를 이용하여 시간에 따른 항만 구조물의 안전성을 확률적으로 해석하고자 한다. 그러나 항만 구조물의 경우는 규모가 작은 기계 장치류와 다르게 실제 내구수명의 자료를 확보하는 것이 상당히 어렵다. 단지 알 수 있는 것은 최초 설계시 적용한 설계하중을 통하여 설정된 설계 내구수명과 재령에 따라 어떤 크기의 하중, 즉, 태풍이 몇개 내습하였는지 정도이다. 항만 구조물의 경우 태풍의 내습에 의하여 심각한 피해가 발생되었을 때만 피해조사와 진단을 통해 사건발생 후 유지관리(CM: Corrective Maintenance)를 실시하지만 예방적 유지관리(PM: Preventive Maintenance)을 위해 정기적으로 피해진행에 대한 점검과 진단을 실시하지 않는다. 따라서 본 연구에서는 관련 분야 전문가의 경험적 판단을 활용할 수 있는 방법을 제시하고자 한다. 즉, 항만 구조물의 설계시 적용된 설계 내구수명과 과거 태풍 내습 관련 이력 자료 등을 고려하여 경험이 풍부한 여러 전문가들이 판단한 내구수명에 대한 자료를 이용하는 방법이다.
그러므로 시간에 따른 누적피해 진행 과정의 불확실성에 따라 확률변수로 고려되는 내구수명의 평균, 시간 의존 신뢰성 이론에서 파괴시간의 평균(Mean Time To Failure: MTTF)으로 정의되는, E ( t ) = ∫ 0 ∞ t f T ( t ) d t
여기서 fT(t)는 내구수명의 확률밀도함수이다. 또한 식(3)은 R(0) = 1, R(∞) ≃ 0을 만족한다. 일반적으로 식(3)의 MTTF는 R(0) = 1인 상태를 기준으로 항만 구조물의 내구수명의 평균을 구하기 위해 사용된다.
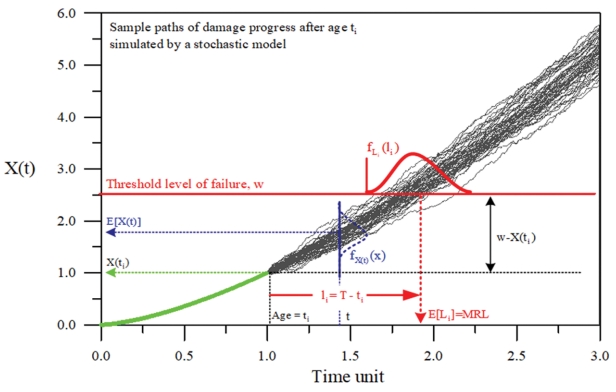
한편 잔류수명(Residual/Remaining Useful Lifetime: RUL)이란 앞에서 언급된 바와 같이 최초상태에서 일정 시간이 경과된 임의의 재령에서 항만 구조물이 파괴에 도달할 때 까지의 수명을 구할 때 사용하는 개념이다. 따라서 Fig. 2에 제시된 바와 같이 재령이 ti인 항만 구조물이 파괴될 때까지의 시간 간격, li = T – ti로 나타낼 수 있고, 다음 식(4)와 같이 정의된다.
여기서 inf는 수학적으로 하한(infimum) 또는 최대하계(greatest lower bound)를 의미한다. 이때 식(2)에서 사용된 개념을 동일하게 적용하면 식(4)를 확률변수인 내구수명의 함수로 다음 식(5)와 같이 나타낼 수 있다.
따라서 항만 구조물의 재령에 따른 잔류수명도 내구수명과 같이 임의의 확률분포, f L i ( l i )
본 연구에서는 복잡한 추계학적 확률모형을 이용하지 않고도 간편한 방법으로 평균 잔류수명, E[Li] ≡ m(ti)를 재령 ti의 함수로 해석할 수 있는 방법을 제시하고자 한다. 따라서 식(5)를 이용하여 확률적 개념으로 약간의 수학적 과정을 거치면 평균 잔류수명을 해석할 수 있는 다음 식(6)을 얻을 수 있다(Ghai and Mi, 1999; Tang et al., 1999; Banjevic, 2009).
시간 의존 신뢰성 이론에서 m(t)를 평균 잔류수명 함수(MRL function)라 정의한다. 앞에서 언급되었듯이 식(6)은 t = 0인 조건에서 R(0) = 1이기 때문에 m(0) = E(T) = MTTF로 식(3)과 같아진다. 따라서 식(6)은 식(3)을 포함하게 된다. 그러나 반대로 t → ∞인 경우에는 R(∞) ≃ 0, M T T F - ∫ 0 ∞ R ( u ) d u
한편 식(6)을 이용하여 항만 구조물의 평균 잔류수명을 해석하기 위해서는 내구수명의 분포함수로 표현된 식(2)를 함께 사용하여야 한다. Banjevic(2009) 등의 연구자들은 감마분포함수(Gamma distribution)나 Weibull 분포함수를 내구수명에 대한 분포함수로 가정한 바 있다. 이와 같은 연구의 대부분은 항만 구조물과 같은 시설물이 아니라 기계류에 대한 해석이었다. 방파제의 대표적 형식인 경사제를 대상으로 하는 본 연구에서는 내구수명의 분포함수를 Lee(2020)의 해석 경험을 바탕으로 다음 식(7)과 같이 정의되는 대수정규분포함수(Log-normal distribution)로 가정하였다(Lewis, 1987).
여기서 Φ(x)는 표준 정규분포함수이다. 쉽게 알 수 있듯이 식(7)에는 분포함수의 모수(parameter), s와 T0가 두 개 포함되어 있다. 이들 모수에 의하여 분포함수의 거동특성이 결정되기 때문에 모수를 결정하는 과정에 원칙적으로 누적피해의 진행과정이 고려되어야 한다. 따라서 임의 재령까지 누적피해에 대한 정확한 시간 이력 관측자료가 필요하다. 그러나 앞에서 언급되었듯이 이와 같은 자료를 확보하는 것은 현실적으로 상당히 어렵다. 단지 최초 설계시 설정된 내구수명과 임의 재령까지 내습한 하중특성, 즉, 태풍의 크기와 발생빈도 등을 대략적으로 알 수 있다. 따라서 본 연구에서는 이와 같은 자료들을 기반으로 관련 분야 전문가들이 해당 항만 구조물의 내구수명에 대하여 판단한 자료를 가지고 분포함수의 모수를 결정할 수 있는 방법을 도입하고자 한다.
동일한 형식의 항만 구조물에서 동일한 재령까지 큰 태풍이 더 많이 내습한 경우는 그렇지 않은 경우보다 상대적으로 더 큰 누적피해가 발생한다(Melby, 1999; Suh et al., 2013). 따라서 임의의 재령에서 파괴가 발생되는 시점까지의 잔류수명은 상대적으로 짧아지게 된다. 이와 같은 현상은 반대의 경우에도 성립한다. 이를 고려하여 분포함수의 모수를 결정하는 방법으로 본 연구에서는 다음 식(8)을 사용하였다.
여기서 T-와 T+는 각각 내구수명의 하한치와 상한치로, 최초 설계시 설정된 내구수명과 임의 재령까지 내습된 태풍의 특성에 따라 전문가의 판단에 의해 대략적으로 결정할 수 있다. 또한 p는 내구수명이 하한치와 상한치 사이에서 발생할 확률을 의미한다. 만약 내구수명의 하한치 T- = T0/α, 상한치 T+ = αT0라 정의하고 그 사이에 존재할 가능성을 p%라 하면 모수는 식(7b)에 의하여 다음 식(9)와 같이 쉽게 결정할 수 있다.
예로 내구수명 50년으로 설계된 임의 항만 구조물의 실질적 내구수명에 대하여 재령 이전 과거 태풍 발생 사상이나 불확실성에 따라 여러 전문가 판단에 의해 각기 다른 하한치와 상한치를 제시한 경우를 생각할 수 있다. 여러 전문가가 제시한 모든 판단 자료를 통계적으로 분석하여 결정된 내구수명의 하한치가 42년, 상한치가 52년, 그리고 실제 내구수명이 그 사이에 존재할 확률이 p= 90%로 결정되었다면, 식(9)에 의하여 T0 = 46.733년, α = 1.113, 그리고 Φ–1 (0.95) = 1.645, s = 0.065로 추정된다.
그러나 평균 잔류수명, MRL은 식(6)을 이용하여 수치적으로 구해야 한다. 이상과 같이 누적피해의 시간 이력 자료를 필요로 하는 추계학적 확률모형과는 다르게 시간 의존 신뢰성 이론과 전문가의 내구수명에 대한 판단자료를 활용하여 항만구조물의 평균 잔류수명을 간편하게 산정할 수 있는 모형이 수립되었다. 본 연구에서 제시된 평균 잔류수명 추정을 위한 간편법은 관련 자료가 부족한 현실을 고려하면 추계학적 확률모형보다 실제에 대한 적용이 용이하다. 따라서 제시된 간편법을 전면이 TTP로 피복된 경사제에 적용하였다. 비교 검증하기 위하여 추계학적 확률모형도 함께 적용하여 각각의 모형으로 경사제의 시간에 따른 신뢰도와 내구수명에 대한 분포함수 뿐만 아니라 평균 잔류수명을 추정하였다.
3. 경사제의 내구수명에 대한 분포함수
본 연구에서 제시된 간편법은 누적피해에 대한 관련 자료를 사용할 수 없는 경우,내구수명에 대한 분포함수를 먼저 가정하고, 전문가의 판단을 기초로 분포함수의 모수를 추정하여 평균 잔류수명을 산정하는 방법이다. 따라서 식(7)과 같이 가정된 내구수명의 분포함수에 대한 검증이 먼저 수행되어야 한다. 이를 위해 본 연구에서는 Lee(2020)의 추계학적 확률 모형도 함께 전면이 TTP로 피복된 경사제에 처음으로 적용하였다.
Suh et al.(2013)은 TTP 중량 산정시 사용한 설계파보다 큰 각기 다른 입사 파랑이 연속적으로 내습할 때, 경사제 전면에 거치된 TTP 피복재의 상대적 피해(relative damage), N0를 관측하여 누적피해의 진행 거동을 살펴보기 위한 수리 모형실험을 실시하였다. 모두 5개, Series A, B, C, D 그리고 E로 구분하여 입사 파랑 내습 시나리오에 따른 TTP 피복재의 누적피해에 대한 거동특성을 해석하였다. 입사 파랑의 지속시간은 파수(number of waves), Nw를 기준으로 약 500파에서 700파 내외이다. 국내에 설치된 경사제 대부분이 TTP 등 콘크리트 이형블록으로 전면 피복된 현실에 비추어 보면 본 실험 결과는 경사제의 유지관리에 충분히 활용될 수 있다고 판단된다. 따라서 본 연구에서도 Suh et al.(2013)의 실험자료를 이용하였다.
앞에서 언급하였듯이 식(7)을 검증하기 위하여 본 연구에서는 Lee(2020)의 WP(Wiener Process) 기반 추계학적 확률 모형도 함께 적용하였다. 즉, WP 기반 추계학적 확률모형을 이용하여 전면이 TTP로 피복된 경사제의 내구수명에 대한 분포함수를 산정하였다. 또한 WP에 대한 다음 식(11)을 이용하여 MCS(Monte-Carlo Simulation) 기법으로도 수치적으로 모의된 누적피해의 피해경로를 이용하여 내구수명에 대한 분포함수도 함께 산정하였다.
여기서 X(t)는 시간 t에서 TTP 피복재의 누적피해를 의미하고, X(0)는 초기피해, a는 피해진행의 평균 기울기, σB는 피해진행의 불확실성을 나타내는 분산계수(diffusion coefficient), W(t)는 표준 브라운 운동(standard Brownian Motion: BM)이다. 또한 피해진행의 거동 특성을 나타내는 시간 의존 함수, ≡(t; b) = btb–1이다. b = 1이면 피해진행이 선형으로 증가하게 된다. 반면 b > 1이면 지수함수적으로, b < 1이면 대수함수적으로 피해진행이 증가한다. 동일하게 ζ ( t ; γ → )
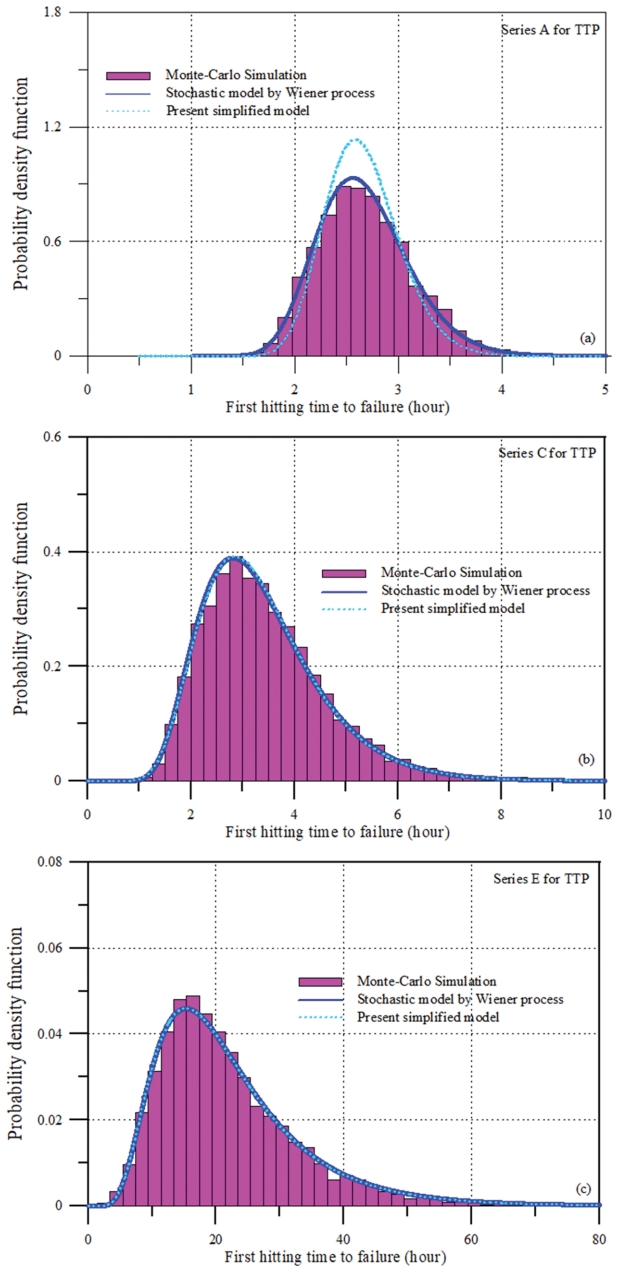
따라서 WP 기반 추계학적 확률모형이나 MCS 기법을 적용하기 위해서는 식(11)에 포함된 3개의 파라미터, a, b 그리고 σB를 먼저 추정해야 한다. Suh et al.(2013)의 Series A, B, C, D 그리고 E의 수리모형실험 결과에 대하여 Lee(2020)의 추정법으로 얻어진 파라미터 추정 결과를 Table 1에 제시하였다. Table 1로부터 알 수 있듯이 Series A와 Series B의 경우는 b > 1서 피해진행이 지수함수적으로 증가한다. 그러나 Series C에서는 b ≃ 1로 선형적으로 증가하게 된다. 반면 Series D와 Series E의 경우는 b < 1다. 따라서 피해진행이 대수 함수적으로 증가하게 된다. 그러나 동일한 피해진행의 형태에서도 σB는 각기 다르게 추정되었다. 이는 피해진행 과정에 불확실성의 정도가 각기 다르게 나타난다는 것을 의미한다. 이와 같은 정성적 분석을 확인하기 위하여 식(11)을 이용하여 MCS 기법으로 Series A와 Series C 그리고 Series E를 수치적으로 모의하였다. b > 1, b ≃ 1 그리고 b < 1인 대표적인 경우로, 그 결과를 Fig. 3에 제시하였다. 그림에서 알 수 있듯이 실험 자료와 MCS로 모의된 자료가 비교적 잘 일치하고 있다. Series A는 지수함수적으로 피해가 진행되고 Series E는 대수 함수적으로 피해가 진행되는 경향을 잘 모의하고 있다. 또한 Series C는 피해진행이 선형적으로 증가하지만, 상대적으로 불확실성의 정도가 크게 나타나고 있다. 이는 Table 1에 제시되었듯이 Series C의 σB가 Series A나 Series E보다 크기 때문이다. 특히 Series E의 경우는 초기에 피해가 크게 나타나고 있는데, 이는 Suh et al.(2013)의 입사파 시나리오 특성에 따른 것이다. 모두 8개의 파랑이 연속적으로 내습한다는 가정하에 실험을 실시하였는데 Series E의 경우 처음과 맨 마지막에 큰 파랑이 내습한다고 가정한 반면, Series A는 마지막에 두 개의 큰 파랑이 내습한다고 가정하였다.
한편 내구수명에 대한 분포함수를 추정하기 위해서는 Fig. 3의 피해경로에 대한 MCS 수치모의 결과를 이용하여 각각의 누적피해 경로가 파괴한계(failure threshold), w에 도달하는 시간을 산정하여야 한다. 이를 위해 본 연구에서는 CEM(2006)에 제시된 TTP 피복재의 파괴한계, w = N0 = 1.5를 적용하였다. 이와 같이 산정된 내구수명의 분포함수를 식(7)과 비교하였다. 식(7)에 포함된 모수는 식(8)의 개념으로 추정하여 Table 2에 제시하였다. p= 0.9에 대하여 내구수명의 하한치와 상한치를 표에 제시한 것처럼 부여하고 식(9)로부터 추정된 것이다. 본 연구에서는 Fig. 3의 피해경로에 대한 결과를 참조하여 하한치와 상한치를 임의로 부여하였는데 이는 실험에서 사용한 설계파고의 재현기간을 모르기 때문이다.
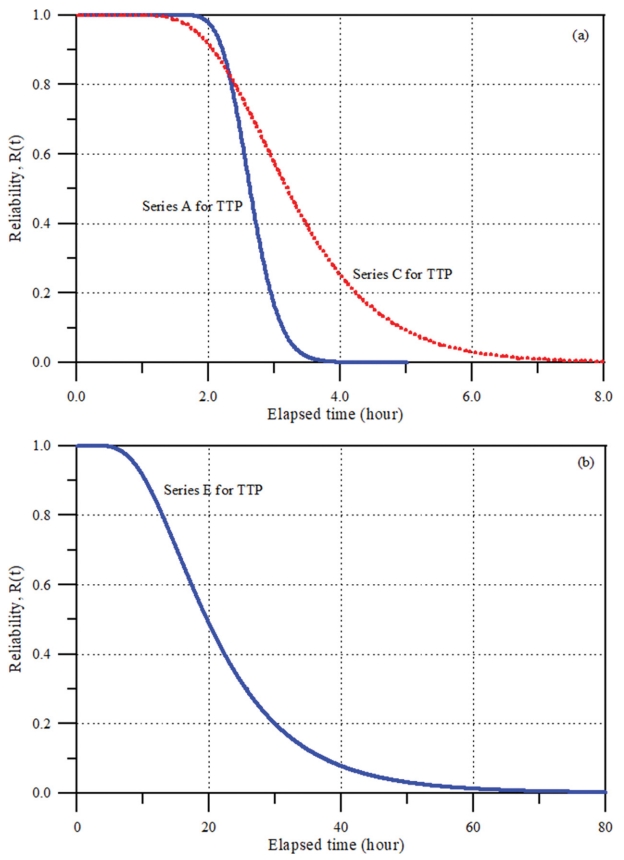
Table 2의 결과와 식(7)을 이용하여 산정된 내구수명에 대한 분포함수를 Fig. 4에 제시하였다. 그림에는 MCS 수치모의로부터 직접 산정된 결과 뿐만 아니라 Lee(2020)가 제시한 WP 기반 추계학적 확률모형의 결과도 함께 제시하였다. 그림에서 볼 수 있듯이 내구수명에 대한 분포함수들이 매우 잘 일치하고 있다. 비록 Series A의 경우 양쪽 꼬리 부분에서 약간 차이가 나지만 정규분포에 가까운 전반적인 거동을 잘 나타내고 있다. 특히 Series C와 Series E에서는 전반적인 분포함수의 거동 뿐만 아니라 우측 꼬리 부분까지도 정확히 나타내고 있다. 한편 내구수명의 평균, MTTF도 산정하여 비교하였는데, Table 3에 식(10b)에 의하여 얻어진 결과를 WP 기반 추계학적 확률모형의 결과와 함께 제시하였다. 모든 경우에서 내구수명의 평균이 매우 잘 일치한다. 따라서 누적 피해의 지수적, 선형적 또는 대수적 진행 거동에 상관없이 TTP로 전면 피복된 경사제의 내구수명에 대한 분포함수는 대수 정규분포로 가정할 수 있다.
4. 경사제의 평균 잔류수명 추정
전면이 TTP로 피복된 경사제의 내구수명에 대한 분포함수로 대수정규분포가 올바로 적용될 수 있음을 확인하였다. Suh et al.(2013)의 실험자료에 Lee(2020)의 WP 기반 추계학적 확률모형과 MCS 기법을 적용하여 TTP로 피복된 경사제의 내구수명에 대한 분포함수와 MTTF가 만족스럽게 비교되었다. 따라서 본 절에서는 식(6)을 이용하여 평균 잔류수명을 산정하였다. WP 기반 추계학적 확률모형도 함께 처음으로 적용하여 RUL의 분포함수도 제시하였다. 특히 평균 잔류수명을 함께 비교하여 본 연구에서 제시된 간편법의 추정 정확도와 적용 범위에 대하여 분석하였다.
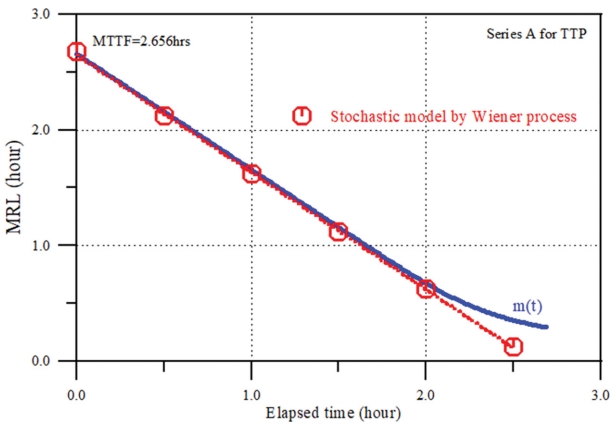
먼저 시간의 진행에 따라 누적피해가 지수적으로 증가하는 Series A에 대하여 식(6)을 이용하여 산정된 경사제의 재령에 따른 평균 잔류수명(MRL) 추정 결과를 Fig. 5에 제시하였다. WP 기반의 추계학적 확률모형에 의한 결과도 함께 제시하였는데, 이는 Fig. 6에 제시한 재령에 따른 잔류수명(RUL)의 분포로부터 산정된 것이다. 그림에서 볼 수 있듯이 본 연구에서 제시된 간편법으로 추정된 평균 잔류수명이 WP 기반의 추계학적 확률모형에 의한 결과와 매우 잘 일치한다. 그러나 재령이 내구수명의 평균(MTTF)에 가까워 짐에 따라 본 연구에서 제시한 간편법이 MRL을 약간 과대 추정하고 있다. 이는 Fig. 3과 Fig. 6에서 볼 수 있듯이 WP 기반의 추계학적 확률모형은 재령의 진행에 따른 누적피해 진행 과정의 불확실성을 올바로 고려하는 데 비해 본 연구에서 제시한 간편법은 단지 내구수명의 분포함수만을 이용하기 때문이다. 특히, 식(6)에서 재령이 커지면 분자보다 분모, R(t)가 급격하게 작아지기 때문이다.
동일하게 시간의 진행에 따라 누적피해가 선형 그리고 대수적으로 증가하는 Series C와 Series E에 대한 평균 잔류수명 추정 결과를 Fig. 7에 제시하였다. 그림에서 알 수 있듯이 초기 재령에서는 본 연구에서 제시한 간편법의 결과가 WP 기반 추계학적 확률모형의 결과와 잘 일치하지만, 재령이 커지면서 차이가 커지고 있다. 즉, 본 연구에서 제시한 간편법이 MRL을 과대 추정하고 있다. 누적피해가 지수적으로 증가하는 Series A와 비교하면 그 차이는 더 확연하다. 이는 누적 피해의 진행 형태에 따라 달라지는 시간에 따른 신뢰도, R(t)의 거동 특성에 기인한다(Bradley and Gupta, 2003; Banjevic, 2009). 이를 확인하기 위하여 Fig. 8에 시간에 따른 신뢰도, R(t)를 제시하였다. 그림에서 볼 수 있듯이 누적피해가 재령에 따라 지수적으로 증가하는 경우는 아주 짧은 시간에 신뢰도가 급격하게 감소하는 반면, 선형으로 증가하는 경우는 일정 시간에 걸쳐 신뢰도가 완만하게 감소하는 것을 알 수 있다. 특히 재령 초기에 큰 피해가 발생하였다가 그 후에 누적 피해가 대수적으로 완만하게 증가하는 경우는 신뢰도가 오랜 시간에 걸쳐 조금씩 감소하는 특성을 나타내고 있다.
따라서 시간에 따른 누적피해의 진행이 지수적인 경우는 거의 내구수명의 평균 전체 구간에 대하여 적용이 가능한 반면, 선형이거나 대수적인 경우는 내구수명의 평균보다 작은 범위에서만 정확성을 담보할 수 있다. 비록 평균 잔류수명을 추정하기 위하여 본 연구에서 제시된 간편법은 누적피해의 시간에 따른 진행 형태에 따라 그 적용 범위가 제한될 수 있다. 그러나 과거 누적피해 이력에 대한 자료가 없어서 추계학적 확률모형을 적용할 수 없는 경우를 고려하면, 본 연구에서 제시된 간편법은 예방적 유지관리 계획을 신속히 수립할 수 있는 대안으로 유용하게 활용될 수 있다.
5. 결 론
항만 구조물의 노후화가 빠르게 진행되고 있는 상황에서 해당 구조물에 부여된 성능에 대한 국민적 기대치는 점점 높아지고 있다. 따라서 시간의 진행에 따라 최초 설계시 부여된 성능이 올바로 유지되도록 생애주기 관점에서 예방적 유지관리가 실시되어야 한다. 이를 위해서는 항만 구조물의 재령에 따른 평균 잔류수명을 먼저 추정해야 한다. 따라서 본 연구에서 평균 잔류수명을 간편하게 추정할 수 있는 방법을 제시하였다. 시간 이력에 따른 누적피해와 관련된 자료를 사용할 수 없는 경우, 내구수명에 대한 분포함수를 먼저 가정하고, 설계 내구수명이나 과거 하중이력 등에 따라 전문가들이 판단한 내구수명의 상한치와 하한치 그리고 그 발생 가능성을 기초로 분포함수의 모수를 추정하여 평균 잔류수명을 산정하는 방법이다.
본 연구에서 제시한 간편법을 전면이 TTP로 피복된 경사제에 적용하여 추정 결과의 정확성과 적용 범위를 확인하였다. 이를 위해 TTP 피복재의 시간에 따른 누적피해에 대한 모형실험 자료가 있는 동일 조건에 대하여 처음으로 WP 기반의 추계학적 확률모형과 MCS 기법도 함께 적용하였다. 시간에 따른 누적피해 자료를 활용하여 WP 기반의 추계학적 확률모형의 파라미터를 추정하여 MCS 기법으로 누적피해의 미래 시간 진행에 따른 피해경로를 먼저 수치적으로 모의하였다. 이를 통해 누적피해 진행이 지수적, 선형적 그리고 대수적으로 증가하는 실제 발생 가능한 모든 경우에 대하여 누적피해가 파괴한계에 도달하는 내구수명에 대한 분포함수를 얻을 수 있었다. 그 결과들을 본 연구에서 가정한 간편법의 분포함수, 대수정규분포함수와 비교하였다. 모든 경우에 대하여 분포함수의 거동 특성 뿐만 아니라 MTTF도 함께 비교하여 전면이 TTP로 피복된 경사제의 내구수명에 대한 분포함수를 피해진행의 형태와 상관없이 대수정규분포로 가정할 수 있다는 것을 확인하였다.
마지막으로 본 연구에서 제시된 간편법으로 추정된 평균 잔류수명을 WP 기반 추계학적 확률모형의 결과와 비교하였다. 먼저 시간의 진행에 따라 누적피해가 지수적으로 증가하는 경우는 내구수명의 평균에 해당하는 재령에 대해서도 비교적 만족스럽게 잘 일치하였다. 그러나 피해진행이 선형적으로 진행하면서 불확실성이 큰 경우나 초기에 큰 피해가 발생된 후 완만하게 대수적으로 진행하는 경우는 재령이 커짐에 따라 본 연구에서 제시한 간편법이 평균 잔류수명을 과대 추정하는 경향을 보였다. 추계학적 확률모형은 재령의 진행에 따른 누적 피해 진행 과정의 불확실성을 올바로 고려하는데 비해, 본 연구에서 제시한 간편법은 내구수명의 분포함수만을 이용하는 데 기인한다. 따라서 항만 구조물의 평균 잔류수명을 추정하기 위하여 본 연구에서 제시된 간편법은 누적피해의 시간에 따른 진행 형태에 따라 그 적용 범위가 약간 제한될 수 있다. 그러나 항만 구조물에 대한 과거 누적피해 이력에 대한 자료가 없어서 추계학적 확률모형을 적용할 수 없는 경우를 생각하면 본 연구에서 제시한 간편법은 누적피해에 대한 시간 이력 자료를 필요로 하지 않기 때문에 평균 잔류수명 기반의 예방적 유지관리 계획을 수립할 수 있는 대안으로 유용하게 활용될 수 있다.