1. 서 론
바닥이 움직여서 파랑을 재현하는 기법은 물리적으로 파랑 발생 매커니즘이 유사한 지진해일을 재현하기 위해 주로 사용되었다. Hammack(1973)은 수평인 바닥이 순간적으로 1회 움직이는 경우의 자유수면변위의 변화에 대해 해석해를 유도하고, 실험을 통해 검증하였다. Lu et al.(2017)은 일부 경사가 있는 바닥이 수평한 상태로 순간적으로 1회 움직이는 경우의 자유수면변위의 변화에 대해 역시 해석해를 유도하고, Boussinesq 방정식을 이용한 수치모델 및 수리실험을 통해 검증하였다. Jung and Son(2018) 및 Jung and Son(2021)은 Hammack(1973)의 해를 이용하여 두 지점에서 수평인 바닥이 시간 차이를 가지고 순간적으로 움직이는 경우에 대한 자유수면변위의 변화에 대해 연구하였다.
최근에는 규칙파를 조파하기 위해 바닥 조파장치를 이용하는 연구들이 Jung et al.(2018) 및 Mahjouri et al.(2021)에 의해 수행되었다. 이들은 바닥을 움직여서 규칙파를 조파하는 경우 구조물에서 반사된 파랑이 조파판에서 재반사 되는 현상을 막을 수 있고, 일반 피스톤 및 힌지형 조파기에 비해 장파의 생성에 더욱 유리함을 알아내었다. Jung et al.(2018)은 Lu et al.(2017)과 같이 라플라스(Laplace) 및 푸리에(Fourier) 변환을 이용하여 바닥 조파장치가 삼각형 형상으로 규칙적으로 움직이는 경우의 규칙파 발생에 대한 해석해를 유도하였으며, 완경사방정식을 이용한 수치해석을 통해 검증하였다. Mahjouri et al.(2021)은 Jung et al.(2018)과 마찬가지로 사각형 및 삼각형 형상의 바닥 조파장치가 규칙적으로 움직이는 경우의 속도포텐셜 및 자유수면변위의 변화에 대해 고유함수전개법(Eigen function expansion method)을 이용하여 해석해를 유도하였다. Jung et al.(2022)은 Jung et al.(2018)의 연구를 확장하여 삼각형 및 사각형 형상 바닥 조파장치에 대한 해석해를 유도하였으며, 구조물에서 반사된 파랑이 바닥 조파장치에서 거의 재반사 되지 않음을 완경사 방정식을 이용한 수치해석을 통해 증명하였다.
기존 연구들은 주로 바닥이 움직일 경우 자유수면변위의 변화에 대해서만 주로 관심을 가졌다. Hammack(1973), Lu et al.(2017), Jung et al.(2018), Jung and Son(2018) 및 Jung and Son(2021)은 속도포텐셜 해석을 통한 유속의 변화에 대해서는 검토하지 않았다. 본 연구에서는 삼각형 및 사각형 형상의 바닥 조파장치가 규칙적으로 움직이는 경우 조파수로 내부에서 속도포텐셜 및 유속변화에 대해 해석적으로 검토하였다. 선형파 이론과 움직이는 바닥에 대한 경계조건, 동역학적 및 운동학적 자유수면 경계조건을 이용하여 바닥 조파장치가 설치된 조파수로 내부의 속도포텐셜을 유도하였으며, 이로부터 각 방향 성분의 유속에 대한 해를 구하였다.
2. 해석해의 유도
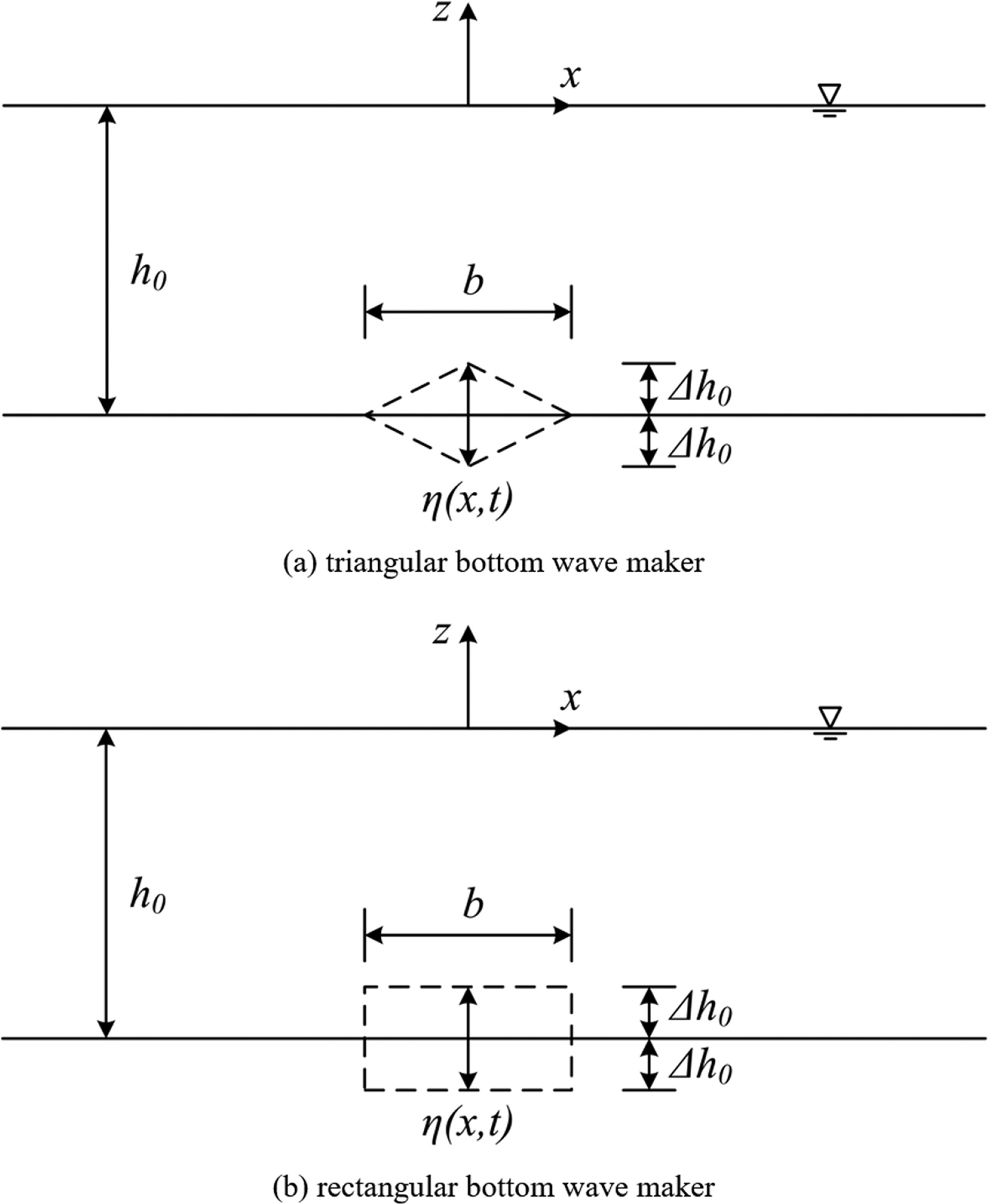
해석해 유도를 위한 좌표 및 변수는 Fig. 1과 같다. 고정된 수심은 h0, 바닥 조파장치의 폭은 b, 바닥 조파장치의 진폭은 △h0로 나타내었으며, 바닥의 움직임을 표현하는 함수는 η(x, t)로 나타내었다. Fig. 1(a) 및 (b)에는 삼각형 및 사각형 형상 바닥 조파장치에 대한 개념도를 각각 나타내었다.
바닥구동 조파수로의 수심은 다음 식과 같이 나타낼 수 있다.
여기서, 바닥의 움직임을 표현하는 η(x, t)는 △h(x)Λ(t)로 표현할 수 있는데 △h(x)는 공간적으로 변화하는 바닥 움직임의 진폭을 나타내며, Λ(t)는 시간이 흐름에 따른 바닥 움직임을 나타낸다.
선형파 이론에 따른 x - z 2차원 공간에서 연속방정식과 선형의 움직이는 바닥에 대한 경계조건, 운동학적 자유수면 경계 조건 및 동역학적 자유수면 경계조건은 다음과 같이 표현된다.
여기서, g는 중력가속도를 나타내며, ϕ(x, z, t)는 속도포텐셜, η(x, t)는 자유수면변위를 나타낸다. 식(4) 및 (5)와 같은 선형의 운동학적 및 동역학적 자유수면 경계조건은 다음 식과 같이 결합할 수 있다.
시간에 대해 라플라스 변환(Laplace transform), 공간에 대해 푸리에 변환(Fourier transform)을 각각 적용하면 식(2), (3) 및 (6)은 다음 식과 같이 변환된다.
여기서, 각진동수(angular frequency) ω는 수심 h0와 파수(wave number) k에 대한 변수로 다음과 같은 관계를 갖는다.
수면변위나 유속이 전혀 없는 초기조건(ζ(x, 0) = ϕ(x, 0, 0) = ∂ϕ(x, 0, 0)/∂t = 0)과 식(8) 및 (9)를 이용하여 식(7)을 풀면 다음과 같은 해가 유도된다.
식(5)를 라플라스 및 푸리에 변환하고 초기조건(ϕ(x, 0, 0) = 0)을 적용하면, 다음 식이 유도된다.
식(14)를 라플라스 및 푸리에 역변환하면 다음과 같다.
식(15)는 Hammack(1973)과 Lu et al.(2017)이 유도한 식과 동일한 식이다. 식(15)는 해석적으로 풀기는 불가능하기 때문에 해석이 가능한 식으로 변환해야 하는데, Hammack (1973)이 평평한 바닥이 순간적으로 1회 움직이는 경우에 대해, 그리고 Lu et al.(2017)이 경사진 바닥이 순간적으로 1회 움직이는 경우에 대해 풀이하였으며, Jung et al.(2018)이 삼각형 형상 바닥 조파장치가 규칙적으로 움직이는 경우에 대해 풀이하였다. 하지만 그들은 식(12)와 같이 표현된 속도포텐셜에 대해서는 어떠한 풀이도 제시하지 않았다.
2.1 삼각형 바닥 조파장치의 속도포텐셜
식(16)을 풀기 위해서는 바닥의 움직임에 대한 정의가 필요하다. 바닥의 움직임은 Fig. 1(a)와 같이 바닥이 삼각형 형상으로 규칙적으로 움직이는 것으로 가정하였다. 바닥의 움직임에 관한 식은 다음과 같이 정의된다.
식(3)을 이용하면 다음과 같은 관계식이 성립한다.
식(19)를 라플라스 및 푸리에 변환하면 다음과 같이 표현할 수 있다.
(21)
해석의 편의를 위해 식(21)은 다음과 같이 구분할 수 있다.
(23)
(25)
식(23)과 식(25)에는 s에 대해 동일한 적분식이 포함되어 있는데, 이 식은 라플라스 역변환에 대한 식이다. 이 식은 합성곱(convolution)을 이용해서 다음과 같이 표현할 수 있다.
식(26)에서 함수 F(t)와 G(t)는 다음과 같다.
따라서, 식(26)은 다음과 같이 표현할 수 있다.
(29)
식(24)에 포함된 s에 대한 적분식은 라플라스 역변환의 정의에 의해 다음과 같이 표현할 수 있다.
따라서,
(34)
식(34)로 표현된 속도포텐셜을 x 및 z 방향으로 미분하면 각 방향의 유속성분(x 방향: U(x, z, t), z 방향: V(x, z, t))을 구할 수 있다. 각 방향의 유속성분은 다음과 같다.
(35)
(36)
바닥이 삼각형 형상으로 움직이는 경우에 대한 자유수면변위는 식(34)를 경계조건인 식(5)에 대입하여 풀 수 있으며, 이는 Jung et al.(2022)이 유도한 식과 동일하다.
2.2 사각형 바닥 조파장치의 속도포텐셜
2.1절에서는 바닥이 삼각형 형상으로 움직이는 경우에 대한 해석해를 제시하였다. 본 절에서는 평평한 바닥이 사각형 형상으로 움직이는 경우에 대한 해석해를 제시한다. 사각형 형상의 바닥 조파장치의 움직임은 다음과 같은 함수로 표현된다.
여기서, 함수 h(x)는 Heaviside step function을 의미한다. 사각형 형상 바닥 조파장치에서의 속도포텐셜은 식(38)을 이용하여 2.1절과 동일한 과정을 거쳐 유도할 수 있으며, 다음 식과 같이 표현된다.
(39)
식(39)를 이용하여 각 방향의 유속성분(x 방향: U(x, z, t), z 방향: V(x, z, t))을 구할 수 있으며, 다음과 같이 표현된다.
(40)
2.3 자유수면변위로부터 속도포텐셜 및 유속 계산
이번 절에서는 기존의 선형이론을 이용하여 자유수면변위로부터 삼각형 및 사각형 바닥 조파장치의 속도포텐셜을 유도하였다. 선형의 동역학적 경계조건인 식(5)로부터 평균수면에서의 속도포텐셜을 다음과 같이 구할 수 있다.
또한 선형파의 해로부터 수직 방향의 임의의 위치에서의 속도포텐셜을 다음과 같이 구할 수 있다(Dean and Dalrymple, 1991).
입자속도 U(x, z, t), V(x, z, t)를 다음과 같이 구할 수 있다.
여기서 바닥 조파장치의 각진동수(ω0)와 파수(k0) 사이의 관계는 다음과 같다.
<삼각형 바닥 조파장치>
(48)
(49)
(50)
<사각형 바닥 조파장치>
3. 수치해석 결과
3.1 시간 흐름에 따른 속도포텐셜 및 유속장 변화
본 절에서는 수치해석을 통해 삼각형 및 사각형 바닥 조파장치가 설치된 수로에서 유속변화에 대해 검토하였다. 해석 조건으로 수심(h0)은 1.0 m, 파장(wave length, L)은 20 m, 조파장치 폭(b)은 5 m, 조파장치가 움직이는 진폭(△h0)은 0.1 m이며, 조파장치가 움직이는 각진동수(ω0)는 식(47)과 같은 선형의 분산관계식을 이용하여 구할 수 있다. 식(47)에서 k0는 파수(wave number)를 나타내며, 목표로 하는 파장(본 실험에서는 20 m)으로부터 계산할 수 있다. 식(34)~(36)의 적분식은 4차 Runge-Kutta법을 이용하여 적분하였다.
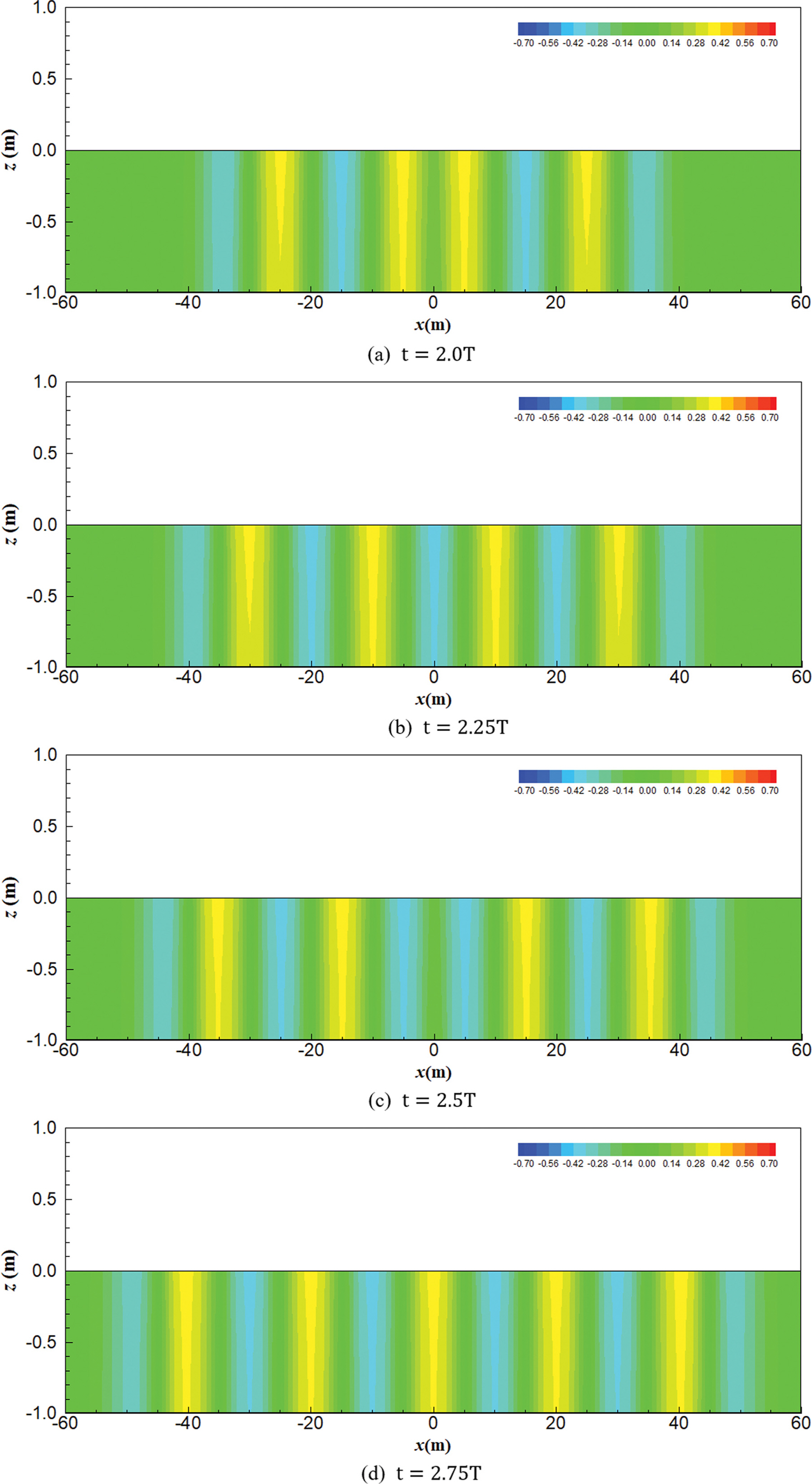
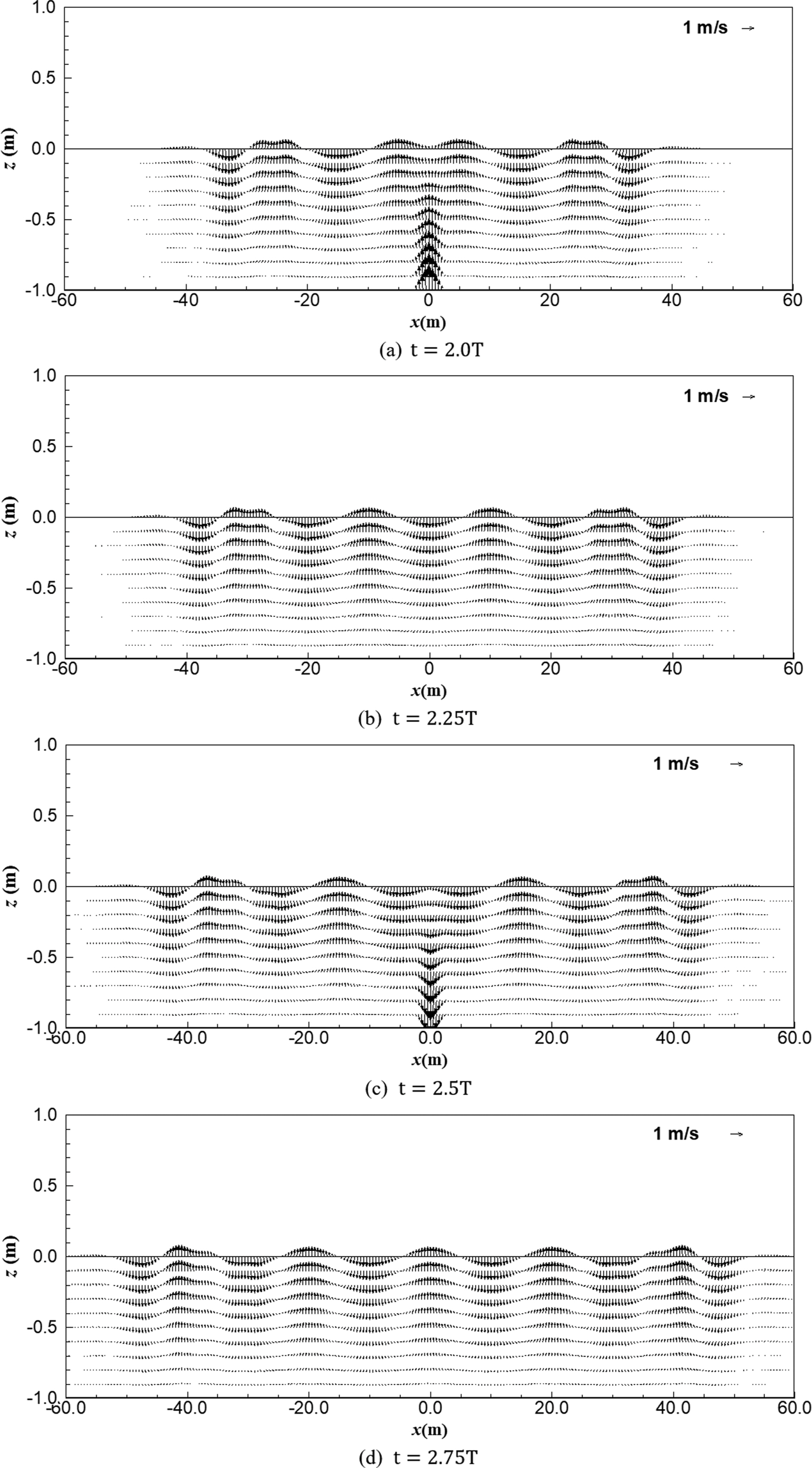
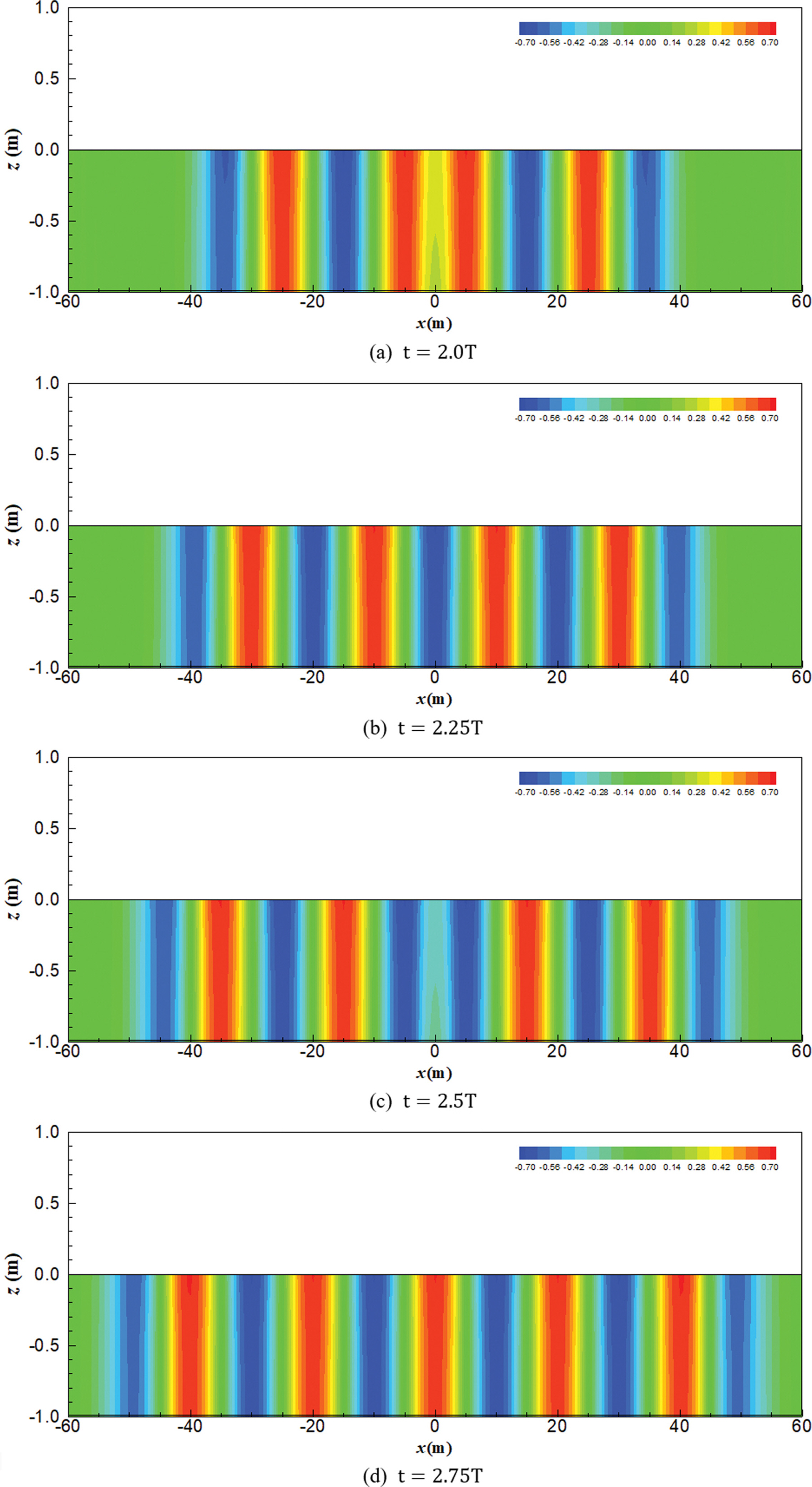
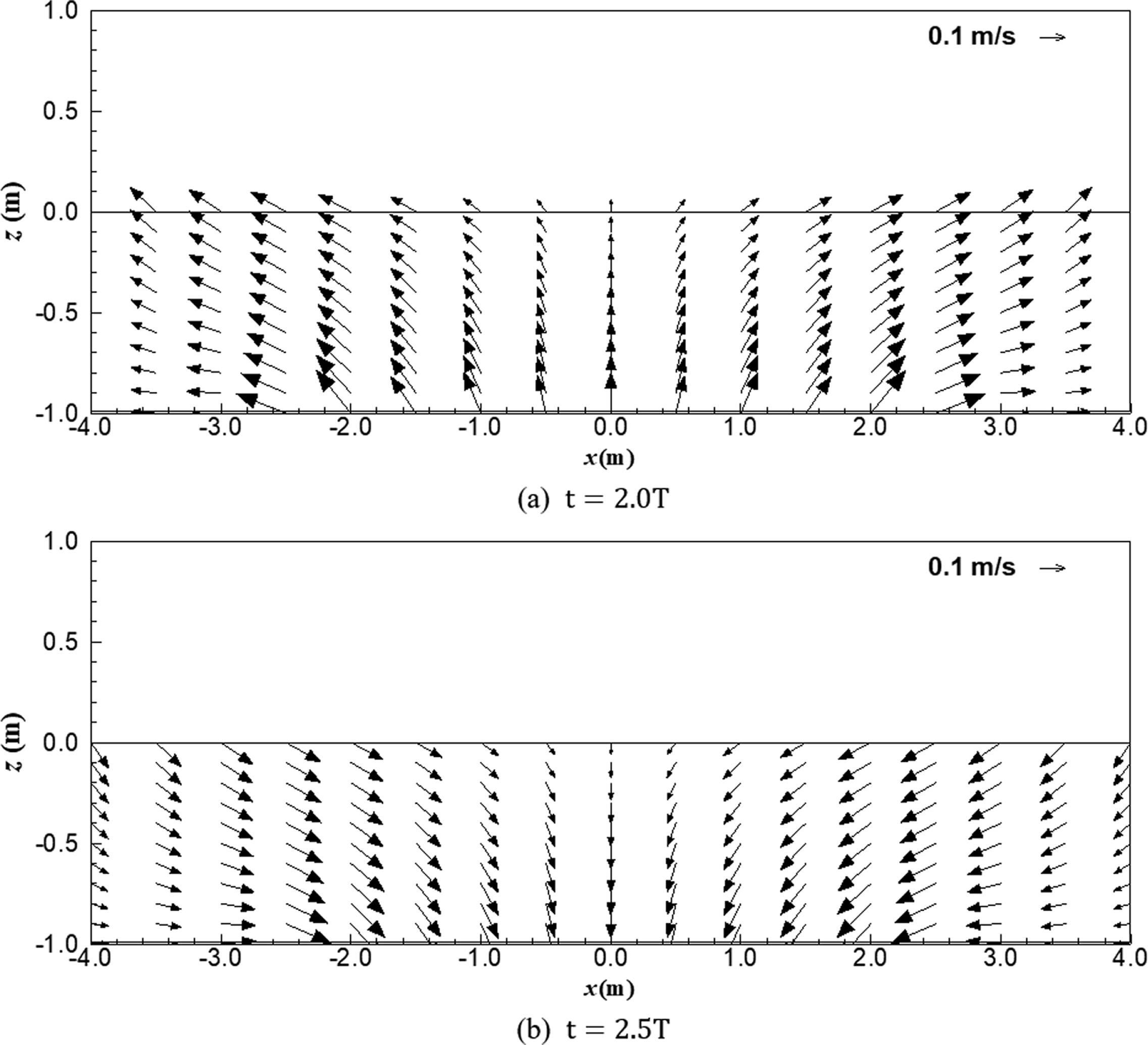
삼각형 바닥 조파장치가 주기적으로 움직일 때 속도포텐셜을 해석한 결과는 Fig. 2에 나타내었다. Fig. 2에서 속도포텐셜은 해석해의 실수부만을 나타낸 그림이다. Fig. 2(a)는 조파 시작 후 2주기(T) 시점에서의 결과이며, 2.25주기, 2.5주기 및 2.75주기 시점에서의 결과를 각각 Fig. 2(b), (c), (d)에 나타내었다. 조파하는 위치인 수로 중앙부에서 양 측면 방향으로 시간이 흐름에 따라 에너지가 전파하는 것을 그림에서 확인할 수 있다. Fig. 3에서는 바닥이 주기적으로 움직임에 따른 유속장의 변화를 나타내었다. Fig. 2와 마찬가지로 2주기, 2.25주기, 2.5주기 및 2.75주기 시점에서의 결과이다. 해석 결과 바닥 움직임에 의해 생성된 파랑이 양 측면으로 전파해 가는 현상을 명확히 볼 수 있다. 그리고, 수로 중앙의 바닥 부근에서 바닥 조파장치의 구동에 따른 강한 유속이 형성되는 것을 확인할 수 있다. Fig. 2 및 Fig. 3은 결과를 잘 보기 위해 x 방향에 비해 z 방향이 더욱 길게 왜곡된 형태의 그림이다. 따라서, Fig. 3의 유속 벡터는 z 방향이 훨씬 강하게 표현되었으므로 본 그림의 reference vector는 x 방향에서만 타당하다.
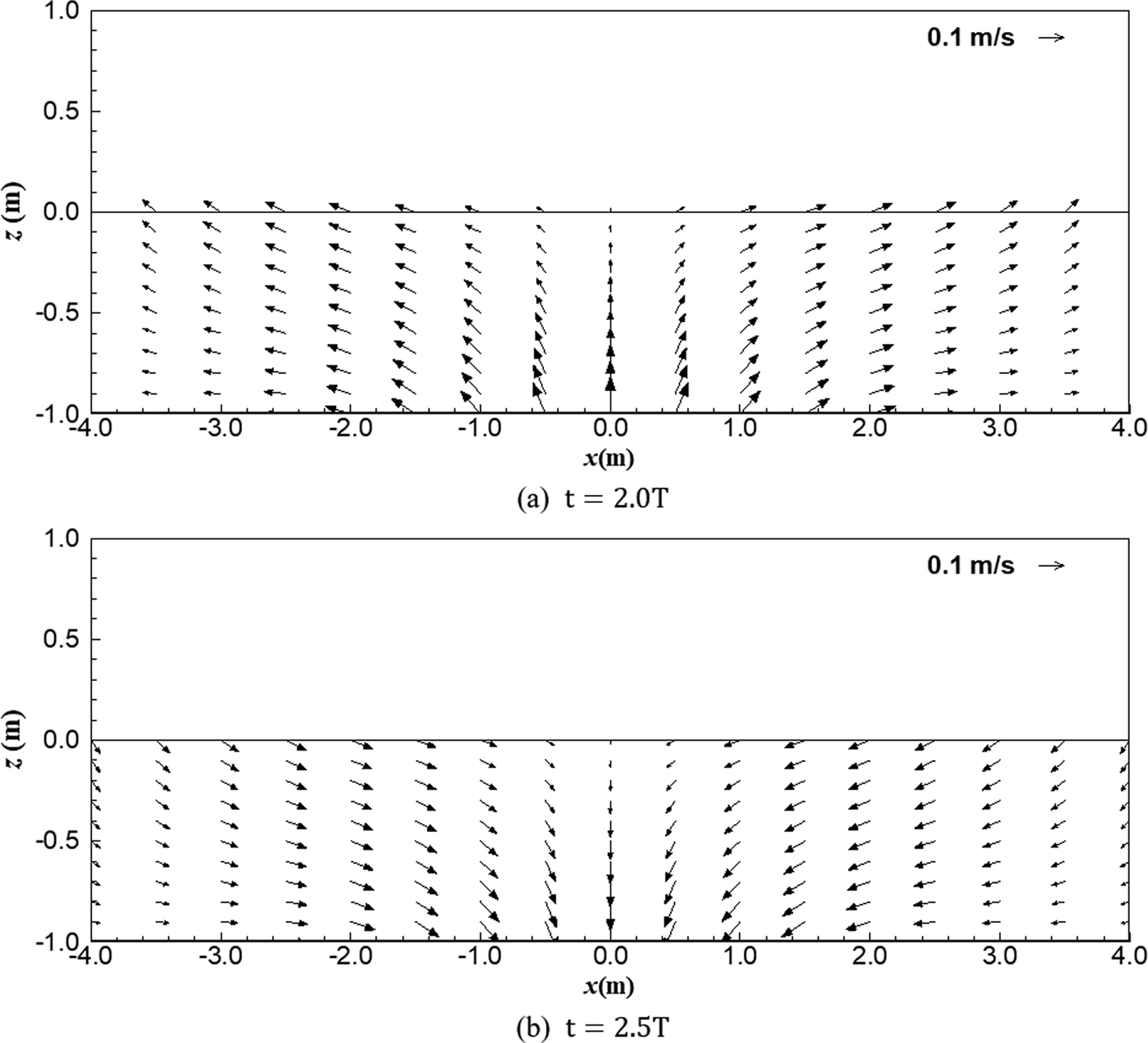
Fig. 4는 2 주기 및 2.5주기 시점에서 삼각형 바닥 조파장치가 위치한 바닥구동 조파수로 중앙부에서 유속벡터를 자세히 나타낸 그림이다. 중앙부만 확대하여 나타내었기 때문에 z 방향으로 왜곡되지 않은 그림이다. 본 그림을 통해 바닥이 움직임에 따른 수직방향 유속이 주변에 영향을 주어 강한 수평방향의 유속을 만드는 것을 볼 수 있다. 즉, 바닥의 움직임으로 유속을 만들기 때문에 바닥 주변에서 유속이 크게 발생하며, 따라서 바닥 주변에서 유속이 강한 천해파의 조파에 바닥 조파장치가 유리함을 다시 한번 확인할 수 있다.
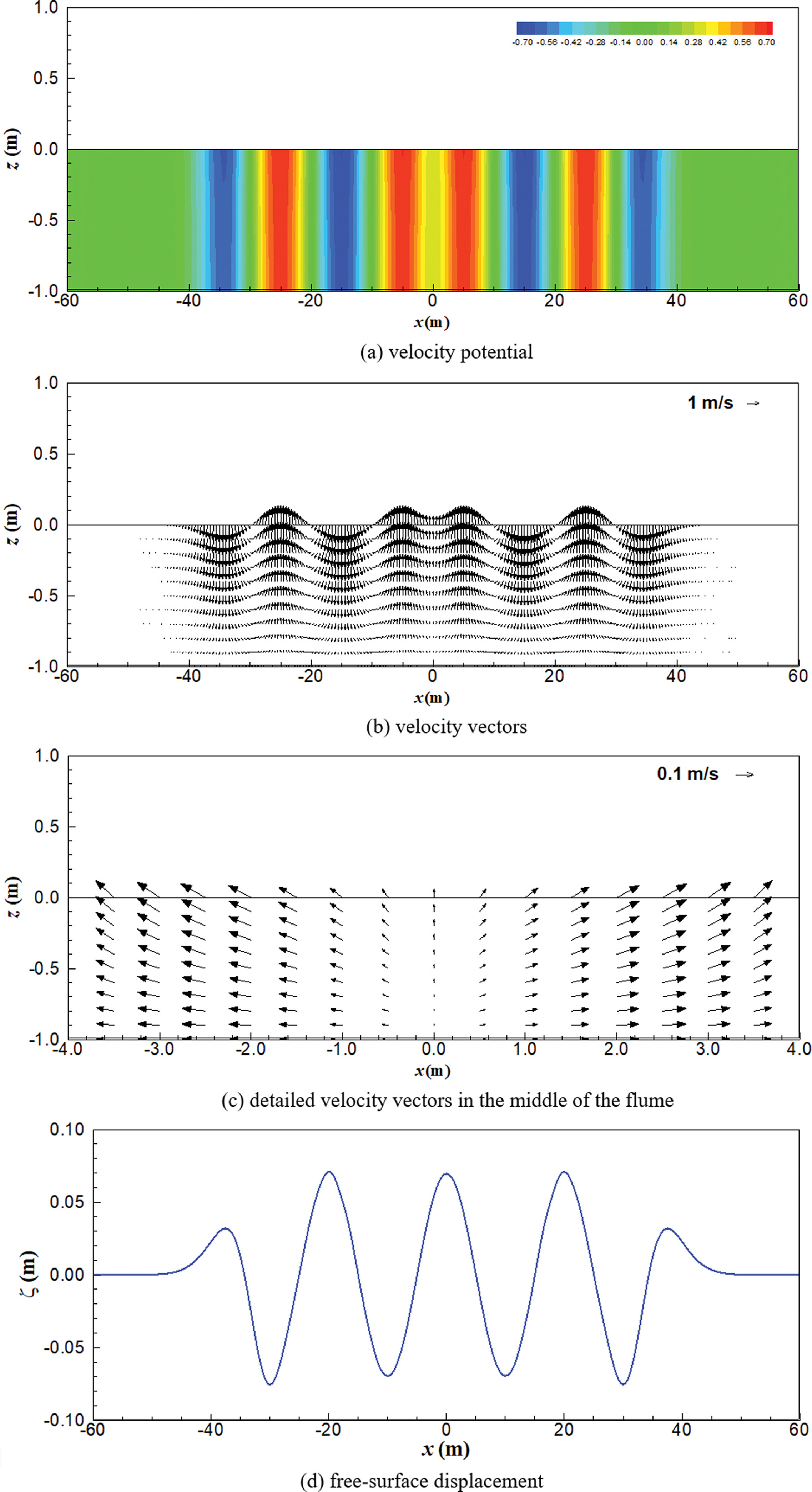
사각형 바닥 조파장치가 주기적으로 움직일 때 속도포텐셜을 해석한 결과는 Fig. 5에 나타내었으며, 유속 벡터도는 Fig. 6에 나타내었다. 사각형 바닥 조파장치의 진폭은 삼각형 조파장치와 마찬가지로 △h0 = 0.1 m를 적용하였다. 사각형 바닥 조파장치가 삼각형 바닥 조파장치와 동일한 진폭으로 움직일 경우 사각형 바닥 조파장치가 삼각형 조파장치에 비해 2배 많은 양의 물을 움직이므로 속도포텐셜과 유속이 삼각형 조파장치보다 더욱 크게 형성되었다. Fig. 7에는 사각형 바닥 조파장치 근처에서의 유속장을 나타내었는데, 바닥 조파장치에 의한 강한 수직방향 흐름이 수평방향 흐름으로 전이 되어 파랑을 형성함을 확인할 수 있다.
3.2 자유수면변위에 따른 선형가정의 결과와 비교
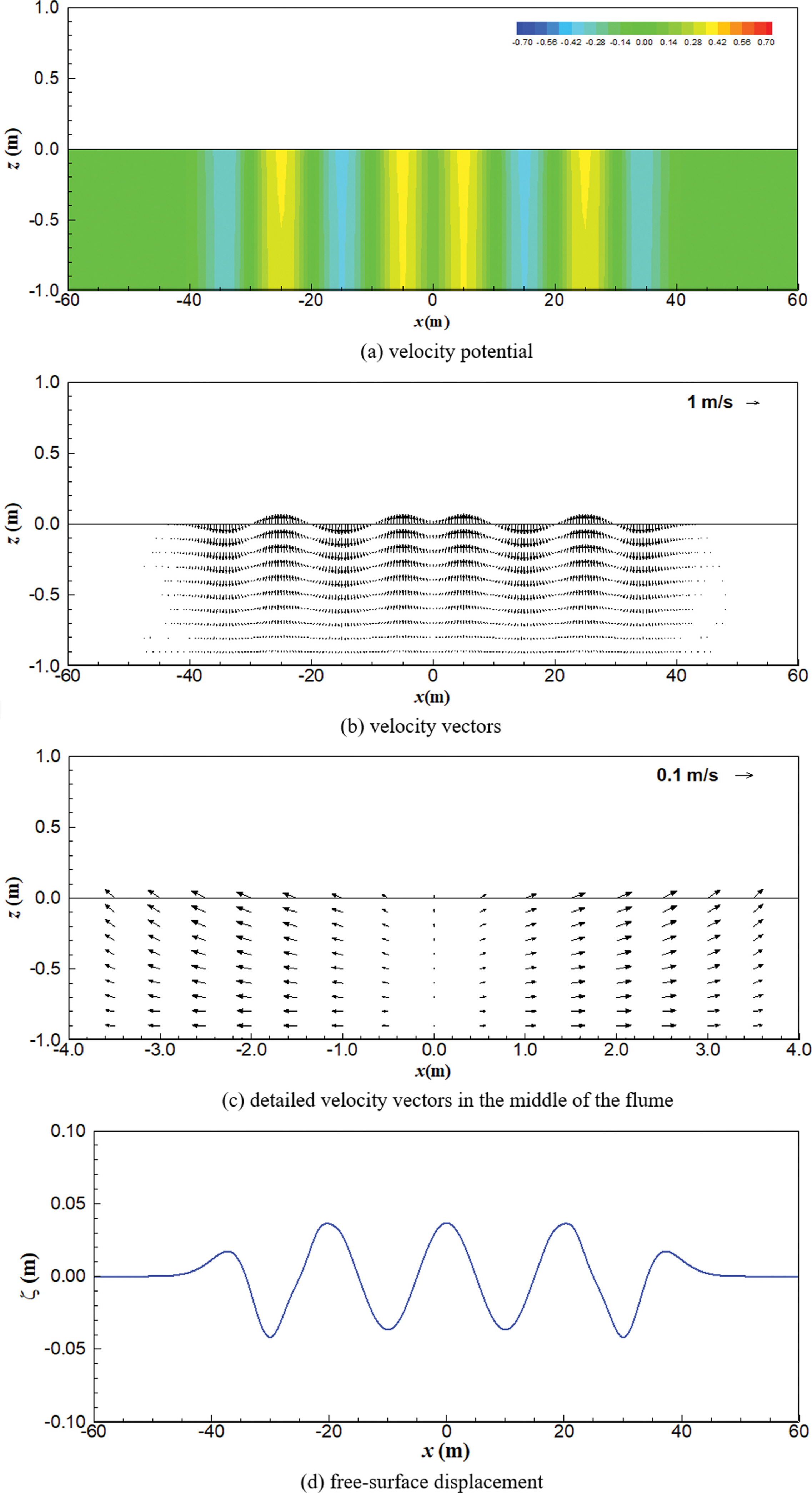
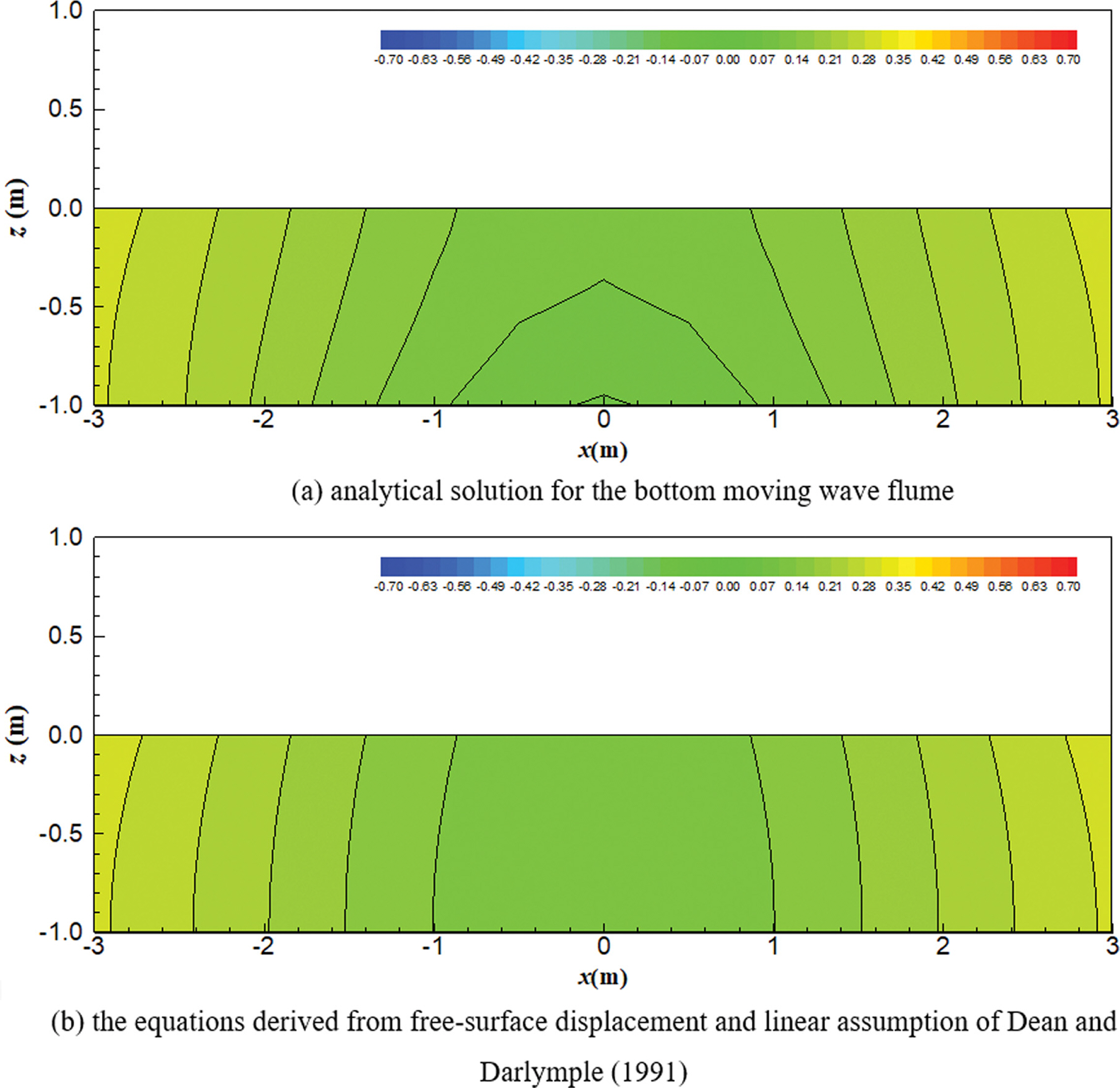
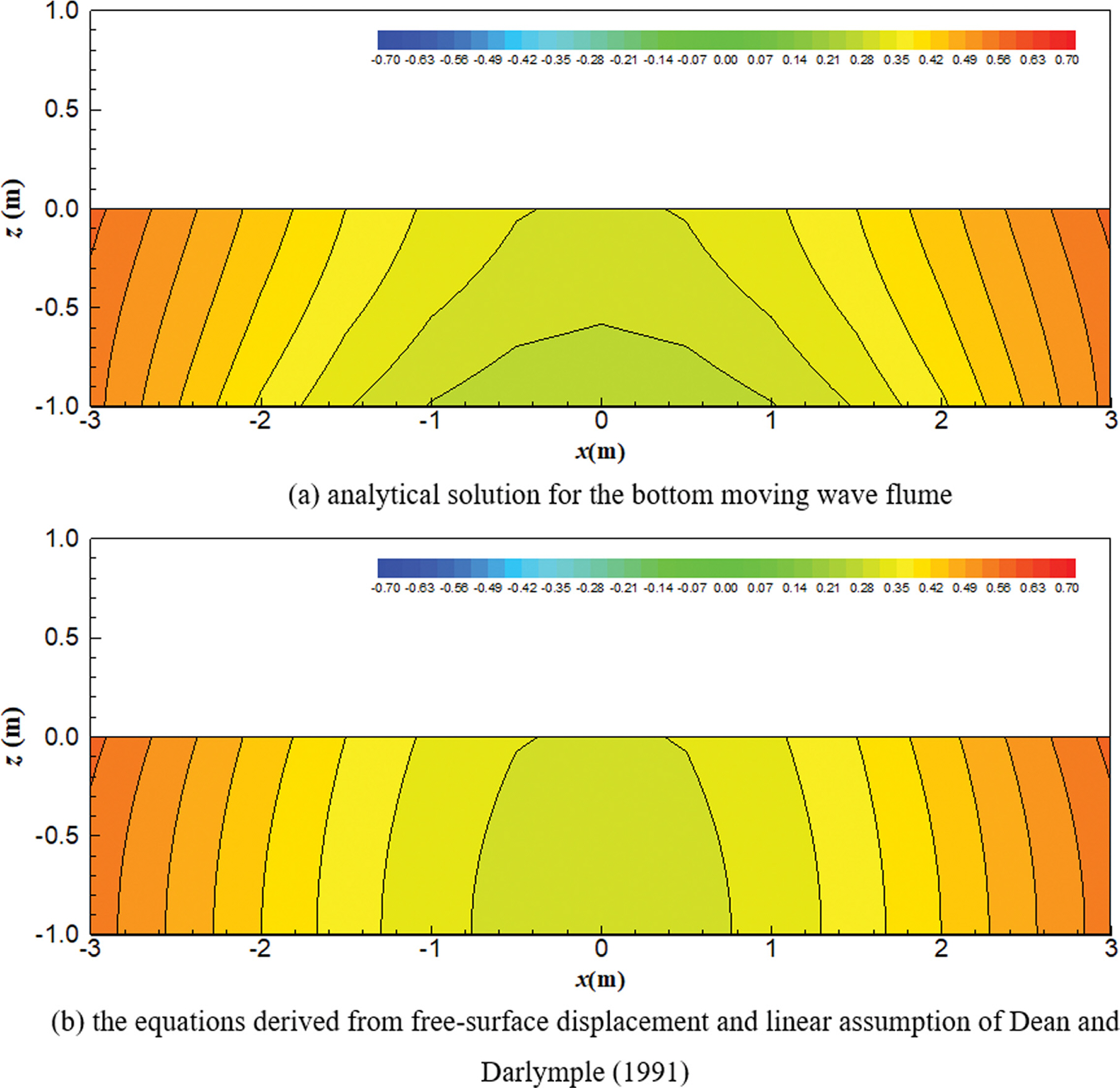
식(39)~(42)와 같이 표현된 자유수면변위 및 Dean and Dalrymple(1991)의 선형가정에 의한 속도포텐셜 및 유속성분과 식(34)~(36)과 같이 직접적인 방법으로 유도한 속도포텐셜 및 유속성분을 비교 검토하였다. 3.1절과 같은 지형 및 바닥 움직임 조건에서 t = 2.0T일 때 삼각형 및 사각형 바닥 조파장치의 속도포텐셜, 유속벡터도 및 자유수면변위를 Figs. 8과 9에 각각 나타내었다. 선형가정에 의해 유도한 속도포텐셜은 Fig. 8(a) 및 Fig. 9(a)와 같은데, 직접 유도한 식(34) 및 식(39)의 결과인 Fig. 2(a) 및 Fig. 5(a)와 약간의 차이가 있다. 전반적으로 |x|>5m인 영역에서는 두 경우가 거의 유사한 결과를 보였다. 하지만 바닥 조파장치가 위치하고 있는 |x| ≤ 5 m인 영역에서는 두 결과가 큰 차이를 보였으며, 이는 Fig. 8(c) 및 Fig. 9(c)에 나타난 유속성분을 보면 그 차이를 더욱 확연히 알 수 있다. 같은 조건인 Fig. 4(a)와 Fig. 7(a)를 비교하면, 전반적으로 자유수면변위 및 선형가정에 의한 결과인 Fig. 8(c) 및 Fig. 9(c)에서는 수로 중앙부에서 바닥 조파장치에 의한 z 방향 유속이 거의 나타나지 않았다. 반면 직접 유도한 식에 의한 결과인 Fig. 4(a) 및 Fig. 7(a)의 경우에는 바닥이 움직임에 의해 수로 중앙부 바닥 근처에서 강한 z 방향 유속이 발생하였다. 자유수면변위와 선형가정을 통한 해석을 위해 Fig. 8(d) 및 Fig. 9(d)와 같이 식(37)과 식 (42)를 이용하여 계산한 자유수면변위를 적용하였는데, 선형 가정은 진행파에 대해 Dean and Dalrymple(1991)이 유도한 해석해에 의한 가정으로 바닥의 움직임과 같은 경계조건은 반영되지 않았기 때문에 z 방향 유속이 실제와 다르게 나타났다. 다시 말해서, 일단 파랑이 생성되고 진행하는 영역인 |x|>5m에서는 두 결과가 거의 비슷하게 나타난다. 하지만, 바닥이 움직이고 있는 영역(|x| ≤ 5 m)에서는 본 연구에서 유도한 속도포텐셜 및 유속이 더욱 타당한 결과를 보임을 알 수 있다.
Fig. 10 및 Fig. 11에서는 바닥 조파장치 부근에서 본 연구에서 유도한 해석해를 통해 직접 계산한 속도포텐셜과 자유수면변위 및 선형 가정을 통해 계산한 속도포텐셜을 비교하였다. 본 연구에서 유도한 해석해의 결과는 바닥 조파기 상부에서 연직 방향으로 속도포텐셜의 변화가 나타나지만, 자유수면변위 및 선형 가정을 통해 계산된 결과는 바닥 조파기 상부에서 연직 방향으로 속도포텐셜의 변화가 거의 나타나지 않는다. 이 때문에 자유수면변위를 통해 간접적으로 계산한 결과에서는 Fig. 8(c) 및 Fig. 9(c)와 같이 바닥 조파기 상부에서 연직방향 유속이 나타나지 않았다.
4. 결 론
본 연구에서는 선형파 이론과 움직이는 바닥 경계조건, 운동학적 및 동역학적 자유수면 경계조건을 이용하여 삼각형 및 사각형 바닥 조파장치가 설치된 수로에서 생성된 규칙파의 속도포텐셜 및 2차원 유속에 대한 해석해를 제시하였다. 제시된 해석해는 복잡한 적분식 형태로써 수치적으로 계산할 수 있다. 자유수면변위 및 Dean and Dalrymple(1991)의 선형가 정을 통한 속도포텐셜 및 유속과 본 연구에서 유도한 해석해와 비교 검토하였다. 검토 결과 바닥의 움직임을 직접 반영한 본 연구에서 유도한 해석해가 바닥 조파장치의 움직임에 따른 유속의 변화를 물리적으로 더욱 타당하게 재현하였다. 본 연구에서 유도된 식은 향후 바닥 조파장치를 이용한 실험을 하기 전에 재현될 파랑의 제원 및 유속을 예측하거나, 바닥의 움직임에 따른 파랑의 생성을 재현할 수 있는 수치모델의 정확도 검증 등에 활용될 수 있을 것으로 생각된다.