요약정점 표층 수온 관측 데이터 중 결측 구간의 데이터를 양방향 순환신경망(Bidirectional Recurrent Neural Network, BiRNN) 기법을 이용하여 보간하였다. 인공지능 기법 중 시계열 데이터에 일반적으로 활용되는 Recurrent Neural Networks(RNNs)은 결측 추정 위치까지의 시간 흐름 방향 또는 역방향으로만 추정하기 때문에 장기 결측 구간에는 추정 성능이 떨어진다. 반면, 본 연구에서는 결측 구간 전후의 양방향으로 추정을 하여 장기 결측 데이터에 대해서도 추정 성능을 높일 수 있다. 또한 관측점 주위의 가용한 모든 데이터(수온, 기온, 바람장, 기압, 습도)를 사용함으로써, 이들 상관관계로부터 보간 데이터를 함께 추정하도록 하여 보간 성능을 더욱 높이고자 하였다. 성능 검증을 위하여 통계 기반 모델인 Multivariate Imputation by Chained Equations(MICE)와 기계학습 기반의 Random Forest 모델, 그리고 Long Short-Term Memory(LSTM)을 이용한 RNN 모델과 비교하였다. 7일간의 장기 결측에 대한 보간에 대해서 BiRNN/통계 모델들의 평균 정확도가 각각 70.8%/61.2%이며 평균 오차가 각각 0.28도/0.44도로 BiRNN 모델이 다른 모델보다 좋은 성능을 보인다. 결측 패턴을 나타내는 temporal decay factor를 적용함으로써 BiRNN 기법이 결측 구간이 길어질수록 보간 성능이 기존 방법보다 우수한 것으로 판단된다.
AbstractThe data of the missing section among the vertex surface sea temperature observation data was imputed using the Bidirectional Recurrent Neural Network(BiRNN). Among artificial intelligence techniques, Recurrent Neural Networks (RNNs), which are commonly used for time series data, only estimate in the direction of time flow or in the reverse direction to the missing estimation position, so the estimation performance is poor in the long-term missing section. On the other hand, in this study, estimation performance can be improved even for long-term missing data by estimating in both directions before and after the missing section. Also, by using all available data around the observation point (sea surface temperature, temperature, wind field, atmospheric pressure, humidity), the imputation performance was further improved by estimating the imputation data from these correlations together. For performance verification, a statistical model, Multivariate Imputation by Chained Equations (MICE), a machine learning-based Random Forest model, and an RNN model using Long Short-Term Memory (LSTM) were compared. For imputation of long-term missing for 7 days, the average accuracy of the BiRNN/statistical models is 70.8%/61.2%, respectively, and the average error is 0.28 degrees/0.44 degrees, respectively, so the BiRNN model performs better than other models. By applying a temporal decay factor representing the missing pattern, it is judged that the BiRNN technique has better imputation performance than the existing method as the missing section becomes longer.
1. 서 론통계적 방식으로 결측 데이터를 보간하는 방식은 실측값의 평균값 또는 중앙값으로 대치하는 방식이 있고, Multivariate Imputation by Chained Equations(MICE) 모델 등을 이용하는 방식이 있다. MICE 알고리즘은 다변수의 결측 데이터 보간에 실용적이며, 큰 데이터 세트의 보간에 유용하다는 장점이 있다. 다만 정규 분포를 따르지 않은 데이터나 결측 데이터가 많은 경우에는 데이터 처리에 단점을 보인다(Van and Oudshoorn, 1999). 또한 데이터 분석과 결측 데이터를 보간할 때 군집화(clustering)가 중요하지만, MICE 알고리즘은 자동으로 군집화를 하지 않기 때문에 복잡성과 한계를 인정하는 것이 중요하다(Azur et al., 2011).
인공지능을 이용한 결측 데이터 보간 방식에는 대표적으로 기계학습 기반의 Random Forest(RF) 방식과 딥러닝 기반의 RNNs가 있다. RF 모델은 데이터를 data set forest로 성장시키기 위해 결측 데이터를 사전에 보간하고 데이터의 근접 거리를 사용하여 보간된 데이터로 업데이트 한다(Tang and Ishwaran, 2017). 내부적으로 교차 검증된 오류 추정값을 제공하지만, 시계열의 시간 정보를 과소평가한다(Feng and Narayanan, 2019). 최근에는 데이터 기반 모델인 딥러닝 방식으로 시계열 데이터를 학습하고 있다. RNN은 시계열 데이터 학습 영역에서 성능 좋은 예측 능력을 제공한다(Lipton et al., 2016). 다만, 시퀀스가 길거나 시간 간격이 클 경우에는 충분히 학습되지 않을 수도 있다(Suo et al., 2019). 또, 이론적으로 시계열 데이터의 기반이 되는 장기 종속성을 구할 수 있지만 기울기 소실 및 폭주(vanishing and exploding gradient) 문제로 인해 효과적으로 구할 수 없는 경우가 많다(Kim and Chi, 2018).
해수면 온도(Sea Surface Temperature, SST) 데이터는 기후 변화 및 모니터링, 수치예보 등 다양한 연구 분야에서 중요한 데이터로 활용되고 있지만, 측정 장비의 오작동 등 원치 않는 외부 간섭으로 인해 발생하는 결측 데이터가 발생하는 경우가 있다. SST의 결측 데이터 보간도 통계적 방식과 인공지능을 이용한 방식의 연구가 진행되었다. 통계적 방식의 보간 방식으로 날씨 및 기후를 예측하기 위한 K-Nearest Neighbor(KNN) 알고리즘과 MICE 모델을 이용하여 추정한(Worku et al., 2018) 연구들이 있다. McNeil and Chirtkiatsakul(2016)은 북대서양 표층온도의 경향과 패턴을 설명하기 위해서 선형보간기술을 이용하여 SST 결측 데이터를 보간한 연구이다.
최근에는 인공지능을 이용하여 SST의 결측 데이터를 보간하려는 연구가 진행되고 있다. Yang et al.(2021)은 Tidal level을 예측하기 위해서 DNN 알고리즘으로 SST 결측 데이터를 보간하였다. 머신 러닝(Machine leaning) 알고리즘을 이용한 SST 결측 데이터 보간 기법을 다른 모델과 비교하는 연구도 진행되고 있다(Mohebzadeh et al.(2021)). 그러나, SST 결측 데이터 보간을 위한 많은 방법들 중에서 인공지능을 이용하는 연구는 많지 않다.
본 연구에서는 SST 관측 데이터에서 일반적으로 발생하는 결측 데이터 문제를 상관관계가 있는 다변수 시계열 데이터(correlated multivariate time series data)를 처리할 수 있는 Bidirectional Recurrent Imputation for Time Series(BRITS)를 이용하여 보간하는 기법을 제안한다. BRITS 모델은 전체 시계열상의 다변수 데이터에서 발생한 임의의 결측 구간의 패턴과 길이를 식별할 수 있는 시간적 감쇠 계수(temporal decay factor)를 적용하여 결측값의 길이가 길어도 추정 성능을 높일 수 있는 장점이 있다. 2장에서는 결측 데이터를 보간하는 모델들의 개념을 설명한다. 3장에서는 결측 데이터를 보간하는 방식을 이해하기 위한 BiRNN의 알고리즘을 설명한다. 4장에서는 BiRNN의 성능을 나타내는 최종 결과와 함께 성능 평가를 설명한다.
2. 결측 보간 모델시계열 데이터에서 결측된 관측값을 처리하는 다양한 방식이 있다. MICE는 다변수 다중 보간이 가능하고, 데이터 기반 모델이자 decision tree를 기반으로 하는 Random Forest 모델도 있다. 본 연구에서는 이 모델들과 BRITS 모델의 성능을 비교하였다.
BRITS는 어떤 가정도 필요 없이 결측값을 보간(imputation)하는 모델로서, 결측값을 양방향 RNN의 변수로 간주한다. 순방향과 역방향 모두에서 지연된 기울기를 얻기 때문에 결측값을 더 정확하게 추정할 수 있다. 여러 개의 상관된 결측값을 처리할 수 있고, 비선형 동역학을 사용하여 시계열을 일반화한다(Cao et al., 2018).
Fig. 1에서 순방향 추정을 보면, 결측값 x5가 발견되면 x4에서 추정한
3. 실험 방식3.1 데이터셋기상청에서 제공하는 해양데이터* 중에서 2016년부터 2018년까지 데이터 중에서 인천 앞바다의 7개 지점(자월도, 이작도, 풍도, 덕적도, 인천, 서수도, 가대암)의 수온, 기온, 기압, 풍속, 풍향, 습도 데이터를 학습 데이터로 적용하였다. Fig. 2에서 기상청 데이터 측정 위치를 지도 위에 표시하였고, 괄호 안 숫자는 측정 지점의 지점 번호이다.
Table 1은 학습에 사용된 데이터들이다. 가대암 지역의 수온 데이터는 2016년 9월부터 2018년 12월까지 연속적으로 측정되지 않아서 학습 데이터에 적용하지 않았다. 이작도, 자월도, 풍도 지점은 수온 데이터만 제공하고 있다.
Table 2는 학습 데이터 세트의 구조이다. 풍속 정보는 벡터로 변환된 정보를 적용하였다. 데이터 전체의 공간은 1,420,416개이고, 결측 데이터 개수는 30,425개로 전체 결측 데이터 비율은 2.14%이다. 덕적도 지점(22101)에서 결측이 가장 적게 발생하였고, 이작도 지점(22461)에서 결측이 가장 많이 발생하였다.
Fig. 3에서 전체 학습 데이터 세트에서 실측값이 있는 구간과 결측된 구간을 matrix로 표현하였다. 가로축은 7개 지점 30개 데이터이고, 세로축은 3년간 시간단위 개수이다. 회색은 실측값이 있는 구간이고, 하얀색은 결측된 구간이다. 연속된 결측 구간이 3일 이하인 경우가 99% 이상이고, 10일 이상 연속 결측 구간은 0.02%뿐이다. 이 두 개 구간을 제외하면 대부분 7일 전후의 연속된 결측 구간이 있는 것으로 분석된다. 기상청에서 제공하는 해양데이터는 1일 연속 결측 구간은 단기 결측 구간으로, 7일 연속 결측 구간은 상대적으로 장기 결측 구간으로 볼 수 있다.
3.2 데이터셋 전처리3.2.1 이상 데이터 제거관측자료의 이상값은 결측과 오측으로 나눌 수 있는데, 본 연구에서는 결측값만 다루기 때문에 학습에 사용된 7개 지점 데이터에서 발생한 이상(오측) 데이터는 Kim et al.(2021)의 연구를 참조하여 보정하였다. 여러 데이터를 학습시키는 다변수 오토인코더를 활용하여 이상(오측) 데이터를 탐지하는 기법으로 보정하였다.
기상청에서는 풍속을 북쪽 0°를 기준으로 시계방향(0°~360°)으로 제공한다. 풍향이 360°에서 1°로, 또는 1°에서 360°로 바뀔 경우 실제 풍향의 변경 폭보다 수치상의 변경 폭이 훨씬 크기 때문에 실제 변경 폭을 모델 학습에 적용할 수가 없다. 따라서 풍향 데이터는 직교좌표계 상의 벡터(동서풍(u)과 남동풍(v))로 변환하였다.
본 연구에서 적용된 기상청 데이터는 모두 시계열성 데이터이므로 시간의 흐름이 학습의 결과에 큰 영향을 줄 수 있다. SST의 특성상 데이터의 변화가 각 시간대 데이터와 큰 연관성이 있으므로, 시간의 변경 폭을 일정하게 만들면서 학습 데이터가 특정 시간의 데이터임을 파악할 수 있도록 시간 데이터를 1과 0으로 이루어진 데이터로 생성하여 학습 데이터에 추가하였다(Table 3).
3.2.2 학습 데이터 전처리학습 데이터는 양방향 학습을 위해서 forward와 backward 정보의 생성에 중점을 두었다. 실측값(evals)과 결측값 식별을 위한 masking(mask), 결측 패턴 설정을 위한 시간 순서(deltas), 결측값 평가를 위한 evaluation(eval_masks), 데이터 세트의 각 항목을 고유하게 식별하기 위한 labels(labels)로 구성된다. 이 데이터들은 standardization 과정을 거쳐서 JSON 파일 형식으로 저장된다.
SST의 시계열 데이터는 시간 순서로 정렬된 T = (t0, t1, …, tn-1)이고, 길이가 n인 X로 표시된다. 변수 차원이 v인 X의 다변수 시계열(multivariate time series)은 X = (xt0, xt1, …, xtn-1)T∈
X의 결측 데이터는 masking matrix
시계열상에서 결측된 데이터의 시간 순서를 설정하기 위해서 결측 전 마지막 시간(t - 1)부터 시간 간격이 식(2)에 의해서 설정된다.
Fig. 4는 시간 순서 T와 결측값이 포함된 다변수 시계열 X에 대한 masking matrix와 결측 데이터의 시간 순서를 보여준다.
3.3 알고리즘기상청에서 제공하는 6가지 데이터들이 서로 상관관계가 없다(uncorrelated)고 가정하고, 시계열상의 데이터를 일방향(unidirectional)으로만 추정을 할 경우, 식(4)와 같이 표현할 수 있지만, 결측값이 있으면 정상적인 계산을 수행할 수 없다. 식(5)와 같이 보완된 데이터를 적용하고, 식(6)에서 결측 값을
일방향(unidirectional)으로만 추정을 할 경우 오류 지연(error delay)이 발생하면서 수렴하는 시간이 길어지고, bias exploding 문제가 발생한다(Bengio et al., 2015). 이 문제를 완화하기 위해서 순방향과 역방향 모두에서 추정을 수행하여 양방향(bidirectional)으로 추정하는 모델을 구현한다. 식(4)에서 식(9)까지 순방향과 역방향으로 각각 수행한다. 식(5)에 의해서 순방향으로 보간 데이터
그리고, 다변수 학습 방법은 예측 측면에서도 단변수 학습 방법보다 더 나은 성능을 생성하고(Miller and Kim, 2021), 보간 측면에서도 결측 구간이 길 경우 다변수 학습 방법이 더 나은 성능을 보인다(Junger and Leon, 2015). 본 연구에서도 보간 성능을 높이기 위해서 기상청에서 제공하는 6가지 데이터들이 서로 상관관계가 있도록 구성하였다.
4. 결 과MICE, Random Forest 모델과 양방향 RNN 기반의 BRITS 모델을 이용하여 각 모델들의 결측값 보간 성능을 비교하였다. 그리고, BRITS type의 모델인 RITS-I, BRITS-I, RITS 모델도 BRITS 모델과 비교하였다.
RITS-I 모델은 일방향(시간 흐름의 순방향)으로 추정하는 RNN 모델이다. 추정된 결측 데이터의 오류값은 다음 실측값이 있는 시점까지 지연되어 모델이 천천히 수렴된다. BRITSI 모델은 시간 흐름의 순방향과 역방향 모두 추정하기 때문에 오류 지연 문제를 완화시킬 수 있다. RITS-I 모델과 BRITS-I 모델은 동시에 측정된 다른 데이터들이 서로 상관 관계가 없는 모델이며(Cao et al., 2018), 본 연구에서는 각 지점의 SST 데이터만으로 학습된다.
한 지점에서 측정된 실측값은 가까운 지점에서 측정된 실측값과 유사한 데이터이고, 과거 데이터와 가까운 지점의 실측값에 따라 결측 데이터를 추정할 수 있다(Cao et al., 2018). SST는 기온, 풍향 등 기상인자의 영향을 받기 때문에(Cho et al., 2010; Qu et al., 2012) 본 연구에 적용된 7개 지점의 데이터들은 공간적, 시간적으로 상관관계가 있다. RITS 모델과 BRITS 모델은 서로 상관관계가 있는 7개 지점의 6가지 데이터를 모두 학습하는 모델이다. RITS 모델은 RITSI 모델과 같이 일방향으로 추정하는 RNN 모델이고, BRITS 모델은 양방향으로 추정하는 기법을 추가한 모델이다.
4.1 결측 구간별 비교2016년부터 2018년까지 데이터 중에서 결측 구간을 무작위로 선택하여 성능 분석에 신뢰성을 더하고자 했다. 측정이 되지 않은 결측 구간은 보간 성능을 평가할 수 없으므로, 보간 성능 평가를 위해서 덕적도 지점의 SST 관측 데이터 중 일부 데이터를 강제로 결측시켰다. SST 강제 결측 구간에 있는 나머지 관계된 5개 데이터를 결측시킬 경우 관측점 주위의 데이터를 사용하여 보간 성능을 높일 수 없으므로 나머지 관계된 5개 데이터는 실측 데이터 그대로 적용하여 학습시켰다. 결측 구간을 연속 3일, 연속 7일을 무작위로 선택하여 실측값을 제거한 후, 모델의 결과로 나온 보간 데이터와 실측값을 모델별로 비교하였다.
Fig. 5와 Table 4는 결측 구간이 7일인 때의 비교 그래프와 PCC 및 RMSE이다. RF 모델과 MICE 모델의 보간 데이터는 일부 구간을 제외한 대부분의 구간에서 실측값과 큰 차이를 보인다. RITS 모델은 결측 구간의 초반 부분은 실측값과 큰 차이 없이 변화 분포를 잘 따라간다. 하지만, 일방향으로만 학습하는 RNN 모델이 근간이 되는 RITS 모델은 결측 구간이 길어질수록 실측값과의 오차가 커지는 것으로 분석된다. BRITS 모델은 결측 구간이 길어져도 실측값의 변화 분포도 잘 따라가면서 오차도 가장 적어 다른 모델보다 나은 성능을 보이고 있다.
Fig. 6과 Table 5은 결측 구간이 3일인 때의 비교 그래프와 PCC 및 RMSE이다. RF 모델과 MICE 모델은 보간된 데이터가 실측값에 비해서 시간 단위로도 변화의 폭이 크게 나타난다. RITS 모델의 경우, 결측 구간의 초반 부분 1일은 실측값의 변화 분포를 잘 따라간다. 하지만, 연속 7일보다 짧은 3일간의 결측 구간임에도 불구하고 실측값의 변화폭이 큰 구간에서는 그 변화 분포를 따라가지 못하면서 일방향 학습 성능의 한계를 보이고 있다. 그에 비해 BRITS 모델은 결측 구간의 마지막 구간에서도 오차가 가장 적은 것으로 분석되어 양방향 학습의 좋은 성능을 보여준다.
4.2 BRITS type 모델 비교BRITS type의 모델인 RITS-I와 BRITS-I, RITS 모델들의 결측값 보간 성능도 비교하였다. 덕적도 지점에서 연속 7일간, 연속 3일간 실측값을 제거한 후, 모델의 결과로 나온 보간 데이터와 실측값을 모델별로 비교하였다.
Fig. 7과 Table 6은 결측 구간이 7일인 때의 비교 그래프와 PCC 및 RMSE이다. 이 구간은 실측값의 변화가 적기 때문에 일방향 모델의 단점이 최소화되면서 RITS 모델도 좋은 성능을 보여준다. SST만으로 학습한 모델인 RITS-I 모델과 BRITS-I 모델의 보간 데이터는 과도한 일변화를 보여준다. SST만으로 학습한 모델에 비해서 서로 상관관계가 있는 6가지 데이터를 모두 학습되는 모델들의 성능이 더 좋은 결과를 보인다. 그 중에서도 전체 구간의 보간 성능에서는 다변수와 양방향으로 동시에 학습한 BRITS 모델이 가장 좋은 결과를 보여준다.
Fig. 8과 Table 7은 결측 구간이 3일인 때의 비교 그래프와 PCC 및 RMSE이다. SST만으로 학습한 모델에 비해서 상관관계가 있는 6가지 데이터를 모두 학습한 모델의 보간 성능이 더 향상되었다. 동시에 일방향 학습 모델은 대부분의 결측 구간에서 실측값과의 오차가 크지만 양방향 학습 모델은 결측 구간의 초반 부분은 일방향 모델과 비슷하게 실측값과 차이를 보이지만 결측 구간일 길어질수록 실측값에 근접하는 것으로 분석된다. 이는 다변수로 학습하면서 동시에 양방향으로 학습하는 모델이 가장 좋은 성능을 보이는 결과로 분석된다. Fig. 8은 3일간의 결측 구간이지만 Fig. 7과 비교해서 실측값의 변화폭이 큰 구간이다. 실측값의 변화폭이 클수록 상관관계가 있는 데이터들을 모두 학습시키면서 양방향으로 학습하는 모델이 가장 우수한 성능을 보이는 것으로 분석된다.
5. 결 론본 연구에서는 BRITS 모델을 이용하여 결측된 SST를 보간하는 모델을 제시하였다. 각각 다른 구간을 가지는 상관된 학습 데이터들의 스케일을 동일하게 만들기 위해서 Standardization을 적용하였고, 보다 정확한 학습을 위해서 학습에 사용된 데이터들 중에서 이상(오측) 데이터들은 다변수 오토인코더를 활용하여 보정하였다. 학습 데이터는 모두 시계열성 데이터이고, SST의 변화가 각 시간대별 변화와 큰 연관성이 있기 때문에 특정 시간 데이터를 1과 0으로 이루어진 데이터로 변환하여 학습 데이터에 추가하였다.
실측값과 보간된 데이터를 비교하기 위해서 실측값이 있는 구간(연속 7일, 연속 3일)을 결측시켰다. 연속 3일 이하 결측 구간(99%)과 연속 15일 이상 결측 구간(0.2%)을 제외하면 대부분 7일 전후의 연속된 결측 구간이다. 타 모델들 중 가장 성능이 좋은 Random Forest와 비교해보면, 결측 구간이 7일인 경우 BRITS/Random Forest 모델의 PCC 값이 각각 0.734/0.796이고 에러율은 각각 0.348/0.597으로 BRITS 모델이 더 좋은 결과를 보인다. 결측 구간이 3일인 경우도 BRITS/Random Forest 모델의 PCC 값이 각각 0.821/0.543이고 에러율은 각각 0.149/0.282로 BRITS 모델이 더 좋은 결과를 보인다.
결측 구간의 시작점의 관측값과 보간 데이터의 차이를 비교해보면, 기존 다른 모델보다 딥러닝 기반 모델의 차이가 약간 더 큰 것으로 분석된다. 기존 모델들은 결측 지점에서 멀리 있는 데이터는 활용하기 어렵고 결측 지점과 가까이 있는 데이터를 활용한다. 딥러닝 모델은 상대적으로 결측 지점에서 이전 방향으로 멀리 있는 데이터도 활용하기 때문에 기존 모델에 비해서 상대적으로 차이가 더 발생할 수도 있다. 이 부분은 향후 추가 연구가 필요하다고 판단된다.
SST는 다양한 주기와 비선형적이라는 일반적인 해양 데이터의 특성을 갖고 있으며, SST에 영향을 주는 인접한 측정 데이터들과 상관관계가 크다. 양방향 학습 모델은 이러한 특성을 고려한 보간 기법으로써, 다변수 데이터 처리 성능이 부족하거나 짧은 결측 구간에서만 좋은 성능을 보이는 기존 모델보다 더 우수한 결측 데이터 보간 성능을 보여준다. 특히, 각 지점에서 측정된 가용한 모든 데이터를 상관관계가 있도록 구성하여 학습할 경우 양방향 학습 모델은 탁월한 성능을 제시한다.
본 연구는 해양데이터의 관측 자료 결측의 문제점을 해결할 수 있는 방안으로 딥러닝 방식을 이용한 방식을 제안한다. 이 방식은 SST 뿐만 아니라 기온, 풍속 등 서로 상관관계가 있는 다른 데이터들의 결측 데이터도 보간이 가능하다. 그리고, 7일 전후의 연속된 결측 구간에서 일변화 변화폭에 대해서 탁월한 성능을 제시한다. 본 연구의 모델로 보간된 데이터를 적용할 경우 데이터 기반 모델의 성능을 향상시킬 수 있을 것으로 기대된다. 마지막으로, 해양 정점관측 데이터들만 사용하여 결측값을 보간하였고, 향후 대기 정점관측 데이터들을 포함할 경우 보간 성능을 더 높일 수 있을 것으로 사료된다.
감사의 글이 논문은 2022년도 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임(20220051, 경기·인천 씨그랜트). 이 논문은 2022년도 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원을 받아 수행된 연구임(2020-0-01389, 인공지능융합연구센터지원(인하대학교)).
Fig. 2.Meteorological Agency data measurement location (from https://data.kma.go.kr). Number in parentheses: number of measuring point. 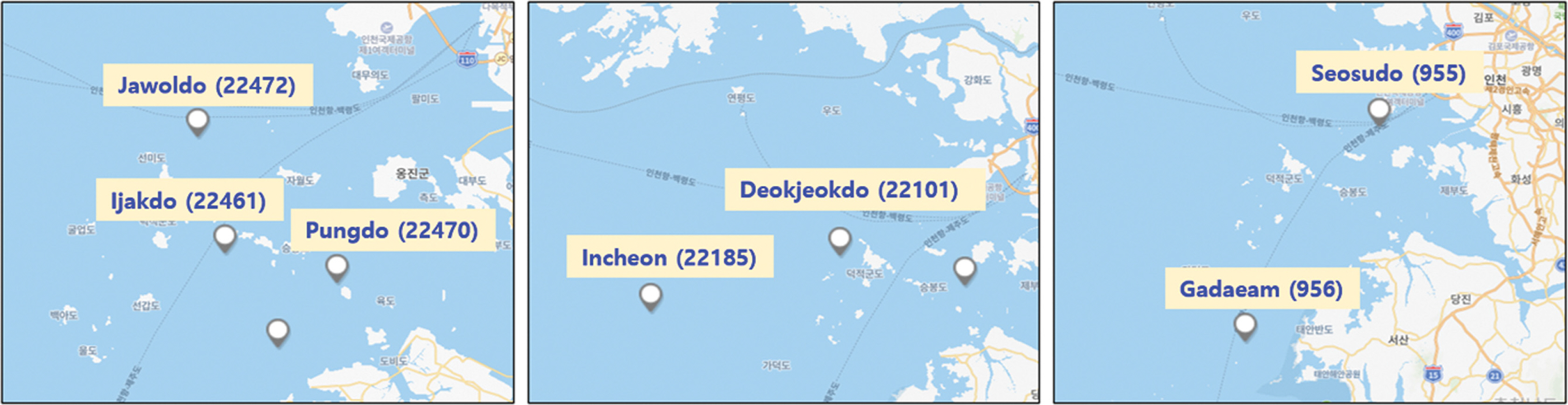
Fig. 3.Training data missing interval distribution Gray: Interval with observation data, White: Interval with missing data Horizontal axis: 7 points 30 data, Vertical axis: 2016–2018 time unit. 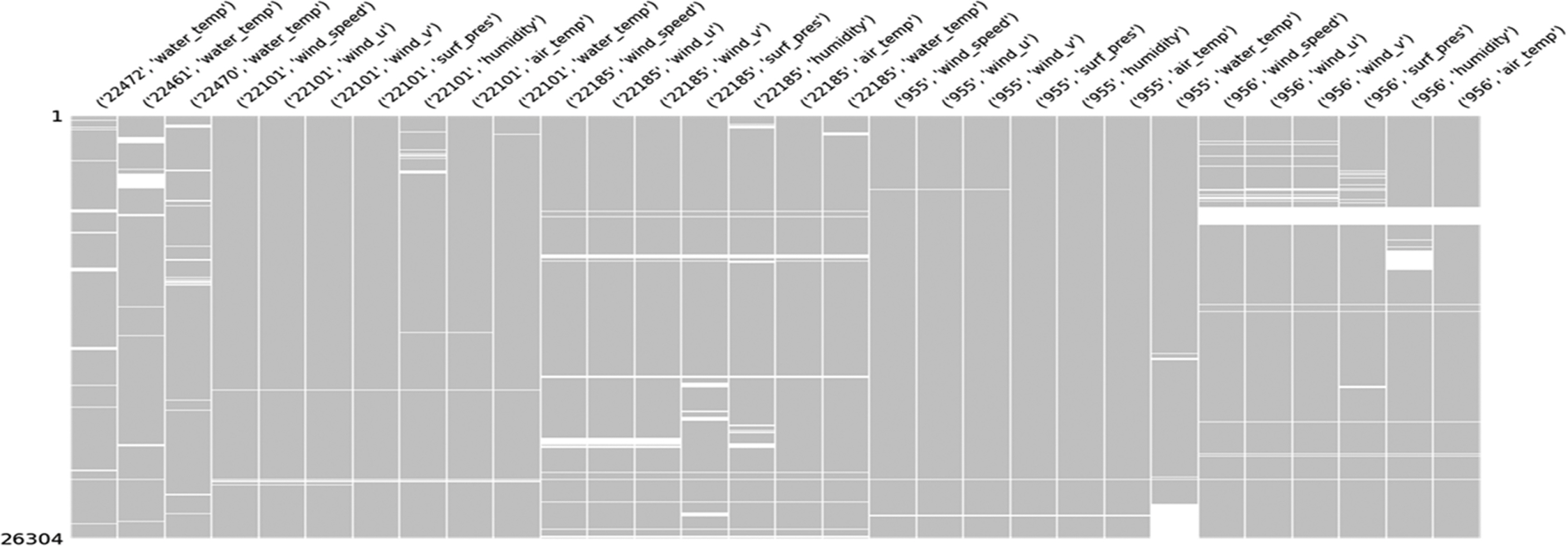
Fig. 5.Comparison graph of observation data and imputation data (Deokjeokdo point). Missing section: 2017.11.09.~2017.11.15. (7 days) black dotted line: observation data, green line:MICE, orange line:RF, blue line:RITS, red line:BRITS. 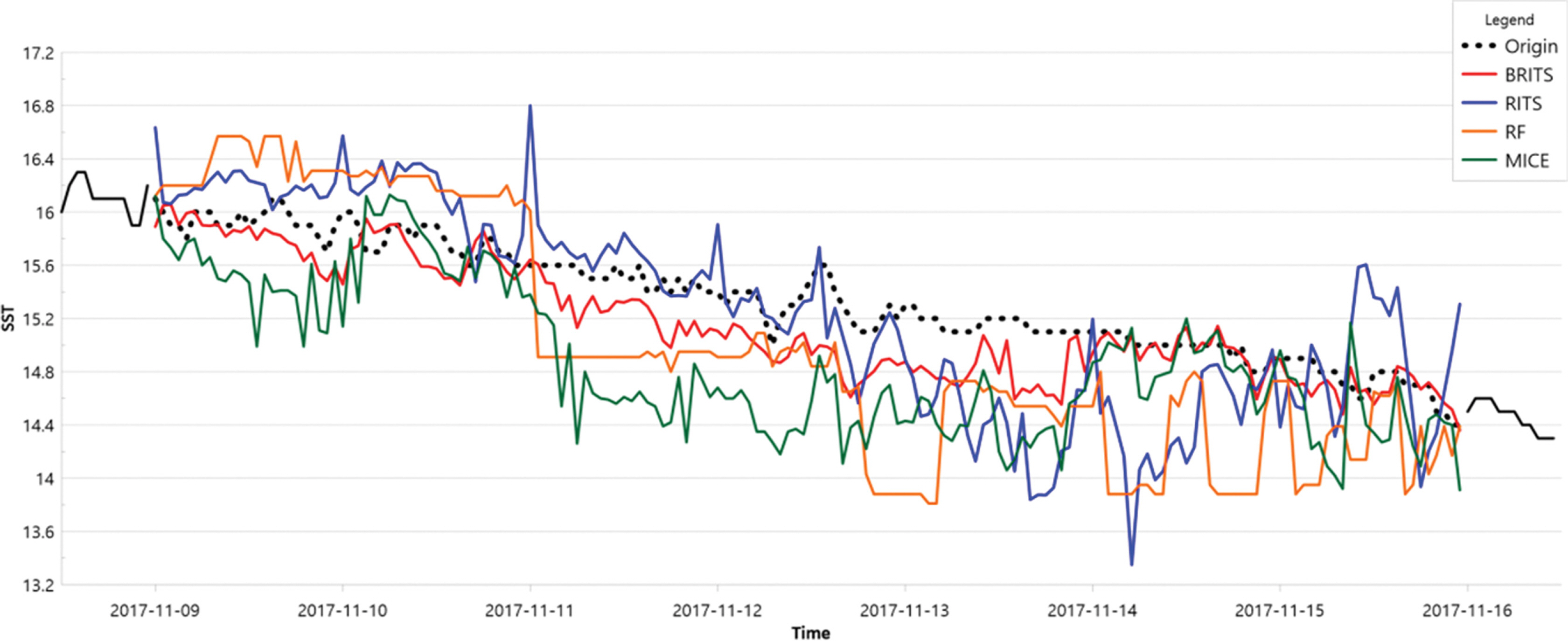
Fig. 6.Comparison graph of observation data and imputation data (Deokjeokdo station). Missing section: 2016.11.11.~2016.11.13. (3 days) black dotted line: observation data, green line:MICE, orange line:RF, blue line:RITS, red line:BRITS. 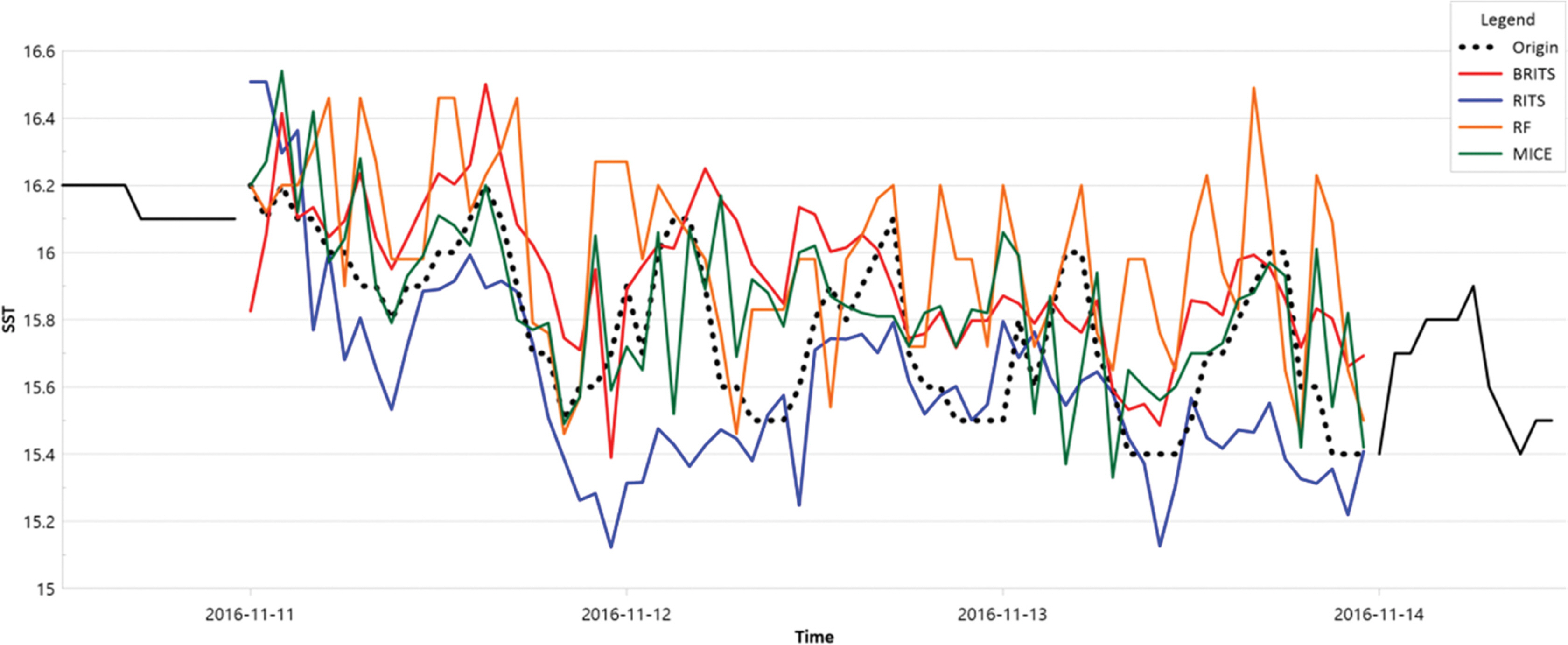
Fig. 7.Comparison graph of observation data and imputation data (Deokjeokdo station). Missing section: 2017.04.15.~2017.04.21. (7 days) dotted black line: observation data, green line: RITS-I, orange line:BRITS-I, blue line:RITS, red line:BRITS. 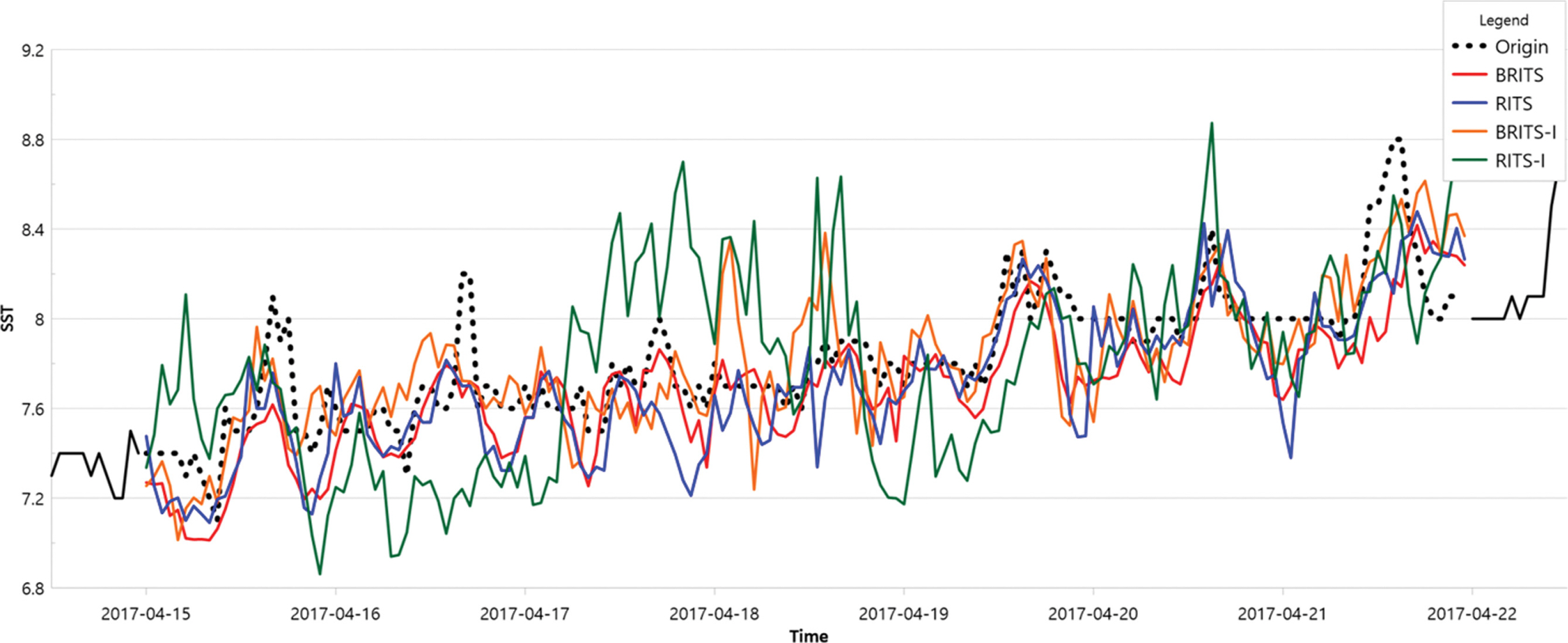
Fig. 8.Comparison graph of observation data and imputation data (Deokjeokdo station). Missing section: 2016.11.11.~2016.11.13. (3 days) dotted black line: observation data, green line: RITS-I, orange line:BRITS-I, blue line:RITS, red line:BRITS. 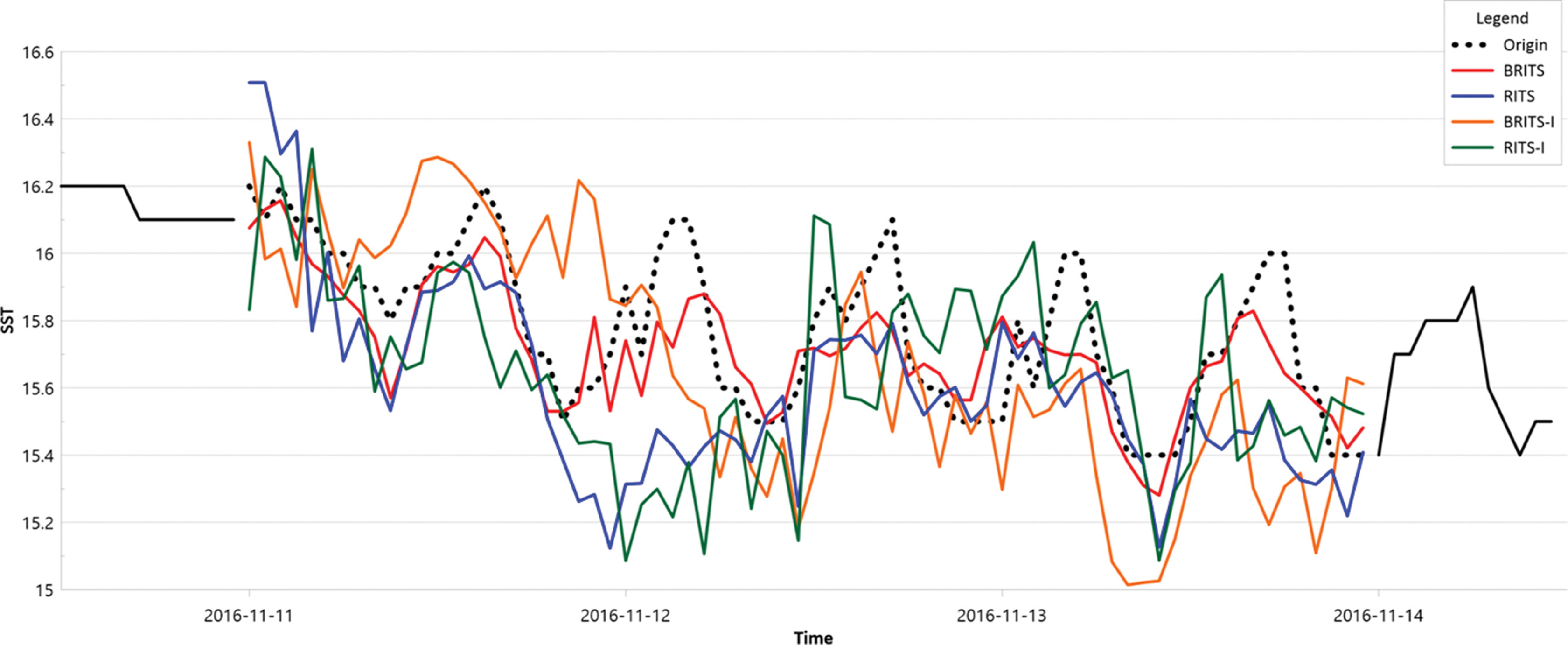
Table 1.Data type and duration of points applied to training * “기상자료개방포털”, 기상청, 2022년 4월 4일 수정, 2022년 4월 5일 접속, https://data.kma.go.kr/cmmn/main.do Table 2.Training data set structure Table 3.Change time data to data consisting of 1 and 0 Table 4.Comparison of PCC and error rate between BRITS and other models (missing interval 7 days)
Table 5.Comparison of PCC and error rate between BRITS and other models (missing interval 3 days)
ReferencesAzur, M.J., Stuart, E.A., Frangakis, C., Leaf, P.J (2011). Multiple imputation by chained equations: what is it and how does it work? International Journal of Methods in Psychiatric Research, 20(1):40-49.
Bengio, S, Vinyals, O, Jaitly, N, Shazeer, N (2015). Scheduled sampling for sequence prediction with recurrent neural networks, Advances in Neural Information Processing Systems, 28.
Cao, W, Wang, D, Li, J, Zhou, H, Li, L, Li, Y (2018). Brits: Bidirectional recurrent imputation for time series, Advances in Neural Information Processing Systems, 31.
Cho, H.Y., Jeong, J.Y., Shim, J.S., Kim, S.J (2010). Variation pattern analysis on the air and surface water temperatures of the yellow sea monitoring buoy, Journal of Korean Society of Coastal and Ocean Engineers, 22(5):316-325 (in Korean)..
Feng, T, Narayanan, S. (2019). Imputing missing data in large-scale multivariate biomedical wearable recordings using bidirectional recurrent neural networks with temporal activation regularization, 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). p 2529-2534. IEEE.
Junger, W.L., De Leon, A.P (2015). Imputation of missing data in time series for air pollutants, Atmospheric Environment, 102, 96-104.
Kim, H.J., Kim, D.H., Lim, C.W., Shin, Y.T., Lee, S.C., Choi, Y.J., Woo, S.B (2021). An outlier detection using autoencoder for ocean observation data, Journal of Korean Society of Coastal and Ocean Engineers, 33(6):265-274 (in Korean)..
Kim, YJ, Chi, M (2018). Temporal Belief Memory: Imputing Missing Data during RNN Training, Proceedings of the 27th International Joint Conference on Artificial Intelligence (IJCAI-2018).
Lipton, Z.C., Kale, D.C., Wetzel, R (2016). Modeling missing data in clinical time series with rnns, Machine Learning for Healthcare, 56, 253-270.
McNeil, N., Chirtkiatsakul, B (2016). Statistical models for the pattern of sea surface temperature in the North Atlantic during 1973–2008, International Journal of Climatology, 36(11):3856-3863.
Miller, D., Kim, J.M (2021). Univariate and multivariate machine learning forecasting models on the price returns of cryptocurrencies, Journal of Risk and Financial Management, 14(10):486.
Mohebzadeh, H., Mokari, E., Daggupati, P., Biswas, A (2021). A machine learning approach for spatiotemporal imputation of MODIS chlorophyll-a, International Journal of Remote Sensing, 42(19):7381-7404.
Qu, B., Gabric, A.J., Zhu, J.N., Lin, D.R., Qian, F., Zhao, M (2012). Correlation between sea surface temperature and wind speed in Greenland Sea and their relationships with NAO variability, Water Science and Engineering, 5(3):304-315.
Suo, Q, Yao, L, Xun, G, Sun, J, Zhang, A. (2019). Recurrent imputation for multivariate time series with missing values, 2019 IEEE International Conference on Healthcare Informatics (ICHI). p 1-3. IEEE.
Tang, F., Ishwaran, H (2017). Random forest missing data algorithms, Statistical Analysis and Data Mining: The ASA Data Science Journal, 10(6):363-377.
Van Buuren, S, Oudshoorn, K. (1999). Flexible multivariate imputation by MICE. p 1-20. Leiden: TNO.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||