Numerical Simulation on Reduced Runup Height of Solitary Wave by Fixed Submerged and Floating Rectangular Obstacles

Choong Hun Shin; Hyung Suk Kim

doi:10.9765/KSCOE.2022.34.6.211

Journal of Korean Society of Coastal and Ocean Engineers > Volume 34(6); 2022 > Article

고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 처오름높이 저감 수치모의

Article

J Korean Soc Coast Ocean Eng 2022; 34(6): 211-221.

Published online: December 27, 2022

DOI: https://doi.org/10.9765/KSCOE.2022.34.6.211

고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 처오름높이 저감 수치모의

신충훈^*, 김형석^**

^*한국수력원자력(주) 선임연구원

^**군산대학교 토목공학과 조교수

Numerical Simulation on Reduced Runup Height of Solitary Wave by Fixed Submerged and Floating Rectangular Obstacles

Choong Hun Shin^*, Hyung Suk Kim^**

^*Senior Researcher, Korea Hydro & Nuclear Power Co., Ltd.

^**Assistant Professor, Department of Civil Engineering, Kunsan National University

Corresponding author: Hyeong Seok Kim, Assistant Professor, Department of Civil Engineering, Kunsan National University, 558 Daehak-ro, Gunsan-si, Jeollabuk-do 54150, Korea, Tel: +82-63-469-4754, Fax: +82-63-469-7434, hskim0824@kunsan.ac.kr

Received November 21, 2022 Accepted November 30, 2022

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

요약

파의 처오름높이는 제방, 호안 및 방파제와 같은 해안 구조물의 설계에 영향을 미치는 가장 중요한 매개변수 중 하나이다. 본 연구에서는 비정수압 수치모형인 SWASH(Zijlema et al., 2011)를 이용해 고정된 수중 및 부유식 사각형 구조물에 의한 고립파의 처오름높이 저감 효과를 분석하였다. SWASH 수치모형이 고립파의 전파, 쇄파 및 처오름현상을 매우 잘 재현하는 것을 확인하였다. 또한 수중 및 부유식 사각형 구조물에 의한 고립파의 파랑변형을 잘 재현하는 것을 확인하였다. 마지막으로 수중 및 부유식 사각형 구조물의 처오름높이 저감 효과를 검토하였다. 부유식 구조물의 에너지 감쇠효과는 수중 구조물보다 크고, 처오름높이 저감에 더 효과적인 것으로 나타났다.

핵심용어: 비정수압모델, 수중 구조물, 부유식 구조물, 고립파, 처오름높이

Abstract

The wave runup height is one of the most important parameters for affecting the design of coastal structures such as dikes, revetments, and breakwaters. In this study, SWASH (Zijlema et al., 2011), a non-hydrostatic pressure numerical model, was used to analyze the effect of reducing The wave runup height of solitary waves by submerged and floating rectangular obstacles. It was confirmed that the SWASH model reproduces the propagation, breaking, and runup of solitary waves quite well. In addition, it was confirmed that the wave deformation of the solitary wave by submerged and floating rectangular obstacles was well reproduced. Finally, we conducted an examination of the effect of reducing the runup height of submerged and floating rectangular obstacles. Reduced runup heights are calculated and the characteristics of runup height reduction according to the dimensions of the obstacle were analyzed. The energy attenuation effect of the floating obstacle is greater than the submerged obstacle, and it is shown to be more effective in reducing the runup height.

Keywords: non-hydrostatic numerical model, submerged obstacle, floating obstacle, solitary wave, runup height

1. 서 론

외해로부터 내습하는 파랑으로부터 연안에 설치된 시설물들을 보호하기 위해 다양한 항만 구조물들이 설치되었으며, 기능적인 효율성을 중요시해 착저 중력식 방파제가 주로 설치되어왔다. 착저 중력식 방파제는 뛰어난 방파기능을 가지고 있으나, 설치에 많은 시간과 비용이 소요되고 원활한 해수유동을 저하시켜 수질 악화를 야기하는 등의 단점이 있다. 이에 대한 대안으로 해수의 흐름을 방해하지 않는 수중 및 부유식 형태의 구조물이 많은 연구자들에 의해 연구되었다. 수중 및 부유식 형태의 구조물은 해수의 흐름을 차단하지 않아 항 내·외 해수교환성은 우수한 반면, 항내 정온도가 다소 저하되고 파장이 긴 장파에는 유효하지 못하다는 단점을 가지고 있다. 이러한 단점에도 불구하고 최근 환경보호에 대한 관심이 높아지면서 수중 및 부유식 형태의 구조물이 적극 활용되고 있는 추세이다.

Frederiksen(1971)은 부유식 및 수중 구조물의 소파 성능에 대한 개념적인 연구를 수행하였고, 이후 다양한 연구가 수행되었다. 수중 구조물에 의한 고립파의 변형을 예측하는 연구(Madsen and Mei, 1969; Seabra-Santos et al., 1987; Goring and Raichlen, 1992)를 시작으로 다양한 수리 및 수치실험을 통해 수중 구조물 위를 통과하는 고립파의 특성(Grilli et al., 1994)과 고립파가 수중 구조물을 통과하며 구조물 뒤쪽에서 발생되는 와류(vortical flow) 구조에 대해 분석하는 연구가 수행되었다(Zhuang and Lee, 1996; Tang and Chang, 1998; Huang and Dong, 1999; Chang et al., 2001; Huang and Dong, 2001; Hsu et al., 2004). Lin(2004)은 직사각형의 수중 구조물 높이와 길이 변화에 따른 고립파의 거동을 수치모의하고, 고립파의 반사계수, 투과계수 및 에너지 감쇠계수를 산정하였다.

국내의 경우, Cho et al.(2002)과 Lee et al.(2003)은 각각 사각형의 수중 구조물과 다양한 형상의 수중 구조물에 따른 규칙파의 반사특성을 수리 및 수치실험을 통해 검토하였다. 또한, 사각형의 다열 수중 구조물에 대해 Jung et al.(2004)와 Jung et al.(2007)은 각각 일방향 불규칙파와 다방향 불규칙파의 반사특성을 수리 및 수치실험을 통해 검토하였다. Kim et al.(2004)은 VOF(Volume Of Fluid) 법을 사용하여 투과성 및 불투과성 수중 구조물에 따른 파랑 변형을 연구하였으며, Hwang et al.(2004)은 VOF 법을 사용해 불투과성 다열 수중 구조물에 대해 불규칙파의 반사 특성을 연구하였다.

부유식 구조물의 경우, 다양한 형상에 관한 연구가 이루어졌고(Hales, 1981; Western Canada Hydraulic Laboratories Ltd., 1981; McCartney, 1985; Sutko and Haden, 1974), 그 결과 부유식 방파제에 대한 개념, 특성, 형상 등에 따른 소파 특성이 제시되었다. 국내의 경우, Yang et al.(2001)은 2차원 유한요소모델을 이용해 사각형 부유식 구조물 배치에 따른 소파 성능 개선 효과를 검토하였으며, Cho(2002)은 해석해를 통해 계류된 사각형 부유식 구조물의 소파 성능에 대하여 검토하였다. Lee(2005)는 비선형수치모델을 이용해 설계조건에 따른 부유식 구조물의 변화특성과 파랑제어기능에 대해 분석하였다. Yoon et al.(2005)은 부유식 구조물의 수리 특성 분석을 위해 수리실험과 RANS(Raynolds Averaged Navier-Stokes) 방정식 모형을 이용한 연구를 수행하였다. 또한 Yoon et al.(2010)은 수리실험과 Navier-Stokes 방정식 모형을 이용한 수치실험을 통해 부유식 구조물의 형상과 흘수에 따른 유동장 변화와 유동장과 와류의 상관관계를 분석하였다.

위에서 살펴본 바와 같이 수중 및 부유식 형태의 구조물의 소파 성능에 대한 다양한 연구가 진행되었으며, 수중 구조물에 의한 처오름높이 저감에 대한 연구(Park et al., 2007; Irtem et al., 2011; Ha et al., 2012; Wang et al., 2018)도 다수 수행되었으나, 부유식 구조물에 의한 처오름높이 저감에 대한 연구는 드물다. 처오름높이는 해안구조물의 안전성을 평가하고, 효과적인 구조물 설계를 위한 중요한 매개변수이다. 또한 최대 처오름높이의 정확한 산정은 연안기반시설의 부지고를 결정하는 기초자료로 매우 중요하다. 따라서, 본 연구에서는 Zijlema et al.(2011)이 개발한 비정수압 수치모형(SWASH)을 활용하여 고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 처오름높이 저감 효과에 대해 분석하였다. 수치모형의 검증을 위해 경사지형에서 고립파의 쇄파 및 처오름에 대한 수치실험을 수행하고 Synolakis(1986, 1987)의 수리실험 결과와 비교하였으며, 고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 변형을 수치실험하고 그 결과를 Lin(2006)의 수치실험 결과와 비교하였다. 검증된 수치모형을 사용하여 고정된 사각형 수중 및 부유식 구조물의 길이 및 높이의 변화에 따른 경사지형에서 발생하는 고립파의 처오름높이 변화를 분석하였다.

2. 수치모형

2.1 지배방정식

본 연구에서는 Delft 대학에서 개발한 비정수압 수치모형인 SWASH(Surface WAves till SHore; Zijlema et al., 2011)를 사용하였다. SWASH 모형은 비정수압 보정항(nonhydrostatic pressure correction term)이 추가된 비선형 천수 방정식을 지배방정식으로 하고 있으며 지배방정식은 다음과 같다.

(1)

∂ζ∂t+∂hu∂x=0

(2)

∂u∂t+∂uu∂x+∂wu∂z=−1ρ∂(ph+pnh)∂x+∂τxx∂x+∂τxz∂z

(3)

∂w∂t+∂uw∂x+∂ww∂z=-1ρ∂pnh∂x+∂τzz∂z+∂τzx∂x

(4)

∂u∂t+∂w∂z=0

여기서 ζ는 자유수면 변위, h는 수심, u(x, z, t)과 w(x, z, t)는 각각 수평방향, 수직방향 유속, ρ는 물의 밀도, ph는 정수압, p_nh는 비정수압, τ_xx, τ_xz, τ_zx, τ_zz는 난류 응력이다. SWASH 모형은 Keller-box기법을 이용해 자유수면 위치의 압력 경계 조건을 손쉽게 정의하고 있으며, Stelling and Zijlema(2003), Stelling and Duinmeijer(2003), Zijlema and Stelling(2005, 2008), Smit et al.(2013) 등의 연구자들에 의해 충분히 검증되었고 많은 문헌에 소개되어 있다. 따라서 수치모형에대한 자세한 내용은 그 문헌들로 대신한다.

3. 수치실험

3.1 수치모형의 검증 - 고립파 쇄파 실험

본 연구에서 적용된 수치모형의 검증을 위해 Synolakis(1986, 1987)에 의해 수행된 고립파의 수리실험을 재현하였다. Synolakis(1986, 1987)는 수리실험을 통해 Fig. 1과 같은 경사지형에서 고립파의 전파과정과 쇄파 및 비쇄파조건에 따른 최대 처오름높이를 제시하고 최대 처오름높이를 산정하는 공식을 제안하였다. Fig. 1에서 h는 수심, H는 파고, β는 경사도, R은 처오름높이를 나타낸다. 바닥 경사(1:19.85, cot(β) = 19.85)에서 다양한 수심과 파고를 이용해 수리실험을 수행하였으며, 보다 자세한 정보는 Synolakis(1986, 1987)를 참조할 수 있다. 본 연구에서는 Synolakis(1986, 1987)가 제시한 쇄파(H/h = 0.3) 및 비쇄파(H/h = 0.0185) 조건을 재현하였으며, 수치실험에 사용한 수심, 파고, 격자조건은 Table 1에 나타내었다.

고립파는 Shin and Yoon(2017, 2018)의 이완법(relaxation method)을 이용해 조파하였으며, 이완영역(relaxation zone) 내에 부가되는 부가되는 매 시간 단계의 수면변위는 Wang(1993)의 식을 이용하였다. 고립파가 계산 영역 내로 잘 전파되는지 확인하고자 Table 1과 동일한 수심 및 계산격자 조건을 이용해 경사지형이 없는 상태로 파고 H = 0.1 m에 대해 수치실험을 수행하였다. 다음 Fig. 2는 이완영역을 제외한 계산 영역에서 시간에 따른 수면변위를 나타낸 결과이다. 고립파가 이완영역을 통과한 이후부터를 t = 0으로 산정하였으며, 고립파의 파형이 잘 유지되면서 계산 영역 전체로 잘 전파하는 것을 확인할 수 있다.

Synolakis(1986, 1987)의 수리실험 결과는 National Tsunami Hazard Mitigation Program(NTHMP)에서 제공하는 자료를 활용하였으며, 수리실험과 수치실험 결과를 비교하기 위해 처오름높이는 수심(h)으로, 시간단위는 T=t-t0h/g로 무차원화하였다. 여기서 t₀는 고립파 파면(wave front)이 경사지형에 도착한 시간이다. Fig. 3과 Fig. 4는 각각 비쇄파 및 쇄파 조건의 수치실험과 수리실험 결과를 비교하여 도시하였다. Fig. 3 비쇄파 조건의 경우, 수심 감소에 따른 파고 증가 후 쇄파 발생 없이 처오름 현상이 발생하고, 시간 경과 후 경사지형에 의한 반사로 인해 처내림 현상이 시작되는 걸 확인 할 수 있다. 반면 Fig. 4 쇄파 조건의 경우, 수심이 감소함에 따라 파고가 증가하다가 쇄파가 발생하면서 파고가 급격히 감소된 후 경사지형을 따라 처오름 현상이 시작되는 것을 확인할 수 있다. 전체적으로 비쇄파 및 쇄파 조건 모두 수치실험 결과가 수리실험 결과를 매우 잘 재현하는 것을 확인할 수 있다.

동일한 바닥 경사 cot(β) = 19.85에서 고립파의 파고의 변화에 따른 최대 처오름높이를 수치실험하고 Synolakis(1987)가 제안한 최대 처오름높이 공식과 비교하였다.

Synolakis(1987)는 다양한 경사에서 고립파의 파고에 따른 최대 처오름높이 변화를 분석해 비쇄파 조건에서의 최대 처오름높이를 산정하는 해석해를 제안하였다. Synolakis(1987)가 제안한 공식은 다음과 같으며, 일반적으로 식(5)는 식(6)과 같은 조건이 충족된 경우에 바람직한 결과를 제공하는 것으로 알려져 있다.

(5)

Rh=2.831cotβ(Hh)5/4

(6)

Hh<0.8183(cotβ)-10/9

쇄파조건의 경우에는 최대 처오름높이를 산정하는 해석해가 존재하지 않는다. Synolakis(1987)는 파고대 수심의 비가 H/h = 0.005~0.665인 77개의 서로 다른 고립파를 이용해 최대 처오름높이를 측정하고 다음과 같은 경험식을 제안하였다.

(7)

Rh=1.109(Hh)0.582

Fig. 5는 수치실험 결과와 Synolakis(1987)가 제안한 해석해 및 경험식을 함께 비교하여 로그 스케일(Log scale)로 도시하였다. 전반적으로 비쇄파 및 쇄파 조건 모두 Synolakis(1987)의 해석해 및 경험식과 잘 일치하는 것을 확인할 수 있으나, 쇄파가 발생하지 않는 한계파고 조건 부근에서는 최대 처오름높이가 과소평가 되고 있는 것을 확인할 수 있다. 본 연구에서 사용한 SWASH 모형은 별도의 쇄파모델을 사용하지 않고 수직 파면의 에너지 소산 메커니즘에 따라 쇄파가 발생하고 이는 쇄파 전면에서 정확한 양의 에너지 소모로 이어진다(Zijlema et al., 2011). 그러나 쇄파가 발생하지 않는 한계파고 조건에서는 이러한 방식으로 정확한 양의 에너지가 소산되지 않는 것으로 예상된다. 오히려 쇄파로 인한 에너지 소산이 과대평가되어 최대 처오름높이가 다소 작게 계산된 것으로 보여진다. 그러나 다소 오차가 있음에도 전체적으로 최대 처오름높이를 정확도 높게 계산하고 있어 SWASH 모형은 고립파와 같은 비선형 파랑의 쇄파와 처오름을 예측하는데 적합한 것으로 판단된다.

3.2 수치모형의 검증 - 고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 변형 실험

본 연구에서 사용한 수치모형을 검증하기 위해 Lin(2006)에 의해 수행된 고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 변형 수치실험을 재현하였다. Lin(2006)은 수치실험을 통해 Fig. 6과 같은 위치(x = 30.0 m)에 고정된 사각형 수중 및 부유식 구조물을 설치하고 각각 x = 1.0 m, 32.5 m, 59.0 m에서 자유수면변위를 관측하였다. 수중 구조물은 바닥으로부터 높이 0.6 m, 폭 5.0 m, 부유식 구조물은 수면으로부터 바닥으로 높이 0.4 m, 폭 5.0 m이며 수면위로는 월파가 발생하지 않도록 충분히 높게 구성하였다. 보다 자세한 정보는 Lin(2006)을 참조할 수 있다. 본 연구에서 수치실험에 사용한 수심, 파고, 격자조건은 Table 2에 나타내었다.

Fig. 7은 고정된 사각형 수중 구조물에 대해 Fig. 6의 각 지점에서의 시간에 따른 자유수면변위를 Lin(2006)의 수치실험결과와 비교하여 도시하였다. Gauge 1은 구조물 전면, Gauge 2는 구조물의 중간, Gauge 3은 구조물 후면 위치에서의 자유수면변위를 나타낸다. Gauge 1에서 확인할 수 있듯이 고립파가 목표 파고에 맞게 잘 전파되고 수중 구조물을 통과하면서 일부가 반사되는 것을 확인할 수 있다. Gauge 2에서는 수중 구조물을 통과하면서 파고가 증폭되는 것을 볼 수 있으며, Gauge 3에서는 구조물을 통과한 고립파의 꼬리부분에서 파고가 감소되는 것을 확인할 수 있다.

Fig. 8은 부유식 구조물에 대해 Fig. 6의 각 지점에서의 시간에 따른 자유수면변위를 Lin(2006)의 수치실험결과와 비교하여 도시하였다. 부유식 구조물의 경우 월파가 발생되지 않는 조건으로 Gauge 2의 자유수면변위가 존재하지 않아 결과에서 제외하였다. Gauge 3에서는 구조물을 통과한 고립파의 파고 크기가 크게 줄어든 것을 확인할 수 있다. 이러한 결과로부터 동일한 부피의 구조물인 경우, 부유식 구조물이 수중 구조물 보다 파랑 에너지를 소산시키는 효과가 뛰어나다는 것을 알 수 있다.

본 연구의 수치실험 결과가 Lin(2006)의 수치실험 결과를 매우 잘 재현하는 것을 확인할 수 있다. 이러한 결과로부터 SWASH 모형은 사각형 수중 및 부유식 구조물에 의한 고립파의 변형을 계산하는데 적합한 것으로 판단된다.

3.3 고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 처오름 저감 수치실험

본 연구에서는 앞서 검증된 수치모형을 이용해 경사지형 앞에 고정된 사각형 수중 및 부유식 구조물이 위치할 때 고립파의 처오름높이 변화를 검토하였다.

수치실험에 사용한 수치수조는 Lin(2006)의 수치실험 조건을 참고해 고립파 조파를 위한 이완영역을 제외한 계산영역의 수치수조의 길이는 100 m이고 수심 1.0 m이며 60 m 위치에서부터 바닥 경사 cot(β) = 19.85의 경사지형을 만들어 Fig. 9와 같이 수심을 구성하였다. 계산영역의 수치수조 30 m 지점에 고정된 사각형 수중 및 부유식 구조물을 위치하도록 구성하였으며 부유식 구조물은 수면위로 월파가 발생하지 않도록 충분히 높게 구성하였다. 수치실험에 사용한 수심, 파고, 격자조건은 Table 3에 구조물 제원은 Table 4에 나타내었다.

Fig. 10은 사각형 수중 구조물의 형상에 따른 고립파의 처오름높이 변화를 나타낸 결과이다. 수중 구조물의 종방향 길이(a)가 0.6 m 미만인 경우에는 종방향의 길이 변화에 따른 처오름높이 변화가 거의 나타나지 않았고, 수중 구조물의 횡방향 길이(b)가 증가함에도 처오름높이 변화는 매우 미미하였다.

수중 구조물의 종방향 길이가 0.6 m 이상일때는 처오름높이가 크게 감소하는 것을 확인할 수 있으나, 횡방향 길이가 작은 경우에는 처오름높이 변화가 거의 나타나지 않았다. 수중 구조물의 횡방향 길이 변화에 따른 처오름높이 변화는 크지 않은 것으로 나타났으며, 이는 횡방향 길이가 길지 않은 경우 고립파의 분산효과가 크지 않아 나타난 것으로, 이는 Ha et al.(2012)의 수치실험 결과와 동일한 결과이다. 이러한 결과로부터 수중 구조물의 종방향 길이가 길지 않은 경우에는 구조물의 횡방향 길이는 처오름높이 변화에 유의미한 영향을 미치지 않는 것으로 보여진다. 구조물의 횡방향 길이가 증가함에도 처오름높이가 크게 감소하지 않는 이유는 수중 구조물을 통과하면서 발생하는 천수효과로 인해 고립파의 파고가 증폭되어 나타난 결과로 보여지며, 구조물의 종방향 길이가 0.6 m 이상일때는 처오름높이가 크게 감소하는 것은 고립파가 수중 구조물을 통과하면서 파봉이 분리되어 나타난 현상으로 예상된다.

Fig. 11은 고정된 사각형 부유식 구조물의 형상에 따른 고립파의 처오름높이 변화를 나타낸 결과이다. 부유식 구조물의 종방향 길이(a)가 작은 경우에도 처오름높이가 감소하나, 횡방향 길이(b)가 작은 경우에는 처오름높이 변화가 거의 나타나지 않았다. 그러나 횡방향 길이가 5 m에서 10 m로 증가되자 종방향 길이 작음에도 처오름높이가 감소하는 것을 확인할 수 있다. 특히 구조물의 종방향 길이가 0.6 m 이상일때는 처오름높이가 크게 감소하는 것을 확인할 수 있다. 이는 수중 구조물과 달리 부유식 구조물의 경우, 종방향 길이가 작음에도 처오름높이가 크게 저감되는 것은 부유식 구조물이 파랑 에너지를 소산시키는 효과가 뛰어나 나타난 결과로 보여진다. 수중 구조물과 달리 부유식 구조물의 경우 횡방향 길이가 증가할 수록 처오름높이가 감소되는 것을 볼 수 있다. 이러한 결과로부터 처오름높이는 부유식 구조물의 횡방향 길이 변화에 유의미한 영향을 받는 것으로 보여진다. 이는 부유식 구조물의 경우 수중 구조물과 달리 천수효과로 인한 파고 증폭이 없고 구조물을 통과하며 에너지가 크게 감소된 영향으로 사료된다.

4. 결 론

본 연구에서는 수치실험을 통해 고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 처오름높이 저감 효과를 검토하였다. 수치실험에 사용한 수치모형을 검증하고자, 일정한 경사지형에서 고립파의 쇄파를 수치실험하고 Synolakis(1986, 1987)의 수리실험 결과와 비교하여 검증하였다. 수치실험결과 쇄파가 발생하지 않는 한계파고 조건 부근에서 약간의 오차가 발생하는 것으로 나타났지만, 비정수압 수치모형이 고립파의 전파 및 쇄파 등의 복잡한 파랑 변형을 비교적 정확하게 예측하는 것을 확인할 수 있었다. 추가로 고정된 사각형 수중 및 부유식 구조물에 따른 고립파의 파랑 변형 정확도를 확인하기 위해 Lin(2006)의 수치실험 결과 비교하였다. 비교 결과, Lin(2006)의 수치실험 결과와 매우 잘 일치하였으며 구조물에 따른 고립파의 파랑 변형 현상을 잘 재현하는 것을 확인할 수 있었다. 검증된 모형을 이용해 고정된 사각형 수중 및 부유식 구조물에 의한 고립파의 처오름높이 저감 효과를 검토하였다. 수치실험을 통해 도출된 결론을 요약하면 다음과 같다.

- 고정된 사각형 수중 구조물의 경우, 구조물의 종방향 길이가 0.6 m 이하일 때는 처오름높이 변화가 거의 나타나지 않았고 0.6 m 이상 일때는 처오름높이가 크게 감소하였다.

- 고정된 사각형 수중 구조물의 경우, 구조물의 횡방향 길이에 대한 처오름높이 변화는 미미하였다.

- 고정된 사각형 부유식 구조물의 경우, 구조물의 종방향 길이가 증가함에 따라 처오름높이가 크게 감소하였으며, 0.6 m 이상일 때는 처오름높이가 크게 감소하였다.

- 고정된 사각형 수중 구조물의 경우, 구조물의 횡방향 길이가 증가할 수록 처오름높이가 감소하는 것을 확인할 수 있었다.

- 수중 구조물보다 부유식 구조물에 의한 에너지 감쇠효과가 커 처오름높이 저감에 효과적인 것으로 보여진다.

본 연구에서는 검증된 비정수압 수치모형을 이용해 사각형 구조물의 처오름높이 저감 효과를 단순 검토한 것으로 기존의 착저중력식 방파제 보다 효과적인 구조물 설계를 위해서는 구조물의 배열 및 형상, 구조물과 파랑간의 상호작용에 의한 동적거동 등에 따른 처오름높이 저감 효과가 분석되어야 할 것으로 보여진다.

감사의 글

이 논문은 2021년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(NRF2021R1A6A1A1A0304518511).

Fig. 1.

Definition sketch for simple beach bathymetry (from Synolakis (1987)).

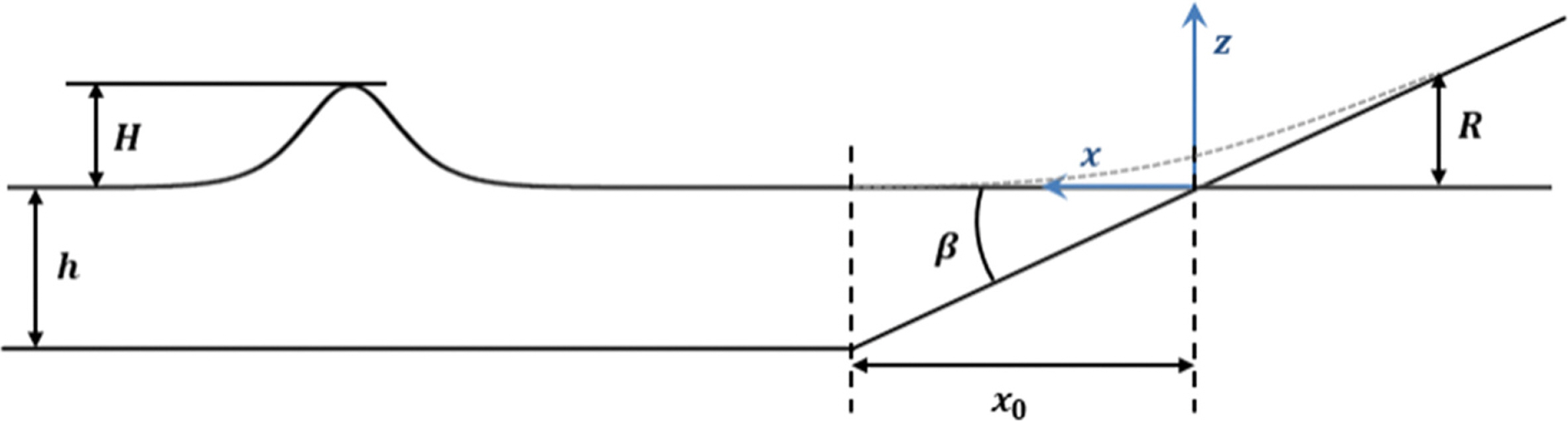
Fig. 2.

Propagation of solitary wave (h =1.0m, H =0.1m).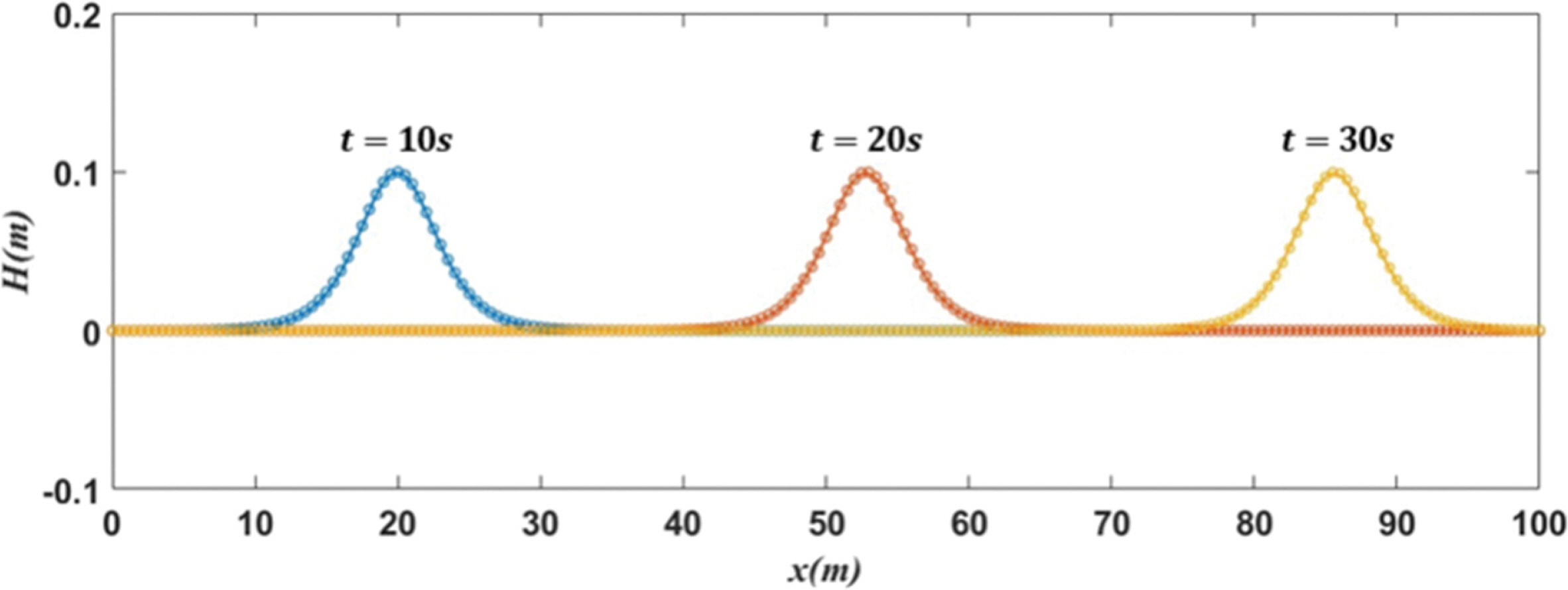

Fig. 3.

Measured (circles) and calculated (lines) free surface profiles at different dimensionless time for H/h = 0.0185.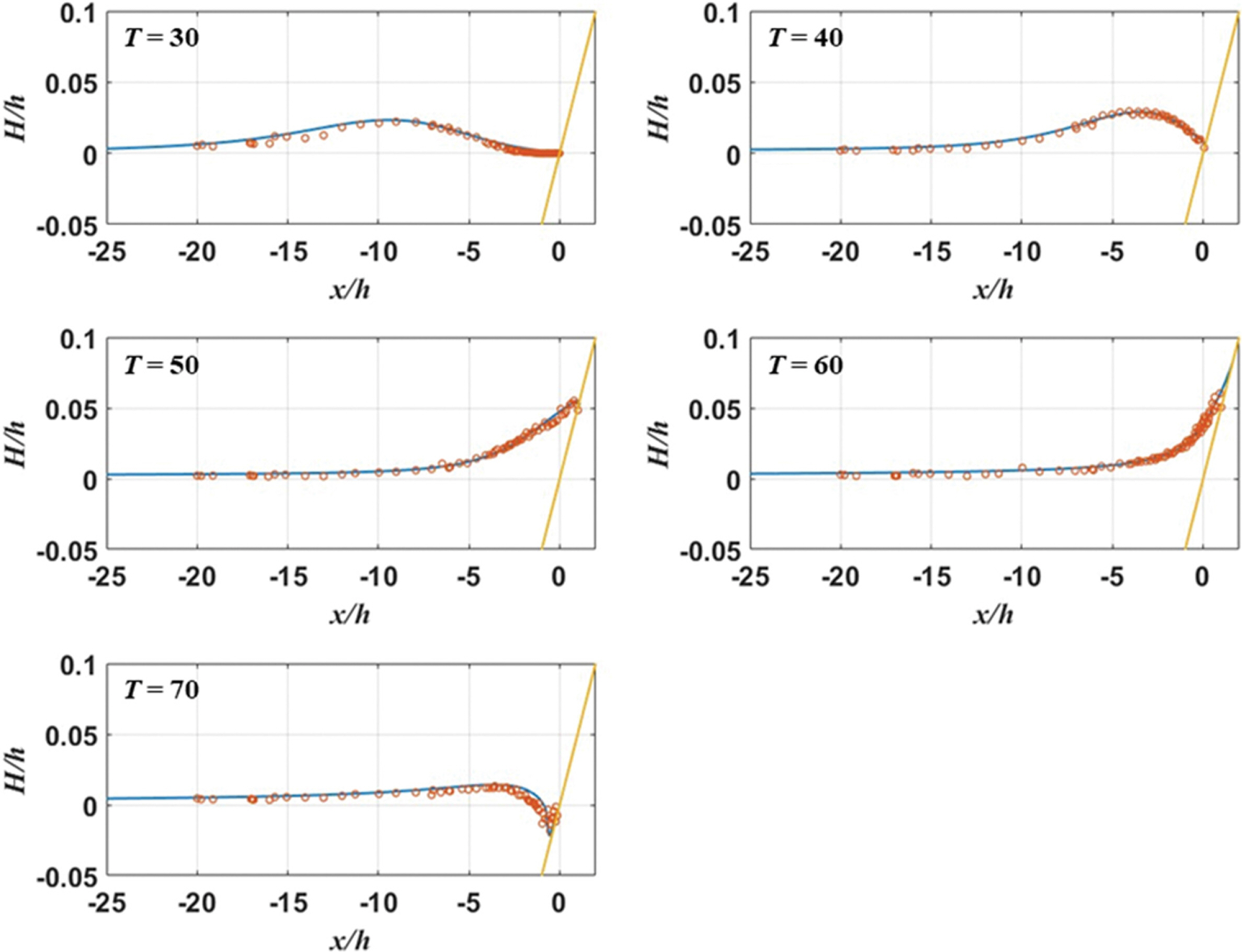

Fig. 4.

Measured (circles) and calculated (lines) free surface profiles at different dimensionless time for H/h =0.3.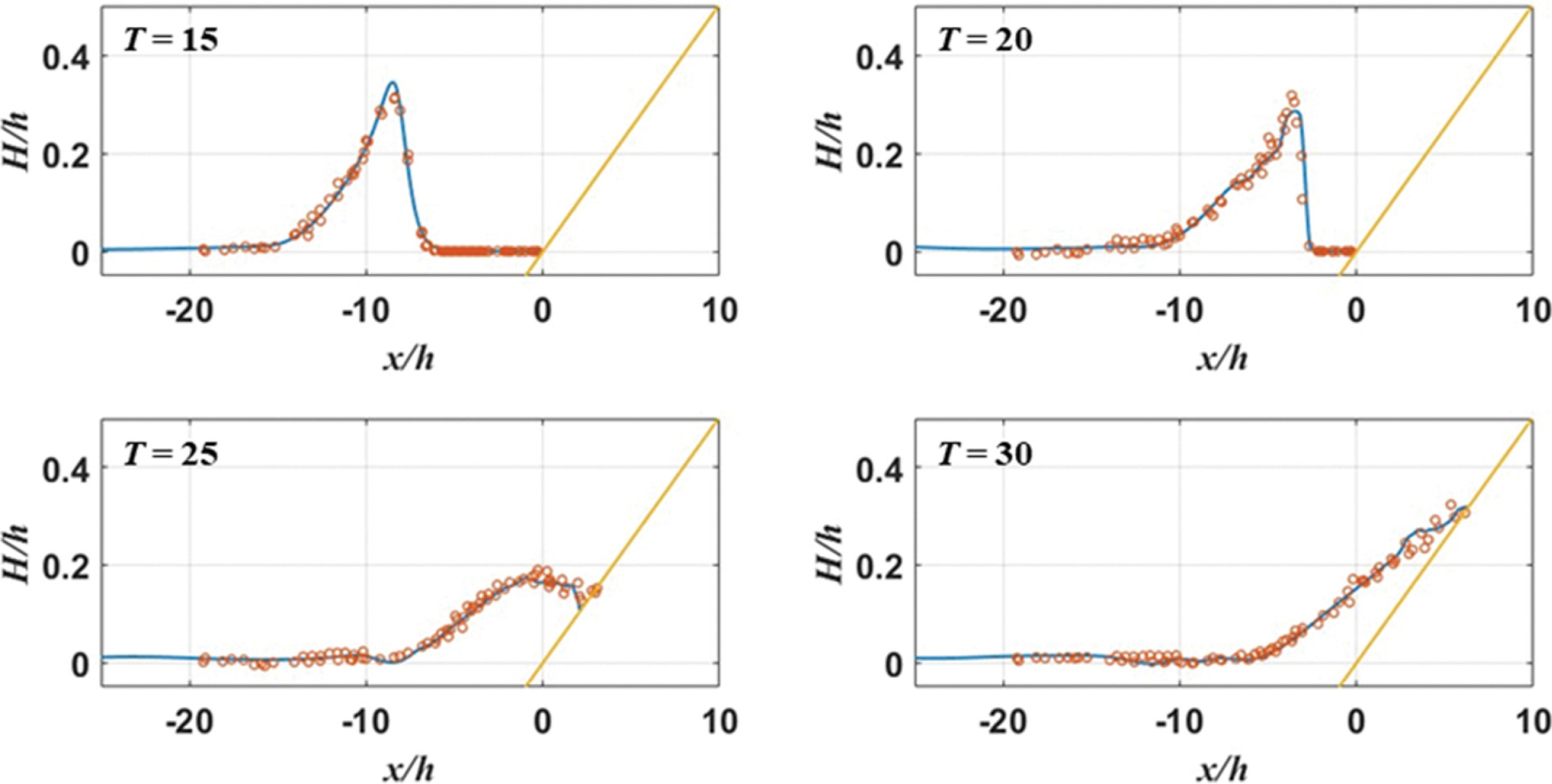

Fig. 5.

Runup heights of solitary wave on a slope.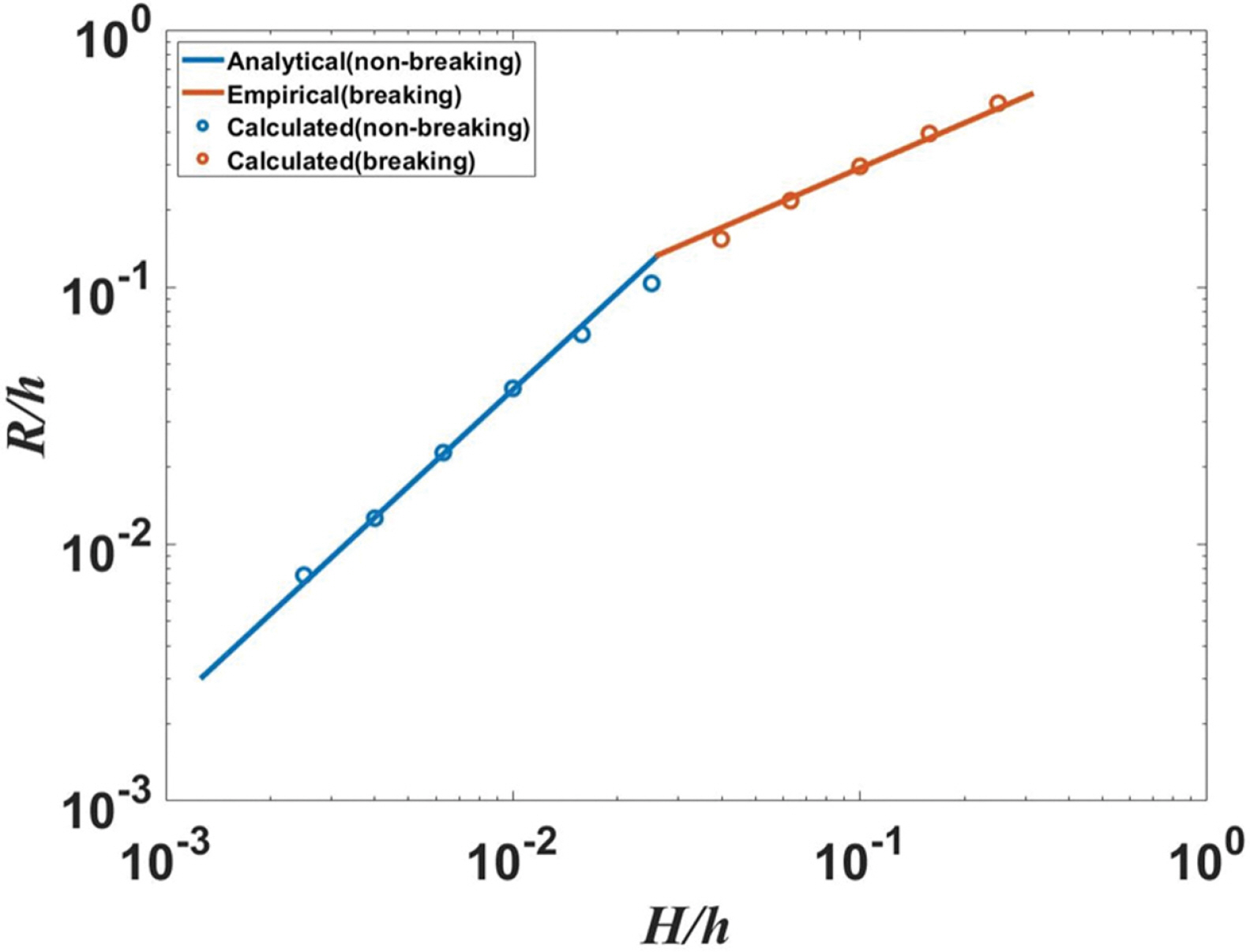

Fig. 6.

Schematic view of numerical model for a solitary wave passing over the submerged and floating rectangular obstacles.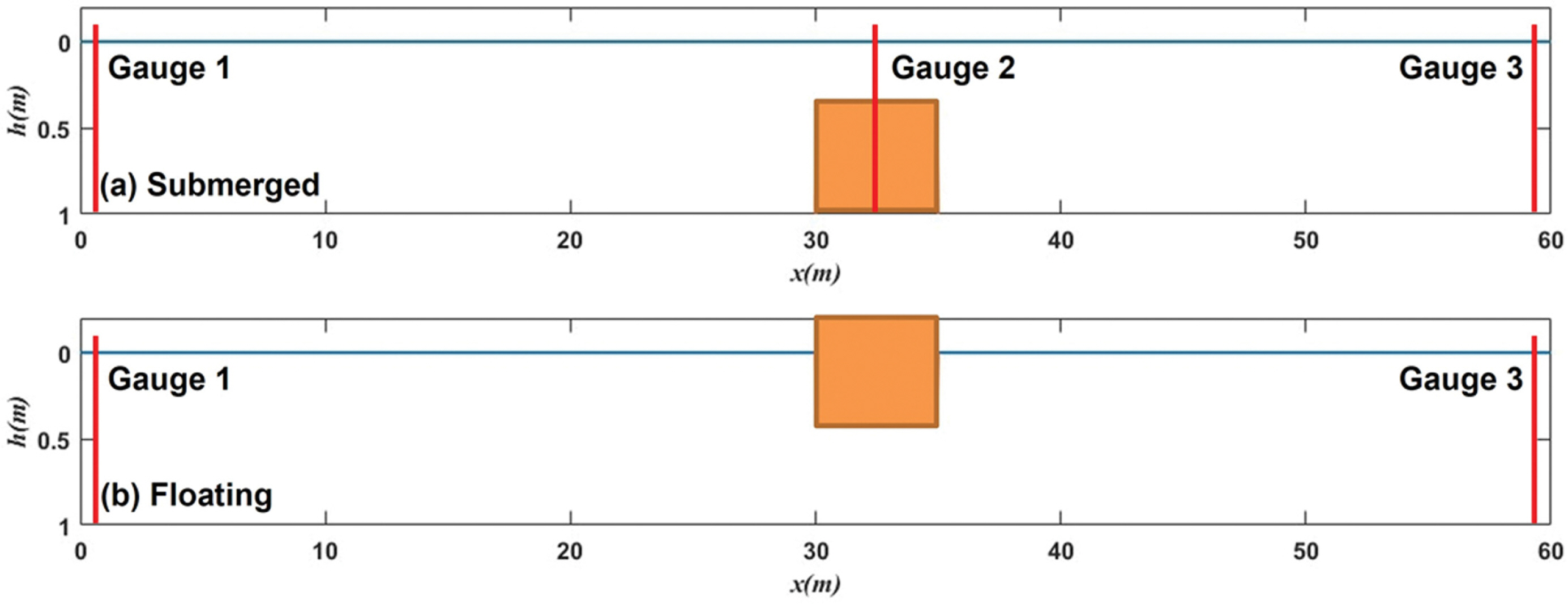

Fig. 7.

Comparisons of time histories of free surface displacement for the submerged obstacle.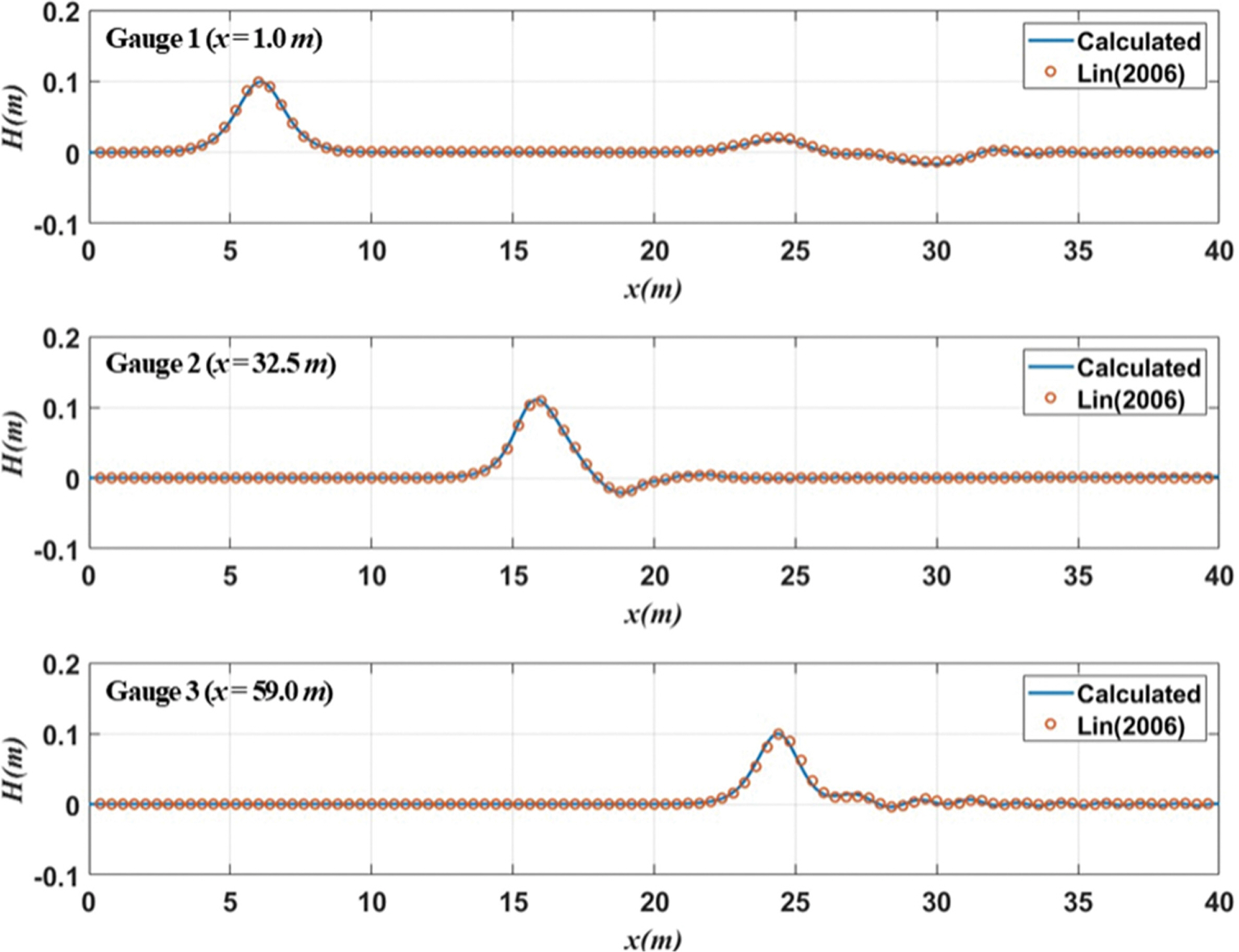

Fig. 8.

Comparisons of time histories of free surface displacement for the floating obstacle.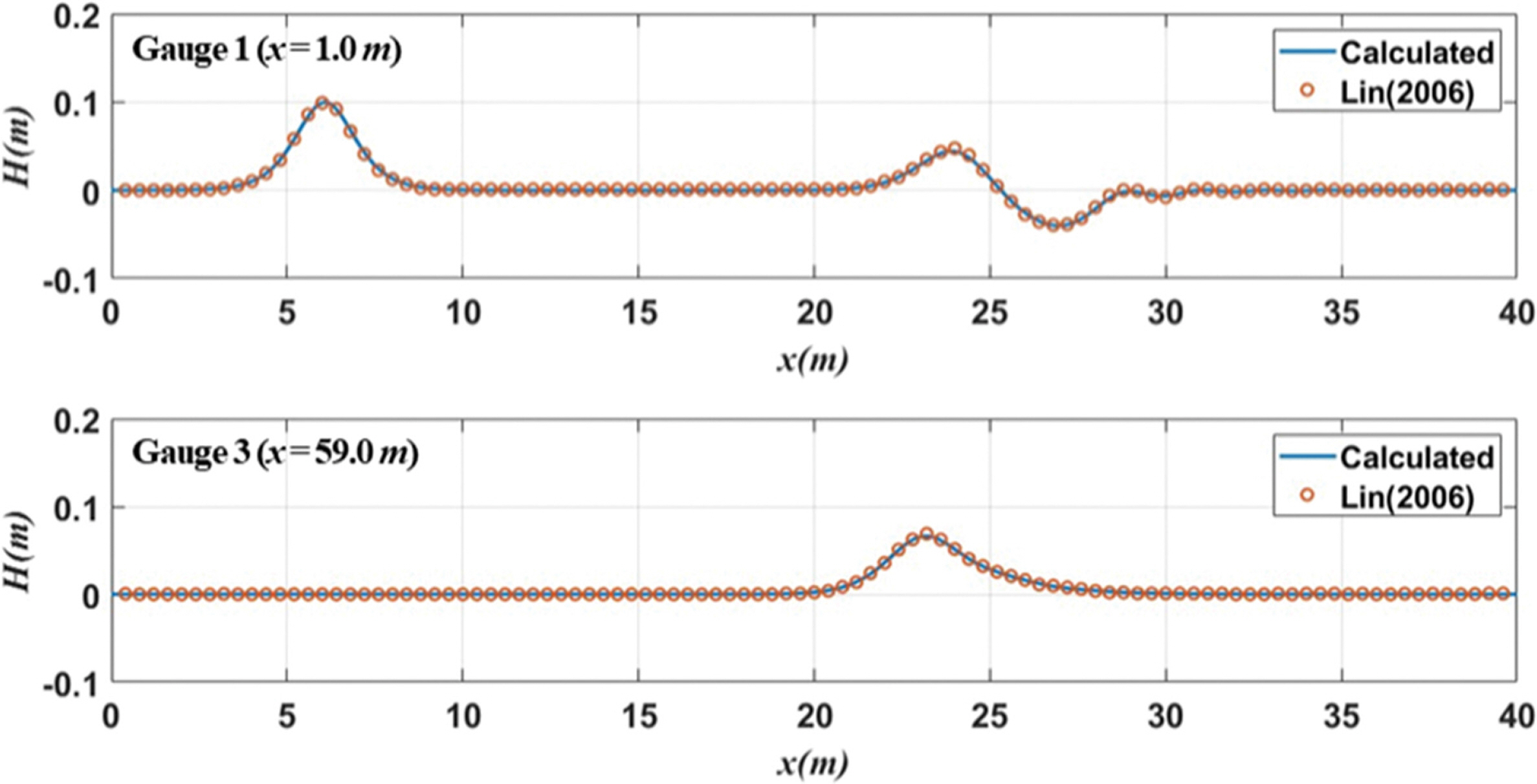

Fig. 9.

Schematic view of numerical model setup for a solitary wave passing over submerged and floating rectangular obstacles.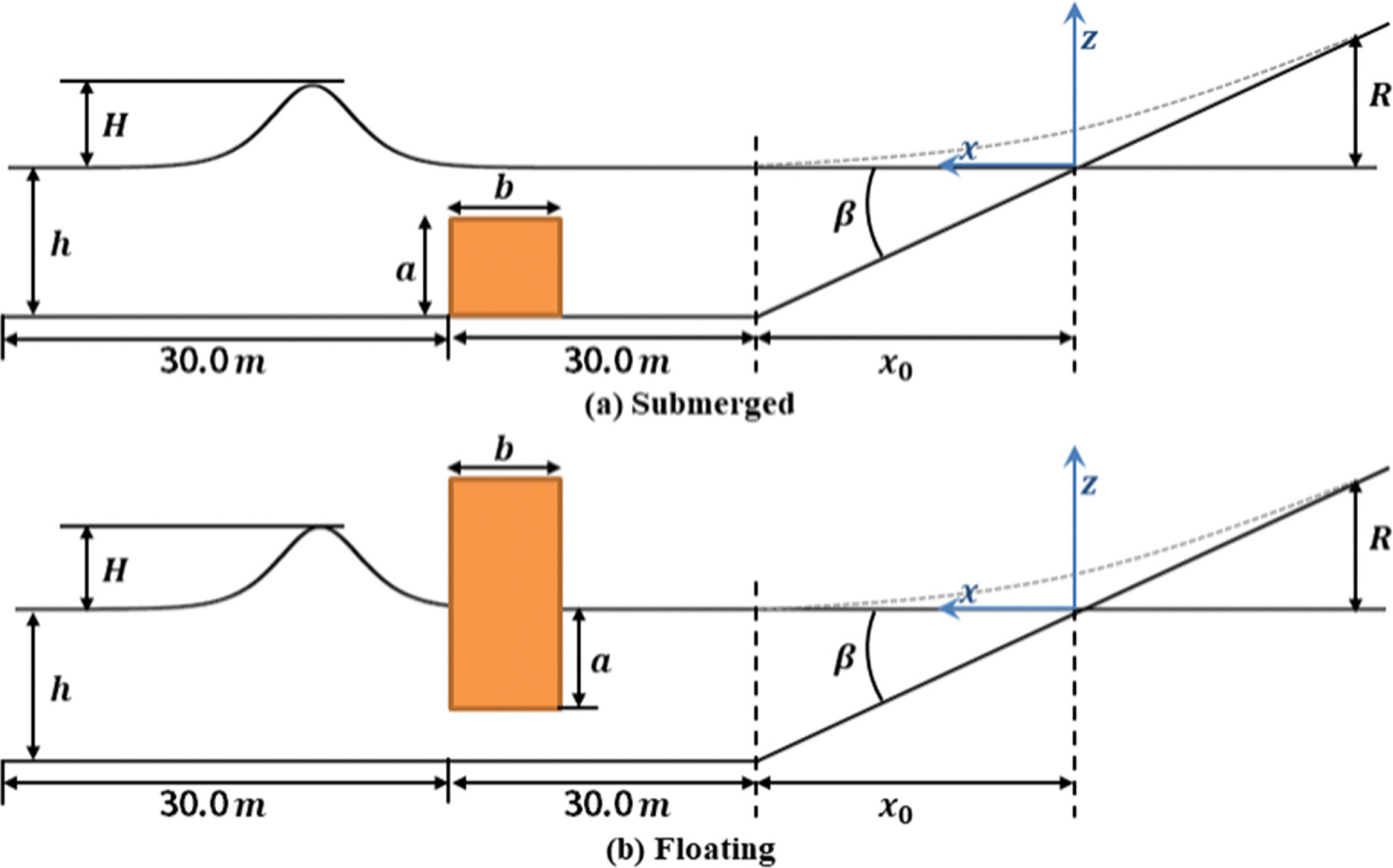

Fig. 10.

Runup heights of solitary wave after passing over a fixed submerged rectangular obstacle.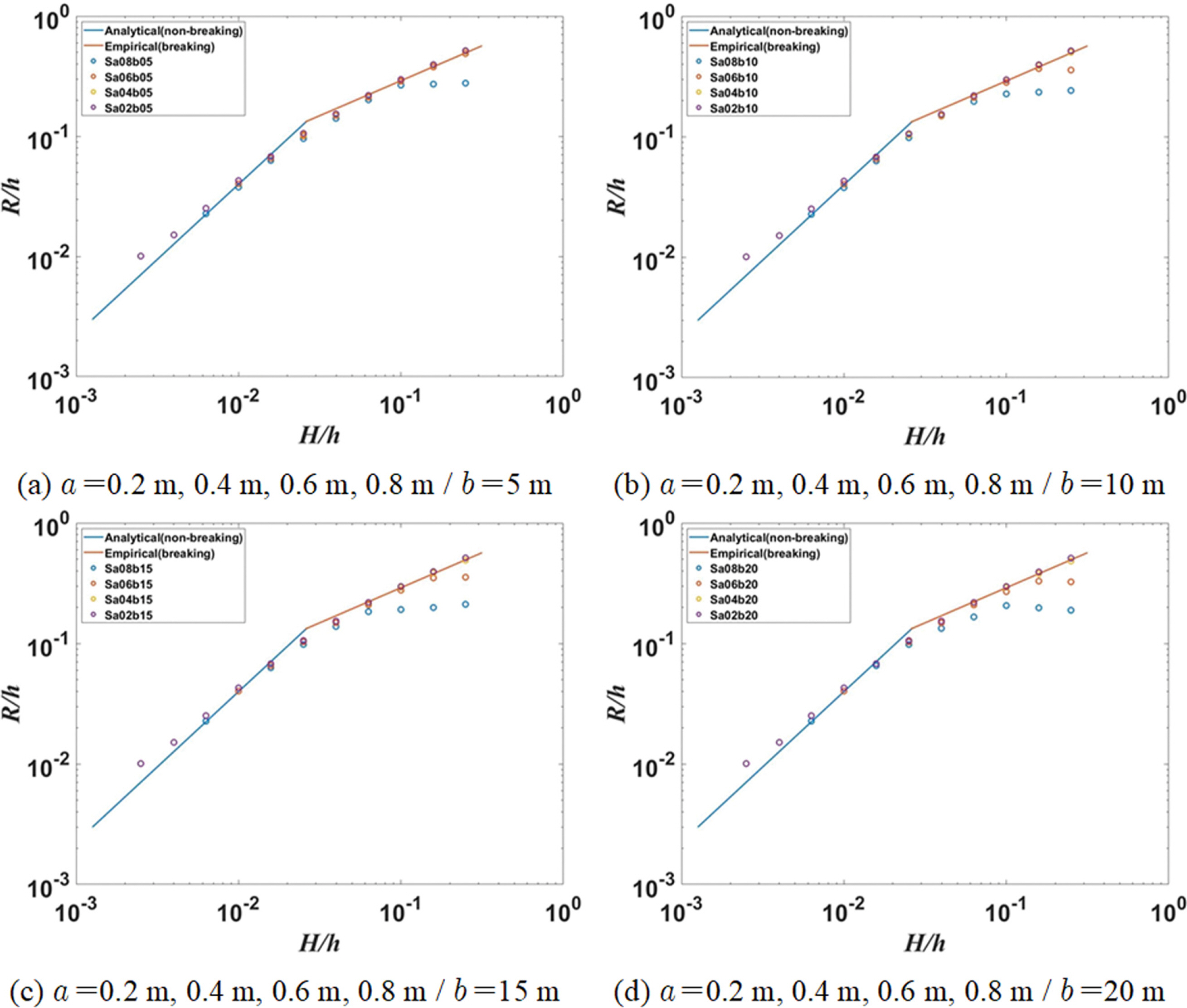

Fig. 11.

Runup heights of solitary wave after passing over a fixed floating rectangular obstacle.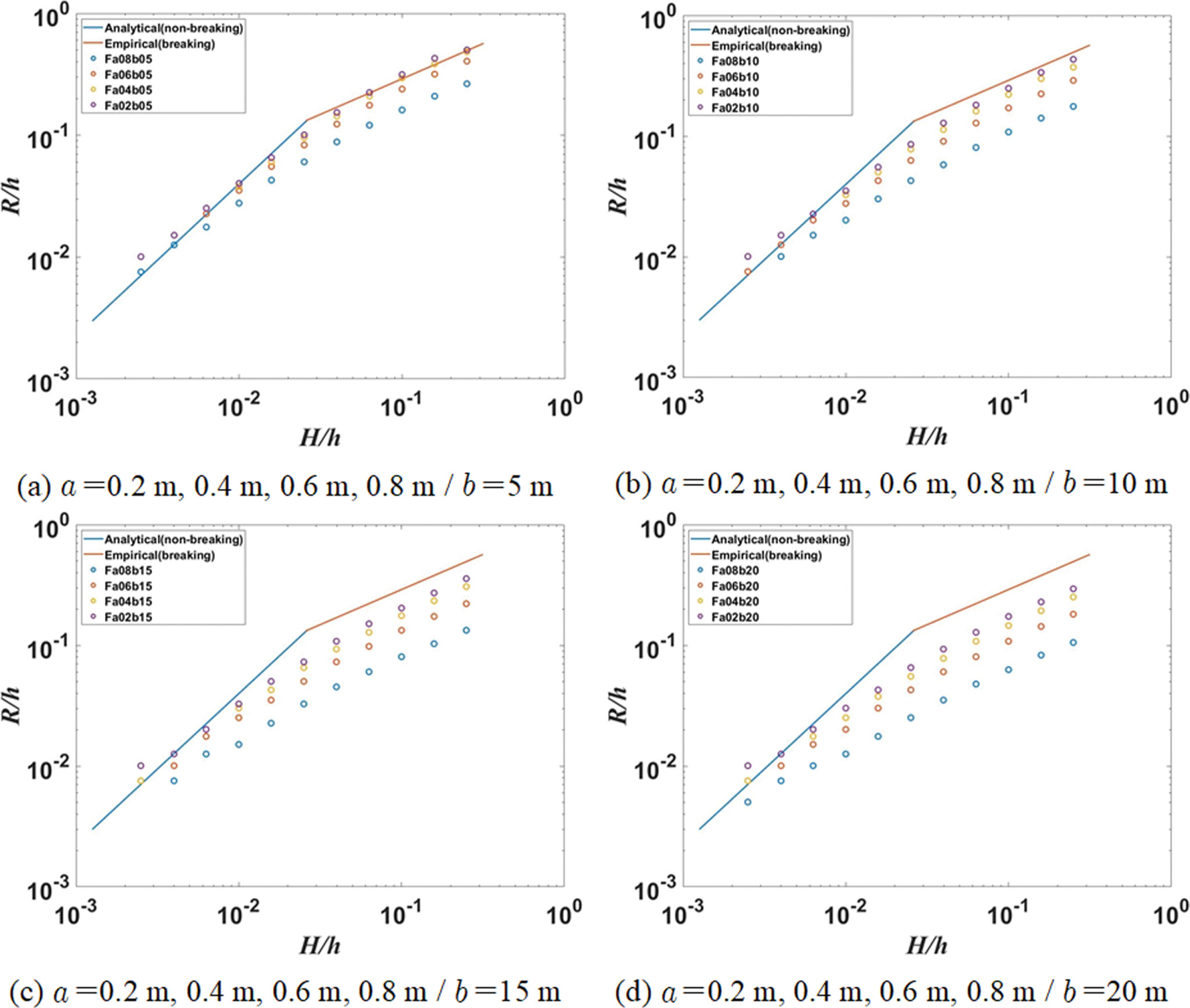

Table 1.

Simulation condition of a solitary wave runup on a simple slope

Description		Component
Description		Non-breaking		Breaking
Water Depth (h)			1.0 m
Wave Height (H)		0.0185 m		0.3 m
Grid size	x-axis direction		0.05 m
	x-axis direction	z-axis direction	3 equidistant vertical layers (σ coordinate)

Table 2.

Simulation condition of a solitary wave passing over obstacles

Description		Component
Water Depth (h)		1.0 m
Wave Height (H)		0.1 m
Grid size	x-axis direction	0.05 m
Grid size	z-axis direction	3 equidistant vertical layers (σ coordinate)

Table 3.

Simulation condition of the run-up of a solitary wave after passing over obstacles

Description		Component
Water Depth (h)		1.0 m
Wave Height (H)		0.0025 m, 0.004 m, 0.0063 m, 0.01 m, 0.0158 m, 0.0251 m, 0.0398 m, 0.0631 m, 0.1 m, 0.1585 m, 0.25 m (11 case)
Grid size	x-axis direction	0.05 m
Grid size	z-axis direction	5 equidistant vertical layers ( coordinate)

Table 4.

Specifications of submerged and floating obstacles

Case	Type	Height a (m)	Width b (m)	Case	Type	Height a (m)	Width b (m)
Sa02b05	Submerged	0.2	05	Fa02b05	Floating	0.2	05
Sa02b10			10	Fa02b10			10
Sa02b15			15	Fa02b15			15
Sa02b20			20	Fa02b20			20
Sa04b05		0.4	05	Fa04b05		0.4	05
Sa04b10			10	Fa04b10			10
Sa04b15			15	Fa04b15			15
Sa04b20			20	Fa04b20			20
Sa06b05		0.6	05	Fa06b05		0.6	05
Sa06b10			10	Fa06b10			10
Sa06b15			15	Fa06b15			15
Sa06b20			20	Fa06b20			20
Sa08b05		0.8	05	Fa08b05		0.8	05
Sa08b10			10	Fa08b10			10
Sa08b15			15	Fa08b15			15
Sa08b20			20	Fa08b20			20

References

Chang, K.A., Hsu, T.J., Liu, P.L.F. (2001). Vortex generation and evolution in water waves propagating over a submerged rectangular obstacle: Part I. Solitary waves, Coastal Engineering, 44(1):13-36.

Cho, I.H. (2002). Wave control performance of moored pontoon-type floating breakwater, Journal of the Korean Society for Marine Environment & Energy, 5(3):35-44 (in Korean)..

Cho, Y.-S., Lee, J.I., Kim, Y.T. (2002). Hydraulic experiments on reflection of regular waves due to rectangular submerged breakwaters, Journal of Korea Water Resources Association, 35(5):563-573 (in Korean)..

Frederiksen, H.D. (1971). Wave attenuation by fluid filled bags, Journal of the Waterways, Harbors and Coastal Engineering Division, 97(1):73-90.

Goring, D.G., Raichlen, F. (1992). Propagation of long waves onto shelf, Journal of Waterway Port Coastal and Ocean Engineering, 118(1):43-61.

Grilli, S.T., Losada, M.A., Martin, F. (1994). Characteristics of solitary wave breaking induced by breakwaters, Journal of Waterway Port Coastal and Ocean Engineering, 120(1):74-92.

Hsu, T.W., Hsieh, C.M., Hwang, R.R. (2004). Using RANS to simulate vortex generation and dissipation around impermeable submerged double breakwaters, Coastal Engineering, 51(7):557-579.

Hales, L.Z.. (1981). Floating Breakwaters : State of the Art Literature Review, Technical Report No. p 81-1. Coastal Engineering Research Center, U.S. Army Corps of Engineers, Fort Belvoir, Virginia.

Ha, T., Jung, W., Cho, Y.-S. (2012). Numerical study on reduced runup heights of solitary wave by submerged structures, Journal of the Korean Society of Hazard Mitigation, 12(5):251-258 (in Korean)..

Huang, C.J., Dong, C.M. (1999). Wave deformation and vortex generation in water waves propagating over a submerged dike, Coastal Engineering, 37(2):123-148.

Huang, C.J., Dong, C.M. (2001). On the interaction of a solitary wave and a submerged dike, Coastal Engineering, 43(3–4):265-286.

Hwang, J.K., Lee, S.H., Cho, Y.-S. (2004). Transformation of irregular waves due to rectangular submerged non-porous breakwaters, Journal of Korea Water Resources Association, 37(11):949-958 (in Korean)..

İrtem, E, Seyfioglu, E, Kabdasli, S. (2011). Experimental investigation on the effects of submerged breakwaters on tsunami run-up height, Journal of Coastal Research, 516-520.

Jung, J.-S., Cho, D.-H., Hwang, J.-K., Cho, Y.-S. (2004). Reflection of random waves propagating over rectangular submerged non-porous breakwaters, Journal of Korea Water Resources Association, 37(9):729-736 (in Korean)..

Jung, J.-S., Kang, K.-Y., Cho, Y.-S. (2007). Analysis of multi-directional random waves propagating over multi arrayed impermeable submerged breakwater, Journal of Korean Society of Coastal and Ocean Engineers, 19(1):29-37 (in Korean)..

Kim, D.S., Lee, K.H., Yoo, H.S., Kim, C.H., Son, B.K. (2004). A study of the wave control characteristics of the permeable submerged breakwater using VOF method in irregular wave fields, Journal of Korean Society of Coastal and Ocean Engineers, 16(3):121-129 (in Korean)..

Lee, J.. (2005). Numerical investigation of wave interaction with a floating breakwater, Ph.D. Dissertation,. Yonsei University.

Lee, J.I., Kim, Y.T., Cho, Y.-S. (2003). Laboratory experiments on reflection of regular waves due to submerged breakwaters, Journal of Korean Society of Coastal and Ocean Engineers, 15(3):167-175 (in Korean)..

Lin, P. (2004). A numerical study of solitary wave interaction with rectangular obstacles, Coastal Engineering, 51(1):35-51.

Lin, P. (2006). A multiple-layer σ-coordinate model for simulation of wave-structure interaction, Computers & Fluids, 35(2):147-167.

Madsen, O.S., Mei, C.C. (1969). The transformation of a solitary wave over an uneven bottom, Journal of Fluid Mechanics, 39(4):781-791.

McCartney, B.L. (1985). Floating breakwater design, Journal of Waterway Port Coastal and Ocean Engineering, 111(2):304-318.

Park, S.H., Lee, S.O., Jung, T.H., Cho, Y.-S. (2007). Experimental study on reduction of rup-up height of sloping breakwater due to submerged structure, Journal of the Korean Society of Hazard Mitigation, 7(5):187-197 (in Korean)..

Seabra-Santos, F.J., Renouard, D.P., Temperville, A.M. (1987). Numerical and experimental study of the transformation of a solitary wave over a shelf or isolated obstacle, Journal of Fluid Mechanics, 176, 117-134.

Shin, C.H., Yoon, S.B. (2017). Improvement of wave generation for SWASH model using relaxation method, Journal of Korean Society of Coastal and Ocean Engineers, 29(4):169-179 (in Korean)..

Shin, C.H., Yoon, S.B. (2018). A numerical study on flow in porous structure using non-hydrostatic model, Journal of Korean Society of Coastal and Ocean Engineers, 30(3):114-122 (in Korean)..

Smit, P., Zijlema, M., Stelling, G. (2013). Depth-induced wave breaking in a non-hydrostatic, near-shore wave model, Coastal Engineering, 76, 1-16.

Stelling, G., Zijlema, M. (2003). An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation, Int. J. Numer. Meth Fluids, 43, 1-23.

Stelling, G.S., Duinmeijer, S.P.A. (2003). A staggered conservative scheme for every froude number in rapidly varied shallow water flows, Int. J. Numer. Meth Fluids, 43, 1329-1354.

Sutko, A.A., Haden, E.L. (1974). The Effect of Surge, Heave and Pitch on the Performance of a Floating Breakwter, Floating Breakwaters Conference Papers, University of Rhode Island, Marine Technical Report Series, 24, 21-39.

Synolakis, C.E.. (1986). The Runup of Long Waves, Ph.D. Thesis,. California Institute of Technology; Pasadena California: 91125: 228.

Synolakis, C.E. (1987). The runup of solitary waves, Journal of Fluid Mechanics, 185, 523-545.

Tang, C.J., Chang, J.H. (1998). Flow separation during solitary wave passing over submerged obstacle, Journal of Hydraulic Engineering, 124(7):742-749.

Wang, K.-H. (1993). Diffraction of solitary waves by breakwaters, Journal of Waterway Port Coastal and Ocean Engineering, 119(1):49-69.

Wang, J., He, G., You, R., Liu, P. (2018). Numerical study on interaction of a solitary wave with the submerged obstacle, Ocean Engineering, 158, 1-14.

Western Canada Hydraulic Laboratories Ltd. (1981). Development of a Manual for the Design of Floating Breakwaters. Department of Fisheries and Oceans, Small Craft Harbours Branch.

Yang, W.S., Cho, W.C., Park, W.S. (2001). Control of wave screening performance of floating breakwaters, Journal of Korean Society of Coastal and Ocean Engineers, 13(3):230-236 (in Korean)..

Yoon, J.S., Lee, M.K., Jung, K.H. (2005). Analysis of flow and turbulence structure for rectangular floating breakwater, Journal of the Korean Society of Civil Engineers B, 25(5B):375-383 (in Korean)..

Yoon, J.S., Son, H.J., Chun, S.Y., Cho, Y.-S. (2010). Experimental study on hydraulic characteristics and vorticity interactions of floating breakwaters, Journal of The Korean Society of Hazard Mitigation, 10(6):175-183 (in Korean)..

Zhuang, F., Lee, J.J. (1997). A viscous rotational model for wave overtopping over marine structure, In Coastal Engineering, 1996, 2178-2191.

Zijlema, M., Stelling, G.S. (2005). Further experiences with computing non-hydrostatic free-surface flows involving water waves, Int. J. Numer. Meth Fluids, 48, 169-197.

Zijlema, M., Stelling, G.S. (2008). Efficient computation of surf zone waves using the nonlinear shallow water equations with non-hydrostatic pressure, Coastal Engineering, 55, 780-790.

Zijlema, M., Stelling, G., Smit, P. (2011). SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters, Coastal Engineering, 58, 992-1012.