요약기존 케이슨방파제의 전면 또는 후면에 추가로 케이슨을 설치하여 구조물의 안정성을 향상시키기 위한 설계 및 시공사례가 보고되고 있다. 본 연구에서는 상용프로그램인 ANSYS AQWA를 이용하여 신규 케이슨이 추가로 설치되는 경우 입사하는 파랑과 케이슨들간의 상호작용 영향에 의해 개별 케이슨에 작용하는 파력 특성을 분석하였다. 앞뒤 케이슨간의 간격변화에 따른 개별 케이슨에 작용하는 파력 특성을 주파수영역에서 수치해석을 수행하였다. 그리고 특이한 파력분포 특성이 발생되는 주파수에 대해서는 불규칙파 조건에서의 시간영역 수치해석을 통해 개별 케이슨에 작용하는 동적파력 특성을 면밀하게 검토하였다.
AbstractThe design and the construction were carried out by installing new caissons on the back or the front of existing caissons to increase the structural stability of caisson breakwaters. In this study, we used the ANSYS AQWA program to analyze the wave forces acting on individual caissons according to the effects of wave-structure interaction when new caissons were additionally installed on existing caisson breakwaters. The wave force characteristics acting on the individual caisson were analyzed according to the distance among caissons in frequency domain analysis. In addition, the dynamic wave force characteristics were closely examined on the basis of the frequency at which the unusual distribution of wave forces occurs in irregular wave conditions using time domain analysis.
1. 서 론지구온난화로 해수면이 상승함에 따라 기존에 설치된 케이슨방파제의 안정성에 문제가 발생되고 있다. 이를 해결하기 위해 기존 케이슨방파제의 전면 또는 후면에 추가로 케이슨을 설치하여 안정성을 향상시키기 위한 설계 및 시공사례가 보고되고 있으나, 현재 이러한 설계에 대한 기준이 없어 설계자의 판단에 따라 다양하게 진행되고 있다. 따라서 기존 케이슨방파제의 안정성을 향상시키기 위해 추가로 케이슨이 설치될 경우 구조물에 작용하는 파력 특성 및 주요 고려사항 등에 대한 데이터 확보가 필요하다(Park et al., 2022).
주파수영역 수치해석으로는 다수의 원형 케이슨으로 구성된 기존 방파제 후면에 신규 원형 케이슨이 추가로 설치될 경우 입사하는 파랑과 원형 케이슨간의 상호작용 영향에 따른 개별 원형 케이슨에 작용하는 파력을 고유함수전개법(Eigenfunction expansion method)을 이용하여 산출하였다(Park, 2019, 2020). 사각형 케이슨과 케이슨 사이에 유체가 존재하는 경우 특정 주기에서 공진으로 유체가 상하로 크게 진동하여 구조물에 작용하는 파력이 과도하게 산출되는 문제를 해결하기 위해 ANSYS AQWA에서 제공되는 감쇠존(Damping zone) 효과를 고려하여 개별 케이슨에 작용하는 파력 특성이 주파수 영역 수치해석을 통해 분석되었다(Park et al., 2022).
시간영역 수치해석으로는 비선형 규칙파 조건에서 입사하는 파랑과 사각형 케이슨 구조물간의 상호작용 영향에 따른 개별 케이슨에 작용하는 파력 특성을 Park(2021)은 상용 프로그램인 ANSYS AQWA를 이용하여 분석하였다. 수치해석 결과 전면 케이슨에 작용하는 파력과 후면 케이슨에 작용하는 파력이 서로 반대 방향으로 작용하는 것을 확인할 수 있었다.
케이슨방파제의 설계는 항만 및 어항 설계기준·해설에서 제시하는 활동 및 전도에 대한 안전율을 만족하도록 정적 수치 해석을 통해 수행되고 있다. 하지만 실제 해양에 설치되는 케이슨방파제는 시간에 따른 동적 파랑의 영향을 받고 있어 시간에 따른 구조물의 동적 거동 평가를 통한 데이터 확보가 필요하다. 따라서 본 연구에서는 케이슨들에 의해 둘러싸인 유체영역에 ANSYS AQWA에서 제공되는 감쇠존 효과를 고려하여 개별 케이슨에 작용하는 파력 특성을 주파수영역 수치 해석을 통해 면밀하게 분석한 Park et al.(2022)의 연구내용 중에서 입사하는 파랑과 케이슨간의 상호작용 효과가 가장 크게 발생한 Dual 4 케이스에 대한 시간영역 수치해석을 수행하였다. 우선 공진이 발생할 수 있는 유체영역에 ANSYS AQWA의 감쇠존 적용 여부에 따른 주파수영역 수치해석을 통해 개별 케이슨에 작용하는 파력 분포 특성을 앞뒤 케이슨 간의 거리변화에 따라 검토하였다. 그리고 케이슨의 구조적 안정성에 큰 영향을 줄 수 있는 특정 주기(주파수)들에 대해서는 입사하는 파랑을 불규칙파 조건(JONSWAP Spectrum)으로 설정한 시간이력 수치해석을 통해 구조물에 작용하는 파력 작용 패턴 및 구조물의 동적 응답 특성을 상세하게 분석하였다.
2. 수치해석 조건 설정포텐셜이론 기반의 수치해석에서는 점성유동(Viscous flow)의 영향이 고려되지 못해 구조물에 작용하는 파력이 과도하게 평가되는 경우가 있는데, 이러한 문제를 해결하기 위해 구조물들에 의해 둘러싸인 유체영역에 감쇠존(Damping zone) 영향을 고려한 수치해석들이 Chen(2005), Fournier et al.(2006), Pauw et al.(2007), Bunnik et al.(2009), Watai et al.(2015), Ganesan T. and Sen(2016), Chen et al.(2021)에 의해 수행되었다. ANSYS AQWA도 인접한 구조물에 의해 둘러싸인 유체영역에서 비정상적인 공진으로 구조물에 작용하는 하중이 과도하게 평가되는 것을 방지하기 위해 식(1)와 같이 공진이 발생되는 유체영역에 감쇠 자유수면 경계조건을 비선형 시간영역 방정식에 적용할 수 있다.
여기서, ω는 파주파수(Wave frequency), g는 중력가속도, αd는 감쇠계수(Damping factor), f1는 구조물간의 간격과 관련된 함수, Φ는 속도 포텐셜이다.
상용프로그램인 ANSYS AQWA를 이용하여 사각형 케이슨 추가 설치에 따른 입사하는 파랑과 케이슨간의 상호작용 영향을 분석하기 위해 Fig. 1과 같이 구조물이 설치된다고 가정하였다. 본 연구에서는 추가로 설치되는 케이슨과 기존 케이슨간의 앞뒤 설치간격에 따른 영향을 집중적으로 검토하기 위해 좌우에 설치된 케이슨의 길이는 추가로 설치되는 케이슨의 길이보다 8배 정도 크게 설정하였고, 좌우 케이슨간의 간격은 항만 및 어항공사 표준시방서에서 케이슨 거치 허용 오차가 5천톤 이상의 경우 150 mm이므로 기존에 설치된 케이슨들은 이 기준을 준용하여 설치되었다고 판단하여 이를 적용하였다. 수치해석에서 수심은 10 m로 고정하였으며 개별 케이슨은 가로 7.5 m, 세로 10 m, 높이 11.3 m이고, 개별 케이슨에 작용하는 파력 특성 분석이 주목적이므로 사석 마운드 및 케이슨들은 강체거동을 하고 콘크리트(단위중량 2.3 ton, 압축강도 41 MPa)로만 구성된다고 가정하였다. Table 1에 나타낸 것처럼 추가로 설치되는 케이슨이 기존 케이슨에 매우 근접하게 설치되는 조건을 반영하기 위해 앞뒤 케이슨간의 거리(GW)를 150 mm로 설정하였고, 기존 케이슨의 안정성 향상을 위해 설치되는 토우 길이만큼 이격된 상태에서 추가 케이슨이 설치되는 조건을 반영하기 위해 앞뒤 간의 거리(GW)를 최대 1,500 mm로 설정하였다. ANSYS AQWA(2022R1 64bit)는 구조물 요소 개수에 제한(최대 60,000 절점, 40,000 요소)이 있어 사석 마운드와 길이가 긴 좌우 케이슨은 최대 요소 사이즈를 3.0 m, 개별 케이슨은 0.4 m, 그리고 감쇠존은 앞뒤 케이슨의 길이에 따라 GW150은 0.06 m, GW750은 0.15 m, GW1500은 0.2 m로 설정하여 최대 요소 개수 제한 조건에 맞게 조절하여 수치해석을 수행하였다. 그리고 시간영역 수치해석에서 케이슨에 작용하는 파력은 케이슨과 사석마운드 하부에 Fixed 조인트를 추가하여 조인트에 작용하는 반력으로 산출하였다. 따라서 본 연구에서는 케이슨과 사석마운드 경계에서 발생하는 변위는 고려되지 않았다.
3. 수치해석 결과 및 고찰구조물과 구조물 사이 공간으로 입사하는 파랑이 들어오게 되면 파랑의 회절(Wave diffraction)이 발생되고, 다수의 구조물이 존재하는 경우 한 구조물에서의 회절현상이 다른 구조물의 회절현상에도 영향을 주므로 인접한 구조물들 사이에서 발생되는 파와 구조물간의 상호작용 영향 평가는 매우 중요하다. 구조물과 구조물 사이 유체가 존재할 경우 특정 주기에서 유체가 공진하여 구조물에 작용하는 하중이 과도하게 산출되는 현상을 검토하기 위해 Fig. 2와 Table 2는 ANSYS AQWA에서 제공되는 감쇠존 옵션 적용 여부에 따른 개별 케이슨에 작용하는 파력 분포 특성을 나타내었다. Park et al.(2022)의 연구에 따르면 감쇠계수가 증가할수록 공진에 따른 구조물에 작용하는 하중이 감소하는 경향이 나타나므로 본 연구에서는 감쇠계수를 1.0으로 설정하여 감쇠효과를 최대화하였다. Fig. 2에서 가로축은 입사하는 파랑의 주기를 나타내고 있으며, 세로축을 케이슨에 작용하는 파력을 입사하는 파랑의 진폭(= 입사파 파고(H)/2)으로 나눈 값이다. 공진이 발생되는 주기 부근에서만 감쇠계수 영향으로 구조물에 작용하는 파력이 감소하고 앞뒤 케이슨간의 간격이 멀어질수록 최대 감소율이 높게 나타났다. 특이한 점은 D-1500의 경우에는 최대 피크파력 발생 주기가 감쇠존 적용 전에는 14.5초 부근이였으나 감쇠존 적용 후에는 15.0초 부근으로 주기 변화가 뚜렷하게 발생하였다.
Fig. 3은 기존 케이슨만 설치된 상황을 Single 조건으로 설정하여 파력을 계산하고 다시 Dual 케이스에서 감쇠계수가 1.0의 경우 개별 케이슨에 작용하는 파력을 Single 조건에 작용하는 파력으로 나눈 비율을 보여주고 있다. Fig. 3에서 비율이 1.0 이상의 경우는 기존 케이슨에 작용하는 파력보다 높은 파력의 영향을 받는 조건을 의미한다. 전체적으로 기존 케이슨 전면 또는 후면에 추가로 케이슨이 설치되는 경우 앞뒤 케이슨간의 간격 변화에 따라 구조물에 작용하는 파력 분포 패턴에 일정한 규칙성 없이 다양한 형태가 나타나는 것을 알 수 있다. 또한 특정 주기부근에서는 Dual 케이스에 작용하는 파력이 Single 케이스보다 상당히 높게 발생되어 신규 케이슨을 추가로 설치하는 것이 기존 케이슨방파제의 안정성을 악화시키는 것으로 나타났다.
케이슨 설계시 구조물에 작용하는 외력은 항만 및 어항설계기준의 고다식으로 산출되는 직립벽에 작용하는 최대파력 및 양압력을 표준으로 사용하고 있다. 초기 케이슨 방파제 설계 시에는 일렬로 설치되는 케이슨에 작용하는 외력에 대해서만 검토되기 때문에 항만 및 어항설계기준을 적용할 수 있다. 하지만 기존 케이슨의 안정성을 향상시키기 위해 추가로 케이슨을 설치하는 경우에는 전면 케이슨에 작용하는 파력과 후면 케이슨에 작용하는 파력의 크기가 다르고, 입사하는 파랑에 의해 앞뒤 케이슨간의 동적 거동이 상이할 수 있어 항만 및 어항설계기준의 고다식 적용에는 다소 한계가 있다. 또한 기존 케이슨과 추가로 설치되는 케이슨간의 상치 콘크리트를 개별로 설치할 것인가 아니면 기존 케이슨의 상치 콘크리트를 철거하고 추가로 설치되는 케이슨의 상치콘크리트와 일체로 설치할 것인가에 대한 검토도 필요하다. 따라서 본 연구에서는 이 부분에 판단 근거를 제공하고자 시간이력 수치 해석을 통해 전면 케이슨과 후면 케이슨에 작용하는 동적 파력 특성을 분석하였다. Fig. 4~8은 주파수영역 수치해석에서 피크파력이 발생된 주기 7.0초, 9.0초, 15초 외 11.0초, 13.0초를 불규칙파(JONSWAP Spectrum)의 첨두주기(Peak period)로 설정하고 JONSWAP spectrum의 첨예도 계수(Peakedness parameter, γ)가 3.3이고 유의파고(Hs)가 8.0 m인 시간이력 수치해석 결과(3,600초 동안)를 보여주고 있다. 이때 각 케이스 별 파력의 절대값이 가장 높게 발생된 시간에서의 동적 거동을 기존 케이슨만 존재하는 Single 케이스와 비교하기 위해 파력의 절대값이 발생된 시점 전후로 30초를 선택하여 총 60초 구간에 대해 상세하게 비교하였다. 또한 시간에 따른 입사 파랑과 구조물에 작용하는 파력의 동적 상관관계를 검토하기 위해 전면 케이슨의 해수면과 접하는 지점에서의 파랑 높이(Wave elevation)를 산출하여 같이 나타내었다. Table 3~7은 입사하는 불규칙파 3,600초 동안 케이슨에 작용하는 파력의 최대 및 최소값과 발생된 시점에서 Zero-crossing 법을 통해 산출된 파랑 주기(T) 및 파랑 높이(A)를 보여주고 있다. Zero-crossing 법은 파랑 높이가 음에서 양으로 바뀌는 지점인 Zero-crossing을 이용하여 각 Zero-crossing 사이에 있는 파고와 파장을 토대로 입사파랑 정보를 분석하는 방법을 의미한다. 또한, 전면과 후면 케이슨에 작용하는 파력값을 Single 조건의 파력값으로 나눈비(Front/Single, Rear/Single)와 후면 케이슨에 작용하는 파력값을 전면 케이슨에 작용하는 파력값으로 나눈 비(Rear/Front)를 같이 나타내었다.
Table 3의 불규칙파 첨두주기 7.0초의 경우 Single 케이스와 D-750 케이스는 입사파의 최대 파고 발생시점인 1,276.6초(T = 6.167초, A = 7.689 m) 부근에서 케이슨에 작용하는 파력이 최대값을 보이고 있으나 그 외 케이스에서는 최대 및 최소 파력값이 서로 다른 시점에서 발생하였다. D-150 케이스의 경우에는 전면 케이슨과 후면 케이슨의 최대 및 최소 파력값은 유사한 시점인 공진주기 7.0초 부근에서 발생하였고 전면 케이슨에 작용하는 파력은 Fig. 3에 나타낸 것과 같이 Single 케이스보다 약 12배 이상 큰 값을 가지는 것을 확인할 수 있었다. 검토된 Single 케이스와 모든 Dual 케이스에 대해 파력의 최대 및 최소값이 주기 6.1초와 7.1초 사이에서 나타나 주로 입사파랑의 첨두주기 부근이지만, 파랑의 높이(A)는 서로 차이가 크게 발생하여 케이스별로 연관성이 없는 것으로 나타났다. Fig. 4의 개별 케이슨에 작용하는 동적 파력은 케이스별로 매우 큰 차이를 보이고 있으며 비선형 파랑 조건을 비교한 Park(2021)의 결과와 유사하게 전면 케이슨에 작용하는 파력과 후면 케이슨에 작용하는 파력이 서로 반대 방향으로 작용하기도 하고 입사하는 불규칙 파랑조건에 따라 같은 방향으로 작용하기도 하는 패턴을 보였다. 명확한 것은 동일한 불규칙파가 구조물에 입사하더라도 파와 구조물간의 상호작용으로 Single 케이스와 Dual 케이스의 동적 파력 특성은 서로 다르다는 것이다.
Table 4의 불규칙파 첨두주기 9.0초의 경우 첨두주기 7.0초와 유사하게 Single 케이스와 D-750 케이스는 입사파의 최대 파고 발생시점인 1,641.3초(T = 7.932초, A = 7.690 m) 부근에서 케이슨에 작용하는 파력이 최대값을 보이고 있으나 그 외 케이스에서는 파력의 최대 및 최소값이 서로 다른 시점에서 발생하였다. D-150 케이스의 경우에는 전면 케이슨과 후면 케이슨에 작용하는 파력의 최대 및 최소값은 유사한 시점 에서 발생하였으나 전면 케이슨의 최대값 발생 주기에는 차이가 있었다. 또한 전면 케이슨과 후면 케이슨에 작용하는 파력의 최대 및 최소값의 차이는 D-150에서가 가장 높게 나타났다. 특이한 점은 D-750의 경우 공진주기가 9.0초이므로 Dual 케이스 중에서 가장 높은 파력값을 가질 것으로 예상되었으나 D-150 케이스보다 낮게 나타났다. Fig. 5의 개별 케이슨에 작용하는 동적 파력도 케이스별로 작용 패턴에 매우 큰 차이를 보였으며 입사하는 불규칙 파랑조건에 따라 전면 및 후면 케이슨에 작용하는 파력은 같은 방향으로 작용하기도 하고 반대 방향으로 작용하기도 하여 일정한 규칙성이 없었다.
Table 5와 6의 불규칙파 첨두주기 11.0초와 13.0초의 경우 D-150 케이스와 D-750 케이스는 첨두주기가 길어짐에 따라 개별 케이슨에 작용하는 파력이 감소하는 경향을 보이고 있으나 D-1500 케이스는 반대로 증가하는 경향이 나타나 Fig. 3의 결과와 유사한 것을 알 수 있다. Fig. 6과 7에서 검토된 시간영역 3,600초 동안 D-150 케이스와 1-1500 케이스의 전면 및 후면 케이슨에 작용하는 파력값에 큰 차이가 발생되었으나 D-750 케이스는 두 파력값의 차이가 미소하게 나타났다.
Table 7의 불규칙파 첨두주기 15.0초의 경우 D-1500 케이스가 파력의 최대 및 최소값이 가장 높게 나타나고 있으나 공진주기인 15.0초보다 짧은 주기인 14.245초에서 전면 케이슨의 최대 및 최소 파력이 발생하였으며 Fig. 3의 결과에서와 같이 Single 케이스보다 5배 이상 큰 값을 가지는 것을 확인할 수 있었다. Dual 케이스의 경우 앞뒤 케이슨간의 거리 변화에 따라 최대 및 최소 파력값의 발생시점에 차이가 발생하고 이로 인해 주기(T) 및 파랑높이(A)도 서로 다르게 나타났다. 일반적으로 구조물에 작용하는 파력은 파고 높이에 비례적으로 증가하는데 Dual 케이스에서는 이러한 경향을 찾을 수가 없었다. 따라서 기존 케이슨의 전면 또는 후면에 추가로 신규 케이슨을 설치하여 구조물의 안정성을 향상시키기 위한 설계를 수행할 시에는 주파수영역 수치해석과 더불어 반드시 시간영역 수치해석을 수행할 필요가 있다. 또한 Fig. 8의 개별 케이슨에 작용하는 동적 파랑 특성에서 확인할 수 있듯이 전면 케이슨과 후면 케이슨의 동적 파랑 특성이 입사하는 불규칙 파랑조건에 따라 서로 다른 경향을 보이고 있으므로 기존 케이슨과 추가로 설치되는 케이슨간의 구조적 안전성을 확보하기 위해서는 전면 케이슨의 상치 콘크리트와 추가 설치되는 케이슨의 상치 콘크리트를 일체로 설치하는 방법 등을 통해 가능한 두 케이슨이 하나의 단일 구조물처럼 거동할 수 있는 방안 마련이 필요할 것으로 판단된다.
4. 결 과본 연구에서는 기존 케이슨의 전면 또는 후면에 추가로 케이슨이 설치될 경우 입사하는 파랑과 케이슨들간의 상호작용 영향에 의해 개별 케이슨에 작용하는 파력 특성을 상용프로그램인 ANSYS AQWA를 이용하여 주파수영역과 불규칙파 조건(JONSWAP spectrum)에서의 시간영역 해석을 통해 분석하였다. 특정 주기에서 유체가 공진하여 구조물에 작용하는 하중이 과도하게 산출되는 현상을 방지하기 위해 감쇠존을 적용하였을 경우에는 공진이 발생되는 주기 부근에서만 감쇠계수 영향으로 구조물에 작용하는 파력이 감소하고 앞뒤 케이슨간의 간격이 멀어질수록 최대 감소율이 높게 나타났다. Dual 케이스에서는 앞뒤 케이슨간의 간격 변화에 따라 구조물에 작용하는 파력 분포 패턴에 일정한 규칙성 없이 다양한 형태가 나타났으며, 특정 주기부근에서는 Single 케이스보다 상당히 높은 파력이 발생하여 케이슨방파제의 안정성이 악화되었다. Dual 케이스의 시간영역 수치해석에서 전면 케이슨에 작용하는 파력 패턴과 후면 케이슨에 작용하는 파력 패턴이 상이하고 입사하는 불규칙 파랑의 주기별로 파력 차이가 크게 발생하고 있어 기존 케이슨과 추가로 설치되는 케이슨 간의 구조적 안전성을 확보하기 위해서는 전면 케이슨의 상치 콘크리트와 추가 설치되는 케이슨의 상치 콘크리트를 일체로 설치하는 방법 등을 이용하여 가능한 두 케이슨이 하나의 구조물처럼 거동할 수 있도록 하는 방안 마련이 필요할 것으로 평가되었다. 본 연구에서는 신규 케이슨을 기존 케이슨 전면 또는 후면에 추가로 설치하여 보강하는 경우에 발생할 수 있는 문제점 및 주요 고려사항 등을 제시하였으며, 향후 수리모형실험을 통해 본 연구 결과와의 비교 및 검토가 수행되어야 할 것으로 판단된다.
감사의 글본 연구는 해양수산과학기술진흥원의 안전한 항만 구축 및 관리기술개발사업인 “재해안전항만구축기술개발(20180323)” 과제 및 ICT 기반 항만 인프라 스마트 재해 대응 기술개발 사업인 “항만 인프라 재해 및 노후화 대응 스마트 유지보수 기술개발(20210659)” 과제를 통해 수행된 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.
Fig. 4.Comparison of wave force between front and rear middle caisson with Tp = 7.0 sec and Hs = 8.0 m in time domain analysis. 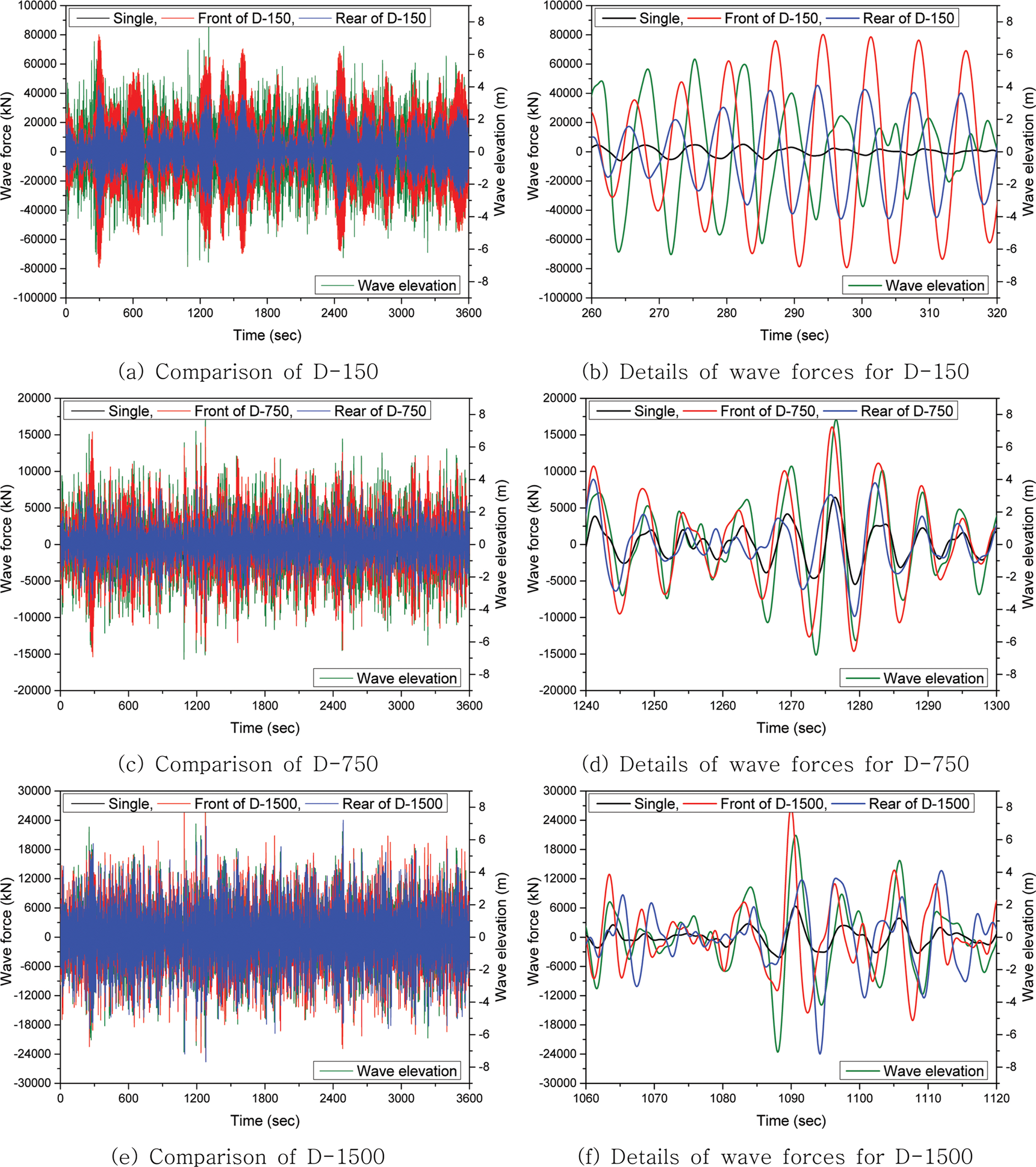
Fig. 5.Comparison of wave force between front and rear middle caisson with Tp = 9.0 sec and Hs = 8.0 m in time domain analysis. 
Fig. 6.Comparison of wave force between front and rear middle caisson with Tp = 11.0 sec and Hs = 8.0 m in time domain analysis. 
Fig. 7.Comparison of wave force between front and rear middle caisson with Tp = 13.0 sec and Hs = 8.0 m in time domain analysis. 
Fig. 8.Comparison of wave force between front and rear middle caisson with Tp = 15.0 sec and Hs = 8.0 m in time domain analysis. 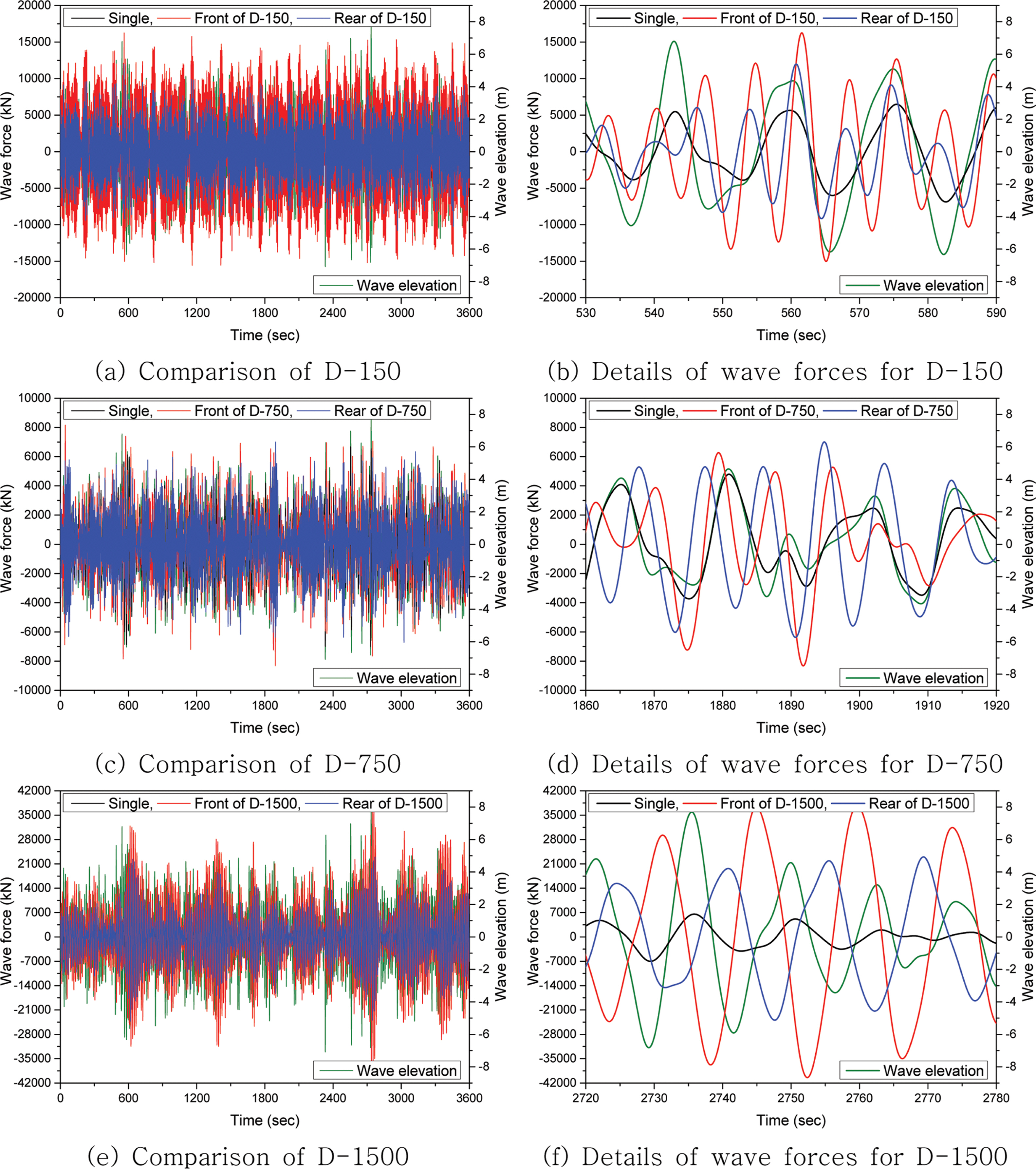
Table 1.Cases of numerical analysis
Table 2.Ratio (with damping/without damping) of wave force for dual case Table 3.Ratio of wave force on middle caisson with Tp = 7.0 sec, Hs = 8.0 m and γ =3.3 Table 4.Ratio of wave force on middle caisson with Tp = 9.0 sec, Hs = 8.0 m and γ =3.3 Table 5.Ratio of wave force on middle caisson with Tp = 11.0 sec, Hs = 8.0 m and γ =3.3 Table 6.Ratio of wave force on middle caisson with Tp = 13.0 sec, Hs = 8.0 m and γ =3.3 Table 7.Ratio of wave force on middle caisson with Tp = 15.0 sec, Hs = 8.0 m and γ =3.3 ReferencesBunnik, T., Pauw, W., Voogt, A.. (2009). Hydrodynamic analysis for side by side offloading, In 19th International Offshore and Polar Engineering Conference. Osaka, Japan.
Chen, X.B.. (2005). Hydrodynamic analysis for offshore LNG terminals, Proceeding of the 2nd International Workshop on Applied Offshore Hydrodynamics. Rio De Janeiro, Brazil.
Chen, M., Guo, H., Wang, R., Tao, R., Cheng, N (2021). Effect of gap resonance on the hydrodynamics and dynamics of a multi-module floating system with narrow gaps, Journal of Marine Science and Engineering, 9(11):1-29.
Fournier, J.R., Naciri, M., Chen, X.B.. (2006). Hydrodynamics of two side by side vessels experiments and numerical simulations, In 16th International Offshore and Polar Engineering Conference. San Francisco, California, USA.
Ganesan, T.S., Sen, D (2016). Time domain simulation of side by side floating bodies using a 3D numerical wave tank approach, Applied Ocean Research, 58, 189-217.
Pauw, W.H., Huijsmans, R.H.M., Voogt, A.. (2007). Advances in the hydrodynamics of side by side moored vessels, In 26th International Conference on Offshore Mechanics and Arctic Engineering. San Diego, California, USA: p 597-603.
Park, M.S (2019). Characteristics of wave forces by installation of new circular caisson on the back of old circular caisson, Journal of Korean Society of Coastal and Ocean Engineers, 31(6):395-402 (in Korean)..
Park, M.S (2020). Wave structure interaction by installation of new circular caissons on old circular caisson breakwater, Journal of Korean Society of Coastal and Ocean Engineers, 32(5):307-321 (in Korean)..
Park, M.S (2021). Interaction effect between caissons by installation of new caisson on existing caisson breakwater in second order stokes wave condition, Journal of Korean Society of Coastal and Ocean Engineers, 33(6):345-356 (in Korean)..
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||