1. 서 론
최근 태풍 국내 내습한 태풍 마이삭(2020년). 하이선(2020년), 힌남노(2022년) 등은 해안가 도로에 많은 월파를 발생시켰고, 이로 인하여 내측 시설물에 많은 피해가 발생하였다. 특히 해안 도로의 경우 배후지에 민가 등의 시설이 위치할 수 있어 월파 발생시 인명피해 및 재산피해가 발생할 수 있다. 국내의 경우 월파에 대비하기 위하여 일반적인 항만 구조물의 경우 설계파고에 대한 상대적인 마루높이, 배후 부지 특성 및 이용성 등을 고려한 평균월파량을 고려하여 마루높이를 산정하고 있다(MOF, 2016).
월파량 산정을 위한 다양한 연구가 수행되었고, 여전히 활발히 진행중이다. 그렇지만 유럽의 경우 van der Meer et al.(2018)이 제시한 EurOtop을 중심으로 월파량 산정기준이 정리되고 있는 것으로 보이며, 이를 이용하여 항만구조물 설계에도 적용되고 있다. EurOtop은 2007년 CLASH프로젝트(Crest Level Assessment of coastal Structures by full-scale monitoring, neural network prediction and Hazard analysis on permissible wave overtopping, De Rouck et al., 2002; Verhaeghe, 2005; van der Meer et al., 2009)의 성과물로서 이후 2018년 최종 개정판이 발간되어 여러 분야에서 활용되고 있다. 현재 EurOtop은 기존 유럽의 여러 나라에서 적용되는 월파량 산정기준을 통합한 연구성과로 볼 수 있다. 당초 2007년 EurOtop 발간시에는 상대적으로 심해 조건에 대한 결과를 제시하였으나, 2018년 개정시에는 수리모형실험(Altomare et al., 2016)을 추가하여 천해에서도 적용할 수 있도록 식이 개선되어 있다.
본 연구에서 수행한 단면수리모형실험에서는 일반적인 항만구조물이 아닌 해안도로에서의 월파량을 계측하였다. 특히 해안도로 전면의 수심을 단면수로에 재현하여 호안도로 배후 부지에서의 월파량을 최대한 정확하게 계측하고자 하였다. 이는 해안 도로의 경우 일반적인 항만시설물은 아니지만 배후 부지의 이용성 및 안정성을 위하여 월파에 대한 예경보 발령 등의 안전 대책이 필요하기 때문이다. 이와 관련하여 해양수산부에서는 시범적으로 해안도로와 인접한 해안주택가에서의 월파예측 모델 기반 경보시스템 개발에 대한 연구를 추진하고 있다. 금번 실험은 위 연구의 일부로서 현장에서 계측된 파랑관측자료, CCTV영상 자료와 금번에 수행한 수치해석과 실험 데이터의 구축을 통해 대상해역에서의 월파량 예측하는 데 목적이 있다(MOF, 2021).
금번 연구에서는 단면수리모형실험을 통하여 다양한 조위 및 파랑 조건에 따른 월파량을 계측하였고, 동일 조건을 대상으로 OLAFoam을 활용한 수치모델링을 통하여 실험결과와 비교하였다. 또한 EurOtop과의 비교를 통하여 OLAFoam의 활용도 및 EurOtop적용시 고려할 사항 등을 제시하고자 한다.
2. 수리 및 수치 모형실험
2.1 수리모형실험
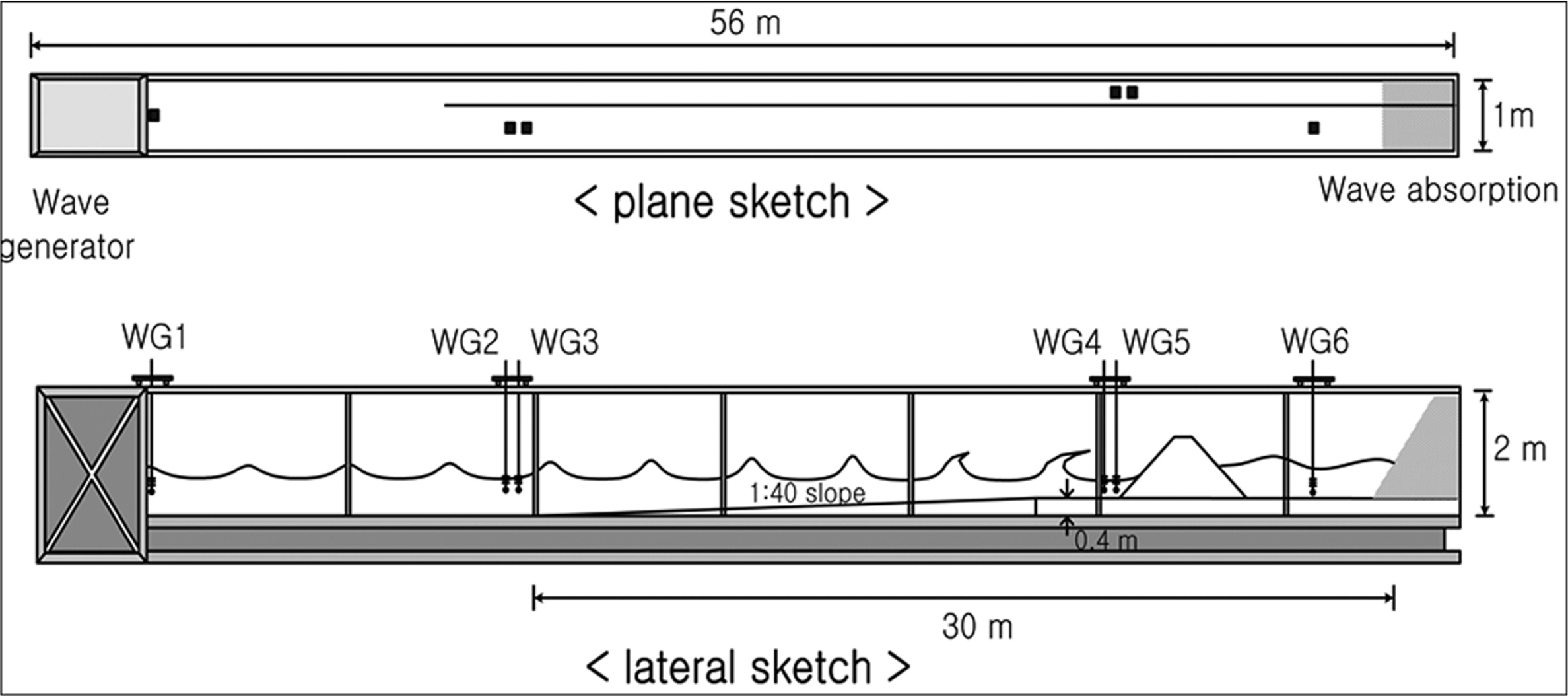
수리모형실험은 한국건설기술연구원의 폭 1.0 m, 높이 2.0 m, 길이 56 m의 수로에서 수행되었으며, 단면수로에는 전기서보피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다(Fig. 1 참조). 그리고 단면수로의 폭 1.0 m는 폭 0.6 m와 폭 0.4 m로 분할되어 있으며, 분할된 수로에서 실험 모형은 폭 0.6 m의 수로에 설치하여 제반 자료를 취득하고, 폭 0.4 m의 수로에서는 입사파의 설정 및 보정을 수행하였다. 또한 흡수식 조파를 실시하여 구조물 및 조파기에서 재반사를 최소화하였다.
단면수로는 전면 30 m 구간을 강화유리로 처리하여 실험 장면 관찰이 용이하도록 되어있으며, 수로 양쪽 끝 부분에는 여러 겹의 다공성 구조로 형성된 소파장치가 설치되어 있다. Fig. 1에서 1번 파고계는 흡수식 조파, 2번과 3번 파고계는 반사계수 및 입사파 측정, 4번과 5번 파고계는 협수로에서 호안도로 위치에서의 입사파 계측에 이용되었다. 2번과 3번, 4번과 5번의 파고계 간격은 2점법을 적용하였으며, 입사파 주기 조건에 따라 적절하게 조절하였다. 수로내에서 발생할 수 있는 반사파와 횡파 등을 제어하기 위하여 단면수로 양끝단에는 충분한 거리의 소파제가 설치되어 있으며(반사계수 10% 미만, 우측수로 끝단 소파제 수평길이 7 m), 흡수식 조파를 적용하였다.
2.2 수치실험
수치실험을 위하여 OpenFoam을 활용하였다(Jacobsen et al., 2012). OpenFoam은 GNU GPL(General Public License)을 기반으로 하는 공개 CFD(Computational Fluid Dynamics) 소스 코드로 전 세계의 다양한 분야의 많은 수치해석 관련 연구자들에 의해 지속적인 개발과 수정이 이루어져 왔다. 파랑의 조파 및 소파기능을 추가하여 개발된 OpenFOAM 라이브러리로는 Waves2Foam(Jacobsen et al., 2012), IHFoam(Higuera et al., 2013), OLAFoam(Higuera et al., 2015) 등이 있다. 금번 연구에서는 Higuera et al.(2015)에 의해 개발된 OLAFoam을 적용하였다. OLAFoam은 multi-paddle piston 방식의 조파기능을 재현하고, 조파와 반사파제어를 위한 감쇠영역에서 cutting-edge 기술을 이용하여 CFD 기반의 수치 계산에서 단점으로 지적되고 있는 계산시간을 절감할 수 있다. 이와 같은 OpenFoam은 국내에서도 많은 연구자들에 의해 활발히 활용되고 있다(Lee et al., 2016; Hwang et al., 2018; Lee et al., 2019).
비압축성유체의 혼상류해석에 대해 소스 코드가 공개된 OLAFoam은 유한체적 이산화법과 VOF법을 이용하며, 그의 지배방정식은 다음의 식(1)과 (2)에 나타내는 연속방정식과 운동량보존방정식으로 구성된다.
(2)
여기서 xi는 공간좌표, ρ는 밀도, ui는 속도벡터, p*는 Pseudodynamic 압력, Xj는 위치벡터, ϕ는 공극률, μeff는 μ + ρνturb이며, νturb 는 난류 동점성계수임. [CT]는 losure term으로 Englend 상수를 사용하면 다음의 식으로 주어진다. α, β는 Engelund(1953) 계수이며, D50 은 유효입경, KC는 Keulegan-Carpenter수로 T O u M D 50 ∅
2.3 실험조건
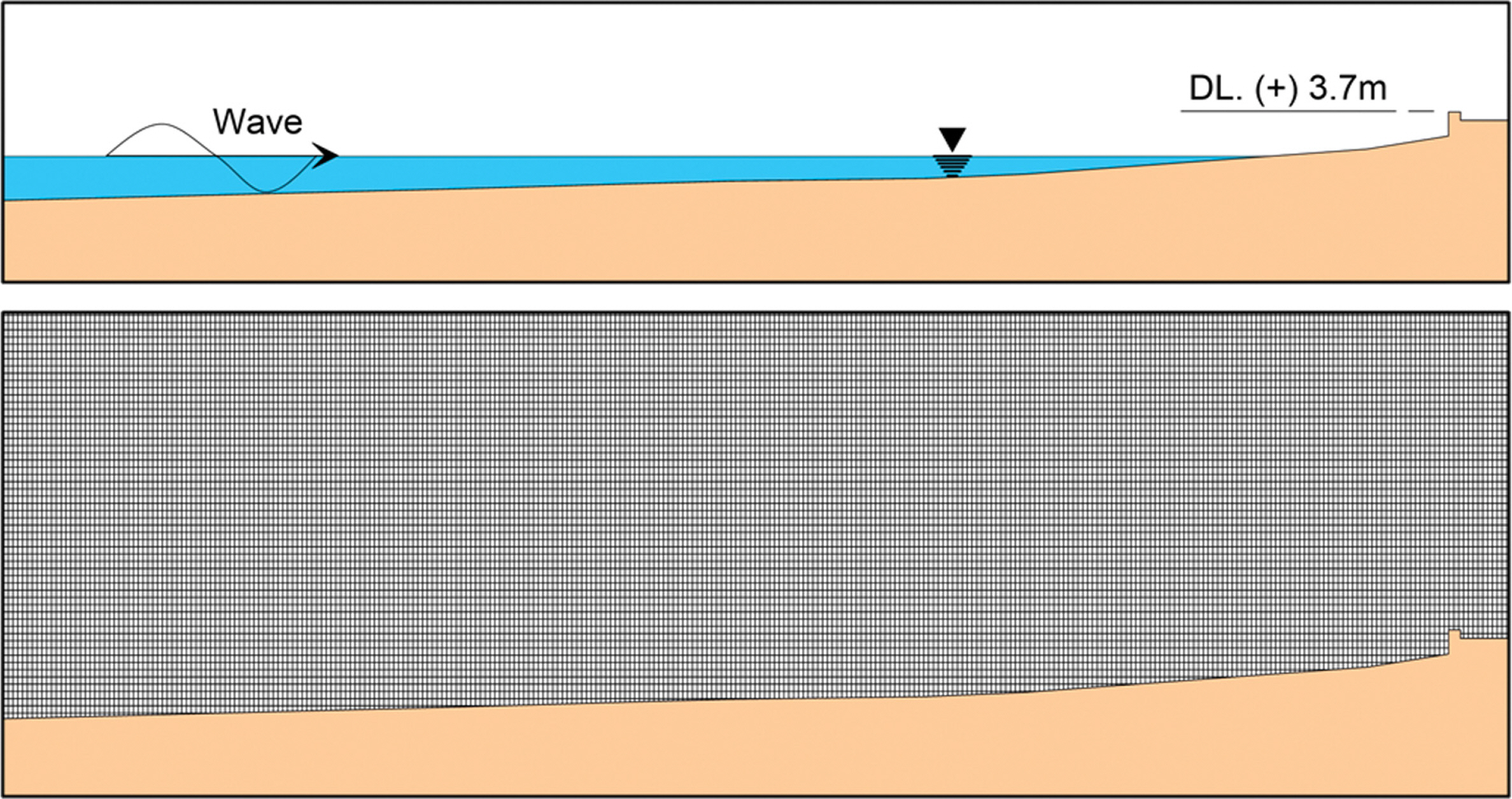
수리모형실험을 위하여 호안도로 전면 해역의 수심을 재현하기 위하여 수심측량을 실시하였고 Fig. 2와 같은 수심조건을 단면수로에 제작하였다. 실험에 적용된 축척은 1/10이며, Froude 상사법칙을 적용하여 실험조건을 축소하였다. 실험수심은 원형상 호안도로 전면해역 198.1 m 범위까지 재현하였다. 실제 해역의 경우 호안 전면에 암반지형과 자갈 사면이 존재하지만 모형수로에서는 고정상으로 재현하였다. 수심은 약최조저조위(App.LLW) DL(±)0.00 m를 기준으로 모형상 0.56 m에 해당한다.
OLAFoam을 이용한 수치해석을 위하여 Fig. 3과 같이 계산영역을 구성하였다. 수치파동수조의 길이는 1,380 m, 높이는 50 m, 격자간격은 dx = 0.5~1.00 m, dz = 0.5 m이며, 총 138,800개으로 계산영역을 구성하였다. 수리모형실험에서는 실험수로의 제작 범위 한계 등으로 인하여 호안도로 전면 해역을 원형상 198.1 m 재현하였으나, 수치해석에서는 상대적으로 넓은 영역(1,380 m)을 재현하였다. DL(±)0.00 m를 기준으로 수치해석 경계면에서의 수심은 원형상 20 m에 해당한다. 지형은 수리모형실험과 마찬가지로 불투과성 해저면 지형을 적용하였다. 금번 수치 모델링에 적용한 경계조건 등을 정리하면 Table 1과 같다.
2.4 실험 방법 및 결과 분석 방법
수치해석의 경우 Table 3에 제시 입사파랑 조건을 DL(±)0.00 m 기준 수심 20 m 지점에서 조파하여 해안도로로 입사하는 파랑을 분석하였다. 반면, 수리모형실험의 경우 상대적으로 깊은 수심 조건을 적용할 수 없으므로 Fig. 4와 같이 해안도로에서 원형상 약 200 m(모형상 20 m) 지점에서 파고를 계측하고 입사파랑으로 적용하였다. 수리모형실험과 수치해석의 비교를 위하여 수치해석의 경우 수리모형실험과 동일하게 해안도로에서 약 200 m 지점에서 입사파고를 계측하고, 이에 대한 월파량을 분석하였다.
실험 분석을 위하여 수치해석의 경우 각각의 실험파 조건에 대하여 300파를 조파한 후 입사파와 월파량을 분석하였고, 수리모형실험의 경우 500파를 조파한 후 파고 및 월파량을 분석하였다. 월파량은 모두 단위시간당 단위폭당 평균 월파량(q, m3 /s/m)으로 분석하였다.
3. 실험 결과
3.2 수치해석
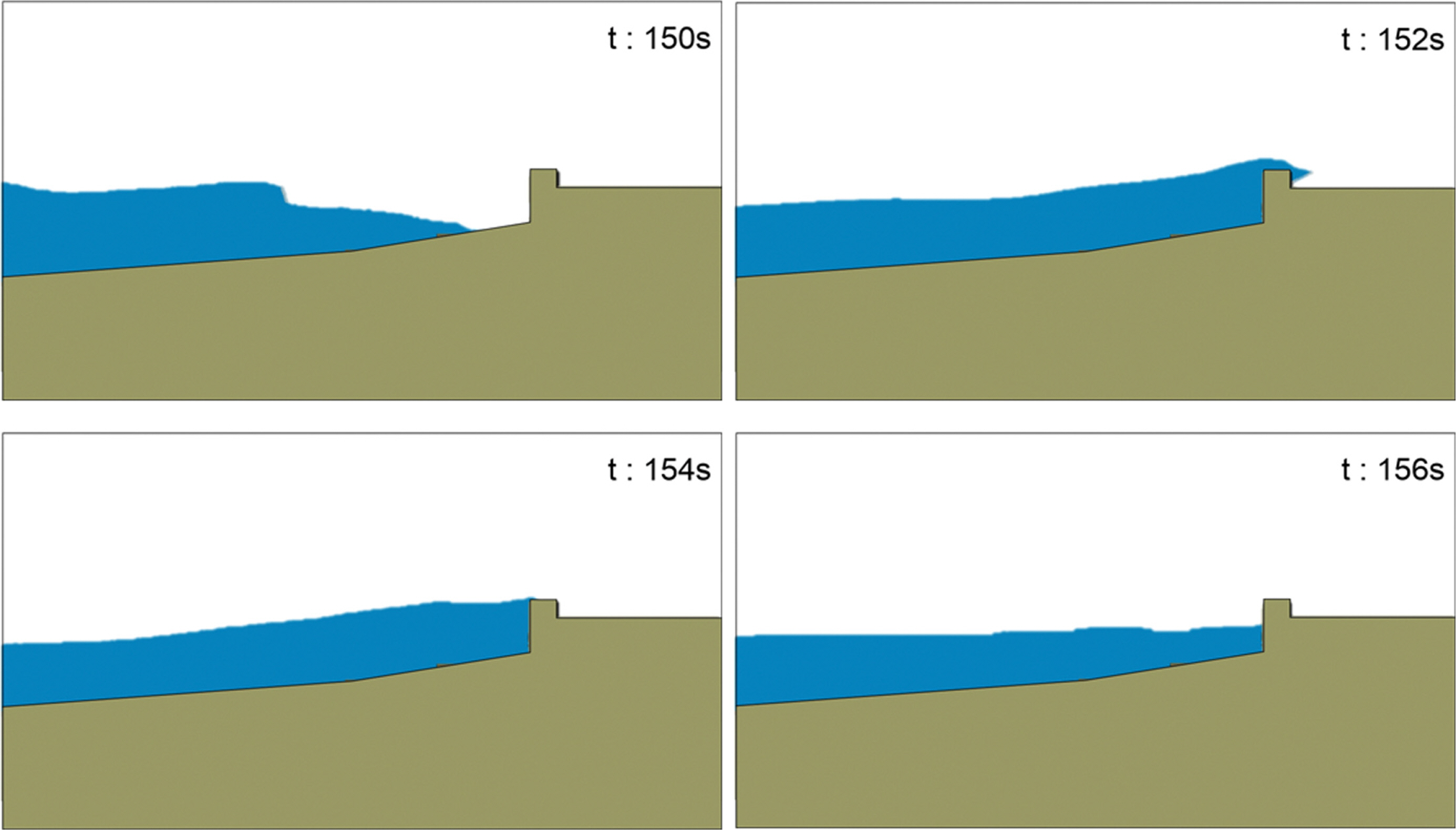
OLAFoam을 활용하여 해안도로에서의 월파량을 계측하였다. Fig. 6은 조위 DL(+)2.0 m 조건에서 Ts = 15 s, Hs = 2.5 m에 대한 월파 장면 스냅샷이다. 월파량 산정을 위하여 호안도로 배후지에 가상의 월파통을 설치하였다. 월파된 유체가 월파통의 자유수면에 영향을 미쳐 노이즈가 발생할 수 있다. 이때 자유수면에 발생된 노이즈는 LPF(Low Pass Filter)를 통해 최소화하였다(10 Hz 미만의 주파수 성분 제외).
3.3 결과 비교 및 분석
2018년 EurOtop에서는 직립식 구조물에 대하여 세 가지 조건으로 구분하여 평균월파량 산정식을 제시하고 있다. 첫 번째는 전빈(foreshore)의 영향이 없는 조건(식(3)), 즉 상대적으로 심해조건, 두 번째는 전면 경사면의 영향이 있는 조건이지만 쇄파 등은 없는 조건(식(4), 상대적으로 천해조건, 비충격파(non-impulsive) 조건, 쇄파 없이 월파만 발생하는 조건), 세 번째는 일부 쇄파가 발생하는 조건(식(5) 및 (6), 충격파(impulsive) 조건)이다. 특히 충격파 조건에서 상대여유고 Rc/Hmo = 1.35를 기준으로 식이 구분되어 있다.
- 전빈의 영향이 없는 직립식 구조물 평균 월파량 산정식
- 전빈의 영향을 고려한 직립식 구조물 평균 월파량 산정식: 비충격파조건
- 전빈의 영향을 고려한 직립식 구조물 평균 월파량 산정식: 충격파 조건
충격파와 피충격파 조건의 구분은 다음과 같다.
수리모형실험결과 분석에서 유의파고(Hs)는 Fig. 4의 파고계 위치에서 H1/3을 계측하여 분석하였다. 반면 식(3)~(7)의 EurOtop에 제시된 유의파고는 spectral wave height(Hm0)로서 수치해석을 통하여 계산된 설계파의 의미로 적용되고 있다. 상대적으로 심해에서는 Hm0와 H1/3이 거의 동일하지만 천해의 경우 차이가 있는 것으로 알려져 있다. 그렇지만 이에 대한 차이로 월파량에서도 차이가 발생한다는 실험결과는 아직 충분하지 않다고 알려져 있다(van der Meer et al., 2018). 이에 따라 본 연구에서는 Hm0와 H1/3를 구분하지 않고 동일한 값으로 적용하였다. 또한 식(5)~식(7)에 있어 파장 Lm-1, 심해파장을 의미하며L m - 1 , 0 = g T m - 1 , 0 2 2 π
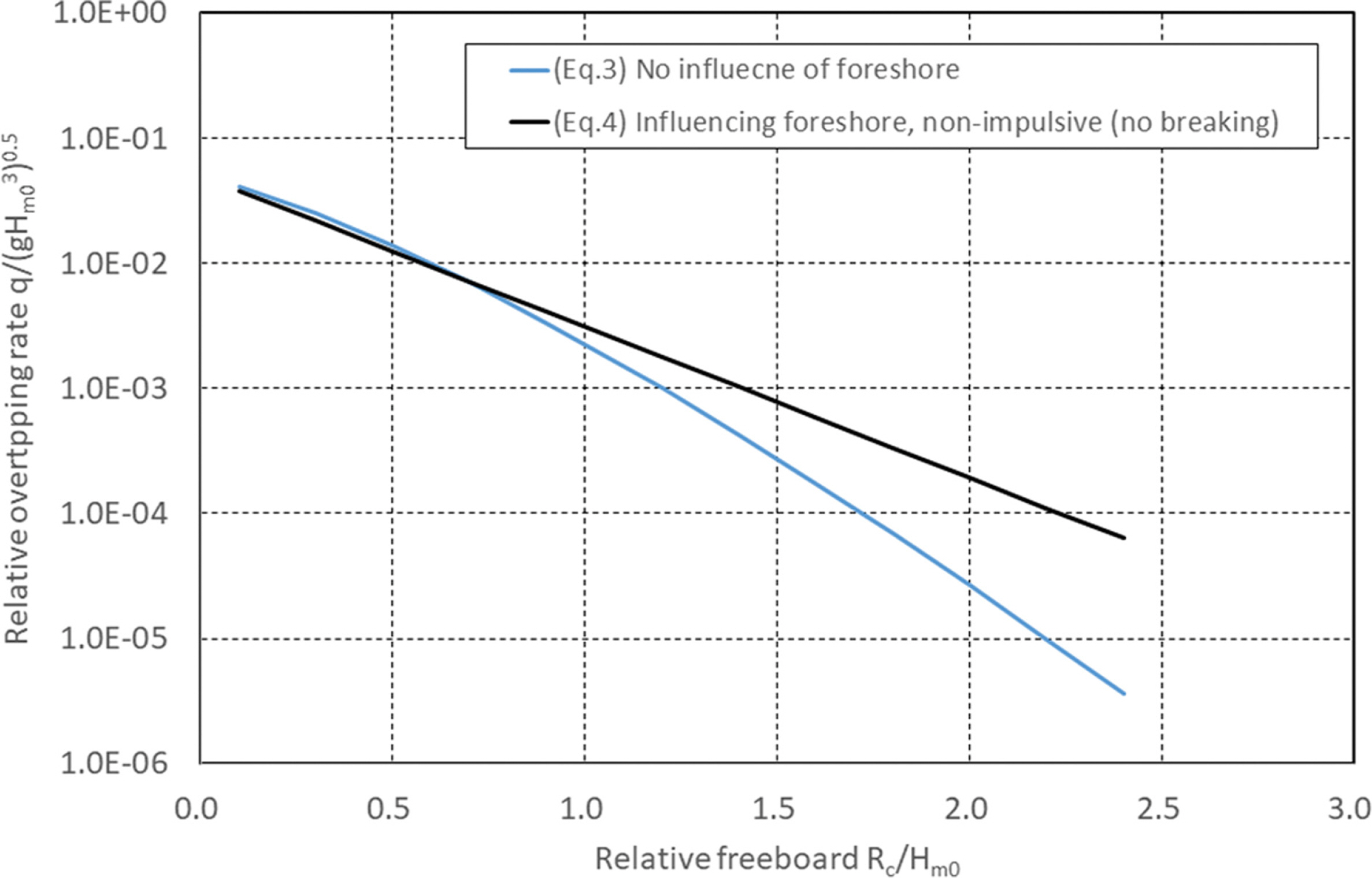
2007년 EurOtop에서는 직립제에 대한 월파량 산정식을 비충격파 조건과 충격파 조건으로 제시를 하였으나, 2018년 제안된 기준에서는 전면 경사면의 영향 유무, 월파 발생 유무 등 다양한 형태의 식을 제시하였다. Fig. 7은 비충격파 조건에서 전면 경사면의 영향 유무를 나타내는 식(3)과 식(4)에 대한 평균 월파량 비교이다. 상대적으로 상대마루높이가 낮은조건(Rc/Hmo < 0.7)에서는 두 식의 차이가 크지 않지만 상대 마루높이가 증가함에 따라 월파량 값에 차이가 발생함을 알 수 있다. Fig. 7 및 다음의 Fig. 8에서 x축은 상대여유고이며, y축은 단위폭당시간당 월파량(q)에 대한 입사파고의 무차원상대월파량이다.
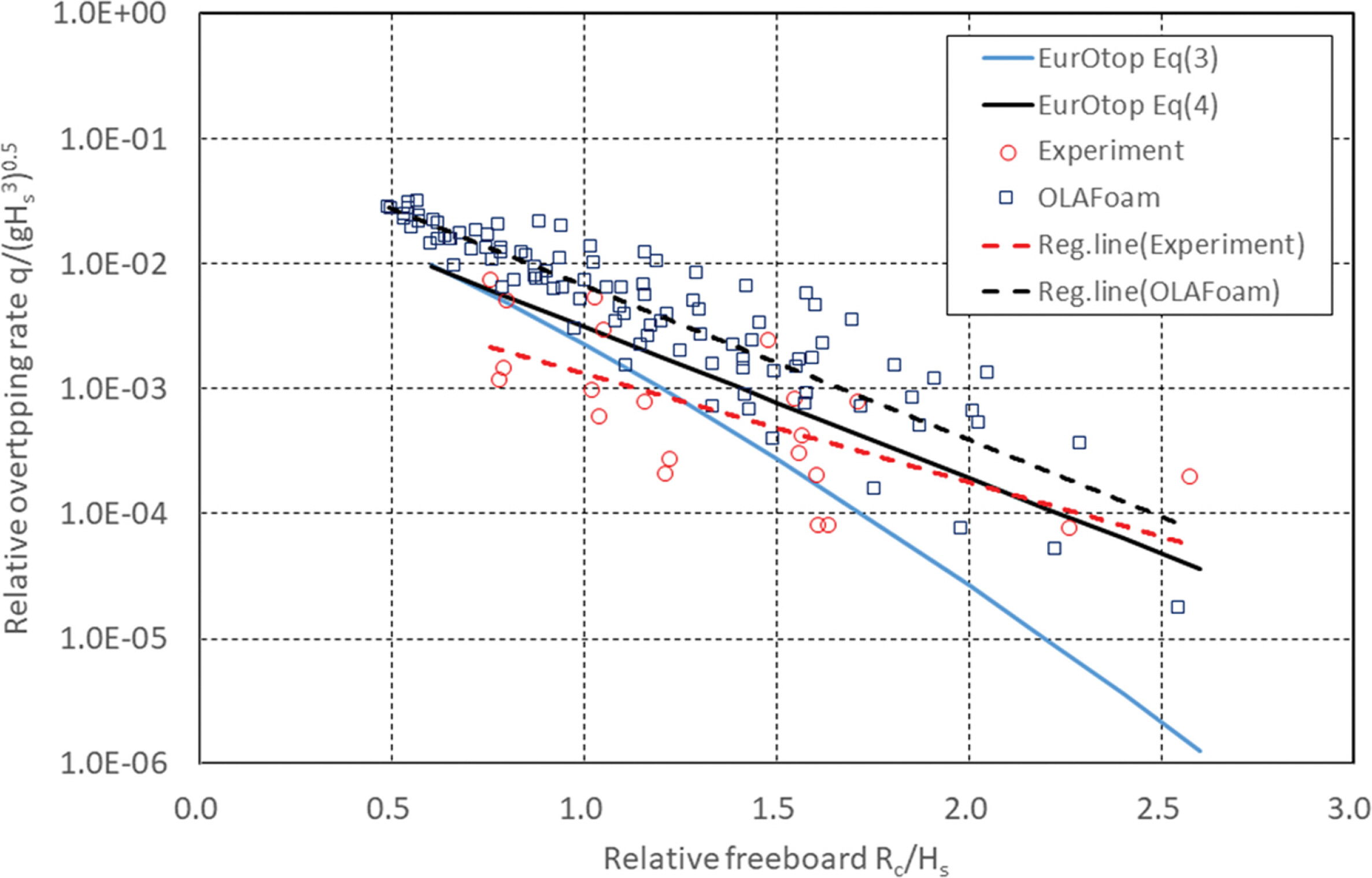
금번에 수행한 수치 및 수리 실험에 적용한 실험조건은 전빈의 영향을 받는 조건이며, 비충격파 조건에 해당한다. 그렇지만 결과 비교는 EurOtop에서 제시하고 있는 식(3)과 (4)와 모두 비교하였다. Fig. 8은 금번에 수행한 수리모형실험과 OLAFoam 및 EurOtop과의 무차원 평균월파량 비교이다. 전면 경사면의 영향을 고려한 EurOtop 식(4)의 월파량이 식(3)에 비하여 상대적으로 수리모형실험 및 수치실험와 유사하게 나타난 것을 알 수 있다. 수리모형실험과 OLAFom결과를 비교하면 상대적으로 OLAFoam의 결과가 크게 나타나는 것을 알 수 있다. 이와 같은 수치와 수리모형실험의 결과 차이는 입력 파랑 설정 조건, 지형 적용 범위 및 실험시간 등에 따라 발생할 수 있을 것으로 보인다. 또한 OLAFoam 및 수리모형실험 결과에 있어 동일 상대여유고 조건에서도 월파량의 편차가 발생하는 것을 알 수 있다. 이는 EurOtop에서 제시한 원데이터(raw data)에서도 나타나는 현상이다. EurOtop의경우 이와같은 데이터의 분산에 대하여 평균값을 적용하는 설계(mean value approach)과 표준편차를 고려하는 방법(design and assessment approach)으로 제안하고 있다.
4. 결 론
금번 연구에서는 해안도로를 대상구조물로 하여 외해에서 파랑 내습시 수리모형실험과 수치해석실험을 통하여 월파량을 계측하고 비교하였다. 특히 수리모형실험의 경우 해안도로 구조물 전면 해역의 수심을 단면수로에 제작하여 대상 해역에서 좀더 정확한 월파량이 계측될 수 있도록 하였다. 그리고 수리모형실험 및 수치실험 결과는 직립식 구조물에 대한 월파량 산정식(EurOtop)과 비교하였다. 특히 전면 경사면의 영향을 유무에 따른 평균월파량을 비교하였으며, 금번 연구를 통하여 다음의 결론을 도출할 수 있다.
(1) EurOtop의 적용에 있어 전면 경사면의 영향 유무에 따른 월파량의 차이는 크게 나타났으며, 구조물 설계시 이에 대하여 유의해야 할 것이다.
(2) 수치모델로 활용한 OLAFoam과 수리모형실험 결과를 비교하면 OLAFoam에 의한 월파량 값이 수리모형실험 결과 보다는 크게 예측된 것으로 나타났다. 그렇지만 이는 실험조건, 지형적용 범위, 실험시간 등의 차이로 발생한 것으로 유추할 수 있다.
금번 연구의 최종 목적은 다양한 입사파랑 조건에 대한 월파량 데이터를 구축하여 호안 도로에서의 월파량을 예측할 수 있도록 하는 것이다. 그리고 수치해석 결과를 수리모형실험 데이터와 비교하는 것이다. 이를 위해서는 월파량 계측 결과에 대한 데이터 검증 및 자료 구축이 지속적으로 진행되어야 할 것이다. 특히 본 연구를 통해 상대적으로 복잡한 수심 형상을 갖고 있는 항만 구조물 및 해안을 대상으로 OLAFoam을 활용하여 월파량 예측이 가능한 것을 알 수 있었다.