요약본 연구에서는 한반도 서해안에 위치한 해상기상관측타워에서 관측된 수면변동자료를 이용하여 첨두주기 산정의 정확도 향상을 위한 평활화 기법을 적용하였다. 평활화 기법 적용에 대한 검증은 파형의 분산값과 관측 자료의 에너지 총량을 통해 수행하였으며, 이후 평활화 적용에 대한 영향을 분석하였다. 분석결과, 파형의 분산값과 관측 자료의 에너지 총량의 상관계수는 0.9994로 나타났으며, 해당 기법 적용에 문제가 없음을 확인하였다. 이후, 평활화 영향 검토를 수행한 결과, 기존 추정 스펙트럼의 신뢰구간에 비해 최대 26% 감소하는 것으로 나타남으로서, 추정되는 첨두주기의 정확도가 향상됨을 확인하였다. 평활화 적용으로 인하여 4~6초 사이에서 확률밀도는 통계적으로 유의미한 차이가 발생하는 것으로 나타났다. 또한, 최적 평활화를 위해 통계적 기법을 이용하여 유의파고 범위에 따른 적정 평활화 개수를 산정하였으며, 평활화 개수는 유의파고가 작아짐에 따라 불안정한 스펙트럼 형상에 의해 증가하는 것으로 나타났다.
AbstractIn this study, a smoothing method was applied to improve the accuracy of peak wave period estimation using the water surface elevation observed from the Oceanographic and Meteorological Observation Tower located on the west coast of the Korean Peninsula. Validation of the application of the smoothing method was performed using variance of the surface elevation and total amount wave energy, and then the effect on the application of smoothing was analyzed. As a result of the analysis, the correlation coefficient between variance of the surface elevation and total amount wave energy was 0.9994, confirming that there was no problem in applying the method. Thereafter, as a result of reviewing the effect of smoothing, it was found to be reduced by about 4 times compared to the confidence interval of the existing estimated spectrum, confirming that the accuracy of the estimated peak wave period was improved. It was found that there was a statistically significant difference in probability density between 4 and 6 seconds due to the smoothing application. In addition, for optimal smoothing, the appropriate number of smoothings according to the significant wave height range was calculated using a statistical technique, and the number of smoothings was found to increase due to the unstable spectral shape as the significant wave height decreased.
1. 서 론불규칙하게 변하는 해양 특성을 구분하기 위한 주요 변수는 파고와 주기이며, 일반적으로 수면 변동 자료(WSE, ηt, Water Surface Elevation)를 통하여 분석을 수행한다. 또한, 파고와 주기는 시간과 장소에 따라 지속적으로 변화하기 때문에 공학적 관점에서 파랑의 다양한 특성을 결정하고 표현하는 것은 필수적이다(Cho et al., 2015). 최근 몇 년간 해양 관측 장비가 발달함에 따라 파랑 정보를 쉽게 취득함으로서 이를 통한 다양한 파랑 분석이 가능하기 때문에 파랑 관측 자료에 대한 중요성이 대두되고 있다. 불규칙한 파랑 특성을 분석하기 위한 방법에는 1) 시간영역에서 수면변동 자료를 직접 분석하는 파열 분석법과 2) 주파수 영역에서 스펙트럼을 분석하는 불규칙 파랑 스펙트럼 분석 방법이 있다(Horikawa, 1978; Mizuguchi, 1982; Goda, 2010). 파열 분석방법은 방파제와 같은 해양 구조물을 설계하는 과정에서 매우 많이 사용되는 방법 중 하나이며, 개개의 파를 구별하여 기준점을 통과하는 파의 파고와 주기를 계산한다. 이에, Stansell et al.(2002)과 Cho et al.(2018)은 파열 분석 방법을 이용하여 관측 시간 간격에 따른 파고의 변화 양상에 대한 연구를 수행한 바 있으며, Nishi et al.(1997)과 Choi et al.(2017)는 Zero-crossing 방법을 적용하여 개발한 파열 분석법을 통해 파랑 변수를 산정하였다. 또한, 파열 분석법을 이용하여 파고정보를 추정하는 경우, 관측 간격이 연속적인 파형의 최대-최소 시점에서 보통 벗어나기 때문에, 스펙트럼 분석 방법을 이용하여 산정된 파고에 비해 과소 추정될 수 있다(Zheng et al., 2006).
스펙트럼 분석법은 파랑의 주요 인자를 산정하는 방법 중 하나이며, 파랑 에너지의 분포를 주파수 함수로 계산하고 가장 큰 에너지 밀도의 주파수에 해당하는 주기 및 면적으로 계산하는 방법이다(Tompson, 1980). 또한, 해양의 무수한 파는 진폭과 주파수가 서로 다른 다양한 정현파로 구성되어 있다고 가정한다. 이에 Pierson and Marks(1952)와 Casas Prat(2008)은 파랑 스펙트럼 분석 방법을 제안하였으며, 이를 이용하여 관측 장비에서 계산된 파랑 변수값(파고 및 주기)을 통해 관심 해역의 스펙트럼 분포 형태 추정, 극치해석, 파랑 변형 수치모형과 같은 연구를 수행하였다.
한편, 기존에 제안된 파랑 스펙트럼 분석 방법에 대한 성능을 고도화하기 위해 다양한 분석이 수행되고 있다. 이에, Liu(2000)와 Liu and Babanin(2004)는 주파수 영역의 해석에 불확실성을 주장하며, 이를 증명하고 보완하기 위하여 웨이블릿 분석을 기반으로 주파수 스펙트럼 분석에 대한 기본 가정을 검토함으로서, 새로운 분석 기법을 개발하고 제안하였다. 또한, 파랑 스펙트럼 분석 방법을 통해 파랑 변수 중 첨두주기를 산정하는 과정에서, 스펙트럼은 너울성 파랑과 풍파가 결합됨에 따라 두 개 이상의 첨두를 나타낼 수 있으며(Aranuvachapun, 1987; Soares and Carvalho, 2012), Rodriguez and Soares(1999)는 수치해석을 통해 다중첨두 형상의 스펙트럼에 대한 연구를 수행하였다.
파열 분석법을 통해 파라미터를 계산하는 과정이 단순하고 정형화 되어있는 반면, 스펙트럼 분석 방법에 적용되는 분석 과정이 매우 다양하고 복잡하다. 실제로 Waveguide, AWAC(Acoustic Wave And Current meter), ADCP(Acoustic Doppler Current Profiler)와 같은 파랑 관측 장비에 설계된 파랑 스펙트럼 분석 방법은 장비마다 그 차이를 보이고 있으며, 추정 방법의 차이는 계산되는 파랑 변수 값에도 영향을 미치게 된다. 또한, 최근 해양공간 활용 범위가 넓어지고, 해양 활동이 활발해짐에 따라 모든 파고 범위에 대한 정확한 분석이 필요하다. 이에 본 연구에서는 파랑 관측 장비를 통해 관측된 수면변동자료를 이용하여 첨두주기 산정의 불확실성 문제를 해결하기 위해 평활화 기법을 적용하였다. 적용된 기법의 타당성 검토를 위해 Parseval 이론을 이용하였으며, 평활화 적용으로 인해 발생하는 영향 검토를 수행하였다. 이러한 연구는 데이터 분석 및 프로그래밍을 수행할 수 있는 오픈 소스 중 하나인 ‘R’을 이용하여 수행하였다.
2. 자료 및 방법2.1 분석 자료수면변동자료는 파랑 변수를 산정하기 위한 가장 기본적인 관측자료로서, 본 연구에서 사용한 관측장비는 Fig. 1과 같이 서해안에 위치한 HeMOSU-1(Herald of Meteorological and Oceanographic Special research Unit-1) 기상타워 (E126º07'45'', N35º27'55'')에 설치된 Waveguide 관측장비를 이용하였다(Lee et al., 2021a). Waveguide 파랑 관측 장비는 5 Hz(0.2 s) 간격으로 수면변동자료를 수집하며, 관측 기간은 2013. 07.~2014. 07.(결측 제외, 약 7개월 자료)이다. 관측자료의 결측은 장비의 시스템 결함 및 유지보수 기간으로 인하여 발생하는 것으로 사료된다. 또한 Waveguide 장비는 1996년 Delft에 의해 개발된 장비로, 파고 및 파향 관측이 가능하며, 기상타워 플랫폼에 설치되어 Waveguide 서버에 의하여 조정되며 자료는 원격장치에 의하여 전송된다. Waveguide는 관측 장비 내 파랑 분석 프로그램인 SWAP(Standard Wave Analysis Package) 방법이 적용된다(Hoekstra et al., 1994). SWAP 방법은 10% 코사인 윈도우(Cosine Window)를 통해 관측 자료를 보정한 후, FFT(Fast Fourier Transform)을 이용하여 주파수 영역에서의 스펙트럼 분석법을 수행하여 1분 간격으로 파랑 변수를 산정하게 된다.
2.2 분석 방법파랑 스펙트럼 분석은 시간영역과 주파수 영역에서 이루어진다. 시간 영역에서는 1) 관측자료의 추세제거를 위한 영점 보정, 2) 주파수 간격의 정수배가 아닌 영역에서 발생하는 에너지 손실(leakage)을 최소화하기 위한 데이터 윈도우, 3) 특정 주기 영역을 제거하기 위한 데이터 필터 방법이 적용되며, 주파수 영역에서는 고속 퓨리에 변환(FFT, Fast Fourier Transform), Periodogram 등을 이용한 시간영역에서 주파수 영역으로 변환을 위한 분석이 수행된다. 시간 영역에서의 분석 과정은 그 과정이 매우 정형화되어 있고 간단하지만, 주파수 영역에서의 해석은 시간 영역에서의 분석 과정보다 보다 복잡하기 때문에 더 정교한 분석이 이루어져야 한다. 일반적으로, 파랑 변수 산정은 주파수 영역에서의 분석을 통해 추정되는 스펙트럼의 면적과 최대 에너지밀도에 해당하는 주파수를 이용하여 수행된다. 그러나, 추정 스펙트럼의 경우 각각의 값에 대한 신뢰구간이 매우 크기 때문에 추정값에 대한 불확실성 문제가 발생할 수 있으므로 이에 대한 추가적인 분석이 필요하다.
관측자료의 보정을 통해 산정된 시계열 자료에 대하여 주파수 영역에서의 해석을 위해 일반적으로 고속 퓨리에 변환을 주로 사용하지만, 본 연구에서는 분석하고자 하는 자료의 개수를 N = 2n개로 한정하지 않고 유동적으로 선정하기 위해 퓨리에 계수를 산정하여 주파수 영역으로의 변환이 가능한 Periodogram 기법을 적용하였다. 이후, 편향-분산 트레이드 오프 이론이 적용되는 데이터 평활화 기법을 적용하였다.
본 연구에서 적용한 평활화 기법은 식(1)과 (2)의 스펙트럼 밀도(Ik)를 추정한 후, 평활화 함수(가중치) ψj를 산정하여 수행되었다.
여기서, Cp는 추정 스펙트럼 에너지 밀도의 손실에 대한 보정 계수이다. 식(2)를 통해 산정된 스펙트럼에 대하여 평활화는 다음 식을 이용하여 산정할 수 있다.
(5)여기서, n은 평활화 개수를 나타내며, ψj는 평활화 함수(필터)를 나타낸다. 상기식 ψj에서 ψ1은 장방형 필터, ψ2는 삼각 필터, ψ3는 포물선 필터이며, 본 연구에서는 계산의 복잡도 및 시간을 고려하여 ψ2인 삼각 필터를 통해 분석을 수행하였다(Lee et al., 2021b). 그러나, 복잡한 분석 과정에서 적용되는 처리 방법에 따라 에너지 레벨이 입력값과 약간의 오차가 발생할 수 있으며, 이를 확인하는 검증 단계가 필수적이다(Goda, 2010). 본 연구에서는 스펙트럼 분석 방법에 대한 검증을 위하여 시간 영역에서의 에너지 총량과 주파수 영역에서의 파형의 분산값이 같음을 나타내는 Parseval 이론을 이용하였으며(Brigham, 1988), 다음 식 같이 표현할 수 있다.
한편, 스펙트럼을 적용하는 경우, 자료의 개수(N)은 1, 2, …, N/2로 제한되며, Δt가 결정되면, 스펙트럼을 해석할 수 있는 최대 주파수(Nyquist frequency)는 fN = 1/(2Δt)로 표현이 가능하며, 이에 해당하는 비율을 고려하여 계산을 수행한다. 또한, 스펙트럼의 면적을 나타내는 파형의 분산값(ηrms)과 관측 자료의 에너지 총량(m0)은 다음 식으로 표현이 가능하다.
여기서, Δf는 주파수 간격으로서 Δf = 1/(NΔt)로 표현이 가능하다.
3. 분석 결과3.1 파랑 변수 산정 결과 검증본 연구에서 수행한 파랑 스펙트럼 분석 결과에 대한 검증을 위한 방법으로 식(7)과 같이 파형의 분산값(
3.2 평활화 영향 검토관측 자료를 통해 산정되는 파랑 스펙트럼 정보는 추정 정보(
스펙트럼 값이 최대가 되는 주파수를 첨두 주파수로 추정하는 과정에서, 신뢰구간을 고려하면 통계적으로 유의미한 차이가 없는 작은 차이(신뢰구간의 크기 보다 작은 차이)로 최대 스펙트럼 위치가 결정되는 경우, 적합한 첨두 주파수를 추정함에 오류가 발생할 수 있다. 스펙트럼 분석에서 중요한 추정 정보중의 하나에 해당하는 첨두 주파수 추정을 위해서는 최대 스펙트럼의 크기가 차순위 스펙트럼과 유의미한 차이를 보이는 수준에서 선택되어야 하며, 결국 신뢰구간의 크기를 줄이는 과정이 필요하다. 이를 위해서는 인접한 스펙트럼 자료를 이용하여 평활화하는 과정(smoothing)이 일반적이다. 이러한 과정을 거쳐 유의미한 차이를 보이는 최대 스펙트럼 정보 추정이 가능하며, 그 최대 스펙트럼에 대응하는 첨두 주파수 추정이 가능해진다.
다음 Fig. 3에는 Hs= 4.07 m, Tp= 12.59 s의 파랑 스펙트럼에 대하여 평활화를 적용했을 때 신뢰구간 변화를 제시하였다.
추정 스펙트럼의 신뢰구간을 산정한 결과, 추정 스펙트럼 에너지 밀도의 첨두 부분에 대한 신뢰구간 범위는 [46.65, 216.49]로 나타났으며, 평활화를 적용하여 산정된 스펙트럼 에너지 밀도의 신뢰구간 범위는 [12.24, 56.81]로 평활화를 적용하기 전에 비해 최대 약 26% 감소하는 경향을 보였다. 이처럼 전체적인 스펙트럼 정보는 평활화 정보를 이용하여 분석하고, 변동성분은 전체적인 변화 양상 성분에 대한 분산 비교 정도로 간주하여 해석한다.
HeMOSU-1 지점에서 발생하는 유의파고 범위에 따라 첨두주기 변화 양상에 대한 분석을 수행하였으며, 그 결과를 Fig. 4에 제시하였다.
분석 결과, 유의파고 4.07 m인 경우, 추정 스펙트럼의 첨두주기와 평활화를 통해 산정된 첨두주기는 변화없이 11.87 s로 나타났다. 유의파고 3.01 m인 경우, 추정 스펙트럼의 첨두주기는 13.38 s, 평활화 스펙트럼의 첨두주기는 11.78 s로 나타났으며, 유의파고 11.14 m인 경우에는 11.14 s에서 10.54 s, 유의파고 1.00 m인 경우, 첨두주기는 7.20 s에서 8.31 s로 변화하는 양상을 보였다. 이는 유의파고가 낮아질수록 다중 첨두 발생 및 파랑 스펙트럼 에너지 밀도가 집중되지 못하는 등의 불안정한 스펙트럼 분포 형태로 첨두주기의 변화가 발생하는 것으로 사료된다. 한편, 추정 스펙트럼에 대하여 평활화를 수행하는 경우, 평활화 개수가 증가함에 따라 스펙트럼은 저주파 영역으로 치우치는 현상(Shifting)이 발생하며, 이는 적용되는 평활화 개수에 대한 자료 손실의 수치적인 영향으로 판단된다. 이러한 문제를 해결하기 위해서는 식(5)에 제시한 바와 같이 평활화의 개수(n)을 합리적으로 결정하는 것이 매우 중요하며, 이를 산정하기 위해 다음 식(10)과 같이 RMSE를 계산하여 오차가 가장 작게 나타나는 n을 산정하였다.
RMSE 산정을 위해 사용된 식(10)에서
최적 평활화 개수를 산정하기 위해 HeMOSU-1 지점의 유의파고 4.00 m에 대하여 평활화 개수를 변화하며 계산한 RMSE 및 신뢰구간의 변화 양상을 Fig. 5에 제시하였다.
분석 결과, HeMOSU-1 지점에서 가장 크게 발현하는 파고에 대하여 신뢰구간의 변화 양상을 분석한 결과, RMSE가 가장 작게 산정되는 평활화 개수는 9개로 나타났다. 이때 스펙트럼의 신뢰구간 범위의 변화(ΔSCI)는 [0.98 142.69] -> [11.90 45.58], 주파수의 해상도 범위 변화(ΔfRE)는 [0.091 0.092] -> [0.07 0.08]로 나타났다. 이처럼 평활화는 스펙트럼 에너지 밀도의 신뢰구간 문제를 감소시키는 장점이 있지만, 주파수 해상도는 식(3)에 제시한 바와 같이 2n + 1만큼 감소하기 때문에 편향-분산 트레이드 오프 현상이 발생하며, 이에 따라 적절한 평활화 개수를 산정하는 것이 중요하다. 이와 같은 과정을 통해 산정된 적정 평활화 개수 결과는 Fig. 6과 같다.
분석 결과, Hs > 4인 경우, HeMOSU-1의 적정 평활화 개수는 7개와 9개로 나타났으며, 3 < Hs < 4인 경우는 11개, 2 < Hs < 3인 경우는 11개로 산정됐다. 1 < Hs < 2의 유의파고 범위에서는 적정 평활화 개수가 15개로 나타났으며, Hs < 1 범위에서는 25개로 산정됐다. 평활화 개수는 유의파고가 작아짐에 따라 증가하는 경향을 보였으며, 이는 파랑 스펙트럼의 불안정한 분포로 인해 평활화를 적용함에 어려움이 있는 것으로 판단된다. 또한, 평활화를 적용함에 따라 평활화된 스펙트럼(
평활화에 의한 첨두주기의 영향을 검토하기 위해 선형 상관관계를 수행한 결과(Fig. 7(a) 참조), 상관계수(CC)는 0.829로 나타났으며, 통계적으로 유의미한 상관관계를 보였다. 또한, 대부분의 주기는 약 4~6초 사이에 주로 분포하는 것으로 나타났다. 평활화의 유무에 따른 첨두주기의 밀도 분포 변화 양상은 Fig. 7(b)에 제시한 바와 같이 평활화의 영향으로 귀무가설이 기각됨에 따라 유의미한 차이가 발생하였다(p-value < 0.05).
상기 분석된 결과를 이용하여 유의파고-첨두주기(Hs - Tp) 사이의 관계 곡선을 도시한 후, 평활화 영향 검토를 추가로 수행하였다(Fig. 8 참조). Fig. 8(b)는 파랑 관측 장비인 Waveguide에서 산정된 결과이며, Fig. 8(a)와 전반적인 경향은 유사하지만, 두 결과의 가장 큰 차이는 산정되는 첨두주기의 간격이다. 이는 파랑 스펙트럼 분석을 수행할 때, Δt에 따라 결정되는 최대 주파수(fN, Nyquist Frequency)에 차이로 사료된다. SWAP 방법을 통해 산출되는 주파수 간격은 ΔfSWAP = 0.010 Hz이며, 본 연구에서 사용한 방법을 통해 산출되는 주파수 간격은 Δfthis study = 0.0017 Hz로 약 10배 차이를 보이고 있기 때문에 산출되는 첨두주기 간격에 대한 차이가 발생하는 것으로 나타났다. 파랑 스펙트럼 분석을 통해 파랑 변수를 산정할 때 주파수 간격(Δf)의 정수배(nΔf) 영역에 해당되는 주기가 산정되기 때문에 주파수 간격이 작을수록 더 다양한 주기가 계산된다. 이를 통해 보다 정확한 결과값을 제시할 수 있으며, 본 연구에서는 주파수 영역에서 발생하는 에너지 손실(leakage)과 같은 문제를 해결하기 위해 시간-주파수 영역에서 충분한 보정을 수행하였기 때문에 SWAP 방법을 통해 산정된 결과보다 정확도가 우수한 것으로 사료된다.
4. 결론 및 제언본 연구에서는 파랑 변수를 산정하기 위한 기초자료인 수면변동자료를 이용하여 추정 스펙트럼의 신뢰구간 문제를 해결할 수 있는 평활화 기법에 대한 연구를 수행하였다. 이를 통해 얻은 결과는 다음과 같다.
1. 파랑 스펙트럼 분석을 통해 파랑 변수를 산정하는 경우, 일반적으로 분석 방법에 대한 검증을 위해 파형의 분산값과 관측 자료의 에너지 총량을 비교하는 Parseval 이론을 적용하여 수행한다. 산정된 두 변수를 이용하여 상관분석을 수행한 결과 상관계수인 CC값은 0.9994로 매우 높은 상관성을 보이고 있었으며, 이를 통해 본 연구에서 적용한 평활화 기법에 대한 타당성을 확보하였다.
2. 파랑 스펙트럼 분석을 통해 산정되는 첨두주기의 불확실성 문제를 해결하기 위해 본 추정 스펙트럼에 대하여 평활화 기법을 적용하였다. 평활화는 추정 스펙트럼의 넓은 신뢰 구간을 감소시키며 추정값의 신뢰성을 확보할 수 있는 기법이다. 기존 추정 스펙트럼의 신뢰구간 범위와 평활화를 통해 산정된 스펙트럼의 신뢰구간은 최대 26% 감소하는 양상을 보였다. 또한, 유의파고 범위에 따라 첨두주기 변화를 확인한 결과, 유의파고가 작아짐에 따라 추정 스펙트럼이 집중되지 않고, 불안정한 형상으로 인하여 평활화에 의한 첨두주기 변화를 보였으며, 이에 따라 적용되는 평활화 개수가 증가하는 것으로 나타났다.
국내에서 제공되는 파랑 관측자료는 기상청, 국립해양조사원 등 서로 다른 관측장비가 적용되며, 관측장비마다 파랑 변수를 산정하는 과정에 차이가 있기 때문에 수면변동자료와 같은 원자료를 제공할 필요가 있다. 본 연구에서는 원자료 확보의 한계로 인하여 서해안 HeMOSU-1 지점에 대한 분석이 이루어졌지만, 보다 더 정확한 파랑 변수 산정을 위해 다양한 국내 해역을 대상으로 다양한 관측 장비를 이용한 파랑 관측 수행이 필요할 것으로 판단된다.
Fig. 3.Change in confidence interval (CI) of observed spectrum and smoothing spectrum (95% Confidence Interval). 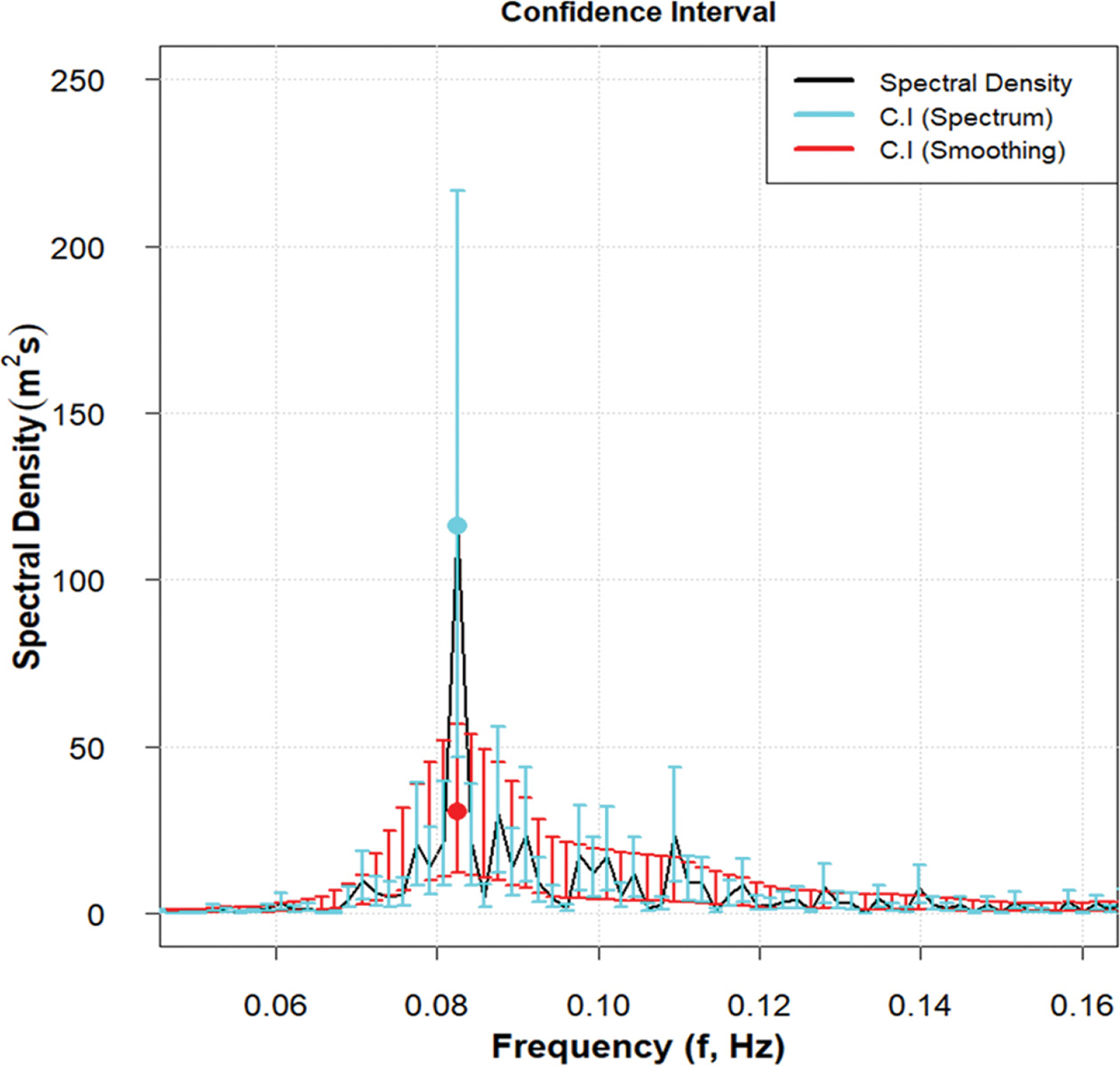
Fig. 6.Estimating the optimal number of smoothing for the significant wave height range for wave spectrum smoothing. 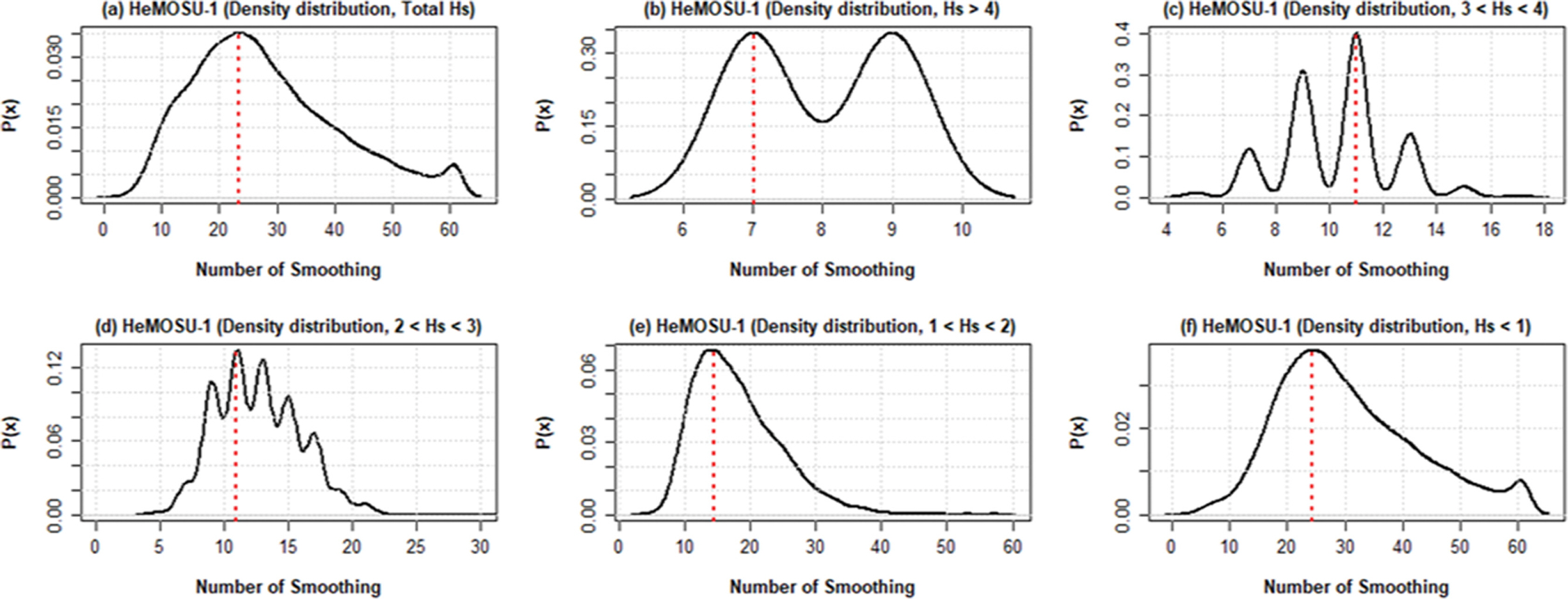
ReferencesAranuvachapun, S (1987). Parameters of JONSWAP spectral model for surface gravity waves—II. Predictability from real data, Ocean engineering, 14(2):101-115.
Brigham, E.O.. (1988). The fast Fourier transform and its applications. Prentice-Hall, Inc.
Casas Prat, M. (2008). Overview of ocean wave statistics.
Cho, H.Y., Choi, H.J., Jeong, S.T., Ko, D.H (2018). Relationship between wave height and sampling interval: revisiting individual wave analysis method, Journal of Coastal Research, 85(10085):1136-1140.
Cho, H.Y., Kweon, H.M., Jeong, W.M (2015). A study on the optimal equation of the continuous wave spectrum, International Journal of Naval Architecture and Ocean Engineering, 7(6):1056-1063.
Choi, H., Jeong, S.T., Cho, H.Y., Ko, D.H., Kang, K.S (2017). Development of wave by wave analysis program using MATLAB, Journal of Korean Society of Coastal and Ocean Engineers, 29(5):239-246 (in Korean)..
Goda, Y.. (2010). Random seas and design of maritime structures (33). World Scientific Publishing Company.
Hoekstra, G.W., Boere, L., Van der Vlugt, A.J.M., van Rijn, T. (1994). Mathematical description of the standard wave analysis package, The Oceanographic Company of the Netherlands bv: Castricum. The Netherlands.
Horikawa, K. (1978). Coastal Engineering, An Introduction to Ocean Engineering. Univ. of Tokyo Press.
Lee, U.J., Ko, D.H., Cho, H.Y., Oh, N.S (2021a). Correlation analysis between wave parameters using wave data observed in HeMOSU-1&2, Journal of Korean Society of Coastal and Ocean Engineers, 33(4):139-147 (in Korean)..
Lee, U.J., Ko, D.H., Kim, J.Y., Cho, H.Y (2021b). Estimation and analysis of wave spectrum parameter using HeMOSU-2 observation data, Journal of Korean Society of Coastal and Ocean Engineers, 33(6):217-225 (in Korean)..
Liu, P.C., Babanin, A.V (2004). Using wavelet spectrum analysis to resolve breaking events in the wind wave time series. In Annales Geophysicae, Copernicus GmbH, 22(10):3335-3345.
Mizuguchi, M (1982). Individual wave analysis of irregular wave deformation in the nearshore zone, Coastal Engineering Proceedings, 18, 32-32.
Nishi, R., Sato, M., Kraus, N.C (1997). Development of wave train analysis package: WAVETRAP, The Research Report of the Faculty of Engineering, Kagoshima Univ, 39, 179-198.
Pierson, W.J., Marks, W (1952). The power spectrum analysis of ocean-wave records, Eos, Transactions American Geophysical Union, 33(6):834-844.
Rodriguez, G.R., Soares, C.G (1999). The bivariate distribution of wave height and periods in mixed sea states, Journal of Offshore Mechanics and Arctic Engineering, 121(2):102-108.
Soares, C.G., Carvalho, A.N (2012). Probability distributions of wave heights and periods in combined sea-states measured off the Spanish coast, Ocean engineering, 52, 13-21.
Stansell, P., Wolfram, J., Linfoot, B (2002). Effect of sampling rate on wave height statistics, Ocean Engineering, 29(9):1023-1047.
Thompson, E.F.. (1980). Energy spectra in shallow US coastal waters, Technical paper. p 80-2. US Army corps of engineers, Coastal engineering research center.
Thomson, R.E., Emery, W.J. (2014). Data analysis methods in physical oceanography, Newnes.
Wand, M.P., Jones, M.C.. (1994). Kernel Smoothing. Chapman and Hall, London.
|
|
||||||||||||||||||||||||||||||||||