Design Wave Period Estimation Using the Wave Height Information

Hong-Yeon Cho; Weon Mu Jeong; Ju Whan Kang; Gi-Seop Lee

doi:10.9765/KSCOE.2023.35.4.84

Journal of Korean Society of Coastal and Ocean Engineers > Volume 35(4); 2023 > Article

파고 정보를 이용한 설계주기 추정

Article

J Korean Soc Coast Ocean Eng 2023; 35(4): 84-94.

Published online: August 31, 2023

DOI: https://doi.org/10.9765/KSCOE.2023.35.4.84

파고 정보를 이용한 설계주기 추정

조홍연^*, 정원무^**, 강주환^***, 이기섭^****

^*한국해양과학기술원 해양빅데이터-AI센터 책임연구원

^**한국해양과학기술원 해양 ICT-모빌리티연구부 책임연구원

^***국립목포대학교 토목공학과 교수

^****한국해양과학기술원 해양빅데이터-AI센터 연수연구원

Design Wave Period Estimation Using the Wave Height Information

Hong-Yeon Cho^*, Weon Mu Jeong^**, Ju Whan Kang^***, Gi-Seop Lee^****

^*Principal Research Scientist & Professor, Marine Bigdata & AI Center, Korea Institute of Ocean Science and Technology, Univ. of Science and Technology

^**Principal Research Scientist, Maritime ICT & Mobility Research Department, Korea Institute of Ocean Science and Technology

^***Professor, Department of Civil Engineering, Mokpo National University

^****Post-Doc. Researcher, Marine Bigdata & AI Center, Korea Institute of Ocean Science and Technology

Corresponding author: Gi-Seop Lee, Post-Doc. Researcher, Marine Bigdata & AI Center, Korea Institute of Ocean Science and Technology, 385 Haeyangro, Youngdo, Busan 49111, Korea, Tel:+82-51-664-3788, freelgs7@kiost.ac.kr

Received July 20, 2023 Revised August 28, 2023 Accepted August 28, 2023

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

요약

재현기간에 따른 설계주기 추정에는 일반적으로 파고-주기 관계곡선을 이용한다. 본 연구에서는 설계주기 추정을 위한 파고-주기 관계곡선의 매개변수를 선형, 로버스트 선형, 비선형 함수를 이용하여 추정하고 그 계수를 비교-평가하였다. 매개변수 추정에 사용한 자료는 해양수산부(2019) 설계파고 추정에 사용한 연 최대 파고-주기 자료이며, 태풍, 비태풍 조건으로 구분하여 매개변수 추정에 이용하였다. 추정 매개변수는 해역의 지점에 따라 뚜렷한 차이를 보였으며, 추정기법의 경우에는 태풍 조건의 자료의 경우 비선형과 선형 기법이 큰 차이를 보이고 있는 것으로 파악되었다. 또한 SPM 공식과 GODA 공식을 평균하여 추정하는 Suh et al.(2008, 2010) 제안 방법은 절편 매개변수는 과소추정, 경사 매개변수는 과대 추정하는 것으로 파악되었으며, 해역의 국지적인 특성 반영에는 한계가 있는 것으로 판단된다.

핵심용어: 설계주기, 파고-주기 관계곡선, 절편 매개변수, 경사 매개변수, AM 파고-주기 자료

Abstract

The wave height and period regression curve is widely used to estimate the design wave period. In this study, the parameters of the curves are estimated, compared, and evaluated using the linear, robust linear, and nonlinear regression methods, respectively. The data used in the design wave height estimation are the annual maxima (AM) wave height and period data sets divided by typhoon and non-typhoon conditions, provided by the Ministry of Oceans and Fisheries (2019). The estimation parameters show significant differences in the local coastal waters and the estimation methods. The estimation parameters based on the Suh et al. (2008, 2010) method show the apparent bias, under-estimation in the intercept (scale) parameter, and over-estimation in the slope (exponent) parameter, respectively.

Keywords: design wave period, wave height and period relation curve, intercept and slope parameters, AM wave height-period data set

1. 서 론

어떤 한 지점의 파랑 자료는 파고(유의파고), 주기(첨두주기), 파향 항목으로 구성되는 벡터 형식의 시계열(time-series) 자료이며, 방향으로 분류하는 경우 파고, 주기 세트의 자료를 파랑자료로 간주한다. 풍파의 경우 파고와 주기는 일반적으로 양의 상관관계를 가지고 있으나, 너울의 경우에는 작은 파고조건에서도 긴 주기를 가지는 경우가 발생한다. 그러나 해안 구조물의 설계에 이용되는 설계파고 조건은 재현기간이 50~100년 정도에 상응하는 파고를 대상으로 하기 때문에 매우 높은 파고 조건에 해당하며, 설계주기도 그 파고에 종속된 경우로 가정하여 적절한 함수를 가정하고 매개변수를 추정하여 계산한다. 따라서 일반적인 설계주기 추정 절차는 설계파고의 추정과 설계파고의 관계공식을 이용한 설계주기 추정 절차가 일반적이다.

본 연구에서는 연 최대(AM, annual maxima) 파고정보를 이용하여 설계 주기를 추정하는 방법을 비교·평가하는 것을 목적으로 한다. 더불어 설계주기 추정 함수로 널리 이용되는 함수의 매개변수의 분포 양상 검토를 수행하고, 자료 기반의 합리적인 제약사항 반영 기법도 제안한다.

일반적으로 널리 이용되는 파고-주기 관계 함수는 다음과 같은 멱(冪, 덮을 멱) 함수, 또는 거듭제곱함수라는 용어를 사용하고 있으나, 다소 생소하고/어려운 한자이기 때문에 이하 “Power 함수” 용어를 영문 포함하여 직접 사용한다.

Tp=αHsβ

Power 함수의 매개변수 추정은 다음과 같은 선형 변환과정을 통하여 간단하게 추정할 수 있다.

lnTp=lnα+β·lnHs→LT=a+b·LH

여기서, LT = lnT_p , LH = lnH_s, a = lnα, b = β 조건에서 선형회귀분석 문제가 되고, 매개변수는 각각 절편(intercept, scale, α) 매개변수, 경사(slope, exponent, β) 용어로 구분한다.

Power 함수 형태를 그대로 이용하는 경우, 풀이 방법은 보다 복잡해지지만 변수의 변동 특성을 그대로 유지하는 비선형(non-linear) 최적화 문제를 푸는 방법으로 매개변수 추정도 가능하다. 그러나 파고-주기 관계함수 추정에 어떤 지점, 어떤(추출된) 자료를 이용하는 가에 따라 그 계수는 차이를 보일 수 있다. 따라서 파고와 주기의 관계함수를 이용하여 추정되는 매개변수는 추정에 사용한 파고-주기 자료의 지점과 조건(태풍, 비태풍; 연안격자, 내부격자)으로 구분된다.

파고와 주기의 상관분석에도 Power 함수 형태를 이용하여 분석하고 있다. 관측 자료를 이용한 분석은 낮은 파고, 특정해역으로 제한되지만, 다양한 분석 결과로 매개변수를 제시하고 있다. Lee et al.(2021)는 서해중부해역에 위치한 HeMOSU-1&2 자료를 이용하여 추정한 결과(α = 4.83, 4.49, β = 0.43, 0.46)를 제시하고 있으며, Jung et al.(2020)은 동해 연안에서 다양한 장비로 측정한 파고-주기자료를 이용하여 추정한 매개변수에 차이가 있음을 보고하고 있다. HF-레이더, 파고부이, AWAC, 기상청(KMA) 부이관측 장비의 경우, 각각 α = 6.58, 5.88, 6.01, 6.55; β = 0.18, 0.23, 0.23, 0.23 정도이다. 한편 Jeong et al.(2019)은 동해 중부해역의 파랑 관측 자료를 이용하여 추정한 매개변수로 α = 6.212, β = 0.323 수치를 제시하고 있다. Ahn et al.(2016)도 강릉연안의 파랑 후측자료를 이용하여 추정한 결과로, α = 7.0, β = 0.25 수치를 제시하고 있다. 이상의 기존 연구결과에서 볼 수 있는 바와 같이 파고-주기 파워 함수 매개변수는 해역에 따라 어느 정도의 유의미한 차이를 보이고 있음을 알 수 있으며, 우리나라 전체 해역을 대상으로 매개변수 변동양상을 분석한 연구는 Suh et al.(2008, 2010) 성과로 제한된다(Table 1 참조).

한편 설계파고와 같은 높은 파고 영역에서 주기 계산은 Suh et al.(2008)은 Goda 공식(Goda, 2010)과 SPM 공식(U.S. Army Coastal Engineering Research Center, 1977)의 평균을 사용할 것을 제안하고 있다. 이 방법은 각각의 공식을 이용하여 설계주기를 계산하여 평균하는 방법, Suh 제안 방법(이하 Suh 방법)으로 간주한다. 그러나 SPM 공식이나 Goda 공식은 모든 파랑-주기 자료를 사용한 조건에서의 곡선은 파랑 자료가 존재하는 하한경계(lower limit) 경계(과소 추정)에 해당하는 것으로 판단된다. 따라서 설계파고를 이용하여 설계주기를 추정하는 과정은 가용한 연 최대 자료를 기반으로 추정하는 방법에 대한 정량적인 추가적인 비교-평가가 요구된다. 본 연구에서는 우리나라 모든 연안 해역을 대상으로 파고-주기 관계곡선의 매개변수를 추정-분석하고, 파고자료를 이용한 적절한 주기분석 기법 제안을 목적으로 한다.

2. 재료 및 방법

2.1 연 최대값(Annual Maxima, AM) 데이터

설계파고를 이용한 설계주기 추정과정에 이용되는 파랑자료는 해양수산부에서 연안 설계파고 추정에 사용한 연 최대파랑자료로 연안 210개 지점, 보다 연안에 근접한 310개 지점의 자료이다. 이 자료는 태풍과 계절풍(이하 비태풍) 자료로 구분되는 장기 후측(hindcasting) 자료이며, 파향 성분을 16 방향으로 구분한 자료이다. 태풍 자료의 경우에는 전체 59년(1959~2017년), 비태풍 조건의 경우에는 전체 35년(1979~2013년) 동안의 자료이다. 파고-주기 관계곡선 추정에 사용된 파랑자료의 위치는 다음과 같다(Fig. 1, MOF, 2019; Cho et al., 2020). 하나의 연안 격자지점 파랑자료는 모두 16 방향으로 구분되어 있으나, 파고-주기 관계곡선 추정 매개변수의 신뢰구간(오차구간)을 절감(사용되는 자료의 개수 증가)하기 위하여 모든 방향을 통합한 자료를 매개변수 추정에 사용한다. 이 경우 파고-주기 자료의 분산이 일정하다고 가정하면, 분석에 사용하는 파랑자료의 개수가 16배 증가하는 영향으로 절감되는 오차구간은 1/4 정도 수준으로 감소하게 된다.

2.2 설계주기 추정방법, Power 함수 매개변수 추정 방법

설계주기를 추정하는 방법은 Power 함수 매개변수 추정이 필수적인 절차로, 다음과 같은 절차를 따르는 경우가 일반적이다.

Step 1: 연 최대 자료 등을 이용하여 설계파고를 추정한다.

Step 2: 연 최대 파고-주기 자료를 이용하여 파고-주기 관계곡선을 추정한다(매개변수 추정).

Step 3: 추정 관계곡선을 이용하여 설계파고에 대응하는 설계주기를 계산한다. 종료.

이상과 같이 절차는 간단하지만, 추정의 핵심은 파고-주기 관계곡선(Power 함수)의 매개변수를 추정하는 과정이다. 본 연구에서는 일반적인 매개변수 추정 방법을 이용하는 경우와, 연 최대 자료의 낮은 파고영역에서 긴 주기를 보이는 자료의 영향을 배제하기 위하여 로버스트 회귀분석 기법을 제안한다. 로버스트 회귀분석은 R 프로그램 {MASS} 패키지에서 제공하는 rlm() 함수(Venables and Ripley, 2002)를 이용하여 수행하였다. 로버스트 회귀분석은 반복기법으로 IWRS(iterated re-weighted least squares, IWLS) 기법을 이용한다(Cho, 2019). 한 연안 격자 지점에서의 회귀곡선 매개변수 추정결과라 할지라도, 방향으로 구분된 자료를 이용하는 경우에는 16개 세트의 추정 세트가 얻어지지만, 추정에 사용한 자료개수 감소로 인한 오차구간이 크게 증가하기 때문에 한 지점의 매개변수는 16 방향의 자료를 모두 통합하여 추정하였다. 이 경우 개략적인 오차구간 감소 정도는 각각의 방향자료를 이용한 경우에 비하여 16배의 자료 증가 효과가 반영되어 1/4 정도로 감소한다. 매개변수 추정결과는 연안 210 + 310 = 520 정점에서 추정되기 때문에 각각의 변동양상 분석은 매우 비효율적인 분석으로, 본 연구의 경우에는 해양수산부에서 구분한 해역을 기준으로 수행한다(Fig. 2 참조).

한편 이 방법과는 별도로 파고와 주기의 결합 확률분포함수(joint pdf.)를 이용하는 방법도 통계적으로는 가능하지만, 50~100년 정도의 재현기간에 해당하는 영역의 자료가 매우 희박하기 때문에 통계적으로 적절한 방법이라 할지라도 상당한 추정오차가 해당되기 때문에 본 연구 분석에서는 제외하였다. 매개변수 추정 결과는 각각의 지점에 대하여 태풍, 비태풍 조건에서 수행하였으며, 추정 결과는 Fig. 2의 해역구분 기준을 이용하여 비교-분석하였다. 결합 확률분포를 이용하는 경우에는 분포함수에 대하여 동일한 확률 contour line 도시가 가능하기 때문에 재현기간에 따른 파고-주기 contour-line 정보가 결과로 제시된다. 그러나 재현기간에 해당하는 확률은 분포의 꼬리부분에 해당하는 매우 작은 확률 영역이고, 가용한 자료의 개수도 매우 적기 때문에 신뢰구간에 대한 평가가 수반되어야 한다.

2.3 매개변수 추정 방법

선형회귀모형은 Power 함수에 로그변환을 적용하면 선형 함수로 간단하게 변환되기 때문에 별도의 추정과정 제시는 생략한다. 로버스트 회귀모형은 잔차의 크기에 따라 가중계수를 차등 부여하여 반복-추정하는 방식으로, 추정 함수에서 크게 벗어나는 자료의 영향을 줄이는 매개변수 추정 방법이다. 한편 비선형회귀모형의 경우에는 최소자승법 기반의 비선형 최적화 함수를 이용하여 추정하는 방법도 가능하다. 두 방법 최적 매개변수 추정에 사용하는 방법이지만, 보다 구체적인 방법은 부록의 수식을 참조한다.

본 연구에서는 nls() 함수를 이용하는 방법을 이용하여 매개변수 추정을 수행하였으며, 비선형함수의 최적 매개변수 추정함수 적용을 위한 초기가정(initial guess)은 α = H, β = 0.5 조건을 부여하였다. 그러나 α = [0, max(H_i)] (파고 전체범위), β = [0, 1] 범위로 확장하여도 반복시간 차이는 있지만 적절하게 최적 매개변수를 안정적으로 추정한다.

2.4 Suh 방법의 주기 추정 공식

Suh et al.(2010) 논문에서는 파고 자료를 이용하여 주기를 추정하는 방법으로 SPM 공식과 Goda 공식의 평균 방법을 제안하고 있다. 두 공식의 평균이 되는 하나의 실질적인 근사 수식은 다음과 같이 추정되며(Fig. 3 참조), 이하 Suh 방법으로 기술한다.

Tp=1/23.85Hs0.50+3.30Hs0.63≈3.55Hs0.57

3. 매개변수 추정 결과

파고-주기 자료의 관계를 표현하는 Power 함수의 매개변수를 추정한 결과는 다음과 같다. 회귀계수 추정결과는 다음과 같이 분류하여 제시한다.

Case 1: 선형변환 - 단순(simple) 선형 회귀모형 매개변수 추정

Case 2: 비선형 회귀분석모형 매개변수 추정결과

Case 3: 선형변환 - 로버스트 선형회귀모형 매개변수 추정

Case 4: Case 2 로버스트 회귀분석 결과에서 지수 매개변수(β) 범위 제한.

Case 4 조건의 범위 제한은 몇몇 지점의 비현실적인 주기 추정 결과를 제시하는 경우를 제거하기 위하여 해양수산부(MOF, 2019) 설계주기 추정과정에서 경험적인 판단에 근거하여 강제로 [0.2, 0.8] 범위로 제한한 경우이다. 그러나 전반적으로 특정한 소수의 경우를 제외하고는 추정 매개변수가 이 범위에 포함되기 때문에 이 경우에 대한 특별한 분석 및 토론은 제외한다. 계산 결과에 대한 다양한 조건 구분에 따른 결과는 다음과 같이 구분한다(Table 2 참조).

매개변수 추정방법에 따른 자료 적합 곡선은 대표지점을 선정하여 제시한다. 대표지점은 해역, 자료유형(태풍(TP), 비태풍 = 계절풍(MS) 조건으로 구분)으로 구분하여 연안 격자(Data cases code: -210 in Table 2)는 11, 118, 178, 210 지점(Fig. 2 참조)을 선택하고, 보다 육지에 근접한 내부 연안 지점(Data cases code: -310 in Table 2)은 11-5, 118-2, 178-1, 210-1 지점(Fig. 2 참조)을 선택하였으며, 그 적합곡선은 Fig. 4와 같다. 분석에 사용한 대표지점의 정확한 위치 좌표는 Table 3과 같다.

매개변수추정은 다양한 조건(Table 2)에서 수행하였으며, 그 결과는 그림으로 제시한다. Power 함수의 α, β 매개변수 추정결과를 해역, 데이터 유형, 추정방법으로 구분하여 비교평가를 수행하였다. 추정 방법 비교는 전통적인 선형(변환) 회귀분석(Simple LR, 그림의 수평축) 기법을 기준으로 로버스트 회귀분석(Robust LR, 그림의 수직축)과 비선형 회귀분석(Power function NLR, 그림의 수직축)과의 차이 비교를 수행한다(Fig. 5 참조). 매개변수는 하나 하나의 지점을 대상으로 각각 추정하였으며, 추정 매개변수는 어떤 한 지점의 파고-주기 특성 변수로 간주할 수도 있다. 모든 연안 격자 지점에서 추정한 매개변수는 해양수산부 해역구분(Fig. 2 참조)을 기준으로 구분하여 제시한다(Fig. 6 참조).

해양수산부 보고서(MOF, 2019)에 제시된 연안격자는 1-210 범위의 일련번호로 부여되어 있으며, 내부 격자 번호는 “-” 기호를 이용하여 연안 격자번호에 종속된 번호를 부여하고 있으나, 순서대로 전체 310개 지점에 일련번호를 부여하여 처리하였다. 연안 격자와 내부 격자를 모두 통합하는 경우에는 210번 이후 번호를 부여하여 전체 1-520(= 210 + 310) 범위의 일련번호를 사용한다. 각각의 일련번호에 대한 해양수산부 구분 지점 번호표는 다음과 같다(Table 4 참조).

4. 토 론

4.1 Power 함수 적합 곡선

Power 함수의 적합 정도는 비태풍, 태풍 조건에서 자료와 추정 곡선의 도시(Fig. 4)로 분석이 가능하다. 그림에서 볼 수 있는 바와 같이, 일반적으로 좁은 영역에 파고-주기 자료가 밀집되어 있으며, 소수의 자료가 너울 영역(낮은 파고, 긴 주기 영역)과 고파 영역(높은 파고, 긴 주기 영역)을 차지하고 있다. 이러한 양상은 태풍, 비태풍 조건 모두 유사한 양상을 보이고 있음을 알 수 있으나, 좁은 영역의 자료 밀집정도는 차이를 보이고 있다. 이런 양상은 비태풍 조건과 태풍 조건의 자료에서 추정 곡선의 차이로 설명이 가능하다. 비태풍 조건의 경우에는 비선형 함수 적합곡선이 다른 방법의 추정곡선과 유사한 변화 양상을 보이고 있으며, Suh et al. 제안 공식은 모든 파고구간에서 낮은 영역을 차지하고 있다. 반면, 태풍 조건에서는 비선형 Power 함수 곡선이 다른 추정 기법과 상당한 차이를 보이고 있다(Fig. 4(b) 태풍 조건 11, 11-5,118, 178, 210 정점). 그러나 고파 영역에서는 Suh 방법의 추정도 적절한 수준으로 판단된다. Suh 방법은 본 연구에서 수행한 매개변수 추정결과의 지점 차이 반영에는 한계가 있다고 판단되나, 해역의 전체적인 특성을 반영한 고파영역의 주기를 추정하는 “어림(approximation)” 공식으로 적절하다고 판단된다. 또한 파고-주기 자료의 분포 양상을 보면 하나의 최적 곡선으로 추정하는 방법보다는 일정 범위를 가지는 구간추정 또는 contour line 정보로 제시되는 형태의 추정이 자료의 분포 및 변동 특성을 보다 적절하게 반영할 수 있을 것으로 판단된다.

4.2 매개변수 추정방법에 따른 영향

매개변수 추정방법 차이는 비태풍 조건에서는 이미 큰 차이를 보이지 않는 것으로 파악되었다. 보다 깊은 분석을 위하여 추정 방법에 따른 추정 매개변수 산포도(scatter plot) 방법을 이용한다(Fig. 5 참조). 그림에서 볼 수 있는 바와 같이 단순 선형회귀 분석과 로버스트 회귀분석 결과는 몇몇 소수 지점을 제외하고는 차이는 미미한 수준으로 판단된다. 반면 비선형 함수를 이용한 추정과 비교하는 경우, 태풍 조건의 경우, 그 차이가 상당한 수준으로 파악된다. 단순 선형회귀 모형추정과 비선형 함수 추정의 양상 차이는 설계주기 추정을 위한 매개변수 선택과정에서 어려운 선택 절차가 포함된다. 일반적으로 비선형 함수 매개변수 추정은 제한되기 때문이지만, 비선형 회귀모형의 장점을 고려할 필요가 있다. 더불어 파고-주기의 산포 정도를 감안하면, 하나의 곡선으로 추정하는 방법에 근본적인 한계가 있는 것으로도 판단할 수 있다. 현재는 하나의 곡선을 이용하는 방법이 널리 이용되고 있으나, 이 방법을 이용하여 주기를 추정하는 경우, 추정 주기의 오차구간(신뢰구간) 추정이 요구된다.

4.3 매개변수의 공간 변화 양상

추정 매개변수의 공간변화 양상은 전통적인 선형 회귀모형 추정 기법의 결과를 기준으로 분석하였다. 그리고 사용한 자료는 태풍, 비태풍 조건으로 구분하였으며, Suh et al. 공식에서 제시한 매개변수를 기준으로 분석을 수행하였다. 그림(Fig. 6)에서 볼 수 있는 바와 같이, 비태풍, 태풍 조건 모두 절편 매개변수는 전반적으로 기준보다 높은 수치로 추정되고 있다. 절편 매개변수는 파고 = 1.0(m) 조건에 해당하는 주기에 해당하기 때문에, Suh 제안 공식을 이용한 공식은 낮은 파고의 주기를 과소추정하게 된다. 반면 경사(지수) 매개변수는 전반적으로 기준보다 낮은 수치로 추정되고 있다. 이는 파고 증가에 따른 주기 증가 비율이 Suh 제안 공식을 이용하는 경우, 과대추정이 예상된다. 전체적인 이런 예상과 더불어 다양한 해역에서 수행한 선형 자료 분석 결과와 본 연구의 분석 결과를 종합하면 Power 함수 매개변수는 해역의 다양한 특성이 반영되어 지수가 결정되기 때문에 어떤 넓은 해역을 대표하는 지수 사용은 한계가 있다.

한편 추정 매개변수의 공간변화도 인접한 해역이라 할지라도 공간변화 정도가 매우 크고, 해역의 수치 범위도 매우 크기 때문에 넓은 범위의 매개변수 제시는 가능하나, 구체적인 수치 제시는 부적절한 방법으로 판단된다. 관심을 가지는 해역, 주기 추정이 필요한 해역에서는 그 지점의 자료를 이용하여 추정하는 절차를 따르는 것이 바람직하다고 할 수 있다. 동일한 지점에서의 매개변수 시간변화 양상도 예상되는 경우에는, 가용자료를 시간으로 구분하여 매개변수 변화 양상을 검토할 필요도 있으나, 본 연구 범위를 벗어나고, 가용한 장기 자료 부족으로 분석에서 제외한다.

5. 결론 및 제언

본 연구에서 수행한 추정 매개변수의 다양한 분석으로부터 다음과 같은 결론과 향후 연구 방향을 제안한다.

1. Suh 방법에서의 제안공식은 일반적인 파고-주기 매개변수의 기준으로는 적절하나, 어떤 특정 해역의 주기 추정에는 한계가 있다. 파고-주기 관계 Power 함수의 매개변수는 해역 특성을 반영하기 때문에 파고 자료를 이용하여 주기를 추정하기 위해서는 그 해역의 특성이 반영된 매개변수를 이용하여 추정하는 방법이 바람직하다.

2. 태풍 조건에서 연 최대 자료를 사용하는 경우, 전통적으로 이용하는 선형 회귀분석기법과 비선형 함수 기반의 매개변수 추정 결과가 상당한 차이를 보이는 경우, 적절한 선택 기준이 제시될 필요가 있다. 본 연구에서는 파고, 주기 자료의 변환 과정이 없는 비선형 함수 기반의 매개변수 추정 기법을 제안한다. 더불어 파고-주기 분포범위가 매우 크기 때문에 향후 연구방향으로는 하나의 곡선을 이용하는 방법보다는 파고-주기 결합(joint) 확률분포를 이용하는 방법을 추천한다. 이 방법의 적용을 위한 장기 자료 확보와 일반적인 양상 분석 연구도 요구된다.

3. 파고-주기 관계를 표현하는 선형 변환과정 없이 직접 비선형 매개변수를 추정하는 공식을 부록에 제안하였다. 이 공식을 이용하는 경우, 두 개의 매개변수를 추정하여야 하는 기존의 방법보다는 간단한 지수 매개변수(β) 하나만을 추정하는 형식의 공식으로 보다 안정된 추정방법으로 판단된다. 다른 절편지수(α)는 앞서 추정된 지수 매개변수를 이용하는 양해(explicit) 형식의 공식으로 계산이 가능하다. 선형 회귀모형은 간단하고, 안정된 매개변수 추정의 장점이 있으나, 자료 변환 과정이 요구된다. 따라서 비선형 함수를 이용하여 매개변수를 추정하는 경우, 안정적인 추정이 보장되는 경우 자료의 속성을 유지한 조건에서 매개변수를 추정한다는 측면에서 비선형 함수를 이용한 방법으로 가장 적절한 방법으로 제안한다.

4. 파고-주기 관계 매개변수 추정은 가용한 자료를 이용하여 추정하기 때문에 관측 자료가 충분하지 못한 경우가 빈번하게 발생할 수 있다. 자료가 부족한 상태에서의 매개변수 추정은 통계적인 불확실성을 증가시키기 때문에 모델 자료를 이용하여 충분한 신뢰할만한 자료를 확보하여 추정할 필요가 있다.

감사의 글

본 연구는 독도의 지속가능한 이용 연구사업(PG-53502)의 지원을 받아 수행되었습니다, 연구비 지원에 감사드립니다. 또한 세세한 심사로 논문 보완에 도움을 주신 익명의 심사위원에게도 감사를 드립니다.

Figure 1.

Location map of the coastal grid and inner-coastal (inside) grid points (MOF, 2019; Cho et al., 2020).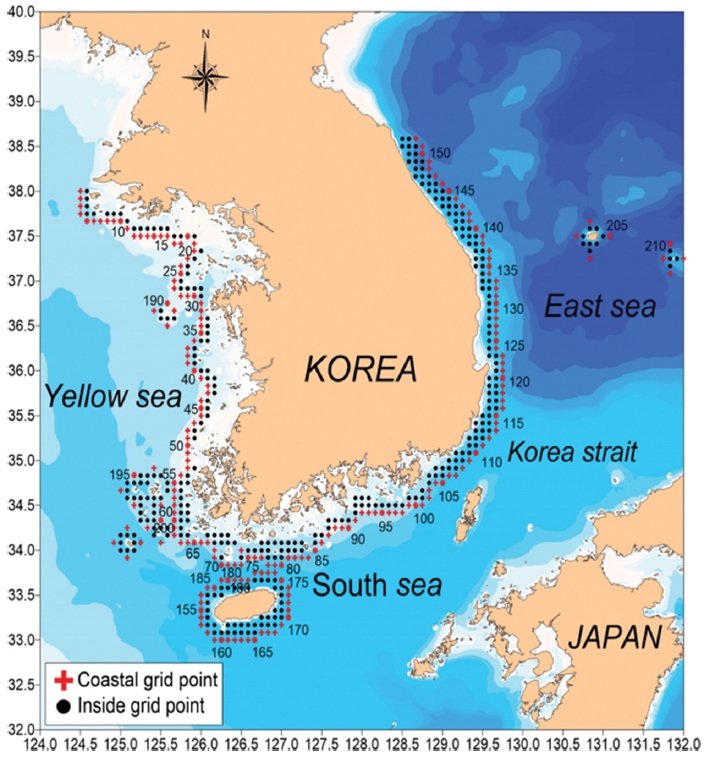

Figure 2.

Station (coastal grid points) numbers and the representative comparison eight station points in the divided coastal zones (MOF, 2019; Cho et al., 2020).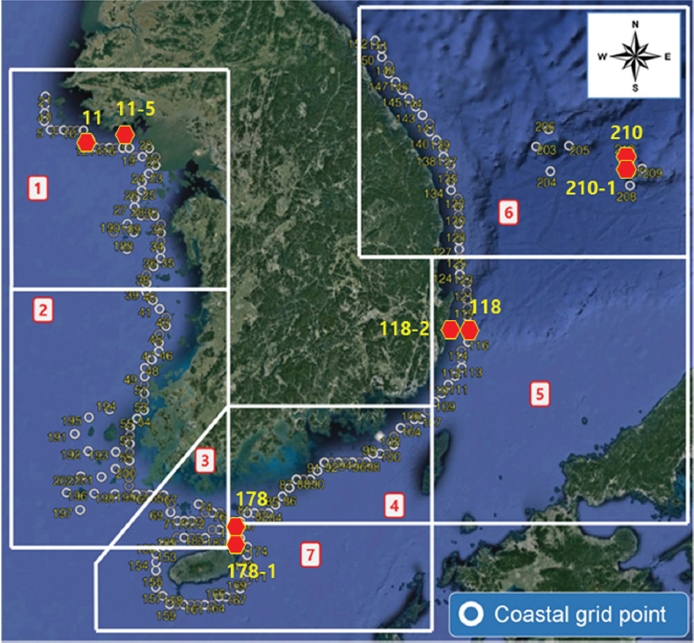

Figure 3.

Comparison plot of the SPM, Goda, and mean functions (Suh et al. method) (blue line = Goda formulae, orange line = SPM formulae, and pink line = mean function).

Figure 4.

Hs-Tp data scatter plot and fitting-curves by the regression methods (red = linear transformation curve fit (Case 1, SL), blue = nonlinear fitting curve (case 2, NL), green = robust linear transformation regression curve (Cases 3 and 4, RL, RL/C), black = SPM + Goda mean curve = Suh method).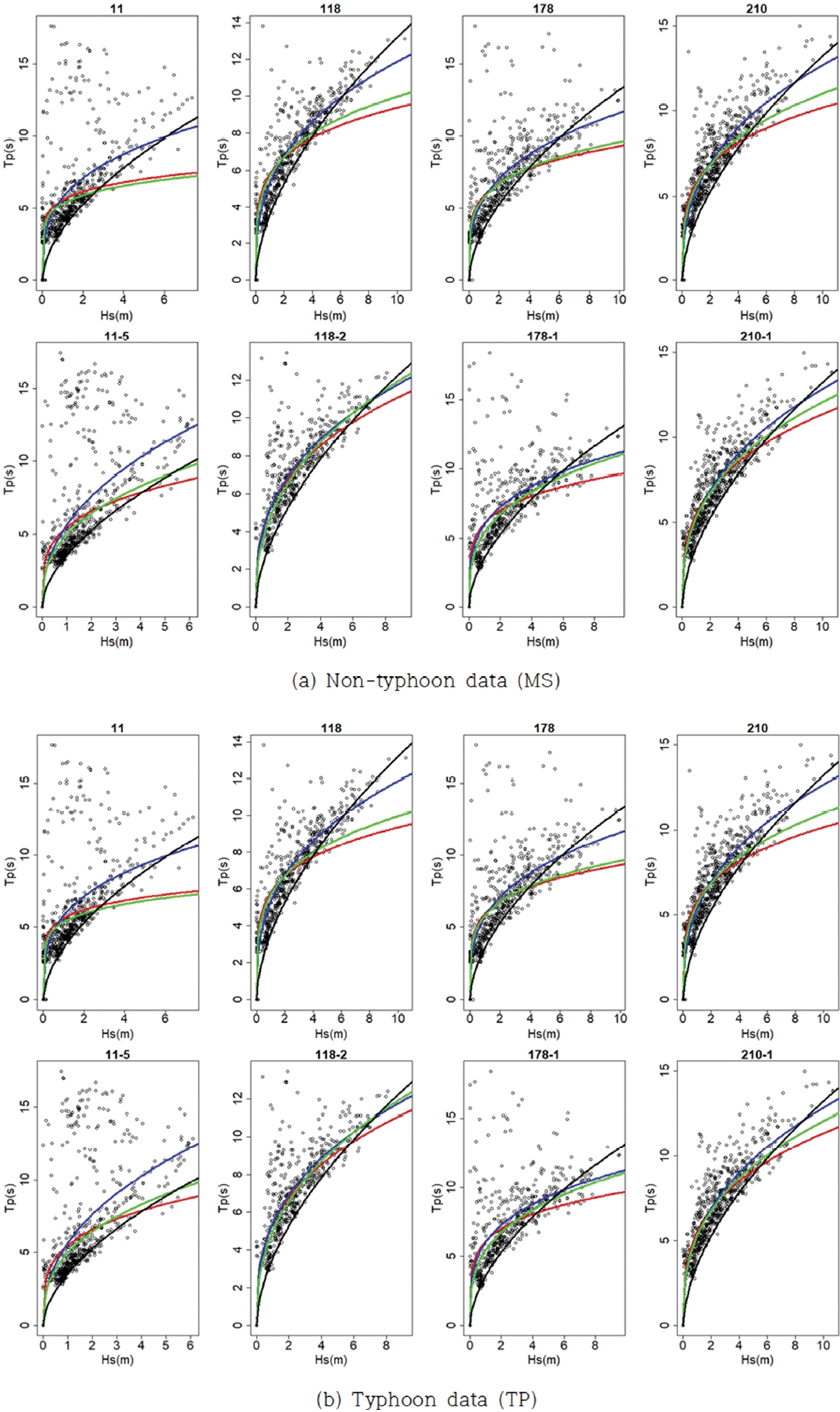

Figure 5.

Parameters scatter plot of the estimation methods (upper panel = simple linear regression (case 1, SL) vs. robust linear regression (case 3, RL), lower panel = simple linear regression vs. power function non-linear regression, Power function NLR; left panel = intercept parameter, right panel = slope (exponent) parameter).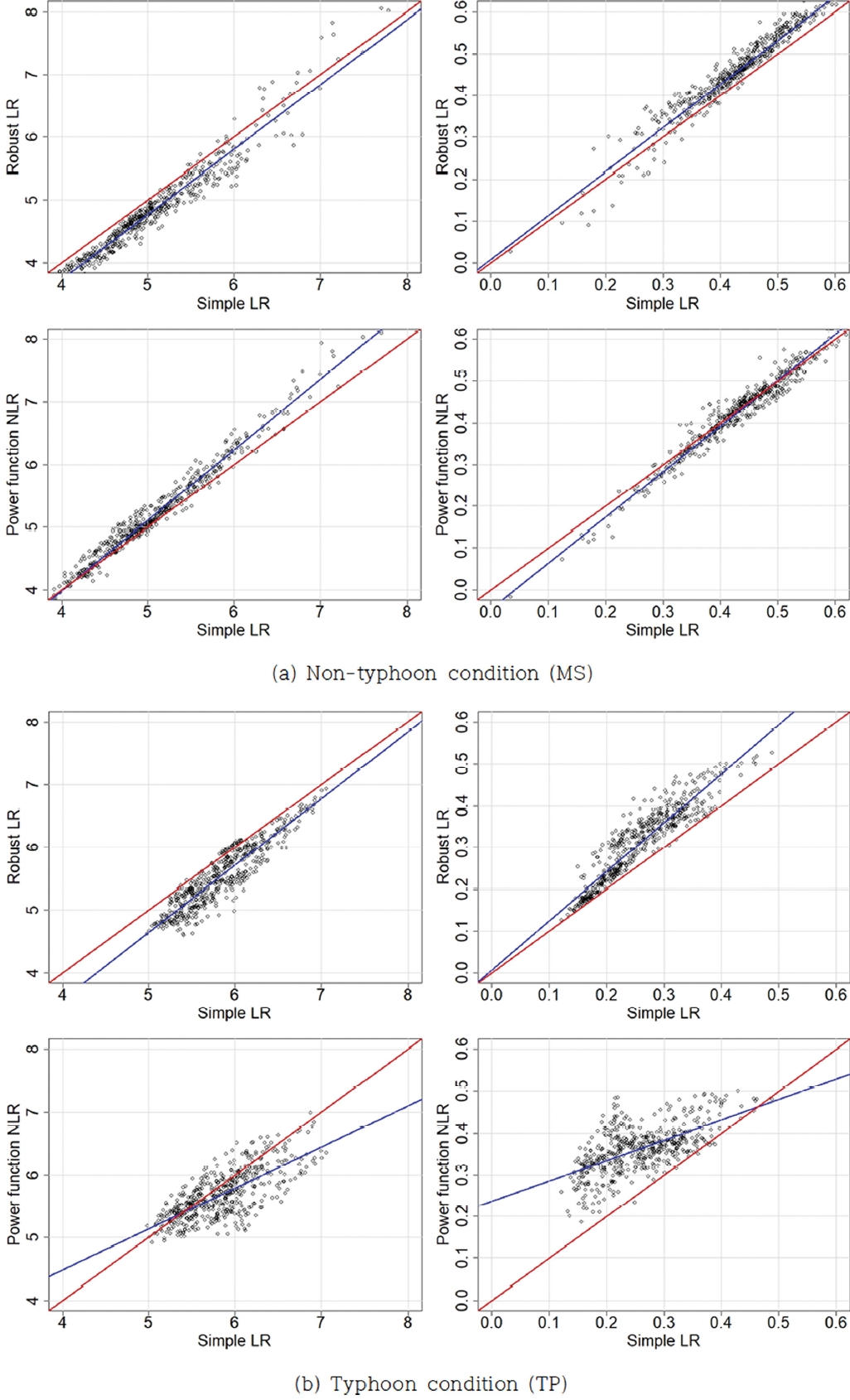

Figure 6.

Estimation parameter change pattern (Roman numbers, I, II, ..., VII = Coastal Division numbers in Fig. 2: Left region of the vertical red line = 210 coastal grid points from 1 to 210 (horizontal axis) in Fig. 2; Right region of the vertical red line = 310 inner (coastal) grid points from 1 to 310 (horizontal axis) in MOF (2019); estimation method = linear regression method). Result codes = (a) SL_MS_0, SL_MS_1, (b) SL_TP_0, SL_TP_1.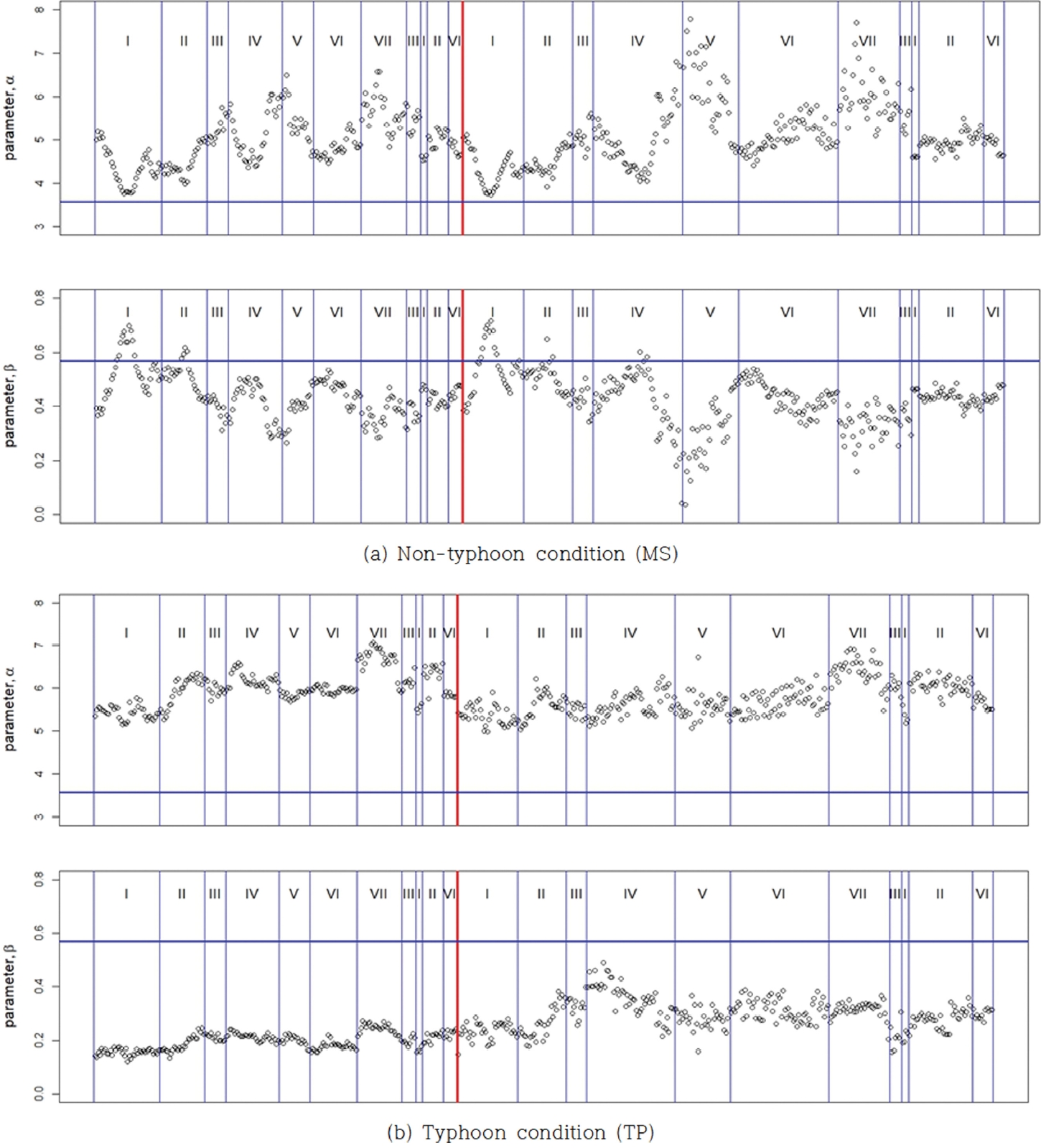

Table 1.

Summary of the power function parameters

Data	Alpha	Beta	Reference
T1/3, H1/3	3.85	0.5	SPM (1977)
T1/3, H1/3	3.54-4.45	0.38-0.60	Kamphuis (2000)
T1/3, H1/3	4.0-4.6	0.5	Goda (2000)
T1/3, H1/3	3.3	0.63	Goda (2003)
Tp, Hm0	6.16/5.59/6.65/6.50	0.26/0.20/0.23/0.22	Suh et al. (2008, 2010)⁽¹⁾
Tp, Hm0	ACW/ES/SS/WS⁽³⁾	ACW/ES/SS/WS⁽³⁾	Suh et al. (2008, 2010)⁽²⁾
	7.92/10.14/8.86/6.57	0.26/0.13/0.20/0.35
	7.92/9.96/6.67/8.82	0.26/0.15/0.34/0.20

Ref. (1) Sites = 4 stations, every monitoring data, (2) Sites = 106 stations, hindcast AM data (1997~2003), (3) ACW/ES/SS/WS = All Coastal Waters/East Sea/South Sea/West Sea, (4) Assumption: T_1/3 = 0.95Tp, Hmo = Hs = H_1/3.

Table 2.

Estimation case code based on the data and methods

	Case 1: SL	Case 2: NL	Case 3: RL	Case 4: RL/C
Data cases	Simple linear regression	Non-linear regression (without constraints) (0.0 < β < 1.0)	Robust linear regression	Robust linear regression with constraints (0.2 < β < 0.8)
MS-210	SL_MS_0	NL_MS_0	RL_MS_0	RL/C_MS_0
MS-310	SL_MS_1	NL_MS_1	RL_MS_1	RL/C_MS_1
TP-210	SL_TP_0	NL_TP_0	RL_TP_0	RL/C_TP_0
TP-310	SL_TP_1	NL_TP_1	RL_TP_1	RL/C_TP_1
TOTAL	SL	NL	RL	RL/C

Table 3.

Location coordinates of the sample stations

Coastal grid point no.	Longitude (E)	Latitude (N)	Inner grid point no.	Longitude (E)	Latitude (N)
11	125.083	37.583	11-5	125.500	38.583
118	129.750	35.750	118-2	129.583	35.750
178	126.750	33.750	178-1	126.750	33.667
210	131.833	37.417	210-1	131.833	37.333

Table 4.

Station (grid) numbers in the divided coastal zones and the assigned sequential numbers of the Inner-coastal grid numbers (Cho et al., 2020; MOF, 2019)

(a) Range of the sequential numbers of the grid points in each divided zone

Divided zone no.	Description of the zones	Grid numbers
Divided zone no.	Description of the zones	Coastal grids (Total 210 grids)	Inner-coastal grids (Total 310 grids)
1	Mid-north coastal waters of the West Sea	1-38, 187-190	1-35, 258-261
2	Mid-north coastal waters of the West Sea	39-64, 191-202	36-63, 262-298
3	Jeju northern waters, mid-west coastal waters of the South Sea	65-76, 179-186	64-75, 251-257
4	Mid-east coastal waters of the South Sea	77-107	76-126
5	Mid-south coastal waters of the East Sea	108-125	127-158
6	Mid-north coastal waters of the East Sea	126-152, 203-210	159-215, 299-310
7	Jeju coastal waters (except Jeju northern waters)	153-178	216-250

Table 4.

(b) Assigned sequential numbers of the Inner-coastal grid points

SN	IGN	SN	IGN	SN	IGN	SN	IGN	SN	IGN	SN	IGN	SN	IGN	SN	IGN	SN	IGN
1	1-1	41	42-1	81	79-1	121	105-2	161	128-1	201	147-1	241	170-4	281	194-4	301	204-1
2	2-1	42	43-1	82	79-2	122	106-1	162	129-1	202	147-2	242	171-1	282	194-5	302	204-2
3	3-1	43	44-1	83	80-1	123	106-2	163	130-1	203	147-3	243	171-2	283	194-6	303	204-3
4	4-1	44	45-1	84	80-2	124	107-1	164	131-1	204	148-1	244	172-1	284	195-1	304	205-1
5	4-2	45	46-1	85	80-3	125	107-2	165	132-1	205	148-2	245	173-1	285	195-2	305	206-1
6	4-3	46	47-1	86	81-1	126	107-3	166	132-2	206	149-1	246	175-1	286	196-1	306	206-2
7	4-4	47	48-1	87	81-2	127	108-1	167	133-1	207	149-2	247	176-1	287	197-1	307	207-1
8	4-5	48	49-1	88	82-1	128	108-2	168	133-2	208	149-3	248	176-2	288	197-2	308	208-1
9	10-1	49	53-1	89	82-2	129	109-1	169	134-1	209	150-1	249	177-1	289	197-3	309	209-1
10	11-1	50	54-1	90	83-1	130	111-1	170	135-1	210	150-2	250	178-1	290	198-1	310	210-1
11	11-2	51	55-1	91	83-2	131	111-2	171	135-2	211	151-1	251	179-1	291	200-1
12	11-3	52	55-2	92	85-1	132	112-1	172	136-1	212	151-2	252	180-1	292	200-2
13	11-4	53	56-1	93	85-2	133	112-2	173	136-2	213	151-3	253	181-1	293	200-3
14	11-5	54	57-1	94	86-1	134	112-3	174	137-1	214	152-1	254	182-1	294	201-1
15	11-6	55	58-1	95	87-1	135	113-1	175	137-2	215	152-2	255	183-1	295	201-2
16	17-1	56	58-2	96	87-2	136	113-2	176	138-1	216	153-1	256	184-1	296	202-1
17	17-2	57	59-1	97	88-1	137	113-3	177	138-2	217	153-2	257	184-2	297	202-2
18	20-1	58	59-2	98	89-1	138	114-1	178	139-1	218	154-1	258	187-1	298	202-3
19	22-2	59	63-1	99	90-1	139	114-2	179	139-2	219	155-1	259	187-2	299	203-1
20	23-1	60	63-2	100	91-1	140	114-3	180	139-3	220	156-1	260	188-1	300	203-2
21	24-1	61	63-3	101	91-2	141	115-1	181	140-1	221	158-1	261	189-1	301	204-1
22	25-1	62	64-1	102	91-3	142	115-2	182	140-2	222	159-1	262	191-1	302	204-2
23	26-1	63	64-2	103	92-1	143	116-1	183	140-3	223	159-2	263	191-2	303	204-3
24	27-1	64	67-1	104	92-2	144	116-2	184	141-1	224	160-1	264	191-3	304	205-1
25	27-2	65	68-1	105	93-1	145	117-1	185	141-2	225	161-1	265	192-1	305	206-1
26	27-3	66	68-2	106	93-2	146	117-2	186	142-1	226	161-2	266	192-2	306	206-2
27	27-4	67	70-1	107	93-1	147	118-1	187	142-2	227	162-1	267	192-3	307	207-1
28	30-1	68	70-2	108	94-1	148	118-2	188	142-3	228	162-2	268	192-4	308	208-1
29	33-1	69	70-3	109	95-1	149	119-1	189	143-1	229	163-1	269	192-5	309	209-1
30	34-1	70	71-1	110	96-1	150	119-2	190	143-2	230	163-2	270	192-6	310	210-1
31	35-1	71	71-2	111	97-1	151	120-1	191	143-3	231	164-1	271	193-1	291	200-1
32	36-1	72	72-1	112	99-1	152	120-2	192	144-1	232	164-2	272	193-2	292	200-2
33	36-2	73	73-1	113	100-1	153	121-1	193	144-2	233	165-1	273	193-3	293	200-3
34	37-1	74	75-1	114	101-1	154	122-1	194	144-3	234	165-2	274	193-4	294	201-1
35	38-1	75	76-1	115	101-2	155	123-1	195	145-1	235	166-1	275	193-5	295	201-2
36	39-1	76	77-1	116	103-1	156	123-2	196	145-2	236	167-1	276	193-6	296	202-1
37	40-1	77	77-2	117	103-2	157	124-1	197	145-3	237	168-1	277	193-7	297	202-2
38	40-2	78	78-1	118	104-1	158	125-1	198	146-1	238	170-1	278	194-1	298	202-3
39	41-1	79	78-2	119	104-2	159	126-1	199	146-2	239	170-2	279	194-2	299	203-1
40	41-2	80	78-3	120	105-1	160	127-1	200	146-3	240	170-3	280	194-3	300	203-2

* SN = sequential numbers (1-310), IGN = Inner-grid point numbers assigned by MOF (2019)

REFERENCES

Ahn, K.M., Hwang, S.M., Chun, H.. (2016). Characteristics of storm waves at Gangneung port based on the wave hindcasting, J, of Korean Society of Coastal and Ocean Engineers, 28(6):375-382.

Cho, H.Y.. (2019). On the robust linear regression, KIDS REPORT, 1(1):21-26 (in Korean).

Cho, H.Y., Jeong, W.M., Baek, J.D.. (2020). Independence and homogeneity tests of the annual maxima data used to estimate the design wave height. J, of Korean Society of Coastal and Ocean Engineers, 32(1):26-38.

Goda, Y.. (2003). Revisiting Wilson’s formulas for simplified wind-wave prediction, J. Waterway, Port, Coastal and Ocean Engineering, 129, 93-95.

Goda, Y. (2010). Random Seas and Design of Maritime Structures. 3rd Edition, World Scientific, Singapore.

Jeong, W.M., Oh, S.H., Cho, H.Y., Baek, W.D.. (2019). Characteristics of waves continuously observed over six years at offshore central East coast of Korea, J. of Korean Society of Coastal and Ocean Engineers, 31(2):88-99.

Jung, D., Song, K.M., Shim, J.S., Lee, S.. (2020). Validation of CODAR 25 MHz high-frequency radar derived waves in Donghae, Korea, J. of Coastal Disaster Prevention, 7(3):127-138.

Kamphuis, J.W.. (2000. Introduction to Coastal Engineering and Management). World Scientific, Singapore.

Lee, U.J., Ko, D.H., Cho, H.Y., Oh, N.S.. (2021). Correlation analysis between wave parameters using wave data observed in HeMOSU-1&2, J. of Korean Society of Coastal and Ocean Engineers, 33(4):139-147.

Ministry of Oceans and Fisheries (2019). Report of the Deepwater Design Wave Estimation in the Korean Coastal Waters (in Korean).

Suh, K.D., Kwon, H.D., Lee, D.Y.. (2008). Statistical characteristics of deepwater waves along the Korean coast, J. of Korean Society of Coastal and Ocean Engineers, 20(4):342-354.

Suh, K.D., Kwon, H.D., Lee, D.Y.. (2010). Some statistical characteristics of large deepwater waves around the Korean Peninsula, Coastal Engineering, 57, 375-384.

U.S. Army Coastal Engineering Research Center (1977). Shore Protection Manual, The 3rd Edition, U.S. Government Printing Office, Washington, D.C., USA.

Venables, W.N., Ripley, B.D.. (2002. Modern Applied Statistics with S. Fourth Edition). Springer, New York.

APPENDICES

Appendix

1. Parameter estimation formulae of the non-linear regression curve.

Power 함수의 선형변환 과정을 수행하지 않고, 최소자승법으로 직접 최적 매개변수를 추정하는 수학적인 절차 및 수식 유도과정을 제시한다. 비선형 함수의 최적화는 일반적으로 반복기법이 요구된다. 본 연구에서 유도한 공식은 경사(지수) 매개변수(β)를 추정하면, 절편 매개변수(α)는 간단한 explicit 형식의 수식으로 직접 계산된다. 따라서 하나의 변수에 대한 비선형 함수의 “해(solution)”를 구하는 반복 절차가 된다. R 프로그램에서 제시하는 nls() 함수는 두 개의 변수(α, β)에 대한 비선형 최적화 문제로, 추정 변수의 개수로 보면 아래 제시되는 과정은 보다 간단한 공식으로 간주된다. 수식은 손실 함수(L)의 정의에서 시작한다.

(A.1)

L=∑i=1nei2=∑i=1nTi-α^·Hiβ^2

여기서, H_i, T_i (i = 1, 2, …, n) = 각각 (유의)파고, 첨두주기 자료, n = 자료의 개수, e = 추정오차(잔차, e_i = T_i - T^i = T_i - α^·Hiβ^)이다. 최적 매개변수 추정은 오차제곱합으로 표현되는 L 함수를 최소화하는 α, β 추정 문제이며, 그 문제풀이는 L 함수를 추정 매개변수로 미분 = 0 조건을 부여하면 된다. 편의를 위하여 hat(^) 기호는 생략한다.

(A.2)

∂L∂α=∂∂α∑i=1nTi-αHiβ2=-2∑i=1nTi-αHiβ·Hiβ=-2∑i=1nTiHiβ-α∑i=1nTiHiβHiβ=0

(A.3)

∂L∂β=∂∂β∑i=1nTi-αHiβ2=-2∑i=1nTi-αHiβ·αHiβ·lnHi=-2α∑i=1nTHiβ·lnHi-α2∑i=1nlnHi·HiβHiβ=0=-2α∑i=1nTHiβ·lnHi-α∑i=1nlnHi·HiβHiβ=0

식(A.2), (A.3)를 각각 정리하면 다음과 같은 결과가 얻어진다.

(A.4)

α=∑i=1nTi·Hiβ∑i=1nHiβ·Hiβ=∑i=1nTi·Hiβ·lnHi∑i=1nHiβ·Hiβ·lnHi

(A.5)

fβ=∑i=1nTi·Hiβ·∑i=1nHiβ·Hiβ·lnHi-∑i=1nHiβ·Hiβ·∑i=1nTi·Hiβ·lnHi=0

(A.6)

∂fβ∂β=f'β=∑i=1nTi·Hiβ·lnHi·∑i=1nHiβ·Hiβ·lnHi+2∑i=1nTi·Hiβ·∑i=1nHiβ·Hiβ·lnHi·lnHi-2∑i=1nHiβ·Hiβ·lnHi·∑i=1nTi·Hiβ·lnHi-∑i=1nHiβ·Hiβ·∑i=1nTi·Hiβ·lnHi·lnHi=+2∑i=1nTi·Hiβ·∑i=1nHiβ·Hiβ·lnHi·lnHi-∑i=1nHiβ·Hiβ·lnHi·∑i=1nTi·Hiβ·lnHi-∑i=1nHiβ·Hiβ·∑i=1nTi·Hiβ·lnHi·lnHi

식(A.5), fβ^=0 비선형 방정식의 해(β^)를 먼저 구하고, 그 값을 이용하여 다음 매개변수(α^)을 계산하면 된다. 파고-주기 관계곡선의 경우, β 범위를 [0, 1] 정도로 한정할 수 있으면 양분법(bi-section method), 또는 다음과 같은 NewtonRaphson 반복추정 기법 등을 이용하여 “해”를 구할 수 있다. f'(β) 함수((A.6) 참고)는 매우 복잡해지는 경우가 빈번하기 때문에 보다 간단하게 적절한 정확도를 가지는 수치미분을 적용하여도 실질적으로 적절한 수준의 “해”를 얻을 수 있다.

(A.7)

βk+1=βk+fβkf'βk, k=0, 1, 2, …, β0=0.5,bk+1-βk≤ε=10-5-10-7

R 프로그램에서 제공하는 함수를 이용하는 경우, 하나의 매개변수(β) 추정으로 한정하는 경우, “해”가 존재라는 상한-하한 범위를 지정하여 양분법(bi-section method)으로 추정하는 uniroot() 함수를 이용하는 방법, 또는 수렴속도가 빠른 Newton-Raphson 알고리즘을 이용하는 nls() 함수를 이용할 수 있다.