1. 서 론
현재 우리나라 항 외곽시설은 오십 년 혹은 백 년 빈도의 파랑을 대상으로 내구력을 담보할 수 있도록 설계되며, 이 과정에서 설계 파랑 선정이나 설계 과정에서 발생할 수 있는 오류는 안전계수를 활용하여 제어된다. 우리나라 신뢰성 기반설계와 관련된 대부분의 연구에서도 단지 전술한 안전율이 하중 증가계수와 저항 감소계수로 세분될 뿐 이러한 시각은 그대로 유지된다. 이렇듯 신뢰성 해석이 지닌 많은 가능성에도 불구하고 우리나라에서만 유독 제한적인 범위에서만 활용되는 이유로는 여러 가지를 생각해볼 수 있으나, 그 중 설계빈도라는 다소 모호한 설계개념에서 벗어나지 못하는 인식체계가 가장 크게 작용하는 것으로 보인다. 그러나 설계빈도라는 개념은 설계 편의를 위해 항 외곽시설에 작용하는 여러 외력의 하나인 파랑의 성격을 어떻게 특정할 것인가를 다룰 뿐 이렇게 특정된 파랑에 대해 견디게끔 설계된 항 외곽시설이 얼마나 강건한지 혹은 허약한지를 우리에게 이야기해주지 않는다. 항 외곽시설이 강건한 정도는 항 외곽시설과 파력의 상호작용으로 인한 구조물의 응답 특성이 담긴 파괴확률로 다룰 수 있으며, 이러한 파괴확률은 전술한 신뢰성 기반설계에서도 중요한 역할을 담당한다(Ang and Tang, 1984). 적정 파괴확률이 담보되도록 신뢰성 기반설계로부터 도출된 항 외곽시설이 의도한 역할을 충실하게 수행할 수 있으려면 신뢰성 해석과정에 활용되는 확률모형이 구조물의 응답에 영향을 미치는 파력, 양력, 조위, 마찰력, 전도 모멘트와 같은 확률변수에 내재하기 마련인 불규칙성을 충분한 정도로 기술할 수 있어야만 한다[Fig. 1 참조](Cho, 2021a, 2021b, 2021c, 2021d, 2021e, 2021f, 2021g, 2021h; Cho and Cho, 2022). 이처럼 확률모형이 지니는 중요성에도 불구하고 현재 직립식 방파제 신뢰성 기반설계와 관련된 대부분의 연구에서는 파력과 양력에 내재하는 불확실성을 특정 재현 빈도의 설계 파랑과 Goda 모형의 overshooting 문제, 파랑 계측과정에서 발생할 수 있는 오류 등을 해결을 위해 도입된 계수를 활용하여 기술된다. 이 과정에서 전술한 보정 계수들은 정규분포를 추종하는 확률변수로 취급된다. 후행하는 신뢰성 해석과정에서 파력과 양력은 상수로 취급되며 보정 계수가 곱해지면서 확률변수의 지위를 회복한다. 그러나 이러한 설계 관행은 하중 계수와 저항 계수 산정을 위한 신뢰성 해석과정에서 파력과 양력이 정규분포를 따른다는 가정이 수행된 것과 같은 결과를 초래하나 이는 우리의 물리적 직관과는 맞지 않는다. 이 밖에도 파력과 양력 보정 계수가 상호 독립적으로 정규분포를 따른다는 사실에서도 확인되듯 이러한 설계 관행에서 파력과 양력은 상호 독립적인 추계학적 과정으로 다루어지게 되나, 이 경우 파괴확률이 과소하게 산출되는 오류를 결과할 수 있다. 이러한 추론의 근거는 양력으로 활동에 저항할 수 있는 유효하중이 감소한 상태에서 파력에 노출되는 경우 방파제가 더 쉽게 활동할 수 있다는 사실에서 찾을 수 있다.
이상에서 살펴보았듯 현재 우리나라의 신뢰성 기반설계 platform은 개선의 여지가 상당해 보인다. 논의를 더 전개하기 위해서는 신뢰성 기반설계를 검토할 필요가 있어 이를 정리하면 다음과 같다: 신뢰성 해석은 먼저, 항 외곽시설에 작용하는 외력과 저항력이 균형을 이루는 한계상태를 특정하고 이어 한계상태를 구성하는 확률변수의 여러 조합 중에 발생 가능성이 가장 큰 설계조합을 찾아내는 작업으로 요약할 수 있다. 이렇게 설계조합이 특정되면 표본공간의 원점으로 부터 설계조합까지의 최소거리로 정의되는 β 지수, 혹은 파괴확률을 산출할 수 있으며, 이러한 지표를 가지고 여러 설계안이 서로 차별화되며 목적하는 구조물의 설계가 구체화 된다. 최근 우리나라 신뢰성 기반설계 관련 연구는 현재 운영 중인 항 외곽시설을 대상으로 신뢰성 해석을 수행하고 이렇게 찾아낸 설계조합을 이루는 확률변수 중 파력, 저항력 값과 실제 설계에 사용된 파랑에 의해 결과된 파력과 저항력의 상대적 크기로 정의되는 하중 계수와 저항 계수 역설계에 천착하여 수행되는 듯 보인다. 전술한 계수는 결정론적 설계법의 안전율을 파력과 저항력으로 세분화한 것으로 과거 설계에 사용된 오십 년 혹은 백 년 빈도의 설계 파가 과소 혹은 과다한 정도를 가늠해 볼 수 있어 공학적 가치가 상당하나, 현재 우리나라 항 외곽시설의 설계 과정에서 전술한 하중 계수와 저항 계수가 활용된 예를 찾기가 쉽지 않다.
이렇게 더딘 체화과정에는 여러 가지 요인이 작용하나, 현재 항 외곽시설 파괴확률 산출과정에서 활동으로 인한 파괴를 중점적으로 다루고 전도파괴, 붕괴 파괴에 대해서는 분리해서 다룰 뿐 세 가지 파괴를 동시에 고려 하지 않는다는 사실이 가장 눈에 띄며, 직립식 방파제 속 채움재 총 소요량과 단위중량과 같은 물성값에 대한 고려가 누락 되어 있다는 사실 등도 일정 부분 기여하고 있는 것으로 판단된다. 전술한 설계 관행이 정당화되기 위해서는 활동, 전도, 붕괴라는 추계학적 사상이 상호 독립적인 과정이어야 하나, 이는 우리의 물리적 직관으로는 받아들이기 어려우며, 국내에서 선호하는 FORM(First Order Reliability Method) 혹은 SORM(Second Order Reliability Method)으로는 다수의 한계상태를 지닌 신뢰성 문제의 해석 자체가 불가능하다는 사실을 상기하면 단지 해석의 편의를 위한 설계 관행으로 보인다. 이 밖에도 오십 년 혹은 백 년 빈도의 설계 파가 항 외곽시설에 작용하는 파력, 양력, 조위, 마찰력, 전도 모멘트와 같은 확률변수에 내재하는 불규칙성을 충분한 정도로 기술할 수 있는지에 대한 우리나라 해안공학계의 오래된 논쟁, 우리나라 해안공학계 일각에서 꾸준히 제기되는 전술한 설계 파 산정 과정에 사용된 확률모형이 해역별로 각기 다른 우리나라 해양환경 특성을 충분히 담아내고 있지 못한 사실도 일정 부분 작용하는 것으로 보인다. 전술한 추론의 근거는 Castillo et al. (2006) 등이 수행한 직립식 방파제 신뢰성 기반 최적 설계에서 찾을 수 있다. 이 연구에서 Castillo et al.(2006)는 특정 빈도 설계 파랑의 사용은 지양하고, 관측자료로부터 산출된 유의파고, 최대 파고, 주기 확률모형을 사용하여 신뢰성 기반 직립식 방파제 최적화를 수행하여 우리나라 신뢰성 기반설계 platform 개발 방향에 대해 시사하는 바가 작지 않으나, 사용된 확률모형이 유럽 북해에 특화되어 우리나라 해양환경에 최적화된 확률모형과 신뢰성 기반 최적화 기법 개발이 필요해 보인다.
이러한 인식에 기초하여 본 연구에서는 하중 계수와 저항 계수의 완성도를 높이기 위한 기초연구의 일부로 직립식 방파제 활동, 전도, 붕괴에 대한 세 개의 한계상태 식과 직립식 방파제의 중량으로 비용함수를 구성하고 적정 파괴확률을 넘어서지 않는 범위에서 직립식 방파제 신뢰성 기반 최적 설계가 수행되며, 이 과정에서 특정 재현 빈도의 설계 파 사용은 지양된다. 최적화 설계 인자로는 방파제 두께, 직립식 방파제 환산 단위중량을 선정하였으며 이 경우 최적화된 환산 단위중량을 활용하는 경우 속 채움재의 수량과 물성값을 가늠해 볼 수 있다. 우리나라 해안공학계의 항 외곽시설 설계 관련 platform의 근간을 구성하는 재현 빈도가 적절하다면 재현 빈도로 산출한 항 외곽시설의 파괴확률은 최적화로 얻은 파괴확률에 수렴해야만 하며, 이때 하중 증가계수는 일이라는 값을 지녀야 한다. 이러한 사실에 준거하면 적정 설계 빈도를 설계 점을 구성하는 년 최대 파력 값과 년 최대 파력 확률분포로부터 역추산할 수 있으며, 이러한 설계빈도 역추산 작업도 함께 수행하였다. 이러한 작업으로 모두에서 언급한 오십 년 혹은 백 년 빈도의 설계 파가 항 외곽시설에 작용하는 파력, 양력, 조위, 마찰력, 전도 모멘트와 같은 확률변수에 내재하는 불규칙성을 충분한 정도로 기술이 가능한지에 대한 우리나라 해안공학계의 오래된 논쟁이 해소될 수 있기를 희망한다. 전술한 직립식 방파제 신뢰성 기반 최적화 과정에서는 오십 년 혹은 백 년 빈도의 파랑으로는 직립식 방파제 활동이나 전도에 가장 큰 영향을 미치는 확률변수인 파력, 양력, 모멘트에 내재한 불확실성을 충분한 정도로 기술할 수 없다는 문제를 해결하기 위해 년 최대 파력, 양력, 전도 모멘트라는 확률변수에 내재한 불규칙성은 Nataf 결합확률분포를 활용하여 충분한 정도로 기술될 수 있도록 노력하였으며, Nataf 결합확률분포는 파력, 양력, 전도 모멘트 사이의 강한 상관성을 기술할 수 있다(Nataf, 1962).
2. 신뢰성 해석
2.1 활동 파괴
신뢰성 기반설계는 항만 외곽시설이 요구되는 역할을 성공적으로 수행할 수 있는 확률을 활용하여 설계가 이루어지며 전술한 확률은 신뢰성이라 불린다. 신뢰성 함수 Z는 항 외곽시설의 활동에 대한 저항력 R과 파력 S의 차이로 정의하며 이 경우 Z는 다음과 같이 기술될 수 있으며,
항만 외곽시설 중 본 논문에서 다루는 직립식 방파제가 목표했던 기능을 수행하기 위해서는 항 외곽시설에 작용하는 파력 S와 활동에 대한 저항력 R의 차이로 정의되는 신뢰성 함수 Z가 다음과 같은 조건을 충족하여야 하며
여기서 μ, FH, FV, d는 각각 마찰계수, 파력, 방파제에 작용하는 양력, 기초 사석 층 정점에서의 수심을 나타내며 해양 환경에 내재한 불확실성으로 인해 확률변수로 다루어야만 한다.
2.2 전도파괴
전도에 대한 안정성이 확보되기 위해서는 다음과 같은 조 건이 충족되어야만 하며
식(6)에서 p1, p4, h c *
상기 식에서 β는 영각, α1, α2, α3는 파랑 주기가 미치는 영향을 설명하기 위해 도입된 계수로 다음과 같이 산출될 수 있으며,
여기서 hb는 방파제에서 5HMAX만큼 떨어진 지점에서의 수심을 나타낸다.
2.3 붕괴 파괴
기초 사석에 작용하는 유효하중 Fe는 허용지지력[490 kN/m2]보다 작게 유지되어야 하며 이를 기술하면 다음과 같으며
여기서 Fe, Te. Mnet, Wnet는 각각 다음과 같이 정의된다.
2.4 Subset Simulation 기법을 활용한 Monte Carlo Simulation
식(2), (3), (14)에 정의된 한계상태로 정의되는 파괴영역이 다섯 개의 확률변수로 구성된 표본 공간상에서 그려내는 형상은 매우 복잡하며 이 경우 현재 우리나라에서 선호하는 FORM 혹은 SORM 같은 해석적 방법으로는 신뢰성 해석을 수행할 수 없다. 이 경우 Monte Carlo Simulation을 활용하면 신뢰성 해석을 수행할 수 있으나, 필요한 정도를 담보하기 위해서는 상당한 횟수의 표집을 반복하여 수행할 수밖에 없어 소요되는 상당한 계산시간으로 설계 과정에서 쉽게 차용되지 못한 것으로 읽힌다. 그러나, 최근 조건부 확률을 활용하여 표집 횟수를 획기적으로 줄이면서도 상당한 정도를 확보할 수 있는 Subset Simulation 기법(Au and Beck, 2001)이 개발되어 보다 효율적으로 Monte Carlo Simulation이 설계 과정에서도 활용될 수 있을 것으로 보인다.
Au and Beck(2001)은 먼저 파괴 사상 F = [g(x) < 0]을 발생 확률이 상대적으로 큰 확률사상[Subset, Fi = [g(x) < yi]의 발생을 전제로 한 조건부 확률을 활용하여 다음과 같이 기술하여 Subset Simulation 기법을 완성하였다.
식(19)에서 각 Subset Fi = [g(x) < yi]의 threshold yi는 다음과 같은 조건이 충족되도록 선정되며
각 Subset Fi의 발생 확률은 0.1~0.2 사이의 값을 지니도록 조절되며 첫 번째 threshold y1의 값은 다소 거친 예비 Monte Carlo Simulation을 수행하여 선정되며, 이후 중간 단계에서의 표집은 수정 Metropolis-Hastings algorithm을 사용한 Markov Chains Monte Carlo(MCMC) 법을 사용하여 수행된다.
3. 신뢰성 기반 최적화 설계
직립식 방파제 두께와 속 채움재 소용량과 단위중량과 같은 물성값을 산출하기 위해 가상의 직립식 방파제를 대상으로 신뢰성 기반 최적화 설계를 수행하였다. 비용함수로는 직립식 방파제 중량 W = ρcg(d + hc)B으로 구성하였으며 목표 β 지수로는 2, 3, 4, 5를 사용하였다. 최적화 설계 인자로는 방파제 두께, 직립식 방파제 환산 단위중량을 선정하여 최적화된 환산 단위중량으로부터 속 채움재의 소요량과 물성값을 가늠해 볼 수 있도록 하였다. 대상 해역은 우리나라를 대표하는 항이 운영 중인 부산, 군산 전면해역으로 선정하였으며 수심은 직립식 방파제의 일반적인 거치 수심을 고려하여 20 m로 취하였다.
직립식 방파제의 한계상태 식 Gi [i = 1, 2, 3]는 활동, 전도, 붕괴 파괴를 고려해 총 세 개로 다음과 같이 구성하였으며,
파력과 양력, 모멘트 사이의 밀접한 상관성은 Nataf 결합확률분포를 사용하여 기술하였다.
전술한 최적화 문제는 다음과 같이 정식화할 수 있으며,
수치 모의에 사용된 구속조건을 나열하면 다음과 같다.
3.1 확률모형
3.1.1 부산
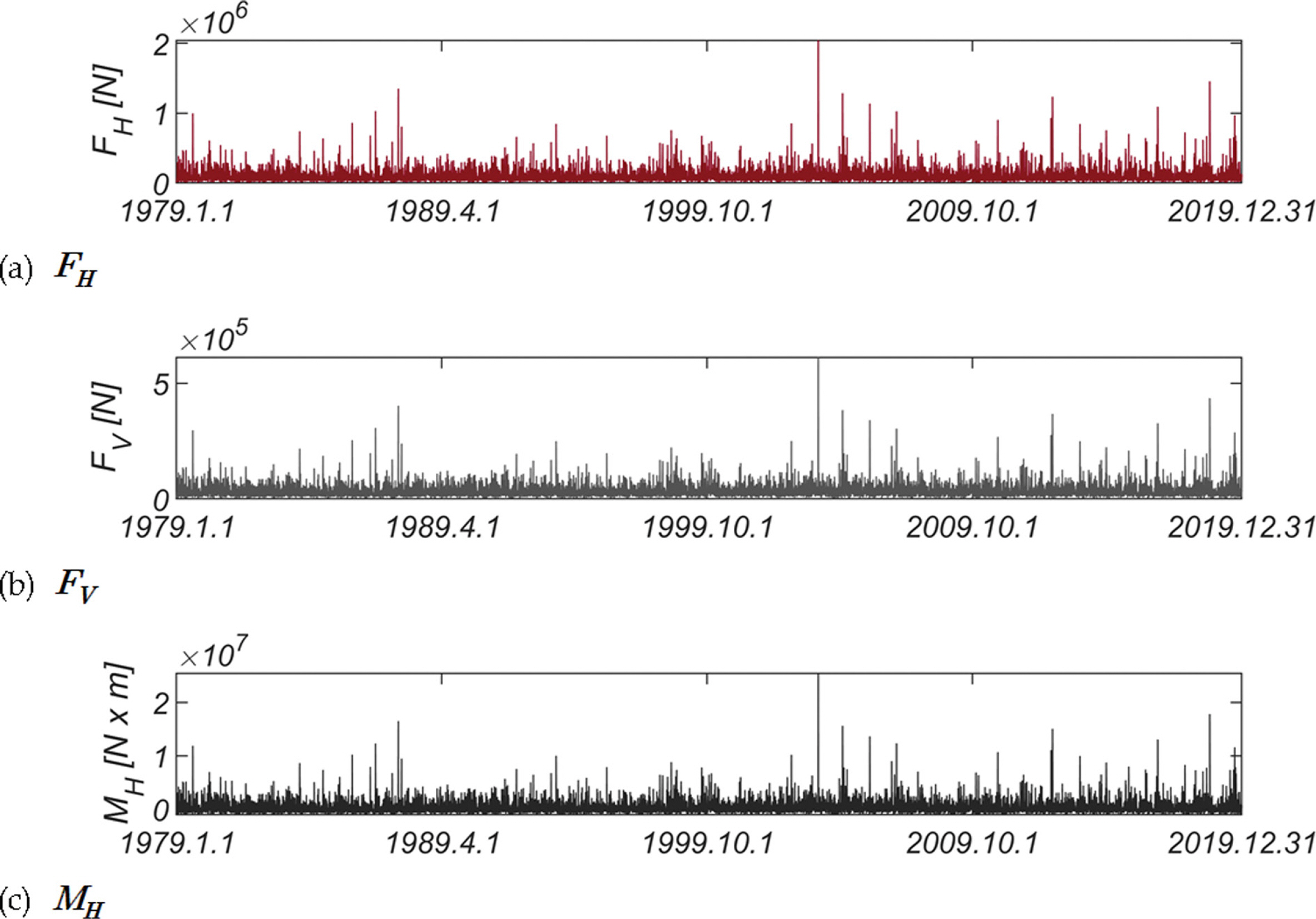
신뢰성 기반 최적화 설계에 필요한 파력, 양력, 전도 모멘트의 확률모형은 우리나라 해양환경의 특성이 담긴 장기 해양 관측자료로부터 특정된 년 최대 파력과 양력, 전도 모멘트 시계열자료 빈도해석 결과로부터 산출하였다[Fig. 2 참조](Jeong et al., 2018; Cho, 2024). 조위는 정규분포를 따르는 것으로 가정하였으며, 조위 표준편차는 JPHA(2007)에서 권하는 값을 사용하였다. JPHA(2007)에 따르면 조위의 표준 편차는 고극조위(H.H.W.L)의 삭망평균만조위(H.W.L.)에 대한 상대적 크기에 의해 결정되며, 고극조위가 삭망 평균만 조위와 비슷한 해역의 경우 0.2μh, 고극조위가 삭망평균만조위보다 2배 이상 큰 해역의 경우 0.4μh의 값을 지니며, 여기서 μh는 평균 조위를 나타낸다. 우리나라의 경우 고극조위(H.H.W.L)의 삭망평균만조위(H.W.L.)에 대한 상대적 크기를 살펴보면 동해안의 경우 2.0에서 2.5 사이의 값을 지니며 남해안과 서해안의 경우 1.0에서 1.5 사이의 값을 지닌다. 한계 상태 식에서 저항력의 크기를 결정하는 마찰계수 μ의 확률 모형으로는 부산, 군산 모두 Takayama(1992), Burcharth et al. (1994)의 연구성과에 준거하여 평균과 표준편차가 각각 μμ = 0.636, σμ = 0.0954인 정규분포를 따르는 것으로 가정하였다. 신뢰성 해석에 사용된 확률 모수는 Table 1에 정리하였다. 수심은 직립식 방파제의 일반적인 거치 수심을 고려하여 20 m로 취하였으며, d는 18.5 m, hc는 5 m, B는 10 m로 각각 취하였다.
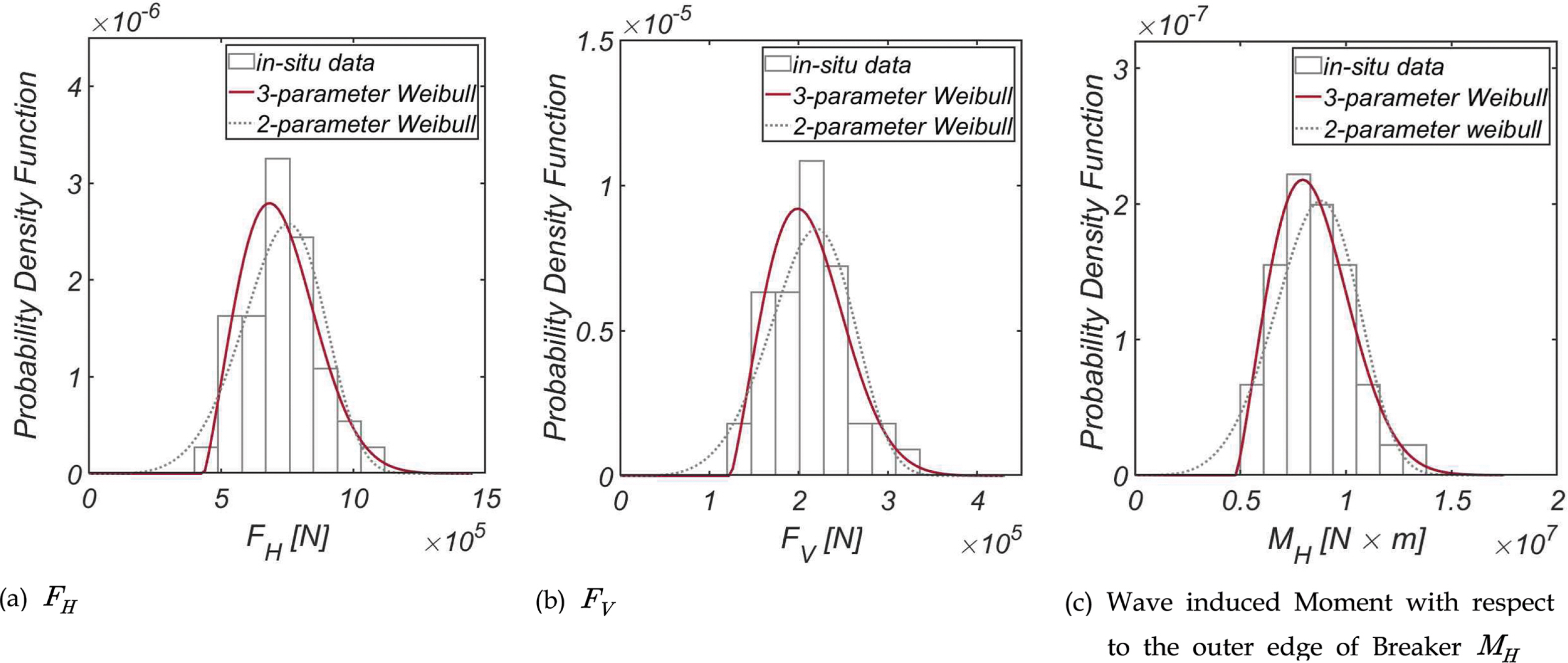
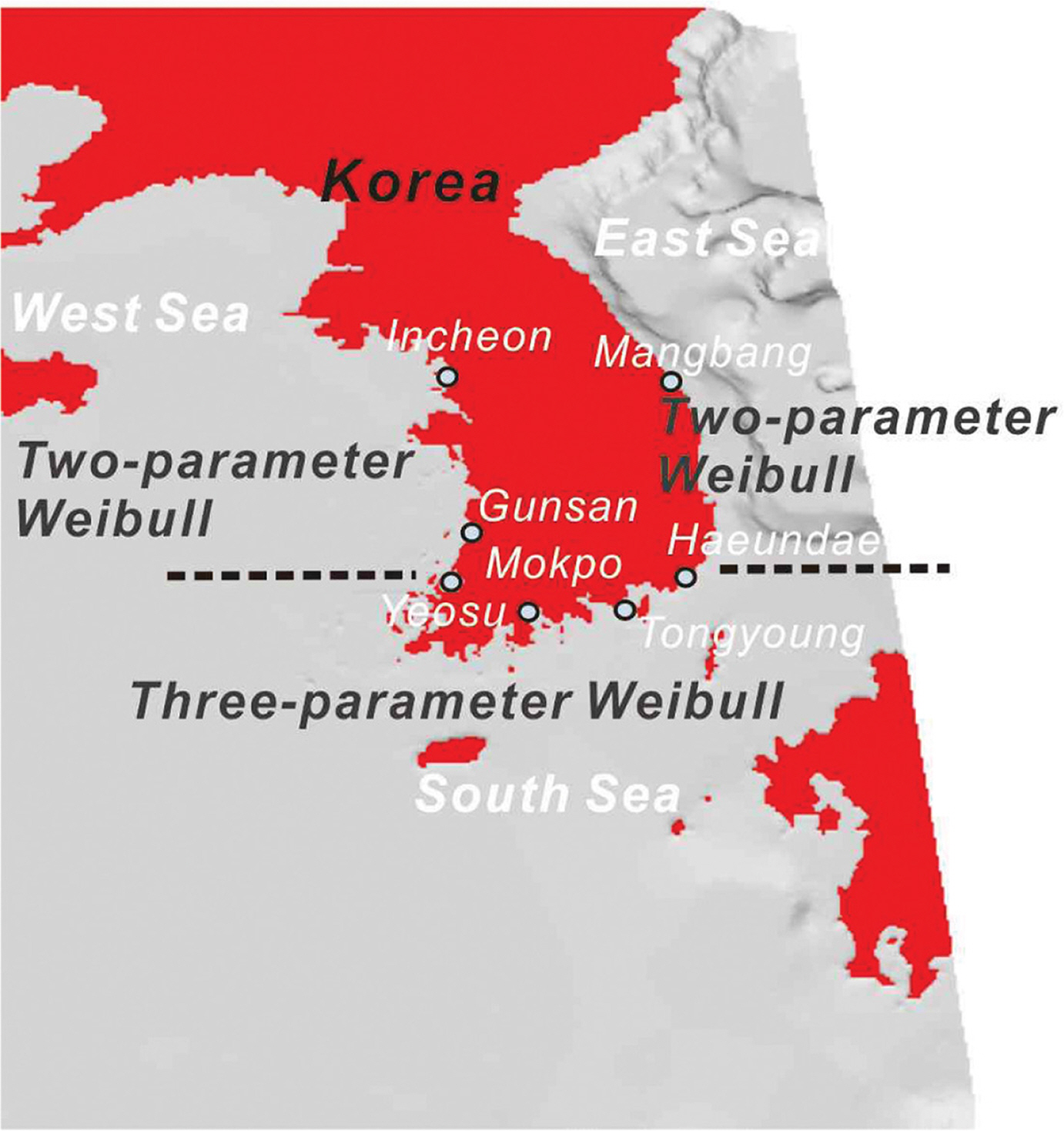
Fig. 3에는 이렇게 산출된 년 최대 파력과 양력, 전도 모멘트의 확률분포를 도시하였으며, 기저 확률분포로 Three-Parameter Weibull 분포를 사용하는 경우 적합도가 가장 우월한 것을 확인할 수 있으며 대표적 극치분포로 알려진 Three-parameter Weibull 분포는 다음과 같이 기술할 수 있으며
여기서 a, b, c는 확률계수로 각각 scale coefficient, shape, location coefficient로 불린다(Cho, 2024).
3.1.2 군산
Fig. 4에는 군산 전면해역에서의 장기 해양 관측자료를 정리하였으며(Jeong et al., 2018), Fig. 5에는 장기 해양 관측자료로부터 부산과 같은 방법을 사용하여 산출한 년 최대 파력과 양력, 전도 모멘트의 확률분포를 도시하였다.
부산과는 다르게 기저 확률분포로 Two-parameter Weibull 분포를 사용하는 경우 적합도가 가장 우월하였으며, 신뢰성 해석에 사용된 확률 모수는 Table 2에 수록하였다.
3.2 신뢰성 기반 최적화 설계
3.2.1 부산
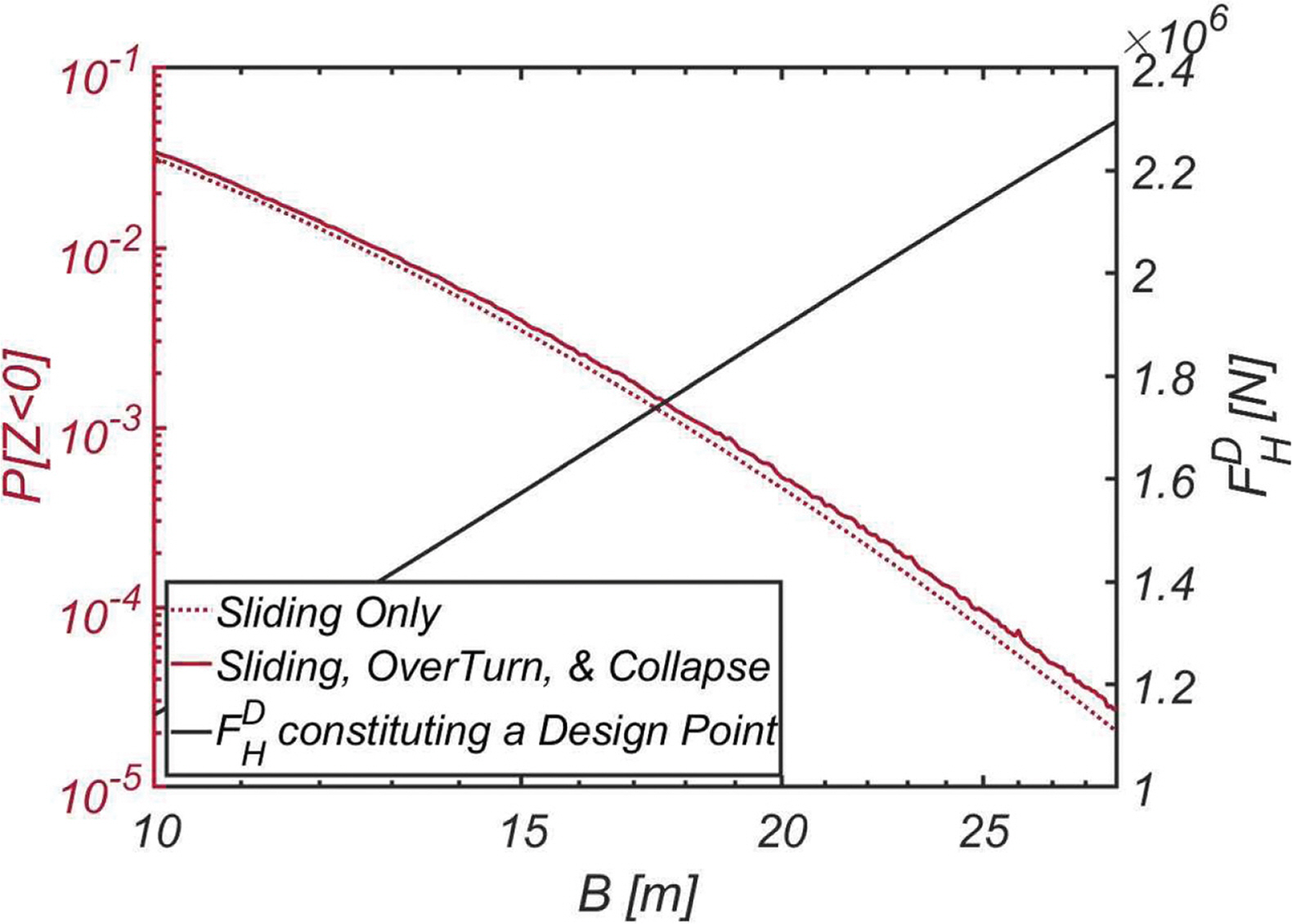
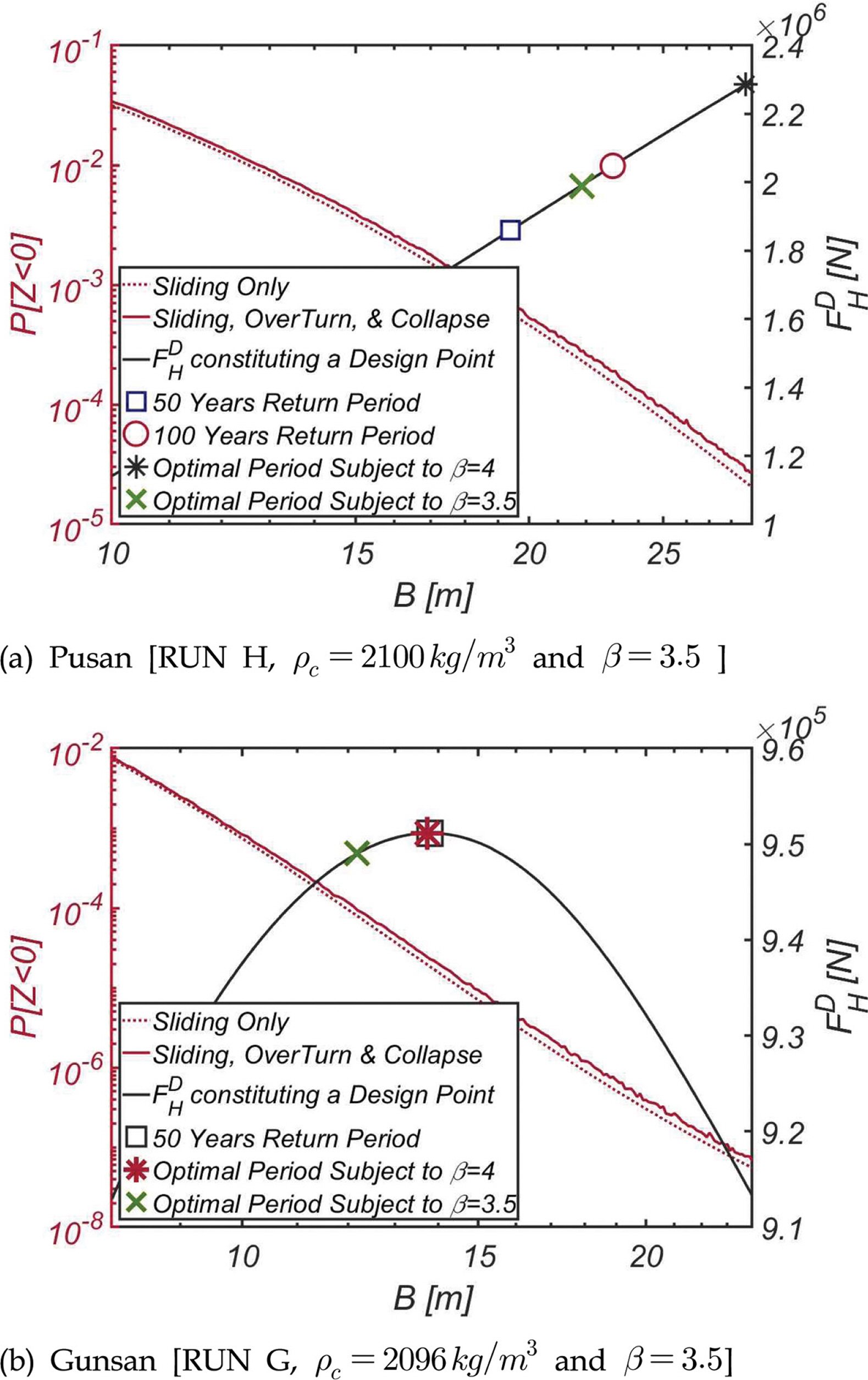
Table 3에는 목표 신뢰성 지수 βt를 2, 3, 4, 5로 바꿔가며 수행된 신뢰성 기반 최적화 설계 결과를 정리하였으며, Fig. 6에는 최적화 과정에서 관측된 β 신뢰도 지수, 초기 가정 값으로 정규화된 방파제 두께, 방파제 등가 밀도 ρc가 변화하는 양상을 정리하였다. 초기 가정 값으로 생긴 오차가 최적화 과정에서 빠르게 이완되며 β 신뢰도 지수, 방파제 두께, 등가 밀도 ρc가 최적화된 값으로 수렴해 가는 과정을 확인할 수 있다. 직립식 방파제 활동 외에도 전도와 붕괴로 인한 파괴가 직립식 방파제 신뢰성에 미치는 영향을 살펴보기 위해 최적화 과정에서 얻은 속 채움재[ρc = 2100 kg/m3, RUN3]로 채운 직립식 방파제 두께를 바꾸어가며 신뢰성 해석을 수행하였으며, 해석 결과는 Fig. 7에 정리하였다. 하중 증가계수와 저항 감소계수에 천착하여 수행되는 현재 우리나라 신뢰성 기반설계 platform과 비교하기 위해 활동 파괴만을 고려한 신뢰성 해석도 두께를 바꾸어가며 같이 수행하였으며, 이렇게 얻은 각 방파제 두께에 해당하는 설계조합을 구성하는 진행 방향 파력 F H D F H D
쉽게 예상해볼 수 있듯 방파제가 두꺼울수록 활동이 시작되는 임계 파력 F H D
3.2.2 군산
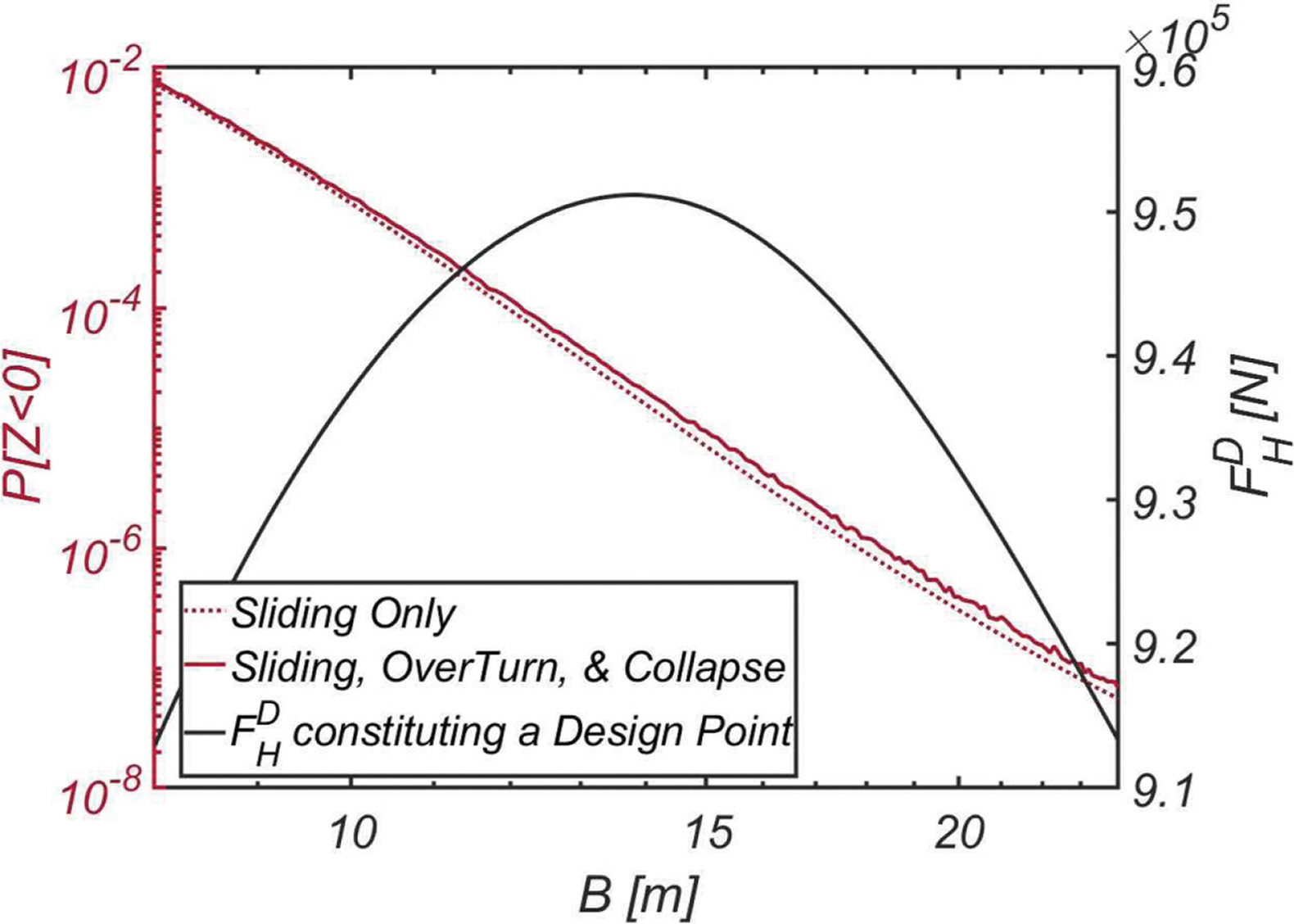
Table 4에는 목표 신뢰성 지수 βt를 2, 3, 4, 5로 바꿔가며 수행된 신뢰성 기반 최적화 설계 결과를 정리하였다. 최적화된 방파제 제원을 부산 전면해역에서의 값과 비교해서 살펴보면 등가 환산밀도는 ρc = 2100 kg/m3 내외로 비슷하나 직립식 방파제 두께가 부산과 비교해 절반에 불과하여 군산 전면해역에서의 해양환경이 상당히 온화하다는 것을 알 수 있다. 최적화 과정에서 얻은 속 채움재 [ρc = 2100 kg/m3, RUN 7]로 구성된 직립식 방파제 두께를 바꾸어가며 신뢰성 해석을 수행하였으며, 해석 결과는 Fig. 8에 정리하였다. 부산과 유사하게 케이슨이 두터울수록 같이 증가하는 양력으로 방파제의 전도파괴 가능성이 증가하는 것을 확연하게 관측할 수 있다. 여기서 한 가지 흥미로운 현상은 B = 13.8 m에서 정점을 찍은 F H D
4. 신뢰성 기반 최적화 설계로부터 역추산한 설계빈도
직립식 방파제 결정론적 설계에 사용된 파랑의 설계빈도가 적절하다면 구조물의 파괴확률은 최적화로 얻은 파괴확률로 수렴해야 하며, 이러한 사실과 년 최대 파력 확률분포로부터 적정 설계빈도를 추산해 볼 수 있다. 이러한 작업은 모두에서 언급한 오십 년 혹은 백 년 빈도의 설계 파가 항 외곽시설에 작용하는 파력, 양력, 조위, 마찰력, 전도 모멘트와 같은 확률변수에 내재하는 불규칙성을 충분한 정도로 기술이 가능한지에 관한 우리나라 해안공학계의 오래된 논제를 해소해 볼 수 있다는 점에서 상당한 공학적 가치를 지닌다.
설계빈도의 적정성을 가늠해보기 위해 Fig. 9에는 직립식 방파제 두께에 따라 파괴확률이 변화하는 양상[RUN H, RUN G]과 각 두께에 해당하는 설계 점을 구성하는 확률변수 중 파력 F H D F H 500 Years F H 100 Years F H 100 Years F H 500 Years
5. 결 론
우리나라 해안공학계에서 신뢰성 기반설계가 결정론적 설계가 지니는 한계를 치유할 수 있는 대안으로 여겨지기 시작한 지 이미 오랜 기간이 경과 했으나, 지난 십여 년간 이루어진 학계의 여러 노력에도 불구하고 여전히 신뢰성 기반설계는 설계 실무에서 적극적으로 활용되지 못하고 있는 것으로 판단된다. 이렇게 더딘 체화과정에는 여러 가지 요인이 작용하나, 현재 항 외곽시설 파괴확률 산출과정에서 활동으로 인한 파괴를 중점적으로 다루고 전도파괴, 붕괴 파괴에 대해서는 분리해서 다룰 뿐 세 가지 파괴를 동시에 고려 하지 않는다는 사실이 가장 눈에 띄며, 직립식 방파제 속 채움재 총 소요량과 단위중량과 같은 물성값에 대한 고려가 누락 되어 있다는 사실 등도 일정 부분 기여하고 있는 것으로 판단된다. 이 밖에도 오십 년 혹은 백 년 빈도의 설계 파가 항 외곽시설에 작용하는 파력, 양력, 조위, 마찰력, 전도 모멘트와 같은 확률변수에 내재하기 마련인 불규칙성을 충분한 정도로 기술이 가능한지에 대한 우리나라 해안공학계의 오래된 논쟁, 우리나라 해안공학계 일각에서 꾸준히 제기되고 있는 전술한 설계 파 산정 과정에 사용된 확률모형이 해역별로 각기 다른 우리나라 해양환경 특성을 충분히 담아내고 있지 못하다는 우려도 일정 부분 작용하는 것으로 보인다.
이러한 인식에 기초하여 본 연구에서는 우리나라 해안공학계에서 신뢰성 기반설계가 빠르게 체화되는 계기를 제공하기 위해 다 수의 한계상태를 지닌 직립방파제의 신뢰성 해석과 신뢰성 기반 최적 설계를 우리나라를 대표하는 항이 운영 중인 부산, 군산 전면해역을 대상으로 수행하였다. 이 과정에서 상당한 정도의 신뢰성 해석을 수행하기 위해, 특정 재현 빈도의 설계 파 사용은 지양하였으며, 이를 위해 직립 방파제의 파괴 여부를 결정하는 확률변수인 파력, 양력, 전도 모멘트에 내재한 불확실성은 장기 파랑 관측자료를 빈도 해석하여 얻은 확률모형을 사용하여 기술하였다. 직립식 방파제의 한계상태는 활동, 전도, 지지력을 고려하여 세 개로 구성하였으며, 파력과 양력, 모멘트 사이의 밀접한 상관성은 Nataf 결합확률분포를 사용하여 기술하였다. 이 밖에도 부분 안전계수 법에 천착하여 수행되는 우리나라 신뢰성 직립식 방파제 기반설계의 뼈대를 이루는 재현 빈도 설계 파의 강건한 정도를 살펴보기 위해 최적 설계된 직립식 방파제의 제원과 년 최대 파력 확률분포로부터 적정 설계빈도를 역 추산하는 작업도 같이 수행하였다.
쉽게 예상해볼 수 있듯 활동만을 고려하는 경우 파괴확률이 과소하게 산출되는 것을 확인할 수 있었으며, 지반 훼손으로 인한 붕괴를 고려하는 경우 직립식 방파제 파괴확률이 다소 증가하였으며, 이러한 경향은 직립식 방파제가 두꺼워지는 경우 현저하게 증가하였다. 신뢰성 기반 최적화 과정을 거쳐 얻은 직립식 방파제의 경우 직립식 방파제가 두꺼워지면 같이 증가하는 양력으로 인한 전도로 파괴확률이 증가하는 것을 확연하게 관측할 수 있었으며, 최적화 과정을 거치며 가벼워진 방파제로 붕괴로 인한 기여분은 미미한 것으로 드러났다. 이러한 모의 결과는 우리의 물리적 직관과 일치하며, 기존의 연구처럼 활동과 전도를 상호 독립적인 파괴 양식으로 다룰 경우, 과소하게 설계된 직립식 방파제가 결과됨을 함의하여 개선이 시급해 보인다. 이 밖에도, 특정 재현 빈도에 근거한 설계 파랑으로는 방파제 파괴확률을 일정하게 담보할 수 없는 것으로 드러났으나, 신뢰 지수가 β = 3.5~4를 만족하도록 최적 설계된 방파제는 전 해역에서 균질한 파괴확률을 확보할 수 있는 것으로 모의 되었다. 이상의 논의를 정리하면 특정 빈도에 근거한 설계 파로는 해역별로 특성이 각기 다른 우리나라 해양환경을 기술하기에는 상당히 버거워 보이며, 따라서 향후 목표 신뢰 지수 β = 3.5~4를 충족하는 신뢰성 기반 최적 설계 도입이 필요한 것으로 판단된다.