요약본 연구에서는 기하학적 방법을 통한 계산을 수행하여 석션앵커의 수직도와 회전오차의 복합작용이 인발지지력에 미치는 영향을 알아보았다. 수직도와 회전오차의 복합영향을 고려한 경우 단순 비례적으로 인발지지력에 영향을 미치지는 않고 서로 상대적으로 영향을 미치는 것으로 나타났다. 수직도와 회전오차를 복합적으로 고려한 기준은 기존문헌이나 DNV 기준에 제시되어 있지 않아 본 연구 결과를 종합하여 인발지지력의 감소폭 3%내를 제안하였다.
AbstractIn this study, geometric calculation was performed to investigate the influence of the combined effect of tilt and misorientation on the pullout capacity of suction anchor used in floating offshore wind turbine. When considering the combined effect of tilt and misorientation, it was observed that they do not proportionally affect the pullout capacity but rather influence each other relatively. Criteria considering both tilt and misorientation are not provided in existing literature or DNV recommendation. Therefore, based on the comprehensive results of this study, a proposed decrease in pullout capacity within 3% is suggested.
1. 서 론부유식 해상풍력 석션앵커의 설계에서는 앵커 설치 및 재설치에 대해 검토해야 한다. 석션앵커의 설치에는 많은 항목에 대한 고려가 필요하다. 앵커 자체의 제원뿐만 아니라 요구되는 앵커의 관입깊이, 부압, 관입속도, 내부 지반융기(히빙), 수직도, 회전오차 등과 지반의 전단강도 등이 필요하다. 재설치 시 점토의 경우 틱소트로피 특성도 필요하다. 이런 특성을 고려하여 설계된 앵커가 예상한 대로 설치가 진행되었는지 확인하기 위하여 앵커 설치 시 모니터링도 반드시 수반되어야 한다. 모니터링 결과에 따라 지형적(지표면 및 지층 경사) 및 지반공학적(지층의 불균질성: seam or lenses 층 및 pocket 영역 존재), 설치장비, 환경적인 이유로 기준에서 벗어나 설치되는 앵커는 설치를 중단하고 앵커를 수거하여 재설치를 해야 한다.
특히 부유식 해상풍력 석션앵커의 설치에 있어 앵커의 수직도(tilt)와 회전오차(misorientation)는 매우 중요한 요소다. 이유는 부유식 해상풍력 운영 중 앵커인발지지력(pullout capacity)에 이 두 요소가 매우 큰 영향을 미칠 수 있기 때문이다. 부유식 해상풍력 석션앵커에는 고정식 해상풍력 석션 앵커에는 없는 계류선과 패드아이(앵커길이 L의 0.7L에 위치)존재하기 때문에 설치 시 수직도와 회전오차에 더 취약하다. 그래서 부유식 해상풍력 석션앵커 설치과정에 수직도 및 회전오차를 ROV를 통한 모니터링을 하고 설계단계에서 정의된 허용기준과 비교한다. ROV는 앵커 윗 부분에 부착해서 작동하고 수직도와 회전오차 모니터링 자료는 설치된 앵커의 최종 승인을 위한 중요한 자료도 사용된다.
Sparrevik et al.(2017)은 수직도는 지반조건(경사와 지반특성)에 따라 차이가 있지만 일반적으로 허용 오차를 ±10°를 언급하였다. 회전오차도 패드아이(padeye) 부분에 작용하는 회전력(torsion)에 따라 달라질 수 있지만 일반적으로 ±10°를 허용할 수 있음을 언급하였다.
하지만 DNV-RP-E303(DNV, 2021)에서는 앵커 설치 시 수직도 오차는 해저면 경사각에 따라 달라진다고 언급하고, 해저면 경사각이 5o보다 작다면 일반적으로 수직도 허용오차는 ±5°로 설정하지만, 해저면 경사각이 5o를 초과하면 수직도 설치 허용오차도 증가시켜야 하므로 각각의 경우에 대해 평가가 이루어져야 한다고 언급하고 있다. 그리고 앵커 설치 시 허용가능한 회전오차는 일반적으로 ±7.5°를 언급하였지만 이 역시 각각의 경우에 대해 평가가 이루어져야 한다고 언급하였다.
부유식 해상풍력에서 석션앵커는 주로 상부구조물에 작용하는 바람과 파도로 인해 계류라인을 통해 전달되는 인발력을 담당하므로 석션앵커의 인발지지력에 대한 연구는 매우 중요하여 부유식 해상풍력 석션앵커의 연구 초기에는 계류라인이 적합하게 정렬된 상태에서 석션앵커의 인발지지력 산정에 중점을 두었다. 즉 앵커 설치 시 수직도나 회전오차의 문제는 발생하지 않은 것으로 가정하고 패드아이 위치나 앵커 장경비와 관련된 인발능력을 산정하는 연구를 수행한 것이다(Ahmed and Hawlader, 2015; Ahn et al., 2015; Fu et al., 2020; Cheng et al., 2021). 하지만 앵커 설치 중 발생하는 수직도나 회전오차 문제가 앵커의 인발력에 영향을 미치는 것으로 알려졌다(Suroor and Hossain, 2015; Saviano and Pisano, 2017; Zhang et al., 2023). 하지만 현재까지 부유식 해상풍력의 석션앵커의 수직도와 회전오차, 그리고 이 둘의 효과를 같이 고려한 연구는 아직까지 미비한 실정이다. 특히 국내의 관련 연구는 극히 저조하여 기초적인 접근으로 기하학적 방법을 이용하여 부유식 해상풍력 석션앵커의 수직도와 회전오차에 따른 인발지지력 변화를 알아보았다.
2. 기존 연구셕션앵커의 경우 설치 중 수직도나 회전오차 등이 문제가 발생하여 제안된 허용 범위를 벗어나면 앵커의 재설치가 필요하다. DNV-RP-E303에 따르면, “석션앵커의 재설치(retrieval)는 앵커 설치단계 동안 우발적인 사고에 대해 앵커를 회수 후 재설치한다”라고 하고 있다. 석션앵커의 재설치는 구속된 앵커 격실 내로 물을 펌핑하여 앵커를 지반 밖으로 밀어내는 과압(overpressure)을 생성함으로써 수행한다.
재설치는 앵커 설치 중 어떤 이유로든 앵커가 해저에서 회수되어 1일 이내에 재배치되는 조건에 대해 주로 계산한다. 앵커 관입해석에 사용된 것과 같은 공식이 재설치에 사용되나, 앵커의 측면전단에 대한 점토의 경우 강도회복효과(틱소트로피)는 반드시 고려되어야 한다. 반면 모래의 경우 밀도 상태에 따라 다를 것이다. 일반적으로 조밀한 모래의 경우 석션앵커 관입으로 전단이 진행하면 부피가 증가하는 (+) dilatancy 발생으로 부의 간극수압 발생으로 강도가 커질 것이다. 느슨한 모래의 경우는 반대로 정의 간극수압 발생으로 강도가 작아질 것이다.
부유식 해상풍력 석션앵커의 재설치 문제는 해저지반의 경사, 앵커 설치 위치의 해류(current) 흐름, 계류선, 패드아이, 지반 내부 지층의 불균질성이 존재(샌드씸, 샌드포켓 등) 등에 의해 앵커의 수직도나 회전오차가 발생하기 때문이다. 특히 부유식 해상풍력 석션앵커에는 계류선과 패드아이가 존재하기 때문에 고정식 석션앵커 보다 수직도와 회전오차에 취약하다.
Fig. 1은 부유식 해상풍력 석션앵커를 목표한 지점까지 관입시키는 일반적인 설치 과정에서 시간에 따른 모니터링 결과를 나타낸 예이다. 앵커를 해저면의 정해진 위치에 착지시키기 위하여 수중에서 앵커의 위치와 방향의 조정, 착지 후 자중에 의한 앵커관입 과정과 부압에 의한 앵커 관입과정, 그리고 관입과정에서의 앵커의 수직도 조정과정이 이루어지는 것을 알 수 있다. 만약 앵커 관입과정에서 수직도가 설계 허용범위를 벗어나면 제거 후 재설치 과정이 필요하다(Colliat et al., 1998).
Fig. 2는 회전오차에 의해 앵커를 회수 후 재설치하는 모니터링 사례이다(Sparrevik, 2002). 그림에서 보는 바와 같이, 석션앵커 재설치과정에서 초기 10 m 근입과정에서는 약 2° 정도의 목표방향에서 오차가 발생하였으며, 이후 점점 증가하여 30 m까지 깊게 굴착되는 과정에서는 약 8° 정도의 오차가 발생하고 있음을 알 수 있다. 따라서 근입과정에서도 회전오차가 발생함을 알 수 있다.
Fig. 3은 석션앵커에서 회전오차를 모식도로 나타난 것으로 패드아이와 계류선이 목표방향에서 벗어난 것을 의미한다. 목표방향에서 벗어나 설치된 석션앵커는 인발력 작용 시 추가적인 토크의 발생으로 인발지지력을 감소시킨다. 석션앵커의 회전오차 관련 몇몇 연구가 진행되었다.
Suroor and Hossain(2015)은 석션앵커 설치과정에서의 부적절한 위치와 해류로 인한 편차로 발생한다고 가정하여, 점토지반에 대해 3차원 유한요소해석을 수행하여 회전오차에 따른 수직력, 수평력 및 torsion의 상호작용에 대한 연구를 수행하였다.
Saviano and Pisano(2017)는 점토지반에서 석션앵커의 회전오차에 의한 수직력 및 수평력에 미치는 영향을 연구하였으며, 인발지지력에 대하여 다양한 회전오차(β)을 적용하여 수치해석을 통해 분석하였다. 연구결과, 장경비가 클수록 수평력은 회전오차에 민감한 것으로 나타났다.
Zhang et al.(2023)은 모래지반에 대하여 회전오차(β)에 의한 Torsion에 대해 계류선(mooring line)의 효과를 고려한 수치해석 연구를 수행하였다. 즉 인발력의 작용점을 패드아이에 두는 경우와 계류선에 두는 경우에 대하여 연구하였다. 검토 결과, 회전오차 각 β가 15°보다 크면 인발지지력의 감소율이 크게 증가하는 것으로 나타났으며, 계류선을 고려한 해석이 계류선을 고려하지 않은 해석보다 인발지지력의 감소가 크다는 것을 보여주였다.
기존 연구 결과를 살펴보면 수직도에 대한 연구보다 회전오차에 대한 연구가 많이 진행되었음을 알 수 있다. 아마 앵커 설치 시 수직도가 문제가 생기면 제거하여 재설치를 하는 행위가 일반적이기 때문으로 판단된다. 반면 회전오차의 경우 설치 시 조정이 경사에 비해 상대적으로 어렵고 설치 이후 해류의 작용으로도 발생할 수도 있으므로 연구가 더 활발하게 이루어진 것으로 보인다.
3. 수직도 및 회전오차의 영향분석3.1 수직도 영향지반의 강도에 따라 지반내 셕션앵커 계류선의 형태(역 현수선형 모양)가 달라지므로 패드아이에 계류선으로부터 작용하는 힘의 각도의 범위도 달라진다. Fig. 4(a)는 점토지반의 비배수전단강도(단순전단시험 DSS 시험으로부터 구한)가 상한값(HE, high estimate)인 경우와 하한값(LE, low estimate)인 경우 두 가지에 대한 계류선 형태를 보여준다. 이 비배수전 단강도 상한값과 하한값은 현장 CPT 시험결과를 통해 산정하는데 앵커 관입 및 앵커 인발력도 상한값과 하한값 두 경우에 대하여 검토하는 것이 일반적이다(Sandven et al., 2014).
Fig. 4(b)와 (c)는 점토지반에서 앵커가 관입과정에서 좌측과 우측의 기울어져 수직도가 -/+ 5°인 것을 나타낸 것이다. 앵커가 좌측으로 기울어진 경우 완전 수직인 경우에 비해 하한값에 해당하는 계류선이 영향을 크게 받으므로 그림으로 표현한 것이고, 반대로 앵커가 우측으로 기울어지면 상한값에 해당하는 계류선이 영향을 크게 받는다.
Sparrevik et al.(2017)은 석션앵커의 수직도 허용 오차를 ±10o를 언급하였지만 DNV-RP-E303에서는 앵커 설치 시 수직도 오차는 해저면 경사각에 따라 달라진다고 언급하고 있다. 해저면 경사각이 5°보다 작다면 일반적으로 수직도 허용 오차는 ±5°로 설정하지만, 해저면 경사각이 5°를 초과하면 수직도 설치 허용오차도 증가시켜야 하므로 각각의 경우에 대해 평가가 이루어져야 한다고 언급하고 있다.
Fig. 5는 global 좌표계와 local 좌표계를 사용하여 최적의 패드아이 위치에서 석션앵커 수직도에 따른 패드아이에 걸리는 수직력과 수평력의 관계를 모식화 시킨 것이다. 수직도가 계류선 방향으로 불량해질수록 수평력은 감소하고 수직력이 증가하는 것을 알 수 있다. 만약 계류선 방향이 아닌 반대방향으로 앵커가 기울어지면 반대로 수평력은 증가하고 수직력은 감소한다.
1) 기울어짐이 없는 경우(δ = 無)에는 Fig. 6(a)와 같이,
- 수직력(V) = Pusinθ
- 수평력(H) = Pu․cosθ
2) 기울어짐이 있는 경우(δ = 有), Local 축 각도는 θ+δ이므로 수직 및 수평분력은 Fig. 6(b)와 같이,
- 수직력(VLocal) = Pu․sin(θ + δ)
- 수평력(HLocal) = Pu․cos(θ + δ)
3) 기울어짐이 있는 경우(δ = 有), Local 축을 투영시켜 Global 축으로 변환하게 되면 Fig. 6(c)와 같이, 수직 및 수평분력을 산정할 수 있다.
- 수직력(VGlobal변환) = Pu․sin(θ + δ)․cosδ
수평력(HGlobal변환) = Pu․cos(θ + δ)․cosδ
Fig. 7은 앞의 Fig. 5에 대한 계산 예로 패드아이에 작용하는 하중의 각도를 45°로 고정하고 계류선 방향으로 기울어짐에 따른 수평력과 수직력을 나타낸 것으로 수평력의 감소가 두드러지게 나타나는 것을 알 수 있다. 즉 수평력의 감소는 앵커 인발지지력의 저하를 유발시킨다. 왜냐하면 셕션앵커에서 최대 앵커저항은 일반적으로 파괴모드가 회전이 없는 순수 병진일 때 얻을 수 있도록 설계하는 것이 전제이기 때문이다(DNV, 2021).
또한, 인발지지력은 local 좌표계로 계산할 경우에는 수평력의 감소에 따라 수직력이 증가하므로 인발지지력은 동일하나, global 좌표계로 계산할 경우에는 기울어짐에 따라 인발지지력이 감소하다 δ가 45°에 도달하게 되면 인발지지력은 최대 70%대로 감소하는 것을 알 수 있다.
Table 1은 Fig. 7의 결과를 표로 정리한 것으로, 계류선방향으로 기울어짐이 δ = 0~10º 범위에서는 local 좌표계 대비 global 좌표계로 보면 인발지지력이 0~1.5% 정도 감소하고, δ = 15~20º 범위에서는 인발지지력이 3.4~6.0% 정도 감소하며, δ = 25~45º 범위에서는 인발지지력이 9.3~29.3%의 감소를 나타내고 있다.
기하학적 방법을 사용한 석션앵커의 수직도가 인발지지력에 미치는 영향을 종합하면, 기울기 δ가 10º 이내에서는 인발지지력의 감소가 계략적으로 2% 이내이지만 10º 이상의 기울어짐은 인발지지력을 크게 감소시키므로 서론에서 언급한 기존문헌(δ = 10º)과 DNV에서 제시한 기준(δ = 5º)이 어느정도 타당한 것을 알 수 있다.
3.2 회전오차 영향서론과 2장에서 언급한 바와 같이 인발지지력에 대한 석션앵커의 회전오차의 영향도 검토도 중요하다. 완벽하게 설치된 앵커에 비해 회전오차가 있는 앵커의 성능은 부가적인 토크 발생으로 감소한다. 회전오차가 있는 앵커의 성능 감소는 오차의 각도에 따라 다르고, 최대 허용 회전오차에 대해 검토가 이루어져야 한다.
서론에서 언급한 바와 같이 Sparrevik et al.(2017)은 회전 허용 오차를 ±10º를 언급하였고, DNV-RP-E303(DNV, 2021)에서는 앵커 설치 시 회전오차는 ±7.5°를 언급하고 있어 각각의 경우에 맞게 검토가 필요하다(Fig. 8).
Fig. 8은 최적의 패드아이 위치에서 앵커가 회전오차에 따라 인발 시 패드아이에 걸리는 수직력과 수평력, 회전토크의 관계를 모식화 시킨 것이다. 수직력은 회전오차와는 관계가 없고 수평력은 회전오차 증가에 따라 감소하는 것을 보여준다.
Fig. 10은 Fig. 9의 대한 계산 예로 패드아이에 작용하는 하중각을 45º로 고정하고 회전오차에 따른 수평력, 수직력, 회전토크를 산정한 결과이다. 아울러 인발지지력에 대해 같이 도시하였는데 회전오차가 증가함에 따라 인발지지력이 감소하여 회전오차가 앵커 인발지지력에 큰 영향을 미침을 알 수 있다.
Table 2는 Fig. 10의 결과를 표로 정리한 것으로, 회전오차가 δ = 0~15º 범위에서는 인발지지력이 0~1.7% 정도 감소하는 것으로 나타났고, δ = 20~75º 범위에서는 인발지지력이 3.0~27.0% 정도 감소하는 것으로 나타났으며, δ = 80~90º 범위에서는 인발지지력이 28.3~30.0%의 감소를 보여주고 있다.
기하학적 방법을 사용한 석션앵커의 회전오차가 인발지지력에 미치는 영향을 종합하면, 회전오차 β가 15° 이내에서는 인발지지력의 감소가 2% 이내로 미비한 것으로 나타났다. 서론에서 언급한 기존문헌 기준 10°와 DNV 기준 7.5°에 대해서는 1% 이내의 인발지지력 감소가 보이는 것으로 나타났다. 즉 본 기하학적 방법에 의한 연구 결과는 기존문헌에서 제시하는 허용회전오차 보다는 큰 δ = 15º까지는 인발지지력의 감소는 미비한 것으로 나타나 약간의 차이가 있는 것으로 알 수 있다.
3.3 수직도와 회전오차 복합 영향앞 절 3.1 및 3.2에서 언급한 바와 같이, 석션앵커가 계류선 방향으로 기울어짐과 회전오차에 따라 수직력에 비해 수평력의 감소가 두드러지게 나타나는 것을 알 수 있었으며, 인발지지력의 감소폭이 커지는 것을 알 수 있었다.
본 절은 수직도와 회전오차의 복합작용에 의한 영향을 분석하기 위해 앵커의 기울짐 δ = 0, 5, 10, 15, 20, 30, 45º에 대하여 회전오차 δ = 0~90º로 변화시켜 계산을 추가적으로 수행하였다.
Fig. 11은 계산 결과로 그림에서 보는 바와 같이, 기울어짐 δ≤ 15°에서는 회전오차 β의 증가에 따라 인발지지력의 감소가 두드러지게 나타나고 있으나, 기울어짐 δ > 20°에서는 회전오차 β의 증가에 따른 인발지지력의 감소는 회전오차 β의 영향이 미비한 것을 알 수 있다. 즉 기울어짐과 회전오차의 영향이 단순 비례적으로 인발지지력에 영향을 미치지는 않고 기울어짐이 작은 경우에 회전오차의 영향이 더 크게 작용하고 기울어짐이 큰 경우에는 상대적으로 회전오차의 영향이 적은 것을 보여준다.
Fig. 12는 Fig. 11의 결과를 기울어짐을 중심으로 다르게 표현한 것으로, 기울어짐 δ = 0°에서는 회전오차 β의 증가에 따라 인발지지력의 상대적인 감소폭이 29.29%로 가장 크게 발생하였으며, 기울어짐 δ = 5~20°에서는 회전오차 β의 증가에 따라 인발지지력의 상대적인 감소폭이 23.40~9.37%로 점점 감소하다가 기울어짐 δ = 45°에서는 회전오차 β의 증가에 따라 인발지지력의 감소가 발생하지 않는 형상을 보여준다.
본 연구에서 사용한 기하학적 방법에서 기울어짐 δ와 회전오차 β가 복합적으로 작용 시, 수직력 계산의 경우 Sine 항과 Cosine 항의 조합으로 이루어져 있고, 수평력 계산의 경우 Cosine 항의 조합으로 이루어져 있어 기울어짐 δ의 증가에 따른 수직력의 감소폭은 δ = 20°까지는 증가하다가 이후 감소하고, 회전오차 β의 증가에 따른 수평력은 비례적으로 감소함에 따라 인발지지력의 감소율이 감소 후 다시 증가하기 때문에 이와 같은 경향이 발생하는 것이다.
Table 3은 연구 전체 결과, 수직도(δ), 회전오차(β), 그리고 수직도·회전오차 복합작용에 대한 인발지지력의 변화를 나타낸 것이다. 수직도와 회전오차에 대한 기존 문헌자료와 DNV 기준을 각각 적용했을 때 기하학적 방법으로 석션앵커의 인발지지력을 검토한 결과 모두 그 감소가 미비한 것으로 나타나 기존에 제시된 기준이 타당함을 알 수 있다.
수직도와 회전오차를 복합적으로 고려한 기준은 기존문헌이나 DNV 기준에 제시되어 있지 않아 3.3의 결과를 종합하여 인발지지력의 감소폭을 3%내로 제안해 보면(표에 녹색 굵은 숫자의 범위), 수직도가 최대 10° 발생한 경우 허용할 수 있는 회전오차는 15°이고, 회전오차가 20° 발생한 경우에 허용 가능한 수직도는 5°이다.
본 연구는 기하학적 측면에서 석션앵커의 수직도와 회전오차를 고려한 연구로 향후 유한요소 수치해석과 모형실험 결과를 통해 추가적인 검토를 하고자 한다.
4. 결 론부유식 해상풍력 석션앵커에서 수직도(기울어짐)나 회전오차가 발생하면 앵커의 인발지지력에 영향을 미친다. 그래서 본 연구에서는 기하학적 측면에서 석션앵커의 수직도와 회전오차에 따른 앵커의 인발지지력의 변화를 산정하여 다음과 같은 결론을 도출하였다.
석션앵커가 계류선방향으로 기울어짐(δ)에 따라 인발지지력이 감소하는 것으로 나타났다. 기울기 δ가 10° 이내에서는 인발지지력의 감소가 계략적으로 2% 이내이지만 10° 이상의 기울어짐은 인발지지력을 크게 감소시켜 기존문헌(δ = 10°)과 DNV 기준(δ = 50°)에서 제시한 값이 타당한 것으로 보여진다.
석션앵커의 회전오차(β)가 인발지지력에 미치는 영향은 β가 15° 이내에서는 인발지지력의 감소가 2% 이내로 미비한 것으로 나타났다. 반면 기존문헌 기준 β = 10°와 DNV 기준 β = 7.5°에서는 1% 이내의 인발지지력 감소가 산정되어 기존기준이 좀 더 보수적이 측면이 있는 것으로 판단된다.
수직도와 회전오차의 영향을 복합적으로 고려한 경우 단순 비례적으로 인발지지력에 영향을 미치지는 않고 기울어짐이 작은 경우에는 회전오차의 영향이 크고 기울어짐이 큰 경우 회전오차의 영향이 작아 서로 상대적으로 석션앵커의 인발지지력에 영향을 미치는 것으로 나타났다.
수직도와 회전오차를 복합적으로 고려한 기준은 기존문헌이나 DNV 기준에 제시되어 있지 않아 본 연구 결과를 종합하여 인발지지력의 감소폭을 3% 내인 수직도가 최대 10° 발생한 경우 허용 회전오차는 15°이고, 회전오차가 20°인 경우에 허용 수직도는 5°이다.
Fig. 2.Observed misorientation of pile subjected to a small moment during penetration (Sparrevik, 2002). 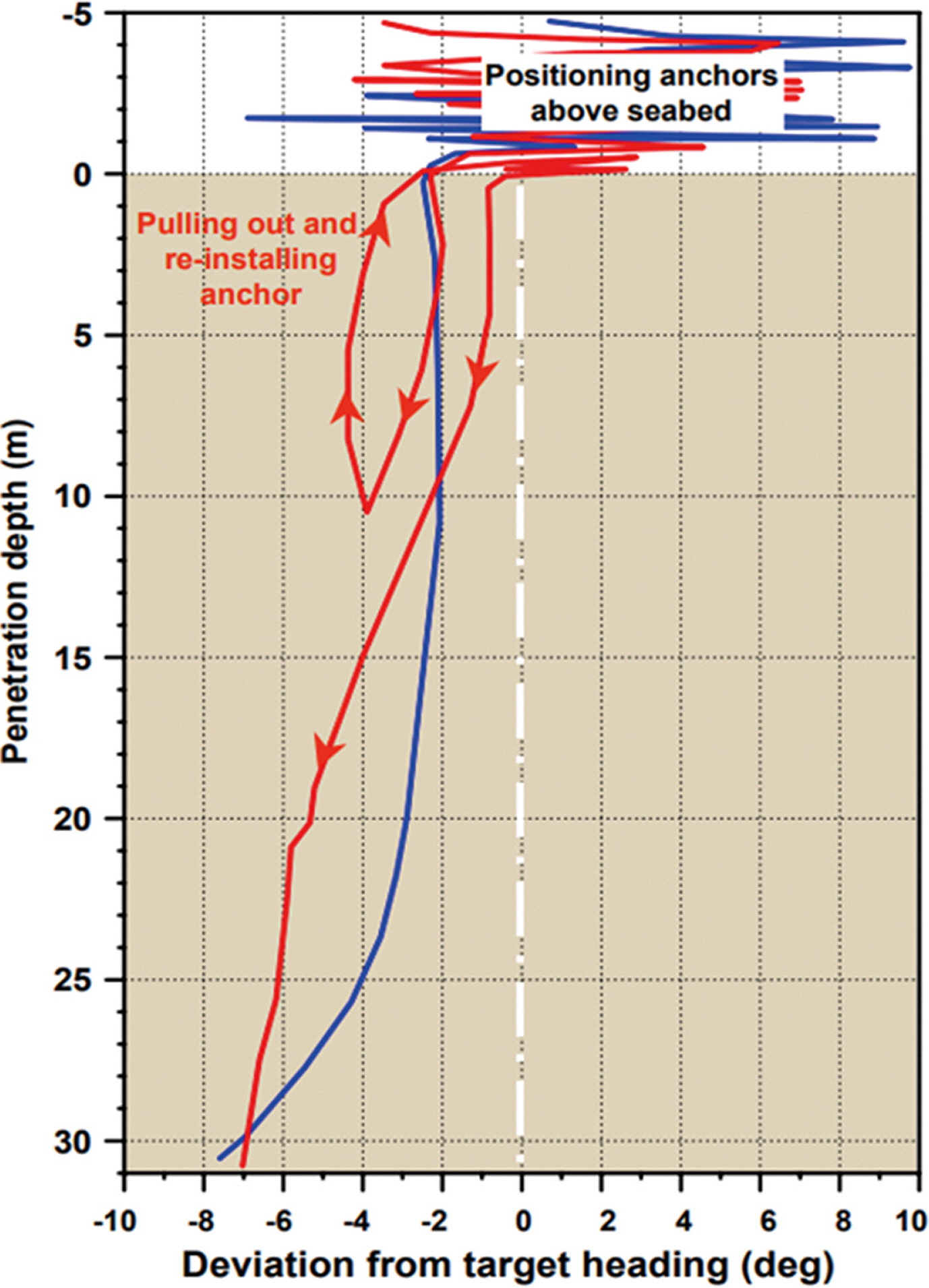
Fig. 4.Effect of inverse catenary in mooring line including tilt tolerances (±5°) based on DNV-RP-E303. 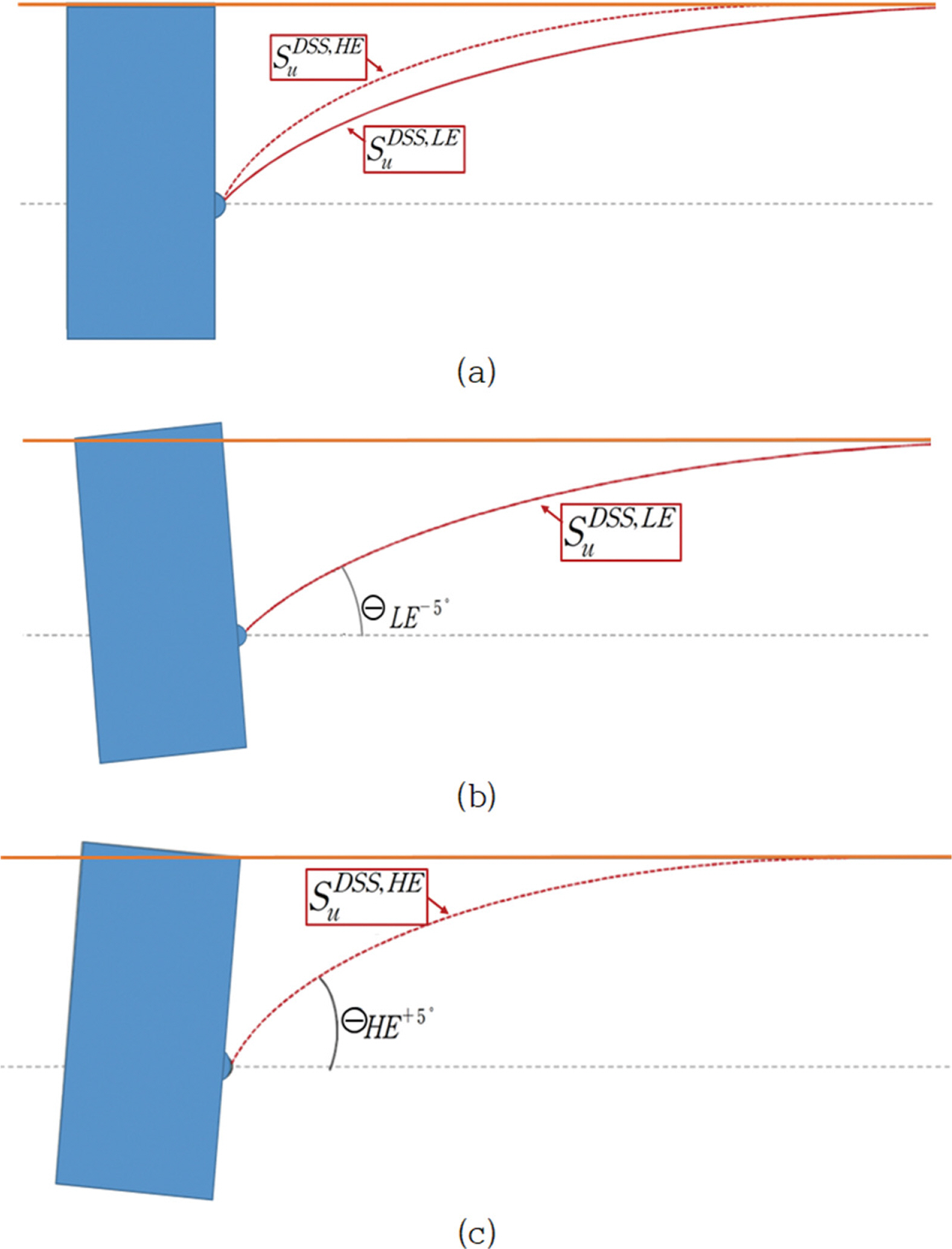
Fig. 7.Effect of tilt angle δ on the vertical - horizontal forces and pullout capacity of suction anchor under loading angle (θ = 45°). 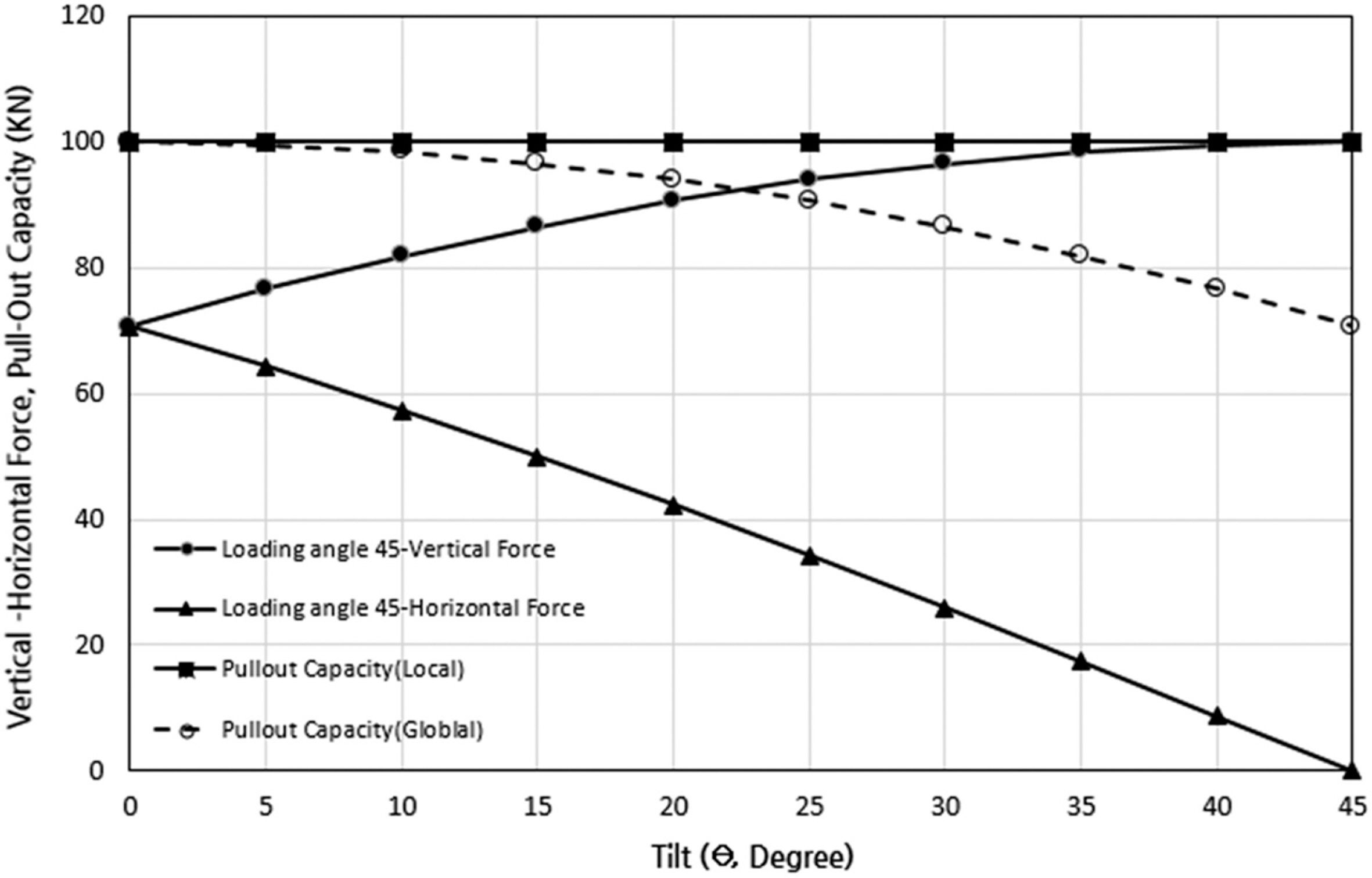
Fig. 10.Effect of misorientaion β on the vertical - horizontal forces, torque, and pullout capacity of suction anchor under loading angle (θ = 45°). 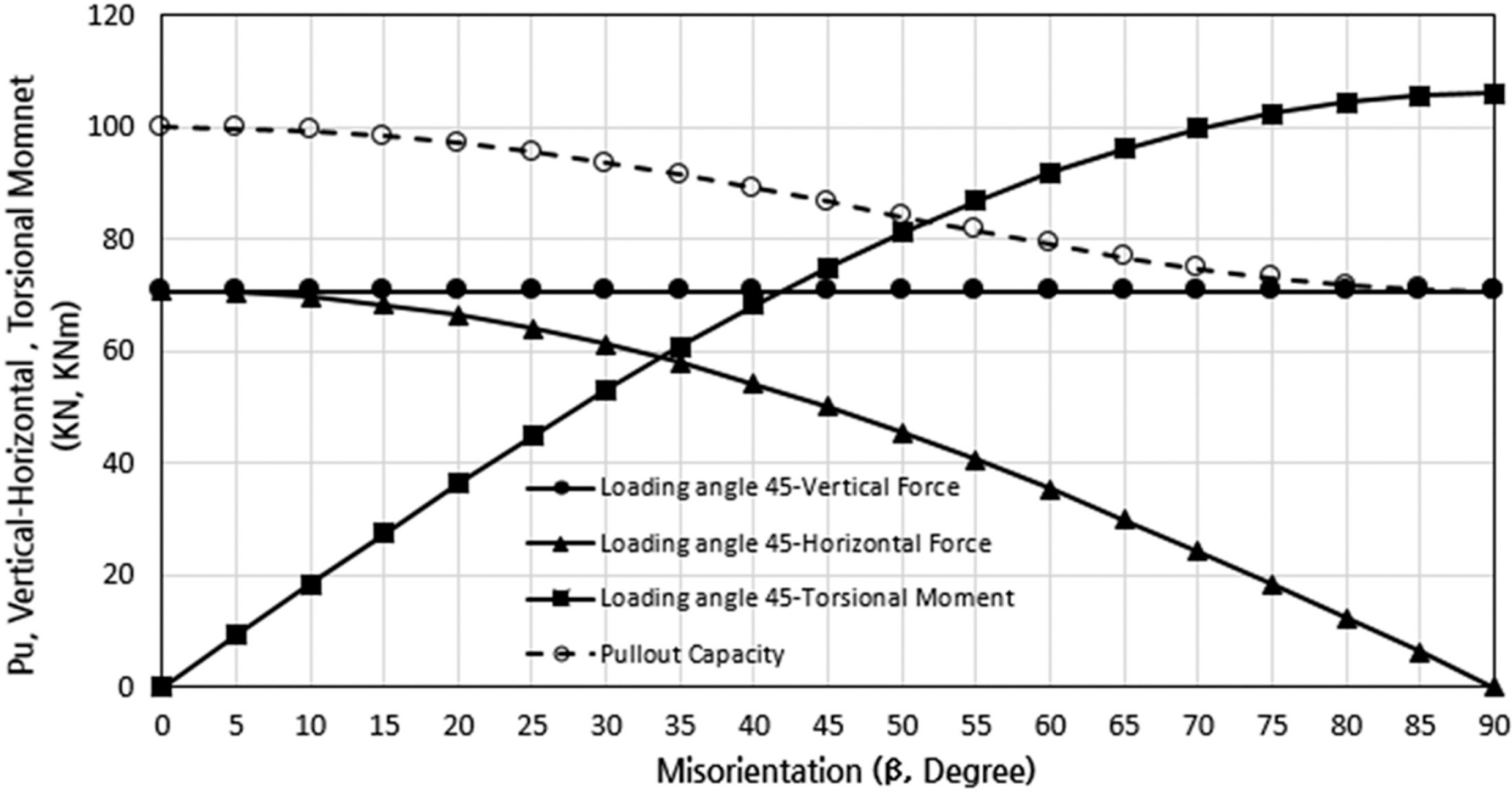
Fig. 11.Combined effect of tilt and misorientation on the pullout capacity of suction anchor under loading angle (θ = 45°) focused on tilt. 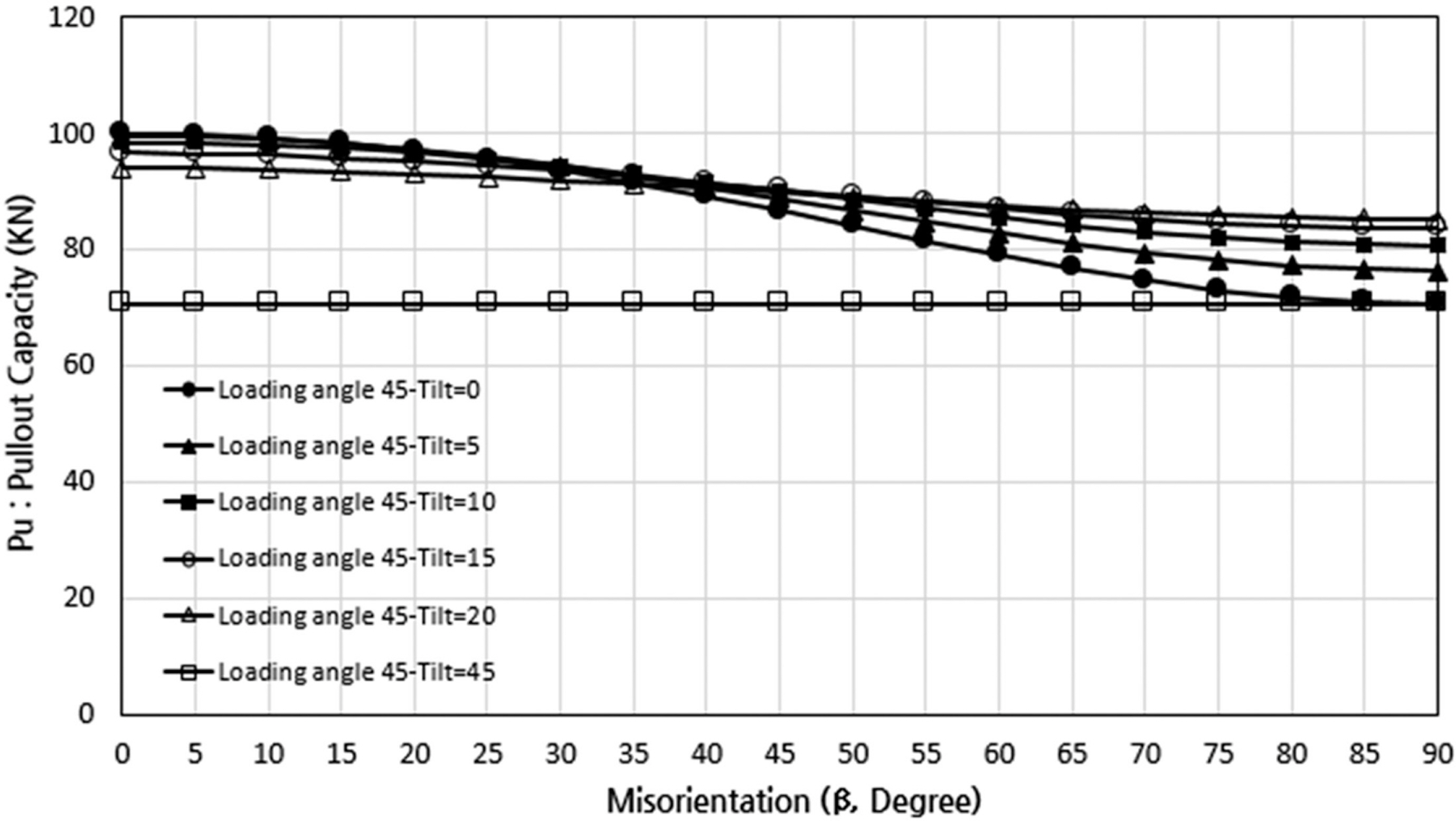
Fig. 12.Combined effect of tilt and misorientation on the pullout capacity of suction anchor under loading angle (θ = 45°) focused on misorientation. 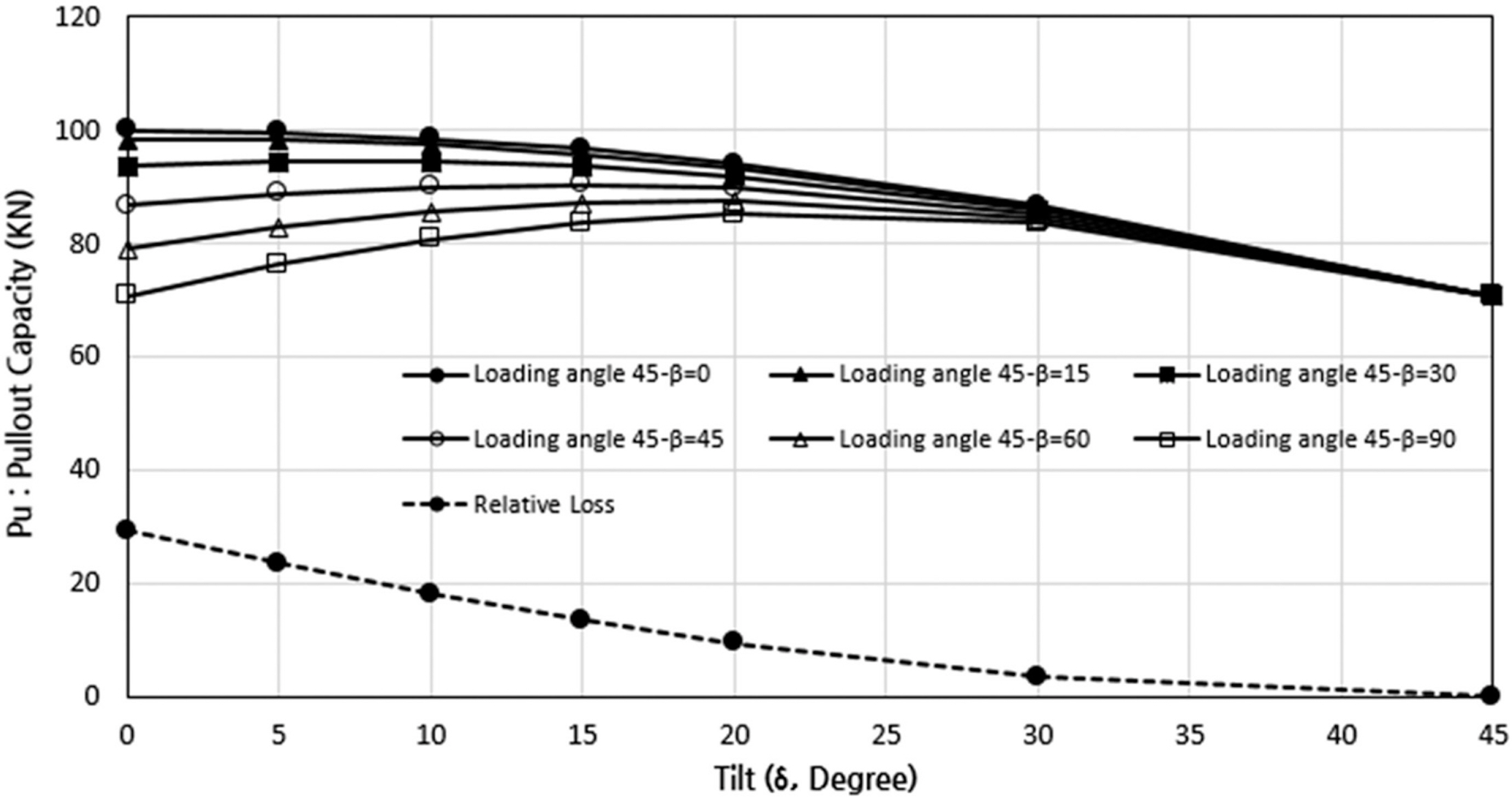
Table 1.Calculation results of the vertical-horizontal forces and pullout capacity according to tilt (Assume Pu = 100 kN, θ = 45o) Table 2.Calculation results of the vertical-horizontal forces and pullout capacity according to misorientation (Assume Pu = 100 kN, D = 3.0 m, θ = 45°, δ = 0°, β = Var.) Table 3.All calculation results of pullout capacity according to tilt, misorientaion, and their combination (Assume Pu = 100 kN, D = 3.0 m, θ = 45°, δ = Var. β = Var.) ReferencesAhmed, S.S, Hawlader, B.C (2015). Numerical analysis of inclined uplift capacity of suction caisson in sand, Int. J. Offshore Polar Eng, 25, 145-155.
Ahn, J, Lee, H, Kim, Y.-T (2015). Finite element analysis of the holding capacity of shallow suction caisson anchors, Mar. Georesources Geotechnol, 33, 33-44.
Cheng, L, Hossain, M.S, Hu, Y, Kim, Y.H, Ullah, S.N (2021). Failure envelope of suction caisson anchors subjected to combined loadings in sand, Appl. Ocean Res, 114, 102801.
Colliat, J.L, Boisard, P, Sparrevik, P, Granet, J.C (1998). Design and installation of suction anchor piles at soft clay site, Waterway, Port, Coastal and Ocean Eng, 124, 179-188.
DNV (2021). Geotechnical design and installation of suction anchors in clay, DNVGL Recommended Practice RP-E303.
Fu, D, Zhang, Y, Yan, Y, Jostad, H.P (2020). Effects of tension gap on the holding capacity of suction anchors, Mar. Struct, 69, 102679.
Saviano, A, Pisanò, F (2017). Effects of misalignment on the undrained HV capacity of suction anchors in clay, Ocean Eng, 133, 89-106.
Sparrevik, P (2002). Suction pile technology and installation in deep waters, Offshore Technology Conf, 14241, 1-9.
Sparrevik, P, Saue, M, Shin, Y, Langford, T (2017). Suction anchor design, installation and monitoring (Part 1), Geotechnical Engineering, 33(5):25-33.
|
|
|||||||||||||||||||||||||||||||||