1. 서 론
다수의 원형 파일을 배열하여 만든 연안/해양 구조물은 방파제, 호안, 항만, 교량, 해상 풍력발전 지지구조물과 같은 연안 및 해양 토목 공사에 널리 사용된다. 따라서 파랑중 다수의 원형 파일에 가해지는 파랑 하중을 정확하게 해석하는 것은 연안/해양 구조물들을 설계할 때 매우 중요하다. 특히 배열된 파일 간의 간격이 좁은 경우에는 인접한 파일들에 의한 간섭 효과로 단일 파일에 가해지는 힘과는 다른 특징을 보인다. 따라서 측정된 실험 데이터에 기초한 관성력 계수와 항력 계수를 가지고 파일에 작용하는 하중을 구하는 모리슨(Morison) 경험 공식은 파일간의 상호작용을 고려하지 못하기 때문에 배열된 파일에 적용하는 것은 적절한 해석방법이 아니다.
단일 원형 파일에 의한 파의 산란 문제는 McCamy and Fuchs(1954)에 의해 해석해가 구해진 이후로 다수의 원형 파일이 배열된 문제로 확장되어 파도와 다수의 파일간의 상호작용 문제를 연구하는데 활용되었다(Ohkusu, 1974; Spring and Evans, 1984; Linton and Evans, 1990; Kagemoto and Yue 1986; Kim, 1993; Maniar and Newman, 1997; Kashiwagi, 2000). 불투과성 파일을 투과성 파일로 확대하여 다수의 투과성 파일과 파도의 상호작용 문제를 다룬 연구들도 있다(Wang and Ren, 1994; Williams and Li, 2000; Cho and Kim, 2010; Cho, 2003, 2009, 2010). 파일의 투과성 효과를 고려하기 위한 해석 방법으로 투과성 파일 전후의 압력차는 투과성 파일을 통과하는 물입자의 속도에 선형적으로 비례한다는 Darcy 법칙을 사용한다. Cho and Kim(2010)은 N개의 투과성 파일들을 간격 없이 일렬로 배열하여 만든 투과성 방파제에 의한 파랑제어 성능을 해석해를 통하여 살펴보았다. 해석해를 검증하기 위하여 공극율 0.093인 투과성 파일(4개, 6개 10개)을 일렬로 입사파의 진행 방향과 직각 방향으로 배열하여 만든 실험모델을 가지고 모형실험을 실시하였다.
본 연구에서는 규칙파와 다수의 파일간의 상호작용에 대한 해석모델을 구하고, 이를 파일이 입사파의 진행방향과 수직으로 일렬로 무한히 배열된 해석모델로 확장하여 양 끝단의 회절 효과가 제거된 모델에 대한 해석해를 구하였다. 125개의 마름모꼴 각관(TSP)을 서로 체결하여 만든 원기둥 모형을 축척비 1/100로 제작하여 2차원 조파수조에서 모형실험을 실시하였다. 직경 40 cm인 원기둥 모형 2개를 제작하여 폭 80 cm인 조파수조 양측 벽면에 밀착 설치하였다. 이는 수조 측벽에서의 이미지 효과로 입사파의 진행 방향에 수직으로 파일이 무한히 배열된 해석모델과 동일하다. 규칙파 실험에서 원기둥 벽면 특정 위치에서의 파압과 처오름 파를 그리고 원기둥 전면에서의 파고를 측정하여 해석해와 비교하였다.
2. 문제의 정식화
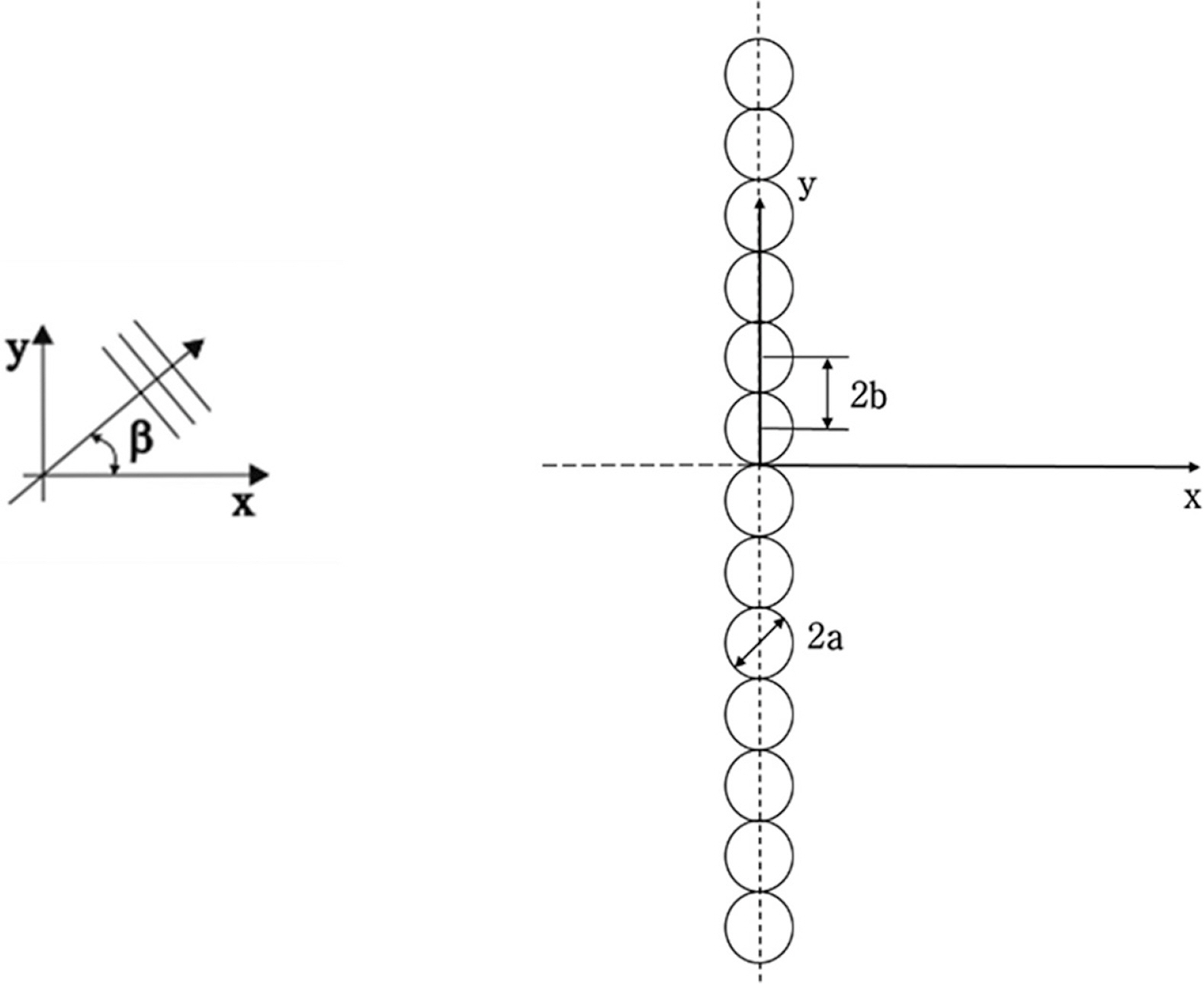
수심이 h인 해저면 바닥 임의의 위치에 고정된 N개의 원형 파일과 파의 상호작용 문제에 대한 해석모델을 먼저 살펴보자. 해석의 편의를 위하여 Fig. 1과 같이 공간상에 고정된 좌표계(x, y, z)와 N개의 파일 중심에 고정된 좌표계(rk, θk, z), k = 1, 2, ..., N를 도입한다. k번째 파일의 중심의 좌표는 (xk, yk)이며 반지름은 ak다. k번째 파일 중심에 대한 j번째 파일 중심의 상대 위치는 (Rjk, ajk)이다. 유체를 비압축성, 비점성으로 가정하고, 유체 유동을 비회전성으로 가정하면 유체입자의 운동은 속도포텐셜로 표현이 가능하다. 유체입자의 운동이 주파수 ω를 갖고 조화운동을 한다면 시간과 공간을 분리하여 속도포텐셜을 ϕ r , θ , z , t = R e - i g ω A ϕ r , θ , z e - i ω t ϕ r , θ , z = η r , θ cosh K z + h cosh K h η s = ∑ k = - N N η s k
입사파가 주파수 ω를 가지고 x축의 양의 방향과 β의 각도를 이루면서 들어올 때 식(1)에서 입사파는 다음과 같이 쓸 수 있다.
여기서 Jn는 제 1종 Bessel 함수이다. 공간 고정좌표계(r, θ)로 표현된 식(2)를 k번째 파일의 중심에 고정된 좌표계(rk, θk), k = 1, 2, ..., N에서 나타내면 아래와 같다.
여기서 I k = e i K x k cos β + y sin β
k번째 파일로부터 발생하는 산란파는 2차원 Helmholtz 방정식과 무한 원방에서의 방사조건(radiation condition)을 만족하며 아래 식과 같다.
여기서 Hn(= Jn + iYn)는 제 1종 Hankel 함수이다. Z n k = J n ' K a k / H n ' K a k
k번째 파일 주위의 파형은 입사파와 k번째 파일에 의한 산란파 그리고 k번째 파일을 제외한 나머지 파일(j = -N, ..., 0, ..., N, j ≠ k)들에 의한 산란파의 합으로 나타낼 수 있다. 이를 수식적으로 표현하기 위하여 아래 주어진 Graf의 Bessel 함수의 덧셈정리(additional theorem)를 적용한다(Linton and Evans, 1990; Kim, 1993; Maniar and Newman, 1997; Evans and Porter, 1999).
(7)
윗식은 rk < Rjk일 때 성립하는 식이다. 식(7)에서 우변의 첫 번째 항은 순수한 입사파를, 두 번째 항은 k번째 파일에 의한 산란파를, 그리고 세 번째 항은 k번째 파일을 제외한 나머지 파일 그룹에 의해 산란된 파가 k번째 파일에 미치는 효과를 나타낸다.
k번째 파일 경계면(rk = ak)에서의 불투과성 경계조건식 (∂ η ∂ r k = 0
식(8)에 주어진 대수방정식을 풀어 A n j
j번째 파일에 작용하는 파랑 하중(Fj(t) = Re{fje-iωt})은 파일에 작용하는 압력을 파일 벽면을 따라 적분하여 구한다.
여기서 [ ]의 상단은 x 방향을, 하단은 y 방향의 파랑 하중을 나타낸다. f s = 4 ρ g tanh K h K 2 H 1 ' K a j '
j번째 파일의 벽면에서의 처오름 파와 벽면에서의 파압은 다음과 같다.
Fig. 2와 같이 동일한 반경(a)이 갖은 파일을 간격(2b)를 가지고 y 축을 따라 무한히 배열하였을 때, 대수방정식(8)은 아래와 같이 바뀐다. 자세한 유도 과정은 부록 A에 수록하였다.
여기서 Ql(x, δ) 아래와 같이 정의된다.
식(11)에 주어진 (2M+1) × (2M+1) 행렬식을 풀어 파일 그룹의 중앙에 놓인 파일에 의한 산란파의 미지수 An, (n = -M, ..., M)을 구하고, 인접한 j번째 파일의 미지수는 A n j = A n e i j δ
입사각이 β = 0일 때, 파일 간의 위상차는 δ = 0이므로 x 방향의 파랑 하중과 처오름 파형식 그리고 파압은 파일의 놓인 위치에 관계없이 동일한 값을 준다.
3. 모형실험
본 연구에서의 다룰 TSP 원형 파일은 기존의 제작 방법과 달리 단면이 사다리꼴인 TSP 각관 125개를 서로 체결하여 만들어 원형에 가까운 내부가 빈 원통 구조물이다. 단일 TSP 원형 파일의 모식도는 Fig. 3과 같다. 이런 특징으로 공장에서 미리 제작한 후 별도의 공정 없이 현장조립으로 설치가 가능하며, 외부의 하중을 TSP 각관내로 분산시켜 별도의 보강재 없이도 구조적으로 안전한 구조물이다. 이 장에서는 TSP 원형 파일을 입사파의 진행 방향과 수직 방향으로 무한개 배열하였을 때 파랑중 원형 파일이 받는 파압과 파일 벽면에서의 처오름 파와 파일 전면 특정 위치에서의 파의 증폭비를 모형실험을 통해 살펴보았다. 실험 결과는 2장에서 개발한 해석모델의 결과와 비교하였다.
수리 모형실험에 이용된 2차원 조파수조는 길이 20 m, 폭 0.8 m, 높이 1 m로 수조 한쪽 끝에 설치된 피스톤 타입 조파장치로 규칙파 및 불규칙파를 생성한다. 본 모형실험에 사용된 파고계는 수면의 변화를 전기용량 값으로 나타나는 용량식 파고계이며 실험모형 전면 3개의 지점과 원기둥 모형 벽면에 설치하였다. 또한 원기둥 벽면 특정 위치에 파압 측정을 위하여 파압계를 설치하였다. kPa당 2.50 mV의 민감도를 갖는 piezo-resistive 타입의 압력센서(Kistler 4043A2)를 사용하였다. 압력 측정범위는 0에서 200 kPa이다.
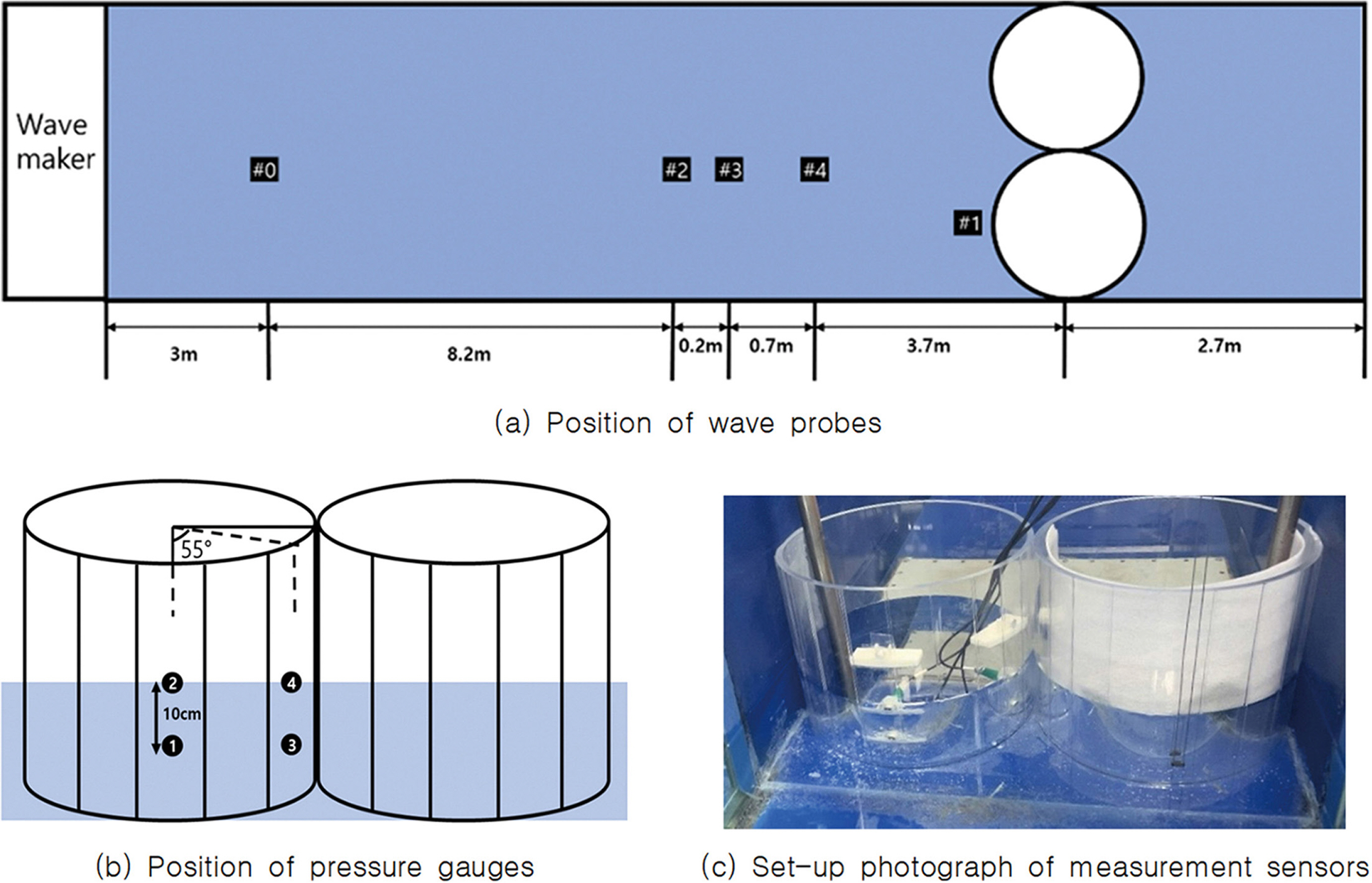
모형실험에 사용한 원기둥 모델의 축척비는 1/100로 직경은 40 cm, 높이는 40 cm이며, 수심 20 cm인 수조 바닥에 고정된다. 입사파의 진행 방향과 수직으로 파일이 무한히 배열된 해석모델과 동일한 조건에서 실험하기 위하여 원기둥 모형 2개를 수조 폭(80 cm)에 맞게 제작하여 바닥에 고정하였다. 이는 수조의 양 측벽에서의 이미지 효과로 무한개의 파일이 배열된 것과 동일한 결과를 준다. 본 실험에 사용한 실험모델은 Fig. 4와 같다. 규칙파 실험에서 주기는 0.5ω2.0 s 범위내에서 17개로 잡았으며 파 기울기는 H/λ = 0.01로 고정시켜 주기에 따라 입사파의 파고를 정하였다.
조파기에서 생성된 파는 윈기둥 모형을 만나면 대부분 반사되어 입사파의 진행 방향과 반대 방향으로 진행한다. 따라서 실험모델 전면 파동장에는 입사파와 반사파가 함께 공존한다. 실험모델 전면에 위치한 파고계에서 측정된 파랑 데이터로부터 순수한 입사파를 얻기 위하여 계측 신호로부터 입사파와 반사파를 분리하여야 한다. 이를 위하여 모델 전면 특정 위치에 3개의 파고계(#2, 3, 4)를 설치하여 입사파와 반사파를 분리하였다 (Mansard and Funke, 1980). 이와 함께 원기둥 벽면에 파고계 1개(#1)를 추가로 설치하여 처오름 파를 측정하였다. 원기둥이 받는 파압을 측정하기 위하여 4개의 파압계를 원기둥 바깥면 특정 위치에 설치하였다(Fig. 5 참조).
4. 계산결과 및 고찰
4.1 모형실험과 비교
모형실험의 모든 결과는 입‧반사 분리기법을 통하여 얻은 입사파의 진폭으로 무차원화시켰다. 앞서 설명하였듯이 입사파와 반사파가 공존하고 있는 위치에서 파고계로 측정된 파랑 데이터로부터 입사파와 반사파를 정확하게 분리하여야 한다. Table 1은 3지점에서 측정된 파랑 데이터로부터 입사파와 반사파를 분리하여 얻은 입사파고와 반사율을 보여주고 있다. 입사파/반사파 분리 기법이 제대로 작동되었는지를 검증하기 위하여 조파기 전면(3 m)에 파고계(#0)를 추가로 설치하여 측정한 입사파고를 함께 수록하였다. 단주기 규칙파 실험에서는 두 결과가 차이를 보이지만 주기가 0.6 s 이상부턴 큰 차이가 나타나지 않았다. 반사율은 예상대로 단주기 영역을 제외하곤 거의 1.0에 가까운 완전반사의 결과를 보여주고 있다.
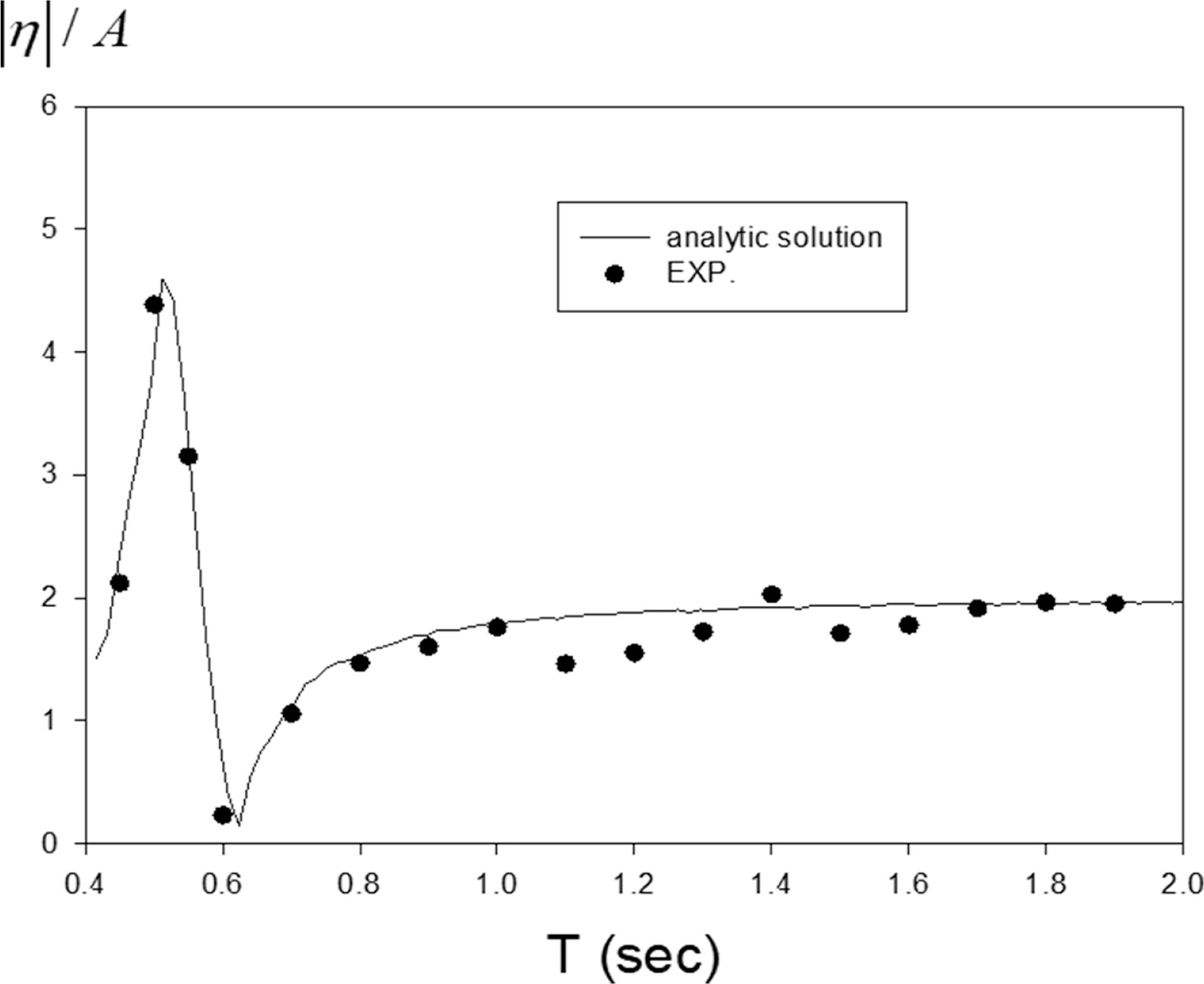
Fig. 6은 원기둥 바깥면에 설치된 파고계 #1(r = a, θ = 180o)에서 얻은 파고를 입사파의 파고로 나눈 처오름 파의 증폭비에 대한 해석결과와 실험결과를 비교한 그림이다. 여기서 실선은 해석결과를 나타내고 기호는 실험결과이다. 입사파의 주기 0.5 s에서 파일 벽면을 따라 상승하는 처오름 파고가 입사파고 보다 약 5배 크게 나타났다가 주기 0.6 s에서 갑자기 줄어들어 0에 가까운 증폭비를 보였다. 이는 단주기 영역에서는 인접한 파일들에 의한 산란파의 중첩이 주기에 따라 특정 위치에서의 처오름 파고를 크게 증가시키거나 감소시킨다. 그러나 주기가 0.8 s보다 큰 장주기 영역에서는 일정한 증폭비(= 2.0)을 보여준다. 즉, 파일의 크기에 비하여 큰 파장을 갖는 장주기파가 입사하였을 때 파일 벽면에서 증폭비는 2.0으로 안티 노드(Anti-node) 점이 형성됨을 보여준다. 전반적으로 해석결과와 실험결과는 서로 잘 일치하였다.
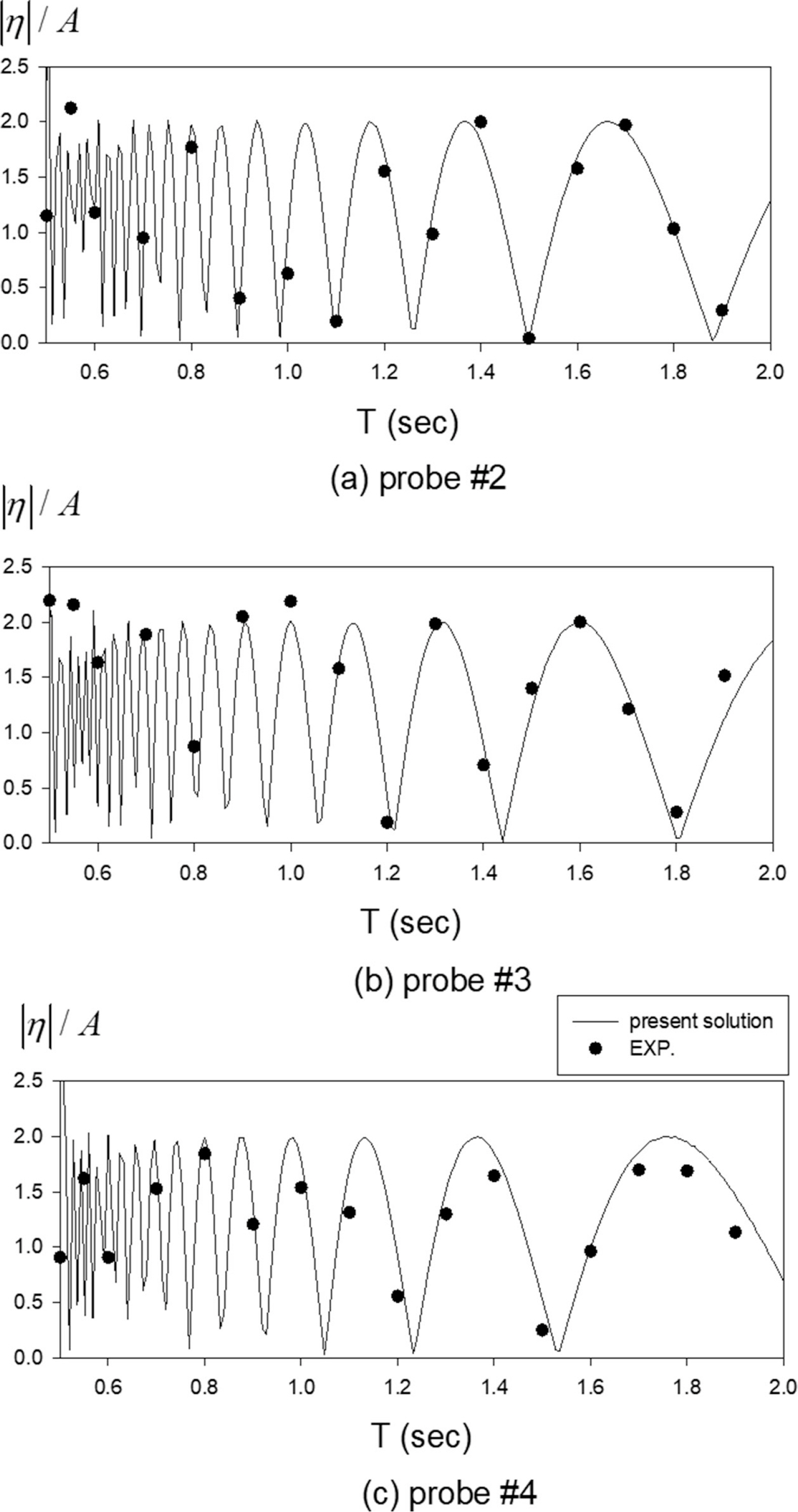
Fig. 7은 파일 모형 전면 3개의 지점에 설치된 파고계(#2, 3, 4)에서 측정된 파의 증폭비를 해석결과와 비교한 그림이다. 파형의 변화가 심한 단주기 영역 T(< 1.0 s)에서는 두 결과의 비교가 쉽지 않으나 장주기 영역에서는 파고계의 위치에 관계없이 해석결과와 실험결과는 서로 잘 일치함을 보여주고 있다. 파일 모형 전면에서 증폭비는 완전반사로 인하여 정지파가 형성되어 주기에 따라 0과 2 사이의 값을 갖는다. 특히 입사파의 파장이 짧은 경우, 정지파의 파장도 짧아져 입사파의 주기 변화에 따라 증폭비가 심하게 변하는 Fig. 7과 같은 특징을 보인다. 반면에 주기가 1 s 이상이 되는 장주기 영역에서는 파고는 주기변화에 덜 민감하게 반응하고 주기가 증가함에 따라 사인 파형의 주기가 증가하는 경향을 보인다. Fig. 6에서 살펴본 파일 벽면에서의 처오름 파의 증폭비는 단주기 영역내에서 크게 변동하는 특징을 보였지만 파일로부터 일정거리 떨어진 위치에서는 파일 모형에 의한 완전반사로 인해 증폭비는 0과 2 사이에서 변한다.
Fig. 8은 파일 바깥면 특정 위치에 설치된 4개의 파압계로 측정한 파압의 진폭값을 ρgA로 무차원화하여 나타낸 그림이다. Fig. 8a는 파압계의 위치(p1, p2)가 파일의 돌출부(θ = 180o)에서 수면 아래 10cm와 수면에 놓인 경우이다. 예상대로 파의 영향이 큰 수면(p2)에서 측정된 파압이 수면 아래(p1)에서의 파압보다 높게 나타났으며 Fig. 6의 파일 벽면에서의 처오름 파의 증폭비와 같이 단주기 영역에서 압력의 변화가 크게 일어났다. 즉, 천수역에서의 파압의 특징인 수면 변위에 선형적으로 변한다(p= ρgη). 두 개의 파일이 만나 좁아지는 특정 지점(θ = 235o)에 설치한 파압계(p3, p4)로 측정한 결과를 Fig. 8b에 그렸다. 파압계 설치지점이 두 개의 파일이 만나는 오목한 지점으로 파가 집중되어 p1과 p2에서 측정된 파압보다 높은 파압을 나타냈었다. 그러나 입사파의 주기가 1.0 s 이상인 장주기파가 들어올 때는 파일 그룹에 의한 완전반사로 정지파가 형성되어 설치 위치와 관계없이 해석해는 2.0에 가까운 값을 보인다. 실험결과는 2.0보다 약간 크고 다소 분산되는 결과를 보여준다. 이는 파압계(p3, p4) 설치 위치에서 형성된 난류의 영향과 높아진 파고에 의한 비선형성으로 인한 결과로 사료된다. 그러나 전반적으로 해석결과와 실험결과는 정성적으로 잘 일치하고 있다.
4.2 파랑 하중과 처오름 파
4.2절에서는 원형 파일이 y 축 방향으로 일렬로 무한개가 배열되었을 때의 파일에 작용하는 파랑 하중을 계산하였다. 계산모델은 실물 크기로 반경(a)과 수심(h)은 20 m이다. 입사각은 β = 0o로 파는 배열된 파일에 수직으로 입사한다. 따라서 파일 간의 위상차는 δ = 0이므로 파일의 배열 위치에 관계없이 동일한 파랑 하중을 준다.
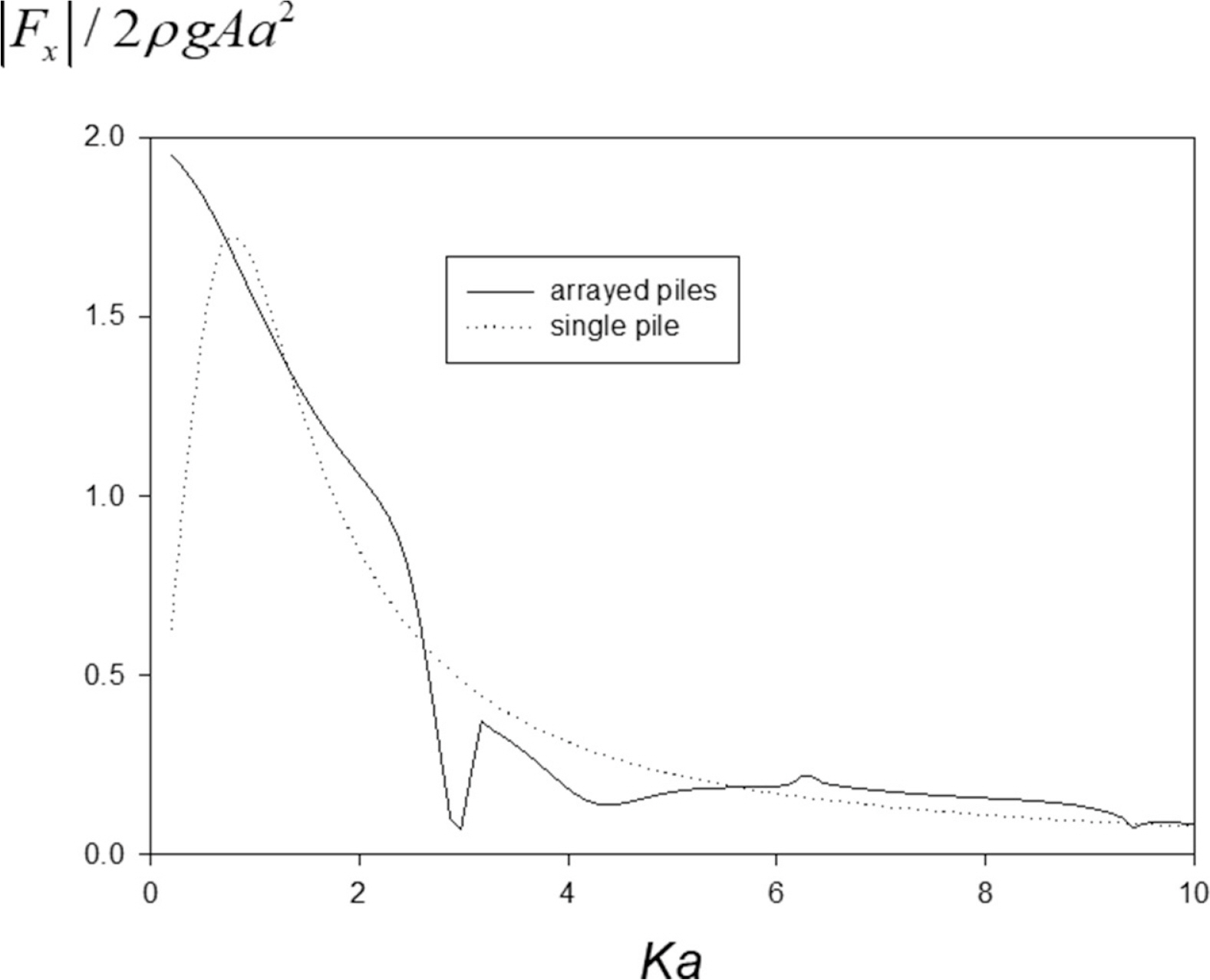
Fig. 9는 파일에 작용하는 무차원화된 x 방향의 파랑 하중(= |Fx|/2ρgAa2)을 보여주고 있다. 여기서 x 축은 입사파의 파장으로 무차원화된 파일의 반경(Ka)이다. 파일간의 간격 없이 파일을 배열하였다(b/a = 1.0). 점선으로 나타낸 단일 파일의 결과와 비교하였을 때 Ka → 0인 장주기 영역에서는 파일 그룹에 의한 완전반사로 무차원화된 파랑 하중은 2.0에 수렴함을 알 수 있다. 이는 단일 파일에 작용하는 파랑 하중과는 전혀 다른 결과이다. 그러나 파장이 짧아짐에 따라 두 결과는 정성적으로 유사하다.
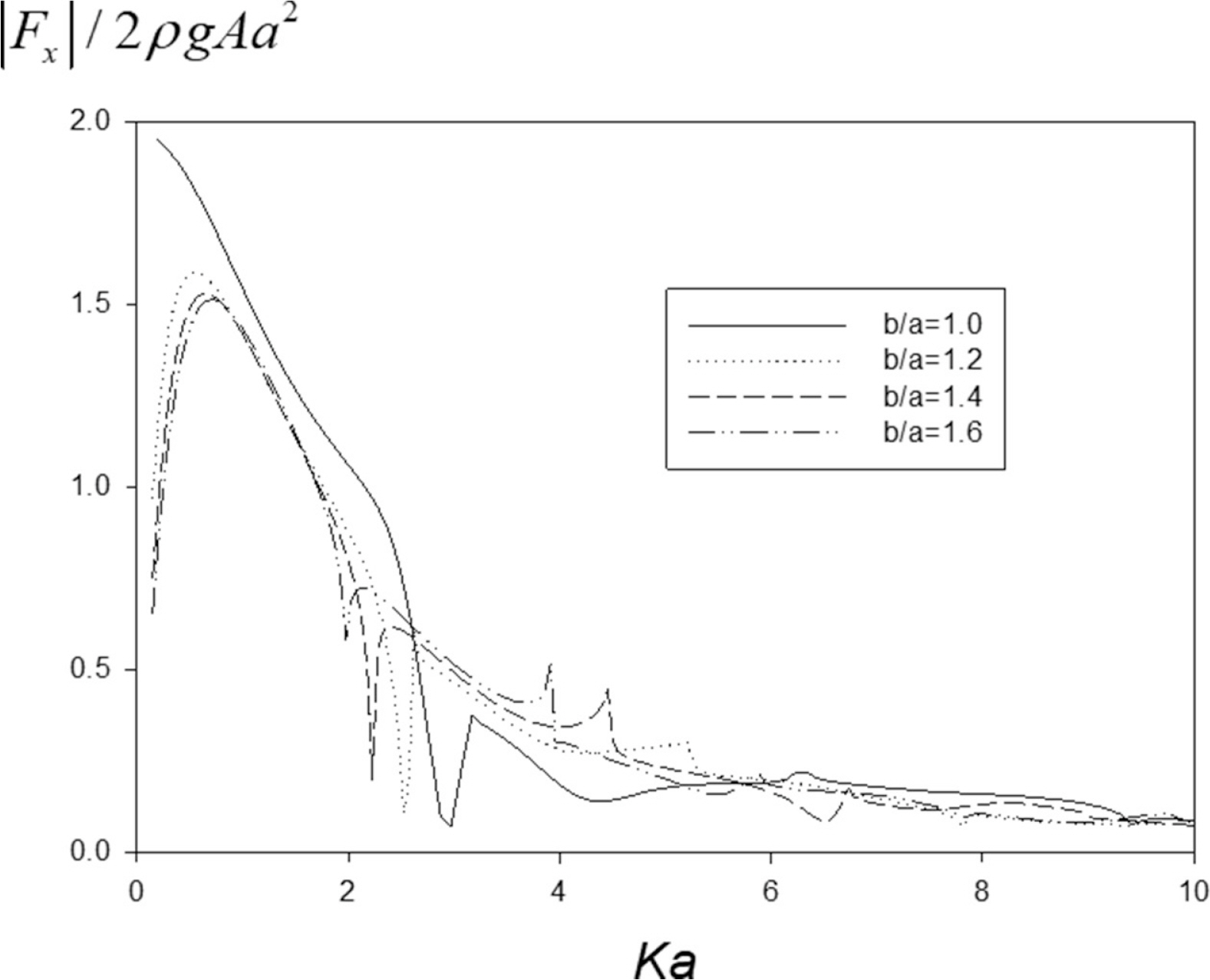
Fig. 10은 무차원화된 파일의 간격(b/a = 1.0, 1, 2, 1.4, 1.6)을 바꿔가면서 파일 그룹내 각 파일에 작용하는 x 방향의 무차원화된 파랑 하중(= |Fx|/2ρgAa2)을 무차원화된 파장(Ka)에 따라 그린 그림이다. b/a = 1.0은 원기둥을 간격 없이 배열된 실험에서와 동일한 모델이다. 예상대로 파일 사이의 간격이 증가할수록 파일에 작용하는 파랑 하중이 줄어드는 것을 볼 수 있다. 이는 일부의 파가 파일과 파일 사이의 열린 공간을 통하여 빠져나가 파랑 하중을 줄이는데 기여하였기 때문이다. 그러나 이러한 파의 투과 효과는 투과율이 큰 장주기 영역에서 주로 나타나며 단주기를 갖는 파는 파일 그룹을 통과하지 못하고 파가 마치 갇혀있는 상태(wave trapping)에 놓여 파랑 하중 감소 효과는 크지 않았다.
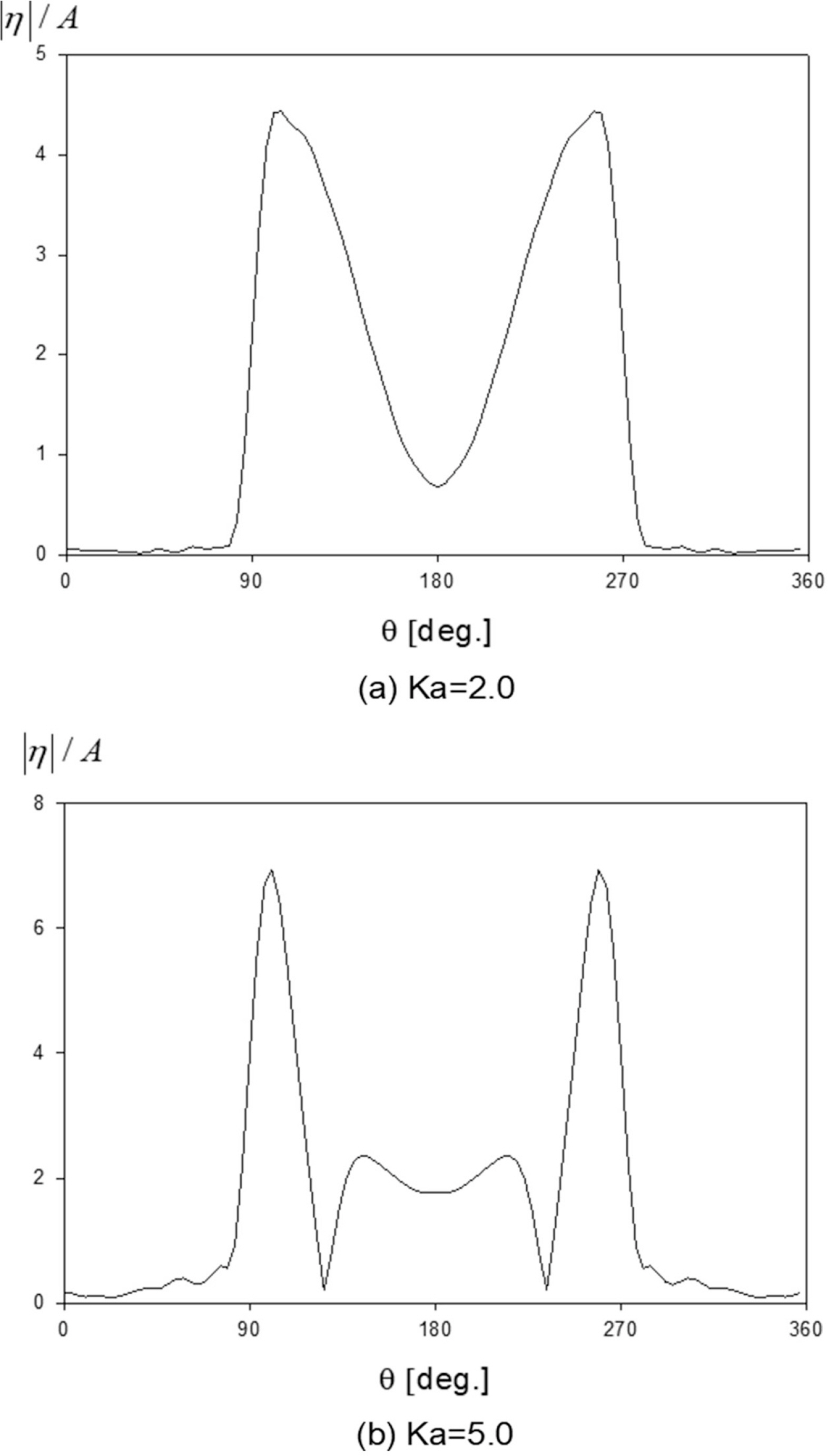
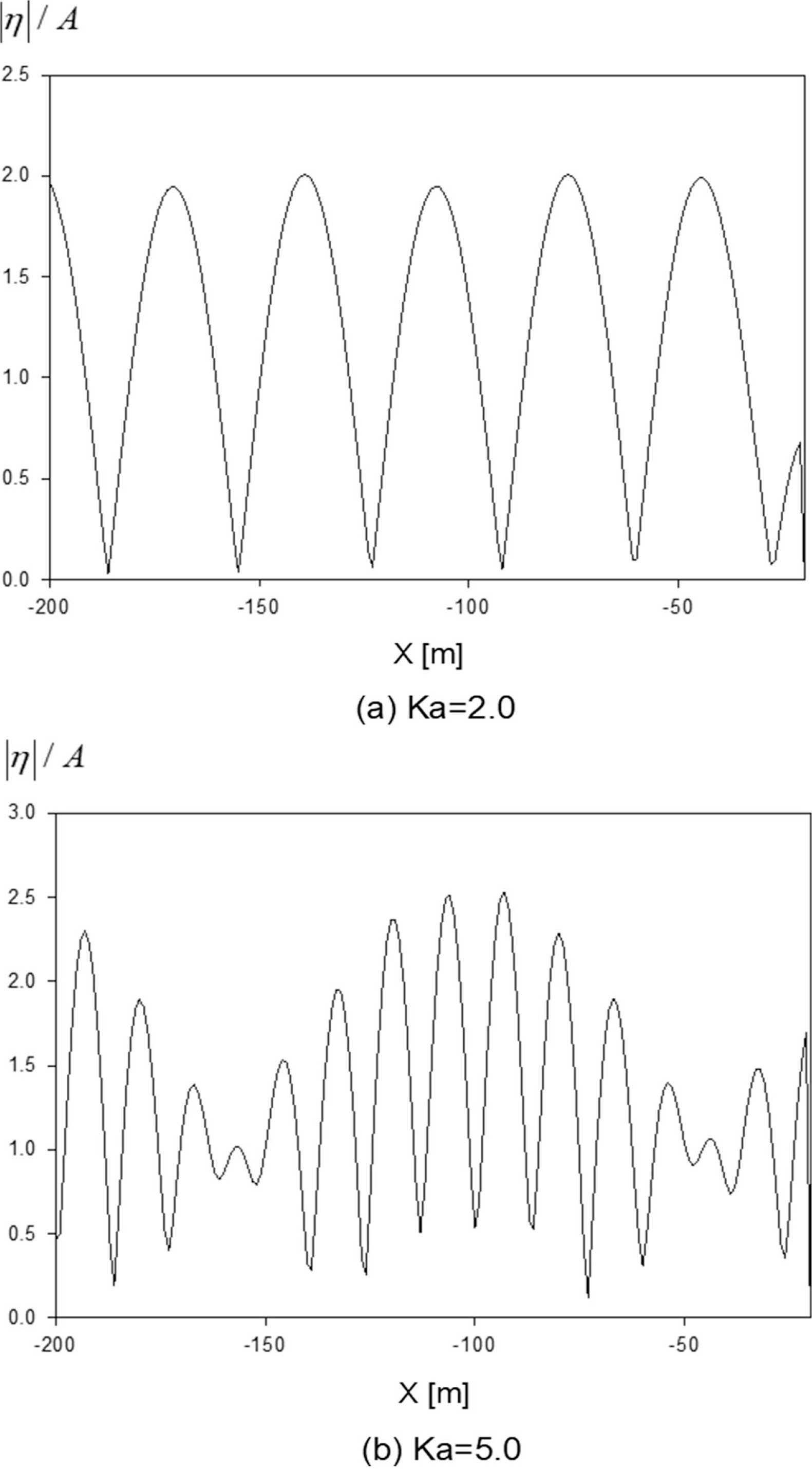
Fig. 11은 무차원화된 파장이 Ka = 2.0, 5.0일 때 파일의 바깥 벽면에서의 처오름 파의 증폭비를 파일의 원주 각도 θ의 함수로 그렸다. 파일이 만나는 양 측면 가까이 (θ = 100o, 260o)에서 처오름 파의 증폭비가 최대가 됨을 보여준다. Fig. 12는 무차원화된 파장(Ka = 2.0, 5.0)에서 x 축에 따른 파의 증폭비를 그렸다. 파장이 긴 Ka = 2.0인 경우 배열된 파일 그룹 전면에는 완전 반사에 의한 정지파가 형성되어 노드와 안티 노드가 주기적으로 형성됨을 볼 수 있다. 상대적으로 파장이 짧은 Ka = 5.0에서는 파일 그룹 전면에서 파의 증폭비는 변조된 특성을 보이며 증폭비가 최대 2.5까지 나타난다. 이는 앞서 설명하였 듯이 파장이 짧은 파가 파일 그룹을 만나면 인접한 파일에 의한 산란파들이 중첩되어 위치에 따라 파가 증폭되거나 상쇄하는 특징을 보이기 때문이다.
5. 결 론
이상의 해석결과와 모형실험결과를 토대로 다음과 같은 결론을 내릴 수 있다.
(1) TSP 파일을 간격 없이 입사파의 진행방향과 수직으로 무한히 배열하여 파일에 작용하는 처오름 파의 증폭비와 파압 그리고 파랑 하중을 입사파의 파장에 따라 살펴보았다. 파일 벽면에서의 파압은 인접한 파일이 만나는 오목한 지점에 가까워질수록 크게 나타났다. 파일 벽면에서 처오름 파의 증폭비는 단주기 영역에서는 인접한 파일들에 의한 산란파의 중첩으로 입사파의 파장에 따라 증가하거나 감소하는 큰 변동성을 보였다. 그러나 장주기 영역에서는 완전반사의 특징인 일정한 증폭비(= 2.0)을 보여준다. 배열된 파일에 작용하는 파랑 하중은 단일 파일의 결과와 비교하였을 때 장주기 영역(Ka → 0)과 다수 파일 그룹에 의한 산란파의 중첩으로 주기에 따른 변동성을 제외하곤 두 결과는 정성적으로 유사하였다.
(2) 파일 사이의 간격이 증가할수록 일부의 파 에너지가 파일과 파일 사이의 열린 공간을 통하여 빠져나가기 때문에 파랑 하중이 줄어든다. 그러나 이러한 파의 투과에 의한 하중 감소 효과는 투과율이 큰 장주기 영역에서 주로 나타나며 단주기 영역에 속한 파는 마치 갇혀있는 상태(wave trapping)에 놓여져 하중 감소 효과는 크지 않았다.
(3) 해석모델 개발과 병행하여 실물의 1/100 축척비를 갖는 모형을 가지로 2차원 조파수조에서 모형실험을 수행하였다. 조파수조 폭에 맞게 2개의 원기둥 모델을 배치하여 입사파의 진행방향과 수직으로 파일이 무한히 배열된 해석모델과 동일한 조건을 구현하였다. 모형실험에서 원기둥 벽면이 받는 파압과 처오름 파, 그리고 실험모델 전면 특정 위치에서의 파의 증폭비를 수리 모형실험을 통해 살펴보았다. 모형 실험의 결과와 해석결과는 정성적으로 잘 일치함을 확인하였다.
(4) 현재의 해석모델은 선형포텐셜 이론에 기반으로 작성되었다. 따라서 파고가 높을 때 나타나는 비선형성과 난류에 의한 점성효과를 고려할 수 없다는 한계를 지니고 있다. 이를 고려하여 모형실험도 가능한 한 비선형성과 점성의 영향이 작은 실험조건에서 실시하여 해석모델과 비교하였다. 앞으로 남은 과제는 비선형성과 점성을 모두 포함할 수 있는 CFD(Computational Fluid Dynamics) 계산을 수행하여 해석 모델의 한계와 가능성을 함께 검토해야 하며, 호안 구조물 개발에 필수적인 불규칙파를 해석모델에 포함시켜야 한다. 또한 제한된 길이의 조파수조내에서 불규칙파를 재현하여 정확한 모형실험결과를 얻는 것도 앞으로 해결해야 할 과제이다.
(5) 제안된 파일 제작공법은 호안 구조물의 기초가 되는 TSP 원형 파일을 공장에서 미리 제작하여 현장에서 간단하게 조립할 수 있어 공사 기간을 크게 줄일 수 있다. 또한 중력으로 지지하는 콘크리트 케이슨 구조물에 비하여 해저면 아래로 파일을 관입하여 설치하므로 연약 지반에서도 설치가 가능하며, 하중을 분산시키는 아칭 효과(arching effect)로 별도의 보강재 없이도 구조적으로 안전하다. 이러한 장점들을 고려할 때 다수의 원형 파일을 배열하여 조성한 호안 구조물은 기존의 중력식 호안 구조물의 보완재로 무한한 잠재력을 지니고 있다.