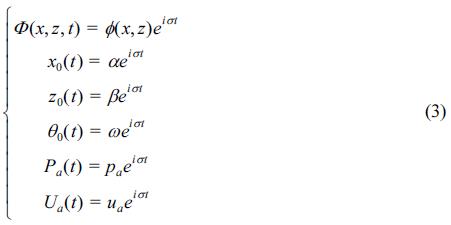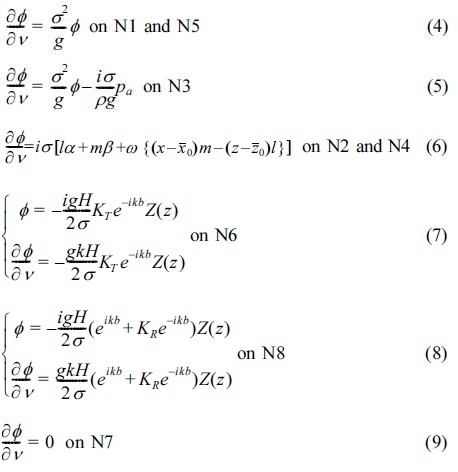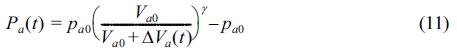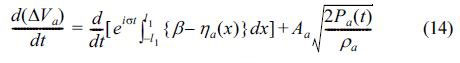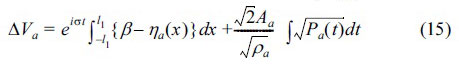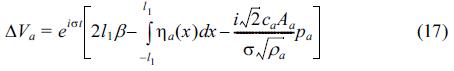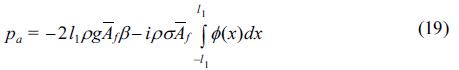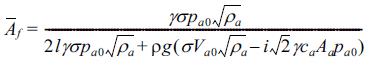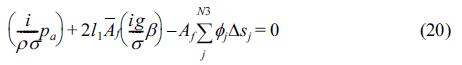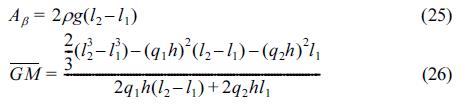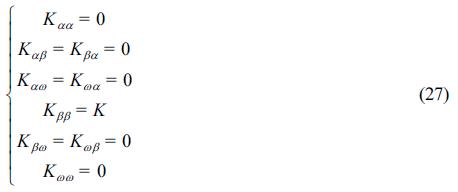1. 서 론
오늘날 전 세계 에너지소비의 대략 93%는 석유와 석탄과 같은 비재생에너지에 의존하고 있는 실정이다. 이러한 화석연료의 연소로 대기중에 방출되는 오염물질이 1차적으로 대기환경 피해를 초래하고, 2차적으로 지구온난화 및 해수면상승과 같은 지구규모의 환경문제를 야기한다. 따라서, 저탄소 청정에너지로 알려진 신재생에너지에 국가차원의 연구·개발 및 투자가 이루어지고 있다. 유럽을 위시한 많은 해양국가에서는 풍력, 파력, 조력, 조류력 및 태양열 등에 의한 발전으로 대표되는 신재생에너지 중에 파력발전 변환장치(WEC; Wave Energy Converter)를 오래전부터 연구·개발하여 왔고, 그 결과로 일부는 상업화의 수준까지 이르고 있다.
WEC는 해안선으로부터 설치위치에 따라 해안용, 근해용 및 심해용으로 각각 대별될 수 있고(CRES(Centre for Renewable Energy Resources), 2006), 해안에서 WEC는 설치와 유지관리가 용이하고, 계류나 긴 수중송전선이 필요없지만 기초지반, 조차 및 해안경관 등의 영향을 받을 수 있다. 이의 대표적인 것으로 포루투갈 Pico에 설치된 진동수주(OWC(Oscillating Water Column))시스템의 LIMPET((Land Installed Marine Power Transmitter) Falcão, 2010; Heath et al., 2000)를 들 수 있다. 근해에서 WEC는 해안선으로부터 대략 500 m 정도 떨어진 수심 20~30 m의 근해역에 설치되고, 해안용의 경우와 거의 동등한 장점을 가지며, 동시에 보다 높은 파력환경을 갖는다. 이의 예로 Fig. 1에 나타내는 WaveRoller를 들 수 있다. 수심 40 m보다 깊은 해역에 설치되는 심해용의 WEC는 파랑으로부터 최대에너지를 추출하기 위하여 수면 혹은 수면 근방에 계획되고, 깊은 수심 때문에 계류가 요구된다. 이의 예로 Fig. 2에 나타내는 Mighty Whale(Hotta et al., 1996)로 불리는 부체식 진동수주형의 WEC를 들 수 있고, 수심 40 m에 설치·계획되어 실증시험까지 완료된 단계에 있다.
한편, 파동의 운동에너지를 변환하는 방식에 따라 Falcão(2010)는 가동물체형, 월파형 및 진동수주형으로 분류하기도 하지만 일반적으로 (1) Attenuator(Falnes, 2007; FEMP(Federal Energy Management Programme), 2009), (2) PA((Point Absorber) Barker et al., 2007), (3) OWSC((Oscillating Wave Surge Converter) AEA, 2006), (4) Overtopping(Powetech, 2009) 및 (5) OWC(ISSC, 2006; EPRI(Electrical Power Research Institute), 2005)으로 분류될 수 있고, 각각의 방식에 해당하는 많은 종류의 WEC들이 국내·외적으로 연구 및 개발되고 있다.
본 연구에서 대상으로 하는 WEC는 위치적으로 근해이고, 형식적으로 구조물 내 압축공기흐름을 통하여 파동에너지를 전기에너지로 변환하는 고정식 및 부체식 OWC이며, 이는 방파제의 기능도 겸비한다. 단독의 WEC를 설치하는 경우 일반적으로 경제성이 떨어지는 문제점이 있으므로 기존 혹은 신설의 방파제에 WEC를 적용하여 파랑제어와 파랑에너지의 이용을 동시에 도모하는 방식이 많이 추진되고 있다. 또한, Fig. 4에 나타내는 바와 같이 본 구조물은 OWC을 이용한 WEC에 Fig. 3에 나타내는 풍력발전시스템을 복합적으로 적용될 수 있으므로 파력과 풍력을 동시에 구비한 복합발전 시스템의 구조물로도 기대될수 있다.
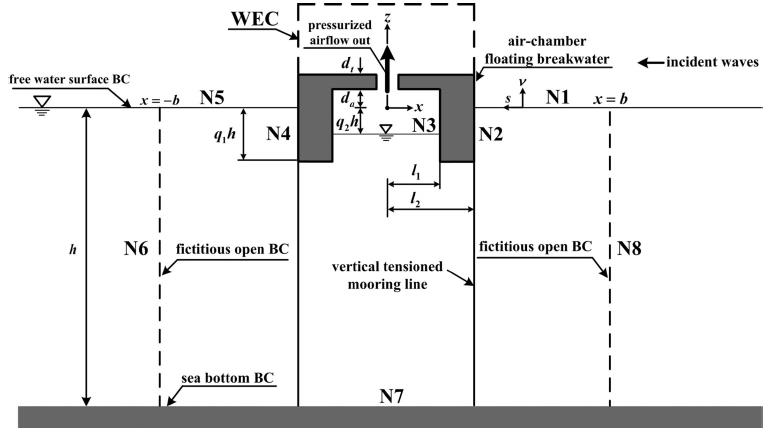
Fig. 4.
Systematic sketch of pressurized air chamber floating breakwater equipped with wave-power generation system.
여기서, 방파제 내부에 압축공기를 주입한 형태를 갖는 구조물은 내부공기압의 조절로부터 파랑제어기능의 향상과 다변화를 기하려고 고안된 형태의 구조물이다(Kim and Iwata, 1991). 압축공기 주입식의 방파제에서는 압축공기실에서 공기흐름이 발생되지 않지만 WEC로 적용되기 위해서는 구조물의 상단에 압축공기의 유출·입구가 구비되어야 하고, OWC의 WEC로의 타당성을 판정하기 위해서는 터빈의 구동력인 유출입구에서 압축공기 흐름속도가 정확히 평가되어야 한다.
OWC의 파력발전구조물에서 파랑-구조물-내부공기의 상호 간섭에 대한 해석해로는 대표적으로 Evans and Porter(1997)의 연구를 들 수 있고, 수치해석에서의 대상파랑을 2차원규칙파랑(Evans and Porter, 1995; Greenhow and White, 1997; Malmo and Reitan, 1985; Kyoung et al., 2006; Nakamura and Nakahashi, 2005), 2차원불규칙파랑(Boccotti, 2007a,b; Gouand et al., 2010; Falcão and Justino, 1999; Gervelas et al., 2011; Falcão and Rodrigues, 2002; Falcão, 2002; Yin et al., 2010), 3차원규칙파랑(EI Marjani et al., 2008; Josset and Clément, 2007; Paixão Conde and Gato, 2008; Cho, 2002), 그리고 3차원불규칙파랑(Delauré and Lewis, 2003)으로 각각 대별할 수가 있다. 수치해석기법으로 구분하면 고유함수전개법(Evan and Porter, 1995; Malmo and Reitan, 1985; Gouaud et al., 2010; Cho, 2002), 경계요소법(Josset and Clément, 2007; Delauré and Lewis, 2003), 유한요소법(Kyoung et al., 2006), Green함수법(Nakamura and Nakahashi, 2005) 및 유한차분법(EI Marjani et al., 2008; Paixão Conde and Gato, 2008; Yin et al., 2010)과 같은 다양한 수치기법이 적용되고 있는 것을 알 수 있다.
여기서, 대부분의 연구에서는 압축공기실 내에서 수면변동에 의해 발생되는 공기압변동을 공기압축성에 관한 상태방정식으로부터 산정하고 있지만 실제로 공기실 내의 압축공기 흐름속도를 직접적으로 평가한 연구는 Lee et al.(2011a, 2011b)과 Liu et al.(2008) 등의 다수를 들 수 있지만 부체식 진동수주형 파력발전시스템에서 압축공기 흐름속도를 직접적으로 산정한 연구 예는 많지 않다.
본 연구에서는 진동수주형 파력발전시스템을 탑재한 방파제에서 방파제로서의 파랑제어기능과 발전구조물로서의 압축공기 흐름속도를 해석하기 위하여 선형속도포텐셜이론에 기초한 경계요소법을 적용하고, 압축공기 흐름해석에 Boyle법칙과 단열변화과정에 기초한 상태방정식을 적용한다. 이로부터 얻어진 해의 타당성은 폰툰형의 고정구조물과 자유부체구조물에 대한 기존의 수치해석결과 및 압축공기주입의 고정구조물에 대한 실험결과와의 비교로부터 검증되며, 실제의 수치해석에서는 공기압축성이 파랑변형율과 공기흐름속도에 미치는 영향을 판단하기 위하여 고정구조물을 대상으로 계산을 수행하고, 더불어 연직긴장 계류시스템(vertical tension mooring system)을 대상으로 주기변화에 따른 진동수주형 파력발전장치를 탑재한 부방파제의 파랑변형율, 구조물의 운동 및 공기흐름속도의 특성 등을 명확히 규명한다.
2. 수치해석이론
2.1 기초방정식
본 연구의 대상인 진동수주형 파력발전시스템을 탑재한 부방파제의 모식도는 Fig. 4와 같다. 그림에서 제체의 외부폭은 2l2, 압축공기실의 폭은 2l1, 흘수는 q1h, 외부 정수면과 압축공기실에서 정수면의 높이차는 q2h로 주어지고, 구조물의 상면을 통하여 파력발전구조물로 유입되는 압축공기의 평균흐름속도와 단위폭당 단면적을 각각 Ua와 Aa로 정의한다.
이 때, 구조물로부터 소멸파(evanescent waves)의 영향이 없어지는 x = ± b에 개경계면(fictitious open boundary)을 설정하면 유체영역은 R(−), R(0), R(+)로 각각 분할되고, 계산영역은 R(0)이다. 각 유체영역에서 비점성, 비압축의 비회전운동의 유체를 가정하면 속도포텐셜이 존재하며, 유체영역 R(0)의 각 경계면상에서 속도포텐셜 Φ(x, z, t)는 다음의 Green공식을 만족한다.
여기서, (x, z)는 고정점의 좌표, (ξ,ζ )는 경계면상에서 유동점의 좌표, r은 고정점과 유동점과의 거리로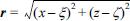 
와 같이 주어지고, G(r)는 다음의 식으로 주어지는 Green함수이다.
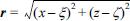와 같이 주어지고, G(r)는 다음의 식으로 주어지는 Green함수이다.
여기서, λ는 고정점이 경계면상에 있을 때 π이고, 고정점이 영역내부에 있는 때 2π로 주어지는 상수이다.
2.2 경계조건
경계면은 Fig. 4로부터 자유수면(경계면 N1과 N5), 구조물표면(경계면 N2과 N4), 압축공기실 내의 수면(경계면 N3), x = ±b 에서 개경계면(경계면 N6과 N8) 및 해저불투과면(경계면 N7)으로 각각 구성되고, 각 경계면에서 속도포텐셜 Φ(x, z, t), 구조물의 중심에서 수평, 연직 및 회전운동 x0(t), z0(t), θ0(t)및 압축공기압 Pa(t)과 압축공기 유출속도 Ua(t)는 다음의 식으로 정의된다.
여기서, φ, α, β, ω, pa, ua는 각 물리량의 시간변화에 대한 복소진폭을 나타낸다.
식(3)에 주어진 물리량의 진폭을 사용하여 각 경계면에서 주어지는 경계조건을 시간함수 eiσt를 생략하여 나타내면 다음과 같다.
여기서,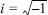 
, ν는 경계면에서 법선방향, ρ는 유체밀도, g는 중력가속도, l과 m은 방향여현으로 l = cos(ν : x), m = cos(ν : x), (x0, z0) 는 중심의 좌표, KR는 복소반사율, KT는 복소전달율, Z(z) = coshk(z + h)/cosh, khH는 입사파고, (x,z)는 공간좌표, h는 정수심, k는 파수, σ는 각주파수를 각각 나타낸다. 그리고, 식(8)에서 속도포텐셜은 입사파와 반사파 성분의 합으로 표현된 것이고, 식(7)의 속도포텐셜은 전달파 성분을 나타내며, 각각에 소멸파 성분은 포함되어 있지 않다. 식(5)의 경계조건은 압축공기실 내에서 동역학적 자유수면경계조건에서 공기압이 대기압과 상이한 것으로 가정하여 압축공기압의 성분을 고려한다.
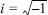, ν는 경계면에서 법선방향, ρ는 유체밀도, g는 중력가속도, l과 m은 방향여현으로 l = cos(ν : x), m = cos(ν : x), (x0, z0) 는 중심의 좌표, KR는 복소반사율, KT는 복소전달율, Z(z) = coshk(z + h)/cosh, khH는 입사파고, (x,z)는 공간좌표, h는 정수심, k는 파수, σ는 각주파수를 각각 나타낸다. 그리고, 식(8)에서 속도포텐셜은 입사파와 반사파 성분의 합으로 표현된 것이고, 식(7)의 속도포텐셜은 전달파 성분을 나타내며, 각각에 소멸파 성분은 포함되어 있지 않다. 식(5)의 경계조건은 압축공기실 내에서 동역학적 자유수면경계조건에서 공기압이 대기압과 상이한 것으로 가정하여 압축공기압의 성분을 고려한다.2.3 이산화방정식
식(4)~(9)에서 주어지는 경계조건식을 식(1)의 Green공식에 적용하여 미소선요소로 분할된 경계요소에 대해 이산화하면 다음과 같은 이산화방정식을 얻을 수 있다.
그리고, δij는 Knonecker의 Delta함수로 i = j의 경우는 δij = 1이고, i ≠ j의 경우는 δij = 0이며, Δs는 경계상에서 절점으로 분할되는 절점간 선요소의 길이, N은 경계면에서 절점의 총수이다.
2.5 공기압축모델
압축공기실 내에서 공기압의 변화 Pa(t)는 공기의 체적변화에 의해 발생되는 것으로 가정하면 Boyle법칙에 기초한 다음의 상태방정식으로 표현될 수 있다(Kim and Iwata, 1991).
여기서, γ는 단열변화과정을 가정하면 γ = 1.4, 이상변화과정을 가정하면 γ= 1.0으로 각각 주어지는 상수이고, pa0와 Va0는 압축공기실에서 초기공기압과 초기공기체적을 나타낸다. Fig. 4로부터 pa0= ρgq2h, Va0= 2l1(q2h + da) da는 Fig. 4에 나타내는 바와 같이 외부정수면에서 압축공기실 내 천단까지의 연직높이)로 나타낼 수 있으며, ΔVa(t)는 초기공기체적에 대한 변화량이다.
한편, 식(11)을 ΔVa(t) « Va0 의 가정하에 급수전개를 수행하고 ΔVa(t)/Va0에 관한 선형항만을 고려하면 다음의 식을 얻을 수 있다.
그리고, 압축공기실 내에서 유출되는 평균공기흐름속도 Ua(t)는 Bernoulli식으로부터 다음과 같이 주어진다.
여기서, ρa는 공기밀도이며, 표준치로 1.2045 kg/m3의 값을 가진다.
단위폭당 압축공기의 유출단면적을 Aa로 두면 압축공기실 내에서 변동체적의 시간변화율을 다음의 식으로 나타낼 수 있을 것이다.
여기서, ηa는 압축공기실 내에서 공간수면변동진폭을 나타낸다.
식(14)를 시간에 대해 적분하여 다음을 얻는다.
한편, 식(15)에서 압축공기의 체적변화와 공기압의 관계를 선형화시키기 위하여 다음을 가정한다.
여기서, ca는 차원을 갖는 상수이며, 식(16)을 (15)에 대입하고, 식 (3)에서 정의된 Pa(t) = paeiσt의 관계를 적용하면 다음을 나타낼 수 있다.
다음으로, 압축공기실 내에서 수면변동진폭 ηa는 Bernoulli식으로부터 다음과 같이 산정된다.
식(17)에 (18)을 대입한 결과를 다시 식(12)에 적용하면 최종적으로 변동공기압의 복소진폭 pa는 다음과 같이 도출된다.
여기서,
식(19)를 이산화하면 다음과 같다.
최종적으로, 압축공기 유출속도의 진폭 ua는 다음의 식에 의해 산정될 수 있다.
여기서, 식(3)에서와 같이 Ua(t) = uaeiσt로 정의된다.
2.6 운동방정식
구조물의 질량과 관성모멘트를 각각 M과 I로 나타내고, 구조물의 좌우측에 있는 계류삭이 구조물의 운동에 저항하는 것으로 하면 구조물의 운동방정식은 구조물에 작용하는 유체압력, 압축공기실 내의 공기압, 복원력 및 계류삭의 반력으로부터 다음과 같이 구성된다.
·수평운동방정식(sway운동)
·연직운동방정식(heaving운동)
·회전운동방정식(rolling운동)
여기서, P는 유체압력으로 선형 Bernoulli방정식으로부터 P = –iρσΦ로 주어질 수 있고, Aβ와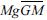 
은 연직과 회전운동에 대한 복원력 성분으로 각각 다음의 식으로 산정된다.
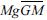은 연직과 회전운동에 대한 복원력 성분으로 각각 다음의 식으로 산정된다.
그리고, Kmn(m = α,β,ω; n = α,β,ω)은 탄성스프링에 의한 연직긴장계류를 가정하면 다음의 식으로 평가될 수 있다(Ijima et al., 1972).
여기서, K는 계류삭의 스프링상수이다.
따라서, 운동방정식(22)~(24)를 이산화하면 다음과 같은 이산화방정식으로 나타날 수 있다.
이상의 이산화방정식(10), (20), (28), (29) 및 (30)을 연립하여 풀면 반사율, 전달율, 압축공기압 및 부체의 운동성분을 산정할 수 있고, 압축공기 흐름속도는 식(21)로부터 도출될 수 있다.
3. 수치해석결과의 검증
본 연구의 수치해석에서 얻어지는 해의 타당성은 기존의 수치해석 및 실험결과와 비교로부터 검증된다. 검증에 적용되는 구조물은 총 4종류의 구조물로 수면상에 고정된 폰툰형 구조물, 계류되지 않은 폰툰형 부체구조물, 수면하에 계류된 폰툰형 부체구조물 및 수면상에 고정된 압축공기 주입식 구조물이며, 각 구조물에 의한 반사율과 전달율의 결과를 중심으로 해의 타당성을 검토한다.
3.1 폰툰형 고정구조물
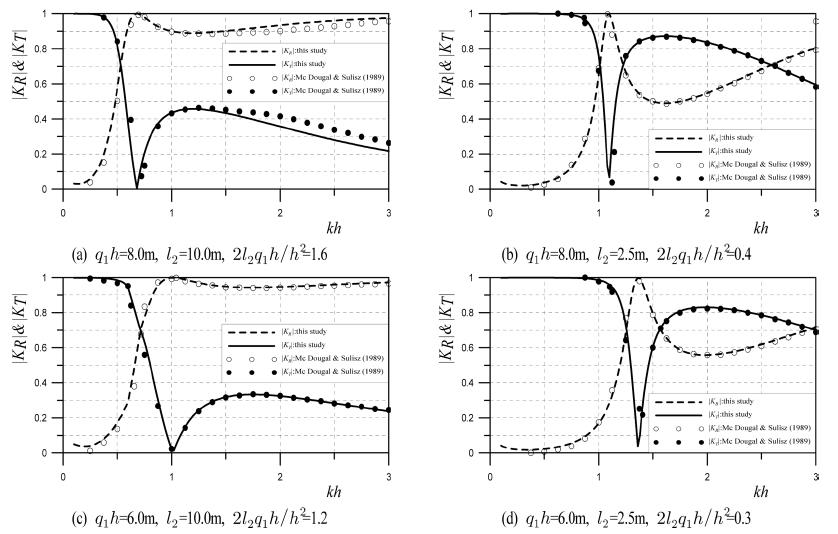
먼저, 수면상 폰툰형 고정구조물에 의한 파랑변형율을 경계요소법으로 해석하고 있는 MaDougal and Sulisz(1989)의 수치해석결과와 본 연구의 해석결과를 비교한 것이 Fig. 5이다. 그림에서 수평축은 kh로 수심 h에 대한 입사파장 L과 비율관계를, 연직축은 반사율 |KR|과 전달율 |KT|를 각각 제시하고 있다. 여기서, Fig. 5의 모든 계산결과에 h = 10.0m를 적용하고 있으며, Fig. 5(a)는 q1h = 8.0m, l2= 10.0 m, (b)는 q1h = 8.0m, l2= 2.5m, (c)는 q1h = 6.0m, l2= 10.0 m, (d)는 =6.0m, =2.5m에 대한 결과이다. 제2장에서 기술된 수치해석이론을 폰툰형 고정구조물에 적용하기 위해서는 압축공기실을 고려하지 않고(혹은 압축공기실의 폭을 0으로 접근시킴), 동시에 구조물의 운동을 고려하지 않으면 된다. 전체적으로 일정한 수심에 대해 입사파장이 길어질수록 혹은 입사주기가 길어질수록 반사율이 감소하고, 동시에 전달율이 증가하는 경향을 나타낸다. 여기서, Fig. 5(a)와 (b) 혹은 (c)와 (d)를 비교하면 구조물의 폭이 좁을수록 반사율이 줄어들고, 동시에 전달율이 커지며, 이러한 경향은 입사파장이 길수록 현저하게 나타난다. 또한, Fig. 5(a)와 (c) 혹은 (b)와 (d)를 비교하면 흘수심이 얕을수록 반사율은 줄어들고, 동시에 전달율은 커지며, 이러한 경향은 역시 입사파장이 길수록 현저하게 나타난다는 것을 확인할 수 있다. 여기서, MaDougal and Sulisz(1989)의 결과와 본 연구의 결과에서 입사파장, 흘수심 및 구조물폭의 변화과정에 따른 반사율 |KR|과 전달율 |KT|의 변화과정이 거의 동일하며, 두 결과에서 나타나는 미미한 차이는 절점수 및 절점간격 등의 차이에 의한 것으로 판단된다.
3.2 자유부체구조물
다음의 Fig. 6에 나타내는 수치해석결과는 경계요소법에 의한 MaDougal and Sulisz(1989)의 결과와 본 연구결과를 비교한 것으로, 계류가 되지 않은 자유부체구조물에 의한 반사율과 전달율을 나타내고 있다. 그림에서 수평축은 kh로 수심 h에 대한 입사파장 L과 비율관계를, 연직축은 반사율 과|KR| 전달율 |KT|를 각각 제시하고 있고, 모두 h = 10.0m에 대해 Fig. 6(a)는 q1h = 8.0m, l2= 10.0 m, (b)는 q1h = 8.0m, l2= 2.5m, (c)는 q1h = 6.0m, l2= 10.0 m, (d)는 q1h = 6.0m, l2= 2.5m를 적용한 결과이다. 이 때, 구조물의 밀도는 해수 밀도의 반으로 가정되므로 구조물의 전체높이는 Fig. 6(a)와 (b)의 경우 16.0 m, (c)와 (d)의 경우 12.0 m로 주어지며, 이로부터 구조물의 단면형상이 결정되어 구조물의 질량과 중심에 관한 관성모멘트가 산정될 수 있다. 자유부체구조물에 대한 본 해석결과는 제2장에서 기술된 수치해석이론에서 압축공기실을 고려하지 않고(혹은 압축공기실의 폭을 0으로 접근시킴), 동시에 계류되어 있지 않으므로 계류삭의 저항력을 고려하지 않으면 간단히 얻어질 수 있다. 그림을 살펴보면 전체적으로 일정수심에 대해 입사파장의 변화에 따라 반사율과 전달율의 변동이 다소 복잡하게 나타나는 것을 알 수 있고, 먼저 동일한 구조물폭 l2= 10.0m를 갖는 Fig. 6(a)와 (c) 및 l2= 2.5m를 갖는 Fig. 6(b)와 (d)를 비교하면, 흘수 q1h가 얕아짐에 따라 파랑변형율이 급변하는 주기대가 보다 단주기측으로 이동되는 것을 알 수 있다. 여기서, l2= 2.5m를 갖는 Fig. 6(b)와 (d)의 경우는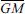 
가 (-)값을 나타내므로 실제로는 복원력이 없는 부체구조물이다. 여기서, MaDougal and Sulisz(1989)의 결과와 본 연구의 결과에서 입사파장, 흘수심 및 구조물폭의 변화과정에 따른 반사율 |KR|과 전달율 |KT|의 변화과정이 거의 동일하며, 역시 두 수치해석결과에서 보이는 미미한 차이는 절점수 및 절점간격 등의 차이에 의한 것으로 판단된다.
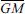가 (-)값을 나타내므로 실제로는 복원력이 없는 부체구조물이다. 여기서, MaDougal and Sulisz(1989)의 결과와 본 연구의 결과에서 입사파장, 흘수심 및 구조물폭의 변화과정에 따른 반사율 |KR|과 전달율 |KT|의 변화과정이 거의 동일하며, 역시 두 수치해석결과에서 보이는 미미한 차이는 절점수 및 절점간격 등의 차이에 의한 것으로 판단된다.
3.3 계류부체구조물
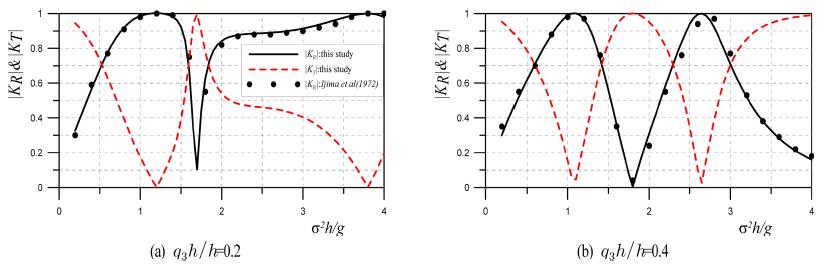
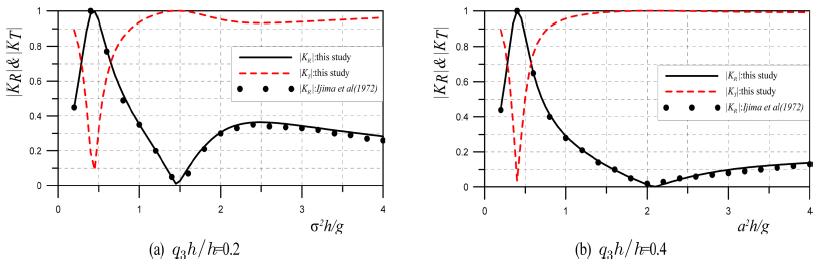
수중에 계류된 폰툰형 부체구조물에 의한 반사율을 고유함수전개법으로 해석한 Ijima et al.(1972)의 결과와 본 연구의 결과를 비교한 것이 Fig. 7과 8에 제시되어 있다. 제2장에 제시된 수치이론을 수중에 계류된 폰툰형 부체구조물에 적용하기 위해서는 경계적분의 순서를 조정하고, 압축공기실의 폭을 0으로 접근시키면서 계류시스템에 따른 계류삭의 저항력을 고려하여야 한다. 여기서, Fig. 7과 8은 open mooring 및 cross mooring의 경우로 각각 l2/h = 0.5, 긴장계류에서 계류삭의 수평길이 h0와 연직길이 l0의 비가 h0/l0= 1/3, 계류삭의 저항계수 K가 K/ρgl2 = 1.0, 구조물의 밀도 ρ'가 ρ'/ρ = 0.8인 값으로 산정된 결과이다. 수평축이 σ2h/g로 일정수심에 대해서는 주기의 변화를, 연직축은 반사율 |KR|과 전달율 |KT|를, 그리고 파라미터는 잠수심 q3h를 수심 h로 나눈 무차원잠수심 q3h/h를 각각 나타낸다. 먼저, Fig. 7을 살펴보면 무차원잠수심이 커질수록 일정수심에 대해 주기의 변화에 따른 반사율의 변동이 급변하는 경향을 나타내고, 반사율이 0으로 되는 주기가 약간 단주기측으로 이동되고 작은 반사율을 나타내는 주변의 주기영역이 넓어지며, 반사율이 1로 되는 장주기측의 주기는 무차원잠수심이 커질수록 보다 장주기측으로 이동되고, 주변의 주기영역이 좁아지는 것을 확인할 수 있다. 다음으로, Fig. 8을 살펴보면 무차원잠수심이 커질수록 반사율이 0으로 되는 주기가 단주기측으로 이동되고 작은 반사율을 나타내는 주변의 주기영역이 넓어지며, 반사율이 1로 되는 주기는 무차원잠수심의 변화에 거의 관계가 없지만 주변의 주기영역이 좁아지는 것을 확인할 수 있다. 그리고, 단주기측에서 나타나는 극대치는 무차원잠수심이 커질수록 보다 단주기측으로 이동되고, 또한 그 값의 크기도 감소하는 것을 확인할 수 있다. 여기서, Ijima et al.(1972)의 결과와 본 연구의 결과에서 입사주기, 잠수심 및 계류시스템의 변화에서 반사율 |KR|의 변화과정이 거의 동일하다는 것을 알 수 있다.
3.4 압축공기 주입식 고정구조물
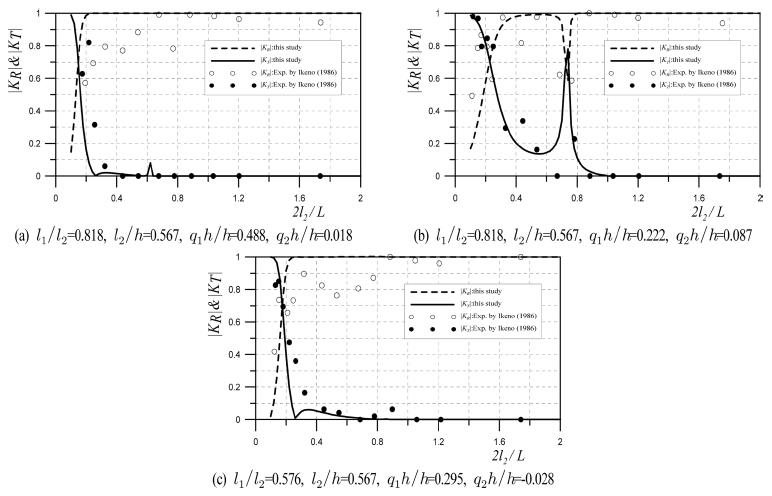
다음에 제시하는 Fig. 9의 결과는 수면상의 압축공기 주입식 고정구조물에 대한 Ikeno(1986)의 수리실험결과와 본 수치해석법에 의한 결과를 비교한 일례이다. 여기서, 제2장에 제시된 본 수치이론을 압축공기 주입식 고정구조물에 적용하기 위해서는 구조물의 운동과 압축공기실 내에서 압축공기 흐름속도를 고려하지 않으면 간단히 얻어진다. 결과에는 γ=1.4(단열변화)와 l2/h = 0.567에 대해 Fig. 9(a)는 l1/l2= 0.818, q1h/h = 0.488, q2h/h = 0.018, (b)는 l1/l2= 0.818, q1h/h = 0.222, q2h/h = 0.087 및 (c)는 l1/l2= 0.576, q1h/h = 0.295, q2h/h = −0.028가 적용되었고, 수평축은 2l2/L(L은 입사파장)을, 연직축은 반사율 |KR|을 각각 나타낸다. 그림을 살펴보면 전체적으로 장주기측에서는 반사율은 작고, 전달율은 큰 값을 나타내는 반면, 단주기측에서는 반사율은 크고, 전달율은 작은 값을 나타낸다. 이러한 결과는 고정폰툰형구조물에 대한 Fig. 5의 결과와 유사하다. 그러나, Fig. 9(b)의 경우와 같이 2l2 ⁄ L ≈ 0.75에서 전달율이 급격히 커지고, 반사율이 떨어지는 현상 및 전체적으로 2l2 ⁄ L ≈ 0.2 근방에서 급격한 파랑변형율의 변동을 나타내는 것은 폰툰형 고정구조물에서 볼 수 없는 현상이다. 하지만, Ikeno(1986)의 수리실험결과와 본 수치해석결과를 비교하면 2l2 ⁄ L ≈ 0.4 근방의 반사율에서 약간 상이한 결과를 나타나지만 전체적으로는 입사파장의 변화에 따라 파랑변형율의 변화과정이 잘 일치하는 것으로 판단된다.
4. 수치해석결과
이하에서 나타내는 결과는 Fig. 4에 제시한 WEC를 탑재한 압축공기 주입식 구조물을 고정시킨 경우에 반사율 |KR|, 전달율 |KT| 및 WEC로 유입되는 무차원압축공기 흐름속도 2|ua| ⁄Hσ, 그리고 계류시킨 경우에 반사율 |KR|, 전달율 |KT|, WEC로 유입되는 무차원압축공기 흐름속도 2|ua| ⁄Hσ, 무차원수평운동 2|α| ⁄H, 무차원연직운동 2|β| ⁄H 및 무차원회전운동 4l2|ω| ⁄H에 대해 입사주기를 중심으로 제시된 파라미터의 변화에 따른 무차원량의 변동특성을 검토한다. 여기서, 계류시스템은 연직긴장계류를 적용한다.
4.1 파력발전시스템을 탑재한 압축공기 주입식 고정구조물
(1) 흘수심의 변화
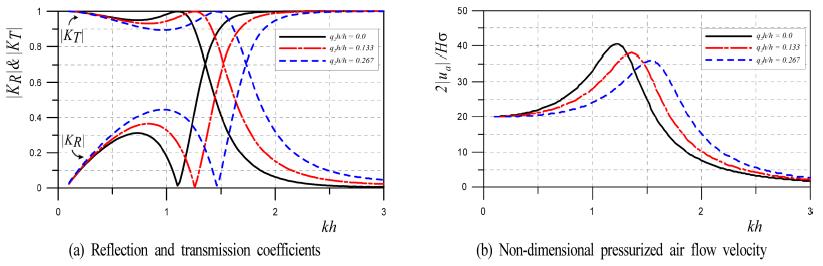
Fig. 10에 나타내는 결과는 h = 15 m, l2= 10 m, l1= 7m, q2h = 1m, ca= 1.0, da= 4m, Aa= 0.7 m2/m, H/L = 0.01(는 입사파고), γ = 1.4에 대해 흘수심을 q1h = 5, 6, 7m로 변화시킨 경우에 파랑변형율 |KR|과 |KT|및 무차원압축공기 흐름속도 2|ua| ⁄Hσ를 제시한 것이다. 반사율은 0.5 < kh < 1.0의 범위에서 극대치를, 1.0 < kh < 1.5의 범위에서 극소치를 나타낸 후에 급격하게 증가하고, kh > 2.0에서는 거의 전반사를 나타낸다. 전달율은 반사율과는 반대의 경향을 나타내며, 반사율과 전달율 모두 kh ≈ 1.3에서는 급변하는 것을 알 수 있다. 여기서, 흘수심이 증가할수록 kh에 따른 파랑변형율의 변화추이가 장주기측으로 이동되는 양상으로부터 흘수심이 깊을수록 보다 장주기파랑의 제어효과가 우수하다는 것을 알 수 있다.
Fig. 10.
Wave transformation and non-dimensional pressurized air flow velocity according to the change of q1h/h(l1/l2= 0.7, l2/h = 0.667, q2h/h = 0.067, ca= 1.0, d2/h = 0.267, Aa/2l2= 0.035, H/L = 0.01, γ = 1.4).
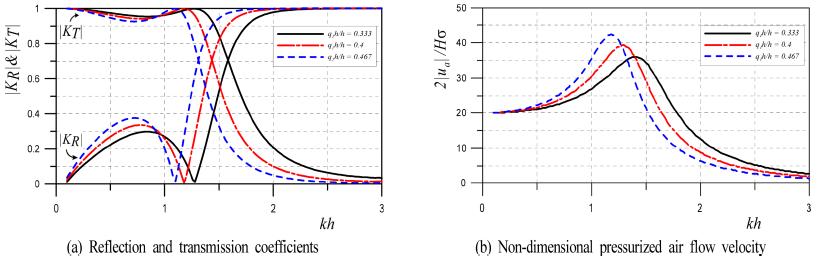
다음으로, 무차원압축공기 흐름속도를 살펴보면 파랑변형율이 급변하는 1.0 < kh < 1.5에서 최대치가 발생하고, 최대치는 흘수심이 깊을수록 장주기측으로 이동되며, 동시에 그의 크기가 증가되는 경향을 나타낸다. 이러한 결과는 구조물 하부를 통과한 압축공기실 내에서 파의 파장과 압축공기실의 폭과의 관계로부터 발생되는 피스톤모드의 공진현상에 의한 것이다. 여기서, kh < 0.5의 장주기측에서는 흘수심의 변화에 따른 값의 차이는 크지 않고, 대략 20 정도의 일정치를 나타내지만 최대치를 나타내는 kh보다 큰 장주기측에서는 흘수심이 깊을수록 큰 값을 나타낸다. 또한, 최대치를 나타낸 kh 이후의 단주기측에서는 kh의 증가에 따라 감소하는 경향을 보이고, 더불어 흘수심이 깊을수록 그의 경향은 심화된다.
다음의 Fig. 11에 나타내는 결과는 10의 조건과 동일하지만 초기압축공기압고가 q2h = 4m인 경우에 흘수심을 q1h = 5, 6, 7 m로 변화시켰을 때 파랑변형율 |KR|과 |KT| 및 무차원압축공기 흐름속도 2|ua| ⁄Hσ를 나타낸다. 전술한 Fig. 10의 경우와 비교하면 흘수심이 증가할수록 kh의 변화에 따른 파랑변형율의 변화양상이 장주기측으로 이동되는 현상은 동일하지만 변동폭이 넓어지는 것을 확인할 수 있다. 따라서, 흘수심이 작을수록, 그리고 초기압축공기압고가 클수록 변동양상은 단주기측으로 이동되는 결과를 나타낸다. 무차원압축공기 흐름속도의 경우는 Fig. 10의 경우와 거의 동일한 변화양상을 나타내지만 초기압축공기압고가 클수록 kh의 변화에 따른 그의 변동과정이 전체적으로 단주기측으로 이동되는 것을 볼 수 있다.
(2) 초기압축공기압고의 변화
Fig. 12에 나타내는 결과는 h=15m, l2=10m, l1=7m, q1h=6m, ca=1.0, da=4m, Aa=0.7m2/m, H/L=0.01, γ=1.4에 대해 초기압축공기압고를 q2h=0, 2, 4m로 변화시킨 경우에 파랑변형율 |KR|과 |KT| 및 무차원압축공기 흐름속도 2|ua| ⁄Hσ를 나타낸 것이다. 그림으로부터 압축공기압고가 증가할수록 kh의 변화에 따른 파랑변형율의 전체 변화양상이 단주기측으로 이동되는 결과를 보이며, 전술한 Fig. 10과 11의 경우와 유사한 변화과정을 나타낸다. 또한, 초기압축공기압고가 증가할수록 무차원압축공기 흐름속도의 변화양상이 파랑변형율과 동일하게 단주기측으로 이동되지만 최대치는 감소하는 결과를 나타낸다. 이러한 사실은 초기압축공기압고가 클수록 압축공기실 내에서 수심이 얕아지고, 이에 따라 파장이 짧아지기 때문에 공진현상을 포함한 변화특성이 단주기측으로 이동되는 것으로 판단된다. 여기서, Fig. 10과 11을 포함하여 고찰하면 무차원압축공기 흐름속도의 최대치가 발생하는 는 파랑변형율에서 극대치(전달율)와 극소치(반사율)가 발생하는 kh의 값보다 약간 큰 값을 나타내므로 보다 단주기측이라는 것을 알 수 있다.
(3) ca의 변화
다음의 Fig. 13에 나타내는 결과는 h = 15m, l2= 10 m, l1= 7m, q1h = 6m, q2h = 0m, da= 4m, Aa= 0.7m2/m, H/L = 0.01, γ =1.4에 대해 식(16)에서 도입하는 상수 ca를 ca= 0.7, 0.9, 1.1로 변화시킨 경우에 파랑변형율 |KR|과 |KT| 및 무차원압축공기 흐름속도 2|ua| ⁄Hσ를 나타낸 것이다. 그림으로부터 ca의 변화는 파랑변형율과 무차원압축공기 흐름속도에 미치는 영향이 없다는 흥미로운 결과를 확인할 수 있다.
(4) 압축공기실폭의 변화
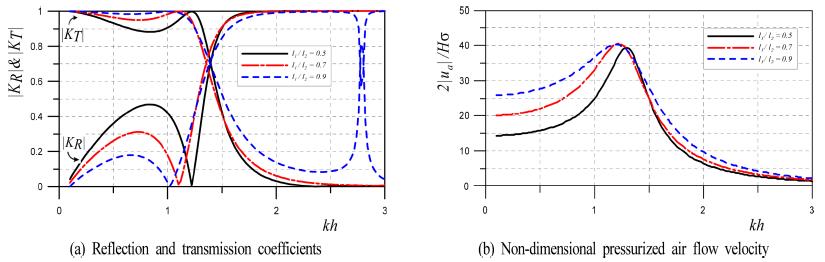
Fig. 14에 나타내는 결과는 h=15m, l2=10m, q1h=6m, q2h=0m, ca= 1.0, da=4m, Aa=0.7m2/m, H/L = 0.01, γ=1.4에 대해 l1=5, 7, 9m로 변화시킨 경우 파랑변형율 |KR| 과|KT| 및 무차원압축공기 흐름속도 2|ua| ⁄Hσ를 제시하고 있다. 그림으로부터 l1의 값이 증가할수록 kh < 1.5의 범위에서 나타나는 파랑변형율의 극대치 및 극소치는 장주기측으로 이동되고, kh < 1.0에서의 극대치는 작아지고, 극소치는 커지는 현상을 볼 수 있다. 무차원압축공기 흐름속도의 변화를 살펴보면 압축공기실폭이 넓을수록 최대치는 장주기측으로 이동되지만 그 값의 차이는 크지 않다. 여기서, 최대치를 나타내는 kh보다 장주기측에서는 압축공기실폭이 넓을수록 상대적으로 매우 큰 무차원압축공기 흐름속도를 나타내지만 최대치를 나타내는 kh보다 단주기측에서는 기본적으로 압축공기실폭이 넓을수록 약간 큰 흐름속도를 나타내지만 그 값의 차이는 크지 않다는 것을 알 수 있다. 이러한 결과는 압축공기실폭이 넓을수록 수면변동량폭이 넓어지고, 이로부터 압축공기실 내에서 많은 양의 공기가 압축되기 때문으로 판단된다. 이에 따라 압축공기 흐름속도가 증가되고, 이러한 현상은 장주기측에서 보다 현저하게 나타난다는 것을 알 수 있다. 한편, 압축공기의 흐름속도에서 그의 최대치는 l1/l2= 0.5의 경우 2l1/L = 0.136에서, l1/l2= 0.7의 경우 2l1/L = 0.178에서, l1/l2= 0.9의 경우 2l1/L = 0.222에서 |ua|max=12.85m/s의 값을 각각 나타내는 것을 확인할 수 있다. 여기서, l1/l2의 비가 커지는 경우 l2가 일정하므로 결국 부력체의 폭이 좁아진다는 의미를 나타내며, 이의 경우 압축공기 최대흐름속도의 발생위치 2l1/L의 값은 부력체폭이 0일 때 공진발생조건인 2l1/L = 0.25에 접근한다는 것을 나타낸다.
4.2 파력발전시스템을 탑재한 압축공기 주입식 부체구조물
압축공기 주입식 부체구조물에서 구조물의 상단에 파력발전시스템을 탑재한 경우 이의 중량과 관성모멘트를 고려하여야 하지만 현 단계에서는 정확한 값을 추정하기 어려우므로 본 계산에서 ρ'/ρ = 0.9(ρ'는 파력발전시스템을 탑재한 경우 구조물의 밀도로 전단면에 걸쳐 균등하며, 구조물의 단면형상은 Fig. 4의 경우와 동일한 것으로 각각 간주된다)를 가정하여 수치계산을 수행한다. 또한, 풍력발전시스템까지도 적용하는 경우에는 그에 따른 중량과 관성모멘트 및 무게중심 등을 고려할 필요가 있다. 여기서, 압축공기 주입식 부체구조물에서 계류시스템은 모든 계산케이스에서 연직긴장계류로 가정되고, 따라서 식(27)에서 Kββ이외의 계류삭에 의한 저항력은 없어진다.
(1) 흘수심의 변화
Fig. 15는 h=30m, l2=10m, l1=7m, q2h=1m, ca=1.0, da=4m, dt=0.5m, Aa=0.7m2/m, H/L = 0.01, γ = 1.4, ρ'=0.9g/cm3에 대해 흘수심 q1h를 q1h =5, 6, 7m로 변화시킨 경우 kh의 변화에 따른 파랑변형율 |KR|과 |KT|, 무차원압축공기 흐름속도 2|ua|⁄Hσ, 무차원수평운동 2|α|⁄H, 무차원연직운동 2|β|⁄H및 무차원회전운동 4l2|ω|⁄H의 변동결과를 나타낸 것이다. 그림으로부터 kh < 2.0의 장주기측에서 1.0 근방의 큰 전달율과 0.1 정도의 작은 반사율을 나타내지만 kh > 2.0의 단주기측에서는 파랑변형율이 크게 변동되는 것을 알 수 있고, kh < 2.0의 장주기측에서 반사율의 극대치를 나타내는 kh의 값은 흘수심이 깊을수록 작아지므로 장주기측으로 이동된다. 여기서, 전술한 4.1절의 고정시 Fig. 10의 경우와 비교하면 흘수심이 클수록 파랑변형율의 변화과정이 장주기측으로 이동되는 현상은 동일한 반면, 파랑변형율의 변화과정은 전체적으로 단주기측으로 이동되는 결과를 볼 수 있다.
Fig. 15.
Wave transformation, non-dimensional pressurized air flow velocity and non-dimensional amplitude of vertical motion according to the change of q1h/h(l1/l2= 0.7, l2/h = 0.333, q2h/h = 0.033, ca= 1.0, da/h = 0.133, dt/h = 0.0167, Aa/2l2= 0.035, H/L = 0.01, γ = 1.4, ρ'/ρ =0.9, Kββ/ρgl2= 1.0).
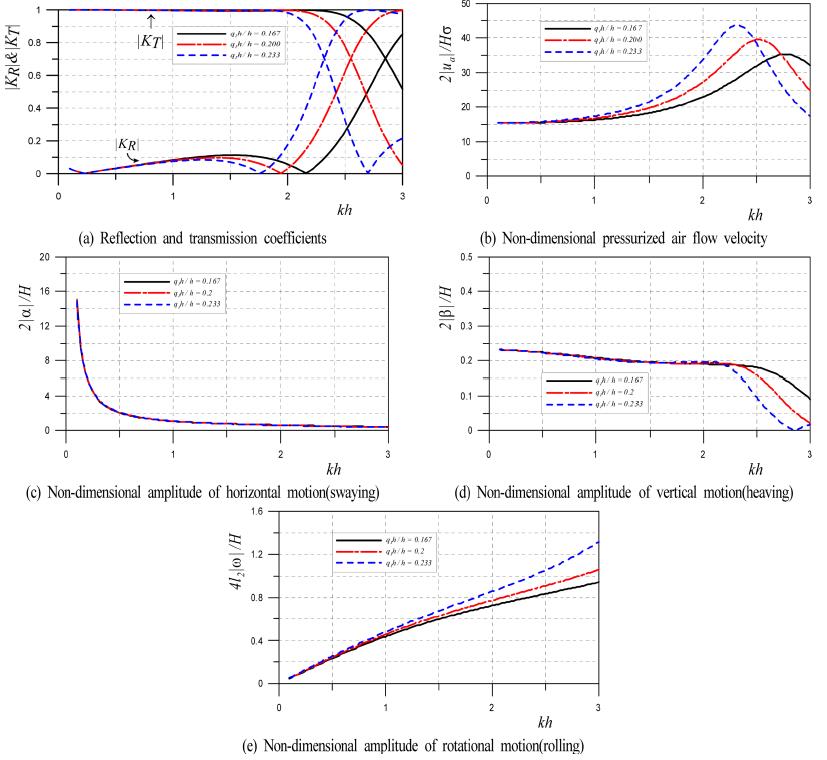
Fig. 15(b)에 나타낸 무차원압축공기 흐름속도를 살펴보면 흘수심이 깊을수록 최대치는 커지고, 동시에 파랑변형율과 같이 장주기측으로 이동되는 결과를 나타낸다. 그리고, 각 흘수심에 대한 공진현상에 의한 최대치가 발생하는 kh는 전달율과 반사율이 교차는 kh와 거의 동일하다는 것을 알 수 있다. 전술한 4.1절 고정식의 경우보다 공기흐름속도의 최대치가 발생하는 위치는 보다 단주기측으로 이동되지만 그의 크기는 거의 동일하다. 그러나, kh < 0.5의 장주기측에서 공기흐름속도는 고정시의 경우보다 작은 대략 15의 값을 나타낸다. 이의 원인으로 연직방향으로 파랑에너지가 분포하는 수심이 크게 깊어졌고, 그에 따른 파장이 변하였기 때문에 고정식의 경우와 직접적으로 비교하기에는 어렵지만 구조물이 운동하는 부체식이라는 점을 들 수 있을 것이다. 또한, 제2장의 이론에서 알 수 있는 바와 같이 압축공기 흐름속도는 압축공기실 내에서 수위변동 및 구조물의 운동, 특히 후술하는 연직운동과 연계되어 있기 때문에 그림으로부터 kh > 2.0의 단주기측에서 압축공기 흐름속도의 변화과정에 파랑변형율과 연직운동의 변동특성이 크게 반영된 것으로 판단된다. 이러한 결과는 압축공기실 내에서 수면변동이 구조물 하부를 통과하는 파랑에너지와 연직운동에 직접적인 영향을 받기 때문인 것으로 여겨진다.
다음으로, 구조물의 운동을 살펴본다. 수평운동의 경우 장주기측으로 갈수록 급격히 증가하는 큰 변위를, 반면에 단주기측에서는 작은 변위를 나타내지만 흘수심의 차이에 따른 변화는 거의 나타나지 않는 것을 볼 수 있고, 특히 kh > 2.0에서 급격하게 변동하는 파랑변형율은 수평운동에 거의 영향을 미치지 못한다는 것을 알 수 있다. 이러한 결과는 본 구조물의 계류시스템이 연직긴장계류이기 때문에 수평파력에 대한 저항력이 매우 작기 때문이다. 연직운동의 경우 kh < 2.2의 장주기측에서 흘수심의 변화에 따른 값의 차이는 거의 없고, kh가 증가할수록 약간 감소하는 경향을 나타낸다. kh > 2.2에서는 무차원연직운동이 급격히 작아지고, 또한 흘수심이 깊을수록 보다 작은 연직운동을 나타내며, 변화과정은 장주기측으로 이동되는 결과를 나타낸다. 여기서, 무차원연직운동에서 흘수심의 변화에 따른 차이가 크게 나타나는 kh의 범위는 파랑변형율과 무차원압축공기 흐름속도의 경우와 직접적인 연관을 갖는 것으로 판단된다. 무차원회전운동의 경우 단주기측으로 갈수록, 그리고 흘수심이 깊을수록 커지는 경향을 나타내며, 장주기측에서는 수평운동과, 단주기측에서는 연직운동과 상호연계성이 크다는 것을 알 수 있다.
Fig. 16은 전술한 15와 동일한 조건을 갖지만 초기압축공기압고를 증가시킨 q2h=4m(q2h/h = 0.133)의 경우에 대해 흘수심을 q1h=5, 6, 7 m로 변화시켰을 때 파랑변형율 |KR|과 |KT|, 무차원압축공기 흐름속도 2|ua|⁄Hσ, 무차원수평운동 2|α| ⁄ H, 무차원연직운동 2|β| ⁄H 및 무차원회전운동 4l2|ω|⁄H를 나타내고 있다. 파랑변형율을 살펴보면 kh>1.7에서 급격하게 변동되고, 극대치와 극소치의 발생은 흘수심이 클수록 보다 장주기측에서 나타나며, 전반적으로 전술한 Fig. 15의 경우보다 단주기측에서 파랑변형율의 변동과정이 복잡하다는 것을 알 수 있다. 이것은 초기압축공기압고가 q2h = 1m에서 4 m로 증가되었기 때문에 구조물 전체 강성이 증대되고, 이로 인하여 전체 시스템이 주기변화에 민감하기 때문인 것으로 판단된다. Fig. 16(b)에 나타내는 무차원압축공기 흐름속도의 변화과정을 살펴보면 Fig. 15(b)의 경우보다 최대치의 발생위치가 보다 단주기측으로 이동되어 있고, q1h/h = 0.167과 0.2의 경우 본 수치계산 kh의 범위 밖의 단주기측에서 그의 최대치가 나타날 것으로 예측된다. 또한, 흘수심이 깊을수록 변동과정이 장주기측으로 이동되는 현상은 Fig. 15(b)와 동일하며, kh < 1.0의 장주기측에서는 Fig. 15(b)와 16(b) 모두 거의 동일한 대략 15 정도의 값을 나타내는 것을 알 수 있다.
Fig. 16.
Wave transformation, non-dimensional pressurized air flow velocity and non-dimensional amplitude of vertical motion according to the change of q1h/h(l1/l2 = 0.7, l2/h = 0.333, q2h/h = 0.133, ca = 1.0, da/h = 0.133, dt/h = 0.0167, Aa/2l2 = 0.035, H/L = 0.01, γ = 1.4, ρ'/ρ = 0.9, Kββ /ρgl2 = 1.0).
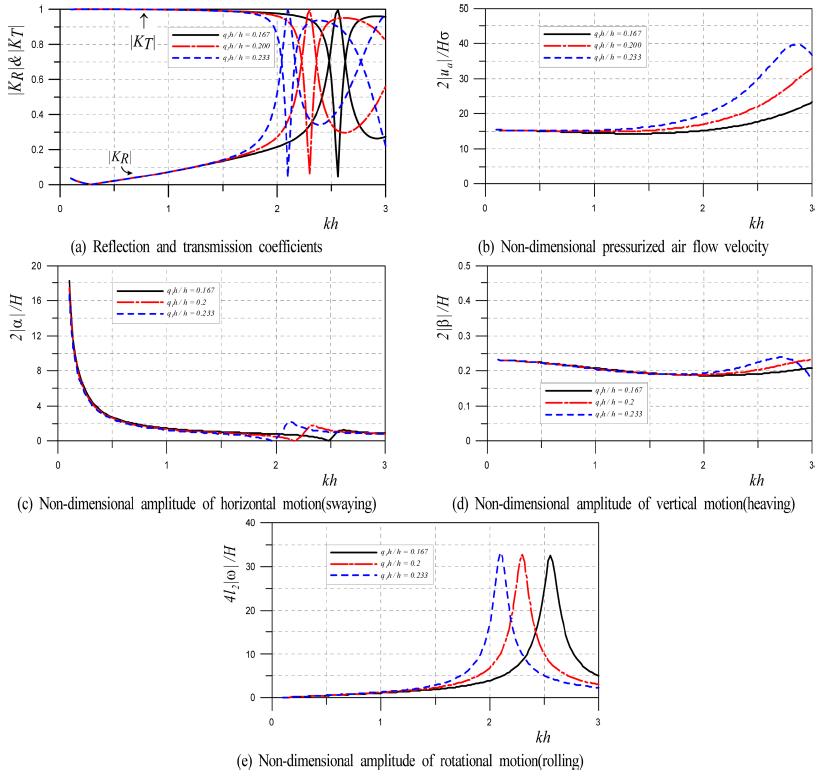
다음으로, 구조물의 무차원수평운동을 검토한다. 전체적으로는 전술한 Fig. 15의 경우와 동일하게 장주기측에서 큰 변위를, 단주기측에서 작은 변위를 나타내며, 흘수심의 변화에 따라서는 Fig. 15와는 상이하게 약간 차이를 나타내지만 크지는 않다. 여기서, kh > 2.0의 단주기측에서 극소치 및 극대치의 발생은 Fig. 15에서는 볼 수 없는 현상이지만 이는 후술하는 회전운동과의 연성이 강하기 때문이다. 연직운동의 경우는 Fig. 15의 경우와 같이 kh < 2.0에서는 흘수심에 거의 영향을 받지 않고, kh의 증가에 따라 약간 감소하는 경향을 나타내지만 kh > 2.0에서는 Fig. 15와 약간 상이한 경향을 나타낸다. 한편, 무차원회전운동을 나타낸 Fig. 16(c)를 살펴보면 kh > 2.0의 단주기측에서 매우 큰 값의 피크치를 나타내며, 이는 흘수심이 깊을수록 장주기측으로 이동된다는 알 수 있다. 이러한 피크치는 Fig. 15에서 나타나지 않는 현상으로, 초기공기압이 증가됨에 따라 본 시스템에서 회전운동의 고유주기가 보다 길어지기 때문에 본 수치계산의 범위내에서 공진이 나타나는 것으로 판단된다.
(2) 초기압축공기압고의 변화
다음의 Fig. 17에 나타내는 결과는 h=30m, l2=10m, l1=7m, q1h=6m, ca= 1.0, da=4m, dt=0.5m, Aa= 0.7m2/m, H/L=0.01, γ = 1.4, ρ' = 0.9 g/cm3에 대해 초기압축공기압고를 q2h=0, 2, 4 m로 변화시킨 경우에 파랑변형율 |KR|과 |KT|, 무차원압축공기 흐름속도 2|ua| ⁄Hσ, 무차원수평운동 2|α|⁄H, 무차원연직운동 2|β|⁄H 및 무차원회전운동 4l2|ω|⁄H를 각각 제시하고 있다.
Fig. 17.
Wave transformation, non-dimensional pressurized air flow velocity and non-dimensional amplitude of vertical motion according to the change of q2h/h(l1/l2= 0.7, l2/h = 0.333, q2h/h = 0.2, ca= 1.0, da/h = 0.133, dt/h = 0.0167, Aa/2l2= 0.035, H/L = 0.01, γ = 1.4, ρ'/ρ = 0.9, Kββ/ρgl2= 1.0)
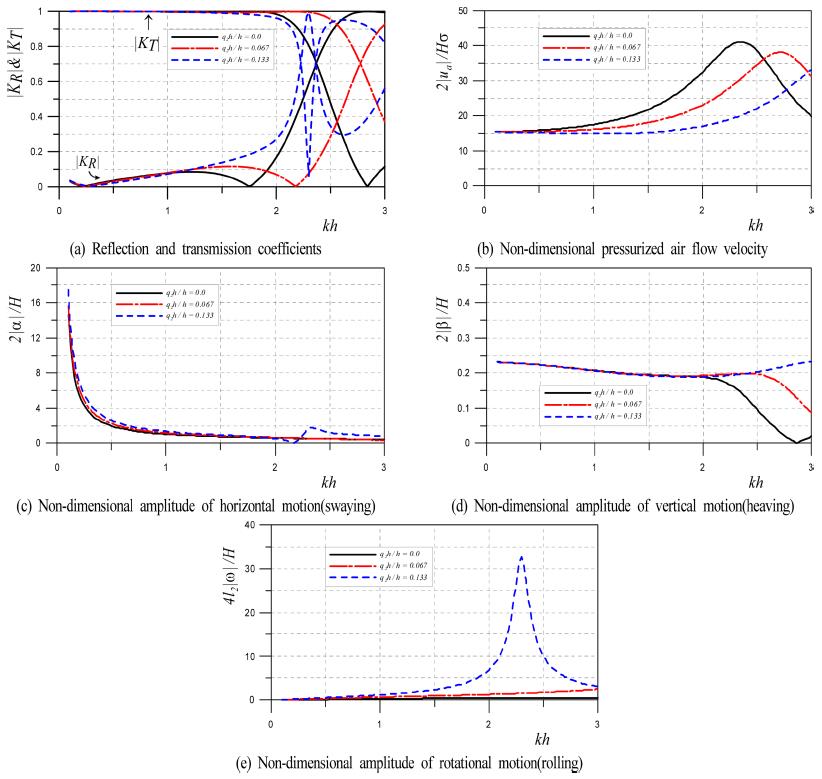
그림으로부터 파랑변형율을 살펴보면 kh < 1.5의 장주기측에서 큰 전달율과 작은 반사율을 나타내고, 더불어 초기압축공기압고의 변화에 크게 좌우되지 않는다는 점에서 전술한 Fig. 15와 16의 두 결과와 유사하지만 kh > 1.5의 단주기측에서는 초기압축공기압고의 변화에 매우 민감하고, q2h/h = 0.133의 경우는 계통적인 변화특성을 나타내지 않는다. 이러한 경향은 후술하는 수평운동과 회전운동에서도 유사하다.
반면, 무차원압축공기 흐름속도는 계통적인 변화특성을 나타내는 것으로 판단되고, 최대치는 초기압축공기고가 작을수록 큰 값을 나타내고, 더불어 장주기측으로 이동되는 결과를 나타낸다. 이러한 결과는 연직운동과 상관이 크고, 특히 kh > 2.0의 범위에서 발생하는 연직운동변위에서 그의 변화기울기가 큰 kh와 거의 동일한 지점에서 무차원압축공기 흐름속도의 최대치가 발생된다는 것을 알 수 있다. 이것은 언급되지 않았지만 전술한 Fig. 15와 16에서도 관찰되는 현상이다. 수평운동, 연직운동 및 회전운동은 전반적으로 Fig. 15와 유사한 변화과정을 나타내지만 q2h/h = 0.133의 경우는 Fig. 16의 변화과정이 포함된 것으로 간주될 수 있다.
(3) ca의 변화
다음은 h = 30m, l2= 10m, l2= 7m, q1h = 6m, q2h = 0 m, da= 4m, dt= 0.5m, Aa= 0.7m2/m, H/L = 0.01, γ = 1.4, ρ' = 0.9 g/cm3에 대해 식(16)에서 ca= 0.7, 0.9, 1.1로 변화시킨 경우 kh에 따른 파랑변형율 |KR|과 |KT|, 무차원압축공기 흐름속도 2|ua| ⁄Hσ 및 무차원운동들의 변화를 나타낸 것이 Fig. 18이다. 그림으로부터 고정시 Fig. 13과 동일하게 파랑변형율, 압축공기 흐름속도 및 각 운동은 ca의 변화에 차이를 나타내지 않는다는 흥미로운 결과를 알 수 있다.
(4) 압축공기실폭의 변화
Fig. 19에 나타내는 결과는 h=30m, l2=10m, q1h=6m, q2h=0m, ca= 1.0, da=4m, dt=0.5m, Aa=0.7m2/m, H/L = 0.01, γ = 1.4, ρ' = 0.9 g/cm에 대해 l1=5, 7, 9m로 변화시킨 경우 파랑변형율 |KR|과 |KT|, 무차원압축공기 흐름속도 2|ua| ⁄Hσ, 무차원수평운동 2|β| ⁄H, 무차원연직운동 및 무차원회전운동 4l2|ω| ⁄H를 나타낸다. 결과로부터 kh < 2.1의 범위에 있는 파랑변형율에서 압축공기실폭이 넓을수록 반사율에서 극대치 및 극소치는 장주기측으로 이동되고, 파랑변형율이 급변하는 kh > 2.0에서는 압축공기실폭이 넓을수록 파랑변형율의 변화과정이 다소 완만해지는 경향을 나타낸다.
Fig. 19.
Wave transformation, non-dimensional pressurized air flow velocity and non-dimensional amplitude of vertical motion according to the change of l1/l2(l2/h = 0.333, q1h/h = 0.2, q2h/h = 0.0, ca= 1.0, da/h = 0.133, dt/h = 0.0167 Aa/2l2= 0.035, H/L = 0.01, γ = 1.4, ρ'/ρ = 0.9, Kββ/ρgl2= 1.0).
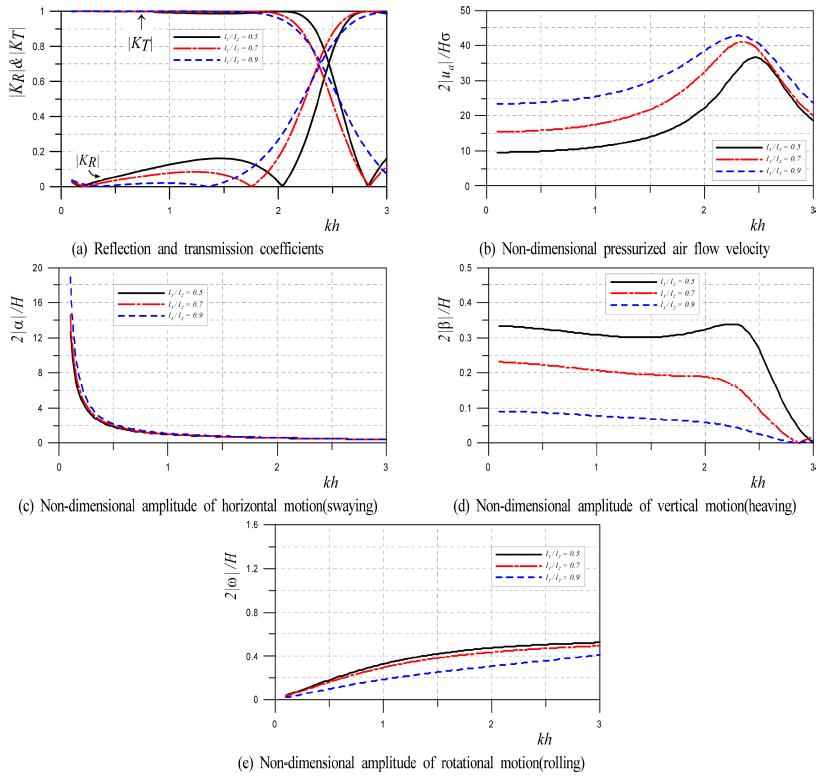
다음으로, 압축공기 흐름속도를 살펴보면 압축공기실폭이 넓을수록 최대치가 발생하는 의 값이 작아지는 결과를 볼 수 있다. 전체적으로 압축공기실폭이 넓을수록 압축공기 흐름속도가 커지며, 이러한 경향은 최대치가 발생하는 보다 작은 장주기측에서 보다 명확하게 주어진다. 압축공기의 흐름속도에서 l1/l2= 0.5의 경우 2l1/L = 0.129에서, l1/l2= 0.7의 경우 2l1/L = 0.172에서, l1/l2= 0.9의 경우 2l1/L = 0.214에서 각각 최대치가 나타난다. l1/l2의 비가 커지는 경우 l2가 일정하므로 결국 부력체의 폭이 좁아진다는 의미를 나타내며, 이의 경우 고정시 Fig. 14에서 언급된 바와 같이 부유시에도 공기흐름에서 최대속도의 발생위치 2l1/L의 값은 부력체폭이 0에 접근할 때 공진발생조건인 2l1/L = 0.25에 접근한다는 것을 알 수 있다. 여기서, 압축공기실폭은 공기흐름속도의 크기를 좌우하는 압축공기실 내 수면변동량과 직접적으로 관계되는 파라미터이다. 수평운동은 지금까지의 경향과 거의 동일한 경향을 나타내며, 압축공기실폭이 넓으면 장주기측에서 약간 커지는 경향을 나타나낸다. 연직운동은 지금까지의 결과에서보다 큰 변동을 나타내며, 전체적으로 단주기로 갈수록 감소하는 결과를 나타낸다. 그리고, 압축공기실폭이 좁을수록 큰 연직운동을 볼 수 있고, 이러한 결과는 연직방향파압이 작용하는 면적이 증가되기 때문이다. Fig. 19에서도 압축공기 흐름속도와 연직운동은 강한 연성을 나타내며, 연직운동의 변화기울기가 크지는 위치에서 압축공기 흐름속도가 최대로 된다는 것을 알 수 있다. 회전운동의 경우는 압축공기실폭이 넓을수록 작은 회전운동을 나타내며, 결과적으로 회전운동에 대해서는 압축공기실폭이 넓을수록 공간적으로 일정한 공기압이 작용하는 넓이가 넓기 때문에 안정적이라는 것을 알 수 있다. 변동과정은 단주기측으로 갈수록 회전운동이 증가되는 것은 Fig. 15의 결과와 유사하다.
(5) 계류삭에서 저항계수의 변화
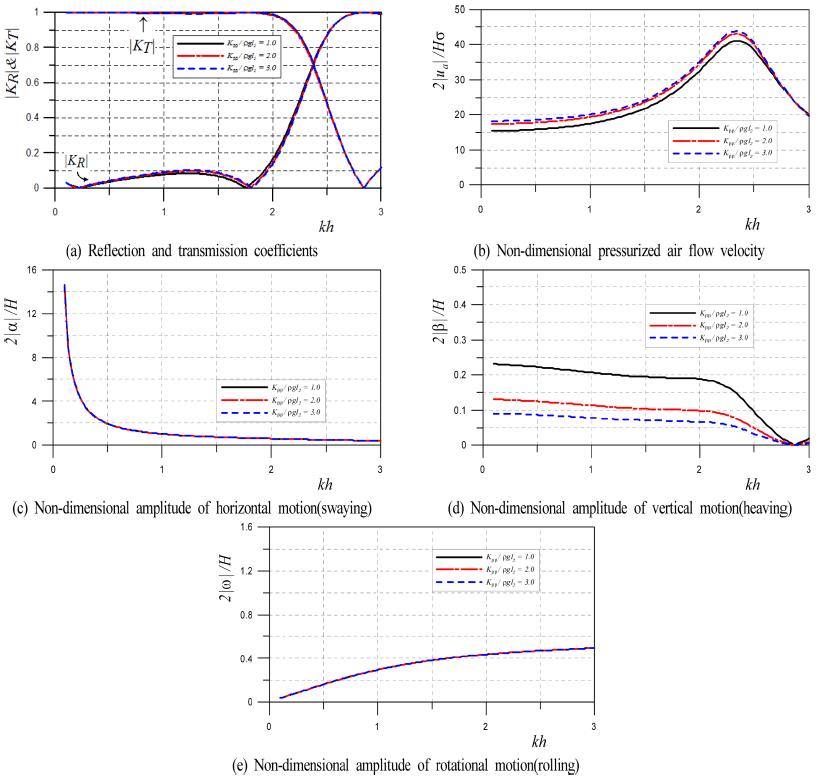
다음의 Fig. 20에 나타내는 결과는 h = 30m, l2= 10m, l1= 7m, q1h = 6m, q2h = 0m, ca= 1.0, da= 4m, dt= 0.5m, Aa= 0.7m2/m, H/L = 0.01, γ = 1.4, ρ' = 0.9 g/cm에 대해 계류삭의 무차원저항계수를 Kββ/ρgl2= 1, 2, 3으로 변화시킨 경우 kh의 변화에 따라 파랑변형율 |KR|과 |KT|, 무차원압축공기 흐름속도 2|ua|⁄Hσ, 무차원수평운동 2|α| ⁄H, 무차원연직운동 2|β|⁄H 및 무차원회전운동 4l2|ω| ⁄H를 나타낸다. 그림의 결과로부터 계류삭에서 저항계수의 변화는 파랑변형율, 수평운동 및 회전운동에 미치는 영향은 미미하지만 연직운동에는 다소 큰 영향을 미치며, 계류삭의 저항계수가 클수록 연직운동은 작아지는 결과를 나타낸다. 따라서, 저항계수가 클수록 압축공기 흐름속도가 커지지만 최대치의 발생위치 kh의 값은 동일하다는 것을 알 수 있다.
Fig. 20.
Wave transformation, non-dimensional pressurized air flow velocity and non-dimensional amplitude of vertical motion according to the change of Kββ/ρgl2 (l1/l2= 0.7, l2/h = 0.333, q1h/h = 0.2, q2h/h = 0.0, ca= 1.0, da/h = 0.133, dt/h = 0.0167, Aa/2l2= 0.035, H/L = 0.01, γ = 1.4, ρ'/ρ = 0.9).
5. 맺음말
본 연구에서는 방파제로 연구·개발된 압축공기 주입식 구조물에 진동수주형 파력발전시스템을 탑재한 경우 방파제로의 기능과 파력발전장치로의 기능을 수치시뮬레이션으로부터 검토하였다. 해석에는 선형속도포텐셜이론에 기초한 경계요소법을, 압축공기 흐름해석에 Boyle법칙과 단열변화과정에 기초한 상태방정식을, 그리고 부체식의 경우는 연직긴장계류시스템을 각각 적용하였다. 해의 타당성은 여러 형태의 구조물에 대한 기존의 수치해석결과 및 실험결과와의 비교로부터 검증되었으며, 실제의 수치해석에서는 여러 파라미터(흘수심, 초기압축공기압고, ca, 압축공기실폭 및 계류삭의 저항계수 등)의 변화에 대해 진동수주형 파력발전시스템을 탑재한 고정식 및 부체식의 구조물에서 파랑변형율, 구조물의 운동 및 압축공기 흐름속도의 변동특성을 논의하였다. 이러한 결과들은 방파제와 진동수주형 파력발전시스템을 복합한 형태의 구조물 계획에서 고정식과 부체식 방파제로써의 가능성, 파력발전구조물로써의 가능성 및 그들의 평가에 중요한 기초자료로 제공될 수 있을 것으로 판단된다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation 
Print 
