1. 서 론
2007년 3월 우리나라 서해안에서 발생한 장주기의 이상파랑으로 2명의 인명피해와 함께 서해안 여러 곳에서 침수 피해가 있었다. 당시의 이상파랑은 주기가 15분 정도로서 지진해일과 유사한 해일의 거동특성을 보였으며, 해일과 함께 이동하는 대기압점프가 확실하게 나타났다. 이 해일은 이동하는 기압 점프(pressure jump)에 의한 대기압의 급변으로 해수면이 국부적으로 상승 또는 하강하게 되고, 기압점프의 이동속도와 해일의 전파속도가 같아질 때 나타나는 Proudman공명 현상이 발생하여 해일고가 크게 증가하였다(Choi et al., 2008). 또한 이렇게 증폭된 해일이 해안에 도달하면서 천수화와 포구 폭 축소에 의해 해일고가 더욱 증대되어 해안을 내습하면서 큰 피해를 발생시켰다. 이러한 발생 및 증폭 기구가 알려지기 전에는 ‘평상적인 파와는 그 특성이 다르고, 발생 원인이 알려지지 않은 큰 파’라는 의미에서 ‘이상파랑’이라는 임시 명칭을 사용하였으나, 전술한 바와 같이 기상변화로 인한 해일로 규명되었으므로 적절한 명칭을 부여하고 앞으로 이를 사용하는 것이 바람직하다.
기압급변부의 이동에 의해 발생하는 장파는 세계 여러 곳에서 나타나며, 그 지역 특유의 명칭으로 불리어왔다. 예를 들어 일본의 Kyushu섬 서쪽해안에 위치한 Nagasaki만에서는 12월에서 다음해 4월 사이에 장파가 내습하는데 이를 Abiki라 부르며, 가까운 중국 산둥반도의 북부 해안에 있는 Longkou항에서도 5월에서 8월 사이에 장파가 자주 내습하는데 특별한 명칭은 없다. 또한 스페인의 지중해 연안의 Balearic제도에서 발생하는 장파는 Rissaga로 불리운다. Monserrat et al.(2006)은 이러한 장파를 종합하여 ‘기상쓰나미(meteorological tsunami; meteo-tsunami)’라 명명하였다. 이와 같이 기상변동에 의한 장파를 국제적으로 기상쓰나미라 부르고 있으며, 이를 우리말로 번역하면 ‘기상지진해일’이라 할 수 있다. 그러나 지진과는 무관하므로 기상장파 또는 기상해일이라 명명하는 것이 좋을 듯하다. 기상 변동에 의한 장파에는 태풍에 의한 폭풍해일도 있으나 2007년의 장파는 폭풍해일에 비해 주기가 짧고, 에너지 면에서도 훨씬 강도가 작다. 기상변동에 의한 장파는 주기가 5~20분 정도이므로 우리나라 동해안에 내습하는 지진해일과 비슷하며, 전파 및 범람양상이 서로 비슷하므로 기상해일이 기상장파보다 좀 더 자연스러워 보인다. 이 연구에서는 임시 명칭인 ‘이상파랑’대신 ‘기상해일(meteo-tsunami)’을 사용한다.
기상해일은 세계 여러 곳에서 발생한 기록이 있으며, 상당한 연구가 수행되어 발표되었다. Monserrat et al.(2006)은 이러한 기상해일의 연구 성과를 정리하여 제시한 바, 대략적인 내용은 다음과 같다. Fontsere(1934), Ramis and Jansa(1983), Tintore et al.(1988) 및 Monserrat et al.(1991)은 스페인의 Balearic Islands에서 발생한 기상해일인 Rissaga에 대해 연구성과를 소개하였고, Colucci and Michelato(1976)과 Candela et al.(1999)은 이태리의 Sycily에서 발생한 기상해일인 Marubbio에 대해, Airy(1878)와 Drago(1999)는 Malta에서 발생한 Milghuba에 대해 각각 연구하였다. 일본에서는 1979년 3월 31일 Nagasaki만에서 발생한 Abiki에 대해 Honda et al.(1908), Hibiya and Kajiura(1982) 및 Akamatsu(1982)가 연구 성과를 발표하였다. Wang et al.(1987)은 발해만 입구부인 산동반도의 Longkou항에서 발생하는 기상해일에 대해 연구하였다. 그밖에도 세계 도처에서 발생하는 기상해일에 대한 연구가 많은 연구자들에 의해 수행되었다.
국내에서는 2005년 2월 9일 제주도 한림읍 옹포리 포구에서 기상해일로 의심되는 범람현상이 발생한 이후, 같은 해 3월 23일에도 남해안에서 해일현상이 발생하였으나 인명피해가 없었고 침수피해도 미미하여 적극적인 사후 조사나 관련연구가 수행되지 않았다. 그 후 2007년 3월 서해안에서 발생한 기상해일로 2명의 인명피해와 함께 서해안 여러 곳에서 침수 피해가 있었고, 2008년 5월에도 충남 보령에서 기상해일이 발생하여 9명의 인명피해가 발생한 이후부터 국내 연구진의 관심을 받기 시작하였다(Lim et al., 2008; Woo et al., 2008). 그러나 당시에는 기상해일에 대한 지식이 축적되지 않은 상태였으므로 해일현상을 임시로 이상파랑 이라 칭하고 해일피해 조사 및 원인파악 정도의 연구가 진행되었다. 그 후 Choi et al.(2008)은 2007년 3월 서해안 이상파랑에 대한 연구를 본격적으로 수행하여 서해의 이상파랑이 기압점프 이동에 의한 해양장파임을 밝히고, 국내 자동기상관측소(AWS: Automatic Weather Station)의 1분 기압자료 및 조위관측자료를 분석하여 대략적인 윤곽을 파악하였으며, 1차원 수치모형을 이용하여 Proudman 공명에 의한 기상해일의 발생과 증폭 등에 대한 연구 성과를 제시하였다. 그 후 Choi(2010)는 이전의 연구결과를 확장하여 비선형 천수방정식을 지배방정식으로 하는 2차원 수치모형을 수립하고, 이를 이용하여 실제 2007년 서해안 기상해일의 수치모의를 수행한 바, 수치모의를 통해 기압점프가 서해상을 북서쪽으로부터 남동진함에 따라 기상해일이 발생하고 증폭되는 과정을 잘 보여주었다. 그러나 Choi(2010)는 계산된 해수위와 조위관측소에서 기록된 해수위와의 비교를 통한 수치모의의 정밀도 검사를 시도하지는 않았다. 이는 수치모의에 사용된 100 m의 격자간격으로는 검조소가 위치하는 해안지역의 지형을 상세히 표현하기 어려워 굴절, 회절, 반사와 만내 공명 등 기상해일의 최종 변형과정을 정도 높게 반영하기 어려웠고, 기압점프를 전면 경사를 가지는 계단형상으로 단순화하여 실제 기압점프 전파양상을 충실히 고려할 수 없었으며, 또한 영광 조위관측소 지점의 기압자료를 포함하지 않아 기압점프 크기를 실제의 1/2에 해당하는 4.0 hPa로 작게 부여했던 것에 기인한 것으로 판단된다.
한편, Woo et al.(2008)은 기상해일의 첫 파봉이 각 조위관측지점에 도달한 시간을 분석하여 기상해일의 이동방향을 추정하였다. Choi et al.(2009)은 2008년 5월 보령 죽도에서 발생한 기상해일을 유발한 기압점프의 이동방향 및 이동속도를 보령과 위도가 비슷한 내륙의 AWS 지점에서 관측한 기압 및 기온 자료를 이용하여 추정하고, 기상 레이더 신호의 이동속도와 동일함을 보인 다음, AWS가 없는 해상에서의 기압점프 이동특성을 기상 레이더 신호를 이용하여 추정하였다. 최근 Eom et al.(2012)은 2007년 서해안 이상파랑 발생 시의 해수면 및 기압분포 관측 자료를 웨이블릿 분석하여 각각의 특성을 파악하였다. 특히 기상청 AWS의 기압자료를 시공간적으로 분석하여 기압점프의 이동방향과 이동속도를 현실적으로 파악하였으며, 이를 이용하여 기상해일 2차원 수치모의를 수행하고 서해안 6개 지점에서의 조위관측 자료와 비교하였다. Eom et al.(2012)의 계산결과는 해일로 인한 최대수면 변위가 일반적으로 관측치의 0.5배 정도로 매우 작게 나타났으며, 반대로 해일의 주기는 2배 정도로 크게 계산되어 기상해일의 발생 및 증폭 기구의 합리성 및 수치모의의 정확성 면에서 아직 많은 문제가 있음을 보이고 있다. 이와 같이 국내에서도 기상해일이 많은 연구자들의 관심대상이 되고 있으나, 이에 대한 심도 있는 연구는 아직 시작단계에 있다.
기상해일이 이전에도 계속적으로 우리나라 서해에서 발생 했던 것인지, 아니면 기후온난화의 영향으로 기상환경이 변화되어 최근 들어 발생하기 시작한 것인지는 분명하지 않으나, 폭풍해일이나 지진해일과는 달리 현재의 기상관측 및 조위관측 시스템으로는 사전에 그 발생과 내습 가능성을 예측할 수 없으므로, 기상해일의 예경보가 가능하도록 향후 기상 관측 및 조위관측 시스템의 신속한 확충 및 개선과 함께 수치모의 기술도 함께 갖추어야 할 것이다. 폭풍해일이나 지진해일 등은 여러 국가가 동시에 영향권에 들어가므로 많은 부분을 일본 등 기상선진국에 의존하는 것이 사실이다. 그러나 우리나라 서해안에 영향을 미치는 기상해일은 중국이나 일본에는 영향을 미치지 않으므로 우리나라 독자적으로 해결하지 않으면 안 된다. 따라서 기상해일에 대한 국가 및 연구자들의 관심과 노력이 특히 요구되는 사안이라 할 수 있다.
본 연구에서는 기상해일의 전파 특성을 잘 나타내줄 수 있는 기본방정식의 선정과 각종 기상 인자 및 해양 조건이 파의 증폭 및 전파에 미치는 영향을 1차원 수치모의를 통하여 좀 더 심도 있게 검토하였다.
2. 2007년 서해안 기상해일 발생현황 및 발생 기구 분석
2007년 3월 31일 0시경부터 서해안 일대에 걸쳐 해일이 발생하여 전남 영광 지역의 법성포 일대에서 주기 17분, 해일고 1.8 m 정도의 해일이 만조와 겹쳐 인근 상가에서 범람이 발생하였다. 이 당시 서해안의 안흥, 군산, 위도 등지에서도 해일현상이 발생하였다.
이 해일은 서해상에서 백령도와 중국의 산동반도를 잇는 선을 따라 길게 발생한 4.0 hPa 정도의 대기압 점프가 남동방향으로 이동하면서 해일을 발생시킨 것으로 보고되었다(Choi et al., 2008). Fig. 1은 당시의 기압분포를 보여주는 기상청의 기상도이다. 2007년 3월 30일 21시의 기상도에서는 동해상에는 고기압대가, 서쪽에는 중국 대륙에 저기압대가 각각 남북으로 길게 자리 잡고 있어 동고서저의 기압 분포를 보여주며, 전반적으로 편서풍의 영향으로 동쪽으로 이동하고 있었다. 3시간 뒤인 31일 0시의 기상도에서는 북한의 평양과 원산 사이에서 갑자기 고립된 고기압대가 나타난 바, Woo et al.(2008)에 따르면 서해상의 등기압선이 S자 형태로 휘어졌으며, 다시 3시간 뒤에는 이 고기압대가 사라져 6시간 전의 형태로 회복되었고, 이 과정에서 백령도와 중국의 산동반도를 잇는 선을 따라 대기압 점프가 길게 발생하였으며, 이 대기압 점프선이 서해상을 남동방향으로 이동하면서 해일을 발생시킨 것으로 추측하고 있다.
Fig. 2.
Mean sea level air pressure measured at AWS at (a) 00:00 KST 31 March 2007, (b) 00:30 KST, (c) 01:00 KST, (d) 01:30 KST (Eom et al., 2012).
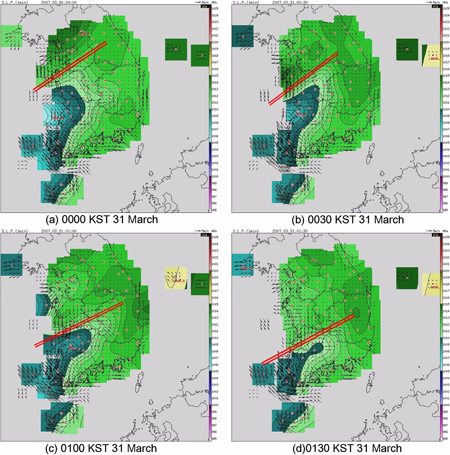
이러한 대기압 점프가 발생하여 이동하다가 사라지는데 3~5시간 정도로 짧고, 대기압 점프에서의 기압변동이 수 분 사이에 이루어지는 점을 고려하면 기상청에서 3시간마다 발표되는 기상도로부터 해일의 발생과 전파과정을 분석하기 위한 자세한 정보를 얻기는 힘들다. Eom et al.(2012)은 우리나라 전역에 걸쳐 기상청에서 운영하는 자동기상관측소(AWS)의 1분 자료를 수집·분석하여 3월 31일 00시 ~ 01시 30분 사이의 기압분포 변화를 Fig. 2와 같이 제시하였다.
Fig. 2에서 보는 바와 같이 00시 00분에는 남서-북동방향으로 좁고 길게 분포하는 기압점프가 태안반도 상을 지나고 있으며, 00시 30분에는 보령을, 01시 00분에는 군산을, 01시 30분에는 영광지역을 지나고 있다. 이 대기압 점프의 전면에서는 기압점프 직전의 저기압대가 역시 남동방향 방향으로 이동하고 있음을 보여준다. 이 대기압 점프선의 이동속도는 대략 25 m/s이다. Fig. 3은 2007년 3월 29일로부터 4월 1일 사이에 AWS가 위치하는 백령도(BRI), 인천(IC), 서산(SS), 군산(KS), 영광(YG)에서 관측된 기압의 1분 자료로서, 3월 30일 22시 41분에 백령도를 통과한 대기압 점프가 남동쪽으로 전파되어 23시 46분에는 격렬비열도를, 31일 00시 01분에는 인천을, 00시 29분에는 서산을 지나고 있다. 그 후 01시 05분에 군산을 통과하고, 01시 29분 영광에 도달하기 까지 서해안을 따라 남하하고 있는 양상을 보여준다. 여기서 대기압 점프 통과시간은 점프 후 최고기압점이 통과하는 시간이므로, 기압점프가 시작하는 시점을 기준으로 하면 각 지점에서 점프통과시간이 조금씩 빨라질 수 있다.
Fig. 3.
Air pressure time histories recorded at various coastal locations for the West Coast abnormal waves in 2007 (Choi et al.,2008).
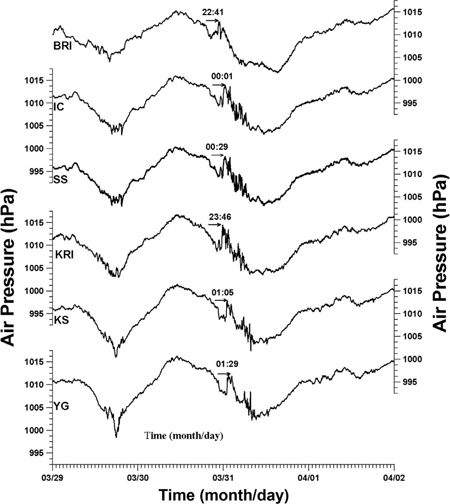
Fig. 4.
Air pressure and free surface displacement time histories recorded at Daesan, Anheung, and Youngkwang stations of KHOA for the West Coast abnormal waves in 2007.
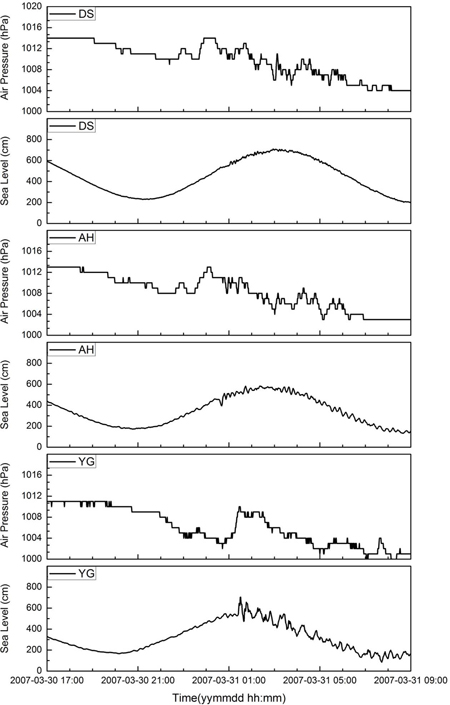
Fig. 5.
Measured time histories of tide-eliminated free surface displacement due to the 2007 abnormal waves at Anheung, Kunsan, Wido, and Youngkwang stations.(Choi et al.,2008).
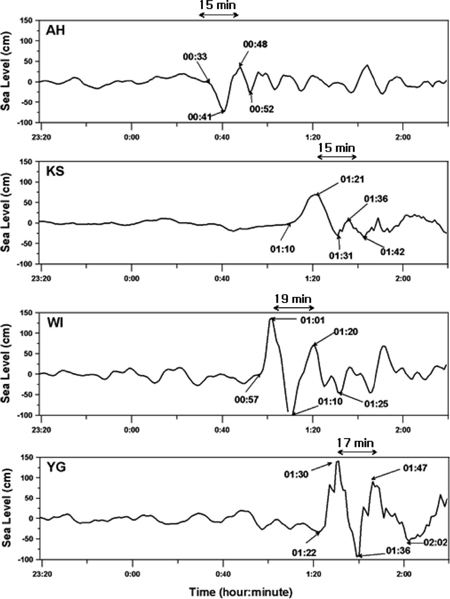
Fig. 4는 국립해양조사원에서 운영하는 조위관측소인 대산(DS), 안흥(AH) 및 영광(YG)에서 동시 측정한 기압과 해수면 변동을 보여주는 바, 대기압 점프의 이동으로 기상해일이 발생함을 잘 보여주고 있다. 영광에서의 경우를 살펴보면 기압점프와 기상해일의 첫 파가 동시에 도착하는 것을 알 수 있다.
Fig. 5는 안흥, 군산, 위도와 영광의 4개 조위관측소에서 관측된 조위자료에서 해일이 발생하지 않았을 경우의 예상조위를 제거하여 기상해일 만에 의한 해수면변위를 보여주고 있다(Choi et al., 2008). 또한 각 지점에서 기상해일의 도달시간, 해일고, 및 첫 2개 해일파 간의 지체시간 즉 주기를 제시하고 있다. 이 기상해일의 주기는 15~19분으로 중간 정도의 장파에 속한다. 대부분의 관측지점에서 4개의 해일파가 도달하였는데, 첫파의 해일고가 가장 크고 2번째와 3번째로 갈수록 해일고가 감소하다가 4번째 파는 다시 증가하는 현상을 보인다. 영광의 경우에는 3번째 파가 나타나지 않았다. 4개 관측점 중 위도의 경우에는 해안으로부터 멀리 떨어진 섬이므로 해안으로부터 반사된 파의 영향이 작을 것으로 판단되며, 따라서 4개의 해일파 모두가 서해상에서 생성되어 전파되어 온 것으로 판단된다.
대기압 점프의 이동에 의한 기상해일의 발생과 증폭 기구는 Proudman 공명으로 설명된다. Proudman 공명은 대기압 점프의 이동속도가 파의 이동속도와 같을 때 공명이 발생하여 파고가 이동거리에 비례하여 증폭되는 현상이다. 대기압 점프의 이동속도가 파의 이동속도보다 커지거나 작아지면 그 차이만큼 증폭정도가 약화된다. 대기압 점프의 이동속도는 대략 18~40 m/s로 알려져 있으므로 Proudman 공명은 수심이 33~160 m의 범위에서 일어날 수 있다. 우리나라 서해는 수심이 100 m 미만이므로 대기압 점프가 발생하면 Proudman공명에 의한 기상해일이 발생할 가능성이 높다. 또한 기상해일은 주기가 10~20분으로 길고 서해의 수심이 육지 쪽으로 가면서 매우 서서히 감소하므로 천수화에 의한 증폭이 크게 발생하여 먼 바다에서 작은 해일도 해안에 도달하면 크게 증폭될 수 있다. 이러한 기상해일의 거동은 지진해일과 매우 유사하여 해안에서 내륙 깊숙이 범람을 발생시킬 수 있다.
3. 기상해일 발생 및 증폭과정 파악을 위한 1차원 수치모의
3.1 기압 점프 형상과 수치모형의 선정
기상해일의 발생과 증폭과정을 이해하고 지배방정식과 수치모형의 타당성을 검토하기 위한 1차원 수치모의를 수행하였다. 기상해일은 대기압 점프가 서해상을 이동하면서 발생하므로 수심에 비해 해일고가 작아 선형이론으로 해석하여도 정밀도가 크게 낮아지지 않는다. 따라서 선형이론을 사용하여 기상해일의 발생과 증폭과정을 검토하였다. Boussinesq 모형으로는 미국 Delaware대학에서 개발한 FUNWAVE 모형에서 비선형 항을 제거하고 사용하였으며, 천수방정식 모형으로는 leap- frog 기법을 사용한 일반적인 선형 천수방정식 모형(LSWE)을 사용하였다.
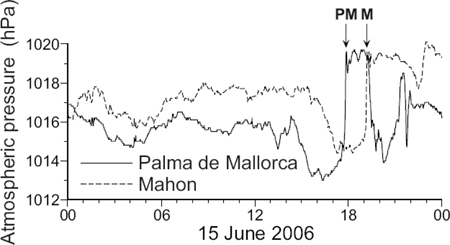
2007년 3월 31일 서해안에서 발생한 기상해일을 유발한 대기압 점프는 Fig. 3에 보인 바와 같이 대기압이 처음에 2 hPa이 급격히 감소한 다음 2.5시간 지속된 후 4 hPa이 5-10분 사이에 급격히 상승하였고 2.5시간 정도 지속되다가 다시 2 hPa이 하강하여 대기압이 음(-)의 sine 커브 형태로 변화하였다. 대기압 점프 발생시 대기압 변화 양상은 2006년 6월 15일 스페인 남부 지중해 연안의 Palma de Mallorca와 Mahon을 강타한 기상해일 발생 시의 대기압 점프의 경우와 매우 흡사하다. 당시 대기압은 Fig. 6에 보인 바와 같이 처음에 3 hPa이 급강하하였고 3시간 후 7 hPa이 10~30분 만에 급상승한 다음 1.5시간 정도 지속되다가 다시 5 hPa이 급강하하여, 서해안 대기압 점프 시와 같이 (-)sine 커브 형상을 보인다.
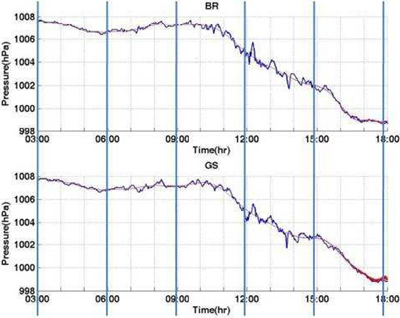
2008년 충남 보령 죽도의 기상해일 발생시 기압은 Fig. 7에 보인 바와 같이 처음 5분 동안 1 hPa이 하강한 다음, 2 hPa이 10분 만에 급상승하였고 또다시 5분 만에 1.5 hPa이 급강하하여 (-)sin 커브를 그리며 원상태로 회복하였다. 2007년의 서해안 기상해일과 2006년 스페인 기상해일의 경우에는 기압 변동이 시작하여 원상태로 회복되는데 약 5시간이 소요된 반면, 2008년 보령 죽도의 기상해일 발생시에는 기압 변동이 원상태로 회복되는 데 20분 정도로 짧게 걸렸다는 점이다.
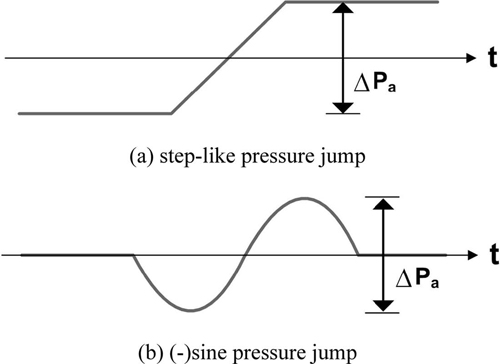
위에서 살펴본 바와 같이 2007년 서해안 기상해일의 경우에는 기압변동 초기의 기압강하가 어느 지역을 통과 후 2.5시간이라는 오랜 시간이 경과한 후 다시 기압 급상승이 통과하며, 또한 마지막 기압 하강도 2.5시간 후에 서서히 이루어지므로 이 세 가지 기압 급변동이 서로 영향을 주지 않고 독립적으로 해일을 발생시킬 것으로 판단된다. 실제 Choi et al.(2008)은 2007년 서해안 이상파랑을 발생시킨 대기압 점프를 이러한 배경설명 없이 상승폭 L = 12 km, 기압상승량 ΔPa= 4.0 hPa의 1단 계단형으로 가정하였다. 반면 2008년 충남 보령의 죽도에서 발생한 기상해일의 경우에는 기압 하강-상승-하강이 20~30분 사이에 이루어지므로 서로 영향을 줄것으로 판단된다. Eom et al.(2012)은 2007년 서해안 기상해일에 대해서도 대기압 점프의 전체적인 형상을 중시하여 주기 60분, 최대 기압상승량 5.3 hPa의 (-)sine형상으로 가정하였다. 따라서 2가지 형태의 기압 급변 형상에 대해 1차원 수치해석을 통해 기상해일의 발생과 증폭 과정을 이해하고자 한다. 그림 Fig. 8과 Fig. 9는 각각 계단형 기압 상승과 음의 sine 형태의 기압 시간변화 및 공간분포를 보여준다. sine형태의 기압변동은 기압 하강으로부터 상승 및 원상태 회복까지 걸리는 시간이 짧아 서로 영향을 미치는 경우이고, 계단형 점프는 기압 급변 과정이 매우 길어 최초 하강 - 중간 상승 - 최종 하강의 과정이 서로 독립적으로 발생할 때 중간의 기압상승 과정만을 표현한다.
Fig. 9.
Spacial distributions of two types of air pressure variations for the analyses of meteo-tsunamis.
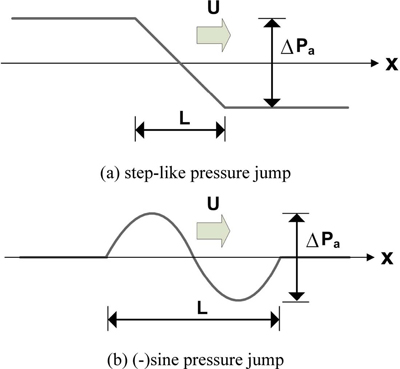
Fig. 10.
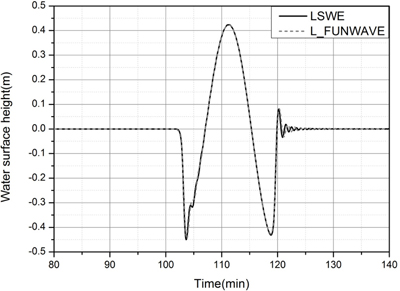
Comparison of time histories of free surface calculated using LSWE and L_FUNWAVE at x=200km for the step-like pressure jump.
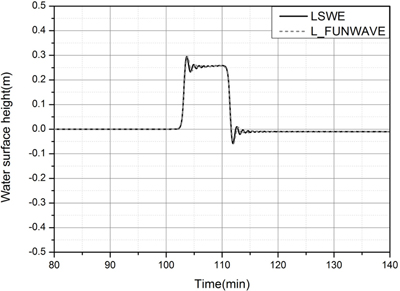
Fig. 11.
Comparison of time histories of free surface calculated using LSWE and L_FUNWAVE at x = 200 km for the (-)sine pressure jump.
수치모의에 사용한 수심은 h = 60m이며, 기압 이동속도 U를 Proudman 공명을 발생시키는 U(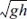 ) = 24.26 m/s로 정하였다. 최대기압 상승량 ΔPa= 4 hPa에 대해 검토하였고, 계단형 점프의 경우 기압상승 구간의 거리 즉 기압점프거리 L을 12 km로, (-)sine형의 경우 최저기압에서 최고기압까지의 변동 거리가 계단형 점프의 경우와 동일하도록 sin형 기압변동 파장 L을 24 km로 하였다. 이러한 수치모의 조건들은 Choi et al.(2008)의 1차원 수치실험을 참고로 구성하였다.
) = 24.26 m/s로 정하였다. 최대기압 상승량 ΔPa= 4 hPa에 대해 검토하였고, 계단형 점프의 경우 기압상승 구간의 거리 즉 기압점프거리 L을 12 km로, (-)sine형의 경우 최저기압에서 최고기압까지의 변동 거리가 계단형 점프의 경우와 동일하도록 sin형 기압변동 파장 L을 24 km로 하였다. 이러한 수치모의 조건들은 Choi et al.(2008)의 1차원 수치실험을 참고로 구성하였다.
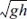 ) = 24.26 m/s로 정하였다. 최대기압 상승량 ΔPa= 4 hPa에 대해 검토하였고, 계단형 점프의 경우 기압상승 구간의 거리 즉 기압점프거리 L을 12 km로, (-)sine형의 경우 최저기압에서 최고기압까지의 변동 거리가 계단형 점프의 경우와 동일하도록 sin형 기압변동 파장 L을 24 km로 하였다. 이러한 수치모의 조건들은 Choi et al.(2008)의 1차원 수치실험을 참고로 구성하였다.
) = 24.26 m/s로 정하였다. 최대기압 상승량 ΔPa= 4 hPa에 대해 검토하였고, 계단형 점프의 경우 기압상승 구간의 거리 즉 기압점프거리 L을 12 km로, (-)sine형의 경우 최저기압에서 최고기압까지의 변동 거리가 계단형 점프의 경우와 동일하도록 sin형 기압변동 파장 L을 24 km로 하였다. 이러한 수치모의 조건들은 Choi et al.(2008)의 1차원 수치실험을 참고로 구성하였다.
Fig. 10은 계단형 기압 점프가 x = 50 km으로부터 U = 24.26 m/s 속도로 이동할 때 x = 200 km에서의 수면변위 시간이력을 각각의 모형으로 계산하여 비교한 것이다. 여기서 선형 Boussinesq 방정식 즉 L_FUNWAVE의 결과를 정확해로 간주할 때, 선형 천수방정식인 LSWE 모형은 L_FUNWAVE의 결과와 비슷한 결과를 보여준다.
Fig. 11은 (-)sine형태의 기압 변동이 이동할 때 x=200km에서의 수면변위 시간이력을 각각의 모형으로 계산하여 비교한 것이다. 이 경우에도 선형 천수방정식인 LSWE 모형은 선형 Boussinesq 방정식인 L_FUNWAVE와 거의 동일한 결과를 준다.
이 2가지 수치실험 결과로부터 선형 천수방정식을 사용하는 LSWE 모형이 계산 시간이 훨씬 짧아 경제적이면서도 지배방정식이 매우 복잡한 FUNWAVE 모형과 비슷한 결과를 주어 기상해일 전파 수치모의에 효율적으로 사용될 수 있음을 알 수 있다. 따라서 본 연구에서는 먼 바다에 대해서는 선형 천수방정식 모형을 사용하고, 기상 해일이 해안 가까이 접근하여 비선형성이 강해지는 상세역에서는 비선형천수방정식 모형을 이용한다.
3.2 계단형 점프에 의한 기상해일 발생 및 증폭 수치모의
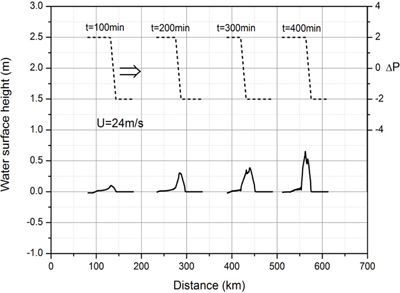
계단형 기압 점프에 의한 기상해일의 수치모의를 수행하여 기압 점프의 특성 즉 최대 기압 상승량 ΔPa, 점프 거리 L, 이동속도 U가 기상해일의 발생과 증폭에 미치는 영향을 분석하였다. 수심 h = 60m에 대해 수치 실험을 수행하였다. Fig. 12는 기압 점프의 이동속도를 수심 60 m에서 Proudman 공명이 발생하도록 U = 24.26 m/s로 놓고, 점프 거리 L = 12 km에 대해 최대 기압 상승량 ΔPa가 1 hPa, 2 hPa, 4 hPa로 변할때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 최대 기압 상승량 ΔPa가 2배가 될 때 마다 기상해일고 즉 최대수면변위도 2배씩 증가하여, 해일고가 최대 기압 상승량에 선형 비례하는 것으로 나타났다.
Fig. 12.
Comparison of time histories of free surface at x = 200 km for the step-like pressure jump: effects of jump intensity.
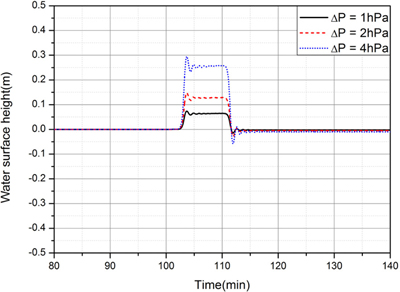
Fig. 13.
Comparison of time histories of free surface at x = 200 km for the step-like pressure jump: effects of jump length.
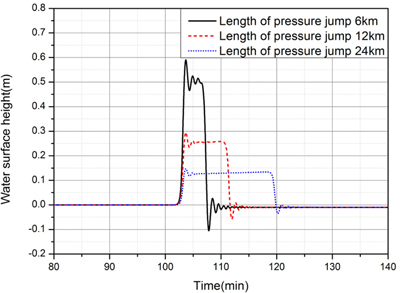
Fig. 14.
Comparison of time histories of free surface at x = 200 km for the step-like pressure jump: effects of jump moving speed.
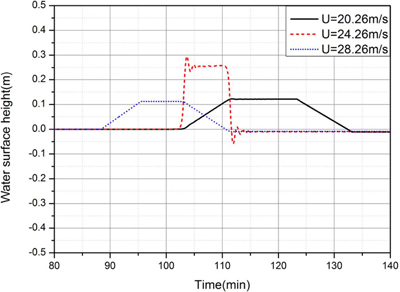
Fig. 15.
Amplification process of meteo-tsunami due to moving distance of the step-like pressure jump.
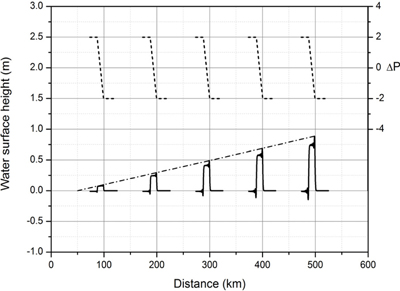
Fig. 13은 수심 h = 60m에서 기압 점프의 이동속도 U = 24.26m/s, 최대 기압 상승량 ΔPa가 4 hPa일 때 점프 거리 L이 6 km, 12 km, 24 km로 길어질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 점프거리 L이 증가할수록 기상해일의 해일고는 감소하는 것으로 나타났다. 특히 최대 기압 상승량 ΔPa가 4 hPa로 동일함에도 불구하고 점프 거리가 2배 증가하면 최대해일고가 1/2로 감소하는 것으로 보아 최대 기압 상승량 ΔPa도 중요하지만 기압상승의 공간 기울기도 중요함을알 수 있다.
Fig. 14는 최대 기압 상승량 가 4 hPa, 기압점프거리가 L = 12 km, 수심이 h = 60m로 동일한 경우 기압 점프의 이동속도 U가 Proudman 공명을 발생시키는 조건인 장파의 전파속도 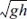 =24.26m/gh s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. Fig. 15는 최대 기압 상승량 ΔPa가 4 hPa, 기압점프거리가 L = 12 km인 기압점프가 수심이 h = 60m인 해상을 Proudman 공명을 발생시키는 조건인 장파의 전파속도
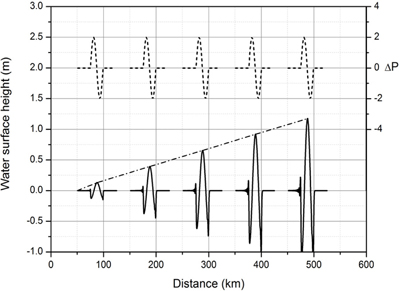
=24.26m/gh s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. Fig. 15는 최대 기압 상승량 ΔPa가 4 hPa, 기압점프거리가 L = 12 km인 기압점프가 수심이 h = 60m인 해상을 Proudman 공명을 발생시키는 조건인 장파의 전파속도 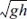 =24.26m/s로 이동할 때 계단형 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 최대 해일고는 기압점프의 이동거리에 선형적으로 증가함을 잘 보여주고 있다.
=24.26m/s로 이동할 때 계단형 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 최대 해일고는 기압점프의 이동거리에 선형적으로 증가함을 잘 보여주고 있다.
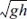 =24.26m/gh s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. Fig. 15는 최대 기압 상승량 ΔPa가 4 hPa, 기압점프거리가 L = 12 km인 기압점프가 수심이 h = 60m인 해상을 Proudman 공명을 발생시키는 조건인 장파의 전파속도
=24.26m/gh s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. Fig. 15는 최대 기압 상승량 ΔPa가 4 hPa, 기압점프거리가 L = 12 km인 기압점프가 수심이 h = 60m인 해상을 Proudman 공명을 발생시키는 조건인 장파의 전파속도 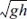 =24.26m/s로 이동할 때 계단형 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 최대 해일고는 기압점프의 이동거리에 선형적으로 증가함을 잘 보여주고 있다.
=24.26m/s로 이동할 때 계단형 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 최대 해일고는 기압점프의 이동거리에 선형적으로 증가함을 잘 보여주고 있다.
3.3 Sine형 기압변동에 의한 기상해일 발생 및 증폭 수치모의
Sine형 기압변동의 이동에 의한 기상해일을 수치모의를 수행하여 기압변동의 특성 즉 최대 기압 상승량 ΔPa, 기압변동파장 L, 이동속도 U가 기상해일의 발생과 증폭에 미치는 영향을 분석하였다. 수심 h = 60m에 대해 수치 실험을 수행하였다. Fig. 16은 기압변동의 이동속도를 수심 60 m에서 Proudman 공명이 발생하도록 U = 24.26m/s로 놓고, 기압변동 파장 L = 24 km에 대해 최대 기압 상승량 가 1 hPa, 2 hPa, 4 hPa로 변할 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 최대 기압 상승량 가 2배가 될 때 마다 기상해일고 즉 최대수면변위도 약 2배씩 증가하여, 해일고가 최대 기압 상승량에 비례하여 증가하는 것으로 나타났다. Fig. 17은 수심 h = 60m에서 기압 점프의 이동속도 U = 24.26 m/s, 최대 기압 상승량 가 4 hPa인 경우 기압변동 파장 L이 12 km, 24 km, 48 km로 길어질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 L이 증가할수록 기상해일의 해일고는 감소하는 것으로 나타났다. 특히 최대 기압 상승량 가 4 hPa로 동일함에도 불구하고 L이 2배 증가하면 최대해일고가 대략 1/2로 감소하여 계단형 점프에서 얻은 결과와 유사하다.
Fig. 16.
Comparison of time histories of free surface at x = 200 km for the (-)sine pressure jump: effects of jump intensity.
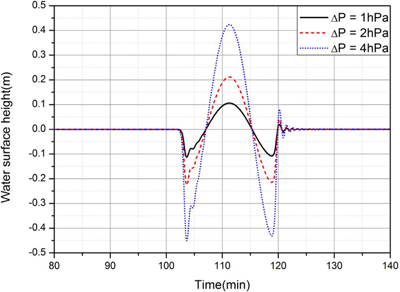
Fig. 17.
Comparison of time histories of free surface at x = 200 km for the (-)sine pressure jump: effects of jump length.
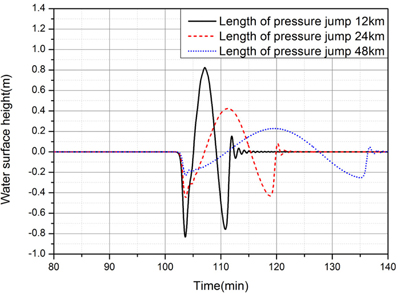
Fig. 18.
Comparison of time histories of free surface at x = 200 km for the (-)sine pressure jump: effects of jump moving speed.
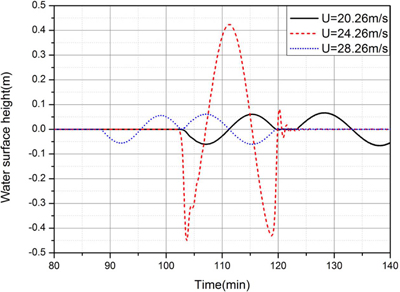
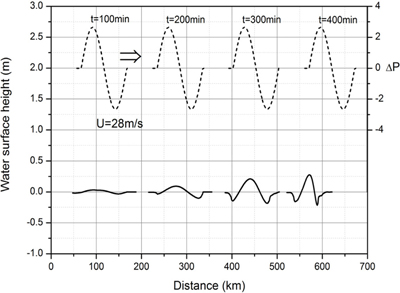
Fig. 18은 최대 기압 상승량 ΔPa가 4 hPa, 기압변동 파장 L = 24 km, 수심이 h = 60m로 동일한 경우 기압 점프의 이동속도 U가 Proudman 공명을 발생시키는 조건인 장파의 전파속도 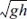 =24.26m/s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. 기압변동의 이동속도가 해일파의 전파속도보다 빠른 U = 28.26m/s인 경우 x = 200 km 지점에 이동하는 기압과 함께 일체화되어 통과하는 구속장파(locked long wave)가 88분경에 도달하고, 후에 장파의 이동속도인
=24.26m/s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. 기압변동의 이동속도가 해일파의 전파속도보다 빠른 U = 28.26m/s인 경우 x = 200 km 지점에 이동하는 기압과 함께 일체화되어 통과하는 구속장파(locked long wave)가 88분경에 도달하고, 후에 장파의 이동속도인 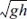 =24 m/s로 이동하는 자유장파(free long wave)가 103분경에 도달하며, 각각의 파는 진폭이 매우 작다. 반면 기압 변동의 이동속도가 장파의 전파속도보다 느린 U = 20.26m/s인 경우 자유장파가 103분경에 먼저 도달하고 구속장파는 기압변동과 함께 123분경에 도달한다. 공명조건인 경우 구속장파와 자유장파가 동일한 속도로 이동하면서 해일을 증폭시킨다.
=24 m/s로 이동하는 자유장파(free long wave)가 103분경에 도달하며, 각각의 파는 진폭이 매우 작다. 반면 기압 변동의 이동속도가 장파의 전파속도보다 느린 U = 20.26m/s인 경우 자유장파가 103분경에 먼저 도달하고 구속장파는 기압변동과 함께 123분경에 도달한다. 공명조건인 경우 구속장파와 자유장파가 동일한 속도로 이동하면서 해일을 증폭시킨다.
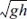 =24.26m/s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. 기압변동의 이동속도가 해일파의 전파속도보다 빠른 U = 28.26m/s인 경우 x = 200 km 지점에 이동하는 기압과 함께 일체화되어 통과하는 구속장파(locked long wave)가 88분경에 도달하고, 후에 장파의 이동속도인
=24.26m/s보다 4 m/s씩 커지거나 작아질 때 x = 200 km 지점을 통과하는 기상해일의 수면변위를 비교한 것이다. 그림에서 보는 바와 같이 기압점프의 이동속도가 공명조건으로부터 빨라지거나 느려지면 기상해일이 증폭되지 못하고 급격히 감소하는 것을 알 수 있다. 기압변동의 이동속도가 해일파의 전파속도보다 빠른 U = 28.26m/s인 경우 x = 200 km 지점에 이동하는 기압과 함께 일체화되어 통과하는 구속장파(locked long wave)가 88분경에 도달하고, 후에 장파의 이동속도인 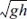 =24 m/s로 이동하는 자유장파(free long wave)가 103분경에 도달하며, 각각의 파는 진폭이 매우 작다. 반면 기압 변동의 이동속도가 장파의 전파속도보다 느린 U = 20.26m/s인 경우 자유장파가 103분경에 먼저 도달하고 구속장파는 기압변동과 함께 123분경에 도달한다. 공명조건인 경우 구속장파와 자유장파가 동일한 속도로 이동하면서 해일을 증폭시킨다.
=24 m/s로 이동하는 자유장파(free long wave)가 103분경에 도달하며, 각각의 파는 진폭이 매우 작다. 반면 기압 변동의 이동속도가 장파의 전파속도보다 느린 U = 20.26m/s인 경우 자유장파가 103분경에 먼저 도달하고 구속장파는 기압변동과 함께 123분경에 도달한다. 공명조건인 경우 구속장파와 자유장파가 동일한 속도로 이동하면서 해일을 증폭시킨다.
Fig. 19는 최대 기압 상승량 ΔPa가 4 hPa, 기압변동 파장이 L = 12km인 (-)sine 형태의 기압점프가 수심이 h = 60m인 해상을 Proudman 공명을 발생시키는 조건인 장파의 전파속도 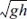 =24.26m/s로 이동할 때 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 기상해일은 이동 거리가 증가할수록 계단형 기압점프의 경우와 같이 해일고가 선형적으로 증가하는 현상을 잘 보여준다.
=24.26m/s로 이동할 때 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 기상해일은 이동 거리가 증가할수록 계단형 기압점프의 경우와 같이 해일고가 선형적으로 증가하는 현상을 잘 보여준다.
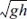 =24.26m/s로 이동할 때 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 기상해일은 이동 거리가 증가할수록 계단형 기압점프의 경우와 같이 해일고가 선형적으로 증가하는 현상을 잘 보여준다.
=24.26m/s로 이동할 때 기압점프의 이동거리에 따른 기상해일의 증폭 과정을 보여준다. 기상해일은 이동 거리가 증가할수록 계단형 기압점프의 경우와 같이 해일고가 선형적으로 증가하는 현상을 잘 보여준다.
4. 2007년 서해안 기상해일의 1차원 수치모의
4.1 기존 기압 점프 형상에 대한 수치모의
Bae(2012)은 기상위성에서 촬영한 구름위성사진을 분석하여 2007년 3월 30일~31일 서해안 기상해일이 중국 랴오닝성 북서쪽에 자리 잡은 대규모 저기압과 산동반도 북쪽 인접해역에서 발생한 강한 상승기류의 상호 작용으로 발생하였다고 보고하였다. 본 연구에서는 Bae(2012)의 추론에 근거하여 2007년 서해 기상해일을 유발한 기압점프가 산동반도 북쪽 인근해역의 좁은 구역에서 발생하여 전남 영광 해역을 향해 서해상을 남동쪽으로 부채꼴 형상으로 퍼져 나갔다고 가정하였다. 따라서 본 연구에서는 Fig. 20(a)에 보인 바와 같이 2007년 기상해일의 발생과 증폭과정을 기압점프가 시작된 중국의 산동반도로부터 최종 상륙지점인 전남 영광지역을 잇는 곡선을 따라 1차원 선형 천수방정식 즉 LSWE모형을 이용하여 수치모의 하였다. 그림 Fig. 20 (b)는 수치모의 대상영역의 수심분포를 보여준다. 1차원 모형에서는 해안선에서 모든 파가 반사되어 실제와 다른 해일형상을 주므로 입사파 형상만을 알아보기 위해 영광 해안지점으로부터 육지쪽으로 일정한 수심을 유지시키고 흡수층을 설치하여 반사파를 약화시켰다.
Fig. 20.
Water depths under MSL used for the 1-D numerical simulation of the meteo-tsunami occurred along the west coast of Korea at Marth in 2007.
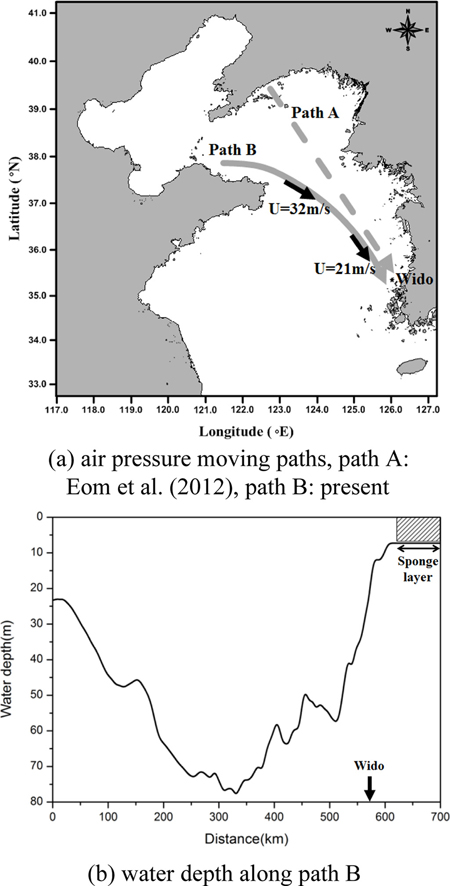
대기압 점프의 형상은 Choi et al.(2008)이 사용한 최대 기압상승량 ΔPa= 4.0 hPa, 기압점프거리 L = 12.0 km, 이동속도 U = 24.0m/s인 1단의 계단형과 Eom et al.(2012)이 사용한 최대 기압상승량 ΔPa= 5.3 hPa, 기압변동 파장 L = 100.8 km, 이동속도 U = 28.0m/s인 (-)sine 형태의 2가지 기압점프 형태를 사용하여 수치모의를 수행하였다. Eom et al.(2012)의 기압점프 이동 경로는 발해만 북쪽 해안으로부터 시작하여 영광 해안까지의 직선 경로를 택하였으나, 본 연구에서는 현실적인 기압점프 발생원 위치를 고려하고, 또한 계단형 기압점프의 경우와 비교를 위해 산동반도와 영광 지역을 잇는 곡선 경로를 택하였다.
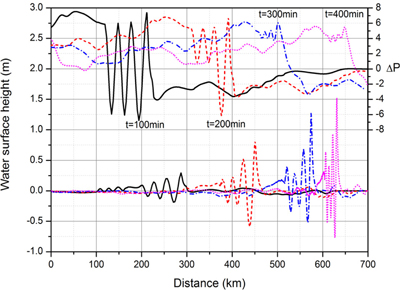
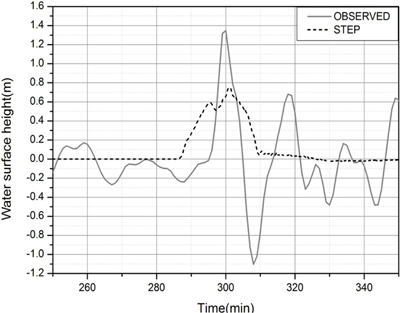
Fig. 21은 계단형 기압점프의 이동에 의한 기상해일의 전파과정을 100분 간격으로 도시한 것으로 1개의 선단파가 시간이 지남에 따라 증폭되어 전파되는 것을 확인 할 수 있다. Fig. 22는 영광 해안에서 해측으로 약 20 km 떨어진 위도에서의 기상해일 수면변위를 보여주는 바, 실측치에 비해 선단파의 해일고가 작고, 선단파 이후 바로 뒤따라오는 일련의 후속파가 나타나지 않았다. 위도는 해안으로부터 멀리 떨어져 있어 해안으로부터의 반사파 영향이 거의 나타나지 않으므로 실측치에서의 선단파 이후의 후속파들은 반사파가 아닌 기압점프에 의해 생성되어 전파되어야 할 것이나, 1단의 계단형 기압점프로는 이러한 일련의 해일파를 발생시킬 수 없음을 알 수 있다.
Fig. 22.
Comparison of observed and calculated free surfaces generated by the step-like pressure jump.
한편 (-)sine 형태의 기압점프를 사용한 경우, Fig. 23에 보인 바와 같이 선단파 통과 직후에 파곡 즉 음의 수면변위가 발생하였으나 후속파가 뚜렷하지 않아 여러 개의 후속파가 나타나는 관측치와는 거리가 멀다.
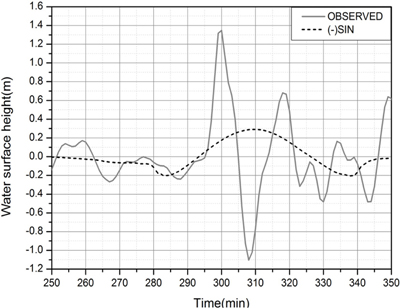
Fig. 24는 (-)sine 형태의 기압점프를 사용한 경우 위도에서의 해일파 수면변위의 시간이력을 도시한 것으로 실제 관측치에 비해 선단파의 해일고가 관측치보다 매우 작고, 파곡부가 불분명하며, 후속파도 잘 나타나지 않는다.
Fig. 24.
Comparison of observed and calculated free surfaces generated by the (-)sine pressure jump at Wido tidal station.
이상에서 살펴본 바와 같이 1단의 계단형이나 (-)sine형태의 이동하는 기압점프 형상으로는 실제 관측치와 비슷한 해일 형상을 재현할 수 없음을 알 수 있었다.
4.2 새로운 기압 점프 형상과 수치모의
본 연구에서는 위도나 영광에서의 기상해일이 17~19분 주기의 3~4개 파봉을 가지는 일련의 파군임에 착안하여 기압점프의 주기를 17분으로 정하고 수치모의를 수행하였다. 이러한 가정은 기압점프 자체가 밀도류의 역학을 따르며, 또한 기압점프 발생 초기에 해당하는 백령도에서 관측된 기압점프 양상이 Fig. 3에 보인 바와 같이 기압점프 발생 15-20분후 소규모의 기압강하가 존재하고, 30-40분 후에는 기압급강하가 발생함에 근거를 두고 있다. 이러한 현상은 보령, 군산, 부안, 영광에서 관측된 기압점프에서도 유사하게 나타났다. 기압점프를 밀도류 역학으로 판단해보면 급격한 기압점프(수리학의 도수현상) 후면에 분산효과에 의해 일련의 고립파가 동반되는 현상과 유사하다. 지진해일에서도 이러한 현상이 나타나는데 역방향 흐름상을 전파하는 고립파가 여러 개의 고립파(soliton)로 분화하는 과정과 유사하다. 산동반도 북부지역에서 발생한 기압점프는 기압점프 발생 전 3-4시간 동안 지속된 기압강하로 인한 서해상의 남동풍을 거슬러 남동방향으로 전파되어 오면서 하나의 매우 긴 고립파 또는 계단형상파가 여러 개의 짧은 고립파로 발전되어 왔을 가능성이 있으며, 그 주기는 15-20분 정도로 추정된다. 각각의 고립파는 전파 도중 국지적인 기상조건에 따라 2번째 고립파의 전파속도가 상대적으로 빨라지면 첫 번째 고립파와 부분적으로 병합되어 파곡부가 점차 소멸되어 보령, 군산, 부안, 영광에서의 기압점프형상과 유사하게 관측될 것으로 판단된다.
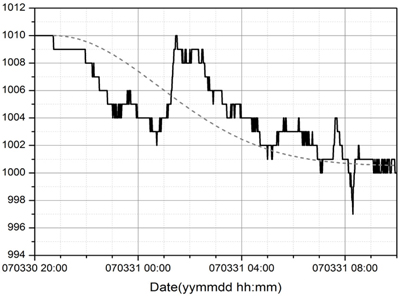
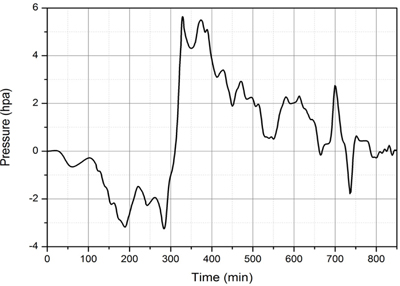
Fig. 25는 영광 검조소에서 관측된 압력 자료이다. 본 연구에서는 실제 관측된 압력자료에서 그림의 점선으로 제시된 배경압력의 변화를 제거하고 앞서 언급한 밀도류 역학에 근거하여 Fig. 26에 제시한 바와 같은 기압점프 형상을 사용하였다. 밀도류 역학의 또 다른 현상은 좁은 지역에서 발생한 초기의 기압점프는 어느 한 방향으로 전파되어 나감에 따라 회절현상에 의해 점차 그 강도가 약해지고, 선단부 경사는 완만해지며, 전파속도도 감소하는 특징이 있다.
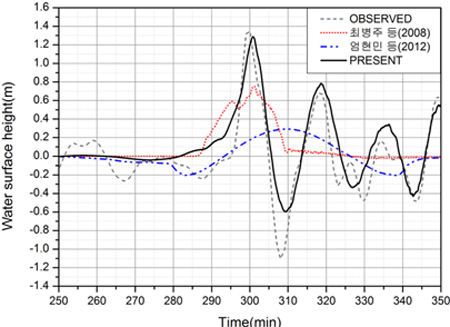
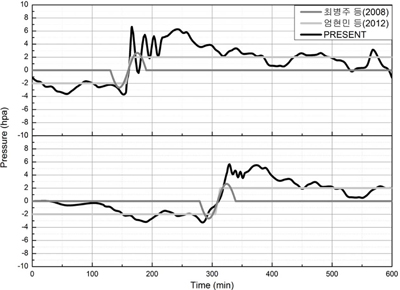
Fig. 27은 이러한 기압점프 형상에 의해 발생되고 전파되는 기상해일 전파양상을 각 시간대별로 도시한 것으로 기압점프의 이동속도와 선단파의 전파 속도가 일치해 시간에 따라 기상해일이 점점 증폭되는 볼 수 있다. 다음 Fig. 28은 서해 중간지점과 영광 통과시 기압점프의 형상을 비교한 결과이다. Fig. 29는 위도에서의 기상해일 수면변위의 시간변화를 보여주는 바, 실측치와 유사하게 선단 파봉부 후면에 파곡이 잘 발달되어 있고, 후속파는 선단파와 약 19분의 차이를 두고 뒤따르는 양상을 보인다. 이러한 기상해일의 정확한 형상은 해안에서의 최대해일고 산정은 물론이고, 특히 발전소의 취수로나 포구에서의 공명현상에 의한 범람 예측을 위한 2차원 수치모의에 있어서 필수적이다.
Fig. 28.
Comparison of pressure jump patterns used by Choi et al.(2008), Eom et al.(2012) and present study: (top) at the middle of path, (bottom) at Youngkwang tidal station.
이상의 수치모의를 통해 계단형이나 (-)sine형태의 간단한기압점프 형상으로는 실제 기상해일을 정도 높게 계산할 수 없으며, 기압점프의 시공간적인 정확한 정보를 필요로 함을 알 수 있다. 그러나 기압점프의 발원지인 중국으로부터 이러한 상세한 기상정보를 얻을 수 없고, 또한 현재의 우리나라의 AWS 지점은 모두 기압점프 진행경로의 하류부인 서해안과 내륙에 분포되어 있어 기상해일의 발생과 증폭에 전적으로 관여하는 서해상 먼 바다에서의 기압점프 크기와 형상 및 이동속도와 이동방향에 대한 정확한 정보를 얻을 수 없다. 해안에서 멀리 떨어진 바다 한 가운데에 기상관측 부이를 설치 및 운영하는 데 많은 경비와 인력을 필요로 하나, 2007년 3월 영광 원자력 발전소와 2008년 5월 보령에서의 인명 손실을 감안하면 원거리 기상관측 및 실시간 정보 제공 등이 필수적이며, 이러한 정보로부터 기상해일 발생 가능성을 판단하고, 피해지역을 예측하며, 신속한 예경보를 발령할 수 있는 시스템을 갖추기 위해 많은 노력이 필요하다. 또한 이러한 자동기상관측소가 확충되어 정보를 공급받을 수 있다 하더라도 예경보시스템에 적용하기 위해서는 기압점프의 발생 및 전파에 관한 근본적인 연구와 함께 기상해일 수치모형의 정확성 및 계산속도 개선 등의 지속적인 노력이 필요하다.
4. 결 론
이번 연구에서는 2007년 3월 서해안에서 발생했던 이상파랑을 기압 급변동의 이동에 의한 기상해일로 간주하고, 기압급변동이 장파의 전파속도로 이동할 때 발생하는 기상해일의 발생 및 증폭 과정을 1차원 수치모의를 통해 파악하였다. 본 연구에서 제안한 기압점프 형상은 기존의 단순한 계단형이나 (-)sine형태의 단순한 형상 대신 주기적인 변동으로 설정하여 해안에서 관측된 기상해일의 주기성은 물론 해일고 등을 잘 재현할 수 있었다. 이 해일의 주기성은 만내 공진에 의한 범람 수치모의에 있어 필수적인 요소이다. 이번 연구를 통하여 기존 연구에서 사용되어 오던 계단형 기압점프나 (-)sine형태의 단순한 기압변동은 실제 관측된 해일의 특성을 제대로 재현할 수 없으며, 기압점프의 보다 상세한 정보가 필수적임을 알 수 있었다. 본 연구의 결과는 향후 실제 기상해일의 2차원 수치모의를 수행함에 있어 필수적인 정보를 제공할 수 있을 것으로 판단된다.