Reliability Analysis of Tripod Support Structure for Offshore Wind Turbine using Stress Concentration Factor

Sang Geun Lee; Dong Hyawn Kim

doi:10.9765/KSCOE.2016.28.2.92

요약

응력집중계수를 이용하여 해상풍력발전기 트라이포드 지지구조물에 대한 신뢰성 해석을 수행하였다. 파랑과 풍하중의 극치분포함수는 POT방법을 사용하여 동적응답을 분석함으로써 추정되었다. 일계신뢰도법을 사용하여 신뢰성해석을 수행하였으며, 한계상태함수는 지지구조물의 이음부에서 발생하는 응력을 기반으로 정의하였다. 보 요소에서 계산된 응력에 응력집중계수를 곱하는 방법과 판 요소를 사용하여 계산하는 두 가지 방법으로 최대응력을 계산하여 신뢰성 해석을 수행하고 결과를 비교 분석하였다.

핵심용어: 해상풍력발전기, 트라이포드 지지구조, 신뢰성해석, 일계신뢰도법, 응력집중계수

Abstract

Reliability analysis of tripod support structure for offshore wind turbine was performed. Extreme distribution function of peak response due to wind and wave loads was estimated by applying peak over threshold(POT) method. Then, stress based limit state function was defined by using maximum stress of support structure which was obtained by multiplying beam stress and concentration factor. The reliability analysis result was compared when maximum stress was calculated from shell element. Reliability index was evaluated using first order reliability method(FORM).

Keywords: offshore wind turbine, tripod support structure, reliability analysis, first-order reliability method, stress concentration factor

1. 서 론

세계적으로 풍력발전 분야에 대한 관심이 집중되고 있으며, 설치 공간에 대한 제약, 소음 그리고 풍질 등의 문제를 해결하기 위한 방안으로 풍력발전기를 해상으로 확장하고 있다. 국내에서도 신재생 에너지원으로 해상풍력발전기에 대한 필요성에 따라 서남해안, 제주도 등 연안에 적합한 해상풍력발전기에 대한 시공 및 연구가 활발하게 진행되고 있다.

해상풍력발전기의 지지구조의 형태는 크게 부유식과 고정식으로 나눌 수 있으며, 주로 시공 및 경험적인 지식이 풍부한 고정식 지지구조물이 주를 이룬다. 대표적인 고정식 지지구조물에는 재킷(Jacket), 모노파일(Mono pile) 그리고 트라이포드(Tripod)가 있다. 이러한 지지구조물은 일반적으로 지반에 의해 지지력을 발휘하기 때문에 지반물성의 변동성이 구조물 안정성에 영향을 미치는 가장 큰 요인 중 하나이다. 또한 풍력발전기의 특성상 기본적으로 풍하중이 작용하며, 해상에 위치한 경우 지지구조물에는 상시 불규칙적인 파랑하중이 작용하기 때문에 해상풍력터빈 지지구조물의 안전성 확보를 위한 설계를 위해서는 설계변수의 불확실성이 고려된 신뢰성 해석이 수행되어야 한다.

해상풍력발전기 지지구조물에 대한 신뢰성 해석시 한계상태함수를 정적응답을 통해 정의한다면 비교적 간단하게 신뢰도지수를 산정할 수 있다. 하지만 해상에 설치된 지지구조물에는 상시 불규칙적인 동적 파랑 및 풍하중이 작용하고 비선형 거동을 하는 지반과 연동되어 있기 때문에 보다 정확한 파괴확률의 산정을 위해서는 동적응답을 기반으로 신뢰성 해석이 수행되어야 한다. 그러나 동적 구조해석은 정적 구조해석에 비해 상당한 해석시간을 필요로 하며, 반복적인 구조해석을 필요로 하는 신뢰성 해석에 직접적으로 적용하기 어렵다는 제한 사항이 있다.

동적 구조해석기반 신뢰성해석시 Cheng(2002)은 구조물 동적 피크응답에 대한 확률분포 추정을 위해 Peak-Over-Threshold(POT) 방법을 사용하였으며, 시뮬레이션 시간을 증가시키면서 추정된 확률분포함수 모수의 수렴정도를 판단하여 최소한의 시뮬레이션 시간을 결정하였다. Agarwal(2008)도 같은 방법으로 접근하였으나, 피크응답에 대한 확률분포 추정을 위해 POT 및 Block maxima 방법 두 가지를 사용하였다. 그러나 두 연구 모두 파랑과 풍하중만을 고려하여 신뢰성 해석을 수행하였고, 지지구조물과 연동된 지반물성의 변동성은 고려되지 않았다. Kim and Lee(2014)는 반복적으로 수행되는 동적 구조해석시간의 단축을 위해 피크응답계수를 도입하여 한계상태함수를 정의하였다. 피크응답계수는 피크응답의 분포를 정적 응답으로 정규화한 확률변수이다. 여기서, 동적 및 정적 하중에 대한 응답은 Mudline에서 나타난 지지구조의 변위이며, 피크응답의 분포는 동적 구조해석을 수행하여 충분한 피크응답의 샘플을 추출한 후 POT 방법으로 분포를 추정하였다. 그리고, 파랑 및 풍하중 외에 지반물성의 확률적 변동성을 신뢰성 해석에 반영하여 지지구조물에 대한 신뢰도지수를 산정하였다.

재킷이나 트라이포드 지지구조물의 이음부는 대부분 용접이음으로 이루어져 있어 급격한 형상변화로 인한 응력 집중이 발생되고 반복되는 하중이 작용함에 따라 피로 파괴의 가장 취약한 지점으로 알려져 있다. 이음부에 대한 응력은 실제 발생하는 국부 응력과 공칭응력의 비로 계산되는 응력집중계수를 산정하여 공칭응력과 응력집중계수의 곱으로 이음부에 대한 응력을 계산하는 것이 일반적이다. Efthymiou(1988), LR(1991), Hansen(1996) 및 Lee(1999)는 설계자가 보다 쉽게 응력집중 계수를 산정할 수 있도록 FEM 및 모형실험결과를 토대로 이음부의 응력집중계수 산정식을 제안하였다. 기하 형상에 대한 영향함수를 정의하여 응력집중계수를 산정하는 방법으로 적용된 용접구조상세 등에 의해 동일한 모델에 대해서도 응력집 중계수가 상이하게 산정된다는 문제점이 있으며, 형상이 복잡해질 경우 적용이 어렵다는 제한사항이 있다.

본 연구에서는 피크응답계수를 도입하여 동적 파랑하중의 확률적 변동성과 추력 및 지반물성의 불확실성이 고려된 신뢰성 해석을 수행하였다. 신뢰성 해석은 Level II 방법인 일계신뢰도법(First Order Reliability Method, FORM)을 사용하여 신뢰도 지수를 산정하였다(Hasofer and Lind,1974). 파괴기준은 이음부에서 발생하는 응력을 기준으로 정의하였으며, 이음부의 응력 평가시 유한요소해석을 통해 산정된 응력집중계수를 사용하였다. 계산된 응력집중계수를 이용하는 방법과 이음부를 상세 모델링하여 해석에 직접 이용하는 방법으로 각 각 신뢰성해석을 수행하여 수렴된 신뢰도 지수 및 소요시간을 비교하였다.

2. 피크응답계수를 이용한 신뢰성 해석

2.1 일계신뢰도법(First Order Reliability Method, FORM)

일계신뢰도법은 신뢰성해석 Level II에 해당하며, 신뢰도지수를 산정하여 파괴확률을 간접적으로 계산하는 방법이다. 신뢰도지수를 산정하기 위해서는 구조물의 파괴 또는 손상을 판단할 수 있는 기준이 필요하며, 확률변수는 정규분포이고 서로 독립변수라고 가정하여 저항요소 R과 하중요소 S로 나타내면 식(1)과 같이 나타낼 수 있다.

(1)

Z=g(R,S)=R−S

여기서, Z > 0는 안전한 경우, Z < 0는 파괴가 발생한 경우이며, Z = 0은 구조물의 안전과 파괴의 경계가 된다. 그러므로 파괴확률은 식(2)와 같이 표현할 수 있다.

(2)

Pf=P(Z<0)

일계신뢰도법에 의하여 파괴확률을 구하기 위해서는 표준화 변수 또는 환산 변수(Reduced Variable)를 사용해야한다. 표준화 변수는 확률변수의 무차원 형태로 식(3)과 같이 표준정규분포 확률변수로 변환할 수 있으며,

(3)

Xi'=Xi−μXiσXi

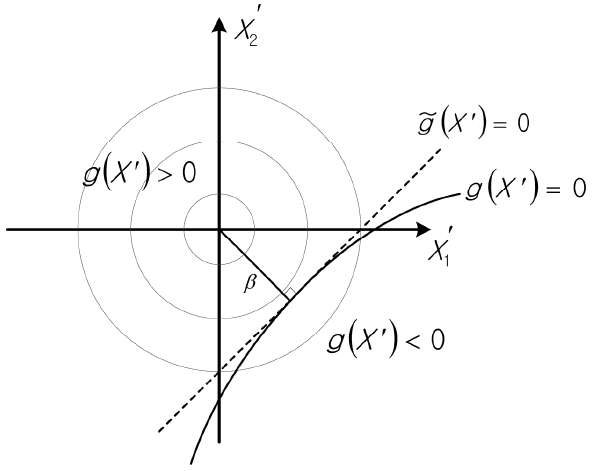
환산변수 공간상에서 한계상태식의 선형 근사 및 신뢰도지수의 개념을 도시하면 Fig. 1과 같다(Hasofer and Lind,1974).

원점과 최단거리에 해당하는 파괴면상의 점을 최확파괴점(Most Probable Failure Point, MPFP)이라고 하며, 이때 원점까지의 최단거리인 신뢰도지수는 식(4)와 같이 계산된다.

(4)

β=∑i=1nxi'*(∂g∂Xi')*∑i=1n(∂g∂Xi')*2

α_i는 x_i′에 대한 민감도 계수 또는 방향 코사인으로 식(5)와 같다.

(5)

αi=(∂g∂Xi')*∑i=1n(∂g∂Xi')*2

2.2 피크응답계수의 적용

지지구조물의 동적 응답은 지지구조물의 역학적 특성, 지반물성 그리고 설계하중 등의 설계변수에 의해 결정되며, 신뢰성 해석을 위한 지지구조물의 한계상태방정식은 식(6)과 같이 정의할 수 있다.

(6)

g=Rall−Rp(X)

여기서, R_all은 구조물 응답에 대한 허용치, R_p(X)는 설계변수에 의한 지지구조물의 동적 피크응답이다. 위 조건에서 파괴확률 계산을 위해 확률변수로 고려되는 설계변수(X)에 따른 동적 피크응답을 구하기 위해 동적 구조해석을 수행하여 응답을 얻어야 한다. 그러나 신뢰성 해석시 음함수로 존재하는 R_p(X)를 양함수로 근사하기 위한 응답면 기법 적용시 반복적인 동적 구조해석을 수행해야 하므로 해석시간적인 측면에서 어려움이 따른다. 이에 파괴확률을 보다 쉽게 구할 수 있도록 식(7)과 같이 피크응답계수 R_n을 정의하였다(Kim and Lee, 2014).

(7)

Rn=Rp/Rst

여기서, R_st는 설계조건에서의 정적응답이며, 지반물성 및 파랑, 풍하중 등에 대한 종속변수이다. 설계변수의 변동성에 따른 지지구조물의 동적 특성 변화가 크지 않은 경우 동적 피크응답과 정적응답은 비례한다는 가정하에 식(7)의 개념을 적용하면, 한계상태함수는 식(8)과 같이 다시 쓸 수 있다.

(8)

g(X)=Rall−RnRst(X)

본 연구에서는 동적 파랑하중의 확률적 변동성을 피크응답 계수로 고려하고자 하였다. 유한요소 모델링된 지지구조물의 각 절점에 작용하는 동적, 정적 파랑하중을 각 각 Fpdis , Fstdis 라 하고, 각 파력의 합을 F_p, F_st로 정의 한다면 동적 파랑하중의 피크응답계수 R_nw는 식(9)와 같이 표현할 수 있다.

(9)

Rnw=Fp/Fst

동적 파랑하중은 정적 파랑하중에 피크응답계수를 곱함으로써 식(10)과 같이 나타낼 수 있다.

(10)

Fp=FstRnw

유한요소해석시 파랑하중은 각 절점에 분포하중으로 입력되어야 하므로, 한계상태식은 식(11)과 같이 다시 표현할 수 있다.

(11)

g(X)=Rall−S(FstdistRnw,X)

여기서, S( )은 유한요소해석을 통해 계산되는 응답이다.

3. 트라이포드 지지구조 및 설계하중조건

3.1 발전기 및 지지구조의 제원

본 연구에서는 상부 타워 및 발전기의 제원은 National Renewable Energy Laboratory(NREL) 5-MW 모델을 참조하였으며(Jonkman et al., 2009), 하부 지지구조는 International Energy Agency(IEA) Wind Annex 23에서 수행된 Offshore Code Comparison Collaboration(OC3) 프로젝트의 모델을 대상으로 하였다(Jonkman and Musial, 2010). NREL의 5-MW 해상풍력발전기는 3-블레이드 Upwind 타입으로 상세한 정보는 Table 1에 정리하였다.

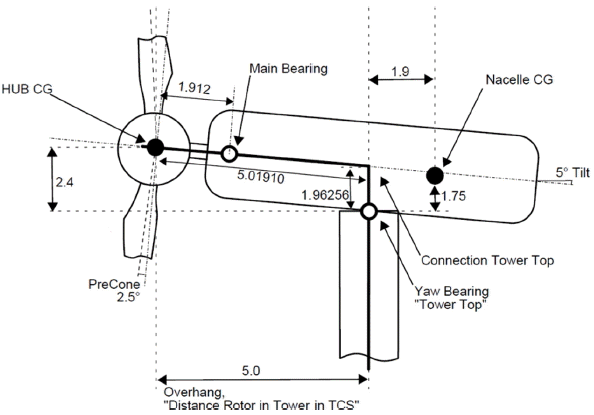
타워 최상부 및 허브의 높이는 각각 해면으로부터 87.5 m, 90 m 이다. 그 밖에 허브와 너셀의 각 무게중심 등 Rotor nacelle assembly(RNA)에 대한 세부 내용을 정리하면 Fig. 2와 같다.

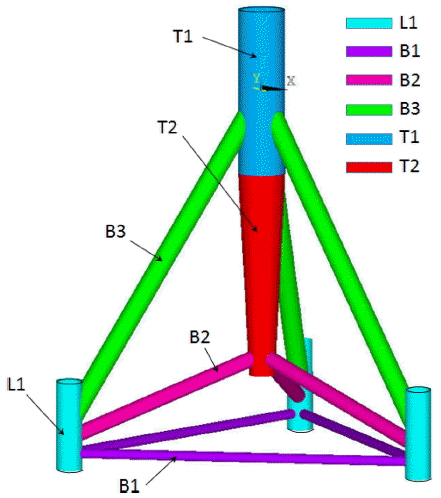
하부 지지구조의 각 멤버에 따라 색상으로 구분하여 Fig. 3에 도시하였으며, 각 부재에 해당하는 외경 및 두께는 Table 2와 같다. L1 부재 중심간 거리는 약 42.958 m이며, B2 부재가 연결되어 있는 T2부재는 변단면으로 이루어져 있다.

기초 파일이 관입되어 있는 지반은 점성토 및 사질토로 이루어진 복합 지반으로 구성하였으며, 각 층의 두께 및 지반 물성를 Fig. 4에 정리하였다.

3.2 설계하중조건

설계하중조건은 DNV 기준에 의해 결정되었으며(DNV, 2013), 해당 기준에서 제시하는 설계하중조건은 해상풍력터빈의 작동상태 및 풍하중, 파랑하중 등에 따라 크게 34가지의 설계하중조건을 제시하고 있다. 본 연구에서는 Table 3과 같이 해상풍력터빈의 작동시 극한하중이 작용하는 상황을 해석조건으로 결정하였다.

풍속조건은 정상 난류모델을 적용하였으며, 풍속은 Cut-in에서 Cut-Out까지 변경하며 해석을 수행하여야 하지만, 정격풍속에서 가장 큰 추력이 발생하므로 본 연구에서는 정격풍속에 대한 추력만을 계산하였다. 난류 바람장 생성 및 추력의 계산은 GH_bladed를 사용하여 계산하였다(GH, 2013). 파랑조건은 위험해상상태 이므로 50년 재현주기에 대한 유의파고 및 피크주기를 사용하게 된다. 파랑에 의한 하중 계산은 기본적으로 식(12)와 같이 모리슨 방정식에 의해 계산할 수 있다(Morison et al., 1950).

(12)

F=CD12ρwD|u|u+CIρwπ4D2∂u∂t

여기서, C_D, C_I는 항력 및 관성력계수, u는 물입자의 속도(조류속 포함), ∂u∂t 는 물입자의 가속도 그리고 ρ_w는 해수의 밀도이다.

조류는 달과 태양 등 천체의 인력에 의해 발생하는 Tidal current와 바람이 작용함에 따라 해수면과의 항력으로 인해 발생하는 Wind-generated current로 구분되며 식(13)과 같이 두 조류속을 합산하여 설계 조류속을 산정하게 된다(DNV, 2013).

(13)

v(z)=vtilde(z)+vwind(z)vtilde(z)=vtilde0(h+zh)1/7 for z≤0vwind(z)=vwind0(h0+zh0) for −h0≤z≤0

여기서 v(z)=total current velocity at level z

z = vertical coordinate from still water level

v_tide0 = tidal current at still water level

v_wind0 = wind-generated current at still water level

h = water depth from still water level

h₀ = reference depth for wind-generated current;

h₀ = 50 m

4. 수치해석

4.1 구조 및 지반 비선형 스프링 모델

추력을 계산하기 위해 해상풍력터빈 전용 구조해석 프로그램인 GH_bladed를 사용하여 발전기 및 지지구조물을 Fig. 5와 같이 모델링 하였다(GH, 2013).

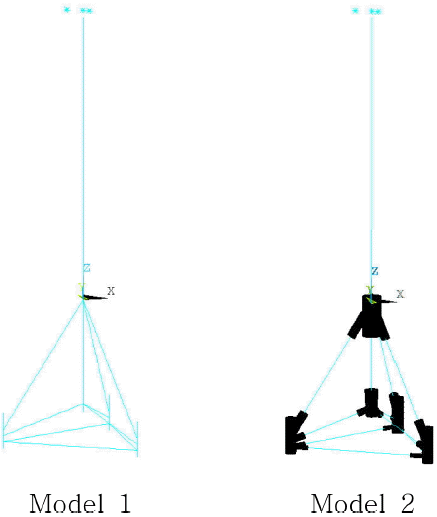
동적 파랑하중에 대한 수치해석을 위해 지지구조 및 비선형 지반 스프링 모델링은 범용 유한요소해석 프로그램인 Ansys ver. 12를 사용하였다(Ansys, 2009). 보(Beam)요소를 사용하여 모델링된 Model 1과 이음부에 대해 판(Shell)요소를 사용하여 상세 모델링하고 그 외 부재에 대해서는 보 요소를 사용하여 결합한 Model 2로 구분하여 Fig. 6에 나타내었다.

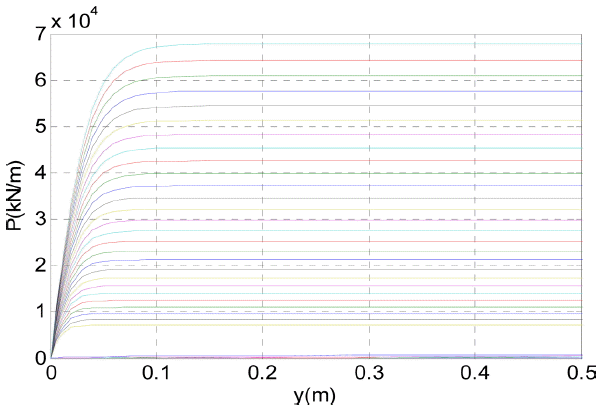
Ansys를 사용한 모델링시 상부 구조물인 허브(Hub)와 너셀(Nacelle)은 무게중심을 고려하여 질량 요소를 사용하여 모델링하였으며, 각 요소간 연결은 질량이 없는 강체(Rigid)요소를 사용하여 정의하였다. 지반은 말뚝과 지반의 비선형 상호작용을 고려하기 위해 비선형 스프링 요소로 모델링 하였다. 이때, 비선형 스프링의 물성은 P-y 곡선을 통해 정의할 수 있다. P-y 곡선은 말뚝변위와 지반반력의 함수관계로 미국석유협회(API)의 해양구조물에 관한 지침서 의해 계산하였으며(API,2007), 1 m 간격으로 계산된 P-y 곡선은 Fig. 7과 같다.

4.2 풍하중

터빈에 작용하는 난류 바람에 의해 허브(Hub)위치에 작용하는 추력을 계산하기 위해 Table 4와 같은 조건을 사용하여 난류 시드(Turbulence seed)에 따라 20set를 생성하고 난류해석을 수행하였다. 3차원 난류 바람장 생성 및 해석에는 GH_bladed를 사용하였으며, 계산된 추력은 Fig. 8과 같다.

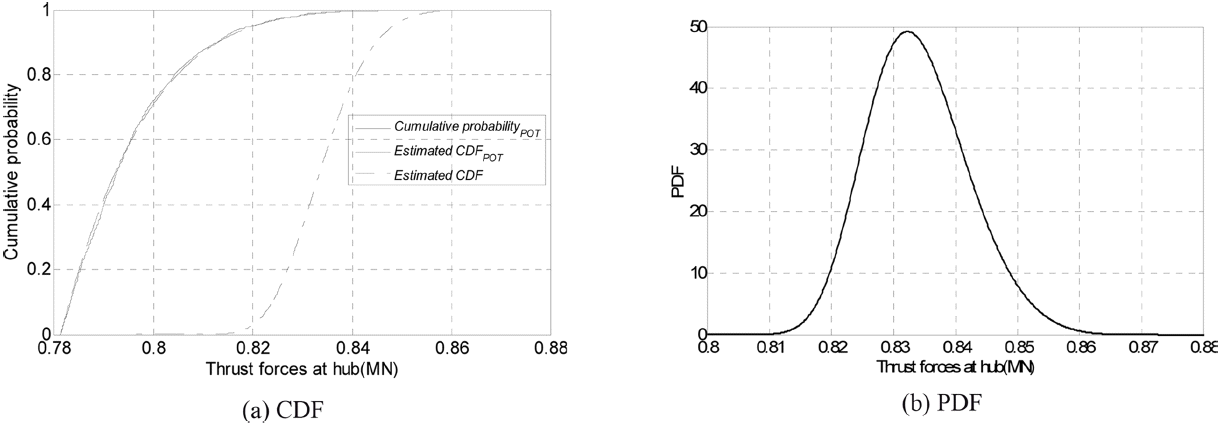
각 시간이력 추력 응답은 POT 방법을 사용하여 Fig. 9와 같이 누적분포함수를 추정하였다. 추정된 확률분포함수의 형태는 Weibull 분포이며, Shape(k), Scale(σ). Location(μ) parameter 는 각각 -0.1813, 0.0076, 0.8307이다.

4.3 파랑하중 및 피크응답계수

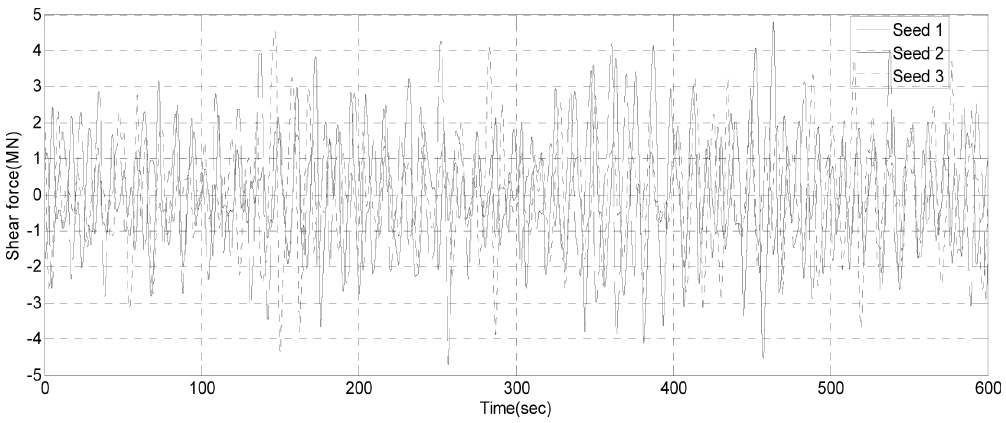
동적 구조해석에 사용된 불규칙파는 유의파고 8.5 m, 피크 주기 12.3 s 로 Table 5과 같이 정의하였으며, 충분한 샘플링을 위해 Random seed에 따라 50set의 동적 구조해석을 수행하였다. Fig. 10은 Mudlind에서의 시간이력 응답을 나타낸 것이다.

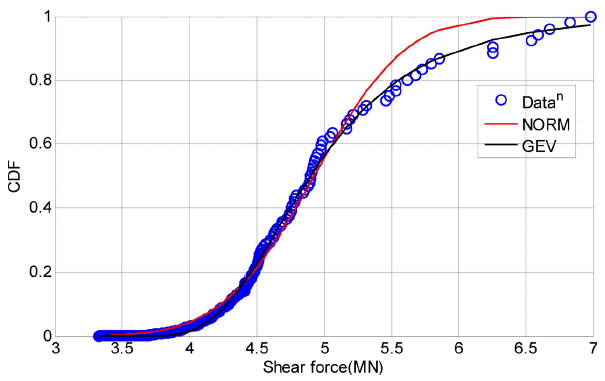
전단력의 시간이력 응답에 대해 POT 방법을 사용하여 Fig. 11과 같이 누적분포를 통해 적합도를 평가한 결과 Weibull 분포가 적합한 것으로 나타났으며, Shape(k), Scale(σ). Location(μ) parameter는 각각 -0.0839, 0.5844, 5.4725로 추정되었다.

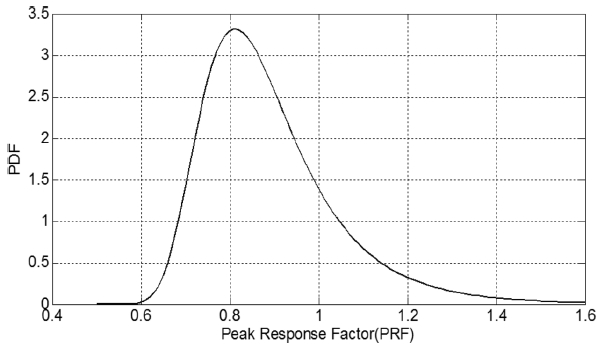
선형 파랑하중이론에 의해 트라이포드에 작용하는 정적 파랑하중을 계산한 결과 5.57 MPa 로 나타났다. 피크응답계수는 식(9)와 같이 동적 피크응답과 정적 응답의 비로 정의되기 때문에 동적 피크응답의 분포를 정적응답으로 정규화하여 Fig. 12와 같이 산정할 수 있다.

4.4 응력집중계수

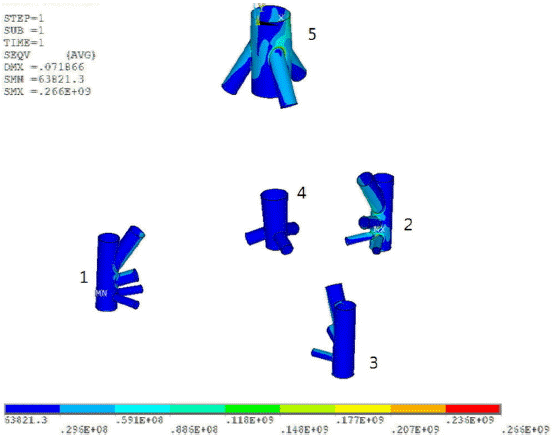
트라이포드 지지구조 이음부의 형상은 여러 부재가 연결되어 복잡한 구조이므로 보다 합리적인 응력 평가를 위해 유한 요소해석을 통해 응력집중계수를 산정하였다. 작용하는 하중의 방향은 0 deg(+x)방향으로 하고, 확률변수들의 평균점에서 정적 구조해석을 수행하여 각 Joint별 응력을 계산한 결과 Fig. 13, Table 6과 같이 이음부 2, 3번 에서 응력이 가장 크게 산정되었다. 하중방향에 대해 대칭 구조이기 때문에 이음부 2, 3번의 응력은 동일하게 나타난 것이며, 응력집중계수 계산 및 한계상태함수는 이음부 2번 이음부를 기준으로 정의되었다.

응력집중계수는 식(14) 와 같이 이음부의 국부에서 발생하는 응력과 공칭응력의 비로 계산할 수 있으며, 국부에서 발생하는 최대 응력 및 계산된 응력집중계수를 정리하면 Table 7과 같다.

(14)

SCF=σhotspot stressσn

4.5 확률변수 및 한계상태함수

지반 토질정수의 확률 변동성은 서남해안 지반조사 결과 단위중량과 내부마찰각은 각 각 3~10%, 7%, 비배수 전단강도의 경우 26%로 나타나고 있어 해당 범위 내에서 확률적 변동성을 가정하였다. DNV 기준에서 지반정수의 범위는 음수가 아닌 특정 범위를 갖고 있기 때문에 일반적으로 대수정규분포 및 Beta분포의 사용을 제안하고 있으므로, 내부마찰각에 대해서는 Beta분포를 적용 하였으며, 단위중량 및 비배수 전단강도에 대해서는 대수정규분포로 가정하였다(DNV, 2012). 그 밖에 신뢰성 해석에 사용된 피크응답계수(X₁), 추력(X₂) 그리고 항복응력(X₉)에 대한 확률특성은 앞서 수치해석을 통해 추정된 결과를 바탕으로 Table 8에 정리하였다.

판(Shell)요소를 사용하여 이음부를 상세 모델링하고 그 외 연결 부재에 대해서는 보(Beam) 요소를 사용하여 결합한 모델의 경우 직접적으로 이음부의 응력을 계산하게 되므로 한계상태함수는 식(15)와 같고,

(15)

Method 1: g1=X9−S(FstX1,X2~X8)

보(Beam)요소만을 사용한 모델의 경우 산정된 응력집중계수를 사용하여 식(16)과 같이 정의할 수 있다.

(16)

Method 2: g2=X9−S(FstX1,X2~X8)SCF

여기서, S( )는 정적 구조해석을 통해 계산되는 응답이며, 응답면 기법을 사용하여 양함수의 형태로 근사하였다. 응답면 추정시 연성항이 고려된 2차 다항식으로 고려하기 위해 Saturated Design 방법을 사용하여 구조해석점을 결정 하였다(Box and Wilson, 1951).

4.6 신뢰성 해석

Method 1, 2 모두 신뢰성해석 결과 신뢰도지수(β)는 Fig. 14와 같이 약 3번의 반복과정 이후 빠른 속도로 수렴되었으며, 신뢰도지수는 각 각 2.4686, 2.4872로 산정되었다.

각 확률변수별 수렴된 민감도 계수 및 파괴점을 Table 9에 나타내었다. 가장 하부에 위치한 점성토의 단위중량(X₅) 그리고 중간에 위치한 사질토(X₆)의 민감도 계수를 살펴보면 거의 0에 근접할 정도로 매우 작은 값으로 수렴한 것을 알 수 있다. 이는 두 확률변수가 Joint 2번의 파괴에 미치는 영향이 매우 적다는 것을 의미한다. 반면, 민감도 계수가 큰 확률변수는 피크응답계수(X₁)와 항복응력(X₉)으로 나타났다. 즉, Joint 2의 파괴를 유발하는 가장 지배적인 하중요소는 파랑하중이며, 저항 요소는 항복응력인 것으로 해석할 수 있다.

두 방법 모두 일계신뢰도법을 이용한 신뢰성 해석시 5번의 반복해석을 수행하였으며, 구조해석에 사용된 PC의 CPU는 쿼드코어 3.4GHz, RAM 16GB, 시스템은 64bit Windows 7 운영체제에서 수행되었다. 해석에 소요된 시간 및 결과를 정리하면 Table 10과 같다.

시간적인 측면에서 볼 때 응력집중계수를 사용한 Method 2 방법이 Method 1에 비해 약 35.7배 빠르고, 산정된 신뢰도지수의 상대오차는 0.74%로 매우 적게 나타났다. 해석에 소요된 시간 및 산정된 파괴확률간의 오차를 평가했을 때 산정된 응력집중계수를 이용하여 이음부의 응력을 평가하는 방법이 합리적인 것으로 나타났다.

4. 접근방법의 제한사항

본 연구에서는 도입된 피크응답계수는 Kim and Lee(2014)의 연구에서 언급한바와 같이 설계변수의 변동성에 따른 지지구조물의 동적 특성 변화가 크지 않은 경우 동적 피크응답과 정적응답은 비례한다고 가정하였다. 동/정적 응답의 비선형성이 큰 경우에는 검증되지 않았기 때문에 구조물의 비선형성에 대한 검토 후 해석에 적용해야 한다. 그리고 유한요소법을 이용한 이음부의 구조해석시 요소의 크기 또는 형상에 따라 응답이 상이하게 나타날 수 있으므로 모델링에 대한 충분한 검토가 선행되어야 한다.

4. 결 론

본 연구에서는 해상풍력발전기 트라이포트 지지구조물에 대한 신뢰성 해석을 수행하였다. Kim and Lee(2014)에 의해 제안된 피크응답계수를 도입하여 동적 파랑하중의 확률적 변동성을 고려하였으며, 풍하중에 의한 발생하는 추력 및 지반물성의 불확실성을 고려하였다. 일계신뢰도법을 사용하여 신뢰도지수를 계산하였으며, 한계상태함수는 이음부에서 발생하는 응력을 기준으로 정의되었다. 이음부의 응력 산정시 이음부를 상세 모델링하여 직접 구조해석에 이용하는 방법(Method 1)과 유한요소해석을 통해 미리 계산된 응력집중계수를 이용하는 방법(Method 2)으로 각 각 신뢰성해석을 수행하였다. 해석 시간적인 측면에서 응력집중계수를 이용한 Method 2 방법이 Method 1에 비해 약 35.7배 빠르고, 산정된 신뢰도지수의 상대오차는 0.74%로 매우 적게 나타났다. 해석에 소요된 시간 및 산정된 파괴확률간의 오차를 평가했을때 산정된 응력집중계수를 이용하여 이음부의 응력을 평가하는 방법이 합리적인 것으로 나타났다.

응력집중계수를 이용한 해상풍력터빈 트라이포드 지지구조물의 신뢰성해석