1. 서 론
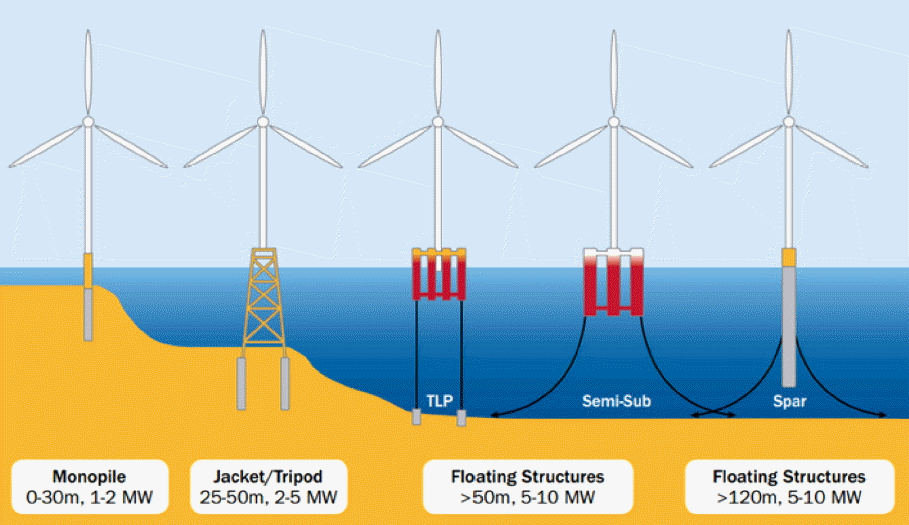
수심 30 m 이내의 천해역에 시공되는 해상풍력터빈(offshore wind turbine, OWT)의 경우 모노파일 형태의 하부구조물이 가장 널리 적용되고 있으며, 2013년 한 해 동안 전체의 79%에 해당하는 총 490기의 해상풍력터빈이 모노파일 하부구조물을 적용하여 시공된 바 있다(EWEA, 2014). 그러나 수심이 상대적으로 깊은 25-50 m의 중수심 조건에서는 재킷 또는 트라이포드 기초가 경쟁력이 있는 형식으로 고려되고 있으며(EWEA, 2013, Fig. 1 참조), 2013년의 경우 트라이포드 하부구조물이 87기(14%), 재킷 하부구조물이 39기(6%) 적용된 바 있다(EWEA, 2014). 재킷 형태의 하부구조물은 이미 해양구조물 분야에서 널리 적용되고 있는 형식이며, 우리나라 서남해안과 같이 연약층 심도가 깊은 경우 적절한 형식이라 할 수 있다. 또한 국내에서는 이어도 종합해양과학기지를 비롯하여 동해 가스전 플랫폼 등 다수의 재킷 하부구조물에 대한 설계, 제작 및 시공 경험이 많아 국내 해상풍력 기초로 재킷이 채택될 가능성이 높고, 기설치 되어 시험운영 중인 제주 월정리 해역의 해상풍력터빈 2기를 비롯하여 올해 완공 예정인 탐라해상풍력단지의 경우에도 재킷 하부구조물을 적용하고 있다. 또한 서남해 해상풍력단지 실증사업에도 재킷이 적용될 예정인 것으로 알려져 있다.
그러나 국내 서남해안의 경우 조류 및 파도의 영향으로 세굴 발생 가능성이 매우 높아서 이에 대한 면밀한 검토가 필요하다. 이와 관련하여 최근 Ko et al. (2015)은 Flow-3D를 이용하여 해상 재킷 구조물 주변의 세굴을 수치적으로 해석한 바 있는데 이들은 서해안에 설치된 HeMOSU-1호 해상 기상탑 재킷 구조물에 대하여 1.32-1.44 m의 최대 세굴깊이를 분석하였고, 그 결과가 현장관측값인 1.5-2.0 m의 세굴깊이와 유사함을 제시한 바 있다. 한편 Lee (2013)는 세굴에 따른 고정식 해상풍력터빈의 고유주파수를 비롯하여 변위, 블레이드 지점부 모멘트 등 동적 응답을 GH_Bladed를 이용하여 분석한 바 있으며, 이 연구를 통하여 모노파일로 지지되는 해상풍력터빈이 세굴에 의하여 가장 큰 영향을 받는 것을 제시한 바 있다. 한편 외국에서는 실제 운영한 지 몇 년이 지난 해상풍력터빈을 대상으로 세굴깊이를 측정한 바 있으며 Margheriini et al. (2006)은 세굴에 대한 쇄파 및 조류의 영향을 축소 모형실험을 수행하여 분석한 바 있으며, 이 연구를 통하여 세굴에 대한 쇄파의 영향은 매우 제한적임을 밝힌 바 있다. 또한 Rudolph et al. (2004)은 현장 관측에 의하여 세굴깊이를 분석하였는데, 모노파일의 경우 Nakagawa and Suzuki (1976)의 세굴 예측식과 유사한 결과를 얻을 수 있었지만 재킷식 해양구조물의 경우 해저면에서의 재킷 레그 슬리브 등 부속 장치의 영향 등으로 세굴이 예측식보다 더 크게 발생함을 제시한 바 있다. 한편 최종 세굴깊이와 관련하여 해상풍력터빈에 대한 DNV-OS-J101 (DNV 2004) 기준에서는 말뚝 직경의 1배~1.5배까지 고려하도록 하고 있으며, 실제 북해에 설치된 모노포드 형식의 해양구조물에 대한 세굴과 관련된 기존 문헌(Peters, 1986)에서는 세굴깊이가 말뚝 직경의 1배 이내이었음을 보고한 바 있다. 그리고 세굴에 의한 고유 주파수 분석을 수행한 기존 문헌에서는 말뚝 직경의 2.5배까지 세굴깊이를 고려한 바 있다(Van Der Tempel et al., 2004).
이와 같이 현재 많이 적용되고 있거나 적용 예정인 모노파일, 트라이포드 또는 재킷과 같은 하부구조물은 고정식 해상풍력기초로, 이를 안전하게 시공 및 적용하기 위해서는 세굴 깊이를 고려한 지반-말뚝 상호작용을 고려하여야 하며, 이때 지반물성치에 포함되어 있는 불확실성을 고려한 신뢰성 해석을 수행하여야 한다. Lee의 연구와 유사한 내용의 기존 연구에서는 세굴깊이와 함께 지반물성치의 불확실성을 고려하여 이러한 고정식 기초로 지지된 해상풍력터빈의 동적 특성, 특히 고유주파수를 분석한 바 있는데, 이를 통하여 모노파일을 적용한 해상풍력터빈의 경우 지반물성치의 불확실성 및 세굴 깊이가 고유주파수의 분포에 큰 영향을 미치는 반면 트라이포드와 재킷을 적용한 해상풍력터빈의 경우 지반물성치의 불확실성 및 세굴깊이가 고유주파수에 미치는 영향이 상대적으로 매우 작음을 밝힌 바 있다(Yi et al., 2015).
이 연구에서는 해상풍력터빈의 동적 특성과 관련된 기존 연구를 확장하여, 모노파일, 트라이포드, 재킷 등 대표적인 하부구조물을 적용한 해상풍력터빈이 설치되는 지반의 지반물 성치 및 하중에 포함되어 있는 불확실성과 세굴깊이를 고려하여 신뢰성 해석을 수행하고자 하였다. 지반물성치의 불확실성은 지반-말뚝 상호작용 해석에서 반영되며, 지반-말뚝 상호작용은 가상고정점 모델(apparent fixity model), 복합 모델 및 Winkler 스프링 탄성모델 등을 이용하여 분석할 수 있는데, 이 연구에서는 p-y, t-z, q-z 등의 지반 스프링을 이용하는 Winkler 탄성 모델을 적용하여 지반과 말뚝의 상호작용을 고려하였다(Winkler, 1867; Hetenyi, 1946; Barber, 1953; Matlock and Reese, 1960; Davisson and Gill, 1963). 그리고 하중은 블레이드 회전 시 발생하는 추력을 기준으로 하여, 추력이 가장 많이 발생하는 정격풍속에서의 추력에 대한 분포를 이용하여 고려하였으며, 신뢰성 해석을 수행할 때 세굴깊이에 따른 신뢰도 지수의 변화를 함께 분석하였다.
2. 이론적 배경
2.1 지반과 말뚝의 상호작용
말뚝 기초는 재킷식 해상 플랫폼에 있어 상부에서 발생하는 하중을 지반에 전달하는 가장 중요한 구조부재라 할 수 있다. OWT에 유발되는 바람, 파랑 및 지진 등의 외력으로 인하여 지지구조물인 말뚝과 지반의 상호작용이 발생되는데 전체 OWT의 거동을 이해하는 데 있어 가장 핵심적인 내용으로 알려져 있다. 일반적으로 말뚝은 실제 지반의 관입 깊이까지 보요소(beam element)를 이용하여 모델링할 수 있으며, 지반의 강성은 관입 깊이까지 모델링한 말뚝의 절점에 비선형 지반 스프링을 추가하여 표현할 수 있다. 이 논문에서는 말뚝은 탄성계수와 단위중량이 각각 210 GPa, 78.5 kN/m3 인 강관으로 설계하였고, 말뚝 주변의 지반은 p-y, t-z, q-z 관계로 나타나는 Winkler의 비선형 지반 스프링으로 모델링하였다. 이 때 횡하중과 말뚝의 변위관계인 p-y 곡선은 점토층과 사질토층에 대하여 API (2005)의 제안식과 Evans and Duncan (1992)의 제안식을 각각 적용하였고, 연직하중과 말뚝의 변위 관계인 t-z, q-z는 다음과 같이 API (2005)에 제시된 식을 적용하였다.
우선 지반과 말뚝 사이의 수평거동과 관련하여, 수평변위 y 발생 시 수평저항력인 p는 다음과 같이 구할 수 있다.
여기서 pu와 ε50은 각각 극한수평저항력과 최대압축응력 50%의 수준에서의 변형률이다. pu는 사질토와 점토질의 경우 각각 달리계산할수있으며, 사질토의경우 pu=min(pus, pud), 즉 정적극한수평저항력(pus)와 동적 극한수평저항력(pud) 중 작은 값으로 구할 수 있다. 한편 점토의 경우, 깊이가 XR 보다 작은 경우 pu=s ⋅ cu ⋅ D+σz′ + D + J ⋅ cu ⋅ z 으로, XR 보다 깊은 경우 pu=9 ⋅ cu ⋅D (z ≥ XR)로 구할 수 있다. 여기서 D는 말뚝 직경이다.
한편, 심도 z 위치에서의 연직변위 w 발생 시 주면마찰저항력 f를 나타내는 t-z 곡선은 다음과 같이 구할 수 있다.
여기서, 최대연직변위 wmax는 2.54 mm이며, 최대주면마찰저항력은 사질토와 점토에 따라 각각 다음과 같이 구할 수 있다. 즉, 사질토의 경우 fmax는 fmax = K ⋅ tanδ ⋅ σz′ ≤ flimit로 구할 수 있고, 점토의 경우 fmax = α ⋅ cu (여기서 α = 0.5ψ–0.5 = ≤ 1, ψ ≤ 1, α = 0.5ψ–0.25 = ≤ 1, ψ > 1, ψ= cu/σz′)로 구할 수 있다. 여기서, K와 δ, σz′, flimit, cu 는 각각 수평토압계수, 지반-말뚝주면 마찰각, 심도 z 위치에서의 유효상재하중, 한계주면마찰저항력, 심도 z 위치에서의 비배수전단강도를 의미한다.
그리고 말뚝선단 연직변위가 z인 경우, 말뚝 선단에서의 저항력 q를 나타내는 q-z 곡선은 다음과 같이 구할 수 있다.
여기서, q ≤ qmax (zb>zmax)이며, 최대 선단저항력인 qmax는 사질토의 경우 qmax = Nq ⋅ σz′ ≤qlimit와 같이 구할 수 있고, 점토의 경우 qmax =9 ⋅ cu를 이용하여 구할 수 있다. 이때, Nq, σz′, qlim, zmax는 각각 선단지지력계수, 말뚝선단 위치에서의 유효상재하중, 한계 단위선단지지력, 에서의 말뚝선단 연직변위이다.
2.2 한계상태함수
신뢰성 해석에 있어서 피로한계상태, 사용한계상태 등 다양한 한계상태함수(limit state function)를 고려할 수 있지만 이 연구에서는 다음과 같이 타워 상부의 수평변위로 정의되는 사용한계상태를 한계상태함수로 고려하여 신뢰성 해석을 수행하였다.
여기서 dallow는 허용 상부 변위로 타워 높이의 1.25%를 적용하였다(Nicholson, 2011).
2.3 Level II 일차이계모멘트방법및 Level III 몬테카를로 시뮬레이션 방법
확률밀도함수가 fX(x)인 확률변수 X에 대하여 구조물의 파괴를 정의하는 한계상태식이 g(x)로 주어질 때, 파괴확률 pf는 다음과 같이 한계상태식이 파괴를 나타내는 영역, 즉 g(x) ≤ 0을 만족하는 x에 대하여 fX(x)를 적분하여 구할 수 있다.
이때 한계상태식의 비선형성이 크거나 해석적으로 적분을 수행하기 어려운 경우, 몬테카를로 시뮬레이션(MCS, Monte Carlo Simulation)과 같은 Level III 신뢰성 해석 방법을 이용하여 파괴확률을 구할 수 있다. MCS에서는 주어진 확률밀도함수를 따르는 난수를 발생시켜 충분한 수의 확률변수 표본집단을 생성한 다음, 생성된 확률변수의 값에 대하여 한계상태식의 값을 확인함으로써 파괴확률을 다음과 같이 구할 수 있다.
여기서 N은 임의 추출한 확률변수 샘플의 수, nf는 각각의 확률변수 샘플에 대한 한계상태식이 0보다 작은 경우의 수를 의미한다. 일반적으로 MCS에 의하여 유의미한 수준의 파괴확률을 구하기 위해서는 예상되는 파괴확률 pf의 역수에 대하여 10배 내지 100배 이상의 값을 전체 추출횟수 N의 값으로 사용하기 때문에 계산시간이 많이 소요된다(Yang et al., 1999). 이와 달리 각 확률변수의 평균과 분산, 그리고 분포형태만을 이용하여 신뢰도 지수(reliability index)를 근사적으로 산정하는 방법이 Level II 신뢰성 해석 방법으로 이를 모멘트 방법이라고도 한다. 서로 통계적으로 독립인 정규분포 확률변수 X의 선형조합으로 정의되는 한계상태식 g = a 0 + ∑ a i x i i = 1 n
여기서, μi와 σi는 각각 확률변수 X의 평균과 표준편차이며, 이때 신뢰도 지수 β는 다음과 같이 구할 수 있다.
여기서, u∗는 표준정규분포 확률변수의 공간에서 구한 MPFP(Most Probable Failure Point)로 한계상태식이 비선형식으로 주어지는 경우 Hasofer and Lind가 제안한 개선된 Level II 신뢰성 해석방법인 일계이차모멘트방법, 즉 AFOSM(Advanced First Order Second Moment)을 적용하여 구할 수 있다(Hasofer and Lind, 1974; Yang et al., 1999).
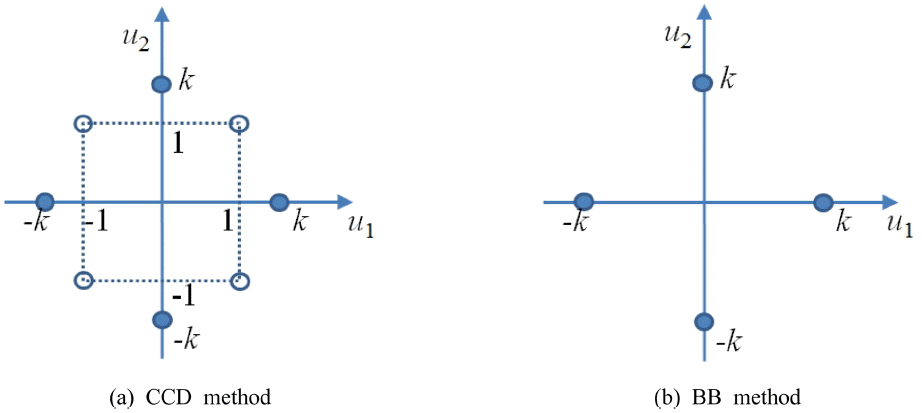
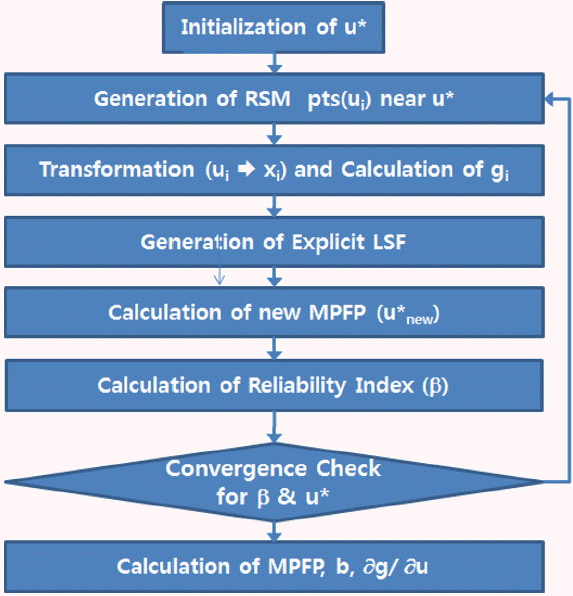
그러나 AFOSM을 적용하여 신뢰성 해석을 수행하는 경우 한계상태식이 확률변수에 대한 양함수(explicit function) 형태가 아닌 음함수(implicit function) 형태로 주어지는 경우에는 식 (9)를 적용하기 어렵고, 따라서 이러한 음함수를 양함수로 근사시켜야 한다. 이 연구에서도 해상풍력터빈에 대하여 지반-말뚝 상호작용을 고려한 해석 프로그램을 사용하였기 때문에, 양함수 형태의 한계상태식을 구하기 위하여 응답면 기법(RSM, Response Surface Method)을 적용하였다(Schueller et al., 1987, Khuri and Cornell 1987). RSM은 적은 횟수의 해석결과를 이용하여 한계상태식을 확률변수에 대한 다항식으로 근사한 후, 이 다항식에 대하여 AFOSM을 적용하여 파괴확률을 산정하는 방법이다. 이러한 응답면 기법에는 Fig. 2에서와 같이 중심합성계획법(CCD, Central Composite Design), Bucher-Bourgund(BB) 방법(Bucher and Bourgund, 1990) 등이 있으며 이 연구에서는 BB 방법을 적용하였다. Fig. 3은 이 연구에서 사용한 응답면 기법을 적용한 AFOSM의 흐름도이다.
3. 예제해석
3.1 해석모델 제원
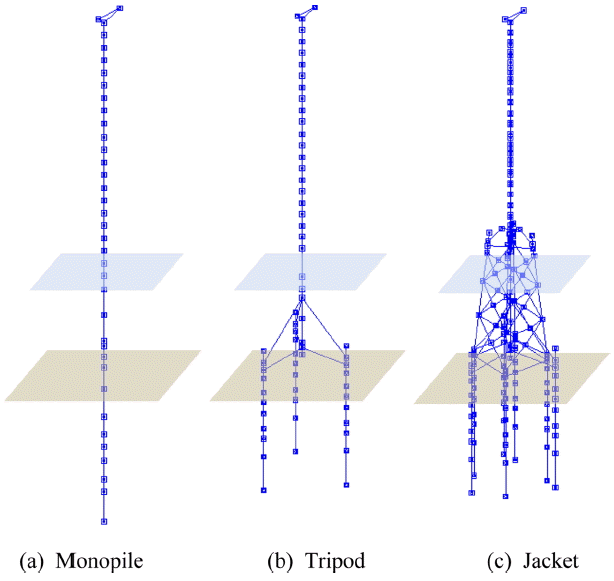
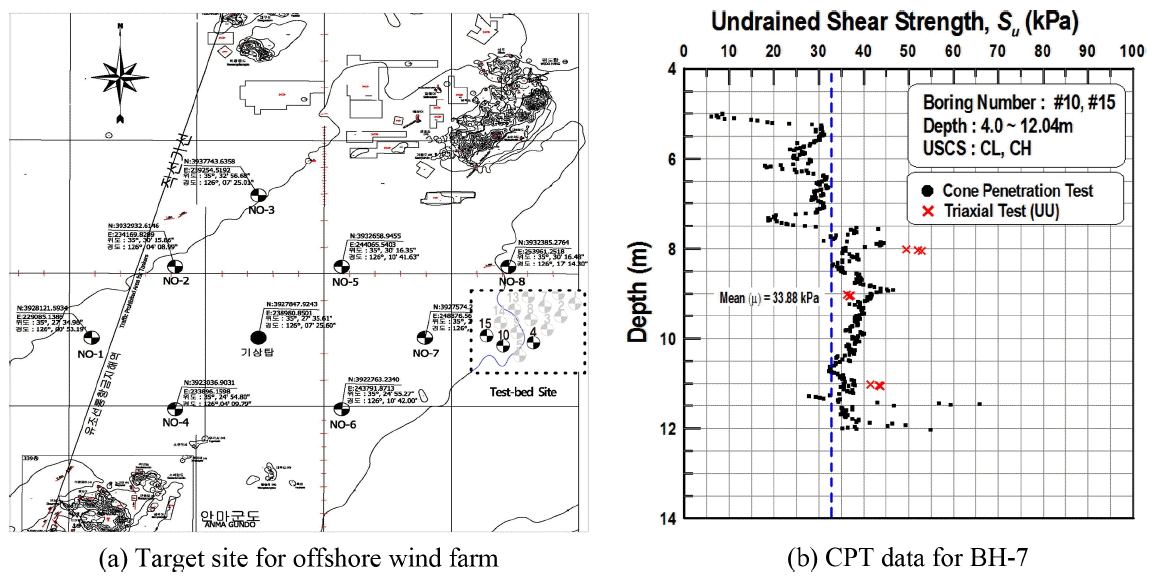
풍력터빈의 타워와 RNA(Rotor Nacelle Assembly) 등은 NREL 5MW 풍력터빈(Jonkman et al., 2009)의 제원을 이용하였다. 설치수심은 모노파일과 트라이포트, 재킷 등의 기초 형식이 서로 경쟁할 수 있는 범위를 고려하여 30 m로 설정하였고, 지반 조건은 2.5GW 해상풍력단지 개발과 관련하여 서남해 해상에서 최근 수행한 바 있는 콘관입시험(CPT, Cone Penetration Test) 결과를 이용하여 산정된 값을 해석에 이용하였다(KOPEC, 2013). 한편 모노파일, 트라이포드, 재킷 등의 기초 구조물 제원은 서남해안 2.5GW 실증사업을 위하여 제시된 조건을 만족하도록 설계된 결과를 이용하였다. 상세 제원은 Fig. 4 및 Table 1에서 제시된 값과 같다. 그리고 수치해석의 단순화를 위하여 블레이드와 허브의 질량은 모두 허브의 질량중심에 그리고 나셀은 나셀의 질량중심에 집중질량으로 모델링하였다. 해수의 영향은 부가질량(added mass)으 로 계산하여 해당 절점에 질량을 추가하여 고려하였다. 한편 플랫폼의 높이를 보면, 모노파일, 트라이포드, 재킷 등의 지지구조물에 따라 그 높이가 각각 15.4 m, 16.0 m, 25.5 m로 재킷의 플랫폼 높이, 즉 TP 높이가 가장 높다. 한편 지반으로 관입되는 말뚝의 제원을 보면 직경과 두께가 모노파일 5.7 m, 70 mm, 트라이포드 2.5 m, 40 mm, 재킷 1.45 m, 40 mm로 모노파일을 제외하면 트라이포드와 재킷의 경우는 대용량 저소음 항타장비 또는 대구경 천공장비 등 대구경 모노파일 시공에 필요한 장비의 도입 없이 기존의 일반적인 시공 장비로도 충분히 시공이 가능함을 알 수 있다. 한편 말뚝관입깊이는 모노파일의 경우만 해저면에서 30 m까지 관입하고, 트라이포드와 재킷은 40 m까지 관입하는 것으로 설계하였다. 세굴깊이는 DNV 기준(DNV 2004) 및 기존 문헌(Van Der Tempel, 2004)을 고려하여 모노파일의 경우 직경이 크기 때문에 직경의 1.5배까지, 그리고 트라이포드와 재킷은 2배까지 고려하였다. 세굴에 대한 수치 모델링과 관련하여 세굴깊이까지의 비선형 지반 스프링을 제거함과 동시에 상재하중의 변화로 발생하는 비선형 지반 스프링의 특성을 고려하여 세굴을 고려한 해석을 수행하였다.
3.2 지반물성치의 불확실성
대상해역에서 실시한 콘관입시험과 비교란 시료를 채취하여 실내에서 수행한 일축·삼축압축시험 결과 등을 토대로 산정한 심도별 지층의 통계적 지반물성치를 Fig. 5와 Table 2에서 정리하였다. 현재까지 공개되어 있는 대상해역의 지반조사 자료를 바탕으로 구한 변동계수(COV, Coefficient Of Variation) 값을 보면 단위중량(γ)에 대해서는 10%, 점착력과 비배수전단강도(c, Su)는 22.5%, 내부마찰각(φ)에 대해서는 6.3% 수준으로, 일반적인 지반물성치의 변동성 범위를 고려 시 c와 Su의 변동성은 비교적 낮은 수준이고, φ의 불확실성은 평균 수준으로 평가되었다 (KOPEC, 2013; Yoon et al., 2014).
3.3 수치해석결과
사용한계상태에 대한 신뢰성 해석을 위하여 지반물성치의 불확실성과 함께 하중의 불확실성을 함께 고려하여 Matlab으로 작성된 In-House Code를 이용하여 수치해석을 수행하였다. 하중의 경우 풍력터빈이 운영 중 발생하는 추력을 비롯하여 타워가 받는 풍하중, 하부구조물에 작용하는 파력, 조류력 등 다양한 외력이 존재하지만 이 연구에서는 추력에 대한 특성만을 고려하여 신뢰성 해석을 수행하였다. NREL 5MW 풍력터빈 제원을 이용하여 연성해석 프로그램인 FAST를 이용하여 추력이 가장 크게 발생하는 정격풍속 12 m/s에 대한 해석을 수행하였으며 이를 통하여 추력의 통계적 분포는 평균 918 kN, 그리고 분산계수가 0.1임을 알 수 있었다(Hyein E&C Co., 2015). 그러나 이 값은 동일한 제원의 육상풍력터빈에 대하여 구한 값으로 추력의 경우 하부구조물이 각각 다른 형태인 해상풍력터빈에 적용할 경우 이러한 풍력터빈의 동특성 변화에 따라 추력도 어느 정도 영향을 받을 수 있지만 이 연구에서는 이러한 영향은 무시하였다. 그러나 엄밀한 해석을 위해서는 해상풍력터빈에 대하여 추력을 구하고 이를 이용하여 신뢰성 해석을 수행하는 것이 필요할 것이라 판단된다.
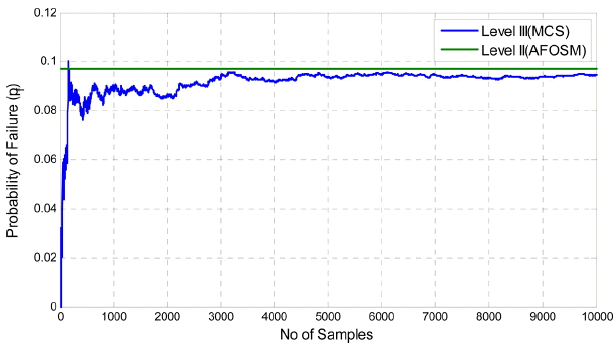
응답면 기법 및 AFOSM을 적용하여 신뢰도 지수를 구하는 절차에 대한 검증 및 Level III MCS 방법과의 계산시간 비교 등을 위하여 신뢰도 지수가 가장 작을 것으로 예상되는 경우, 즉 모노파일로 지지되는 해상풍력터빈에 세굴이 직경의 1.5배까지 발생한 경우에 대하여 MCS 결과와 비교하였다(Fig. 6 및 Table 3). Level II AFOSM 방법으로 구한 파괴확률(0.097328)은 Level III MCS에 의한 결과(0.094400)보다 3.1% 크게 분석되었으며, 신뢰도 지수는 1.2969로 MCS에 의한 결과(1.3141)보다 1.3% 작게 분석되어 공학적으로 허용가능한 수준의 차이임을 알 수 있다. 한편 계산시간과 관련된 실행횟수의 경우 Level II AFOSM 방법의 경우 총 57회의 실행만으로 충분한 결과를 얻을 수 있음을 알 수 있다. 다만 그림에서 알 수 있듯이 샘플의 수가 3,000번 이상인 경우 파괴확률이 어느 정도 일정하게 유지됨을 알 수 있다. 그러나 이 경우는 파괴확률이 가장 클 것으로 예상되는 경우이며, 신뢰도 지수가 3 이상인 경우 파괴확률이 0.0013 미만이므로 이러한 경우에는 파괴확률 역수의 10배~100배의 샘플을 사용한다고 할 때 총 7,000~70,000개의 샘플이 필요함을 알 수 있다. 한편 아래의 MCS로 구한 파괴확률의 경향을 보면 파괴확률인 0.0944에 대한 역수의 100배(1,059개)를 취하더라도 상당한 차이가 있음을 알 수 있다.
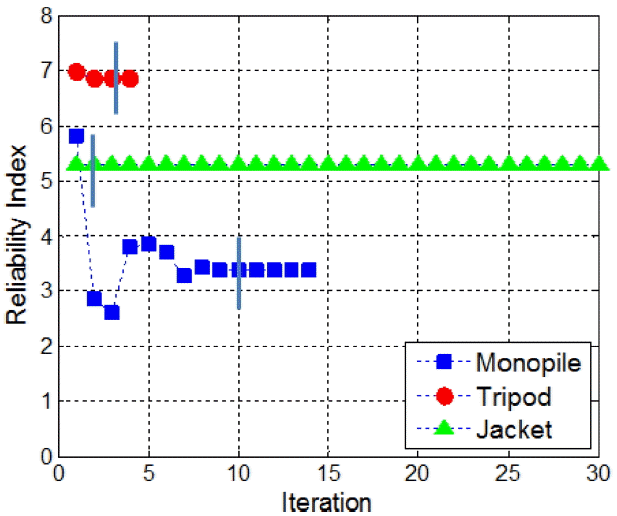
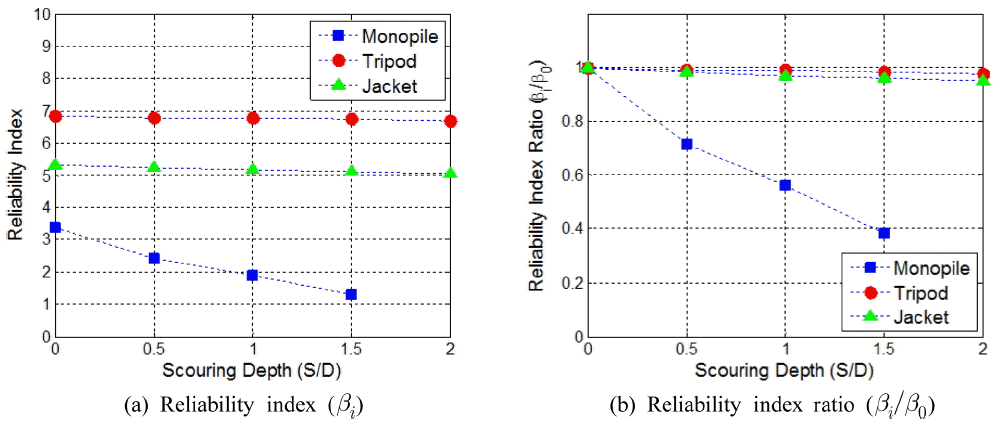
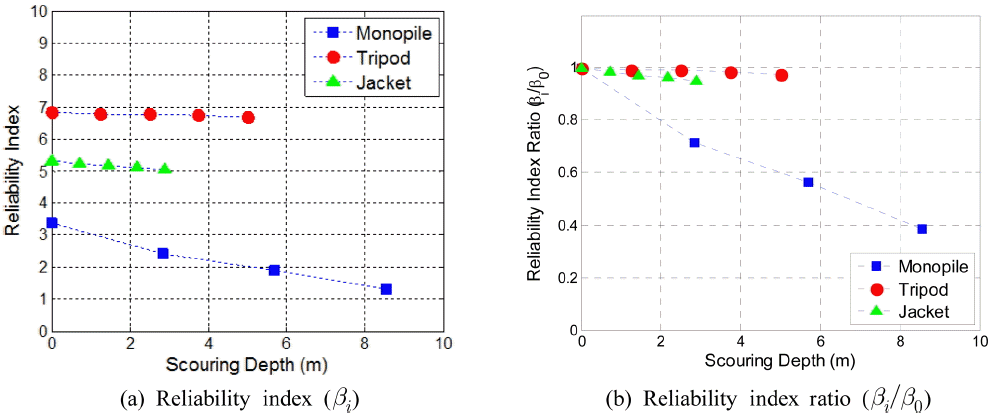
Fig. 7은 세굴이 없는 경우 모노파일, 트라이포드, 재킷으로 지지되는 풍력터빈의 신뢰도 지수를 응답면 기법 및 AFOSM을 이용하여 구하는 과정을 제시한 것이다. i번째 단계에서의 신뢰도 지수를 βi 라고 할 때, 수렴 여부는 Δβi = βi-βi-1 < βtolerant로 판단하였고, 수렴조건을 βtolerant = 0.001로적용한결과로수렴 조건을 βtolerant = 0.01로 증가시키는 경우의 종료 지점을 별도로 표기하였다. 모노파일의 경우 βtolerant = 0.01로 할 경우, 10회의 반복계산으로, 트라이포드와 재킷의 경우 각각 3회와 2회의 반복계산만으로도 충분한 결과를 얻을 수 있음을 알 수 있다. 모노파일의 반복횟수가 더 큰 것은 모노파일의 경우 지반 비선형성이 더 크게 작용하였기 때문으로 이해할 수 있다. Fig. 8은 모노파일을 비롯하여 트라이포드 및 재킷으로 지지되는 풍력터빈에 대하여 말뚝 직경 대비 상대적인 세굴깊이를 고려하여 구한 신뢰도 지수 및 신뢰도 지수의 변화를 정리한 결과를 보여주고 있다. 이 결과를 보면 트라이포드와 재킷으로 지지되는 풍력터빈의 경우 세굴깊이에 따라 신뢰도 지수가 크게 영향을 받지 않는 반면 모노파일로 지지되는 풍력터빈의 경우 세굴깊이가 증가함에 따라 신뢰도 지수가 3에서 1까지 크게 감소되는 것을 알 수 있다. 한편 Fig. 9는 절대적인 세굴깊이에 따른 신뢰도 지수 및 지수의 변화를 정리한 것으로 동일한 세굴깊이에 대해서도 모노파일의 신뢰도 지수 변화가 가장 큰 것을 알 수 있다. 예들 들어 세굴깊이가 대략 3 m 내외인 경우 모노파일형 OWT의 경우 신뢰도 지수가 30% 감소하는 반면, 트라이포드와 재킷형 OWT는 각각 2%, 5% 내외의 감소를 보인다. 이는 상대적인 세굴깊이에 대한 신뢰도 지수의 변화뿐만 아니라 절대적인 세굴깊이에 대해서도 모노파일형 OWT의 신뢰도 지수가 가장 큰 영향을 받는 것을 의미한다.
한편, Fig. 8과 Fig. 9를 보면 세굴을 고려하지 않은 경우에 대해서 모노파일형 OWT의 신뢰도 지수가 가장 작게 평가되고 있음을 알 수 있는데, 이와 관련하여 세 가지 서로 다른 지지구조물을 채택한 OWT에 대하여 세굴을 고려하지 않았을 경우의 고유주파수를 비교하였다. 고유진동수 분석을 위해서는 전술한 바와 같이 해수의 영향을 고려하여 부가질량을 추가적으로 모델링하였으며, 지반의 비선형성을 고려하기 위하여 10 kN의 수평하중이 작용할 때의 등가지반강성(equivalent soil stiffness)을 이용하였다. 모노파일, 트라이포드, 재킷형 OWT에 대하여 각각의 고유주파수는 0.2480 Hz, 0.2690 Hz, 그리고 0.3256 Hz로 분석되었다. 모노파일형 OWT의 고유주파수가 가장 작고, 재킷형 OWT의 고유주파수가 가장 크게 나왔는데, 사용한계상태를 타워 상부의 수평변위로 고려한 신뢰성 해석에서와 달리 고유주파수 분석에서는 질량의 영향까지 고려되었기 때문에 신뢰도 지수와의 경향과는 다른 결과를 얻을 수 있음을 알 수 있다. 즉 구조물의 강성 자체는 트라이포드형 OWT가 가장 크지만, 트라이포드형 OWT는 상대적으로 질량이 크기 때문에 재킷형 OWT 보다 고유주파수가 작게 분석되었음을 알 수 있다.
본 연구에서는 동일한 수심 30 m에 대하여 서로 다른 지지구조형식을 적용한 결과를 비교하였지만, 실제 25 m 내의 천해에서는 모노파일이, 30-50m 범위의 중수심에서는 트라이포드나 재킷이 경제성이 높은 지지구조형식으로 알려져 있으며, 25-30 m 범위의 수심에서는 장비 등 다른 여건을 고려하여 최적의 지지구조형식을 정해야 하는 것으로 알려져 있다. 동일한 수심에 대하여 비교한 본 연구에서는 모노파일의 고유주파수가 가장 낮고, 트라이포드와 재킷형 OWT의 고유주파수가 높고, 강성 또는 트라이포드와 재킷형 OWT가 커 신뢰도 지수에서도 이러한 영향이 반영되고 있음을 알 수 있다.
Level II 신뢰성 해석을 수행하는 과정에서 구할 수 있는 민감도 행렬(sensitivity matrix), 즉 MPFP 점에서의 신뢰도 지수를 확률변수로 편미분한 값은 어떠한 확률변수가 신뢰도 지수에 영향을 어느 정도 미치는지를 분석하는데 중요한 정보를 제공한다. 민감도가 큰 확률변수는 신뢰도 지수에 크게 영향을 주는 반면 민감도가 작은 확률변수는 신뢰도 지수에 영향을 크게 주지 않기 때문에 상대적으로 중요도가 작다고 할 수 있다. Table 5에서는 모노파일, 트라이포드, 재킷으로 지지되는 해상풍력터빈에 대하여 세굴깊이에 따른 9개 확률변수(Table 4 참조)의 민감도를 정리한 것이다. 이 결과로부터 트라이포드와 재킷으로 지지되는 해상풍력터빈의 경우 9번째 확률변수, 즉 추력에 대한 민감도가 가장 크고 다른 확률변수의 경우 민감도가 매우 작은 반면, 모노파일로 지지되는 해상풍력터빈의 경우 7번째와 8번째 확률변수, 즉 사질토층의 내부마찰각과 점토층의 비배수전단강도, 추력에 대한 민감도가 상대적으로 높음을 알 수 있다. 또한 세굴이 증가할수록 추력에 대한 민감도와 내부마찰각의 민감도는 감소하는 반면, 네 번째 점토층의 비배수전단강도에 대한 민감도는 증가하는 것을 알 수 있다. 이러한 민감도를 통하여 세굴깊이가 증가함에 따라 모노파일로 지지되는 해상풍력터빈의 신뢰도 지수가 크게 감소하는 원인을 이해하는데 도움을 받을 수 있음을 알 수 있다. 즉 트라이포드와 재킷으로 지지되는 해상풍력터빈의 경우 지반물성치가 신뢰도 지수에 미치는 영향이 작고 따라서 세굴깊이가 증가하더라도 신뢰도 지수가 크게 감소하지 않지만 모노파일로 지지되는 해상풍력터빈의 경우 지반물성치의 영향을 크게 받기 때문에 세굴에 의하여 지반의 지지력이 감소하게 되면 신뢰도 지수가 크게 감소하게 된다.
4. 결 론
NREL 5MW 풍력터빈 제원을 이용한 수치해석을 통하여 모노파일, 트라이포드, 그리고 재킷으로 지지되는 해상풍력터빈에 대한 신뢰성 해석을 수행하였다. 이 연구에서는 여러 한계 상태 중 사용한계상태를 대상으로 하여 너셀 위치에서의 수평 변위 및 허용수평변위를 이용하여 한계상태함수를 정의하였으며, 신뢰성 해석에서는 지반물성치 및 추력에 포함되어 있는 불확실성을 고려하여 지반의 단위중량 및 비배수전단강도 그리고 내부마찰각과 같은 지반물성치와 추력을 확률변수로 고려하였고, 세굴깊이에 따른 신뢰도 지수와 함께 민감도 행렬을 분석하였다. 이 연구를 통하여 다음과 같은 결론을 도출하였다.
(1) 트라이포드와 재킷기초의 해상풍력터빈은 신뢰도 지수에 대한 세굴깊이의 영향은 크지 않았으나 모노파일로 지지되는 해상풍력터빈의 경우 세굴깊이가 증가함에 따라 신뢰도 지수가 크게 감소하였다.
(2) 트라이포드와 재킷 기초의 해상풍력터빈은 지반물성치에 대한 민감도가 작고 지반물성치에 포함되어 있는 불확실성의 크기가 신뢰도 지수에 미치는 영향이 매우 작았다. 따라서 초기설계단계에 지반물성치를 정확하게 모르거나 충분하지 않아 지반-말뚝 상호작용을 고려하기 어려울 경우에도 트라이포드와 재킷으로 지지되는 해상풍력터빈에 대해서는 비교적 정확한 신뢰성 해석이 가능할 것으로 사료된다.
(3) 모노파일로 지지되는 해상풍력터빈의 경우 신뢰도 지수에 미치는 지반물성치의 영향이 상대적으로 큰 것을 알 수 있었다. 특히 단위중량보다는 비배수전단강도와 내부마찰각이 큰 영향을 주었으며 따라서 모노파일로 지지되는 해상풍력터빈에 대하여 높은 신뢰도 지수를 가지기 위해서는 지반물성치에 대한 분산계수를 줄일 수 있도록 정밀한 현장지반 조사가 필요하리라 사료된다.
(4) 트라이포드와 재킷으로 지지되는 해상풍력터빈의 경우 상대적으로 세굴에 대하여 강건한 장점이 있음을 알 수 있다. 하부구조물 형식은 설치 수심이나 가용한 장비 등을 고려하여 최적 형식을 결정할 수 있으나 수심이 20-30 m인 중수심의 경우, 해상지반 조건이 우리나라 서해안처럼 세굴 발생이 우려되는 경우에는 이와 같은 세굴에 대한 강건성(robustness) 역시 하부구조물의 최적 형식을 결정하기 위한 기준으로 사용될 수 있을 것으로 사료된다.
(5) 본 연구에서는 타워 상부에서의 수평변위를 사용한 사용한계상태만을 대상으로 하였기 때문에 지반물성치의 불확실성 및 세굴에 의한 영향이 모노파일로 지지된 해상풍력터빈의 신뢰도 지수에 대하여 큰 영향을 준 것으로 분석되었으나, 추후 응력 등을 이용한 한계상태함수를 적용한 신뢰성 해석을 수행하여 그 결과를 분석할 필요가 있다. 또한 이 연구에서는 지반물성치의 확률분포를 정규분포함수로 가정하였는데, 대수정규분포 등 다른 확률분포를 가지는 경우에 대한 신뢰성 해석도 수행할 필요가 있을 것으로 사료된다.