1. 서론
모든 항만 구조물은 사용 시간이 진행됨에 따라 피해가 발생한다. 구조물을 구성하는 주요 성분들의 재질적 내구성 감소에 따라 피해가 발생하기도 하고, 임의 크기의 하중이 갑작스럽게 발생하여 순간적인 피해를 일으키기도 한다. 성능 감소는 해당 구조물의 사용성이나 안정성에 중대한 영향을 미치게 된다. 따라서 구조물을 최적으로 유지관리 하는 것이 필요하다. 특히 항만 구조물의 경우 파괴에 따른 사회적 영향 정도가 다른 시스템 보다 크기 때문에 장래의 환경 변화에 따라 구조물을 올바르게 유지관리하는 것이 필요하다. BS3811(1984)에 의하면 유지관리(maintenance)란 해당 시설물이 요구되는 기능을 올바로 수행할 수 있는 상태를 유지하거나 복구하는 기술적·행정적 관련 행위들이라 정의하고 있다.
일반적으로 유지관리는 CM(Corrective Maintenance)과 PM(Preventive Maintenance)으로 구분된다(Wang, 2002). 전자를 사후 보전형이라 하고 임의의 시스템이 파괴되면 복구 행위에 의해 해당 시스템을 원래 상태로 되돌리는 것이고, 후자는 파괴되기 전에 예방적으로 시스템이 그 기능을 유지하도록 관리하는 것이다. 토목 구조물과 같이 파괴에 따른 피해가 큰 경우에는 CM 보다는 PM이 적용되어야 한다. 따라서 파괴되기 전에 언제 PM이 수행되어야 가장 경제적인지를 결정해야 한다. 이는 유지관리와 관련하여 필요로 하는 비용에 대한 경제성 분석을 통하여만 가능하다. 현재까지 제시된 경제성 해석 모형은 다음과 같은 세 가지로 구분할 수 있다. 하나는 구조물의 재령을 기반으로 하는 ABM 모형(Age-Based Maintenance)이고 다른 하나는 순수하게 누적피해만을 기반으로 하는 DBM 모형(Damage-Based Maintenance)이다. 마지막이 이 둘을 동시에 고려하는 CBM 모형(Condition-Based Maintenance)이다. ABM은 하중 내습에 따른 구조물의 누적피해에 대한 모니터링 없이 미리 정해진 일정 시간 간격으로 유지관리를 실시하는 방법으로 우리나라 시설물의 안전관리에 관한 특별법(시특법)에서 사용하는 개념이다. 따라서 이 방법은 누적피해가 사용한계에 도달하지 않아도 일정 시간이 경과하면 무조건 보수보강을 실시하는 개념이다. 그와 반대로 DBM은 순수하게 피해에 대한 모니터링에 의존하여 누적피해가 정해진 사용한계를 초과할 때만 보수보강을 실시하는 개념이다. 따라서 DBM은 누적피해의 정확한 모니터링과 예측에 전적으로 의존한다. 이를 위해서는 하중 내습시마다 점검을 실시하여 하중과 피해의 관계를 기록하는 RM(Regular Maintenance)이 필요하다. 한편 CBM은 DBM과 같이 누적피해가 정해진 사용한계나 파괴한계를 초과하던지 아니면 ABM에서 미리 정해진 유지관리 기간에 도달하던지 어느 것이나 먼저 발생하는 것에 따라 보수보강을 실시하는 개념이다. 따라서 CBM을 적용하기 위해서는 구조물의 누적피해과정(stochastic-cumulative damage process)과 하중발생과정(shock occurrence process)에 대한 추계학적 해석이 필요하다. 너무 자주 유지관리를 수행하면 관련 비용이 증가하고 그 반대의 경우는 예기치 못한 파괴로 인해 피해비용이 커질 수 있다. 따라서 올바른 시점에 비용과 성능이 균형된 최적화된 기준으로 어느 정도의 보수보강이 이루어져야 하는지를 결정해야 한다.
최근 Deloux et al.(2009), Dovan and Berenguer(2010), Niu et al.(2010), Tinga(2010), Weide et al.(2010), Zhaoet al.(2010), Zhao and Nakagawa(2010), Bouvard et al.(2011), Fouladirad and Grall(2011), Ito and Nakagawa(2011), Tian and Liao(2011), Weide and Pandey(2011), Chien et al.(2012), 그리고 Lee(2013a) 등이 CBM에 대한 연구를 수행하였다. 이상의 연구들은 하중발생 과정과 추계학적 누적피해과정을 어떻게 고려하느냐에 따라 구분된다. 하중발생 과정은 Kahle and Wendt(2004), Lee(2013a)에 자세히 언급되었듯이 HPP(Homogeneous Poisson Process), NHPP(Non-Homogeneous Poisson Process), MPP(Mixed Poisson Process) 그리고 DSPP(Doubly Stochastic Poisson Process)로 구분된다. 한편 구조물의 추계학적 누적피해과정에 대한 예측기법은 선형피해모형(additive damage model)과 비선형피해모형으로 구분되고, 비선형피해모형은 다시 포화피해모형(saturated damage model)과 가속피해모형(accelerated damage model)으로 구분된다(Weide et al., 2010). 앞에서 언급된 대부분의 연구자들은 HPP와 선형피해모형을 이용하여 여러 문제들을 해석하였다. Weide et al.(2010)은 NHPP와 선형피해모형을, Weide and Pandey(2011)는 HPP와 비선형피해모형을 해석하였다. 특히 Zhao and Nakagawa(2010), Ito and Nakagawa(2011), Chien et al.(2012) 등은 하중발생 과정을 이산시간 확률과정으로 고려하여 해석하였다. 연속적인 시간에 따른 하중발생 과정을 일정한 시간 간격으로 이산화하여 구조물의 누적피해를 예측하는 개념이다. 그러나 이들 모형에서는 유지관리와 관련된 각종 비용에 대한 시간의 가치를 고려하지는 못했을 뿐만 아니라 선형피해모형을 사용하여 추계학적 누적피해의 비선형성을 고려하지 못했다. 또한 이상의 대부분의 연구들은 소규모 기계적 부품 장치들에 대한 해석 아니면 이론 개발에 대한 것이다. 비록 Lee(2012), Lee(2013b), Lee et al.(2013) 등이 경사제 피복재에 대한 다중하중발생과 누적피해의 관계를 확률론적으로 해석하였지만 CBM을 적용하지는 않았다. Lee(2013a)와 Lee and Kim(2013)이 처음으로 ABM을 경사제 피복재에 적용하였지만 비용의 시간에 따른 가치를 고려하지 못하였다.
따라서 이와 같은 문제를 해결하기 위하여 본 연구에서 경사제 피복재 등 임의의 항만 구조물에 적합한 유지관리모형을 개발하고자 한다. 경사제 피복재의 누적피해를 이산시간 확률과정으로 고려하여 유도된 CBM의 할인비용모형은 유지관리와 관련된 각종 비용에 대한 시간의 가치를 고려할 수 있다. 또한 선형의 피해율 대신 비선형 피해강도함수를 도입하여 구조물의 추계학적 누적피해의 비선형성도 해석할 수 있다. 특히 피해강도함수에 포함된 관련 변수들을 산정하기 위하여 표본경로기법을 사용하였다. 먼저 제 2절에 이산시간 확률과정속에서 이자율을 고려하여 기대비용을 산정할 수 있는 수학적 모형을 유도하였다. 제 3절에서는 본 연구에서 개발된 모형을 검증하고 민감도 분석을 수행하였다. 제 4절에서는 표본경로기법을 이용하여 개발된 추계학적 기대비용모형을 경사제 피복재에 적용하였다. 마지막으로 제 5절에 결론을 언급하였다.
2. 조건기반 유지관리의 기대비용모형
임의의 항만 구조물이 그 기능을 시작하고 첫 번째 태풍, 하중이 내습하여 해당 구조물에 Y1의 피해를 유발한다고 생각할 수 있다. 계속하여 두 번째 하중에 의하여 Y2의 피해가 발생하면 그 시간 t까지 발생한 구조물의 누적피해, Z(t)=Y1+ Y2가 된다. 따라서 t시간 동안 N(t)개의 하중이 내습한 구조물의 누적피해를 다음 식(1)과 같이 정의할 수 있다.
식(1)은 t시간 동안 몇 개의 하중이 발생하고 각각의 하중에 의하여 어떤 피해가 발생하는지를 추계학적으로 해석하기 위하여 수립된 식이다. 시간에 따른 하중발생이 포아송 확률과정에 의하여 불규칙하게 발생하고, 피해의 크기가 독립이고 동일한 임의의 확률분포를 따르는 확률변수라고 하면 식(1)을 연속시간 확률과정 중 하나인 CPP(Compound Poisson Process)라 한다. 따라서 두 개의 확률과정을 해석해야 한다. 그러나 만약 하중이 일정한 시간 간격으로 발생한다고 가정할 수 있다면 순간피해 Yi에 대한 확률분포만을 이용하여 상대적으로 간단히 해석할 수 있다. 이와 같은 접근방법을 이산시간 확률과정이라 하며 아래 수학적 모형 수립에 이용되었다.
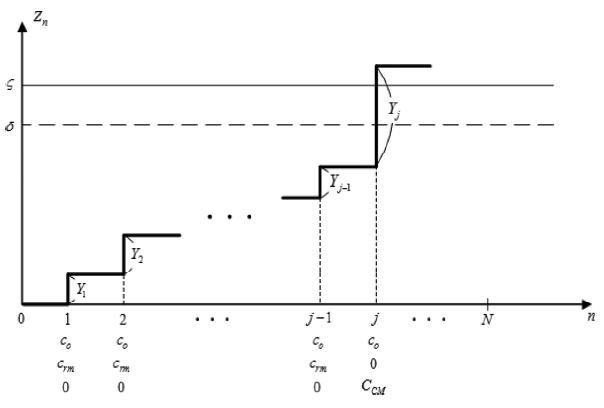
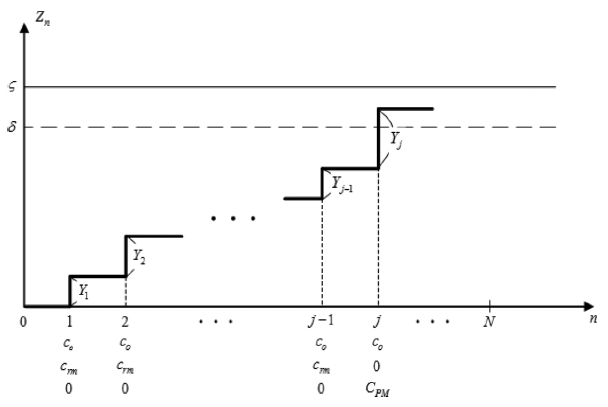
전절에서 언급한 CBM 개념에 따라 최적의 PM 시기를 결정하기 위한 기대비용모형을 수립하기 위해서는 Fig. 1~Fig.3과 같이 각 하중에서 발생하는 누적피해의 크기에 따라 수행되는 유지관리의 모든 정책을 고려해야 한다. j번째 하중에서의 누적피해를 Z j = ∑ i = 1 j Y i
먼저 Fig. 1은 Zj≥ζ, j≤N 이기 때문에 CM을 통해 파괴된 구조물이 완전 보수보강된다고 가정한 경우이다. 이 경우 소요되는 기대비용, E(C1)은 다음 식(2)와 같이 유도할 수 있다.
여기서 P j C M = P ( Z j - 1 < δ < ζ ≤ Z j ) ∑ i = 1 0 ( · ) ≡ 0
유사하게 Fig. 2는 δ ≤ Zj< ζ, j ≤ N 이기 때문에 파괴되지는 않았지만 사용한계 이상의 누적피해에 의해 성능이 감소된 구조물을 PM을 통해 완전 보수보강하는 경우이다. 이때 소요되는 기대비용 E(C2)는 다음 식(3)과 같이 유도된다.
여기서 P j P M = P ( Z j - 1 < δ ≤ Z j ≤ ζ )
마지막으로 Fig. 3은 ZN< δ < ζ인 마지막 경우로 하중 발생 개수가 임의의 N 일 때 PM을 수행하여 그 때까지의 누적피해에 의해 성능이 감소된 구조물을 완전 보수보강하는 경우이다. 따라서 기대비용 E(C3)는 다음 식(4)와 같이 유도된다.
위의 식에서 쉽게 알 수 있듯이 기대총비용을 산정하기 위해서는 먼저 각각의 식에 포함된 확률, P j C M P j P M P j C M P j P M
한편 유지관리의 경제성 분석에서는 이상에서 유도된 기대총비용을 직접 사용하지 않고 두 개의 완전보수보강이 이루어지는 시간간격(renewal cycle: RC)의 기대치로 나눈 단위 시간당 기대총비용의 개념이 사용된다(Ross, 1980; Lee, 2013a). 두 개의 완전보수보강이 이루어지는 시간간격의 기대치는 식(6)을 이용하여 다음 식(7)과 같이 간단히 정의할 수 있다.
식(7)은 임의로 설정한 N개의 하중이 발생하면 무조건 PM이 수행된다는 정책에 기반하여 유도된 식으로, 우변의 첫 항이 N개의 하중이 발생하는 동안 CM이 이루어질 기대시간, 두 번째 항이 PM이 이루어질 기대시간 그리고 마지막 항이 N번째에서 PM이 수행될 기대시간이다.
따라서 식(2)와 (3) 그리고 식(4)를 모두 더한 기대총비용 E(C)를 식(7)로 나누면 단위 시간당 기대총비용, 기대총비용율(expected total cost rate) CR(δ, ζ, N, r)을 다음 식(8)과 같이 정의할 수 있다.
식(8)은 비용의 시간에 따른 가치변화를 고려하여 본 연구에서 유도된 식이다. Chien et al.(2012)은 동일한 방법으로 모형을 제시하였으나 비용의 시간에 따른 가치변화를 고려하지 않았다. 따라서 식(8)에서 r = 0.0이라 하면 두 결과는 정확히 일치해야 한다. 식(8)에 r = 0.0이라는 조건을 부여하고 식(6)을 대입하여 복잡한 수학적 과정을 거쳐 간단히 정리하면 다음 식(9)를 얻을 수 있다.
여기서 G ( y ) = 1 - G ( y )
특히 본 연구에서 유도한 식(8)의 CBM은 ABM과 DBM을 모두 포함한다. 만약 N→∞라고 가정하면 수학적으로는 P(∞ < δ) = 0.0이 되고, 이는 식(4)의 기대비용을 고려하지 않는다는 의미이기 때문에 식(8)은 DBM이 된다. 무수히 많은 하중이 내습하여 발생한 각각의 순간피해를 더한 누적피해가 사용한계를 넘지 않으면 아무런 보수보강을 실시하지 않는다는 개념이다. 또한 사용한계 δ를 파괴한계 ζ로 보내면 P j P M = P j ( Z j - 1 < δ = ζ ≤ Z j < ζ ) = 0 . 0
이상에서 살펴본 바와 같이 식(8)을 이용하여 기대총비용율을 산정하기 위해서는 각각의 하중 내습에 따른 순간피해의 분포함수 G(y)를 올바르게 정의하여야 한다. 지금까지 수행된 대부분의 CBM 연구에서는 편의상 피해율이 1/λ로 일정하다는 가정하에 개별 하중에 의한 피해 분포함수로 지수분포, G(y)=1− e −y/λ를 사용하였다. 이는 선형피해모형을 적용한다는 제약성을 내포하는 것이다. 그러나 경사제 피복재와 같이 많은 실제 구조물의 누적피해과정은 비선형이다. 따라서 본 연구에서는 이와 같은 비선형성을 고려하기 위하여 피해율이 아닌 Weide and Pandey(2011)가 제시한 피해강도 함수를 사용하였다.
식(1)에서 N(t)=t/Δt라고 생각하면, Δt는 하중 발생간격이다. 따라서 시간의 진행에 따라 임의의 구조물에 다중하중이 작용하여 발생되는 기대 누적피해 E[Z(t)]는 식(1)에 의하여 다음 식(11)과 같이 정의할 수 있다.
여기서 P[N(t)=j]는 t시간 동안 j개의 하중이 발생할 확률로 서론에서 언급한 HPP, NHPP, MPP 그리고 DSPP를 이용하여 산정할 수 있다. 또한 E[Zj]는 j개의 하중이 내습한 구조물의 누적피해의 기대치로 다음 식(12)를 이용하여 구할 수 있다.
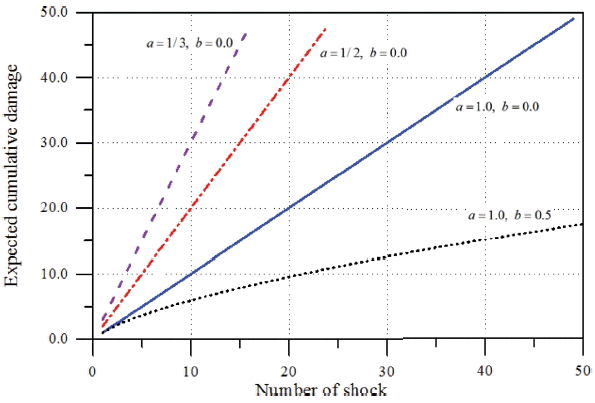
여기서 a와 b는 임의의 계수로 그 값에 따라 서론에서 언급한 누적피해 예측모형이 구분된다. 이론적으로 b =0인 경우를 선형피해모형이라 하고, b ≠0인 경우를 비선형모형이라 한다. 특히 b < 0 경우를 가속피해모형, b > 0 경우를 포화피해모형이라 한다.
따라서 식(12)를 식(11)에 대입하면 최종적으로 시간에 따른 기대 누적피해를 산정할 수 있는 다음 식(14)를 얻을 수 있다(Weide and Pandey, 2011; Lee, 2015).
3. 모형의 검증 및 민감도 분석
각기 다른 시간에 소요되는 비용의 시간 가치를 고려하기 위하여 본 연구에서 유도된 CBM의 할인비용모형 식(8)을 검증하기 위하여 두 가지 경우를 해석하였다. 하나는 이자율을 고려하지 않은 경우에 대한 결과이고 다른 하나는 이자율을 고려한 경우이다.
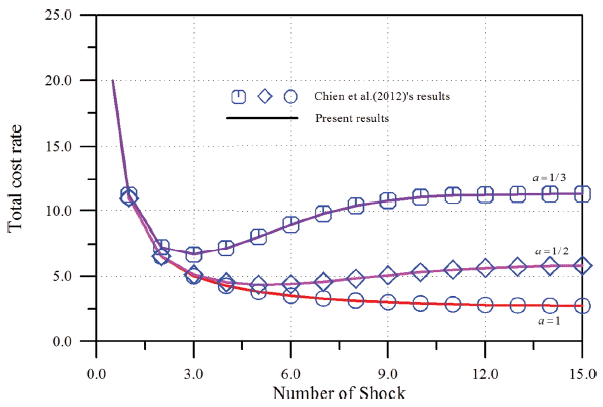
먼저 이자율을 고려하지 않은 경우의 결과는 Chien et al. (2012)의 결과와 비교하였다. 이들은 가장 단순한 선형피해에 대하여 피해율을 변화시키면서 해석하였다. 이자율을 고려하지 않았을 때 본 연구에서 유도된 식(8)이 순수하게 수학적으로 Chien et al.(2012)의 모형과 일치함을 이미 전절에서 보인 바 있지만 계산의 정확성을 위하여 비교하였다. 여러 조건 중에서 비교 대상으로 ζ = 20, δ = 16의 한계조건을 선정하였다. 또한 관련 비용으로 co= crm= 1.0와 CCM= 200, CPM= 10을 선택하였다. 선형피해에 대한 해석이고 이자율을 고려하지 않은 결과이기 때문에 본 연구에서 유도된 모형에서 r = 0.0, b = 0.0이 된다. 또한 동일한 피해강도 a = 1/3, 1/2 그리고 1.0에 대하여 해석하였다.
식(8)을 이용하여 기대총비용율을 산정하기 전에 식(14)를 이용하여 피해율 변화에 따른 누적피해의 거동 특성을 먼저 살펴보았다. 이때 하중발생 사상은 HPP와 NHPP 그리고 MPP를 모두 고려할 수 있는 다음 식(15)와 같이 정의되는 DSPP를 사용하였다(Kahle and Wendt, 2004)
여기서 ν는 하중발생의 불확실성을 고려하기 위하여 도입된 확률변수로 임의의 분포함수, fν(x)를 따른다. 또한 α와 β는 하중발생강도함수(shock occurrence intensity function), dη(t)/dt의 계수이다. 일반적으로 하중발생 사상을 해석하는 모형은 ν 가 상수인지 확률변수인지에 따라 구분된다. 먼저 ν > 0.0 상수인 경우, α ≠0.0 일 때 β = 0.0인 경우를 HPP, β ≠0.0인 경우를 NHPP라 한다. 반면 ν 가 fν(x)를 따르는 확률변수인 경우, α ≠0.0 일 때 β = 0.0인 경우를 MPP, β ≠0.0인 경우를 DSPP라 한다.
각각의 피해강도에 대하여 하중발생에 따른 기대 누적피해를 계산하여 Fig. 4에 제시하였다. 단위시간당 한 개의 하중이 발생한다고 가정하여 α = 1.0, β = 0.0와 ν = 1.0을 사용하였다. 이미 언급하였듯이 Fig. 4에서 b = 0.0인 경우가 선형피해에 대한 결과이다. 그림에서 볼 수 있듯이 단위 하중당 피해율이 1/a를 잘 만족하고 있다. 따라서 피해강도가 작을수록 기대 누적피해는 상대적으로 크게 증가하는 경향을 나타내고 있다. 비교 목적으로 비선형 피해, b = 0.5에 해당하는 포화피해에 대한 결과도 함께 제시하였다. 선형피해모형의 결과와 다르게 하중 발생개수가 증가함에 따라 증가율이 상대적으로 완만하게 증가하는 포화피해모형의 비선형성을 잘 나타내고 있다.
누적피해의 거동특성에 대한 분석을 기반으로 식(8)을 이용하여 기대총비용율을 산정하여 Fig. 5에 제시하였다. 그림서 쉽게 볼 수 있듯이 Chien et al.(2012)의 결과와 정확히 일치한다. 또한 식(10)을 만족하는 N*와 CR(δ, ζ, N*, 0)을 산정하여 Table 1에 비교하였는데 이 결과도 거의 일치하는 것을 알 수 있다. 따라서 식(8)을 이용한 수치모형이 올바르게 수립되었음을 알 수 있다.
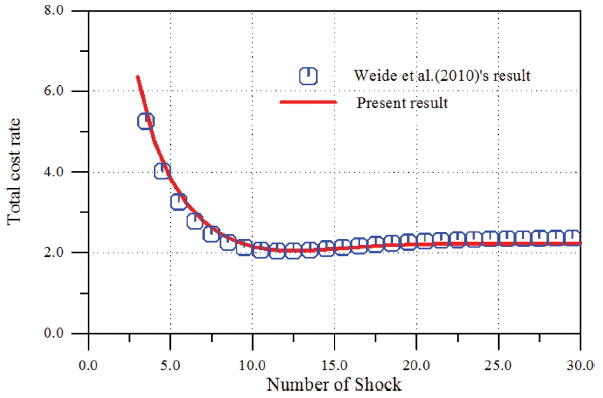
이상의 결과는 이자율을 고려하지 않았을 때의 결과이다. 따라서 각 비용의 시간에 따른 가치변화를 고려하였을 때에 대하여도 검증할 필요가 있다. Weide et al.(2010)이 가장 최근에 이자율을 고려하여 CBM의 기대비용모형을 연구하였다. 이들은 ζ = 30, δ = 28의 한계조건과 일정 피해율 2.0을 사용하였다. 이는 a = 1/2, b = 0.0에 해당하는 것이다. 또한 Weide et al.(2010)은 시간에 따른 하중발생 과정을 HPP로 가정하였으며 관련 비용도 다르게 고려하였다. 따라서 이런 조건들과 등가가 되도록 본 연구의 계산 조건을 다음과 같이 설정하였다. 먼저 단위시간당 하중이 하나 발생한다고 가정하였으며, co= crm= 0.5, CCM= 99.5, CPM= 19.5이다. 이자율도 동일하게 r = 0.05을 사용하였다. 비교 결과를 Fig. 6에 제시하였는데 두 결과가 전 구간에 대하여 비교적 잘 일치한다. 또한 최적의 N*와 CR(δ, ζ, N*, r)을 Table 2에 제시하였는데 거의 동일하다. 따라서 본 연구에서 유도된 CBM의 할인비용모형은 수학적으로나 수치적으로 만족스럽게 수립되었음을 알 수 있다.
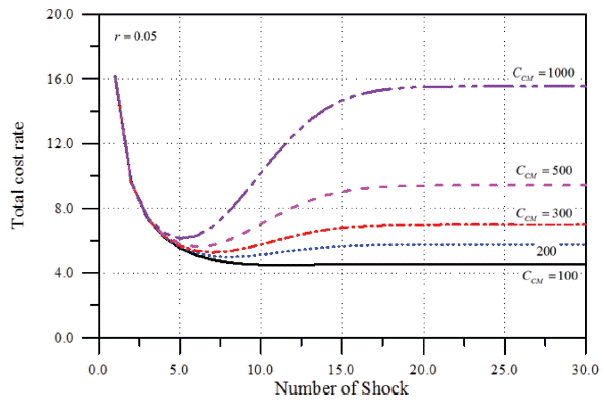
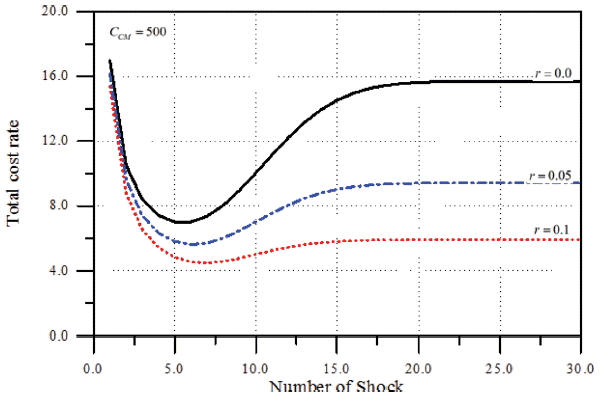
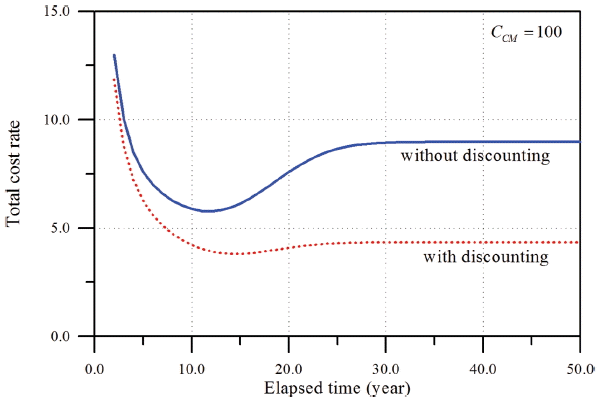
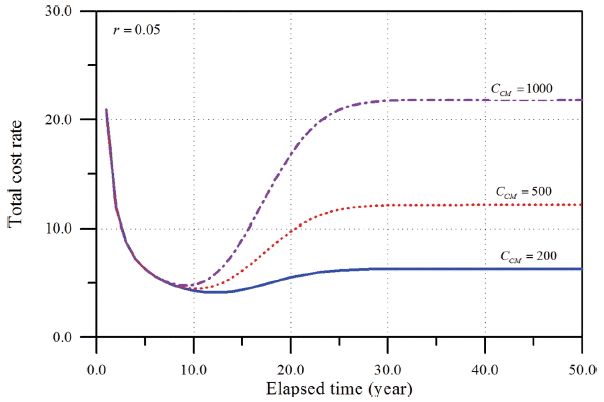
앞에서 살펴보았듯이 본 연구에서 수립된 CBM의 할인비용모형이 만족스럽게 검증되었다. 따라서 이하에서는 본 연구에서 개발된 모형을 이용하여 CCM과 r의 변화에 따른 영향을 분석하였다. CCM 이 커진다는 것은 해당 구조물의 중요도가 높다는 의미이기 때문에 구조물의 중요도에 따른 결과의 변화를 보기 위함이다. 또한 이자율을 변화시키는 것은 비용의 시간에 따른 가치가 CBM의 할인비용모형에서 어떻게 거동하는지를 평가하기 위함이다. 먼저 한계조건은 ζ = 20, δ = 18이고 비선형피해모형에 대하여 해석하였다. 따라서 피해강도함수의 계수는 a = 0.5, b = 0.1을 사용하였다. 또한 관련 비용으로 co= crm= 2.0와 CPM= 15을 가정하였다. 먼저r = 0.05인 조건에서 CCM 을 100에서 1000까지 변화시키면서 해석한 결과를 Fig. 7에 제시하였다. 그림에서 볼 수 있듯이CCM이 커지면, 즉 구조물의 중요도가 높을수록 더 자주 PM을 실시하여야 한다. 또한 최소 기대총비용율이 커지는 것을 알 수 있다. Table 3에 식(10)을 만족하는 최적의 PM 조건을 제시하였다. 한편 주어진 CCM= 500에 대하여 이자율 0.0, 0.05 그리고 0.1까지 변화시키면서 계산한 결과를 Fig. 8에 제시하였다. 결과에 의하면 이자율이 높을수록 PM 시점이 늦춰지며 비용도 감소하는 경향을 보이고 있다. Table 4에 최적의 PM 조건을 제시하였다. 이상의 중요 변수, CCM과 r의 변화에 따른 결과를 실제 문제에 비추어 보면 그 거동특성이 합리적임을 알 수 있다.
4. 경사제 피복재에 대한 적용
전절에서 살펴보았듯이 본 연구에서 유도된 식(8)의 CBM 기대비용모형이 수학적으로나 수치적으로 만족스럽게 수립되었음을 알 수 있었다. 또한 모형을 구성하는 주요변수, CCM과 r의 변화에 따른 거동특성도 해석하였다. 따라서 본 절에서는 앞에서 유도된 CBM 기대비용모형을 경사제 피복재에 적용하였다. 이는 경사제 피복재의 피해가 다른 성분들의 피해를 동반 유발하는 중요한 공변수(covariate)라고 생각하였기 때문이다.
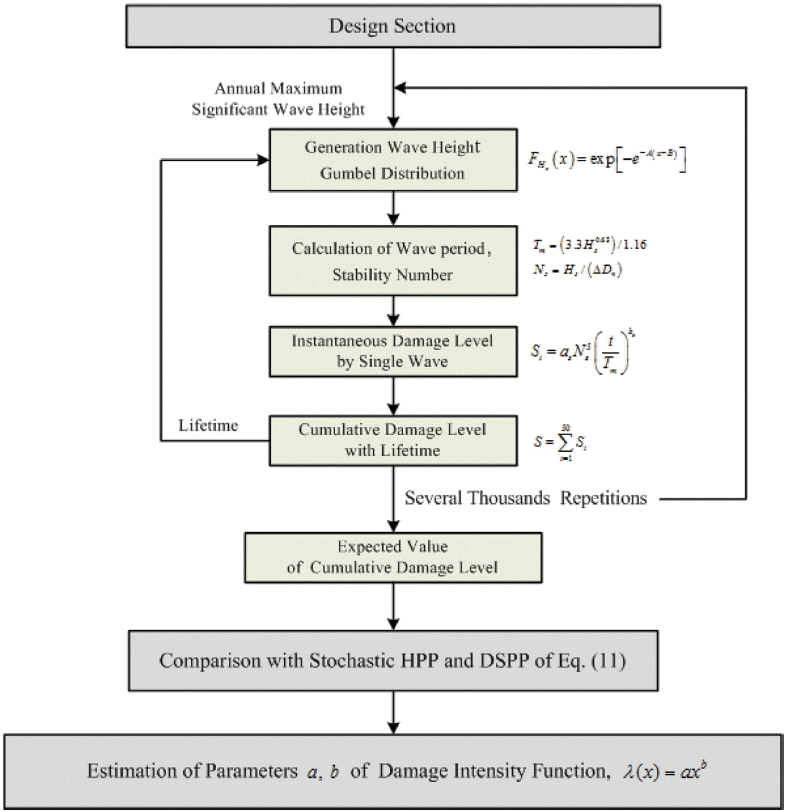
CBM 기대비용모형을 경사제 피복재에 적용하기 위해서는 먼저 식(13)의 피해강도함수의 계수, a와 b가 결정되어야 한다. 이는 다중하중에 따른 경사제 피복재의 누적피해를 추정해야 만 가능하다. 본 연구에서는 누적피해를 추정하기 위하여 Lee(2015)가 제시한 MCS(Monte-Carlo Simulation)기반 표본경로기법(sample path method)을 이용하였다. 표본경론기법을 수행하는 절차를 Fig. 9에 제시하였다. van der Meer(1988)가 제안한 피해수준(damage level), S = A e / D n 2
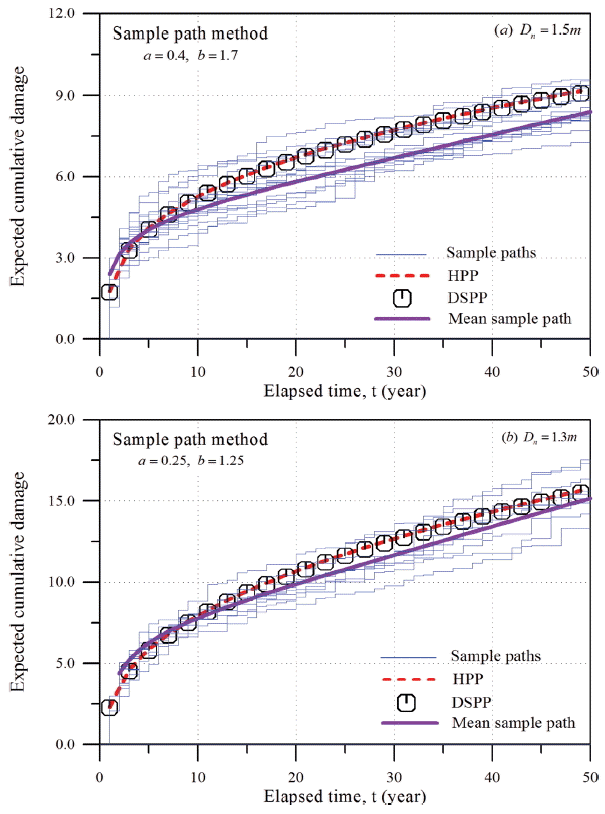
각 태풍이 약 3.0시간 지속된다는 가정하에 표본경로기법을 이용하여 추정된 기대 누적피해수준을 Fig. 10에 제시하였다. 하중발생 과정을 HPP와 DSPP로 각기 다르게 고려하여 식(14)를 이용하여 산정된 결과도 함께 비교하였다. HPP는 식(15)에서 α = 1.0, β = 0.0과 ν = 1.0인 경우이고, DSPP는 하중발생 과정에 불확실성을 고려하였다는 의미이다. 따라서 ν를 상수가 아닌 확률변수로 고려하였다. 본 연구에서는 다음 식(16)과 같이 정의되는 Erlang 분포를 따른다고 가정하였다(Kahle and Wendt, 2004).
여기서 k는 형상계수(shape parameter), θ는 축척계수(scale parameter)로 HPP와 DSPP의 평균이 같다는 점을 이용하여 산정할 수 있다.
그림에서 볼 수 있듯이 기대 누적피해수준이 포화피해모형을 따르는 등 전반적인 거동들이 Melby(1999), Castillo et al.(2012) 등이 언급한 특성들과 잘 일치하고 있다. 참고로 Fig. 10에는 Dn= 1.3 m에 대한 결과도 함께 제시하였는데 이는 피복재의 직경이 달라질 때 기대 누적피해수준의 거동을 보기 위함이다. 그림에서 쉽게 볼 수 있듯이 동일한 하중조건에서 피복재의 직경이 작아짐에 따라 기대 누적피해수준이가 크게 증가하고 있다. 특히 각각의 그림에서 HPP와 DSPP의 결과가 잘 일치한다는 것은 누적피해에 미치는 하중발생과정의 불확실성이 작다는 의미이다. 이는 하중 발생사상을 이산시간 확률과정으로 고려할 수 있다는 것을 의미한다. 따라서 각 표본경로의 평균을 산정하던지 식(14)와 비교하면 계수 a와 b를 결정할 수 있다. 그림에 제시하였듯이 본 연구에서는 보수적인 관점에서 각 표본경로의 평균보다 약간 큰 기대 누적피해수준에 대하여 a와 b을 추정하였다.
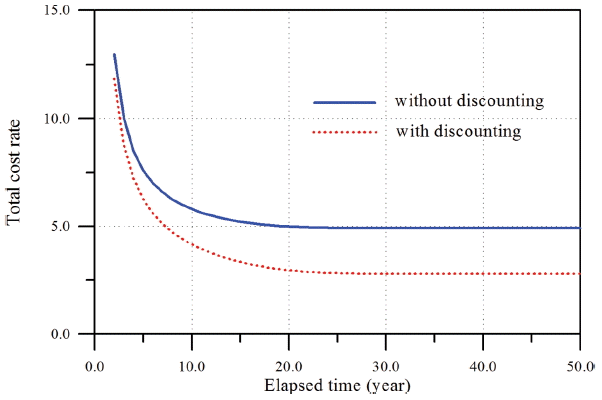
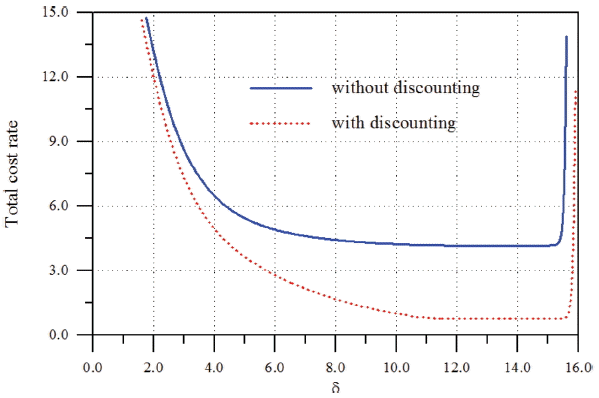
따라서 이 추정 결과를 이용하여 CBM의 할인비용모형을 해석할 수 있다. 이하에 Dn= 1.5 m인 경우의 a = 0.4와 b = 1.7에 대한 해석 결과를 제시하였다. 먼저 피해수준의 개념에 따라 경사제 피복재에 대한 파괴한계와 사용한계를 정의하였다. 본 연구에서는 PIANC(1992)의 기준에 따라 파괴한계로 ζ = 14.0, 사용한계로 δ = 6.0을 사용하였다. 또한 매년 소요되는 운용 및 검사비용으로 co= crm= 2.0, 그리고 이자율 r =0.05을 사용하였다. 먼저 CPM= 20.0과 CCM= 100.0에 대하여 이자율을 고려한 경우와 고려하지 않은 결과를 비교하여 Fig. 11에 제시하였다. 그림에서 알 수 있듯이 CR(δ, ζ, N, r)<CR(δ, ζ, N − 1, r)과 CR(δ, ζ, N + 1, r)=CR(δ, ζ, N, r)을 만족한다. 특히 이자율을 고려하지 않았을 때 CR(δ, ζ, N + 1, 0) = CR(δ, ζ, N, 0)을 처음으로 만족하는 N = 31, CR = 4.914인 반면, 이자율을 고려하였을 때는 N = 32, CR = 2.797이다. 그러나 CR(δ, ζ, N + 1, r)>CR(δ, ζ, N, r)의 조건은 만족하지 않는다. 이는 N의 전 영역에 대하여 최적의 N*와 CR(δ, ζ, N*, r)을 찾을 수 없다는 의미이다. 이와 같은 경우에 CBM은 DBM이 된다. 이를 확인하기 위하여 N →∞는 조건에서 사용한계 δ를 변화시키면서 CR(δ, ζ, ∞, r)을 산정하여 Fig. 12에 제시하였다. 그림에서 볼수 있듯이 δ = 6.0에서 CR(6, ζ, ∞, 0) = 4.914와 CR(6, ζ, ∞, 0.05) = 2.797로 Fig. 11의 결과와 일치한다. 앞에서 언급하였듯이 DBM은 CBM과 다르게 CR(δ, ζ, ∞, r)이 최소가 되는 δ*(< ζ)를 찾아 기대 누적피해도가 δ* 이상이 되는 시점에 PM을 실시하는 것이다. Fig. 12에 의하면 r = 0.0 일 때 δ* = 11.8에서 CR(δ*, ζ, ∞, 0) = 4.180으로 최소가 되고, r = 0.05 일 때는 δ*= 12.1에서 CR(δ*, ζ, ∞, 0.05) = 0.776로 최소가 된다. 따라서 이론적으로는 기대 누적피해수준이 이들 δ*를 초과하는 시점에 PM을 실시하는 것이 가장 바람직하다. 그러나 Fig. 10의 기대 누적피해수준에서는 구조물의 내구년수 50년 동안에 이들 최적의 사용한계를 초과하는 사상이 발생하지 않고 있다. 따라서 PM 시기를 결정하기 위해서는 Fig. 10과 Fig. 11을 함께 사용하여야 한다. 먼저 Fig. 10(a)를 이용하여 기대 누적피해수준이 사용한계인 6을 초과하는 시점을 찾는다. 보수적인 관점에서 대략 13년 정도가 된다. 다음으로는 Fig. 11에서 13년에 해당하는 CR(δ, ζ, N, r)을 결정하면 된다. r = 0.0 일 때 CR = 5.393이고, r = 0.05 일 때는 CR = 3.603이다.
한편 본 계산 예에서 기대 누적피해수준이 파괴한계 ζ = 14.0를 초과할 가능성이 거의 없다. 이는 P j C M ≈ 0 . 0
이상과 같이 본 연구에서 개발된 CBM의 할인비용모형을 이용하여 여러 조건을 변화시켜가면서 가상적인 임의의 경사제 피복재 단면을 해석하였다. 이는 매년 각기 다른 태풍이 내습하여 피해를 유발할 때 경사제 피복재와 같은 항만 구조물을 장래 어떻게 합리적으로 유지관리하여야 하는지를 제시하기 위함이다. 즉, 예방적 유지관리를 가장 경제적으로 수행할 수 있는 최적시점을 산정할 수 있을 뿐만 아니라 피해규모도 산정할 수 있어 유지관리의 범위를 비교적 쉽게 결정할 수 있다. 그러나 본 연구에서는 실제 피해 자료를 이용한 해석이 수행되지 못했다. 따라서 실제 구조물의 피해에 대한 실무적인 적용성 검토가 앞으로 더 수행되어야 한다. 또한 본 연구에서 유도한 CBM의 할인비용모형이나 표본경로기법은 경사제 피복재외에 다른 구조물에도 적용이 가능하다. 따라서 직립제나 안벽과 같은 항만 구조물로 모형의 적용 영역을 확장할 수 있는 추가적인 연구가 필요하다.
5. 결론
태풍의 내습에 따라 경사제 피복재를 예방적으로 최적 유지관리할 수 있는 조건기반 유지관리의 할인비용모형을 개발하였다. 복합 포아송 확률과정에서 하중발생 사상을 이산시간 확률과정으로 고려하는 추계학적 누적 피해모형과 보수보강 비용에 대한 경제성 모형을 결합하여 수학적으로 유도하였다. 특히 본 논문에서 유도된 조건기반 유지관리의 할인비용모형은 시간에 따른 비용의 가치 뿐만 아니라 누적피해의 비선형성도 고려할 수 있다. 또한 관련 변수에 따라 피해기반 유지관리 모형이나 재령기반 유지관리 모형으로의 변환이 가능하여 기존에 제시된 예방적 유지관리모형을 모두 포함할 수 있다.
본 연구의 결과는 이자율을 고려하지 않은 경우와 고려한 경우로 구분하여 기존 모형들의 결과와 비교하여 만족스럽게 검증되었다. 또한 구조물의 중요도와 이자율과 같은 주요 변수들에 대한 민감도 분석도 자세히 수행하였다. 구조물의 중요도가 높아질수록 PM의 최적시기는 빨라지나 이자율이 커질수록 반대의 경향이 나타났다.
한편 본 연구에서 유도된 추계학적 기대비용모형을 이용하여 임의의 경사제 피복재 단면을 해석하였다. 표본경로기법을 이용하여 임의의 태풍 내습에 따른 경사제 피복재의 기대누적피해수준을 예측하여 피해강도함수의 계수들을 올바로 추정할 수 있었다. 특히 하중발생 과정을 HPP 모형 뿐만 아니라 DSPP 모형으로도 처음 해석하여 기대 누적피해수준에 미치는 하중발생의 불확실성에 대한 영향도 분석하였다. 하중발생사상을 이산시간 확률과정으로 고려해도 된다는 것을 확인하였다. 예방적 유지관리모형의 해석 결과에 의하면 경사제 피복재의 설계조건에 따라 기대 누적피해수준의 거동특성이 크게 달라지고, 이에 따라 PM을 수행하기 위한 최적의 조건도 달라진다. 마지막으로 구조물의 중요도와 이자율 그리고 파괴한계 설정에 따라 PM을 가장 경제적으로 수행하기 위한 피해 상태와 최적 시점을 정량적으로 제시하였다. 따라서 본 연구에서 제시된 모형들을 이용하면 예방적 유지관리를 가장 경제적으로 수행할 수 있는 최적시점을 산정할 수 있을 뿐만 아니라 피해규모도 파악할 수 있어 유지관리의 범위를 합리적으로 결정할 수 있다.
그러나 본 연구에서는 가상적인 임의의 경사제 피복재 단면을 대상으로 해석하였다. 따라서 실제 구조물의 피해에 대한 실무적인 적용성 검토가 앞으로 더 수행되어야 한다. 또한 본 연구에서 유도한 CBM의 할인비용모형이나 표본경로기법은 경사제 피복재외에 다른 구조물에도 적용이 가능하다. 따라서 직립제나 안벽과 같은 항만 구조물로 모형의 적용 영역을 확장할 수 있는 추가적인 연구가 필요하다.