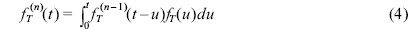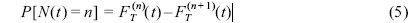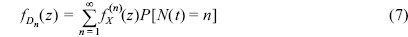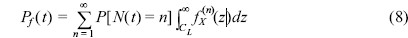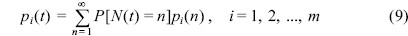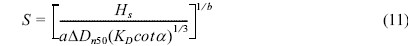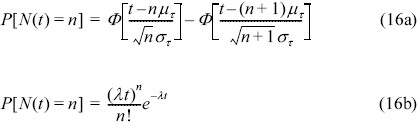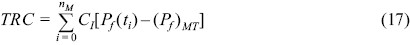1. 서 론
안정성이나 기능성과 관련하여 모든 시스템의 상태는 예외 없이 시간이 진행됨에 따라 항상 변화한다. 현재의 상태는 과거의 상태에 의존하게 되고 또 미래의 상태에 영향을 주게 된다. 이와 같이 시간의 진행에 따라 임의의 상태에서 다른 상태로 변화하는 과정을 올바로 해석하기 위해서는 확률과정(stochastic process)에 대한 이해가 필요하다. 여러 분야에 가장 일반적으로 적용될 수 있는 모형이 MP(Markov Process) 모형이다. MP 모형은 이행확률(transition probability)을 근간으로 시스템의 시간에 따른 상태 변화를 예측하는 모형이다. 이행확률이란 시스템의 상태가 단위사건 후 다른 상태로 바뀔 가능성을 정량화하기 위해 도입된 개념이다. MP 모형에서는 현재 시스템의 상태는 바로 전단계의 시스템 상태에만 의존한다는 개념을 사용한다. 이는 현재 시스템의 상태에 영 향을 주는 과거의 모든 이력을 바로 전단계의 시스템 상태로 고려할 수 있다는 의미이다.
경사제 피복재의 경우도 시간의 진행에 따라 각기 다른 피해정도를 나타낼 수 있는데, 이는 바로 전단계의 피해정도와 현재 불규칙하게 내습하는 파랑의 수와 규모에 직접적으로 의존하기 때문이다. 따라서 MP 모형을 경사제 피복재의 시간에 따른 피해정도를 예측하는 데 올바로 적용하기 위해서는 앞에서 언급된 과거의 피해정도와 불규칙하게 내습하는 파랑의 특성 등이 함께 고려되어야 한다. 경사제 피복재의 경우는 과거의 피해가 계속 누적되는 물리적 특성을 갖고 있다. 따라서 전단계의 피해정도가 과거의 모든 피해이력을 모두 내포하게 된다. 이는 전단계의 피해가 현재 어떤 규모의 파랑에 노출되면 어떤 피해로 변할지에 대한 이행확률을 산정하는 것이 이론적으로 가능하다는 것을 의미한다. 그러나 전단계의 피해정도와 현재 내습하는 파랑 모두 불규칙한 확률변수이다. 만약 동일 경사제 피복재에 대해 지난해의 피해규모와 올해 임의의 태풍 내습으로 인해 발생한 피해규모를 비교 할 수 있는 실측자료를 가지고 있다면 이행확률을 정확히 산정할 수 있다. 그러나 한 단면에 대하여도 확률적으로 의미 있는 많은 양의 자료를 축적한다는 것은 여러 가지 제약성에 따라 대단히 어려운 일이다. 특히 지역적으로 각기 다른 조건에 노출된 여러 단면에 일반적으로 적용할 수 있는 이행확률을 실측자료로부터 산정한다는 것은 거의 불가능하다. 이와 같은 이유로 현재까지 MP 모형을 이용하여 경사제 피복재 등과 같은 항만 구조물의 시간에 따른 안정성에 대한 상태 변화를 해석한 연구 사례는 없었다. 그러나 경사제 피복재 등과 같은 항만 구조물을 효율적으로 유지관리하기 위해서는 시간의 진행에 따른 안정성에 대한 상태 변화를 예측하는 것이 필요하다. 기존 구조물에 대한 보수·보강 계획 뿐만 아니라 새로운 구조물 설계시 생애주기비용 등을 산정하기 위해서는 확률과정 모형에 기초한 안정성의 시간 의존 거동특성을 반드시 해석해야 한다.
Mori and Ellingwood(1994), Van Noortwijk and Klatter(1999), Van Noortwijk and Peerbolte(2000), Kallen and Van Noortwijk(2005), Buijs et al.(2009), Van Noortwijk(2009), 이철응(2012) 등이 PP(Poisson Process) 모형을 이용하여 여러 가지 문제를 추계학적으로 해석하였다. 개별사상에 의한 피해가 독립적이고 동일한 지수분포를 따른다고 가정하여 누적피해 분포함수의 형태모수(shape parameter)를 시간의 함수로 고려하는 방법이다. 형태모수의 시간에 따른 변화는 일반적으로 Bayesian 정리를 이용하여 산정하며, 이를 GP(Gamma Process) 모형이라고도 한다. 이상에서 볼 수 있듯이 현재까지 이루어진 시간의 진행에 따른 안정성의 거동특성에 대한 연구에서는 주로 PP 모형을 이용하고 있다. 일반적으로 PP 모형은 MP 모형의 한 부분으로 고려된다. 왜냐하면 MP 모형의 이행확률이 시스템의 상태와 무관하다고 가정하면 PP 모형이 되기 때문이다. 따라서 PP 모형에서는 피해강도함수(damage intensity function)만을 이용하여 시간에 따른 피해의 통계적 거동특성을 해석하게 된다. 따라서 전단계의 피해정도와 현단계의 하중 조건에 대한 상관성을 직접적으로 고려할 수 없다. 만약 허용한계와 사용한계 그리고 파괴한계로 구분되는 피해상태가 있을 때 MP 모형을 이용하면 현재의 하중조건에 따라 허용한계에서 사용한계로 또는 허용한계에서 파괴한계로 변화될 확률과 시간까지도 각기 따로 해석할 수 있다. 그러나 PP 모형에서는 이와 같은 해석을 할 수 없다. 단지 피해강도함수의 특성에 따라 얼마의 시간이 지나면 허용한계에서 사용한계를 거쳐 파괴한계에 도달하는지를 해석할 뿐이다. 그럼에도 불구하고 PP 모형이 주로 사용되는 이유는 적용에 필요한 변수가 적고, 각 변수들을 추정하는 것이 비교적 쉽기 때문이다.
본 연구에서는 경사제 피복재의 안정성과 관련된 시간에 따른 피해 거동특성을 해석할 수 있는 MP 모형을 개발하였다. 먼저 경사제 피복재의 피해정도에 따른 상태를 정의하기 위하여 피해수준(damage level)의 개념을 도입하였다. 또한 발생 가능한 피해수준과 내습하는 파랑의 수와 규모를 모두 확률변수로 고려하여 MCS(Monte-Carlo simulation) 기법을 이용하여 이행확률을 산정하고 분석하였다. 또한 경사제 피복재의 설계와 관련된 관련 변수들의 변화에 따른 파괴확률 등 안정성을 해석하였다. 특히 해석된 결과를 이용하여 생애주기 기간 동안 경사제 피복재를 합리적으로 유지관리할 수 있는 방법을 제안하였다.
2. 추계학적 Markov 확률모형
시간의 진행에 따라 규모가 각기 다른 불규칙한 하중이 반복적으로 작용하면 구조물의 저항력은 점점 감소하다 임의의 극한한계에 도달하면 파괴된다. 이와 같은 시간 의존 문제를 추계학적 모형으로 해석하기 위해서는 두 가지 확률과정을 함께 고려하여야 한다. 하나는 하중의 발생개수와 관련된 CP(Counting Process) 해석이고 다른 하나는 각 하중에 의하여 발생되는 DP(Damage process) 해석이다.
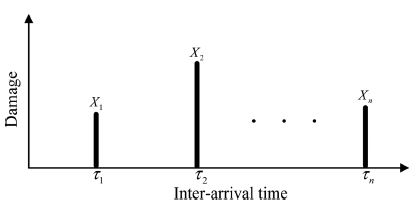
먼저 Fig. 1에 나타낸 바와 같이 첫 번째 하중이 발생한 시간을 확률변수 τ1이라 하고 첫 번째 하중과 두 번째 하중 사이의 시간간격(inter-arrival time)을 τ2라고 정의하면 τn은 n − 1번째 하중과 n번째 하중 사이의 시간간격이 된다. 따라서 n번째 하중이 발생하는 시간(arrival time), Tn은 다음 식 (1)과 같이 정의할 수 있다.
또한 하중 발생개수와 관련된CP 해석을 수행하기 위해서는 t 시간 동안 발생한 하중의 개수, N(t) 를 다음 식 (2)와 같이 나타낼 수 있어야 한다(Ross, 1980).
물리적으로 식 (2)는 n번째 하중이 t 이전에 발생하였다면 t 시간 동안 n개 이상의 하중이 발생하였다는 것을 의미한다. 따라서 다음 식 (3)이 성립한다.
식 (1)에서 {τ1, τ2, ...}이 독립적이고 동일한 분포함수를 따른다고 가정하면 식 (2)에 의하여 정의된 CP는 RP(Renewal Process)가 된다. 만약 τi가 임의의 분포함수 fT(t)를 따르다고 가정하면 Tn의 분포함수는 다음 식 (4)와 같이 된다.
쉽게 알 수 있듯이 식 (4)는 하중발생 시간에 대한 조건부 확률밀도함수(conditional probability density function)이다. 따라서 식 (3)과 식 (4)를 함께 이용하면t 시간 동안 개의 하중이 발생할 확률은 다음 식 (5)와 같이 정의된다.
여기서 FT(n)(t)는 ƒT(n)(t)의 누적분포함수이다. 예로 식 (4)의 ƒT(t) 를 지수분포라 가정하면 식 (5)는 Poisson 분포가 된다. 이상에서 하중 발생개수와 관련된 CP 해석이 수행되었다. 따라서 이하에서는 DP 해석을 수행하겠다.
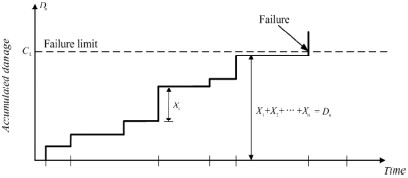
한편 Fig. 2에서 임의의 크기를 갖는 첫 번째 하중이 구조물에 유발한 피해를 확률변수 X1이라 하고 이를 순차적으로 나열하면 n번째 하중에 의한 피해를 Xn이라 정의할 수 있다. 따라서 누적피해(cumulative damage), Dn은 다음 식 (6)과 같이 정의된다.
식 (6)의 가{X1, X2, ...} 독립적이고 동일한 분포함수를 따른다고 가정하고 앞에서 정의한 식 (4)와 식 (5)를 이용하면 누적피해, Dn의 분포함수, ƒDn(z)는 전확률법칙(law of total probability)에 의해 다음 식 (7)과 같이 정의된다.
만약 누적피해 Dn이 임의의 파괴한계, CL보다 크다면 구조물은 파괴된다. 따라서 파괴확률을 Pƒ(t)라 정의하면 다음 식 (8)이 성립한다.
식 (8)은 t 시간 동안 발생 가능한 모든 하중 개수와 각각의 하중에 의하여 발생한 누적피해를 함께 고려한 것이다. 따라서 우변의 각 부분을 정의하면 시간에 따른 파괴확률을 쉽게 계산할 수 있다.
지금까지의 대부분의 연구는 하중발생강도(load occurrence intensity)와 피해강도함수(damage intensity function)만을 사용하는 PP 또는 GP 모형을 사용하였다. 그러나 PP 또는 GP모형은 전단계의 피해정도에 따른 현단계의 하중조건에 대한 상관성을 분석할 수 없다. 이와 같은 문제를 해결하기 위하여 본 연구에서는 식 (8)을 다음 식 (9)와 같은 MP 모형으로 변환하였다.
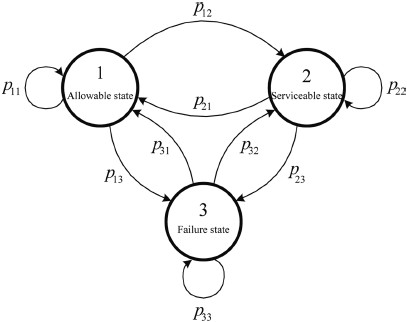
여기서 pi(t)는 t 시간에 구조물이 임의의 i 상태에 있을 확률이다. 만약 구조물의 상태를 허용한계, 사용한계 그리고 파괴한계로 구분하여 Fig. 3과 같이 각각을 i = 1, 2 그리고 3으로 정의한다면, 식 (9)의 p3(t) = Pƒ(t)가 된다. 또한 p1(t)과 p2(t)는 각각 t 시간에 구조물이 허용한계와 사용한계에 있을 확률이 된다. 그러나 식 (8)에서는 1 − Pƒ (t)만을 계산 할 수 있기 때문에 각각의 한계를 구분하여 해석하는 것이 불가능하다. 따라서 식 (9)의 MP 모형은 식 (8)의 PP 모형을 포함하게 된다.
또한 pi(n)은 임의의 초기상태에서 시작한 구조물이 t 시간 동안 발생한 n개의 하중에 의하여 i 상태로 변화될 확률을 의미하며 다음 식 (10)으로부터 산정할 수 있다(Taylor and Karlin, 1984).
여기서 pi(0)는 초기에 구조물이 i 상태에 있을 확률이고 pij는 전단계에서 i 상태에 있던 구조물이 단위 사건후 j 상태로 변화될 이행확률을 의미한다. 윗 첨자 T는 행렬변환(Transpose)을 의미한다. 식 (10)에서 쉽게 알 수 있듯이 시간에 따른 하중 발생 개수와 구조물의 각 상태간 상관성은 이행확률 행렬을 통하여 모두 고려된다.
따라서 식 (9)의 MP 모형에서는 이행확률을 올바로 산정하는 것이 중요하다. 예로 허용한계상태에 있던 구조물이 단위 사건후 사용한계상태나 파괴한계상태로 변할 확률, 와 를 산정해야 한다. 이때 허용한계상태에 있던 구조물이 사용한계상태로 변할지 파괴한계상태로 변할지는 내습하는 하중의 크기에 의존한다. 따라서 모든 상태에 대하여 그리고 내습할 수 있는 모든 하중의 크기에 대하여 구조물에 발생한 피해에 대한 연속적인 자료가 있어야 한다. 즉, 과거의 피해이력, 전단계의 피해가 어느 수준이었는데 어떤 크기의 하중들이 내습하여 어느 피해수준으로 바뀔지에 대한 확률적 해석이 수행되어야 이행확률을 산정할 수 있다. 경사제 피복재와 같은 항만 구조물에서 이와 같은 자료를 얻는 다는 것은 현실적으로 매우 어려운 일이다. 따라서 본 연구에서는 MCS 기법을 이용하여 이행확률을 산정하였다.
3. 경사제 피복재에의 적용
먼저 경사제 피복재의 피해상태를 정의하기 위하여 Van der Meer(1988)가 제시한 피해수준, S를 이용하였다. PIANC(1992)에 제시된 결과에 따라 각각의 상태에 대한 피해수준의 범위를 Table 1에 제시하였다. PIANC(1992)에서는 허용한계를 S = 2, 사용한계를 S = 6 그리고 파괴한계를 S = 14로 정의하였다. 여기서 허용한계는 설계시 허용하는 피해수준을, 사용한계는 사용성에 제약을 받기 시작하는 한계를 의미한다. 그리고 파괴한계는 피복재의 피해로 인해 경사제 제체의 안정성에 문제가 생기는 피해수준을 의미한다. 따라서 일반적으로 설계할 때는 피해수준이 2이하가 되도록 설계하나 실제로 사용성 관점에서 보면 6보다 작은 수준까지도 허용할 수 있다는 의미이다. 또한 사용한계가 6이라는 의미는 그 이상의 피해수준이 발생되면 사용성에 일부 제약을 받을 뿐 파괴되지는 않는다는 의미이다. 마지막으로 피해수준이 14 이상이 되면 경사제 피복재는 파괴에 도달한다.
이와 같이 설정된 각 상태에 대한 정의를 가지고 경사제 피복재의 바로 이전 단계 피해수준이 내습하는 파고의 불규칙성에 의하여 어느 피해수준으로 바뀔지에 대한 해석을 수행하였다. 이를 위해서는 파고와 피해수준의 관계식이 필요하다. 본 연구에서는 다음 식 (11)과 같은 PIANC(1992)에 정의된 수정 Hudson 공식을 이용하였다.
여기서 Hs는 유의 설계파고, Dn50은 피복재의 대표직경이다. 또한 Δ = ρs/ρω − 1, ρs와ρω는각각 피복재와 해수의 밀도, a와 b는 경험상수, 그리고 KD 안정계수 그리고 cotα는 제체경사이다. 식 (11)에서 볼 수 있듯이 경사제 피복재의 피해수준은 동일한 하중이 작용하더라도 여러 변수들에 의존한다. 본 연구에서는 경험상수, a = 0.7, b = 0.158, 그리고 Δ = 1.6, KD= 4.0, cotα = 1.5를 사용하였다(Burcharth, 1992). 또한 Dn50은 임의의 재현기간, R에 대한 유의 설계파고, HSR을 이용하여 결정하였다. 이는 임의의 재현기간 R년의 설계파고로 설계된 피복재가 매년 다르게 내습하는 파고에 의하여 어떠한 피해 거동을 보이는지 해석하기 위함이다.
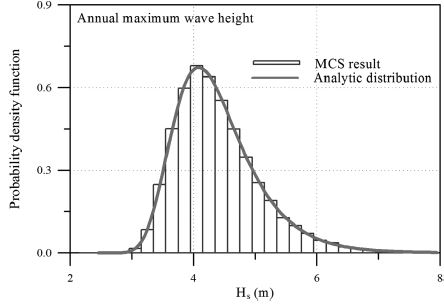
식 (11)을 이용하여 하중 내습에 따른 피해수준을 산정하기 위해서는 태풍의 특성을 잘 나타낼 수 있는 파고의 분포가 필요하다. 일반적으로 재현기간에 따른 설계파고 등을 산정할 때 사용하는 개념이 년 최대 유의파고(annual maximum significant wave height)이다. 태풍이 몇 개 내습하던지 그 해 발생한 태풍의 유의파고 중 최대치만을 이용하여 극치분포로 나타내는 개념이다. 따라서 극치분포를 알면 역으로 매년 내습하는 최대 유의파고를 재현할 수 있다. 본 연구에서는 이와 같은 개념을 가지고 이행확률을 산정하였다. 먼저 임의 크기의 파고가 내습하기 이전 단계 피해수준을 S = 0이라 가정한 후, 극치분포로부터 생성된 유의파고를 식 (11)에 대입하여 불규칙하게 내습하는 유의파고에 대한 피해수준을 산정한다. 이는 S = 0의 이전 피해수준이 어느 상태의 피해수준으로 변화했는지를 해석하기 위함이다. 동일하게 이전 피해수준을 변화시키면서 앞의 과정을 반복한다. 전체 계산 결과를 Table 1에 제시된 각각의 상태에 대한 정의와 비교하여 순차적으로 이행확률을 산정한다. 예로 p12는 허용한계상태에서 시작하여 사용한계상태로 변화될 확률이기 때문에 6 미만의 이전 피해수준에서 시작한 모든 경우 중 몇 개가 6 이상 14미만으로 변화했는지를 계산하면 쉽게 얻을 수 있다.
이와 같은 과정을 수행하기 위하여 본 연구에서는 다음 식(12)의 Gumbel 극치 분포함수를 사용하였다.
여기서 축척계수, A와 위치계수, B를 각각 1.83 m−1와 4.08 m로 가정하였다(Burcharth, 1992). 재현기간, R에 따른 설계유의파고, HSR 은 다음 식 (13)과 같이 정의할 수 있다.
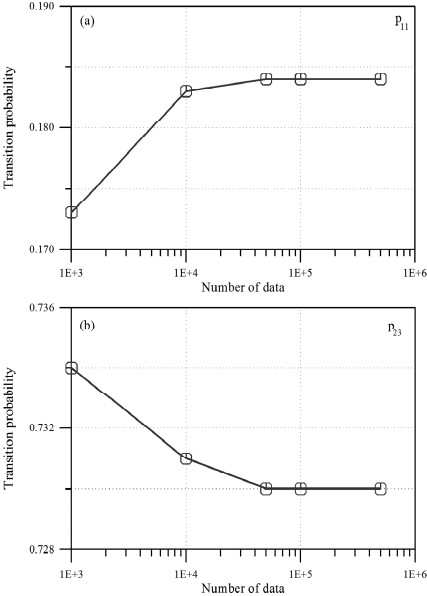
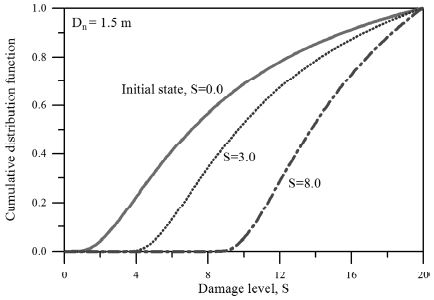
식 (12)를 이용하여 MCS로 생성된 년 최대 유의파고의 분포를 Fig. 4에 제시하였다. 그림에서 볼 수 있듯이 생성된 자료가 식 (12)와 매우 잘 일치한다. 이 자료를 식 (11)에 대입하여 피해수준과 이행확률들을 계산하였다. 먼저 생성된 자료의 개수에 따른 영향을 살펴보았다. Dn50 = 1.50m을 가지고 허용한계에서 시작된 피복재가 허용한계, 사용한계 그리고 파괴한계로 이행할 각각의 확률, p11, p12 그리고 p13과 사용한계에서 시작된 피복재가 사용한계 및 파괴한계로 이행할 확률, p22 및 p23을 산정하였다.Fig. 5에 대표적 결과를 제시하였는데 50,000개 이상의 자료를 생성하게 되면 이행확률이 일정한 값으로 수렴하는 것을 쉽게 알 수 있다. 또한 이전단계의 피해수준에 임의의 불규칙한 파고가 내습하였을 때 어떤 피해수준으로 이행하는지를 살펴보기 위하여 누적피해수준의 분포함수를 살펴보았다. 이는 이행확률을 산정하기 위하여 본 연구에서 제안한 방법의 타당성을 검증하기 위함이다. 이론적으로 식 (6)에서 Xi가 지수분포이면 누적피해, Dn의 분포함수는 Gamma 분포를 따른다(Taylor and Karlin, 1984). 따라서 본 연구에서는 이와 같은 개념을 이용하여 누적피해, Dn= S의 분포함수를 다음 식 (14)에 제시한 Gamma 분포와 비교하였다.
여기서 ν는 물리적으로는 피해강도를 의미하는 축척계수(scale parameter), n은 형상계수로, 다음 식 (15)를 이용하여 추정할 수 있다.
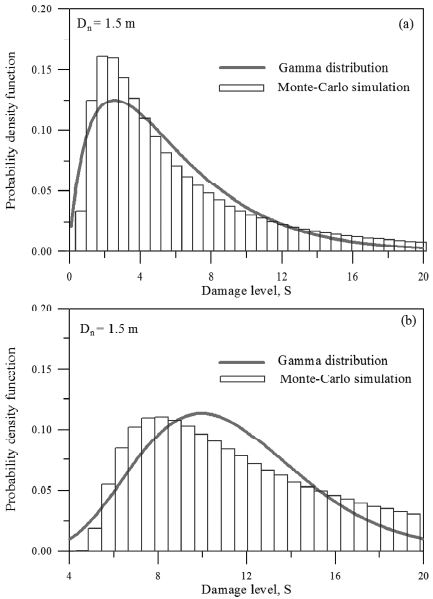
여기서 μS와σ2S 은 각각 평균과 분산으로 MCS 기법으로 생성된 누적피해의 통계적 특성을 이용하여 산정할 수 있다. 모두 두 개의 누적피해에 대한 분포함수를 비교하였다. 이전 피해수준이 각각 S = 0과 S = 4인 경우에 식 (12)의 파고가 불규칙하게 내습하는 경우이다. 임의의 피복재에 어떤 불규칙한 파고가 내습하는 경우를 해석하기 위하여 피복재의 대표입경 Dn50= 1.50m로 가정하였다. 먼저 Fig. 6(a)는 이전 피해수준이 S = 0에 대한 경우이고 Fig. 6(b)는 S = 4에 대한 경우의 결과이다. 특히 Fig. 6(b)에서 실선은 누적피해 수준의 물리적 거동범위, S ≥ 4를 맞추기 위하여 식 (14)를 이용하여 산정된 절단확률밀도함수(truncated probability density function)이다. 두 그림에서 알 수 있듯이 MCS로 산정한 결과가 식 (14)의 이론적 확률밀도함수와 비교적 잘 일치하고 있다. 따라서 본 연구에서 제시한 접근 방법이 올바르다는 것을 알 수 있다. Fig. 7에 이전 피해수준에 따른 누적분포함수를 제시하였다. 또한 피복재의 입경 변화에 따른 이행확률을 Table 2에 제시하였다.
모두 6가지 경우에 대하여 제시하였는데 Case 1과 Case 6은 피복재의 대표입경이 각각 1.50 m와 2.50 m에 대한 것이고, 나머지 Case 2에서 Case 5까지는 순서대로 재현기간이 10년, 30년, 50년 그리고 100년 설계파고에 해당하는 대표입경에 대한 것이다. 먼저 Table 2(a)는 각각의 경우에 대하여 이전 피해수준이 허용한계일 때 불규칙 파고 내습 후 허용한계로 이행할 확률, p11, 즉, 허용한계에 계속 머물 확률이다. 또한 Table 2(b)는 허용한계 및 사용한계에서 사용한계로 이행할 확률, p12와 p22를 제시한 것이다. 마지막으로 Table 2(c)는 허용한계 및 사용한계 그리고 파괴한계에서 파괴한계로 이행할 확률, p13과 p23 그리고 p33을 제시한 것이다. Fig. 3의 나머지 이행확률, p21= p31 = p32= 0.0이다.
Table 2.
Transition probability with respect to nominal diameters of armor units
(a)
|
Transition probability |
Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| p11 | 0.184 | 0.572 | 0.770 | 0.834 | 0.895 | 0.956 |
물리적으로 보면 사용한계나 파괴한계에 있던 피해수준이 다시 허용한계로 돌아갈 수 없음을 의미한다. 또한 파괴상태에 있던 피해수준은 불규칙파가 내습하면 원래 파괴상태를 벗어날 수 없기 때문에 p33= 1.0이다. 이를 MP 모형에서 흡수상태(absorbing state)라 한다. Table 2에서 쉽게 알 수 있듯이 모든 경우에 대하여 p11+p12+ p13= 1.0, p21+p22+ p23= 1.0을 만족한다. 또한 피복재의 대표입경이 커짐에 따라 허용한계에서 사용한계나 파괴한계로 이행할 확률, p12와 p13는 감소하고 있다. 이와는 반대로 허용한계에서 허용한계로, 사용한계에서 사용한계로 이행할 확률, p11과 p22는 증가하고 있다. 이는 피복재의 중량이 커지면 불규칙 파고의 내습시 피해에 대한 저항력이 커진다는 것을 의미한다.
4. 경사제 피복재에 대한 결과 분석
이상과 같이 본 연구에서 제시한 방법으로 산정된 이행확률은 수학적으로 또는 물리적으로 만족해야하는 여러 가지 조건들을 잘 충족한다. 따라서 이하에서는 산정된 이행확률을 식 (9)에 대입하여 시간의 진행에 따른 경사제 피복재의 누적피해에 따른 파괴확률 등 유지관리에 필요한 여러 가지 문제를 해석하겠다. 이를 위해서는 식 (9)에서 쉽게 알 수 있듯이 먼저 시간의 진행에 따른 하중의 발생사상을 정의하여야 한다. 본 연구에서는 추계학적 확률과정 해석시 가장 일반적으로 적용되는 두 가지 경우에 대하여 해석하였다. 하나는 하중 사이의 발생 시간 간격이 평균, μτ, 표준편차, στ를 갖는 정규분포를 따르는 경우이고, 다른 하나는 발생강도 λ를 갖는 지수분포를 따르는 경우이다. 따라서 식 (5)에 의하면 각각의 경우는 다음 식 (16)과 같이 쉽게 유도할 수 있다.
본 연구에서는 하중의 크기를 나타내기 위하여 년 최대 유의파고를 사용하였기 때문에 λ = 1.0을 사용하였다. 또한 동일한 하중 발생사상을 해석하는 것이기 때문에 지수분포와 정규분포의 평균과 분산이 같다는 개념에 의하여 μτ = στ = 1/λ이 된다. 그러므로 식 (16)과 Table 2의 이행확률을 식 (9)에 대입하면 임의의 시간에 경사제 피복재가 파괴될 확률, p3(t)를 구할 수 있다.
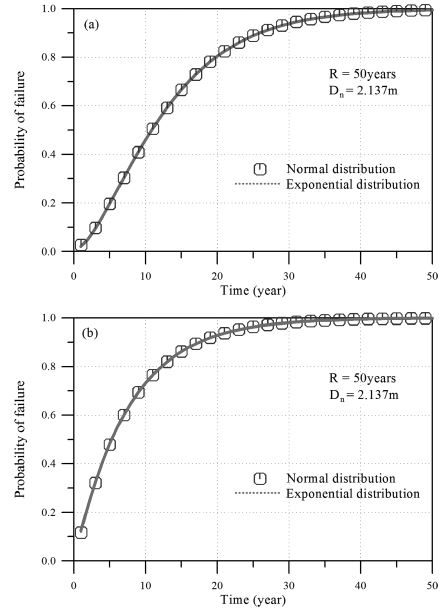
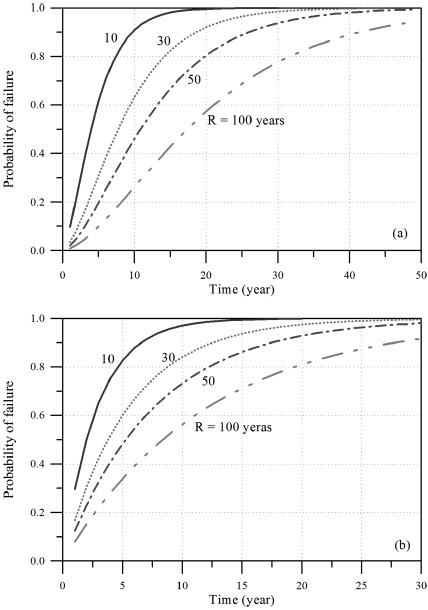
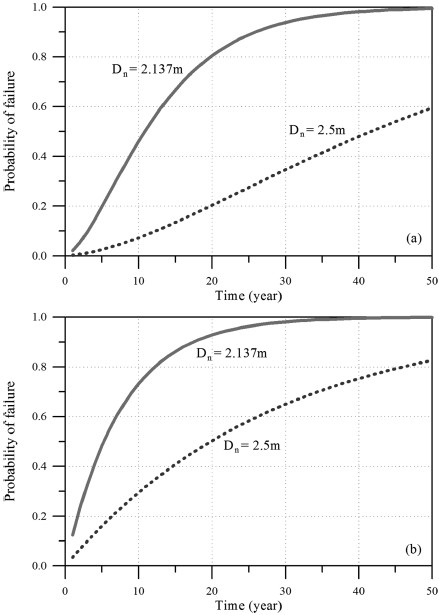
먼저 피복재의 시간의 진행에 따른 파괴확률을 Fig. 8에 제시하였다. 재현기간, R = 50년 설계파고로 설계된 피복재의 거동특성이다.Fig. 8(a)는 최초 허용한계에서 시작한 경우이고, Fig. 8(b)는 사용한계에서 시작한 경우이다. 각각의 그림에는 두 가지의 하중 발생 시간 간격의 분포함수에 따른 결과를 함께 비교하였다. 그림에서 보는 바와 같이 동일한 조건에서는 하중 사이의 발생 시간 간격의 분포함수에 따른 차이는 거의 나타나지 않고 있다. 그러나 이전단계의 피해수준에 따른 차이는 명확하게 나타나고 있다. 동일한 시간 경과에 따라 Fig. 8(b)의 결과가 Fig. 8(a)의 결과보다 큰 파괴확률을 나타내고 있다. 이는 최초 파괴수준의 영향이 반영된 결과이다. 즉, 허용한계보다 큰 피해수준을 갖는 사용한계에서 시작한 피복재가 동일한 파랑 조건에 노출되면 더 빨리 파괴한계에 도달한다는 것을 정량적으로 나타낸 결과이다. 이와 같은 결과는 일반적으로 많이 사용되는 PP 모형에서는 해석할 수 없다. 또한 Fig. 9에 설계파고의 재현기간, 즉, 경사제 피복재의 대표입경 차이에 따른 파괴확률의 시간 의존 거동특성을 제시하였다. 동일하게 Fig. 9(a)는 최초 허용한계에서 시작한 경우이고,Fig. 9(b)는 사용한계에서 시작한 경우이다. 두 그림에서 쉽게 볼 수 있듯이 피복재의 대표입경이 작게 설계될수록 파괴확률은 급격하게 증가하고 있다. 마지막으로 재현기간 50년에 대한 설계파고로부터 결정된 피복재의 대표입경, Dn50= 2.137 m를 2.500m로 크게 하였을 때, 즉, 안전율(2.500/2.137 =1.17)을 고려하였을 때 파괴확률의 거동특성을 비교하여 Fig. 10에 제시하였다. Fig. 10(a)는 최초 허용한계에서 시작한 경우이고, Fig. 10(b)는 사용한계에서 시작한 경우이다. 그림에서 볼 수 있듯이 파괴확률은 두드러지게 차이가 난다. 따라서 본 연구에서 개발한 추계학적 MP 확률모형을 이용하면 설계변수의 변화에 따른 경사제 피복재의 파괴확률을 시간의 함수로 산정할 수 있다.
한편 본 연구에서 추계학적 MP 확률모형을 개발한 중요한 또 다른 목적은 시간에 따른 파괴확률의 거동특성을 이용하여 경사제 피복재의 합리적인 유지관리 방법을 제안하는 것이다. 유지관리란 구조물이 파괴되기 전에 즉, 기능성이 상실되기 전에 합리적인 방법으로 보수보강을 실시하여 경제적으로 그 기능성을 최대한 길게 확보하는 것이다. 이와 같은 개념에 의하여 본 연구에서는 두 가지 방법을 제안하고 정량적으로 해석하였다. 하나는 현행 시설물의 안전관리에 관한 특별법(시특법)에 정해진 일정한 기간, TM간격으로 보수보강을 실시하는 방법이고, 다른 하나는 일정한 목표파괴확률, (Pf)TM을 정하고 시설물이 그 목표파괴확률에 도달하면 보수보강을 실시하는 방법이다.
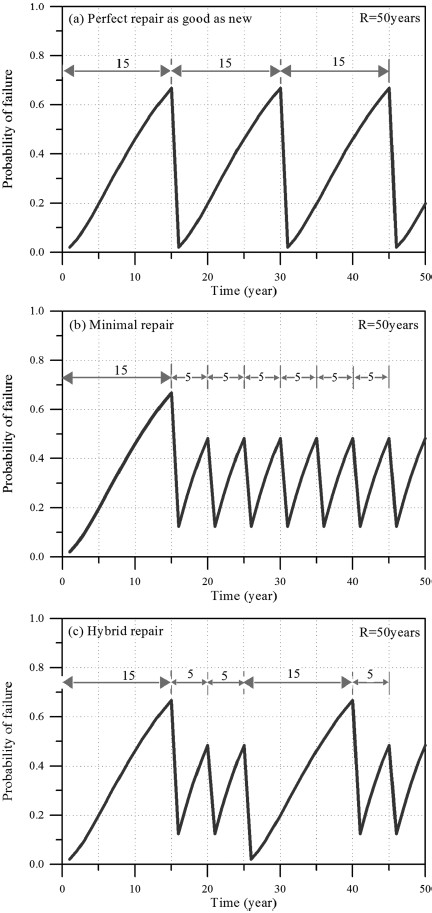
먼저 시특법에 따라 일정한 시간간격으로 보수보강을 실시하는 경우의 결과를Fig. 11에 제시하였다. 특히 Fig. 11에서는 재현기간 50년의 조우확률(encounter probability)을 고려하여 시간간격을 결정하였다. 즉, 재현기간 50년의 설계파가 내용년수 50년 동안에 발생할 확률은 대략 0.64이다. 따라서 TM= 15를 가정하여 모두 3가지 경우에 대하여 해석하였는데, Fig. 11(a)는 15년 주기로 새것처럼 보수보강하는 경우이고 Fig. 11(b)는 첫 15년 경과 후에 최소한의 보수보강을 실시한 후, 5년 간격으로 최소 보수보강을 반복적으로 실시하는 경우이다. 마지막으로 Fig. 11(c)는 앞의 두 경우를 종합하여 25년 간격으로 새것처럼 보수보강을 실시하되 그 중간에 파괴가 발생하지 않도록 15년과 5년이 되는 해에 최소 보수보강을 실시하는 방법에 대한 결과이다. 새것처럼 보수보강을 실시한다는 것은 보수보강 목표파괴확률, (Pf)MT를 설계시 부여하는 허용/목표파괴확률, (Pf)T과 동일하게 부여한다는 의미이고, 최소수준의 보수보강을 실시하는 경우는 구조물의 중요도에 따라 사용성을 만족하는 수준내에서 임의의 보수보강 목표파괴확률을 부여할 수 있다는 의미이다.
재현기간 50년에 대한 결과이기 때문에 내구년수를 50년 으로 보면 첫 번째 방법은 내구년수 동안 모두 3번의 새것처럼 보수보강을 실시하여야 한다. 반면 두 번째 경우는 모두 7번의 최소수준의 보수보강이 실시되어야 한다. 마지막으로 세 번째 방법에서는 1번의 새것처럼 보수보강과 4번의 최소수준의 보수보강이 이루어져야 한다. 시특법에는 시설물의 종류에 따라 일정한 시간 간격으로 안전점검을 실시하고 등급에 따라 보수보강의 정도나 방법을 결정하도록 규정되어 있다. 항만 구조물의 가장 대표적인 경사제 피복재의 경우는 아직 이 조차 마련되어있지 않다. 따라서 이에 대한 대책을 마련할 필요가 있다. 그런 의미에서 Fig. 11의 결과는 방법론적인 접근법을 제시하기 위한 하나의 예를 나타낸 것이다.
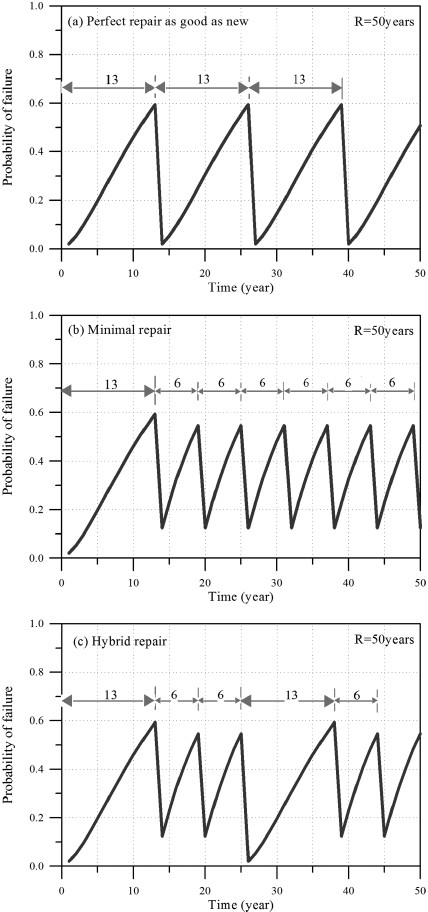
한편 일정한 목표파괴확률을 정하고 시설물이 그 목표파괴확률에 도달하기 전에 보수보강을 실시하는 방법이다. 목표파괴확률, (Pf)TM= 60%를 가정하여 앞의 접근법과 동일하게 모두 세 가지 관점에서 해석을 수행하였다. 먼저 Fig. 12(a)는 목표파괴확률에 도달하기 직전에 새것처럼 보수보강을 실시하는 방법에 대한 해석 결과이다. 또한 Fig. 12(b)는 최소수준의 보수보강을 자주 실시하는 경우에 대한 결과이고, Fig. 12(c)는 앞의 두 가지 경우를 혼합한 경우에 대한 해석 결과이다. 각각의 결과를 종합하면 대략 13년 간격으로 새것처럼 보수보강을 실시하던지 아니면 준공 후 첫 13년 되는 해에 최소수준의 보수보강을 실시하고 그 후 매 6년 간격으로 최소수준의 보수보강을 실시해야 된다. 또한 25년 간격으로 새것처럼 보수보강을 실시하되 그 중간에 파괴가 발생하지 않도록 13년과 6년이 되는 해에 최소수준의 보수보강을 실시해야 한다는 사실을 쉽게 알 수 있다.
마지막으로 앞에서 제시한 각각의 접근방법, 즉, 일정한 시간간격으로 보수보강하는 방법과 목표파괴확률에 따라 보수보강하는 방법에 대한 경제성 분석을 실시하였다. 경제성 분석은 인명손실과 같은 간접비용을 고려하지 않고 단순히 보수보강 비용만을 고려하여 수행하였다. 내구년수 동안 소요되는 총 보수보강비용을 TRC라 하면 다음 식 (17)을 정의할 수 있다.
여기서 nM은 내구년수 동안 수행되어야 하는 총 보수보강 횟수이고 CI는 구조물의 초기공사비를 의미한다. 또한 Pf (ti)과 (Pf)MT는 각각 보수보강 시점의 파괴확률과 보수보강 후 도달해야하는 목표파괴확률을 의미한다. 이는 피해정도에 따른 보수보강 비용이 달라진다는 것을 고려하기 위함이다. 여기서 일정한 시간간격으로 보수보강하는 방법에서 ti = i TM이 만족해야하고 목표파괴확률에 따라 보수보강하는 방법에서는 Pf (ti) = (Pf)TM이 만족되어야 한다. 식 (17)에서 t0는 초기상태를 의미한다. 따라서 초기상태에서 Pf (To) = (Pf)MT =(Pf)T를 만족한다. 만약 보수보강하기 전에 갑작스럽게 파괴되었다면 그 시점의 파괴확률 Pf (ti) = 1.0이 된다. 이는 구조물을 새롭게 건설해야 한다는 의미가 된다. 따라서 이 두 경우에서 (Pf)MT는 설계 목표파괴확률로 정의하면 된다. 식(17)을 이용하여 앞에서 제시된Fig. 11과 Fig. 12에 대한 초기공사비에 대한 총 보수보강 비용의 비를 산정하여 Table 3에 제시하였다. 본 연구에서는 새것처럼 보수보강을 실시하는 경우의 보수보강 목표파괴확률, (Pf)MT = (Pf)T= 2.0%, 최소수준의 보수보강을 실시하는 경우의 (Pf)MT = 12.5%를 사용하였다. 그러나 새것처럼 보수보강을 실시하는 경우와 최소수준의 보수보강을 실시하는 경우의 보수보강 목표파괴확률, (Pf)MT의 변화에 따른 추가적인 연구가 필요하다.
Table 3.
Ratio of total repairing cost to initial construction cost according to the maintenance methodologies of armor units of rubble-mound breakwater with the lifetime of 50 years
| Method based on a planned period, TM | Method based on a target probability, (Pf)TM | |||||
|---|---|---|---|---|---|---|
| Fig. 11(a) | Fig. 11(b) | Fig. 11(c) | Fig. 12(a) | Fig. 12(b) | Fig. 12(c) | |
| TRC/CI | 1.941 | 2.697 | 2.267 | 1.722 | 3.008 | 2.313 |
Table 3에 의하면 모든 경우에서 내구년수 동안에 소요되는 총 유지관리비용이 초기공사비보다 많이 소요됨을 알 수 있다. 또한 유지관리 시점을 어떤 방법으로 결정하느냐에 따라 비용의 차이가 많음을 알 수 있다. 본 예에서는Fig. 12(a)의 방법이 가장 경제적인 유지관리 방법임을 확인 할 수 있다. 따라서 이와 같은 해석으로 유지관리를 하게 되면 방법간에 비교가 가능하고 가장 경제적인 유지관리 방법을 찾을 수 있다. Table 3의 결과는 경사제 피복재의 유지관리를 위한 방법론을 제시하기 위한 예를 나타낸 것이다. 따라서 본 연구에서 고려하지 못한 간접비용이나 이자율과 관련된 현가문제도 추가적으로 해석되어야 한다.
5. 결 론
경사제 피복재의 안정성과 관련된 시간에 따른 피해 거동특성을 해석할 수 있는 MP 모형을 개발하였다. PP 모형에서는 해석할 수 없는 전단계의 피해정도와 현단계의 하중 조건에 대한 상관성을 직접적으로 고려할 수 있는 추계학적 확률 해석 모형이다. 하중발생에 대한 CP/RP 해석과 피해사상에 대한 DP 해석을 결합하여 수학적 모형을 수립하였다. 경사제 피복재의 피해수준 개념을 도입하여 피해정도에 따른 상태를 정의하였다. 특히 발생 가능한 피해수준과 내습하는 파랑의 수와 규모를 모두 확률변수로 고려하여 MCS 기법을 이용하여 이행확률을 산정하였다. 생성된 자료의 수에 따른 영향 및 누적피해수준의 분포함수를 분석하여 본 연구에서 개발한 이행확률 산정 방법의 타당성을 검증하였다. 재현기간에 따른 설계파고의 크기와 안전율에 따라 모두 6가지 경우에 대하여 이행확률을 산정하였다. 산정된 이행확률들은 확률적으로나 물리적으로 만족해야하는 제약조건들을 잘 충족한다.
한편 하중 발생사상도 정규분포와 지수분포로 구분하여 두가지 경우에 대하여 해석하였다. 동일 조건에서 경사제 피복재의 시간진행에 따른 파괴확률을 비교해 본 결과 두 가지 경우의 결과가 거의 동일하게 나타났다. 현재 대부분의 PP 모형에서 하중발생 사상을 정의하기 위하여 주로 지수분포를 사용하고 있는데 이를 정규분포로 대체하여도 결과의 차이는 나타나지 않는다는 의미이다. 또한 본 연구에서는 경사제 피복재의 설계와 관련하여 중요한 변수로 생각되는 재현기간 및 안전율의 변화에 따른 시간 의존 파괴확률을 산정하여 그 거동 특성을 자세히 비교 분석하였다. 특히 PP 모형에서는 해석할 수 없는 이전단계의 피해수준이 사용한계인 경우에 대한 해석도 수행하였다. 이전단계의 피해수준이 사용한계에 있는 경우의 결과를 허용한계에서 시작한 경우의 결과와 비교하여 시간의 진행에 따라 파괴확률이 어떻게 변하는지를 정량적으로 해석할 수 있었다.
마지막으로 유지관리에서 가장 중요한 보수보강 시점을 결정할 수 있는 두 가지 접근방법을 제시하였다. 하나는 시특법에서 사용하는 일정시간 간격으로 보수보강을 시행하는 방법이고 다른 하나는 목표파괴확률을 이용하는 방법이다. 두가지 접근방법에 근거하여 모두 6가지 경우로 보수보강될 때 파괴확률의 시간에 따른 변화를 해석하였다. 특히 각각의 경우에 대하여 경제성 분석을 함께 실시하여 내구년수 동안 소요되는 총 보수보강비용을 산정 비교하였다. 보수보강의 방법에 대한 규정보다는 보수보강을 수행하면 구조물의 안정성이 최초설계수준(허용한계수준)으로 돌아가거나 최소수준(사용한계수준)으로 돌아간다는 가정하에 보수보강시점을 결정 할 수 있는 추계학적 모형을 개발한 것이다.
따라서 본 연구에서 개발된 추계학적 MP 확률모형을 이용하면 경사제 피복재의 설계와 관련된 변수들의 변화에 따른 시간 의존 파괴확률을 해석할 수 있다. 또한 경제성 분석을 통해 내구년수 동안 경사제 피복재를 가장 경제적으로 유지관리할 수 있는 방법들 간의 상호 비교가 가능하다. 그러나 본 연구의 경우는 추계학적 MP 확률모형을 개발하고 그 적용 예를 제시한 것이기 때문에 설계 목표파괴확률이나 보수보강 목표파괴확률에 따른 다양한 조건에서의 해석이 추가적으로 수행되어야 한다.