1. 서 론
친수 및 여가활동을 위하여 호안 및 방파제와 같은 연안구조물의 사용자가 증가함에 따라 부주의 등으로 인한 안전사고가 빈번히 발생하고 있다. 특히, TTP와 같은 소파블록으로 피복되어 있는 중력식 호안 및 중력식 방파제 등은 이러한 안전사고를 가중시키는 요인으로 작용하고 있다. 언론보도(JTBC, 2015)와 Kim et al.(2017)에 따르면 2014년 실족으로 인한 추락사고가 총 95건(이 중에 사망사고는 26명), 2015년에 실족으로 인한 추락사고가 총 100여건(이 중에 사망사고는 약 20%)이 발생하였다. 이러한 안전사고는 TTP 표면에 부착되는 미끄러운 해조류에 의한 실족사고와 반사율의 저감을 위해 TTP 사이에 형성된 공극으로의 추락사고, 경우에 따라서는 사망사고로도 이어지는 불상사가 빈번히 발생하고 있다. 그리고, 매년 반복되는 폭풍파랑의 내습으로 중력식 호안 및 중력식 방파제에 피복된 TTP의 안정중량 부족으로 인한 산란과 기초지반의 세굴 등으로 인한 TTP의 활동으로 전술한 안전문제는 보다 악화되고, 또한 경관상에 악영향을 주면서 친수공간으로의 이미지가 저하되어 사용자 측면에서 악영향을 초래한다.
따라서, TTP 피복의 호안과 방파제에 항상 내재되어 있는 안전와 경관의 문제 등을 해결하기 위하여 저자 중의 1인은 유공회파(有孔回波) 블록을 고안하고, 제체의 내파안정성을 향상시키기 위하여 블록과 블록을 현장타설 말뚝으로 결속하는 공법(특허번호: 제10-2016-0107522호)을 개발하였다. 이러한 형식의 구조물을 격자블록결속 호안(interlocking revetment bound latticed blocks) 혹은 격자블록결속 방파제(interlocking breakwater bound latticed blocks)로 칭하며, 다음의 Figs. 1과 2에서 실제현장에 설치된 호안의 사례를 제시한다.
본 연구에서는 전술한 유공회파블록제의 기능성을 보다 향상시킨 것으로, 어항 등과 같은 소규모 항에서 항내정온도 및 낚시와 같은 레크리에이션과 친수할동 등에서 안전을 동시에 확보할 수 있으며, 더불어 우수한 경관을 유지할 수 있는 격자블록결속에 의한 신형식의 원형유공케이슨 방파제를 개발한다. 이 방파제의 형식은 전술한 유공회파블록제에서 현장 타설 말뚝으로 블록과 블록을 결속하는 공법은 동일하지만 반사율을 보다 저감시키기 위하여 유공회파블록의 배후에 슬리트케이슨 방파제와 같이 유수실을 적용한 경우이다. 여기서, 블록과 블록을 결속하여 내파안정성을 도모하는 공법은 대규모 항만의 외곽 방파제에서 케이슨과 케이슨을 뒷채움재 혹은 케이블 등으로 결속하여 장대케이슨을 계획 · 확보하는 Park et al.(2016)와 Seo et al.(2015)의 연구와 동일한 것으로 판단되며, 이러한 결속 방파제는 특히 경사입사파에 대해 내파안정성이 탁월한 큰 장점을 가진다. Fig. 3에서 본 연구의 격자블록결속에 의한 원형유공케이슨 방파제의 시공순서를 모식적으로 나타낸다. 구성요소인 개개의 블록은 소규모항에서 외곽방파제 혹은 호안을 대상으로 하기 때문에 중량이 크지 않아 육상에서 공장제작이 가능하고, FD 선을 이용하지 않고 일반 Barge 선으로 이송이 가능하기 때문에 공기가 짧고, 경제적이다. 하지만, 본 원형유공케이슨 방파제가 실해역을 대상으로 다수 계획되고 있지만 그의 기능성과 내파 안정성이 명확히 규명되어 있지 않으므로 기존의 슬리트케이슨 방파제나 혼성방파제에 대한 결과들이 그대로 적용되는 실정을 감안하면 원형유공케이슨 방파제에 대한 기능성(반사율과 월파량)과 내파안정성(파압분포)이 시급히 해결되어야 하는 과제인 것으로 판단된다.
이상에서 나타낸 본 연구의 격자블록결속에 의한 원형유공케이슨 방파제는 격자블록결속에 의해 내파안정성을 향상시킨다는 구조적인 특성을 제외하면 일반적인 슬리트케이슨 방파제와 유사한 형상을 갖는다. 따라서, 본 연구에서 검토 · 논의하는 월파량과 반사율(기능성) 및 작용파압(안정성)에 대한 기존의 슬리트케이슨 방파제의 주요 연구결과들을 요약하면 다음과 같다.
먼저, 대표적인 예로 Jarlan(1961)의 연구를 들 수 있고, 이로부터 슬리트케이슨이 처음 계획 · 설계되었다고 하여도 과언이 아니다. Boivon(1964)는 슬리트케이슨 전면에서 파고를 실험으로 측정하여 전면의 유공율과 유수실 폭이 반사율에 영향을 미치는 주요 인자이며, 횡슬리트, 종슬리트 및 원통형의 유공과 같이 전면의 유공형상이 반사율에 미치는 영향은 크지 않다고 결론지었다. Kondo(1979)는 선형천수파이론을 기반으로 유수실이 1개 혹은 2개인 슬리트케이슨의 반사율을 평가하는 해석모델을 개발하였으며, 유수실이 1개보다는 2개의 경우가 반사율 저감에 더 효과적이라는 것을 규명하였다. 반면, Fugazza and Natale(1992)는 포텐셜이론과 수리실험을 기반으로 한 해석모델로부터 유수실이 1개인 경우가 실제 적용범위에서 가장 크게 반사율을 저감시킨다는 Kondo(1979)와는 다른 결론을 지었으며, 반사율은 유수실 폭과 관련되고, 유수실 폭이 파장의 1/4배일 경우가 가장 작은 반사율에 도달하다는 사실을 규명하였다. Huang et al.(2011)은 광범위한 주파수 영역에서 복수의 유수실인 경우가 작은 반사율을 얻을 수 있다고 결론지었다. Tanimoto and Yoshimoto(1982)는 슬리트의 유공벽 높이와 수심의 비가 0.33~0.83의 범위일 경우 유수실 폭과 파장의 비가 0.15~0.20의 범위에서 반사율이 가장 작다는 사실을 수리실험으로부터 규명하였다. Suh et al.(2006)은 Galerkin 고유함수법(Galerkin-eigenfunction method)과 유한차분법에 기초하여 기초사석의 마운드 상에 설치된 슬리트케이슨에 의한 반사율을 추정하였으며, 2차원수리실험을 실시하여 검증하였다. 그러나, 수치해석에서는 속도포텐셜의 소멸파 성분이 무시되었고, 2차압력강하조건에 선형화된 모델이 적용되었다. Garrido and Medina(2012)는 Jarlan 형식의 방파제에 인공신경망을 기반으로 반경험적 모델을 적용하여 추정한 결과와 수리실험결과를 비교하였으며, Meringolo et al.(2015)은 SPH(Soothed Particle Hdrodynamics)법을 이용하여 2차원파동장에서 파와 슬리트케이슨과의 상호작용을 연구하였다.
다음으로, 슬리트케이슨에 작용하는 파압분포에 대해서는 대표적으로 Takahashi 방법(Takahashi et al., 1992, 1996; Tanimoto and Takahashi, 1994)과 Tabet-Aoul and Lambert 방법(Tabet-Aoul and Lambert, 2003), 그리고 DUT(Dalian University of Technology) 방법이 제안되어 있다. 여기서, Takahashi 방법은 Goda 식(Goda, 2000)을 수정한 방법으로 Goda 식에서 파압보정계수 λ1, λ2, λ3를 구조물에 작용하는 파의 위상에 따라 재산정하여 적용하였다. Takahashi(1996)는 6개의 파위상에 따라 보정계수 λ1, λ2, λ3를 제시하고 있지만 이글루블록이나 워록과 같은 블록 방파제에 대해서는 λ1, λ3 = 0.8~1.0, λ2 = 0을 적용하고, Tanimoto et al.(1981)은 곡면슬리트케이슨, 다공케이슨, 종슬리트케이슨 등의 경우 평균적으로 λ1, λ3 = 1.0, λ2 = 0을 적용하였다. Tabet-Aoul and Lambert 방법은 수리실험결과를 기반으로 Takahashi 방법과 동일하게 Goda 식을 수정한 방법으로 Takahashi(1996)가 제시한 6개의 파위상에서 파곡시의 파위상에 대한 위상조정계수(phase adjustment factor)와 전면 유공벽의 유공율을 파라메터로 추가하였다. 그러나, Chen et al.(2005)는 유수실 폭과 파장의 비가 0.1보다 작은 경우 Tabet-Aoul and Lambert 방법은 수리실험결과보다 작은 값이 산출된다는 것을 나타내었다. DUT 방법은 1998년부터 중국에서 수치해석, 이론해석 및 수리실험으로부터 슬리트케이슨에 작용하는 파압분포를 검토한 방법이다. 또한, Chen et al.(2003, 2007)은 2차원유한차분법에 기반한 RANS 방정식을 이용하여 규칙파 및 불규칙파의 작용 하 슬리트케이슨에 작용하는 파압을 산정하였고, Li et al.(2002, 2003a), Teng et al.(2004), Liu et al.(2006, 2007, 2008)는 확장고유함수법을 이용하여 슬리트케이슨에 작용하는 파압을 산정하였으며, Liu(2003), Jiang(2004), Ma(2004), Li et al.(2003b, 2005a, 2005b)는 2차원 및 3차원수리실험으로 평행입사파와 경사입사파가 슬리트케이슨에 작용하는 파력을 산정하였다. 또한, Lee et al.(2010)은 혼상류의 2차원 및 3차원수치해석법으로부터 슬리트케이슨에서 반사율과 작용파압에 대한 2차원해석결과와 3차원해석결과의 차이점을 검토하였으며, Lee et al.(2011)은 Lee et al.(2010)과 동일한 구조물과 해석법을 적용하여 규칙파와 고립파의 작용시 각각의 작용파압을 산정하여 차이점을 비교 · 검토하였다. 한편, 본 연구의 원형유공케이슨 방파제와 같이 전면이 원형인 유공을 갖는 케이슨 방파제에 대한 연구로는 Tanimoto et al.(1976)을 들 수 있으며, 그들은 원통형으로 천공된 케이슨 방파제를 대상으로 불규칙파를 작용시켜 유수실 폭의 변화에 따른 반사율의 변화를 실험으로 추정하였고, Tamrin et al.(2014)은 원통형으로 천공된 블록을 대상으로 규칙파를 작용시켜 반사율을 실험으로 추정하였으며, Franco and Franco (1999)는 3차원수리실험을 통하여 원통형유공케이슨 방파제에서 월파량을 산정하였다.
이상에서는 다양한 형상의 유공을 갖는 슬리트케이슨에 대한 기존의 연구를 검토하였으며, 이들의 대부분은 기능성과 안정성 모두에 관점을 둔 접근도 있지만 대부분은 기능성 혹은 안정성 중의 하나에 관접을 두고 수치적 혹은 실험적으로 검토하였다. 여기서, 검토된 단면은 정수면을 중심으로 상하의 일부 구간에만 슬리트를 적용한 경우가 대부분이고, 또한 3차원보다는 2차원적인 접근이 대부분이었다. 또한, 수치해석적인 접근에서는 포텐셜이론 등과 같은 선형적인 접근이 주를 이루었으며, 본 연구에서와 같이 쇄파를 동반한 강비선형의 파동장도 정밀하게 추정할 수 있는 수치적인 접근은 거의 없었다.
한편, 최근들어 GNU-GPL(공중사용허가서) 라이선스 기반의 다양한 CFD 오픈소스 코드가 공개됨에 따라 이러한 오픈소스 코드를 활용한 공학적 문제를 해결하고자 하는 사례가 증가하고 있다(Chen et al., 2014; Horgue et al., 2015; Safti, 2013). 특히, CFD 오픈소스 코드 중에 OpenFOAM®(Open source Field Operation And Manipulation)은 연속체역학 전산해석 프로그램으로, 영국의 Imperial college에서 개발이 시작되어 2004년 OpenCFD Ltd.에서 GNU-GPL(공중사용허가서) 라이선스로 공개된 오픈소스 코드이다. 공개된 이후로 OpenFOAM®은 다양한 분야에서 그 사용목적에 따라 지속적인 개발과 수정이 이루어져 왔으며, 수정된 코드의 재배포도 활발하게 이루어지고 있다. 해안 및 해양공학 분야에 있어서도 Higuera et al.(2015)에 의해 OpenFOAM®에 수치적인 조파기능과 반사파의 제어기능이 추가적으로 고려된 OLAFOAM(olaFOAM Reference Manual; https://github.com/phicau/OLAFOAM/blob/master/reference.zip)이 공개되었지만 국내에서는 Lee et al.(2016)을 제외하면 이를 활용한 연구 예는 거의 없다.
따라서, 본 연구에서는 Navier-Stokes solver의 VARANS 방정식에 기초한 OLAFOAM(Higuera et al., 2015)을 적용하여 Fig. 3에서와 같이 전면의 원형유공은 완전히 천공되어 배면의 유수실과 연결되는 구조로 되어 있는 원형유공케이슨 방파제가 기초사석마운드 상에 놓인 경우를 대상으로 수리특성을 파악하기 위한 3차원수치해석을 수행하였다. 슬리트케이슨에 작용하는 파압을 산정에 대한 OLAFOAM의 적용성 검증을 위해 Wang et al.(2011)의 결과 및 불규칙파 조파에 대한 비교 · 검증을 수행하였다. 검증된 수치해석결과를 바탕으로 불규칙파랑이 작용하는 신형식의 3차원원형유공케이슨 방파제를 대상으로 유수실 폭, 입사파고 및 주기의 변화에 따른 반사율, 월파량, 그리고 전면 유공벽, 케이슨 저면 및 유수실 후면벽에 작용하는 파압분포 등과 같은 수리학적 특성을 비교 · 검토하였다.
2. 수치해석이론
여기서, t는 시간, xi는 공간벡터좌표, ρ는 후술하는 액체와 기체 상태를 고려한 혼상유체의 밀도, ui와 uj는 속도벡터, p*는 Pseudo-dynamic 압력, Xj는 위치벡터, φ는 공극률, D50은 중앙입경, μeff는 μ + νturb로 μ는 점성계수이고, νturb는 난류동점성계수이며, [CT]는 투과성 구조물에 유체저항으로 다음의 식(3)과 (4)으로 주어진다.
여기서, α, β는 Engelund 공식(1953)을 van Gent(1995)가 수정하여 제시한 마찰계수로 자세한 사항은 후술되지만, α는 선형마찰계수이고, β는 비선형마찰계수이다. KC는 Keulegan-Carpenter 수로 TouM/D50φ를 나타내며, To은 진동주기이고, uM은 최대진동속도이다. 또한, C는 del Jesus(2011)의 연구결과에 따라 일정치 C = 0.34로 주어지는 계수이다. 식(4)에서 제시된 바와 같이 투과성 구조물에 의한 저항항에서 α와 β는 매질의 형상, 종횡비 또는 매질의 방향 등에 의해 영향을 받는 상수이며, van Gent(1995)가 제시한 α = 1000과 β = 1.1의 값이 해안공학 분야에 널리 적용되고 있지만 다양한 실험을 통하여 얻어진 값을 많은 문헌에서 확인할 수 있다.
한편, OpenFOAM®을 이용하여 저항계수를 재산정한 Jensen et al.(2014)는 Reynolds 수에 따라 층류흐름(Forchheimer flow), 층류와 난류가 혼합된 흐름(Forchheimer/turbulent flow) 및 난류흐름(turbulent flow)으로 각각 나누어서 수치적으로 해석하고, 실험결과와 비교하였다. 층류흐름에 대해서는 모래는 아니지만 모래입경에 속하는 중앙입경 D50 = 2 mm, 공극률 φ = 0.34의 다공성매질에 단파를 작용시켜 수행한 Billstein et al.(1999)의 실험이었고, 층류와 난류가 혼합된 흐름애 대해서는 중앙입경 D50 = 1.59 cm, 공극률 φ = 0.49의 쇄석에 단파를 작용시킨 Liu et al.(1999)의 실험이었으며, 난류흐름의 경우는 중앙입경 D50 = 2.5 cm, 공극률 φ = 0.41의 유리구슬에 단파를 작용시킨 Billstein et al.(1999)의 실험이었다. 최종적으로, Jensen et al.(2014)는 이러한 3가지 흐름상태의 모두를 만족하는 저항계수값으로 α = 500, β = 2.0을 제시하였으며, 따라서 본 수치해석에서의 저항계수값으로 Jensen et al.(2014)의 결과인 α = 500, β = 2.0을 적용하였다.
또한, 자유수면의 추적을 위해 계산 셀 내에서 유체의 점유율을 나타내는 VOF 함수를 이용하며, VOF 함수에 대한 이류방정식으로는 액체가 기체로부터 압축되는 것을 방지하고 VOF 함수의 값이 0 ≤ F ≤ 1의 값을 유지하기 위하여 인공압축항(artificial compression term) (∂uic/∂t)F(1 − F)를 고려한 식(5)를 적용한다.
여기서, u i c = m i n [ c α | u i | , m a x ( | u i | ) ]
불규칙파는 선형파이론으로부터 얻어진 성분파의 주파수에 하나씩 순번을 붙여서 이를 무한급수의 합으로 고려된다. 수치조파에서는 조파지점에서 수면파형 η, 수평 및 연직유속 u, w의 시간변동이 필요하며, 이들은 각각 식(6)~(8)로 주어진다.
여기서, εm은 random한 위상각, fm은 주파수, am은 진폭, km은 파수, M은 성분파의 수, h는 수심이다. 그리고, 연직좌표 z는 정수면에서 연직상방을 (+)으로 취하며, εm 및 fm의 선택방법은 후술되며, 진폭 am은 다음의 식(9)로 정의된다.
여기서, Δf는 주파수폭, S(f)는 파랑에너지밀도이며, 불규칙파의 스펙트럼은 불규칙파를 모의하는 데에 널리 사용되고 있는 식(10)의 Modified Bretshneider-Mitsuyasu(Goda, 1988) 스펙트럼을 적용하였다.
여기서, H1/3은 유의파고, T1/3은 유의파주기를 각각 나타낸다. 또한, 주파수 fm의 선택방법에는 주파수스펙트럼을 등구간으로 분할하는 방법과 각각의 성분파의 진폭이 거의 같도록 하는 등에너지로 분할하는 방법 등이 있다. 본 연구에서는 Modified Bretshneider-Mitsuyasu(Goda, 1988)의 스펙트럼에 대해 등에너지로 스펙트럼을 분할할 수 있는 Goda(2000)에 의해 제안된 다음의 식(11)을 이용하여 주파수 fm을 선택하였다.
3. 수치해석결과의 검증
3.1 슬리트케이슨에 작용하는 파압(동압)
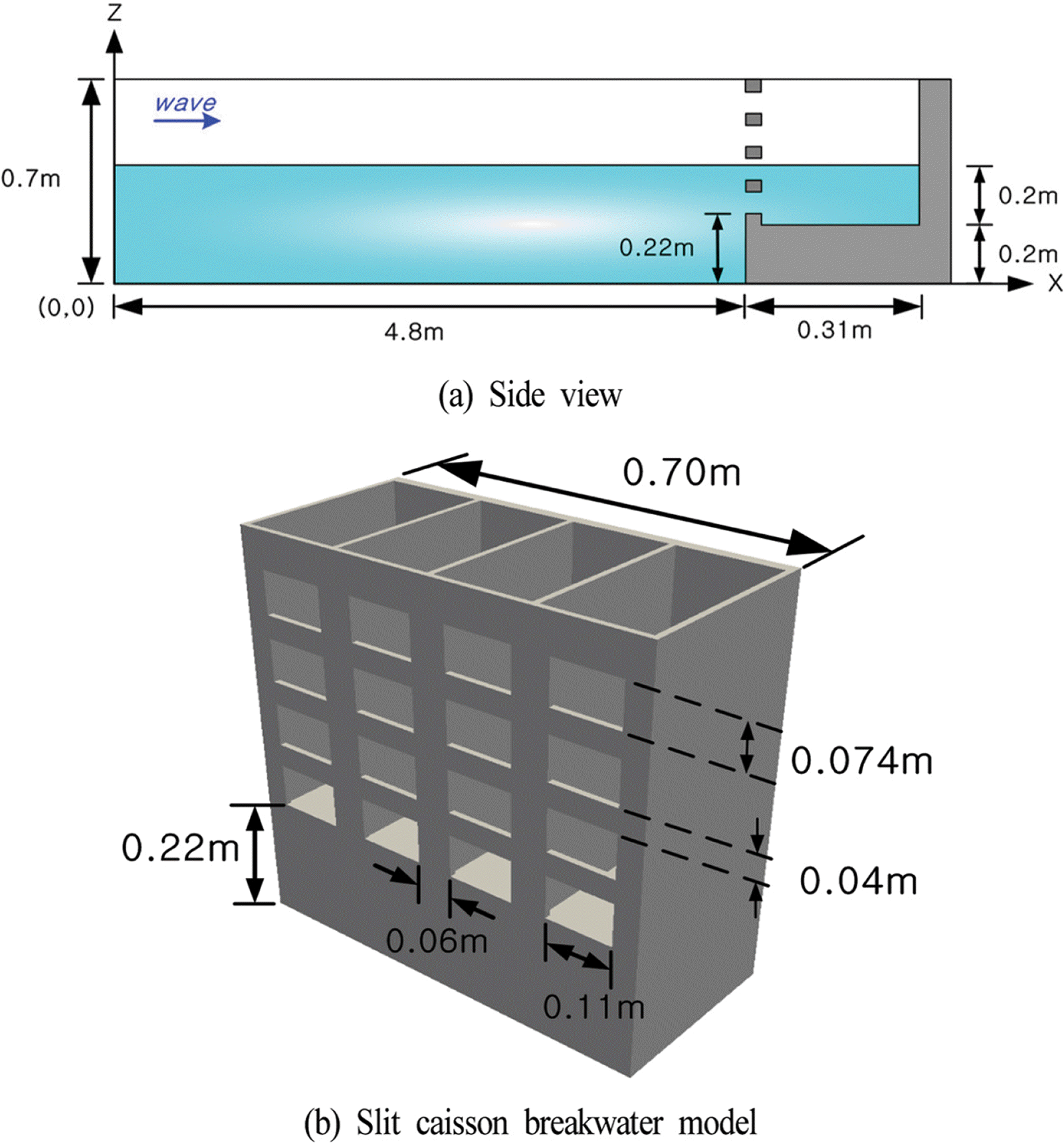
Wang et al.(2011)은 Fig. 4(a)와 같은 일정수심 h = 0.4m의 3차원파동장에 설치된 높이 0.7 m의 슬리트케이슨에 규칙파를 작용시켜 전면 유공벽과 유수실 후면벽에서 파압(동압) 변동을 수리실험으로부터 측정하였다. 수리실험에 사용된 조파수조는 길이 56 m, 폭 1.0 m, 높이 0.7 m이며, 조파판의 반대 수조 끝단에 슬리트케이슨을 설치하였다. Fig. 4(b)는 슬리트케이슨에서 유공벽의 제원을 나타내며, 슬리트의 두께 및 유수실 측벽의 두께는 1 cm로 구성하였다. 입사파랑은 파고 H = 6 cm, 주기 T = 1.4 s의 규칙파를 적용하였으며, Fig. 5는 전면 유공벽과 유수실 후면벽에서 파압계의 부착위치를 나타낸다.
OLAFOAM에 의한 본 수치해석에서는 계산비용의 감소를 위해 수리실험에 비해 축소된 길이 5.12 m의 수치조파수조를 적용하였고, 슬리트케이슨은 조파판으로부터 4.8 m 이격된 지점에 설치하였다. 벽면경계조건으로는 바닥 및 양측면에 Slip조건을 적용하였으며, 격자크기는 Δx = 1.0 cm, Δy = 0.5 cm, Δz = 1.0 cm로 총 격자수는 5,076,000개로 구성하였다. 수치조파에 적용된 파는 Cnoidal 파이고, 적용된 난류모델은 LES모델(Ghosal et al., 1995)이다.
Fig. 6은 Fig. 5에 나타내는 슬리트케이슨의 전면 유공벽과 유수실 후면벽에 작용하는 파압의 시간변동에 대해 본 연구의 수치해석결과와 Wang et al.(2011)의 실험결과를 비교한 것으로, 그림에서 1~3지점은 전면 유공벽에 대한 경우를, 4~6지점은 유수실 후면벽에 대한 경우를 각각 나타낸다. 여기서, 1지점에서 3지점으로 갈수록, 그리고 4지점에서 6지점으로 갈수록 정수면에 가까워지고, 3과 6지점은 바로 정수면에서 수평파압을 나타낸다. 그림을 살펴보면 정수면 아래에 위치한 1과 2지점에서는 비선형파압의 발생으로 비대칭적인 파압변동을 나타내며, 4와 5지점에서도 동일한 비선형파압에 의한 비대칭변화를 나타내지만 1과 2지점보다는 그의 정도가 약하다는 것을 알 수 있다. 이는 전면 유공벽과 후면 불투과벽체의 형상적인 차이와 반사파의 발생위치의 차이로 판단되며, 1과 2지점에 영향을 미치는 반사파는 전면 유공벽의 불투과벽체와 유수실 후면의 불투과벽체로 각각 구성되기 때문에 각각은 위상차를 가지고 1과 2지점에서의 파에 영향을 미친다. 정수면에 위치하는 3과 6지점에서는 파곡부분이 통과할 때 공기중으로 들어나기 때문에 부압은 거의 나타나지 않고 정압이 크게 나타난다. 각 지점에서 최대파압의 크기를 살펴보면 1->2->3지점으로 갈수록, 그리고 4->5->6지점으로 갈수록 증가하므로 정수면에서 가장 큰 파압을 나타내는 것을 알 수 있다. 수리실험결과 및 수치해석결과를 비교하면 6지점의 파곡부분에서 약간의 차이는 인정되지만 전반적으로 대응성은 매우 탁월한 것으로 판단된다. 따라서, OLAFOAM에 의한 수치해석결과는 슬리트케이슨의 전면 유공벽과 유수실 후면벽에 작용하는 파압의 변동과정에서 실험치를 고정도로 재현하므로 슬리트케이슨과 유사한 형태를 갖는 원형유공형케이슨으로의 적용성이 높은 것으로 판단된다.
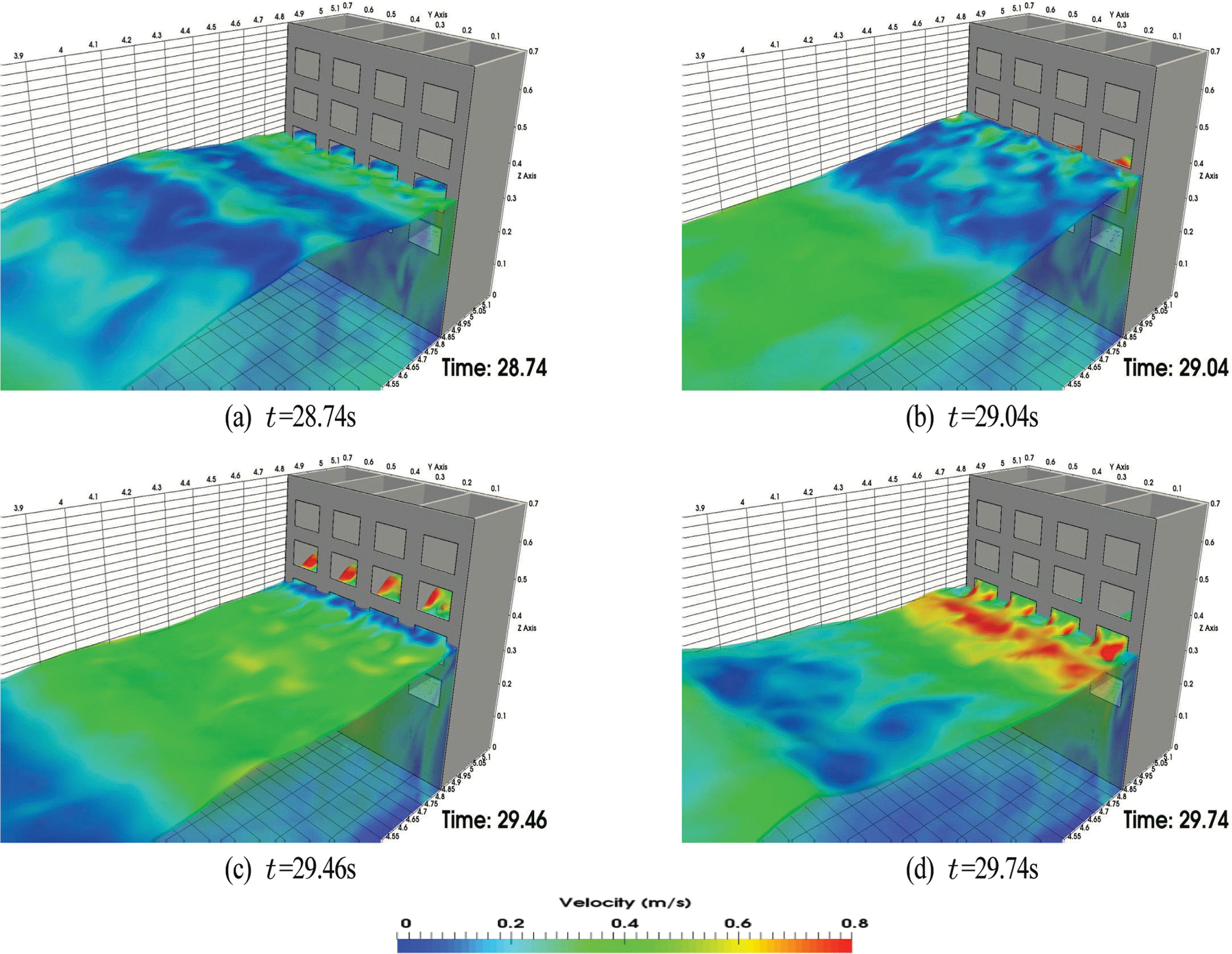
Fig. 7은 슬리트케이슨 주변에서 수위의 3차원적인 시 · 공간변화과정을 가시화한 결과이다. 그림을 살펴보면 입사파에서 파봉 근방의 위상에서 파가 전면 유공부로 유입되고, 반대로 파곡 근방의 위상에서 전면 유공부로 다시 유출되는 일련의 시간변동에 따른 수위변동과정을 시각적으로 확인할 수 있다.
3.2 3차원불규칙수치파동수조에서 조파검증
본 연구의 OLAFOAM에 의한 불규칙파의 조파성능을 검증하기 위하여 구조물이 설치되지 않은 수심 h = 10.1m의 3차원수치파동수조에서 유의파고 H1/3 = 3.0m, 유의주기 T1/3 =11.0 s를 목표로 불규칙파를 조파하였다. 적용한 스펙트럼은 식(11)에 제시한 Modified Bretshneider-Mitsuyasu 스펙트럼(Goda, 1988)을 적용하였으며, 150개의 성분파를 선형중첩하여 조파하였다. 그리고, 파랑의 반사 및 재반사가 해석영역의 파동장에 미치는 영향을 방지하기 위하여 수조 끝단에는 감쇠경계를 적용하였고, 조파판에는 조파와 감쇠가 동시에 작용하는 Pure active wave absorption 경계를 적용하였다. 이러한 조건으로부터 계산된 불규칙파형과 주파수스펙트럼이 Figs. 8(a)와 8(b)에 각각 제시되어 있고, 동시에 Fig. 8(b)에는 목표한 Modified Bretshneider-Mitsuyasu 스펙트럼(Goda, 1988)도 병기되어 있다. 그림을 살펴보면 장시간의 해석에도 평균수위상승과 같은 특이한 사항이 나타나지 않았으며, 영점상향교차법에 의한 파별해석으로부터 얻어진 유의파고 H1/3 =3.067 m, 유의주기 T1/3 = 11.014 s와 입력치가 매우 잘 일치하는 결과를 얻을 수 있었다.
4. 수치해석 결과
4.1 계산조건
Fig. 9와 같은 일정수심 h = 10.1m를 갖는 3차원파동장에 설치된 원형유공케이슨 방파제를 대상으로 3차원수치파동수조를 구성하였다. 수조의 크기는 폭 19.2 m, 높이 22 m이며, 길이는 반사율을 측정하기 위해 조파판과 구조물 사이 2L(L: 파장), 구조물 길이 42 m, 구조물 배후에서 수조 끝단까지 55 m를 고려하여 전체 2L + 97 m로 구성되었다. 그리고, 수조 끝단에는 반사파를 제어하기 위해 감쇠영역을 적용하였다. 바닥경계조건 및 양측면경계는 Slip 조건이고, 격자는 Δx =0.5 m, Δy = 0.4m, Δz = 0.5m의 크기를 가지며, 적용한 난류모델은 LES 모델이다.
Fig. 10은 케이슨의 제원을 나타내며, 케이슨의 폭은 20 m, 높이는 11.2 m이며, 전면 유공벽에 해측으로 직경 1.2 m의 원형 구멍이, 육측으로 직경 0.6 m의 원형 구멍이 원뿔 관통형을 형성하고 있다. 정수면 근방에 형성되는 일반적인 슬리트케이슨과는 달리 본 케이슨은 원형유공이 케이슨 하단부터 천단까지 형성되어 있고, 유공율은 해측에서 44.18%, 육측에서 11.04%이다. 유수실은 0.8 m의 격벽으로 총 6개로 나눠져 있고, 각 유수실의 길이는 2.4 m이며, 폭은 1, 2, 3, 4, 5, 6 m로 각각 구성되었다. 또한, 유수실은 상치구조물이 없고, 케이슨 바닥부터 천단까지 연결되어 있다. 유수실 격벽은 폭 0.5 m, 길이 1.8 m의 직사각형 유공부를 가지며, 폭이 1 m일때 유공부는 1열로, 폭이 1 m 씩 증가할 때 유공부의 열이 하나씩 추가되며, 유수실 폭이 6 m일 때는 6열의 유공부로 구성된다. Fig. 9에 나타내는 바와 같이 케이슨 아래는 높이 1.6 m의 기초사석과 그 위에 두께 1.2 m의 피복석이 놓여 있고, 전 · 후의 비탈면은 1:1.5의 경사를 가진다. 기초사석은 공극률 φ = 0.28, 중앙입경이 D50 = 2.75 cm이고, 피복석은 공극률이 φ = 0.3, 중앙입경이 D50 = 20 cm인 투과성 재료이며, 저항계수로는 Jensen et al.(2014)이 제시한 α = 500, β = 2.0의 값을 적용하였다.
본 연구에서는 유수실과 구조물 전면에 유공부가 없는 혼성방파제의 경우도 동일한 조건 하에 수치해석을 수행하여 월파량, 반사율 및 파압분포 등의 결과를 본 연구의 원형유공케이슨의 경우와 비교하였으며, 이하에서는 유수실 폭이 1.7 m인 경우를 CASE 1, 폭이 2.7 m인 경우를 CASE 2, 폭이 3.7 m인 경우를 CASE 3, 폭이 4.7 m인 경우를 CASE 4, 폭이 5.7 m인 경우를 CASE 5, 폭이 6.7 m인 경우를 CASE 6로 나타내었고, 혼성방파제의 경우를 CASE 0으로 나타내었다.
Table 1에 나타낸 바와 같이 불규칙파랑의 조건은 파고변화에 따른 구조물의 성능비교를 위하여 유의주기(T1/3 = 11 s)를 고정하고, 유의파고를 H1/3 = 2.5, 3.0, 3.5 m로 조정하였으며, 주기변화에 따른 구조물의 성능을 비교하기 위하여 유의파고(H1/3 = 3.0m)를 고정하고, 유의주기를 T1/3 = 11.0, 13.0, 15.0 s로 조정하였다.
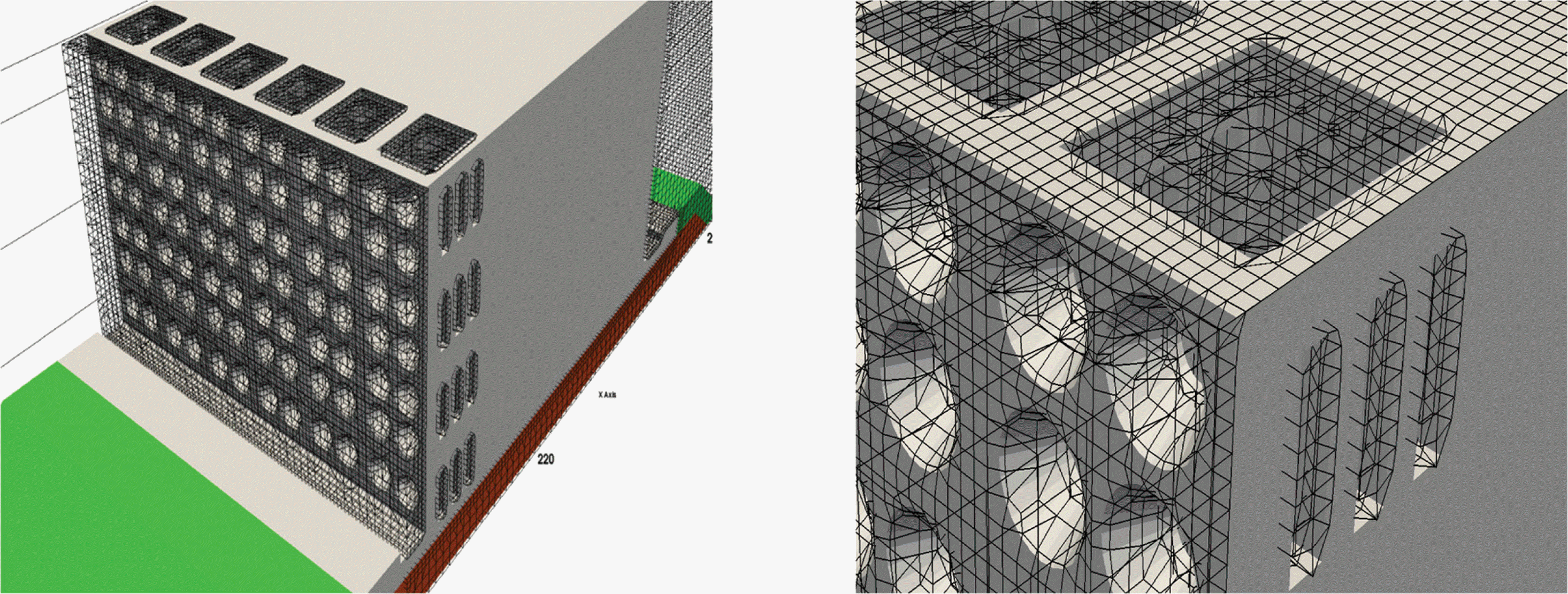
Fig. 11은 OpenFOAM®이 제공하는 SnappyHexMesh를 사용하여 케이슨 전면 유공벽 주변 및 유수실의 격자를 구성한 예를 나타낸다.
4.2 월파량
Fig. 12는 단위폭당 월파량을 나타낸 것이며, 케이슨 폭을 따라 케이슨 천단의 끝단에서 수조 상부경계까지 각 격자에 유속계를 설치하고, 각 유속계에서 산출된 유량을 합한 후에 경과시간과 케이슨 폭 19.2 m를 나누어 단위폭당 월파량으로 산정하였다. Fig. 9(a)는 유의주기(T1/3 = 11.0 s)를 고정하고, 유의파고를 H1/3 = 2.5, 3.0, 3.5 m로 변화시켜 산정한 결과이고, Fig. 9(b)는 유의파고(H1/3 = 3.0m)를 고정하고, 유의주기를 T1/3 = 11.0, 13.0, 15.0 s로 변화시켜 산정한 월파량이다. 그림을 살펴보면 각 케이스에서 월파량은 Q = 0.0012~0.117m3/s/m의 범위 내에 존재하며, 적용된 모든 케이스의 원형유공케이슨 방파제가 혼성방파제보다 월파량이 작다는 것을 확인할 수 있다. 이러한 결과는 기본적으로 본 원형유공케이슨방파제가 혼성방파제보다 반사율이 작기 때문이다. 그리고, 원형유공케이슨에서도 유수실 폭이 넓을수록 월파량이 감소하는 결과를 나타내며, 또한 유의파고가 클수록, 유의주기가 길수록 월파량이 증가하는 경향을 보인다. 이러한 경향 역시 전술한 반사율과 밀접한 연관성을 가지기 때문이다. 또한, 월파량은 주기에 비해 파고에 보다 민감함을 확인할 수 있다.
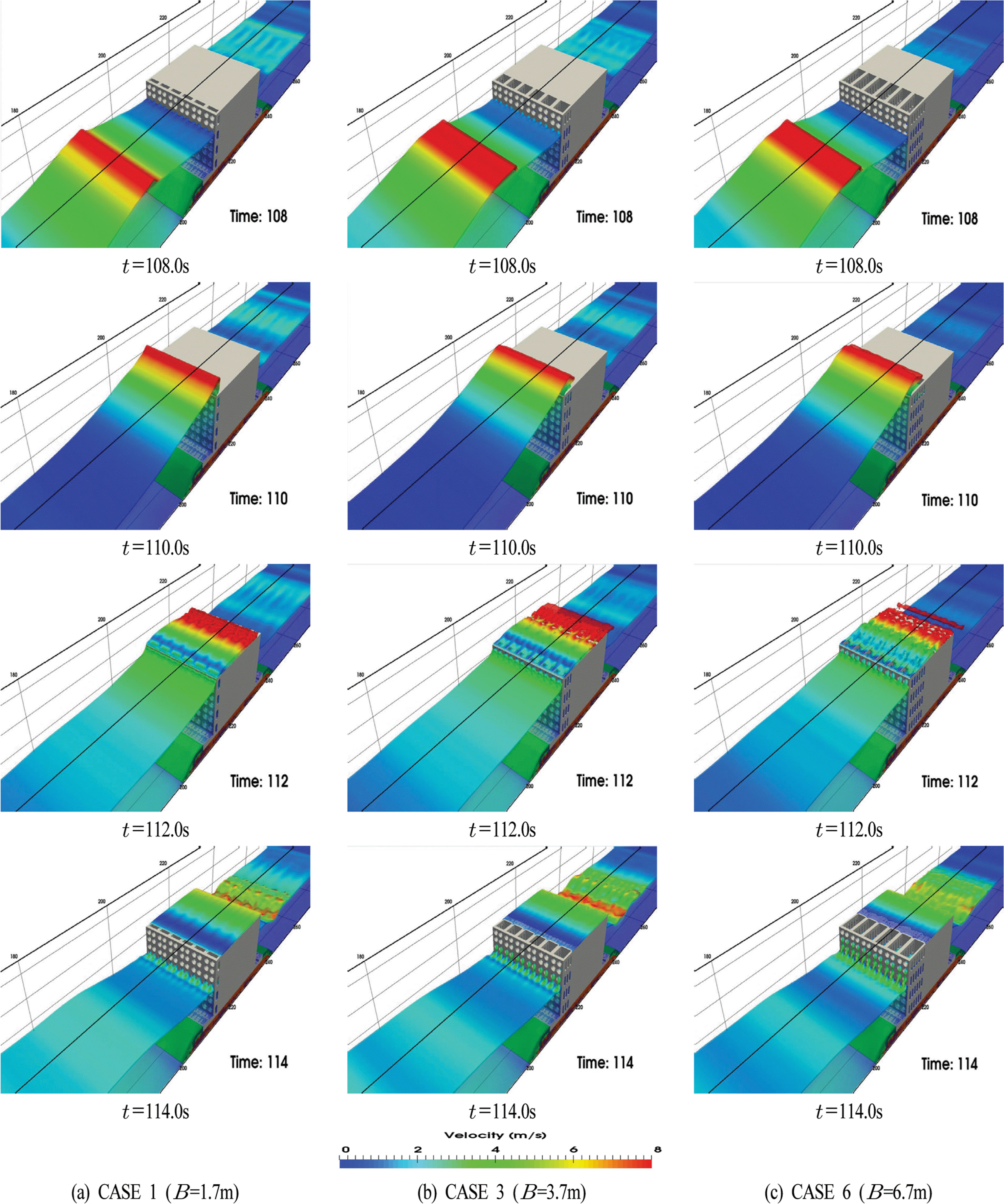
Fig. 13은 CASE 1, CASE 3 및 CASE 6에서 유의파고 H1/3 = 3.5 m, T1/3 = 11.0 s의 경우에 구조물 주변에서 수위의 시 · 공간적인 3차원변화과정을 나타낸 것이다. 그림으로부터 전면 유공부를 통한 입사파의 유수실로 유입, 반사 및 유출, 그리고 주변에서 파랑변형과 천단상으로 월파과정 등을 시각적으로 명확히 확인할 수 있다. 또한, 유수실 폭이 넓을 수록 케이슨 천단 상으로의 월파량이 작아진다는 것도 확인할 수 있다.
4.3 반사율
Fig. 14는 유수실 폭에 따른 반사율 KR의 변화를 나타낸 것으로, 전술한 Fig. 12와 같이 Fig. 14(a)는 유의주기(T1/3 = 11.0 s)를 고정하고, 유의파고를 H1/3 = 2.5, 3.0, 3.5 m로 변화시킨 경우이고, Fig. 14(b)는 유의파고(H1/3 = 3.0m)를 고정하고, 유의주기를 T1/3 = 11.0, 13.0, 15.0 s로 변화시킨 경우이다. 반사율을 추정하기 위하여 케이슨 전면으로부터 L + h(h: 수심)만큼 떨어진 지점에 파고계를 간격 0.5L로 수조의 길이 방향으로 두 열(하나의 열에 수조의 폭방향으로 5개의 파고계를 설치하고 독치를 평균하였음)로 설치하였으며, Goda and Suzuki(1976)에 의한 2점법을 사용하여 반사율을 추정하였다. Fig. 14에는 Tanimoto et al.(1976)에서 의한 얻어진 반사율의 상한치와 하한치도 같이 병기하였으며, 동시에 유수실 폭에 따른 결과를 명확하게 구분할 수 있도록 상세도도 추가하였다. 여기서, Tanimoto et al.(1976)은 유수실 폭 B와 파장 L과의 비 B/L에 대해 B/L > 0.05의 경우에만 실험을 수행하였고, B/L < 0.05의 경우에는 추세선을 이용하여 반사율을 추정하였다. 본 연구에서는 B/L = 0.012(T1/3 = 15.0 s, B = 1.7m)~0.065(T1/3 = 11.0, B = 6.7m)의 범위에 속하며, Fig. 14(a)는 B/L = 0.065의 경우이고, Fig. 14(b)는 B/L = 0.05의 경우이다. 그림을 살펴보면 각 케이스에서 반사율은 KR = 0.567~0.731의 값을 나타내며, 모든 케이스가 Tanimoto et al.(1976)에 의한 실험결과의 범위에 존재하는 것을 확인할 수 있다. 여기서, 입사파고가 증가할수록 감소하고, 주기가 길수록 반사율이 증가하는 경향을 나타낸다. 유수실 폭의 변화에 따른 반사율을 비교하면 유수실 폭이 넓을수록 감소하며, 유공과 유수실이 없는 혼성제 CASE 0의 경우는 원형유공케이슨의 다른 케이스보다 상대적으로 큰 반사율을 나타낸다. 이러한 결과는 유수실 내에 파랑에너지가 포획되고, 좌우 격벽 및 전면벽 유공부 배면의 유수실 내에서 와류 및 난류로 인한 파랑에너지의 소산이 커지고, 이로 인하여 반사율이 작아지기때문이며, 본 연구의 계산범위 내에서 이러한 현상은 유수실 폭이 넓을수록 보다 현저하게 발생되는 것으로 판단된다. 또한, 월파량의 특성과 비교하면 전술한 바와 같이 월파량이 많을수록 전반적으로 반사율이 작아지는 결과를 확인할 수 있다. 즉, 월파량이 많다는 것은 구조물 배후로 전달율이 크다는 것을 나타내고, 따라서 파랑에너지보존으로부터 반사율이 작아지는 것을 나타낸다.
4.4 파압분포
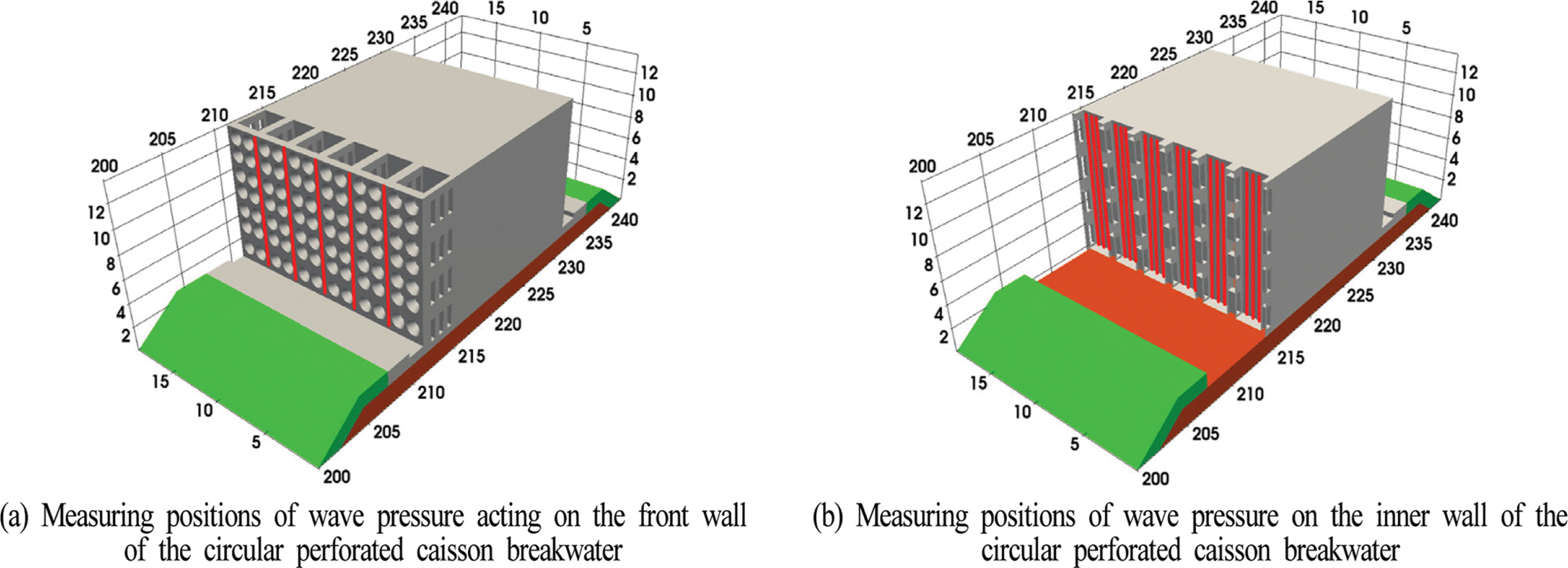
Fig. 15는 전면 유공벽에 작용하는 최대파압과 유수실 후면벽에 작용하는 최대파압의 측정위치를 나타낸 것이다. 전면 유공벽에 작용하는 파압은 유공이 없는 케이슨 바닥에서부터 상단까지 폭방향으로 5열에서 측정되었고, 유수실 후면벽에 작용하는 파압은 각 유수실에서 3열로 바닥에서부터 상단까지 측정되었으며, 각각을 평균하여 파압을 산출하였다. 산정된 파압은 ρgH1/3로 무차원화되었고, 연직깊이 Z는 수심 h로 무차원화되었다.
Table 2는 수치해석결과와 Goda 식(Goda, 2000; 전면벽에서 파압) 및 Takahashi 식(Takahashi et al., 1992, 1996; Tanimoto and Takahashi, 1994; 유수실 후면벽에서 파압)과를 비교하기 위해 구조물이 설치되지 않은 진행파 조건 하에서 구조물 설치위치에서 얻어진 수위변동에 영점상향교차법을 적용하여 최대파고 Hmaxoutput을 산출하였으며, 이로부터 최대파고와 유의파고의 비 Hmaxoutput/H1/3도 산출 · 병기하였다. 또한, Goda 식 및 Takahashi 식에서 최대파고는 대상으로 하는 파군 중에서 가장 큰 파력이 작용하는 최대파를 적용하며, 이는 출현확률이 해역에 따라 일정치로 나타나지 않는 점을 고려하여 유의파고 H1/3의 1.8배에 해당하는 값을 사용하기 때문에 Hmax = 1.8H1/3의 값도 병기하였다. 이하의 Figs. 16~21는 본 수치해석결과와 Goda 식 및 Takahashi 식에 의한 결과를 비교한 것이며, 그림에서는 Goda 식 및 Takahashi 식의 적용시 구조물이 설치되지 않은 조건 하에서 구조물 설치 위치에서 산출된 Hmaxoutput과 Hmax = 1.8H1/3을 적용한 결과도 함께 제시한다.
4.4.1 전면유공벽에 작용하는 최대파압
(1) 유의파고의 변화
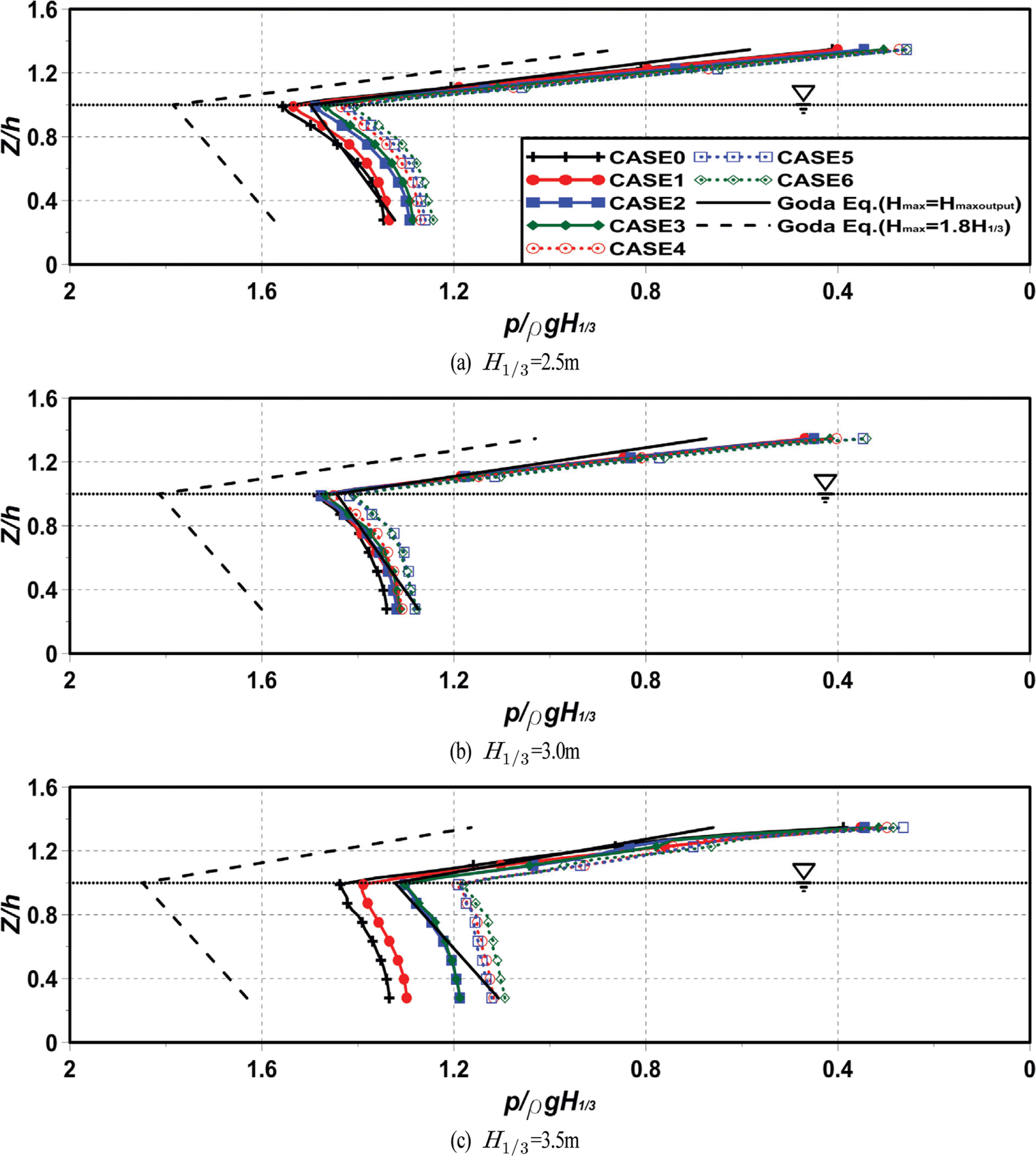
Fig. 16은 유의주기(T1/3 = 11.0 s)를 고정하고, 유의파고의 변화에 따른 전면 유공벽에 작용하는 최대파압분포를 나타낸 것이다. 여기서, Fig. 16(a)는 유의파고 H1/3 = 2.5m인 경우, Fig. 16(b)는 유의파고 H1/3 = 3.0m인 경우, Fig. 13(c)는 유의파고 H1/3 = 3.5m인 경우이다. 그림을 살펴보면 전체적으로 무차원파압은 혼성방파제의 직립부에 작용하는 Goda 파압분포와 유사하게 정수면에서 가장 큰 값을 나타내고, 깊이의 증가에 따라 지수함수적인 감소를 나타낸다. 각 케이스 별로 정수면에서 무차원파압을 비교하면 유의파고 H1/3 = 2.5m인 경우는 p/ρgH1/3 = 1.41~1.56의 범위, 유의파고 H1/3 = 3.0m인 경우는 p/ρgH1/3 = 1.41~1.48의 범위, 유의파고 H1/3 = 3.5m인 경우는 p/ρgH1/3 = 1.18~1.44의 범위에 속하며, 입사파고가 클수록 정수면에서 무차원파압이 작아지는 경향을 나타낸다. 유의파고 H1/3 = 3.5m에서 무차원파압이 상대적으로 많이 작아지는 것은 입사파가 쇄파된 후에 구조물에 작용하기 때문인 것으로 판단된다. 다음으로, 유수실 폭이 넓을수록 무차원파압이 작아지는 것을 알 수 있으며, 이는 유수실 폭이 증가하면 파랑에너지의 포획이 보다 많게 되고, 유수실 내에서 와류 및 난류 등으로 인한 파랑에너지 소산이 보다 많아 반사율이 작아지기 때문이다. 이러한 유수실 폭에 따른 파압의 결과는 단일 및 이중 유수실 유공케이슨에 작용하는 수평파력을 수리실험을 통해 측정 · 비교한 Oh et al.(2013)의 결과와 동일한 경향을 보인다. Goda 식과 비교하면 최대파고를 구조물이 설치되지 않은 조건 하에서 구조물 설치위치에서 산출된 최대파고 Hmaxoutput을 적용한 경우 CASE 0, CASE 1, CASE 2 및 CASE 3은 불안정측에 놓이지만 최대파고로 유의파고 H1/3을 1.8배한 Hmax를 적용하면 모두 안정측에 놓인다는 것을 알 수 있다. 따라서, 본 연구의 원형유공케이슨 방파제의 전면 유공벽에 작용하는 파압 산정에 Hmax = 1.8H1/3을 고려한 Goda 파압분포를 적용하면 보수적인 설계로 되지만 과다설계로 될 가능성이 매우 높다는 것을 나타낸다.
(2) 유의주기의 변화
Fig. 17은 유의파고(H1/3 = 3.0m)를 고정하고, 유의주기의 변화에 따른 전면 유공벽에 작용하는 최대파압분포를 나타낸 것이며, Fig. 17(a)는 유의주기 T1/3 = 11.0 s인 경우, Fig. 17(b)는 입사파고 T1/3 = 13.0 s인 경우, Fig. 17(c)는 입사파고 T1/3 = 15.0 s인 경우이다. 전술한 Fig. 16과 같이 Goda 파압분포와 유사하게 정수면에서 가장 큰 값을 나타내며, 깊이의 증가에 따라 지수함수적인 감소를 나타낸다. 각 케이스 별로 정수면에서 무차원파압을 비교하면, 유의주기 T1/3 = 11.0 s인 경우는 p/ρgH1/3 = 1.41~1.48의 범위, 입사파고 T1/3 = 13.0 s인 경우는 p/ρgH1/3 = 1.57~1.41의 범위, 입사파고 T1/3 = 15.0 s인 경우는 p/ρgH1/3 = 1.38~1.64의 범위에 놓이고, 유의주기가 길어질수록 정수면에서 무차원파압이 증가하는 경향을 나타낸다. Fig. 16과 같이 유수실 폭이 넓을수록 무차원파압이 작아지며, Goda 식과 비교하면 최대파고 Hmaxoutput을 적용한 경우는 불안정측에 속하는 케이스가 있지만 최대파고 Hmax를 적용하면 모두 안정측에 속하는 것을 알 수 있다.
4.4.2 케이슨 저면에 작용하는 최대양압
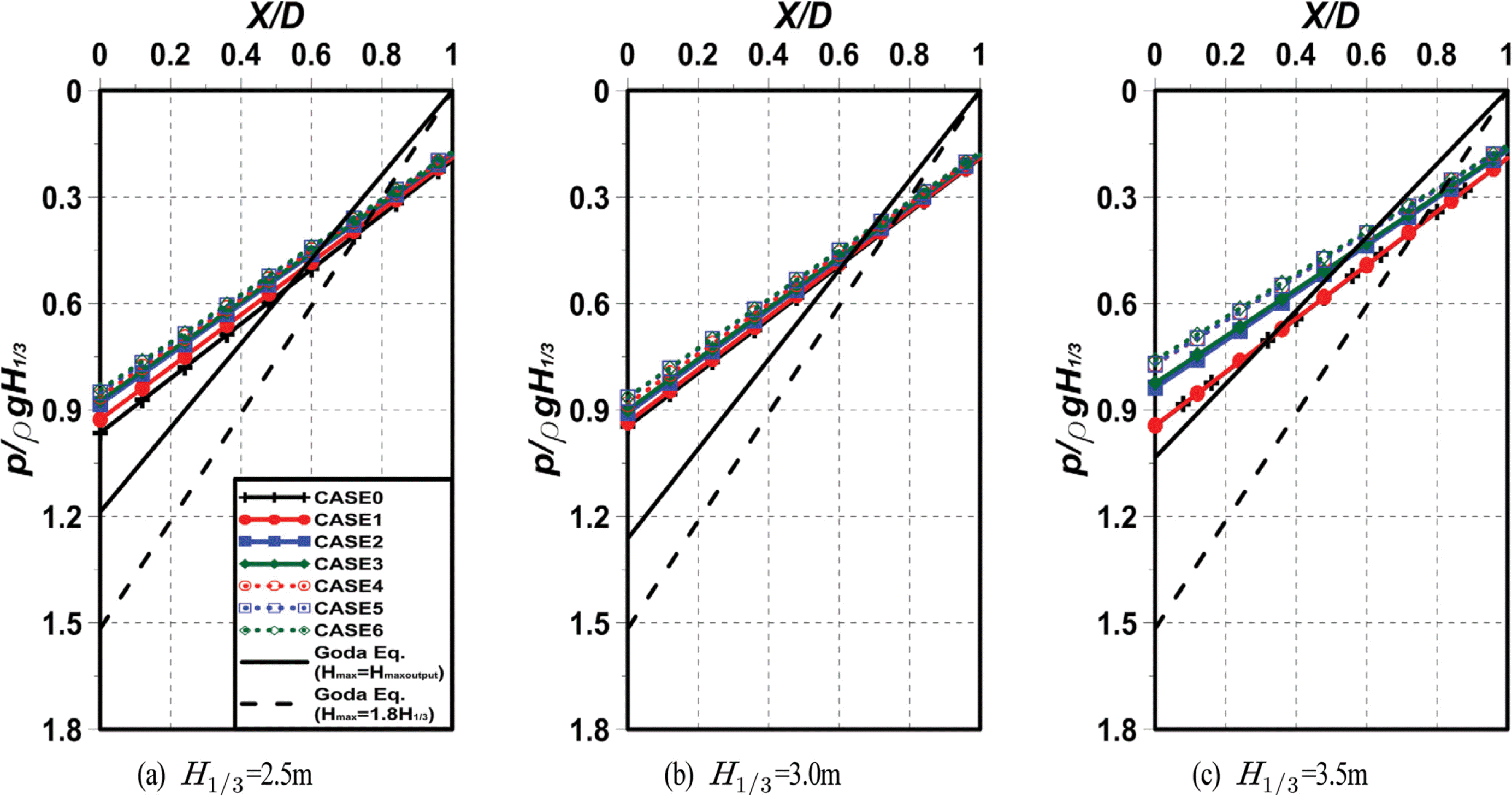
(1) 유의파고의 변화
Fig. 18은 유의주기(T1/3 = 11.0 s)를 고정하고, 유의파고의 변화에 따른 케이슨 저면에 작용하는 최대양압분포를 나타낸 것이며, Fig. 18(a)는 유의파고 H1/3 = 2.5m인 경우, Fig. 18(b)는 유의파고 H1/3 = 3.0m인 경우, Fig. 18(c)는 유의파고 H1/3 = 3.5 m인 경우이다. 그림을 살펴보면 모든 케이스가 직선분포를 나타내지만 수치해석결과는 항내측 저면 끝단에서 무차원양압이 p/ρgH1/3 = 0.15~0.19의 값을 나타내며, 이는 p/ρgH1/3 = 0인 Goda 식의 결과와는 큰 차이를 나타낸다. 항외측 저면 끝단에서 무차원양압은 p/ρgH1/3 = 0.75~0.96의 값을 나타내며, 최대파고 Hmaxoutput 및 Hmax를 적용한 Goda 식의 결과는 전체적으로 안정측에 속한다. 또한, 유수실 폭이 넓을수록 무차원양압이 작아지는 경향을 나타내며, 이는 피복석과 기초사석을 침투하는 과정에서 파랑에너지가 감쇠되기 때문이다. 여기서, 본 연구의 원형유공케이슨 방파제의 케이슨 하부에 작용하는 양압의 산정에 Hmax = 1.8H1/3을 고려한 Goda 양압분포를 적용하면 보수적인 설계로 되지만 과다설계로 될 가능성이 높다는 것을 또한 알 수 있다.
(2) 유의주기의 변화
Fig. 19는 유의파고(H1/3 = 3.0m)를 고정하고, 유의주기의 변화에 따른 케이슨 저면에 작용하는 최대양압분포를 나타낸 것이며, Fig. 19(a)는 유의주기 T1/3 = 11.0 s인 경우, Fig. 19(b)는 유의주기 T1/3 = 13.0 s인 경우, Fig. 19(c)는 유의주기 T1/3 = 15.0 s인 경우이다. 그림을 살펴보면 전술한 Fig. 15와 같이 모든 케이스가 직선분포를 나타내지만 수치해석결과는 항내측 저면 끝단에서 무차원양압이 p/ρgH1/3 = 0.17~0.22의 값을 나타내며, 이는 p/ρgH1/3 = 0인 Goda 식의 결과와는 큰 차이를 나타내고, 항외측 저면 끝단에서 p/ρgH1/3 = 0.82~1.08의 값을 나타낸다. 또한, 유수실 폭이 넓을수록 무차원양압이 작아지는 경향을 볼 수 있다. 여기서, 최대파고 Hmaxoutput 및 Hmax를 적용한 경우는 전체적으로 안정측에 속한다.
4.4.3 유수실 후면벽에 작용하는 최대파압
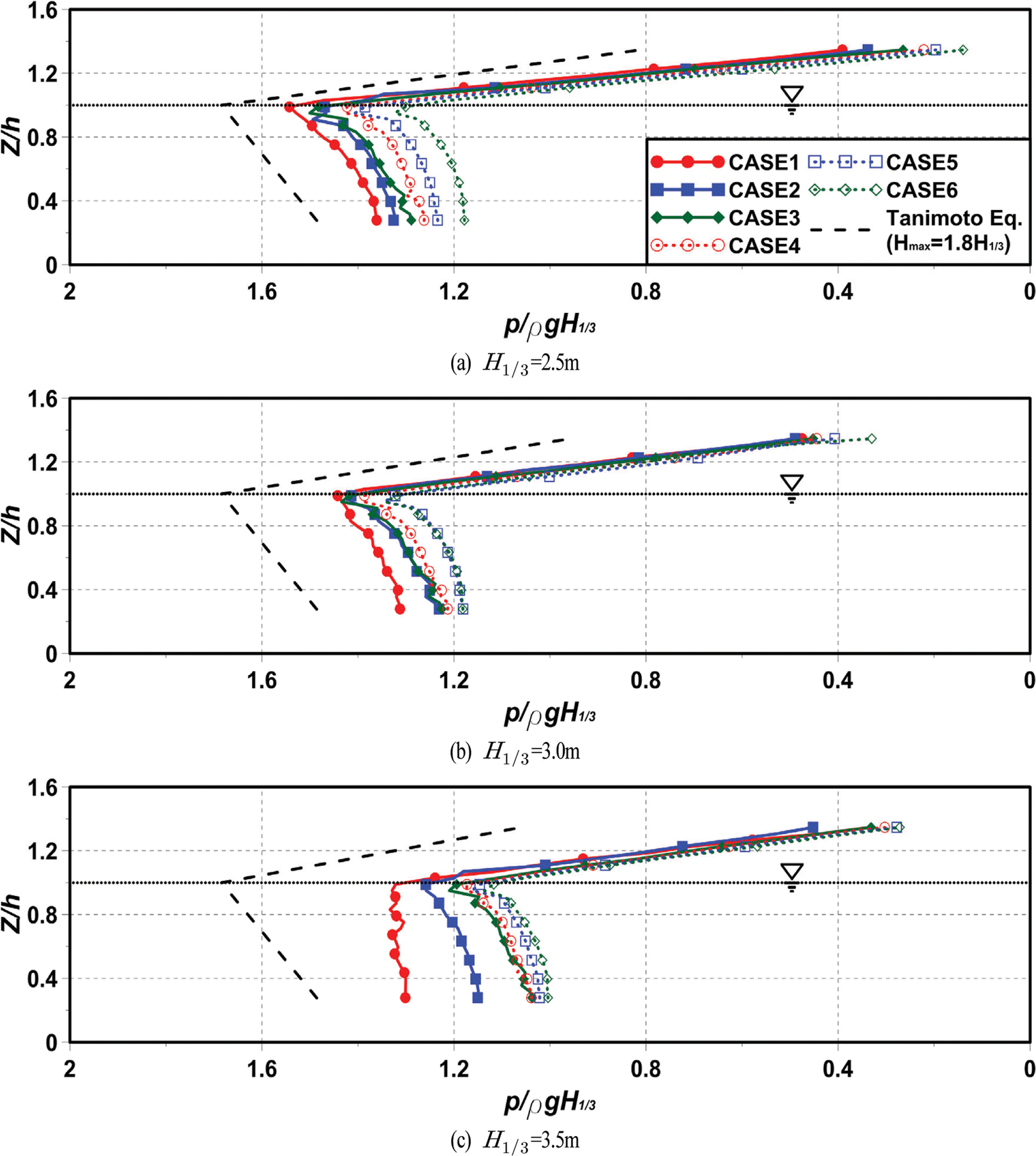
(1) 유의파고의 변화
Fig. 20은 유의주기(T1/3 = 11.0 s)를 고정하고, 유의파고의 변화에 따른 유수실 후면벽에 작용하는 최대파압분포를 나타낸 것이며, Fig. 20(a)는 유의파고 H1/3 = 2.5m인 경우, Fig. 20(b)는 유의파고 H1/3 = 3.0m인 경우, Fig. 20(c)는 유의파고 H1/3 = 3.5m인 경우이다. 그림을 살펴보면 전체적으로 무차원파압은 직립 소파케이슨의 직립부에 작용하는 Takahashi 파압분포(Takahashi et al., 1992, 1996; Tanimoto and Takahashi, 1994)와 유사하게 정수면에서 가장 큰 값을 나타내고, 깊이의 증가에 따라 지수함수적인 감소를 나타낸다. 각 케이스 별로 정수면에서 무차원파압을 비교하면 유의파고 H1/3 = 2.5m인 경우는 p/ρgH1/3 = 1.30~1.54의 범위, 유의파고 H1/3 = 3.0m인 경우는 p/ρgH1/3 = 1.32~1.44의 범위, 유의파고 H1/3 = 3.5m인 경우는 p/ρgH1/3 = 1.12~1.32의 범위에 속하며, 전술한 바와 같이 유의파고 H1/3 = 3.5m인 경우는 쇄파된 파가 구조물에 작용하기 때문에 무차원파압이 상대적으로 많이 작아지는 것으로 판단된다. 다음으로, 유수실 폭이 넓을수록 무차원파압이 작아지며, 이는 전술한 바로 유수실로 유입되는 파랑에너지가 유수실 내에서 소산이 크게 되고, 또한 유수실 폭이 넓을수록 이러한 경향은 보다 현저히 발생되기 때문인 것으로 판단된다. Takahashi 식과 비교하면 모두 안정측에 속하는 것을 알 수 있다.
(2) 유의주기의 변화
Fig. 21은 유의파고(H1/3 = 3.0m)를 고정하고, 유의주기의 변화에 따른 유수실 후면벽에 작용하는 최대파압분포를 나타낸 것이며, Fig. 21(a)는 유의주기 T1/3 = 11.0 s인 경우, Fig. 21(b)는 유의주기 T1/3 = 13.0 s인 경우, Fig. 21(c)는 유의주기 T1/3 = 15.0 s인 경우이다. 그림을 살펴보면 전체적으로 무차원파압은 직립 소파케이슨의 직립부에 작용하는 Takahashi 파압분포(Takahashi et al., 1992, 1996; Tanimoto and Takahashi, 1994)와 유사하게 정수면에서 가장 큰 값을 나타내며, 깊이의 증가에 따라 지수함수적인 감소를 나타낸다. 각 케이스 별로 정수면에서 무차원파압을 비교하면 유의주기 T1/3 = 11.0 s인 경우는 p/ρgH1/3 = 1.32~1.44의 범위, 유의주기 T1/3 = 13.0 s인 경우는 p/ρgH1/3 = 1.31~1.48의 범위, 유의주기 T1/3 = 15.0 s인 경우는 p/ρgH1/3 = 1.25~1.55의 범위에 속하며, 전술한 Fig. 20과 같이 유수실 폭이 넓을수록 무차원동파압이 작아지고, Takahashi 식과 비교하면 모두 안정측에 속하는 것을 알 수 있다.
4. 결 론
본 연구에서는 OLAFOAM을 이용하여 규칙파동장 하에서 3차원슬리트케이슨에 의한 파압변동에 대한 기존의 실험결과와의 비교 · 검토 및 3차원수치파동수조에서 불규칙파를 조파하여 목표한 불규칙파의 재현과 주파수스펙트럼을 비교 · 검토하여 OLAFOAM의 타당성을 검증하였다. 이에 근거하여 OLAFOAM으로부터 슬리트케이슨과 유사한 본 연구의 원형유공케이슨이 설치된 3차원수치파동수조에 불규칙파를 조파하여 유수실 폭과 유의파고 및 유의주기의 변화 등에 따른 원형유공케이슨에서 월파량, 반사율, 파압분포 및 그들의 상호연관성을 면밀히 검토 · 분석하였다. 이로부터 도출된 중요한 사항을 다음에 요약 · 기술한다.
(1) 월파량에 대해, 유수실 폭이 넓을수록 월파량이 감소하며, 입사파고가 클수록 또는 주기가 길수록 월파량은 증가한다.
(2) 반사율에 대해, 유수실 폭의 변화와 파고 및 주기의 변화에 상관없이 모두 Tanimoto et al.(1976)의 실험치의 범위 내에 속하며, 유수실 폭이 넓을수록, 파고가 증가할수록 감소하고, 주기가 길수록 증가한다. 이는 월파량과 비교하여 월파량이 많을수록 반사율이 작아지는 결과를 나타낸다.
(3) 파압분포에 대해, 일반적으로 유수실 폭이 넓을수록 전면 유공벽에 작용하는 파압이 작아지며, 유수실 폭이 좁은 경우 Goda 식(Goda, 2000)보다 불안정측에 속하는 경우도 있지만, Hmax = 1.8H1/3을 적용하면 모두 안정측에 속한다. 케이슨 저면에 작용하는 양압은 Goda 식과는 상이하게 항내측 케이슨 끝단에서 0이 아닌 값을 나타내지만 전체적으로는 Goda식에 의한 두 결과가 안정측에 속한다. 유수실 후면벽에 작용하는 파압도 Hmax = 1.8H1/3을 적용한 Takahashi 식(Takahashi et al., 1992, 1996; Tanimoto and Takahashi, 1994)의 결과가 안정측에 속한다. 따라서, Goda 식과 Takahashi 식에 의한 파압 산정결과를 적용하는 경우는 보수적인 것으로 되지만 과다설계로 될 소지가 매우 높다.
(4) 본 연구에서는 원형유공케이슨 방파제의 기능성(반사율과 월파량)과 안정성(파압)을 3차원 OLAFOAM(Higuera et al., 2015)이라는 고정도 해석법을 적용하여 수치적으로 검토 ·논의하였지만 추후 수리실험을 통하여 본 수치해석결과를 직접적인 방법으로 검증할 필요가 있고, 입사파의 파라미터, 구조물의 형상에 관한 파라미터 및 배치조건 등을 충분히 고려하여 파압분포 등에 관한 적절한 추정식을 제시할 예정에 있다.