요약유한길이의 혼성방파제 선단에서 발생되는 회절파의 영향으로 방파제 길이를 따라 중복파고가 변동하고, 이로 인하여 케이슨에 작용하는 파압이 공간적으로 변동하며, 또한 케이슨의 활동거리가 상이한 사행피해가 발생한다는 것은 잘 알려져 있다. 제체에 작용파력의 공간적인 변동은 2차원적인 실험이나 수치해석으로서는 접근될 수 없는 문제이다. 본 연구는 olaFlow 모델을 적용하여 고천단의 사석마운드 상에 놓인 케이슨의 선단 주변에서 회절파의 발생과 배후역으로의 영향 및 제체에 작용하는 충격쇄파압을 포함한 파압의 공간적인 변동 등을 2차원 및 3차원수 치기법으로 접근한다. 또한, 수치해석에서는 혼성방파제 주변에서 평균파고, 평균수평유속 및 평균난류운동에너지의 변동특성을 면밀히 분석·검토한다. 이로부터 동일한 입사파랑에 대해 케이슨에 작용하는 파압분포가 방파제의 길이에 따라 크게 변동하며, 2차원수치해석에서는 발생되지 않았든 충격쇄파압이 3차원수치해석에서는 발생되는 경우가 나타나고, 충격쇄파압의 발생 시 경우에 따라 기존의 설계조건보다 매우 큰 파압이 정수면 근방의 케이슨 전면 벽체에 작용되는 등의 중요한 결과를 확인할 수 있었다.
AbstractIt has been widely known that the effect of diffracted waves at the tip of composite breakwater with finite length causes the change of standing wave height along the length of breakwater, the spatial change of wave pressure on caisson, and the occurrence of meandering damage on the different sliding distance in sequence. It is hard to deal with the spatial change of wave force on trunk of breakwater through the two-dimensional experiment and/or numerical analysis. In this study, two and three-dimensional numerical techniques with olaFlow model are used to approach the spatial change of wave force including the impulsive breaking wave pressure applied to trunk of breakwater, the effect of rear region, and the occurrence of diffracted waves at the tip of caisson located on the high crested rubble mound. In addition, it is thoroughly studied the mean wave height, mean horizontal velocity, and mean turbulent kinetic energy through the numerical analysis. In conclusion, it is confirmed that the larger wave pressure occurs at the front wall of caisson around the still water level than the original design conditions when it generates the shock-crushing wave pressure checked by not two-dimensional analysis, but three-dimensional analysis through the change of wave pressure applied to the caisson along the length of breakwater.
1. 서 론항내 시설물과 정박된 선박의 보호 및 부두에서 원활한 하역·선적을 위해 정온수역이 요구되고, 이에 따라 혼성방파제로 대표되는 방파구조물을 외곽에 배치·건설하는 것이 항만 내 수역시설의 배치에 대한 보편적인 접근이다. 파의 입사에 따라 구조물 전면에서 중복파시스템이 형성되고, 파시스템이 1차원적이라면 입사파가 구조물로부터 완전반사되어 구조물 전면에서는 완전중복파동장이 형성되며, 이 때 파고는 입사파고의 두 배로 된다. 하지만, 방파제는 개구부를 가진 유한 길이로 배치되고, 이로 인한 선단 부근에서 회절파의 영향으로 구조물의 길이에 연한 공간위치에 따라 중복파고가 변동한다는 것은 일반적으로 알려진 사실이다(Morihira and Okuyama, 1965).
이와 같이 방파제를 따른 중복파고에서 변동은 방파제에 작용하는 파압의 공간적인 변동을 야기하고, 과도한 작용파압으로 혼성방파제의 케이슨에서 활동파괴가 발생되는 경우 각 케이슨의 항내 측 활동거리에 차이를 나타내게 된다(Ito and Tanimoto, 1971). Ito and Tanimoto(1971)는 이러한 현상을 방파제 선단으로부터 회절파의 영향으로 설명하였고, 이로 인한 피해를 사행피해(meandering damage)로 칭하였다.
해외에서 이러한 사행피해가 다수 보고되어 있고(Takahashi et al., 1993), 최근 국내에서도 설계 내구년의 초과에 따른 노후화와 더불어 설계당시에 예측하지 못한 이상파랑과 큰 충격파압의 작용으로 유사한 피해사례가 발생되고 있다. Photo 1은 2018년 10월에 남해안을 내습한 25호 태풍 콩레이에 의해 부산항 외곽방파제에 활동피해가 발생된 사례를 나타낸다. 사진으로부터 케이슨이 항내 측으로 활동되었고, 그의 활동거리가 케이슨에 따라 상이한 것을 볼 수 있다. 이후에 실시된 정밀계측에 따르면 항내 측으로 케이슨에 따라 20~80 cm 정도의 상이한 활동거리가 발생된 것으로 나타났다. 또한, 여기서는 제시되지 않지만, 정수위 근방의 일부 케이슨 전면 벽체가 부분적으로 파손되어 속채움모래가 유실된 것으로 조사되었다. 이와 같은 피해는 일반적으로 충격쇄파력의 작용에 의해 야기되는 것으로 알려져 있고, 실제로 일본에서 이러한 사례가 보고된 바도 있다(Takahashi et al., 1993; Tsuda and Takayama, 2006). 여기서, 이러한 현상은 2차원적으로는 접근될 수 없는 요소이며, 또한 여러 요소가 연관되어 나타나므로 이를 통합적으로 규명하기 위해서는 3차원적인 접근이 요구된다.
한편, 혼성방파제의 직립부에 작용하는 파압을 수치적으로 검토하려는 연구가 일찍이 90년대부터 Sulisz(1997)과 Kim et al.(2000) 등에 의해 일부 시도되었지만, 이들은 포텐셜이론의 비쇄파를 대상으로 하였다. 하지만, 최근에는 혼상류에 대한 Navier-Stokes 운동방정식, VOF(Volume Of Fluid) 법에 의한 쇄파 및 난류 등을 고려할 수 있는 고정도의 3차원 수치해석법이 개발되어 왔으며, 이를 적용한 수치연구로부터 (1) 직립부에 작용하는 충격력, (2) 충격력에 의한 케이슨의 활동거리 및 (3) 방파제 선단에서 회절파와 작용파력의 공간 적인 변동 등이 정밀하게 예측되고 있다. 쇄파충격력의 해석은 일찍이 Bagnold(1939)에 의해 제안되었고, 이후에 Takahashi and Tanimoto(1983) 및 Takahashi et al.(1994) 등에 의해 정식화되었다. 이에 따르면 쇄파 시에 연행되는 공기가 중요한 역할을 담당하며, 충격력을 약화시키면서 비이상적으로 크게 되는 것을 방지하는 것으로 알려져 있다. 그리고, 활동거리에 대한 추정은 Ito and Tanimoto(1971)에 의해 처음 수행되었고, 충격력을 삼각형펄스로 근사한 Shimosako et al. (1994) 등에 의해 또한 정식화되었다. 이러한 충격력과 이로 인한 활동거리에 대한 일본에서의 연구는 주로 실험과 모델에 의한 것이 대부분이다. 최근, 이를 수치적으로 접근하려는 시도가 Cuomo et al.(2011), Castellino et al.(2018) 및 Chen et al.(2019) 등에 의해 다수 시도되고 있다. 한편, 국내에서는 반무한 방파제를 대상으로 회절파와 작용파력의 공간적인 변동을 검토한 Jung et al.(2016)의 연구 등이 있지만, 본 연구와 같은 유한길이의 방파제의 경우에 방파제 선단에서 회절파와 작용파력의 공간적인 변동에 대한 수치적인 예측은 상대적으로 연구사례가 많지 않고, 또한 이는 2차원적인 해석법으로는 접근될 수 없는 문제다. 여기서, 3차원불규칙파의 작용 하에서 회절파와 작용파력에 관한 연구로 Higuera et al. (2014)을 들 수 있지만, 이들은 3차원해석에서 소요되는 막대한 계산시간과 컴퓨터용량을 줄이기 위하여 2차원과 3차원의 해석을 결합한 Hybrid 기법을 적용하였으며, 따라서 준 3차원해석법이라고도 할 수 있다.
본 연구에서는 혼성방파제의 케이슨에 충격쇄파력의 작용을 유도하기 위하여 고천단의 사석마운드 상에 케이슨이 설치된 혼성방파제를 고려하며, 그리고 액체와 기체의 혼상류 해석, 난류해석 및 쇄파해석이 가능한 CFD(Computational Fluid Dynamics) code인 olaFlow(Higuera et al., 2018) 모델을 적용한다. 이로부터 방파제 선단부 주변에서 회절파의 발생과 배후역으로의 영향 및 공간위치에 따른 케이슨의 항 내·외측에 작용하는 충격쇄파압을 포함한 파압의 변동 등을 2차원 및 3차원수치기법으로 해석하고, 동시에 기존의 설계 공식(Goda, 2010; Takahashi et al., 1994)에 의한 결과와도 비교·검토한다. 또한, 혼성방파제 선단 주변에서 평균파고, 평균수평유속 및 평균난류운동에너지의 변동특성을 면밀히 분석·검토한다.
2. 수치해석2.1 이론적인 배경본 연구에서 사용한 olaFlow 모델(Higuera et al., 2018)은 비혼합·비압축성의 혼상유체(액체 및 기체)를 해석하기 위하여 다음 식(1)의 연속방정식과 식(2)의 VARANS(Volume-Averaged Reynolds-Averaged Navier-Stokes) 방정식을 유한체적법에 기초하여 이산화한다.
여기서, t는 시간, ρ는 유체의 밀도, xi는 공간벡터좌표, ui와 uj는 각각 유체속도벡터, Xj는 위치벡터, gj는 물체력벡터이며, 첨자 i와 j는 각각에 대한 Cartesian 성분을 의미한다. 그리고, p*는 Pseudo-dynamic 유체압력, ϕ는 해석영역 내에 위치하는 투과성구조물의 공극률을 나타낸다. 또한, μeff는 μ + νturb로 μ는 점성계수, νturb는 난류동점성계수이고, [CT]는 투과성구조물에 의한 저항 항으로 다음의 식(3)과 (4)로 주어진다.
여기서, D50은 해석영역 내에 위치하는 투과성구조물의 중앙입경을 나타내며, α와 β는 선형과 비선형의 마찰계수이다. 또한, KC는 Keulegan-Carpenter수로 TouM/D50ϕ를 나타내며, To은 진동주기이고, uM은 유체입자의 최대진동속도이다.
액체와 기체의 경계면은 계산격자 내에서 유체가 점유하는 체적을 나타내는 VOF 함수 F를 이용하는 VOF 법을 적용하며, VOF 법에서는 액체셀의 경우 F = 1, 기체셀의 경우 F = 0, 그리고 액체와 기체를 모두 포함하고 있는 경계셀의 경우는 0 < F < 1의 값을 갖는다. VOF 함수 F는 다음의 이류 방정식(5)에 의해 계산된다.
여기서, uic는 인공압축항으로 |uic| = min[cα|ui|, max(|ui|)]과 같이 주어지며, 본 연구에서는 cα = 1을 적용하였다. 또한, 각각의 계산셀에서 유체의 밀도와 점성계수는 VOF 함수를 가중치로 적용하여 다음과 같이 산정될 수 있다.
또한, LES(Large Eddy Simulation) 모델(Ghosal et al., 1995)을 적용하여 전술한 난류동점성계수 νturb를 산정하였으며, 그 밖의 olaFlow 모델에 대한 상세한 수치해석기법은 Lee et al.(2016) 혹은 olaFlow 매뉴얼(https://gitgub.com/phicau/olaFlow/master/reference.zip)을 참조하기 바란다.
2.2 검증2.2.1 2차원혼성방파제 주변에서 수위 및 지반 내 간극수압사질지반 상에 설치된 혼성방파제 주변에서 수면변동과 직립케이슨 하의 사석마운드 및 사질지반 내부에서 중복파로 인한 과잉간극수압변동을 수리모형시험으로부터 측정한 Mostafa et al.(1999)에 의한 결과와 파동장과 지반거동의 해석에 각각 VARANS 방정식(Hsu et al., 2002)과 Biot 방정식을 각각 적용하여 접합한 PORO-WSSI 모델(Jeng et al., 2013)에 의한 수치해석결과 및 본 연구에서 적용하는 olaFlow(Higuera et al., 2018) 모델에 의한 결과를 비교하여 olaFlow모델의 적용에 대한 타당성을 검증한다.
Fig. 1은 Mostafa et al.(1999)이 적용한 혼성방파제의 제원과 수면변동 및 과잉간극수압변동의 측정 및 비교위치를 나타내며, 격자는 ∆x =1cm와 ∆z = 0.5 cm의 크기를 가지고, 해저면과 케이슨표면에는 불투과경계조건 및 Slip 조건이 적용되었다. 이 때, 입사파랑 조건은 파고 Hi = 5 cm, 주기 T = 2.2 s이다. 또한, 혼성방파제의 사석마운드는 공극률이 ϕ = 0.33, 중앙입경이 D50 = 2.7 cm로, 그리고 해저지반은 공극률이 ϕ = 0.3, 중앙입경이 D50 = 0.08 cm의 사질지반으로 각각 구성되었다. 구조물의 저항계수 α와 β에 대해 사석마운드에는 Jensen et al.(2014)이 제시한 α = 500과 β = 2.0을, 해저지반에는 Burcharth and Christensen(1991)이 균등하고 둥근 모래입자에 대해 제시한 α ≤ 240, β ≤ 2.8의 범위에 있는 α = 40.0과 β = 2.0을 각각 적용하였다.
Fig. 2는 Fig. 1에서 제시된 A와 B지점에서의 무차원수면변동 η/Hi(η는 수면변동)에 대해 olaFlow 모델에 의한 본 연구의 계산결과, Mostafa et al.(1999)의 실험결과 및 Jeng et al.(2013)의 수치계산결과를 함께 나타낸 그림이다. 그림으로부터 확인되는 바와 같이 사석마운드 전면 비탈면 상인 A 지점에서는 전면경사로 인한 천수와 케이슨으로부터 반사파와의 간섭으로 비선형파가 발달되어 비대칭파가 형성된다. 그리고, 케이슨 전면의 사석마운드부의 천단인 B지점은 중복파의 배 근방에 위치되기 때문에 케이슨으로부터 반사파로 인한 중복파가 중첩되어 큰 수면변동을 나타내며, olaFlow 모델에 의한 본 연구의 계산결과는 Jeng et al.(2013)의 수치해석결과와 함께 전체적으로 Mostafa et al.(1999)의 실험결과를 정도 높게 예측한다는 것을 확인할 수 있다.
Fig. 3은 Fig. 1에 제시된 사석마운드 내의 ①지점과 사질지반 내의 ②와 ③지점에서 무차원과잉간극수압 p/ρgHi(ρ는 유체밀도, g는 중력가속도, p는 과잉간극수압)에 관해 olaFlow 모델에 의한 본 연구의 계산결과, Mostafa et al.(1999)의 실험결과 및 Jeng et al.(2013)의 수치해석결과를 함께 나타낸 그림이다. 전체적으로, 사석마운드 및 해저지반의 내부에서 셋 해석결과는 각각 좋은 대응을 나타내며, 특히 혼성방파제 전면 해저지반인 ②지점에서 형성되는 부분중복파동장 하의 비선형과잉간극수압도 정도 높게 예측하고 있을 뿐만 아니라 Jeng et al.(2013)의 수치계산결과보다 Mostafa et al.(1999)의 실험결과를 보다 정확하게 재현한다는 것을 확인할 수 있다. 따라서, olaFlow(Higuera et al., 2018) 모델은 파-혼성방파제의 상호작용뿐만 아니라 해저지반까지 고려된 경우의 상호작용해석에도 적용성이 매우 높은 것으로 판단된다.
2.2.2 3차원투과성직립벽 주변에서 수위 및 파압다음에, 투과성직립이안제를 대상으로 수위 및 파압에 관한 수리실험과 IH3VOF 모델에 의한 수치해석을 수행한 Lara et al.(2012)에 의한 결과와 olaFlow(Higuera et al., 2018) 모델을 적용하여 도출된 본 연구의 결과를 비교하여 olaFlow 모델의 적용에 대한 타당성을 검증한다.
Lara et al.(2012)은 Fig. 4와 같이 수심 h = 0.4 m를 갖는 3차원파동장에 설치된 높이 0.6 m, 길이 4.0 m, 폭 0.5 m의 투과성직립이안제에 규칙파를 작용시켜 직립벽 주변에서 수위변동과 파압변화를 각각 측정하였다. 수리실험에 사용된 조파수조는 길이 17.8 m, 폭 8.6 m, 높이 1.0 m이며, 투과성직립벽은 조파판에서 10.5 m로 이격되어 있고, 우측벽에 접해 있다. 양측벽과 수조 끝단은 완전반사가 발생되도록 불투과 성직립벽으로 구성되었다. 이 때, 투과성직립벽의 공극률은 ϕ = 0.51, 중앙입경은 D50 = 1.5 cm, 입사파고는 H = 9 cm, 주기는 T =4s이다.
수치해석에 사용된 수치파동수조의 크기는 전술한 수리실험수조의 경우와 동일하지만, 구조물의 천단상으로 월파가 발생되지 않으므로 계산효율상 계산결과에 영향이 없는 것으로 판단되는 수조 높이를 투과성직립벽의 경우와 동일한 0.6 m로 구성하였다. 격자크기에서 수조 길이방향의 경우 조파지점에서부터 8m까지는 ∆x = 5~2.5 cm의 가변격자로, 8~12.5 m의 범위에서는 ∆x = 2.5 cm로, 12.5~17.8 m의 범위에서는 ∆x = 5~2.5 cm의 가변격자로 각각 구성하였고, 수조 폭방향의 크기는 ∆y = 2.5 cm, 연직방향의 크기는 ∆z = 1.25 cm로 각각 일정한 격자로 구성하였으며, 따라서 적용된 격자의 총 개수는 대략 880만개에 달한다. 수치조파에 Cnoidal 파이론을, 난류모델에 LES 모델(Ghosal et al., 1995)을 각각 적용하였으며, 조파 개시 후 20 s 동안 파랑의 전파과정을 시뮬레이션 하였다. 여기서, 해저면 및 수조의 후면과 양측 벽면에는 불투과경계조건과 Slip 조건이 각각 적용되었다. 투과성직립이안제에 대한 저항계수 식(4)의 α와 β는 전술한 바와 같이 Jensen et al.(2014)이 제시한 α = 500과 β = 2.0을 적용하였다. 여기서, Figs. 4(b)와 (c)는 수위 및 파압변동에 관한 수리실험 및 수치해석결과의 산정위치로, Fig. 4(b)가 수위변동의 경우를, Fig. 4(c)가 파압변동의 경우를 각각 나타내며, Table 1에 수위계의 설치좌표를, Table 2에 파압계의 설치좌표를 각각 제시한다. 이하에서는 6개 지점(3~7 및 9지점)에서 산정된 수위와 6개 지점(1~6지점)에서 파압에 대한 각 실험결과를 olaFlow에 의한 수치해석결과와 상호 비교·검토한다.
Fig. 5는 수치해석결과와 실험결과를 비교한 투과성직립이안제 주변에서 수위변동을 나타낸 것으로, 그림에서는 IH3VOF 모델에 의한 Lara et al.(2012)의 수치해석결과도 같이 병기되어 있다. 그림을 살펴보면 3과 4지점은 투과성직립이안제 전면에서 수위변동을 나타낸 것으로, 8 s 이후에 쌍봉형의 수위변동이 나타나며, 앞의 파봉은 입사파에 의한 것이고, 뒤는 투과성직립이안제로부터의 반사파에 의한 것이다. 5와 6지점에서의 수위변동은 투과성직립이안제와 후면 불투과 벽체로부터의 회절파 및 반사파의 영향을 동시에 받는 경우로, 6지점의 16 s 근방에서 발생되는 쌍봉형의 수위변동은 후면 불 투과 벽체에 의한 반사파의 영향이다. 다음의 7지점은 투과성직립이안제에 의한 회절파가, 9지점은 후면 불투과 벽체에 의한 반사파가 각각 영향을 크게 미치는 지점이다. 수리실험 및 수치해석결과의 대응성은 6과 7지점의 16 s 이후 쌍봉형 수위변동에서 약간이 차이가 나타나지만, 전반적으로 매우 잘 구현되는 것으로 판단되며, 특히 이러한 결과는 3, 4, 5, 9지점에서 확인할 수 있고, 또한 Lara et al.(2012)의 IH3VOF에 의한 수치해석결과보다 본 수치해석결과가 피크에서 약간 적은 값을 보이지만, 전체적으로는 거의 동일한 값을 나타내는 것을 알 수 있다.
Fig. 6은 투과성직립이안제 주변에서 파압변동에 관한 수치해석결과와 실험결과를 비교한 것으로, Fig. 5와 동일하게 IH3VOF 모델에 의한 Lara et al.(2012)의 수치해석결과도 병기하였다. 그림을 살펴보면 투과성직립이안제 전면에서 파압 변동을 나타낸 1과 2지점의 경우는 실험치와 거의 동일한 값을 나타내는 것을 확인할 수 있다. 또한, 투과성직립이안제과 후면 불투과 벽체로부터의 회절파 및 반사파의 영향을 동시에 받는 3~6지점에서 파압변동은 전반적으로 실험치를 잘 재현하고 있지만, 수위변동에서와 같이 3, 5, 6지점의 16 s 근방에서 후면 불투과 벽체에 의한 반사파의 영향에 의해 생성되는 쌍봉형의 파압변동에서 약간의 차이가 인정된다. 그러나, 전체적으로 실험치를 잘 재현하고 있는 것을 알 수 있다. 따라서, olaFlow 모델(Higuera et al., 2018)에 의한 수치해석 결과는 투과성직립이안제에 의한 파랑변형과 작용파압의 변동과정에서 실험치를 잘 재현하고 있으므로 혼성방파제와 같은 투과성구조물로의 적용성이 높은 것으로 판단된다.
3. 혼성방파제의 수치해석결과3.1 혼성방파제의 배치와 단면형상 및 수치해석 조건본 연구의 혼성방파제에 대한 3차원배치 및 2차원단면형상을 Fig. 7에 나타내며, 이는 쇄파충격파압을 유도하기 위하여 고천단의 사석마운드부를 적용한 Higuera et al.(2014)의 경우를 참조하였다. 그림에 나타내는 바와 같이 일정수심 h = 20 m에 x 방향으로 260 m, y 방향으로 170 m, 그리고 연직 방향으로 35 m의 크기를 갖는 3차원수치파동수조에 케이슨 길이 Le = 90 m와 사석마운드 길이 Ls = 137 m의 혼성방파제가 설치되었으며, 이 때 개구폭 Lo = 33 m을 가진다. 단면은 사석마운드층, 중간피복층과 바깥쪽 TTP 층의 3개 피복층 및 케이슨으로 각각 구성되었으며, 피복층은 일반적인 경우보다 고천단이 적용되었고, 구조물의 수중부는 모두 1:2의 비탈경사를 가진다. 사석마운드는 높이 13 m, 공극률 ϕ = 0.45과 중앙입경 D50 = 0.3 m로 구성되었고, 이의 다공성매질에 대한 저항계수는 Jensen et al.(2014)의 실험으로부터 α = 500과 β = 2.0가 적용되었다. 중간피복석은 두께 1.6 m, 공극률 ϕ = 0.5과 중앙입경 D50 = 0.8 m로 구성되었고, 저항계수는 사석 마운드와 동일하게 α = 500과 β = 2.0가 적용되었다. 또한, TTP 층은 난적을 대상으로 두께 3.4 m, 공극률 ϕ = 0.55와 중앙입경 D50 = 1.7 m로 가정되었으며, Kondo and Takeda(1983)에서 제시된 α = 1200, β = 1.7를 적용하였다. 그리고, 케이슨은 13 m의 높이를 가지며 불투과구조물로 처리되었다.
격자크기는 수치해석의 계산효율을 위하여 수조의 조파지점에서 구조물이 설치되는 지점 앞 30 m까지는 ∆x = 1~0.5 m의 가변격자를, 그리고 ∆y = 0.5 m와 ∆z = 0.5 m의 격자크기를 적용하였으며, 이후 수조 끝단까지는 동일한 ∆x = ∆y = ∆z = 0.5 m의 정방격자를 적용하여 총 10,472,000개의 격자를 사용하였다. 그리고, 시간간격은 충격파압의 작용과 계산시간을 고려하여 ∆t = 0.05 s로 적용되었다. 수조의 저면과 양측 벽면 및 혼성방파제의 케이슨에는 불투과경계조건 및 Slip 조건이 적용되었고, 또한 수조의 조파위치와 끝단에는 감쇠경계가 적용되었다. 그리고, 난류는 LES 모델(Ghosal et al., 1995)로 해석되었다.
Table 3은 본 수치해석에 적용한 규칙파랑의 제원과 월파여부를 나타내며, 총 4케이스에 대해 수치해석을 수행하였다. 여기서, 200 s 동안에 10개의 지점에 설치된 수위계의 수위변동에 대한 시계열로부터 정상상태를 조사하였다. 시계열데이터로부터 100 s 이후에 물리량이 정상상태에 도달하는 것을 알 수 있었고, 따라서 이하에 제시되는 모든 수치결과는 정상상태에 대한 데이터로부터 도출되었다는 것을 부기한다.
3.2 수면변동
Fig. 8은 Table 3에 제시된 모든 케이스에 대해 혼성방파제 전면과 선단부 근방에서 수면변동에 대한 시간별 Snapshot을 나타낸 것이다. 주기가 상대적으로 짧은 Figs. 8(a)와 (b)를 보면 방파제의 중앙부보다 우측의 선단 부근과 좌측의 내측에 상대적으로 높은 파봉이 나타나고, 동시에 선단부 주변으로 파가 돌며, 이어서 우측의 선단과 좌측의 내측보다 중앙부에 상대적으로 높은 수위가 형성되면서 회절파가 배후로 보다 전파되는 상황을 시각적으로 명확히 판단할 수 있다. 다음에, 주기가 보다 긴 Figs. 8(c)와 (d)의 경우는 전술의 경우와는 달리 방파제의 우측의 선단과 좌측의 내측보다 중앙부에 상대적으로 높은 파봉이 나타나고, 동시에 선단부에서 파는 배후로 회절되면서 수위가 낮아지고, 중앙부 근방의 파는 방파제의 내측으로 전파되어 방파제의 내측에서 높은 수위가 형성되는 것을 알 수 있다. 여기서, 선단부에서 파가 회절되면서 배후로 돌아들어가는 상황은 유사하지만, 주기에 따라 방파제 전면에서 최고수면이 형성되는 위치가 상이하게 나타나는 것을 알 수 있고, 이로부터 방파제에 작용하는 파압이 공간위치에 따라 변동될 것이라는 사실을 예상할 수 있을 것이다.
3.3 무차원평균파고
Fig. 9는 파고와 주기의 차이에 따른 무차원평균파고
여기서, 주기에 따른 회절상황을 살펴보면 주기가 짧을수록 선단부 근방에서 회절의 정도가 상대적으로 약간 약하고, 파의 직진성이 조금 강하게 나타나는 것으로 판단된다. 그리고, 주기가 짧은 Fig. 9(a)의 경우는 구조물 전면에서 파집중이 두 곳에서 나타나지만, Fig. 9(b)의 경우는 파집중이 명확하게 나타나지는 않는다. 반면, 주기가 긴 Figs. 9(c)와 (d)의 경우는 구조물 전면에서 파집중이 선단에 가까운 한 곳에서만 나타난다. 이러한 현상은 상대적으로 주기가 짧은 경우에 약하고, 주기가 긴 경우에 강한 방파제 선단에서 회절파와 수조의 좌측 벽체로부터 반사파와의 중첩에 의한 결과로 판단된다. 이와 같이 방파제 전면에서 공간위치에 따른 파집중의 발생은 방파제에 작용하는 파압의 공간적인 변동을 야기할 것이며, 이러한 결과는 주기가 길수록 강할 것으로 예상된다. 따라서, 작용파압에 대한 케이슨의 중량이 부족한 경우에는 항 내 측으로 케이슨의 수평활동이 발생할 수 있고, 케이슨에 작용하는 파압의 공간적인 차이 때문에 사행파괴가 동반될 수 도 있다(Ito and Tanimoto, 1971).
다음에, 방파제의 배후면에서는 선단에서 회절된 파가 방파제를 따라 전달되고, 좌측 벽체로부터 반사되어 배후면에서도 중복파가 형성되는 것을 확인할 수 있다. 여기서도 주기가 짧은 경우는 두 곳에서 파집중이 나타나지만, 주기가 긴 경우에는 벽체 바로 전면의 한 곳에서만 파집중이 나타나며, 분포공간도 넓다는 것을 알 수 있다.
3.4 평균수평유속해저 혹은 사석마운드부의 표면에서부터 정수면까지 연직 방향으로 3개 층으로 분할하고, 최저층에서 수평유속을 연직 방향으로 시간평균한 평균수평유속의 공간분포를 나타낸 것이 Fig. 10이다. 여기서, 각 층의 연직높이는 동일하다.
전반적으로 우측 선단부의 피복재 표면 상에서 평균수평유속은 굴절·회절의 영향으로 대부분이 케이슨에 수직에 가까운 방향으로 향하며, 입사파고 및 주기에 관계없이 피복재 상에서 평균수평유속이 빨라지고, 약간 항내 측에서 가장 빨라진다. 이러한 경향은 파고가 크고, 주기가 짧을수록 강하게 나타나는 것을 확인할 수 있다. 그리고, 케이슨 전면의 피복재 상에서 평균수평유속의 경우 선단부 근방에서 강한 굴절·회절의 영향으로 케이슨을 따른 흐름성분이 탁월하고, 내측으로 갈수록 강한 중복파의 영향으로 케이슨에 수직한 성분이 탁월해지는 경향을 나타낸다. 케이슨 전면의 해저 상에서는 반시계방향의 순환류가 형성되고, 이는 주기가 긴 T = 15 s의 경우에 보다 명확하게 나타나는 것을 알 수 있다.
다음에, Fig. 11은 전술한 연직 3개 층의 전체에 대해 연직방향으로 시간평균한 평균수평유속을 나타낸 것이다. 그림을 살펴보면 우측의 선단부 근방에서는 전술한 최저층의 경우와 거의 동일한 경향을 나타내지만, 파고가 큰 Hi =3 m의 경우는 주변보다 큰 유속이 분포하는 공간이 약간 확대되며, 또한 주기가 긴 T = 15 s에서는 평균수평유속이 항내 측에서 미미하지만 줄어드는 결과를 나타내는 것을 알 수 있다. 여기서, 케이슨 전면에서 평균수평유속의 경우를 살펴보면 선단부 근방에서는 전술한 최저층과 같이 케이슨을 따른 흐름 성분이 존재하지만, 그의 분포는 선단부의 우측 일부에 국한되고, 전체적으로는 케이슨에 수직한 성분이 탁월하다는 것을 알 수 있다. 그리고, 전면에서 순환류의 경우는 전술한 최저층에서와 달리 그의 형성이 명확하지 않은 것을 알 수 있다.
3.4 평균난류운동에너지
Fig. 12는 전술한 평균수평유속에서와 같이 동일한 높이로 분할된 3개 층에서 최저층의 경우에 난류운동에너지를 연직방향으로 시간평균한 평균난류운동에너지의 공간분포를 나타낸 것이다. 전반적으로 입사파고 및 주기에 관계없이 선단부의 피복재 상에서 강한 평균난류운동에너지가 집중되고, 또한 구조물 전면의 피복재 상에서 큰 값을 볼 수 있다. 여기서, 동일한 주기에 대해 파고가 증가하는 경우 혼성방파제의 전면과 선단부의 피복재 상에서 평균난류운동에너지가 상대적으로 크게 증가하고, 동일한 파고에 대해서는 주기가 증가하는 경우에 큰 변화가 나타나지 않지만, 값의 크기가 약간 줄어들면서 다소 넓게 분포되는 경향을 나타낸다. 이러한 결과는 전술한 평균수평유속에서와 유사한 현상이며, 따라서 평균수평유속과 평균난류운동에너지가 상관되어 있다는 것을 확인할 수 있다.
다음으로, Fig. 13은 전술한 Fig. 12와 동일한 조건 하에 전체 층에 대한 난류운동에너지를 연직방향으로 시간평균한 평균난류운동에너지의 공간분포를 나타낸 것이다. 전술한 최저층에서 평균난류운동에너지의 공간분포와 비교하면 분포양상이 전반적으로 유사한 경향을 나타내지만, 값의 크기는 전체 층에 대한 경우가 다소 작은 값을 나타내는 것을 확인할 수 있다. 이러한 사실로부터 난류운동에너지는 구조물의 전면과 선단부의 피복재 상에서 상대적으로 강하게 나타나며, 특히 선단부의 피복재 상에서 강하다는 것을 확인할 수 있다.
한편, 해저지반과 혼성방파제를 통합적으로 수치해석한 Ye et al.(2014)은 평균난류운동에너지가 이상과 같이 크게 집중되는 곳에서 구조물이 파괴되거나 사석이 이동될 가능이 높고, 결과적으로 쇄굴이 진행될 가능성이 높은 것으로 지적하고 있다. 또한, Kim and Lee(2017)는 선단부 우측의 피복석이 상대적으로 배후로 잘 이동되며, 파에 매우 취약하다는 결과를 수리실험으로부터 제시하고 있다. 따라서, 수리실험으로 부터 난류운동에너지와 수평유속의 시·공간변화를 평가하는 것은 계측관계 상 매우 어렵기 때문에 본 연구와 같은 고정도의 수치해석으로부터 구조물의 취약성을 규명하는 것도 하나의 유용한 방법인 것으로 판단된다.
3.5 케이슨에 작용하는 무차원최대파압
Fig. 14는 혼성방파제의 케이슨에 작용하는 최대수평파압과 양압의 공간분포를 검토하기 위하여 나타낸 구간별 단면의 위치이며, 총 5개의 단면위치에서 무차원최대수평파압 및 양압을 각각 추정하였다.
3.5.1 2차원해석(1) 무차원최대수평파압2차원해석과 3차원해석에 의한 최대수평파압의 결과를 각각 비교·분석하기 위하여 2차원수치해석도 함께 수행하였다. 이 때, 모든 파랑조건과 구조물의 단면제원은 3차원의 경우와 동일하다. Fig. 15는 Fig. 7(b)에 제시된 2차원단면에 대해 파고와 주기의 변화에 따른 무차원최대수평파압 pmax/ρgHi의 연직분포와 무차원최대양압 pu, max/ρgHi의 수평분포를 나타낸 것이며, 단면의 각 지점에서 작용파압의 위상차를 고려하지 않고 최대파압만을 나타낸 것이다. 그림 중에는 olaFlow 모델(Higuera et al., 2018)에 의한 2차원수치해석결과뿐만 아니라 Goda(2010)의 파압공식에 의한 결과와 Takahashi et al.(1994)에 의한 충격파압의 결과도 함께 제시되었다. 케이슨 전면에서 수평파압을 살펴보면 모든 케이스에서 Takahashi 등에 의한 충격파압이 Goda의 파압보다 큰 값을 나타내고, Figs. 15(b)와 (c)의 경우를 제외하면 olaFlow 모델에 의해 수행된 2차원수치해석결과는 상대적으로 Goda의 파압에 근접한 결과를 나타낸다.
일반적으로, 충격파압은 (i) 입사파가 방파제에 거의 직각으로 입사(20° 보다 적은 입사각)하고, (ii) 사석마운드부의 천단이 높으며, (iii) 동시에 폭이 넓고, (iv) 해저경사가 1/50보다 급하며, 그리고 (v) 환산심해파형경사가 0.03보다 적은 경우 등에서 발생하는 것으로 알려져 있다. 그러나, 이러한 기준은 상당히 정성적이고, 다른 많은 요소에 의해 영향을 받기 때문에 저천단의 사석마운드에서도 충격파압이 발생하는 등의 불확실성이 매우 크며, 보다 명확한 판정을 위하여 수리모형실험이 권장된다(Goda, 2010). 한편, 수치해석결과가 실험치를 합리적으로 재현한다는 보편적인 가정에 근거하면 본 연구에서 Goda의 파압이 수치해석결과를 보다 타당하게 재현한다는 사실로부터 충격쇄파력계수 αI (Takahashi et al., 1994)와 파압계수 α2(Goda, 2010)가 거의 동등한 값으로 추정되어 충격파압이 발생되지 않아야 한다. 그러나, 본 연구의 조건 하에서 Goda의 파압보다 큰 충격파압이 발생되는 결과로부터 추론하면 충격압의 명확한 발생여부와 그 값의 정확한 예측에 불확실성이 크게 포함된다는 것을 인지할 수 있다.
다음에, 2차원수치해석의 연직분포에서 최대수평파압이 정수면 근방과 정수면 하에서 발생되는 Fig. 15(b)의 경우와 Goda의 파압보다는 Takahashi 등의 충격파압에 가까운 연직분포를 나타내는 Fig. 15(c)의 경우를 고찰한다. 먼저, Fig. 15(b)의 경우에 해당하는 케이슨 전면에서 파형의 전파과정을 나타낸 Fig. 16을 살펴보면 시간의 경과와 더불어 물입자의 수평속도가 위상속도보다 빨라져 권파형의 쇄파가 발생되고, 이어서 케이슨의 직립부를 강타하면서 직립부 전면 상으로 처오름이 발생되는 과정을 가시적으로 확인할 수 있다. 이러한 과정에서 정수면 근방에서 최대수평파압은 쇄파로 인한 충격압과 이어지는 처오름에 의한 동압 중에 큰 수평파압이 Fig. 15(b)의 정수면 근방에서 최대수평파압으로 나타난다. Fig. 15(b)에서 정수면 하의 최대파압은 Fig. 16보다 시간이 더 경과된 Fig. 17의 파형에서 정수면 하의 최대수평파압이 발생되는 것을 확인할 수 있었다. 여기서, 충격압이 발생하지만, 최대파압은 Goda의 파압보다 작다는 것을 알 수 있다.
그리고, Fig. 15(c)의 케이슨 전면에서 파형의 전파과정을 나타낸 다음의 Fig. 18을 살펴보면 파가 입사하면서 케이슨의 직립부 전면 상에서 처오름이 발생되고, 이어서 직립부 전면으로부터 반사파가 형성되어 반대방향으로 전파되는 과정을 확인할 수 있다. 이러한 전파과정에서 쇄파현상이 나타나지 않으므로 충격파압이 발생되지 않는 것을 알 수 있다. 따라서, Fig. 15(c)에서 주어진 수치해석결과는 충격파압에 보다 근접한 값의 연직분포를 나타내지만, 충격파압에 의한 결과가 아니라는 것을 알 수 있다.
마지막으로, Goda(2010)의 파압공식과 Takahashi et al. (1994)에 의한 충격파압공식에는 직립케이슨을 월류한 전달파와 사석마운드부 내부를 통한 파에너지의 전파를 고려하지 않기 때문에 케이슨 배면에서 제시된 수평파압은 전부 2차원수치결과이며, 이는 공극률을 갖는 사석마운드부 내부를 통한 전달파의 성분에 의한 결과이다. 이러한 파압은 케이슨 전면에서의 값에 비해 매우 적은 값을 나타내는 것을 알 수 있다.
(2) 무차원최대양압양압의 경우 항내 측에서 파가 존재하지 않는 것으로 고려되는 삼각형분포에 대한 Goda(2010)의 양압과 Takahashi et al.(1994)의 양압은 동일한 결과를 나타내며, 2차원수치해석 결과와 비교하면 이들의 결과는 매우 큰 값을 나타낸다. 이러한 차이는 Goda와 Takahashi 등의 양압공식에서는 사석마운드부를 통한 전달파와 케이슨 전면의 투과매질에서 파에너지의 감쇠를 고려하지 않기 때문이다. 여기서, 수치해석결과는 케이슨의 전면과 배면의 바닥에서 수평파압이 동시에 고려된 경향을 나타내며, 대략적으로 케이슨의 전면과 배면에서 큰 수평파압을 나타내는 경우가 큰 양압을 나타낸다. 케이슨 저면을 따른 수평분포는 비선형적으로 변화되며, 또한 주기가 길고, 파고가 큰 경우가 전반적으로 큰 양압을 나타내는 것을 알 수 있다.
3.5.2 3차원해석(1) 무차원최대수평파압
Fig. 19는 Fig. 14에 제시된 케이슨 직립부의 전면 다섯 곳의 단면위치(S.01~S.05)에서 파고와 주기의 변화에 따른 무차원최대수평파압 pmax/ρgHi의 연직분포와 무차원최대양압 pu, max/ρgHi의 수평분포를 나타낸 것으로, olaFlow 모델(Higuera et al., 2018)에 의한 3차원해석결과이다.
먼저, 상대적으로 주기가 짧고, 파고가 작은 Fig. 19(a)의 경우를 살펴보면 S.01과 S.05에서 큰 최대수평파압을, 중간의 단면위치 S.03에서 가장 작은 값을 각각 나타낸다. 이러한 결과는 Fig. 9(a)에 나타내는 무차원평균파고의 공간분포와 일치하는 경향을 나타낸다. 여기서, 전술한 Fig. 15(a)에 제시된 2차원의 경우보다 3차원이 케이슨의 단면위치에 따라 큰 파압 혹은 작은 파압의 분포를 나타나내만, 전체적으로 2차원의 경우가 3차원보다 상대적으로 작은 측의 값을 나타낸다. 여기서, S.01과 S.05에서 3차원수치결과가 전술한 Fig. 15(a)의 2차원수치결과보다 큰 수평파압이 작용되는 이유를 Fig. 20에 나타낸 S.01에서 수위의 시간변동으로부터 고찰한다.
Fig. 20으로부터 물입자의 속도가 위상전파속도보다 빨라 쇄파가 발생되면서 동시에 케이슨 전면을 강타하고, 이후에 전면에서 처오름이 매우 높게 나타나는 것을 알 수 있다. 이러한 충격파압의 작용과 그에 따른 높은 처오름으로 인하여 전술한 바와 같이 정수면 근방에서 2차원수치결과보다 훨씬 큰 수평파압이 작용된 것으로 판단된다. 그리고, 2차원해석에서 충격파압이 발생되지 않은 반면에 3차원에서 충격파압이 발생되는 이유는 3차원의 경우에 파의 집중현상으로 파고가 증폭되었기 때문이다. 파고의 크기가 충격파압에 미치는 영향에 대해서는 입사파고와 사석마운드부 상의 천단수심과의 비가 파라미터로 적용되는 Takahashi et al.(1994)의 충격파 압산정식으로부터 알 수 있을 것이다. 한편, 여기서는 제시되지 않지만, 단면위치 S.03에서 수평파압은 전술한 Goda의 파압보다 적은 값을 나타내며, 이의 경우는 충격파압의 발생이 나타나지 않는다. 여기서, 3차원파압분포를 2차원파압추정공식으로부터 평가하기 위해서는 단면위치에서 입사파고가 주어져야 하지만, 3차원적인 현상으로 파가 집중되는 단면위치에서 2차원적인 입사파고를 알 수 없기 때문에 3차원적인 파압을 정확히 평가하기 위해서는 3차원적인 실험 혹은 정밀한 수치해석법으로 접근될 필요가 있다.
상대적으로 주기가 짧고, 파고가 큰 Fig. 19(b)의 경우를 살펴보면 정수면 근방과 정수면 하에서는 Fig. 19(a)와 상이하게 구조물의 중간 부분인 S.03에서 가장 큰 최대수평파압을, 다음에 선단부에 가까운 S.05에서 큰 값을 나타내는 반면, 단면위치 S.02에서 가장 작은 값을 나타낸다. 이는 Fig. 9(b)에 나타낸 파고분포와 직접적으로 대응되지 않는 결과로, Fig. 8(b)에서 나타내는 바와 같이 파고가 큰 단면위치에서 발생되는 월파로 인하여 작용파압이 줄어든 것으로 판단된다. 여기서, 2차원수치해석결과와 비교하면 케이슨의 위치에 따라 3차원의 경우보다 큰 파압도 나타나고, 작은 파압도 나타나지만, 전체적으로 2차원이 평균적으로 3차원보다 작은 측의 값을, 특히 정수면 근방에서 상당히 작은 값을 나타낸다. 여기서, 단면위치 S.03의 정수면 상에서 상당히 큰 수평파압이 작용하는 것을 다음의 Fig. 21로부터 검토한다. Fig. 21에서 케이슨 전면에 쇄파충격압이 작용되고, 동시에 전면 상의 높은 위치까지 처오름이 발생된다. 이러한 처오름은 전술한 Fig. 20의 경우보다 상대적으로 높고, 또한 2차원의 Fig. 16보다도 쇄파강도가 강하며, 처오름도 상당히 높다. 따라서, 이상과 같은 상대적으로 높은 쇄파강도와 처오름에 의해 큰 수평파압이 발생된 것으로 판단된다.
다음에, 상대적으로 주기가 길고, 파고가 작은 Fig. 19(c)의 경우는 S.05 → S.04 → S.03 → S.02 → S.01의 순서로 최대수평파압이 작아지는 경향을 나타내며, 이는 Fig. 9(c)에서 나타낸 각 단면위치에서 파고의 공간분포 결과와 잘 일치한다. 2차원수치해석결과와 비교하면 케이슨의 위치에 따라 2차원의 경우보다 큰 파압과 작은 파압의 분포를 나타내지만, 전체적으로 3차원파압이 2차원파압보다 큰 측의 값을 나타낸다. 여기서, 단면위치 S.05의 정수면 상에서 큰 수평파압이 작용하는 것을 다음의 Fig. 22로부터 검토한다. Fig. 22에서 케이슨 전면에 쇄기파와 같은 쇄파가 형성되고, 이어서 케이슨 전면과 충돌하면서 전면 상의 높은 위치까지 처오름이 발생된다. 이러한 쇄파의 작용과 처오름은 2차원의 Fig. 18에서는 주어지지 않는 현상이다.
마지막으로, 상대적으로 주기가 길고, 파고가 큰 Fig. 19(d)의 경우는 전술한 Fig. 19(c)와 동일하게 S.05 → S.04 → S.03 → S.02 → S.01의 순서로 최대수평파압이 작아지는 경향을 나타내며, 이는 Fig. 9(d)에서 나타낸 각 단면위치에서 파고의 공간분포와 거의 일치한다. 여기서, Fig. 19(b)에서 달리 월파가 발생하는 상황에서도 파고분포와 수평파압이 대응하는 것은 주기가 상대적으로 길기 때문에 월파가 거의 동일한 시간에 구조물 전체길이에 걸쳐 발생하기 때문이며, 따라서 월파로 인한 파압의 감소가 전체의 단면위치에 상대적으로 균등하게 영향을 미치는 것으로 판단된다. 2차원수치해석 결과와 비교하면 모든 단면위치에서 3차원이 2차원보다 큰 값을 나타낸다. 여기서, 단면위치 S.04의 정수면 상에서 큰 수평파압이 작용하는 것을 다음의 Fig. 23으로부터 검토한다. Fig. 23에서 케이슨 전면에 높은 강도의 권파형쇄파가 발생되고, 이어서 케이슨 전면과 크게 충돌하면서 전면 상에 처오름이 발생된다. 이러한 쇄파강도는 전술한 다른 케이스의 경우보다 강하지만, 처오름은 상대적으로 작다. 또한, Figs. 19(c)와 (d)에서 2차원의 경우에 나타나지 않는 쇄파가 3차원의 경우에 발생하는 것은 파의 회절현상에 따른 파에너지의 집중현상으로 파고가 증폭되었기 때문이다.
한편, 항내 측 케이슨의 배면에 작용하는 수평파압은 전면에서 형성되는 중복파압과는 달리 사석마운드 내를 통해 전달된 파와 회절된 파로 인한 파압성분이다. 3차원의 경우는 케이슨의 단면위치에 따라 큰 차이를 나타내며, 대략적으로 주기가 짧은 경우에는 선단부 근방에서, 주기가 긴 경우에는 내측 근방에서 큰 값을 나타내는 것을 알 수 있다. 그리고, 동일한 주기에 대해는 파고가 작은 경우가, 동일한 파고에 대해서는 주기가 긴 경우가 전체적으로 큰 값을 나타내는 것을 확인할 수 있다.
이상과 같이 항내·외측에서 정수면 위의 수평파압분포에 관한 수치결과가 정수압분포보다 작은 값을 나타내는 것은 Ramsden(1993)이 지적하고 있는 바와 같이 연직벽체를 따른 흐름에서 연직가속도가 존재하기 때문이다.
4. 결 론본 연구에서는 오픈소스인 olaFlow 모델(Higuera et al., 2018)을 이용하여 일정수심의 2차원 및 3차원파동수조에 혼성방파제를 설치하고 규칙파를 조파하였다. 이로부터 파고와 주기 변화에 따라 구조물 주변에서 무차원평균파고, 평균유속, 평균난류운동에너지의 각 공간분포 및 케이슨의 항내 측에 작용하는 2차원 및 3차원의 무차원최대수평파압 및 양압의 분포를 수치적으로 도출하여 공간위치에 따른 그의 변동 특성 등을 기존의 2차원적인 파압추정공식(Goda, 2010)의 파압공식과 Takahashi et al.(1994)의 충격파압공식과 비교·분석하였다. 이로부터 다음과 같은 결론을 얻을 수 있었다.
(1) 무차원평균파고 : 구조물의 바로 전면에서 중복파고가 구조물의 길이방향으로 위치에 따라 변동하며, 곳에 따라 파가 집중되는 현상이 나타난다. 무차원평균파고의 공간집중에 의한 증폭현상은 주기가 길수록, 동시에 파고가 작을수록 높게 나타난다. 주기가 길고 입사파고가 작은 경우에 선단부 근방에서 파집중에 의한 증폭이 3 이상의 값을 나타내는 곳도 발생하므로 파에너지의 공간적인 집중이 상당히 높다. 방파제의 배후면에서는 선단에서 회절된 파가 방파제를 따라 전달되고, 좌측 벽체로부터 반사되어 배후면에서도 중복파의 형성에 의해 공간적인 위치에 따라 파집중이 발생된다.
(2) 평균수평유속 : 우측 선단부의 피복재 표면 바로 위 및 피복재 상의 전체높이에 대한 각각의 평균수평유속은 굴절·회절의 영향으로 대부분이 케이슨에 수직에 가까운 방향으로 향하며, 입사파고 및 주기에 관계없이 피복재 상에서 평균수평유속이 빨라진다. 이는 파고가 크고, 주기가 짧을수록 강하게 나타난다. 구조물 전면의 피복재 상에서 평균수평유속의 경우 선단부 근방에서 강한 굴절·회절의 영향으로 구조물을 따른 흐름성분이 탁월하고, 내측으로 갈수록 강한 중복파의 영향으로 구조물에 수직한 성분이 탁월하다.
(3) 평균난류운동에너지: 우측 선단부의 피복재 표면 바로 위 및 피복재 상의 전체높이에 대한 각각의 평균난류운동에너지는 입사파고 및 주기에 관계없이 선단부의 피복재 상에서 강하게 집중되고, 또한 구조물 전면의 피복재 상에서도 큰 값을 나타낸다. 이러한 결과는 전술한 평균수평유속의 경우와 매우 유사하며, 따라서 두 현상에서 상관이 매우 높고, 선단부 근방에서 구조물의 파괴 및 피복재의 이동과 밀접한 연관을 가지는 것으로 판단된다.
(4) 무차원최대수평파압과 양압: 무차원최대수평파압은 전체적으로 케이슨의 전면에 형성되는 중복파고의 영향을 직접적으로 받는 것이 일반적이지만, 경우에 따라서는 월파 등의 영향으로 일률적이지 않은 경우도 발생한다. 특히, 케이슨의 공간위치에 따라 3차원의 경우가 2차원보다 큰 값을 나타내는 경우가 많고, 또한 케이슨의 공간위치에 따라 크게 변동한다. 2차원해석에서는 발생하지 않는 충격파압이 3차원해석에서는 파의 공간적인 집중에 의한 파고증폭현상으로 발생되고, 이에 상대적으로 매우 큰 수평파압이 발생되는 단면위치도 있으며, 반면 Goda의 파압보다 작은 파압이 작용되는 단면위치도 이었다. 이러한 결과로부터 활동피해 시에 케이슨의 이동거리가 상이한 사행피해가 예상되며, 2차원의 단면적인 평가가 위험 측으로 될 소지가 존재한다. 무차원최대양압의 경우 항내 측에서 파가 존재하지 않는 것으로 고려되는 삼각형분포의 Goda결과와 2차원 및 3차원수치해석결과와는 매우 상이한 값을 나타내며, 전체적으로 항내 측에서 회절파, 좌측 벽체로부터 반사파, 월류로 인한 파 및 사석마운드부를 통한 파에너지의 전달이 존재하기 때문에 케이슨의 배면에서 0의 값을 나타내지 않는다.
Fig. 9.Spatial distribution of simulated non-dimensional mean wave heights according to changes of wave height and period. 
Fig. 10.Spatial distribution of mean horizontal velocities over the lowest layer according to changes of wave height and period. 
Fig. 11.Spatial distribution of mean horizontal velocities over the total layers according to changes of wave height and period. 
Fig. 12.Spatial distribution of mean turbulent kinetic energies over the lowest layer according to changes of wave height and period. 
Fig. 13.Spatial distribution of mean turbulent kinetic energies over the total layers according to changes of wave height and period. 
Fig. 15.Spatial distribution of non-dimensional maximum horizontal and uplift pressures acting on the caisson in case of two dimensional analysis. 
Fig. 17.Water level profile at the time of maximum wave pressure under still water level in case of No. 02_H3T10. 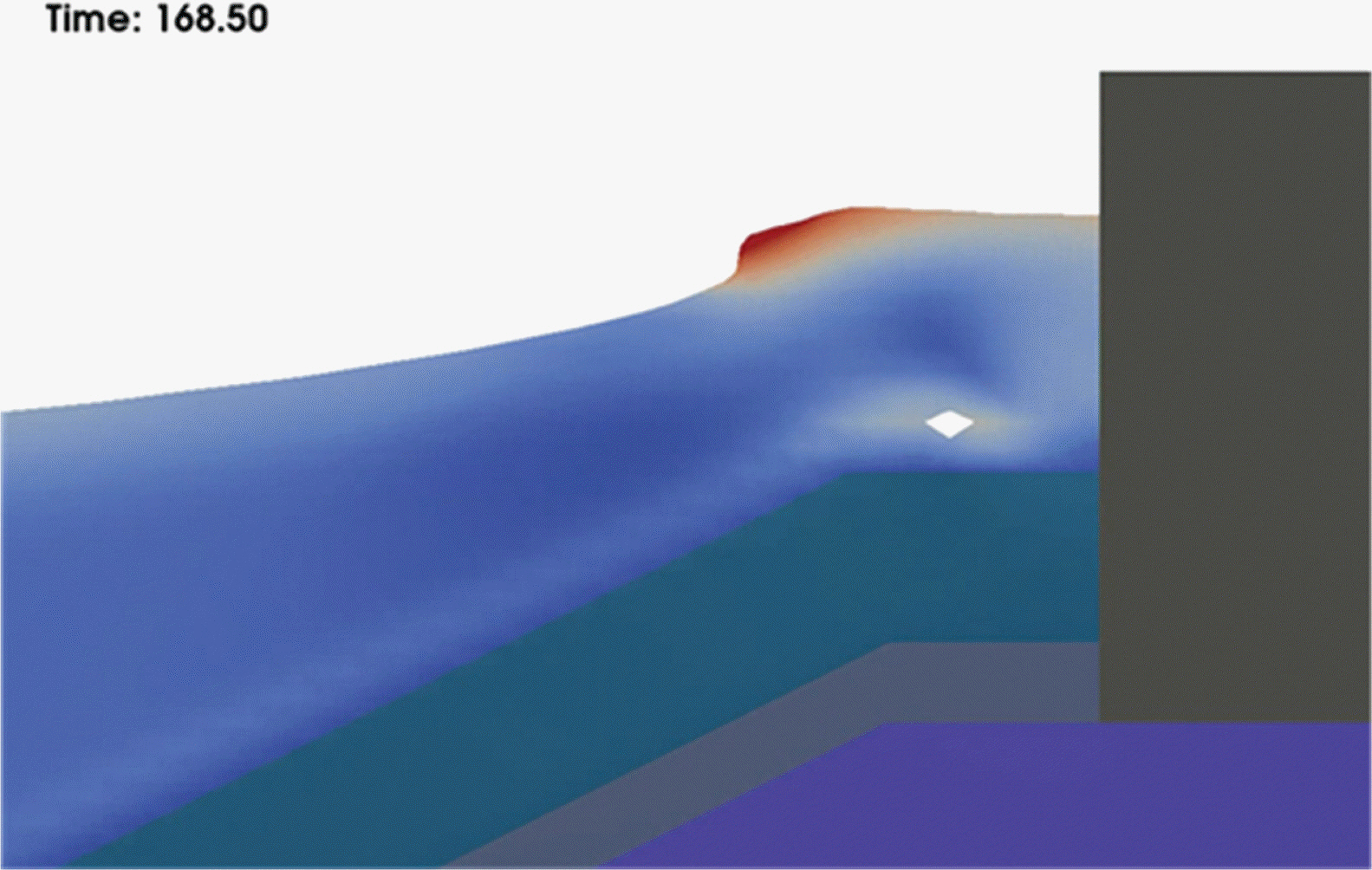
Fig. 19.Spatial distribution of non-dimensional maximum horizontal and uplift pressures on the caisson according to the changes of incident wave height and period. 
Table 1.Wave gauge positions
ReferencesBurcharth, HF, Christensen, C. (1991). On stationary and nonstationary porous flow in coarse granular materials: European Community, MAST G6-S: Project 1, Wave Action on and in Coastal Structures.
Castellino, M, Sammarco, P, Romano, A, Martinelli, L, Ruol, P, Franco, P, Girolamo, P (2018). Large impulsive forces on recurved parapets under non-breaking waves, A numerical study, Coastal Engineering, 136, 1-15.
Chen, X, Hofland, B, Molenaar, W, Capel, A, Marcel, RA, Gent, V (2019). Use of impulses to determine the reaction force of a hydraulic structure with an overhang due to wave impact, Coastal Engineering, 147, 75-88.
Cuomo, G, Lupoi, G, Shimosako, K, Takahashi, S (2011). Dynamic response and sliding distance of composite breakwaters under breaking and non-breaking wave attack, Coastal Engineering, 58, 953-969.
Ghosal, S, Lund, T, Moin, P, Akselvoll, K (1995). A dynamic localization model for large-eddy simulation of turbulent flows, J. Fluid Mechanics, 286, 229-255.
Goda, Y. (2010). Random seas and design of maritime structures. 3rd Edition. World Scientific Publishing, Co. Ltd., Singapore.
Higuera, P, Lara, JL, Losada, IJ (2014). Three-dimensional interaction of waves and porous coastal structures using Open- FOAM. Part I: Formulation and validation, Coastal Engineering, 83, 243-258.
Higuera, P, Liu, PF, Lin, C, Wong, WY, Kao, MJ (2018). Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope, Journal of Fluid Mechanics, 847, 186-227.
Hsu, TJ, Sakakiyama, T, Liu, PLF (2002). A numerical model for wave motions and turbulence flows in front of a composite breakwater, Coastal Engineering, 46(1):25-50.
Ito, Y, Tanimoto, K (1971). Meandering damage of composite type breakwater, Tech. Note of Port and Harbour Res. Inst, 112 (in Japanese)..
Jeng, DS, Ye, JH, Zhang, JS, Liu, PF (2013). An integrated model for the wave-induced seabed response around marine structures : Model verifications and applications, Coastal Engineering, 72, 1-19.
Jensen, B, Jacobsen, NG, Christensen, ED (2014). Investigations on the porous media equations and resistance coefficients for coastal structures, Coastal Engineering, 84, 56-72.
Jung, JS, Lee, CH, Cho, YS (2016). Distribution of forces at points on a vertical structure of semi-infinite breakwater considering diffraction, Journal of Korean Society of Coastal and Ocean Engineers, 28(4):240-249 (in Korean)..
Kim, DS, Hong, SH, Kim, JS, Jeong, YT (2000). Linear wave pressure distributions and loads acting on the vertical caisson of composite breakwater, and resulting wave reflection and transmission coefficients, Journal of Korean Society of Civil Engineers, 20(5B):747-754 (in Korean)..
Kim, YT, Lee, JI (2017). Hydraulic experiments on stable armor weight and covering range of round head of rubblemound breakwater armored with tetrapods: Non-breaking conditions, Journal of Korean Society of Coastal and Ocean Engineers, 29(6):389-398 (in Korean)..
Kondo, S, Takeda, H. (1983). Wave dissipating structures. Morikita Publishing Co. Ltd, (in Japanese)..
Lara, JL, del Jesus, M, Losada, IJ (2012). Three-dimensional interaction of wave and porous coastal structures: Part II: Experimental validation, Coastal Engineering, 64, 26-46.
Lee, KH, Bae, JH, An, SW, Kim, DS, Bae, KS (2016). Numerical analysis on wave characteristics around submerged breakwater in wave and current coexisting field by OLAFOAM, Journal of Korean Society of Coastal and Ocean Engineers, 28(6):332-349 (in Korean)..
Morihira, M, Okuyama, I (1965). Computing method of sea waves and diffraction diagrams, Tech. Note of Port and Harbour Res. Inst, 21 (in Japanese)..
Mostafa, AM, Mizutani, N, Iwata, K (1999). Nonlinear wave, composite breakwater, and seabed dynamic interaction, Journal of Waterway, Port, Coastal, and Ocean Engineering, 125(2):ASCE. 88-97.
Ramsden, JD. (1993). TSUNAMI: Forces on a vertical wall caused by long waves, bores, and surges on a dry bed. PhD Thesis,. California Institute of Technology.
Shimosako, K, Takahashi, T, Tanimoto, K (1994). Estimating the sliding distance of composite breakwaters due to wave forces inclusive of impulsive forces, ICCE, 1580-1594.
Sulisz, W (1997). Wave loads on caisson founded on multilayered rubble base, Journal of Wtrwy., Port, Coast., and Oc. Engrg, ASCE, 123(3):91-101.
Takahashi, S, Tanimoto, K (1983). Generation mechanism of impulsive pressure by breaking wave on a vertical wall, Rept. Port and Harbour Res. Inst, 22, 3-31 (in Japanese)..
Takahashi, S, Tanimoto, K, Shimosako, K (1993). Experimental study of impulsive pressure on composite breakwaters-Fundamental feature of impulsive pressure and the impulsive pressure coefficient-, Rept. Port and Harbour Res. Inst, 31(5):33-72 (in Japanese)..
Takahashi, S, Tanimoto, K, Shimosako, K. (1994). A proposal of impulsive pressure coefficient for design of composite breakwaters, Proceedings of the International Conference on Hydrotechnical Engineering for Port and Harbour Construction. 489-504.
Tsuda, M, Takayama, T (2006). Design procedures for a caisson wall against impulsive wave forces, Annual J. Civil Engrg, Ocean, JSCE, 22, 667-672 (in Japanese)..
|
|