1. Introduction
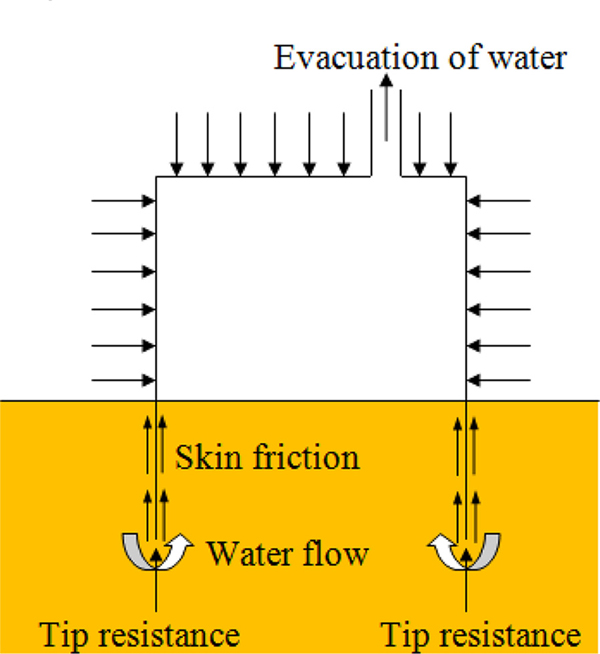
Wind energy is a promising source of energy for the near future, and plans for expanding the capacity in offshore will continue to increase. Various types of foundations have been proposed and researched for the construction of offshore wind towers, including gravity-based foundations, monopile foundations, jacket foundations, and bucket foundations. Some of the recent research and development projects (Houlsby et al., 2005) have indicated that a bucket foundation (or suction caisson) can be used as an offshore wind turbine foundation under suitable soil conditions. A bucket foundation is installed by using suction as the driving force based on the pressure difference inside and outside the bucket. Lowering the pressure in the cavity causes water flows, which reduce the effective stresses around the tip of the skirt. Hence, the penetration resistance is reduced. Therefore, it does not require heavy installation equipment (Fig. 1).
The shape of a bucket foundation is basically an open shell with a large radius/height ratio. This shape has many advantages for in relation to external loading and its stability (Houlsby et al., 2005). However, an opened cylindrical shell can be faced the buckling failure at the installation stage. Especially, this failure would be more severe for a bucket foundation that made in the form of a steel thin- walled steel cylinder, compared to a thick- walled cylinder.
In a previous studies (Pinna et al., 2000; Pinna et al., 2001; Pinna et al., 2003), these problems were widely researched by using the variational method. In these research were focused on examining the factors influencing the buckling load of for the caisson, including the boundary conditions of the shell, geometric imperfections, material plasticity, embedding ratio, and the amount of lateral restraint offered by the surrounding soil. However, because of the limitations from of the analysis scheme, only unstiffened open cylindrical shells models were considered in the analysis.
In this study, the bucket foundations that have thin-walled cylindrical sections with stiffeners and top caps were modeled and analyzed in relation to the buckling behavior. The surrounding soil was also considered in the form of a soil spring. Through the a parametric analysis, factors such as, the shape of cylindrical shell shape, the longitudinal stiffener, and the driven depth, the and buckling behaviors of the bucket foundation were estimated.
2. Buckling of Cylindrical Shell
One of the most important papers concerning the buckling of cylinders with a perfect geometry was that by Donnell (1935). Donnell derived one set of equations based on the assumption that the simplest set of possible relationships is correct.
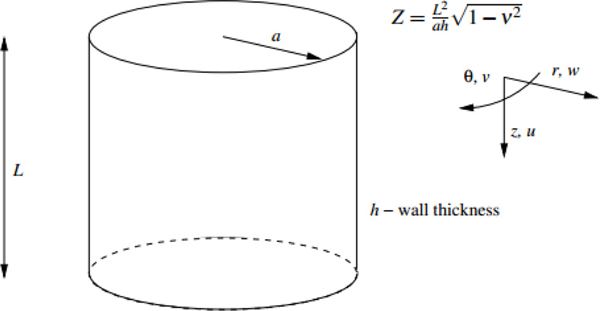
Batdorf (1947a,b) considered the Donnell equations further, making a comparison between Donnell's results and other theoretical solutions, where higher order terms were included. A comparison has also been made with experimental data for different load conditions. Batdorf's work is also notable because it introduced the non-dimensional parameter Z, which has subsequently become known as the Batdorf Z parameter. This Z parameter can be more easily explained by using the variational method. By applying the variational method to potential energy expressions, the buckling load can be non-dimensionalized by
where L is length, a is radius, h is thickness of bucket foundation cylinder (Fig. 2); D is shell bending stiffness,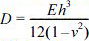 
; E is Young’s modulus, and v is Poisson's ratio; Pcris the load at buckling or the load at the change of state from the pre-buckled to buckled state; hydrostatic pressure is used as buckling load.
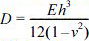; E is Young’s modulus, and v is Poisson's ratio; Pcris the load at buckling or the load at the change of state from the pre-buckled to buckled state; hydrostatic pressure is used as buckling load.
In addition, according to the Det Norske Veritas (DNV) recommended practice for the buckling strength of shells (DNVRP-C202, 2010), the buckling load can be calculated as:
where ρ is coefficient, in case of hydrostatic pressure, ρ = 0.6; ψ is coefficient, in case of hydrostatic pressure, ψ = 2; ξ is coefficient, in case of hydrostatic pressure, ξ = 1.04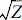
; Z is Batdorf's parameter, or curvature parameter,
.
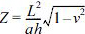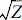; Z is Batdorf's parameter, or curvature parameter,.
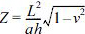3. Buckling Analysis System
3.1 Analysis Model
In the analytical models employed in previous studies, the bucket foundations were modeled just simply as thin-walled cylindrical shells. However, in this study, to consider the real shape of a bucket foundations, the thin-walled cylindrical shell was stiffened by 12 T-shaped longitudinal stiffeners, each of which consisted of both a web and a flange. Two types of models were prepared,: the one was modeled for a verification procedure and the other was modeled for a parametric study. For the parametric study model, the cap of the bucket foundation was also considered. The material of the structures was steel, and its 210 Gpa and 0.3 used as the elastic modulus and Poison ratio, respectively.
The confinement effects of the surrounding soil were considered using soil springs that attached to each nodes of the cylindrical shell under the seabed. These springs were connected from the nodes of the shell to the center points of the cylinder. Therefore, the compressive actions of the springs were used to represent the internal constraints of the internal soil constraints, and the tensile actions of the springs were used to represent that of the external soil constraints. For a given driven depth, these springs were recalculated by using soil parameters such as the depth and soil stiffness. The friction and vertical effects of the surrounding soil were ignored.
To estimate the buckling capacities of the bucket foundations, a series of buckling analyses was performed using eigen analysis. Therefore, the dynamic effects of the loading and material properties were not considered. Even though the soil springs could act in a nonlinear manner, only the initial spring constants were used in the analysis because a linear eigen analysis was performed.
3.2 Loads
During the installation phase, two types of loads are applied to a bucket foundation, hydrostatic pressure and self weight. Because the driving force for a bucket foundation is the negative pressure caused by the evacuation of the water inside it, the pressure difference between the inner pressure and external hydrostatic pressure acts as the load. The hydrostatic pressure can simply be given as
where R is hydrostatic pressure; ρ is mass unit of sea water; h is depth of considered point. Because the buckling behaviors corresponding to a longitudinal load are considered, the force obtained by the above pressure multiplied by the area of the cap acts as the main buckling load. The hydrostatic pressures act at the face of the cylinder as a confined pressure.
The boundary conditions play an important role in determining the buckling load of a shell structure. Boundary conditions are present at the lower and upper edges of the cylinder. The lower, open end of the shell generally has either a free or pinned boundary condition. At the beginning of driving, because the cylinder walls are slightly embedded by the self weight, the boundary conditions fall between the free and pinned conditions.
3.3 Analysis Procedure
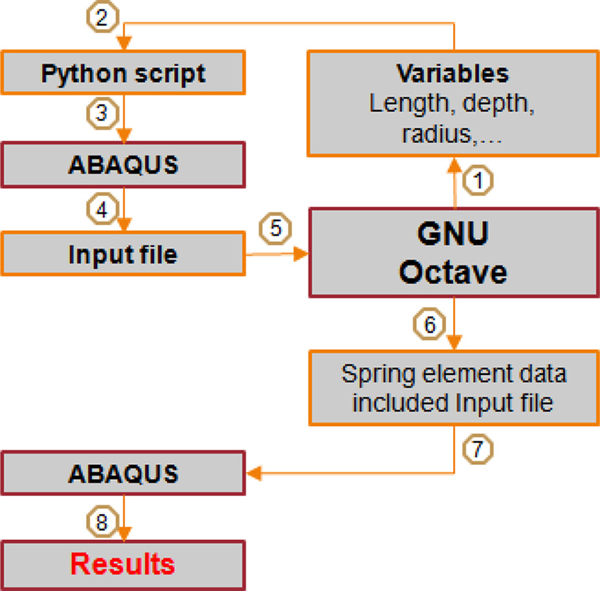
A numerical parametric study requires many repetitions of the analysis. This is tedious and time consuming. To overcome this inefficiency, all the dimensions of the models were parameterized; that is, all the dimensions could be changed and analyzed automatically.
This process includes sequence steps. These steps are shown in Fig. 3. ABAQUS(Simulia, 2011), GNU Octave(Eaton, 2007) and python were used as analysis s/w and script, respectively.
4. Analysis Results
The effects of selected parameters on the buckling behaviors were estimated using the verified buckling analysis system. These parameters were the longitudinal stiffeners and driven depth. In the estimation of these parameters, the effects of the surrounding soil and the cap of the bucket foundation were also considered.
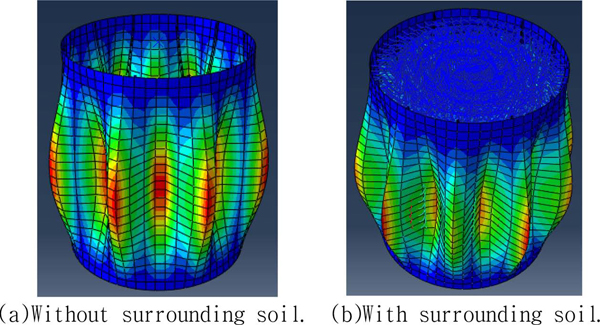
The typical buckling mode shapes are shown in Fig. 4. The boundary condition for these mode shapes was the pinned-pinned condition. Even for the surrounding soil represented by the spring constraint deformation, the general deformation characteristic was not changed.
4.1 Verification
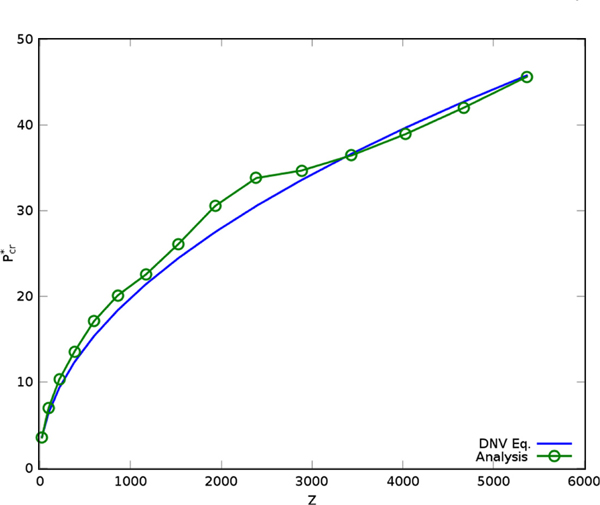
To verify the analysis system, relationship of Pcr* and Batdorf's parameter for the unstiffened cylindrical foundation was compared with that of the DNV recommendation, as shown in Fig. 5. The used boundary was the pinned-pinned condition. In this figure, the analysis results of this study show good agreements with the code formula driven obtained the analytical method.
4.2 Effects of longitudinal stiffener
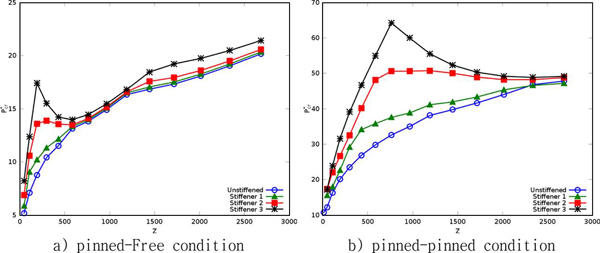
To estimate the effects of the longitudinal stiffener at the skirt, three types of T-shaped stiffeners were added longitudinally to the unstiffened base model. The dimensions of these stiffeners are listed in Table 1. The bending stiffness of a plate stiffened in a single-directionally stiffened plate can be denoted represented as an orthogonal plate. The Dc and Dl in Table 1 are orthogonal bending stiffness of circumferential and longitudinal direction, respectively.(Chu and Kim, 2002)
The boundary condition models were considered for both the pinned-free and pinned-pinned conditions. In the initial state of the installation, the end of the cylinder is driven into the seabed by its self weight, and the real boundary condition for the bucket foundation would be located between the two conditions. It depends on the soil properties of the site.
In Fig. 6, the variations of Pcr* are shown for pinned-free conditions and pinned-pinned conditions, respectively. The effect of longitudinal stiffeners made the amplification of Pcr* in whole range of Z. These amplification ranges were focused in Z < 500 and 500 < Z < 1500 for the pinned-free conditions and the pinned-pinned conditions, respectively. The effects were especially obvious in some Z-value, and both the width of Z and the amplification ratio were much better in under the pinned-pinned conditions. The Z value of a bucket foundation with normal dimensions (L = 10 m, a = 5 m, h = 0.02 m) was about 900, and this value was located at a highly amplified region of the pinned-pinned conditions. Because, the stiff soil conditions are closer to the pinned-pinned conditions than those to the pinned-free conditions, the longitudinal stiffeners can be a very effective tools for bucket foundations that installed at stiff soil sites.
4.3 Driven depth
To estimate the effect of the driven depth on the buckling load, a bucket foundation model having a radius of 5 m, length of 12 m, wall thickness of 0.02 m was considered.
In addition, to consider the effect of surrounding soil, the four vertically layered an offshore site condition was assumed. Theses layer properties are listed in Table 2. The properties of soil spring representing these properties were estimated using Malock equation and O'Neil's equaions(KGS,2002) for clay and sand layer, respectively. The spring constants used in model could be obtained by multiplying the area of each shell element by the spring coefficients listed in Table 2. The spring coefficients were calculated at the middle of each layer.
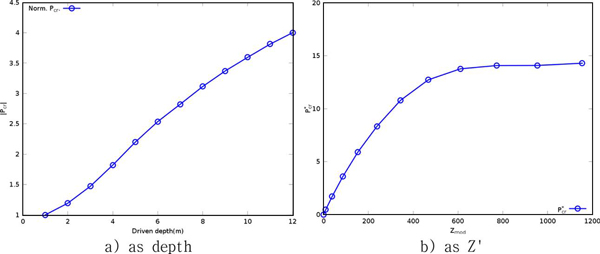
As the driven depth increased, the lateral confinement increased. Fig. 7a) shows the change in the buckling load, which was normalized by using the value of the initial state. In this figure, the buckling load capacity increases almost linearly.
Generally, the buckling capacities of structures do not change in the service state. However, in the installation state, this increased with the driven depth because the soil constraints increased. Therefore, the additional driving force using auxiliary equipment can be controlled by referring to these results.
With an increase in the driven depth, the new Z value (Z') can be calculated for the upper part not embedded to seabed. The curve of dimensionless buckling capacity Pcr* about Z' is shown in Fig. 7b). This curve is almost constant in the region after Z' = 600. This behavior is different from the previous results that the buckling stiffness was increasing with the Z value. This difference is apparently because of the lower boundary condition of this case, because it is closer to a pinned-clamped condition than to a pinned-pinned condition.
5. Conclusion
In this study, the parametric buckling behaviors of a bucket foundation for an offshore wind tower were researched. As a result, it was found that longitudinal stiffeners could dramatically increase the buckling capacity over a practical range of Z values. In addition, the confinement effect of the surrounding soil increased the buckling capacity linearly with the driven depth. However, the curve of dimensionless buckling capacity Pcr* about modified Z parameter (Z') was different from previous results that increasement as Z value.
These results can be applied to the design and installation process for the maximum efficiency of structures.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation 
Print 
