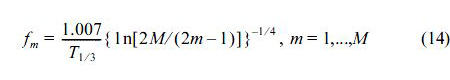1. 서 론
최근 환경오염 문제와 화석에너지 고갈 등의 문제로 인하여 신재생에너지에 대한 연구개발 투자 및 실용화가 활발히 이루어지고 있으며, 그 중 파력발전은 청정도와 경제성이 높기 때문에 국내외에서 많은 개발이 진행되고 있다. 파력발전은 파동의 운동에너지를 변환하는 방식에 따라 분류될 수 있으며, Falcão(2010)에 의하면 가동물체형, 월파형 및 진동수주형으로 분류된다. 실해역에 파력발전구조물이 설치된 사례로 1985년에 노르웨이의 해안에 건설되어 몇 년 동안 가동된 월류형 파력발전구조물인 TAPCHAN(Tapered Channel Wave Power Device)을 들 수 있고, 1985년 노르웨이 Toftestallen(Bnke and Ambli, 1986), 1990년 일본 Sakata(Ohneda et al., 1991), 1990년 인도 Vizhinjam(Ravindran and Koola, 1991), 1999년 포르투갈 Pico(Falcão, 2000), 2000년 스코틀랜드 Islay(LIMPET(Land Installed Marine Power Transmitter); Heath et al., 2000)에 각각 건설된 진동수주형(OWC; Oscillating Water Column) 파력발전구조물을 들 수 있으며, 파랑에너지로부터 추출되는 전기동력은 60~500 kW의 범위에 있다. 여기서, 유용성이 가장 큰 것으로 알려진 진동수주형은 공기실 내부에서 파의 상하운동을 공기흐름으로 변환하여 공기터빈을 구동시키는 방식으로, 입사파랑의 주파수가 공기실의 고유주파수와 일치하게 되면 공진현상이 발생하게 되고, 결과적으로 공기실내에 수면의 상하운동을 크게 증폭시킬 수 있으므로 에너지효율을 극대화시킬 수 있다 (조, 2002).
이상의 OWC파력발전구조물에 있어서 파랑-구조물-내부공기의 상호간섭에 대한 해석해로는 대표적으로 Evans and Porter(1997)의 연구를 들 수 있고, 수치해석에서의 대상파랑을 2차원규칙파랑(Evans and Porter, 1995; Greenhow and White, 1997; Malmo and Reitan, 1985; 경 등, 2006; Nakamura and Nakahashi, 2005), 2차원불규칙파랑(Boccotti, 2007a,b; Gouand et al., 2010; Falcão and Justino, 1999; Gervelas et al., 2011; Falcão and Rodrigues, 2002; Falcão, 2002; Yin et al., 2010), 3차원규칙파랑(EI Marjani et al., 2008; Josset and Cle'ment, 2007; Paixão Conde and Gato, 2008; 조, 2002), 그리고 3차원불규칙파랑(Delaure' and Lewis, 2003)으로 각각 대별할 수가 있다. 수치해석기법으로 구분하면 고유함수전개법(Evan and Porter, 1995; Malmo and Reitan, 1985; Gouaud et al., 2010; 조, 2002), 경계요소법(Josset and Cle'ment, 2007; Delaure' and Lewis, 2003), 유한요소법(경 등, 2006), Green함수법(Nakamura and Nakahashi, 2005) 및 유한차분법(EI Marjani et al., 2008; Paixão Conde and Gato, 2008; Yin et al., 2010)이 있으며, 다양한 수치기법이 적용되고 있는 것을 알 수 있다.
여기서, 공기실 내의 공기압의 변동은 공기실 내의 수면변동으로부터 발생되는 것으로 하여 공기압축성에 관한 상태방정식으로부터 변동공기압을 산정하는 것이 거의 대부분이다. 이로부터 Wells터빈을 통과한 후의 공기압과의 차이로부터 Wells터빈에 의한 전기에너지로의 변환효율을 검토하며, 실제로 공기실 내의 공기흐름속도를 직접적으로 평가하는 연구는 혼상류해석법에 의한 이 등(2011)의 연구를 제외하면 거의 이루어지지 않고 있는 실정이다. 최근, RANS(Reynolds Averaged Navier-Stokes Solver) 및 k−ε난류모델에 기초한 FLUENT Code를 적용하여 유한차분법으로 해석하는 기법(EI Marjani et al., 2008; Paixão Conde and Gato, 2008; Yin et al., 2010)이 적용되고 있지만, 3차원적인 공기흐름을 충분히 재현하고 있지는 못하다.
본 연구에서는 해수교환을 통해 항내정온도의 유지 및 수질의 개선능력을 향상시키고, 동시에 파랑에너지의 추출이 가능한 해수교환용 OWC파력발전구조물에서 공기흐름을 해석하기 위하여 규칙파랑뿐만 아니라 불규칙파랑을 해석할 수 있는 3차원수치모델인 3D-NIT(Three-Dimensional Numerical Irregular wave Tank)모델(이 등, 2012)을 적용한다. 해석에서는 자유수면추적에 VOF법(Hirt and Nichols, 1981)을, 난류해석에 k−ε모델을 각각 적용하며, 무반사조파시스템을 구현한 3차원수치조파수로를 적용한다. 공기흐름해석에 3D-NIT모델의 적용성을 검증하기 위하여 파랑변형율(반사율, 전달율) 및 해수교환통수로에서의 평균유속에 관한 기존의 수치해석결과와 실험결과 및 일본 연안개발기술센터에서 개발한 CADMAS-SUFR(沿岸開發技術硏究センタ, 2001)에 의한 수치해석결과와 본 연구의 3D-NIT모델에 의한 수치해석결과를 각각 비교·검토하였다.
이와 같이 검토된 본 해석법의 타당성 하에 본 3D-NIT모델을 불규칙파동장하의 해수교환용 OWC파력발전구조물에서 공기실 내 공기흐름의 해석에 적용하여, Bretschneider and Mitsuyasu스펙트럼(Mitsuyasu, 1970)에 근거한 입사주파수스펙트럼의 변화에 따른 공기흐름 주파수스펙트럼의 변화특성, 구조물의 존재여부에 따른 공기실 위치에서 주파수스펙트럼의 변화특성, 구조물에 의한 파랑변형율의 변화특성 및 공기흐름과 유체흐름에 의한 동력 등을 검토한다. 이러한 결과로부터 실해역에서 이용가능한 파랑에너지밀도가 가장 높게 분포하는 파랑조건이 결정되면 해수교환용 OWC파력발전구조물에서 공기흐름속도, 파랑변형율 및 공기실 내에서 수위변동의 특성 등을 용이하게 판단할 수 있을 것이며, 향후 해수 교환용 OWC파력발전구조물의 계획, 설계 및 시공 등에 중요한 기초자료를 제공할 수 있을 것이다.
2. 수치해석모델의 개요
2.1 기초방정식
3차원불규칙파수치파동수로에 기초한 본 연구의 3D-NIT모델은 기존의 2차원수치파동수로의 계산수법을 기본으로 3차원으로 확장한 것이며, 자유수면 해석모델에 VOF법을, 난류해석에는 k−ε모델을 각각 적용하였고, 3차원수치파동수로의 기초방정식은 3차원비압축성의 점성유체를 대상으로 한 연속식 및 Navier-Stokes방정식을 PBM (Porous Body 모델)에 근거하여 확장한 다음의 식(1)~(4)와 같이 주어진다.
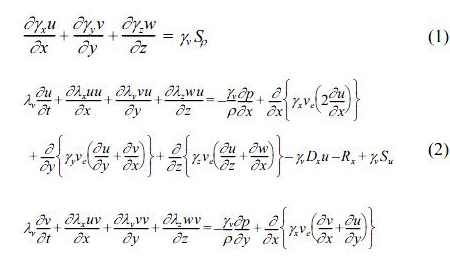
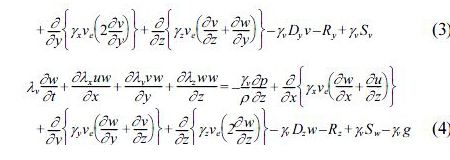
여기서, t는 시간, x, y는 수평방향좌표, z는 연직방향좌표, u,v, w는 x, y, z방향의 유속성분, ρ는 유체밀도, p는 유체 압력, ve는 분자동점성계수 v와 와점성계수 vt의 합, g는 중력가속도, γv는 체적공극율, γx, γy, γz는 x, y, v방향의 면적공극율Dx, Dy, Dz는 경계에서 반사파의 제어를 위해 설치한 스폰지층에서의 에너지감쇠계수, Sp, Su, Sv, Sw는 해석영역내의 조파를 위한 조파소스항, λv, λx, λy, λz는 구조물에 의한 관성력효과를 나타낸 파라미터로 다음의 식 (5)와 같이 표현된다.
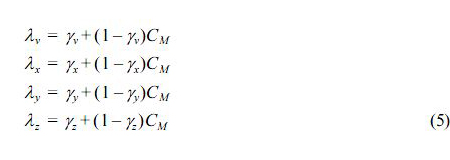
여기서, CM은 관성력계수, Rx, Ry, Rz는 투과층에서 저항력으로 식(6)과 같이 주어진다.
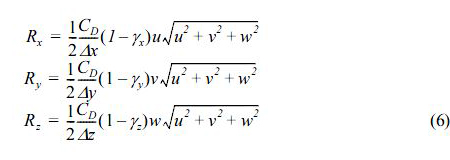
여기서, CD는 항력계수, Δx, Δy, Δz는 x, y, z방향의 격자간격이다.
본 연구에서는 이상의 기초방정식에 기초한 3D-NIT모델을 적용하여 규칙파 및 불규칙파에 의한 OWC파력발전구조물에서 공기흐름속도 및 수위변동 등의 해석을 수행하였다. 대상의 구조물은 불투과성이기 때문에 실제의 수치계산에서는 체적공극율, 면적공극율 및 투과층 내에서 저항력 등은 무시되었고, 또한 계산영역의 양측면과 바닥에는 불투과경계조건이 적용되었다.
2.2 3차원수치파동수로에서 불규칙파의 조파
3D-NIT모델을 적용하여 불규칙파를 검토하는 경우에 조파지점에서의 수위변동 및 물입자속도(수평 및 연직유속)을 사용자가 독자적으로 입력데이터로 작성할 필요가 있다. 일반적으로 불규칙파랑은 선형이론으로부터 얻어진 규칙파의 중첩으로 조파되지만, 해석시간이 증가됨에 따라 평균수위가 상승하는 문제가 발생하여 계산이 불가능하게 된다.
본 연구에서는 3D-NIT모델을 이용하여 불규칙파를 검토하는 경우에 문제로 지적되는 평균수위상승을 억제하면서 안정적으로 불규칙파가 조파될 수 있는 시스템을 기술(Fujiwara, 2005; 이, 2007)하며, Goda의 방법(1985)에 따른 불규칙파의 조파방법도 간략히 기술한다. 규칙파의 조파방법은 선형이론으로부터 얻어진 성분파의 주파수에 하나씩 순번을 붙여서 이를 무한급수의 합으로 고려하는 것이다. 조파지점에 있어서는 수면파형η, 수평 및 연직 유속(u, v)의 시간적인 변동이 필요하게 되며, 이들은 각각식(7)~(9)로 주어진다.
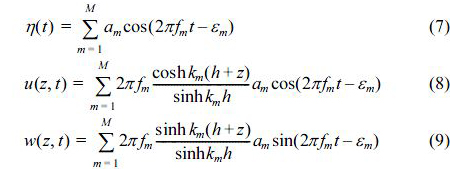
여기서, εm은 random한 위상각, fm은 주파수, am은 진폭, km은 파수, M은 성분파의 수, h는 수심이다. 단, 연직좌표 z는 정수면에서 윗방향을 (+)로 취하고, εm 및 fm의 선택방법은 후술되며, 진폭 am은 다음의 식 (10)으로 정의된다.

여기서, Δf는 주파수폭, S(f)는 파랑에너지밀도이며, 불규칙파의 스펙트럼은 불규칙파를 모의하는 데에 널리 사용되고 있는 식(11)의 Bretschneider and Mitsuyasu스펙트럼(Mitsuyasu, 1970)을 적용하였다.
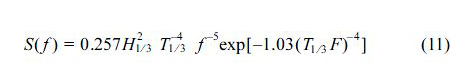
여기서, H1/3은 유의파고, T1/3은 유의파주기를 각각 나타낸다. 일반적으로 수치해석을 통해 불규칙파를 검토하는 경우 전술한 바와 같이 해석시간이 증가됨에 따라 평균수위가 상승하는 문제가 지적되어 있다(CDIT, 2001). 본 연구에서는 평균 수위상승을 억제하는 방법으로 조파지점에서 수평유속을 산출할 때 각 성분파에 대응하는 Stokes파의 질량수송속도를 뺀 다음의 식(12)를 적용한다(Fujiwara, 2005; 이, 2007).
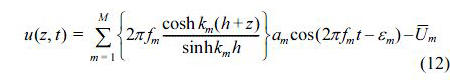
여기서, Stokes파의 질량수송속도 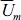 은 성분파를 나타내는 m을 제외하여 나타내면 다음의 식(13)과 같이 주어진다.
은 성분파를 나타내는 m을 제외하여 나타내면 다음의 식(13)과 같이 주어진다.
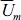 은 성분파를 나타내는 m을 제외하여 나타내면 다음의 식(13)과 같이 주어진다.
은 성분파를 나타내는 m을 제외하여 나타내면 다음의 식(13)과 같이 주어진다.
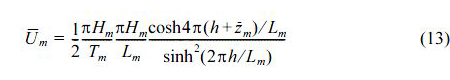
여기서,  m은 물입자의 평균위치를 나타낸다.
m은 물입자의 평균위치를 나타낸다.
 m은 물입자의 평균위치를 나타낸다.
m은 물입자의 평균위치를 나타낸다.
3. 수치해석의 검증
3.1 해수교환구조물에 의한 파랑변형율
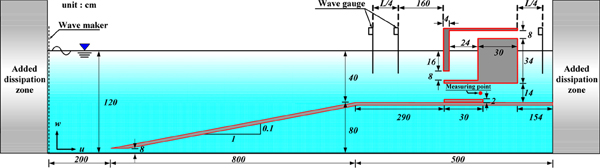
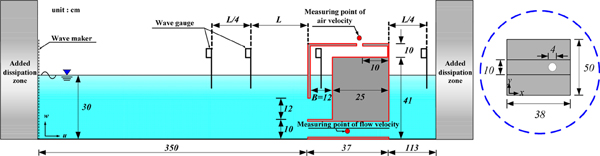
본 절에서는 3D-NIT모델에 의한 3차원수치파동수로에서 파랑과 구조물과의 상호간섭현상에 대한 타당성을 검증하기 위하여 Nakamura(1999)가 제시하고 있는 Fig. 1의 해수교환구조물의 반사율 및 전달율에 대한 수리모형실험 및 수치모형실험의 결과(Nakamura et al., 2003)와 비교ㆍ검토하며, 이와 병행하여 CADMAS-SUFR(沿岸開發技術硏究センタ, 2001)에 의한 수치해석도 수행하여 그 결과를 함께 제시한다.
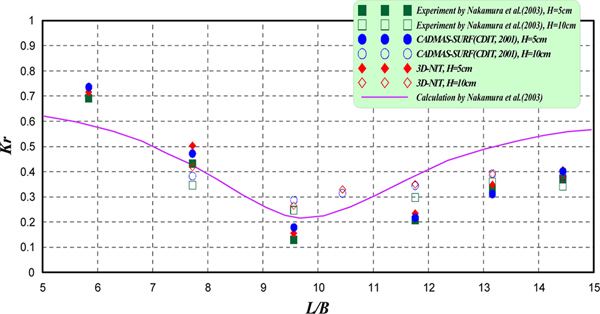
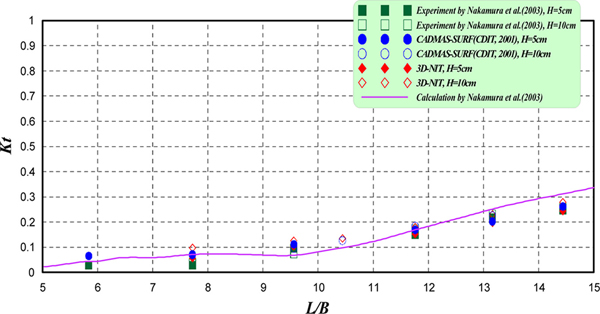
수치해석의 검증을 위하여 본 3차원수치파동수로는 Nakamura(1999)가 수행한 수리 및 수치해석조건과 동일한 입사파랑(규칙파)의 제원으로 구성되었으며, Figs. 2,3에 해수교환구조물에 의한 반사율Kr, 전달율 Kt를 파장 L과 유공부의 폭 B와의 비인 L/B에 대해 산정된 결과를 제시한다. Fig. 2의 결과를 살펴보면, 반사율의 경우 입사파고 H = 5 cm와 H = 10 cm에 대한 실험치(Nakamura, 1999; Nakamura et al., 2003), CADMAS-SUFR(沿岸開發技術硏究センタ, 2001)에 의한 수치해석치 및 본 해석결과 모두 공진현상이 나타나는 L/B = 9.56의 값에서 최소치를 취하고, L/B의 양측으로 갈수록 반사율이 증가하는 경향을 나타낸다. 또한, L/B = 11.76~14.44인 비교적 장주기파랑의 경우에 기존의 실험결과와 거의 동일한 결과를 나타내고 있으며, L/B = 5.84~9.56 인 비교적 단주기파랑의 경우에 수치해석치가 기존의 실험치보다 약간 높은 결과를 나타낸다. 이는 계산영역을 크기가 일정한 직사각형의 격자로 분할하는 과정에서 단주기파랑 및 장주기파랑을 모의하는 격자크기를 동일하게 설정하였기 때문이라 판단되지만, 실험치와의 대응성은 만족스러운 것으로 판단된다. Fig. 3의 결과를 살펴보면, H = 5 cm와 H = 10 cm에 대한 실험치(Nakamura, 1999; Nakamura et al., 2003), CADMAS-SUFR(沿岸開發技術硏究センタ, 2001)에 의한 수치해석치 및 본 해석결과 모두 L/B의 값이 커질수록 전달율이 증가하는 경향을 나타내며, 본 해석결과와 Nakamura et al.(2003)에 의한 실험치 및 CADMAS-SUFR(沿岸開發技術硏究センタ, 2001)에 의한 수치해석치의 대응성을 살펴보면, H = 5 cm및 H = 10 cm에 대해 모두 매우 잘 일치하는 것을 알 수 있다.
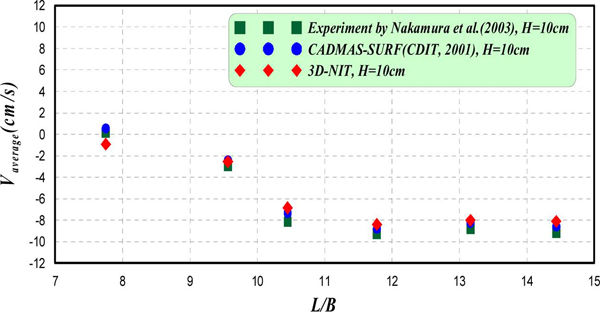
3.2 해수교환통수로에서의 평균유속
본 절에서는 3D-NIT모델에 의한 3차원수치파동수로에서 해수교환통수로에서의 유체흐름에 대한 타당성을 검증하기 위하여 전술한 Fig. 1의 해수교환통수로에서의 평균유속에 대한 수리모형실험의 결과와 비교ㆍ검토하며, 이와 병행하여 CADMAS-SUFR(沿岸開發技術硏究センタ, 2001)에 의한 수치해석도 수행하여 그 결과를 함께 제시한다. Fig. 3과 동일한 계산조건에 대하여 해수교환통수로에서의 평균유속을 파장 L과 유공부의 폭 B와의 비인 L/B에 대해 산정된 결과를 Fig. 4에 나타낸다. Fig. 4의 결과를 살펴보면, L/B = 10 이하인 비교적 단주기파랑의 경우에 (−)방향유 속의 경향이 미미하지만, L/B = 10 이상인 비교적 장주기파랑의 경우 (−)방향유속이 크게 나타나고 있으므로 해수교환의 효과가 큰 것으로 판단되며, 본 해석결과와 Nakamura et al.(2003)에 의한 실험치 및 CADMAS-SUFR(沿岸開發技術硏究センタ, 2001)에 의한 수치해석치의 대응성은 매우 만족스러운 것으로 판단된다.
4. 수치해석의 결과
본 연구에서의 해수교환을 고려한 OWC파력발전구조물은 Fig. 1의 해수교환구조물에 이 등(2011)의 연구에서 제시된 OWC파력발전구조물의 최적형상을 적용한 구조물로, 이를 Fig. 5에 제시하며, Table 1에 수치해석에 적용된 입사파랑의 제원을 나타낸다.
먼저, 본 연구에서 제시한 해수교환용 OWC파력발전구조물의 해수교환능을 판단하기 위해 해수교환통수로에서의 유체흐름속도를 측정하며, 본 3D-NIT모델의 조파이론으로부터 Bretschneider and Mitsuyasu(Mitsuyasu, 1970)에 의한 입력조파스펙트럼과 조파위치에서의 수위변동으로부터 산정된 주파수스펙트럼, 그리고 구조물의 공기실 위치까지 전파된 불규칙파랑의 수위변동으로부터 얻어지는 주파수스펙트럼을 구조물의 유무에 따라 비교·검토한다. 또한, 해수교환용 OWC파력발전구조물의 공기실 내에서 수위변동에 식 (15)를 적용하여 추정되는 공기흐름속도에 대한 주파수스펙트럼의 특성을 분석하며, 본 연구에서 제시하는 구조물에 의한 반사율 Kr 및 전달율Kt(Goda and Suzuki, 1976)와 유의주기와의 관계를 검토하며, 공기흐름 및 유체흐름에 의한 평균동력을 검토한다.
Table 1
Conditions of incident waves
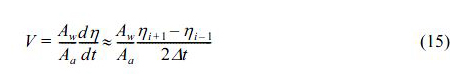
여기서, V는 공기실 내에서 평균공기흐름속도, Aw는 공기실의 단면적(Fig. 5에서 Aw = 600 cm2), Aa는 터빈부의 단면적(Fig. 5에서 Aa = 12.57 cm2), η는 공기실 내에서 평균수면진동, Δt는 시간차분간격을 나타낸다.
4.1 해수교환통수로에서의 유체흐름속도
4.2 파랑스펙트럼
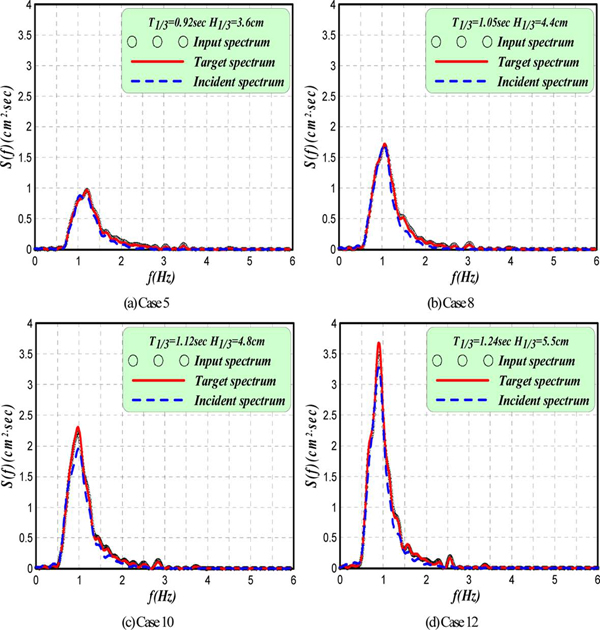
3차원수치파동수로에 기초한 본 3D-NIT모델에 의한 불규칙파의 조파성능을 검토하기 위하여 Table 1의 파랑조건을 적용하여 Bretschneider and Mitsuyasu스펙트럼으로부터 불규칙파랑(주파수성분은 M = 150개)을 조파한다. 이로부터 조파위치에서 발생하는 수위변동에 의한 주파수스펙트럼(편리상 Target spectrum으로 칭함) 및 구조물이 존재하지 않을 때 구조물의 위치에서 수위변동에 의한 주파수스펙트럼(편리상 Incident spectrum으로 칭함)을 본 수치모델로부터 산정한 결과 및 입력조파스펙트럼(편리상 Input spectrum으로 칭함)을 각각 Fig. 7에 나타낸다.
먼저, Input spectrum과 Target spectrum을 살펴보면 유의주기가 T1/3 = 0.92, 1.05 sec인 경우는 주파수의 변화에 따른 두 스펙트럼의 변화과정은 거의 일치하는 것을 알 수 있고, 특히 첨두주파수에서 스펙트럼의 값도 거의 동일한 것을 알 수 있다. 그러나, 유의주기가 길어지는 Case 10와 12의 경우에는 주파수의 변화에 따른 두 스펙트럼의 변화과정은 거의 일치하지만, 첨두주파수에서 Target spectrum의 값이 약간 큰 것을 볼 수 있고, 특히 유의주기가 긴 경우에 이러한 현상이 명확히 나타나는 것을 알 수 있다. 이러한 결과는 근본적으로 Input spectrum인 Bretschneider and Mitsuyasu스펙트럼이 심해에서 주어지는 스펙트럼인 반면, 본 연구에서 주어진 상대수심이 천해이기 때문인 것으로 판단된다. 두 스펙트럼의 모양에는 차이가 있으나, 전체 면적이 유사하여 유의파고는 오차범위내에서 거의 같게 나왔다. 즉, 입력조파된 불규칙파랑의 유의주기 및 유의파고와 조파위치에서 발생하는 불규칙파랑의 유의주기 및 유의파고가 잘 일치되는 것으로 판단된다.
다음으로, 구조물이 존재하지 않을 때 조파된 불규칙파랑이 구조물이 위치하는 지점까지 전파된 경우에 수위변동으로부터 산정되는 Incident spectrum을 Target spectrum과 비교하면 전체적으로 Incident spectrum의 파랑에너지가 감쇠되고, 이러한 현상은 첨두주파수대에서 크게 나타나며, 특히 유의주기 및 유의파고가 큰 경우에 현저하게 나타나는 것을 알 수 있다. 이것은 조파된 Target spectrum이 수심이 얕은 수조상을 전파하면서 나타나는 파랑에너지의 분산에 의한 결과로, 첨두주파수대에서 고파랑에너지의 분산이 크게 나타나는 것으로 추산된다. 또 다른 원인으로는 유체점성에 의한 파랑에너지의 감쇠 등을 들 수 있을 것이다. 이상과 같이, 주파수의 변화에 따른 Input spectrum, Target spectrum 및 Incident spectrum의 각 변화특성 및 전파과정에서 나타나는 Target spectrum의 파랑에너지 분산과정 등의 특성이 일반 해안공학적인 사실과 잘 합치되는 것으로 판단된다.
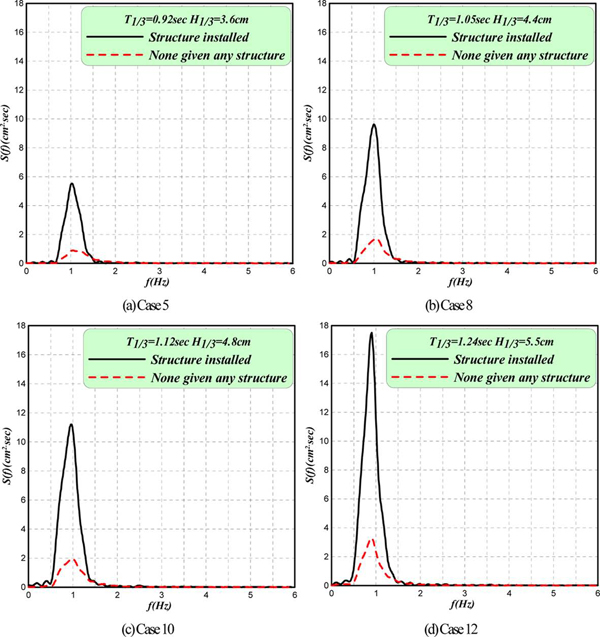
다음의 Fig. 8은 해수교환용 OWC파력발전구조물의 설치유무에 따른 공기실 위치에서 수위변동으로부터 추산된 스펙트럼을 나타낸 결과이다. 제시된 모든 결과에서 구조물이 존재할 때 모든 주파수대에서 파랑에너지가 증대되는 것을 알 수 있고, 이는 첨두주파대 근방에서 최대로 나타나는 것을 확인할 수 있다. 이러한 결과로부터 공기실 내에서 다중반사 등에 의해 파고가 증폭되는 것을 알 수 있고, Nakamura and Nakahashi(2005)에 의하면 Piston mode의 공진에 의해 입사 파랑에너지를 포획하여 반사율을 감소시키는 결과로 귀착되는 것으로 알려져 있다. 또한, 이러한 Piston mode의 공진이 발생하면 공기실 내의 수위변동과 구조물 전면에서 수위변동에서는 큰 위상차가 발생하고, 반사율이 최소로 되는 주기대에서 180o의 역위상이 발생한다는 사실이 지적되어 있다. 따라서, 공기실 내에서 발생하는 이러한 파고증폭으로 인하여 공기흐름의 유출부에서는 공기흐름속도가 증가되고, 결과적으로 파력발전의 유용성이 증대되는 결과로 이어질 것이다.
4.3 해수교환용 OWC파력발전구조물에서 공기흐름속도에 관한 주파수스펙트럼
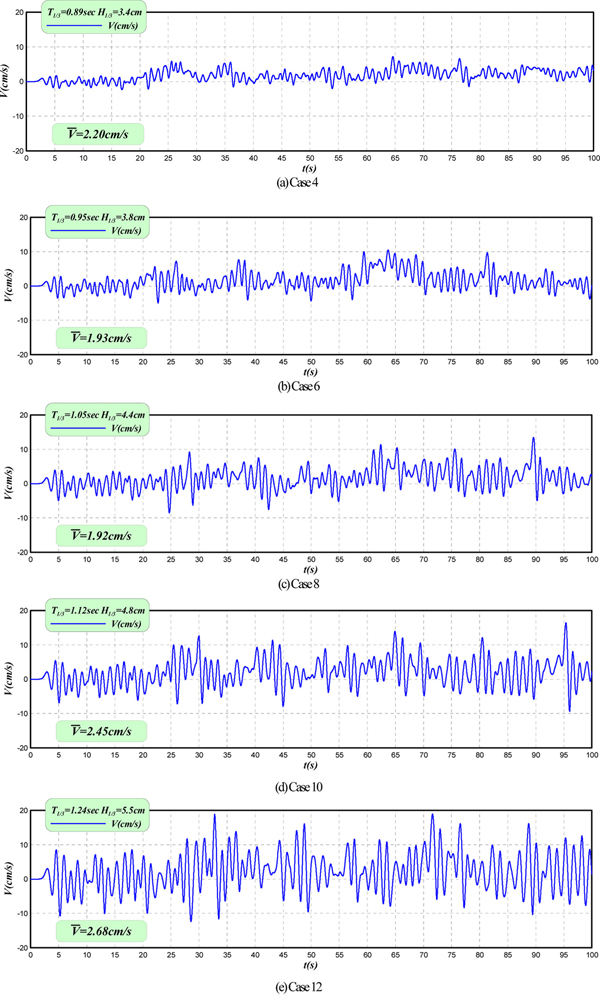
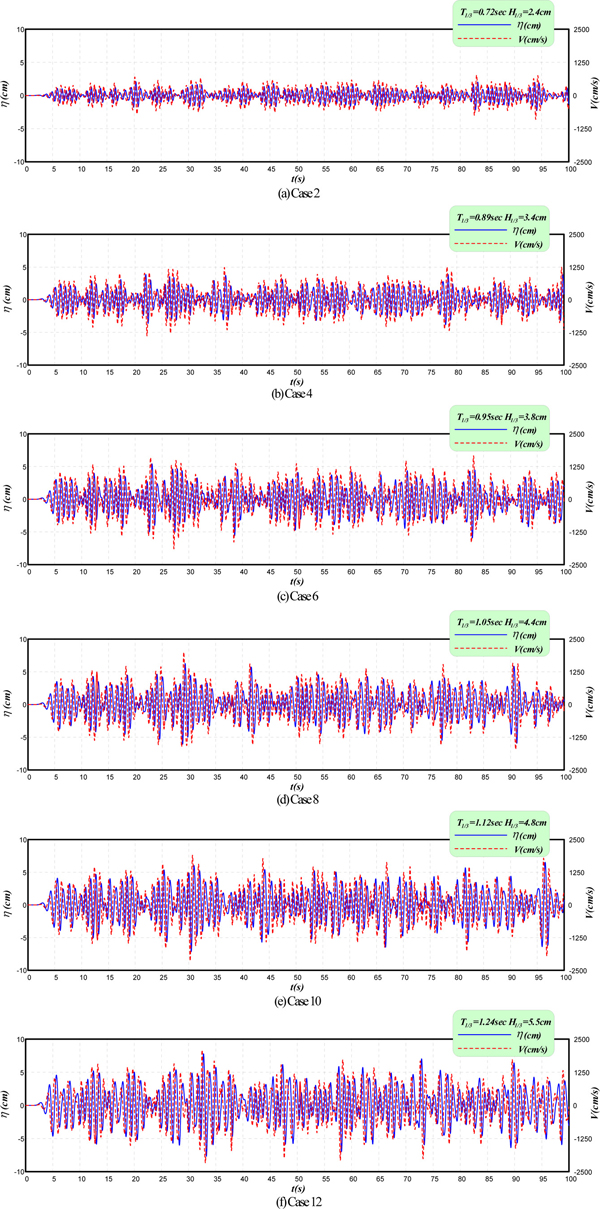
먼저, 3차원불규칙파동장하 해수교환용 OWC파력발전구조물의 공기실 내에서 수치적으로 얻어지는 불규칙수면변동에 식 (15)를 적용하여 추산된 불규칙공기흐름속도의 시간변화V(cm/sec)를 불규칙수면변동 η(cm)과 함께 Fig. 9에 제시한다. 전체적인 경향은 유의주기 및 유의파고가 클수록 공기실 내에서 수위변동과 이에 따른 공기흐름속도가 크게 나타나고, 두 변동량의 시간변화에서는 항상 위상차이가 존재한다는 것을 알 수 있다. 이러한 결과는 식 (15)로부터도 알 수 있는 바와 같이 파봉과 파곡의 전후에서는 수위변동량이 나타나지 않기 때문에 공기흐름속도는 0으로 주어지고, 반면에 수위의 영점상향 혹은 하향교차점에서는 수위변동량이 크게 나타나므로 이에 따라 공기흐름속도가 크게 주어지기 때문이다. 그림에서는 이와 같은 관계가 규칙적으로, 그리고 반복적으로 표현되고 있는 것을 알 수 있다.
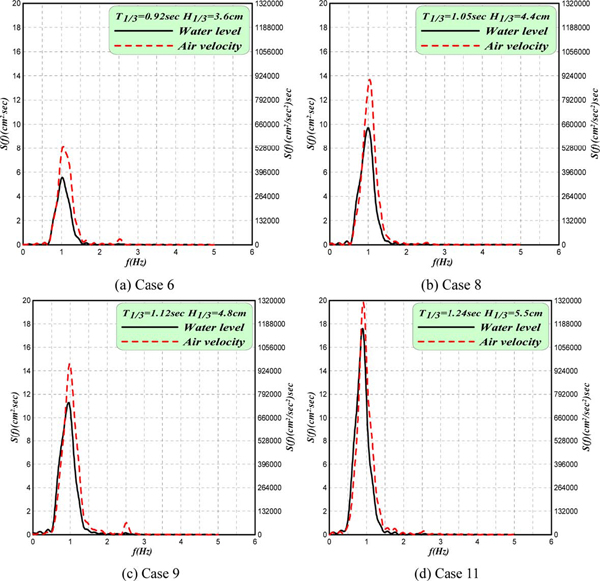
Fig. 9의 수위변동으로부터 추산된 공기흐름속도의 주파수스펙트럼을 수위변동의 주파수스펙트럼과 함께 Fig. 10에 나타낸다. Fig. 10의 결과를 살펴보면 공기흐름속도의 주파수스펙트럼 첨두치가 수위변동의 경우보다 약간 단주기측으로 이동된 결과를 나타낸다. 이것은 Fig. 9에서 언급한 바와 같이 두 변동량의 시간변화에서 위상차이가 존재하기 때문으로, 즉 수위변동의 크기가 바로 공기흐름속도로 변환되는 것이 아니라 수위변동의 시간변화율이 공기흐름속도로 변환되기 때문이다. 그리고, 수위변동의 시간변화량에서 일반적으로 동일한 유의파고의 조건하에서는 유의주기가 길수록 변환되는 공기흐름속도는 감소될 것이고, 반면에 동일한 유의주기의 조건하에서는 유의파고가 클수록 변환되는 공기흐름속도는 증가할 것으로 예측된다. 따라서, 이러한 사실에 근거하여 Fig. 10를 살펴보면 상대적으로 유의파고가 큰 경우가 수위변동의 시간변화로부터 공기흐름속도로 변환되는 비율이 크다는 것을 알 수 있다.
Fig. 11에는 불규칙파랑에 대한 구조물의 반사율 Kr 및 전달율 Kt의 변화를 공기실 폭 B와 유의파장 L1/3과의 비인 B/L1/3의 변화에 대해 제시한다. 결과를 살펴보면 특정한 B/L1/3=0.092에서 최소의 반사율을 나타내고, 좌우로 갈수록 반사율이 증가하는 경향을 나타내며, 유의주기 및 유의파고가 커질수록 전달율이 크게 나타난다.
4.4 공기흐름 및 유체흐름에 의한 평균동력
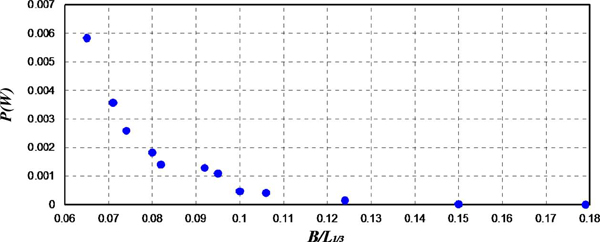
Fig. 9의 수위변동으로부터 추산된 공기흐름속도 및 해수교환통수로에서의 유체흐름속도에 다음의 식 (16)을 적용하여 산정한 평균동력 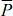 의 변화를 공기실 폭 B와 유의파장 L1/3과의 비인 B/L1/3의 변화에 대해 제시한다. 이 때, 공기흐름의 경우 양방향흐름의 발전이 가능한 Wells터빈에 의해 동력을 생산하기 때문에 양방향흐름을 고려한 반면, 유체흐름의 경우 (+)방향의 흐름만 적용하여 평균동력을 산정한다.
의 변화를 공기실 폭 B와 유의파장 L1/3과의 비인 B/L1/3의 변화에 대해 제시한다. 이 때, 공기흐름의 경우 양방향흐름의 발전이 가능한 Wells터빈에 의해 동력을 생산하기 때문에 양방향흐름을 고려한 반면, 유체흐름의 경우 (+)방향의 흐름만 적용하여 평균동력을 산정한다.
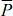 의 변화를 공기실 폭 B와 유의파장 L1/3과의 비인 B/L1/3의 변화에 대해 제시한다. 이 때, 공기흐름의 경우 양방향흐름의 발전이 가능한 Wells터빈에 의해 동력을 생산하기 때문에 양방향흐름을 고려한 반면, 유체흐름의 경우 (+)방향의 흐름만 적용하여 평균동력을 산정한다.
의 변화를 공기실 폭 B와 유의파장 L1/3과의 비인 B/L1/3의 변화에 대해 제시한다. 이 때, 공기흐름의 경우 양방향흐름의 발전이 가능한 Wells터빈에 의해 동력을 생산하기 때문에 양방향흐름을 고려한 반면, 유체흐름의 경우 (+)방향의 흐름만 적용하여 평균동력을 산정한다.

여기서, 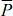 는 평균동력, t는 시간, ρ는 공기 및 유체밀도(공기밀도: 1.23 kg/m3유체밀도: 1000 kg/m3), A는 터빈부의 회전면적(공기터빈부의 회전면적: 0.001257 m2, 유체터빈부의 회전면적: 0.045 m2) V는 공기흐름 및 유체흐름속도를 나타낸다. 유체흐름에 의한 발전방식은 해수교환통수로에서의 유체흐름속도를 이용한 발전형식이며 동력 산정시 터빈에 의한 저항은 무시하였다. 유의주기 T1/3및 유의파고 H1/3의 변화에 따른 공기 및 유체흐름에 의한 평균동력
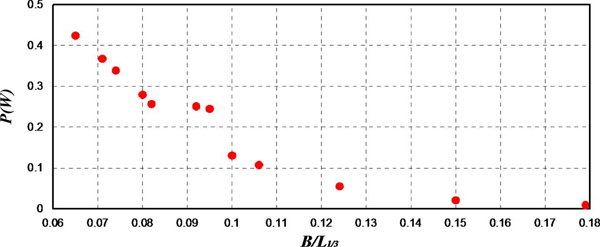
는 평균동력, t는 시간, ρ는 공기 및 유체밀도(공기밀도: 1.23 kg/m3유체밀도: 1000 kg/m3), A는 터빈부의 회전면적(공기터빈부의 회전면적: 0.001257 m2, 유체터빈부의 회전면적: 0.045 m2) V는 공기흐름 및 유체흐름속도를 나타낸다. 유체흐름에 의한 발전방식은 해수교환통수로에서의 유체흐름속도를 이용한 발전형식이며 동력 산정시 터빈에 의한 저항은 무시하였다. 유의주기 T1/3및 유의파고 H1/3의 변화에 따른 공기 및 유체흐름에 의한 평균동력 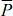 의 변화를 Figs 12 , 13 에 각각 나타낸다.
의 변화를 Figs 12 , 13 에 각각 나타낸다.
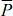 는 평균동력, t는 시간, ρ는 공기 및 유체밀도(공기밀도: 1.23 kg/m3유체밀도: 1000 kg/m3), A는 터빈부의 회전면적(공기터빈부의 회전면적: 0.001257 m2, 유체터빈부의 회전면적: 0.045 m2) V는 공기흐름 및 유체흐름속도를 나타낸다. 유체흐름에 의한 발전방식은 해수교환통수로에서의 유체흐름속도를 이용한 발전형식이며 동력 산정시 터빈에 의한 저항은 무시하였다. 유의주기 T1/3및 유의파고 H1/3의 변화에 따른 공기 및 유체흐름에 의한 평균동력
는 평균동력, t는 시간, ρ는 공기 및 유체밀도(공기밀도: 1.23 kg/m3유체밀도: 1000 kg/m3), A는 터빈부의 회전면적(공기터빈부의 회전면적: 0.001257 m2, 유체터빈부의 회전면적: 0.045 m2) V는 공기흐름 및 유체흐름속도를 나타낸다. 유체흐름에 의한 발전방식은 해수교환통수로에서의 유체흐름속도를 이용한 발전형식이며 동력 산정시 터빈에 의한 저항은 무시하였다. 유의주기 T1/3및 유의파고 H1/3의 변화에 따른 공기 및 유체흐름에 의한 평균동력 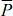 의 변화를 Figs 12 , 13 에 각각 나타낸다.
의 변화를 Figs 12 , 13 에 각각 나타낸다.
그림에서 주어지는 전체적인 경향은 두 경우 모두 유의주기가 길수록 평균동력이 커진다는 것을 알 수 있으며, 공기흐름에 의한 평균동력이 유체흐름에 의한 평균동력보다 크다는 것을 알 수 있다. 이는 유체의 밀도 및 터빈부의 면적이 공기의 밀도 및 터빈부의 면적보다 크지만, 공기흐름의 속도가 유체흐름의 속도보다 크기 때문이다. 즉, 동력은 흐름속도의 3제곱에 비례하므로 흐름속도가 2배가 되면 동력은 8배가 되기 때문이다.
5. 결 론
파랑에너지를 추출하고, 동시에 항내 정온도 유지 및 수질 개선이 가능한 해수교환용 OWC파력발전시스템에 있어서 불규칙파동장하 공기실 내의 불규칙공기흐름속도의 추정에 본 연구에서 제시하는 3D-NIT모델의 적용성을 검토할 목적으로, 기존의 수치해석결과, 수리실험결과 및 CADMAS-SURF(沿岸開發技術硏究センタ, 2001)에 의한 수치해석결과와 비교하여 해의 타당성을 확립하였다. 이상으로부터 본 모델을 불규칙 파동장에 설치된 해수교환용 OWC파력발전구조물의 주변파동장 및 공기실 내에서 공기흐름속도의 추정에 적용하여 다음과 같은 중요한 사항을 알 수 있었다.
(1) 본 연구에서 제시하는 해수교환용 OWC파력발전구조물은 해수교환의 기능을 충분히 갖는다.
(2) Bretschneider and Mitsuyasu스펙트럼에 기초한 Input spectrum과 조파지점에서 계측된 수위변동으로부터 산정된 Target spectrum은 잘 일치하며, 조파된 불규칙파랑의 전파에 따라 파랑에너지의 분산 및 유체점성 등에 의해 Incident spectrum의 첨두주파수대에서 파랑에너지의 감쇠가 발생하며, 이러한 경향은 유의주기와 유의파고가 커질수록 현저하게 나타난다.
(3) 해수교환용 OWC파력발전구조물의 설치 유무에 따른 공기실 위치에서의 수위변동으로부터 추산된 스펙트럼에서 구조물이 존재할 때 모든 주파수대에서 파랑에너지가 증대되며, 이는 첨두주파대 근방에서 최대로 나타난다.
(4) 공기실 내에서 수위변동과 이에 따른 공기흐름속도의 시간변화에서는 항상 위상차이가 존재하며, 공기흐름속도에 관한 주파수스펙트럼의 첨두주파수가 수위변동에 대한 주파수 스펙트럼의 경우보다 약간 단주기측으로 이동된다.
(5) 해수교환용 OWC파력발전구조물에서 파랑변형율의 경우 특정한 B/L1/3에서 최소의 반사율을 나타내며, 유의주기와 유의 파고가 커질수록 전달율은 증가한다.
(6) 해수교환용 OWC파력발전구조물은 해수교환 및 공기흐름에 의한 동력생산은 유체흐름에 의한 동력생산에 비해 유리하다.