Estimation of the Input Height of Irregular Waves Generated at a Wave Maker by Using Gaussian Process Regression and Artificial Neural Networks

Jung-Eun Oh; Sang-Ho Oh

doi:10.9765/KSCOE.2024.36.6.225

Journal of Korean Society of Coastal and Ocean Engineers > Volume 36(6); 2024 > Article

가우시안 과정 회귀 및 인공신경망에 의한 불규칙파 조파기 입력파고 추정

Article

J Korean Soc Coast Ocean Eng 2024; 36(6): 225-232.

Published online: December 31, 2024

DOI: https://doi.org/10.9765/KSCOE.2024.36.6.225

가우시안 과정 회귀 및 인공신경망에 의한 불규칙파 조파기 입력파고 추정

오정은^*, 오상호^**

^*국립창원대학교 산업기술연구원 연구원

^**국립창원대학교 스마트그린공학부 건설시스템공학전공 부교수

Estimation of the Input Height of Irregular Waves Generated at a Wave Maker by Using Gaussian Process Regression and Artificial Neural Networks

Jung-Eun Oh^*, Sang-Ho Oh^**

^*Researcher, Industrial Technology Research Center, Changwon National University

^**Associate Professor, Department of Civil Engineering, School of Smart and Green Technology, Changwon National University

Corresponding author: Sang-Ho Oh, Associate Professor, Department of Civil Engineering, School of Smart and Green Technology, Changwon National University, 20 Changwondae-ro Uichang-gu Changwon-si, Gyeongsangnam-do 51140 Korea, Tel: +82-55-213-3779, coast.oh@gmail.com

Received November 20, 2024 Revised December 7, 2024 Accepted December 9, 2024

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

요약

2차원 조파수조 내에서 취득된 불규칙파 실험 데이터를 이용하여 조파기 입력파고를 예측하는 인공신경망(NN) 및 가우시안 과정 회귀(GPR) 모델을 수립하고 그 성능을 평가 및 비교하였다. 두 모델 모두 불규칙파 조파 시 목표파고를 재현할 수 있는 입력파고를 매우 높은 정확도로 추정할 수 있었으며, NN 모델에 비해서는 GPR 모델의 성능이 더 우수한 것으로 나타났다. 본 연구 결과를 바탕으로 조파수조에서 수리실험을 수행할 때 조파기 입력파고 설정 시 시행착오를 줄임으로써 실험에 소요되는 시간을 줄일 수 있을 것으로 기대된다.

핵심용어: 인공신경망, 가우시안 과정 회귀, 조파, 불규칙파, 수리실험

Abstract

A neural network (NN) and Gaussian process regression (GPR) model for predicting the input wave height of the wave generator were established, and their performance was evaluated and compared using irregular wave data acquired in a two-dimensional wave flume. Both models were able to predict the input wave height that can produce the target wave height of irregular waves with a very high accuracy. Among the two models, the GPR model showed better performance than the NN model. Based on the results of this study, it is expected to reduce the time required for experiments by shortening trial and error in setting the input wave height of the wave generator when conducting physical experiments in a wave flume.

Keywords: artificial neural network, gaussian process regression, wave generation, irregular waves, physical experiment

1. 서 론

해안공학 분야에서 다루는 여러 물리적 현상들은 복잡하고 비선형적인 특성으로 인해 물리 기반의 수치 모델링과 현장 관측 또는 수리실험에 의해 규명하기 어려운 경우가 많다. 특히 수치 모델링은 특정 조건과 상황에 맞춘 방정식을 바탕으로 하기 때문에 해양 및 기상 조건과 지형 등 다양한 변수의 영향을 모두 반영하기 어렵다. 또한 복잡한 방정식을 풀기 위해 고성능의 계산 자원이 필요하고 모델링 시간이 오래 걸리는 단점이 있다. 뿐만 아니라 모델링 결과가 초기 조건 및 경계 조건에 민감하므로 입력 자료의 정밀도가 낮을 경우 결과의 신뢰성이 낮아질 수 있다. 현장 관측 및 수리실험도 해안 지역에서 발생하는 물리적 현상을 재현하는데 장비 및 인력을 운영하는데 많은 비용이 들고, 실제의 현상을 완벽히 재현하거나 계측해 내기 어렵다.

이러한 한계점을 극복하기 위해 최근에는 머신러닝 등 데이터 기반 연구방법을 이용하여 해안 현상을 분석하고 예측하는 연구가 증가하고 있다. 특히 양질의 데이터를 충분히 얻을 수 있다면 취득된 데이터에 내재된 복잡한 패턴을 머신러닝 기법으로 학습하고 비선형적 관계를 포착할 수 있다. 또한, 수치 모델링에 비해서는 계산 자원의 소모가 적고 빠르게 결과를 산출할 수 있다는 장점이 있다. 뿐만 아니라 여러 다양한 해상 및 기상 조건에서 취득된 서로 다른 이질적 성격의 데이터를 통합하여 분석하는 것이 가능하며, 확보된 데이터 수가 늘어날수록 예측 정확도가 더욱 향상될 수 있다.

그렇기 때문에 최근 해안공학 분야에서는 다양한 데이터 기반 연구가 활발하게 이루어지고 있다(Goldstein et al., 2019; Pourzangbar et al., 2023; Abouhalima et al., 2024). 최근 이루어진 몇 가지 연구 사례를 들면 Liu et al.(2024)은 북대서양 열대성 저기압의 데이터에 포함된 일부 결측값들을 다른 데이터를 이용하여 합리적으로 대치하는 모델을 개발하였다. Giaremis et al.(2024)은 순환신경망(RNN) 기법의 한 종류인 LSTM(Long Short-Term Memory) 기법으로 폭풍해일의 예측 정확도를 향상시킨 연구성과를 소개하였고, Lucero et al.(2023)은 머신러닝을 활용하여 Wavewatch III 파랑추산 모델의 후측 결과를 개선하였다. 또한, Cheng et al.(2023)은 단일 기둥 주변에서의 간극수압을 머신러닝에 의해 예측하는 연구를 수행하였다. 이 외에도 수많은 데이터 기반 연구가 이루어지고 있으며 그 숫자 또한 점점 더 증가하는 추세이다.

여러 가지 데이터 기반 연구 방법 중에서 가우시안 과정 회귀(Gaussian Process Regression: GPR)는 특정 함수 형태를 가정하지 않고 데이터에 적합한 함수 분포를 정의하여 모델링하므로 불확실성 및 노이즈가 포함되어 있는 복잡한 데이터를 효과적으로 예측하는 것으로 알려져 있다(Kim and Lee, 2022). 이러한 장점으로 인해 해안공학 분야에서도 최근 GPR을 활용한 몇몇 연구가 이루어지고 있다(Liu et al., 2024; Shashank et al., 2024; Parker et al., 2019). 국내의 경우 Oh and Oh(2022)가 조파기에서 생성된 규칙파의 입력파고를 추정하기 위해 가우시안 과정 회귀와 인공신경망 기법을 활용한 연구를 수행한 바 있다. 이 연구를 통해 2차원 조파수조 내에서 계측이 이루어지는 위치에서의 목표파고를 재현하기 위한 규칙파 입력파고를 사전에 추정하는 데이터 기반 모델을 개발함으로써 실험파 생성에 소요되는 시간을 단축할 수 있음을 보였다.

본 연구에서는 이 선행 연구를 불규칙파에 대해 확장하여 2차원 조파수조 내에서 다양한 수심, 파고 및 주기 조건에서 계측된 불규칙파 실험데이터를 기반으로 조파기 입력파고를 예측하는 가우시안 과정 회귀 모델과 인공신경망 모델을 각각 수립하고 그 성능을 검증하였다.

2. 수리실험 자료

조파수조 내 입력파고 예측 모델 수립을 위한 불규칙파 실험 자료는 길이 50 m, 폭 1.2 m인 2차원 조파수조에서 취득되었다(Oh and Lee, 2018). 이 수조의 조파판은 Fig. 1에 파란 색으로 표시된 것처럼 수조 한 쪽 끝으로부터 3.4 m 위치에 설치되어 있다. Oh and Oh(2022)에 기술된 것처럼 파도 발생장치를 구동하는 전용 소프트웨어에 입력되는 파고와 실제로 조파기에서 생성되는 파고는 약간 다르다.

본 연구에서는 총 196개의 불규칙파 자료를 분석에 이용하였으며, Fig. 1에 붉은 색으로 표시한 것처럼 수조의 길이 방향으로 총 2개 지점(x = 9 m, x = 30 m)에서 파랑을 계측하였다. Fig. 1에서 x는 조파수조 끝을 기준으로 파 진행방향으로의 좌표계를 의미한다. x = 9 m에서의 파랑은 조파판 설치 위치(x = 3.4 m)와 같은 수심에서 계측된 것이며, x = 30 m에서의 파랑은 0.35 m 더 얕은 수심에서 계측된 것이다. Table 1에는 모든 데이터에 대해서 x = 9 m에서의 수심, 유의파고(H_s) 및 첨두주기(T_p)의 범위를 제시하였다. 대부분의 수리실험이 실험실 환경에서 주기 1~3 s 범위에서 주로 수행되었기 때문에 이 범위에서의 데이터가 대부분이며, 주기 3 s 이상의 데이터도 일부 존재한다.

Fig. 2에는 조파기에 입력한 파고와 x = 9m 및 x = 30m에서 계측된 불규칙파 파고를 각각 비교한 결과를 나타내었다. x = 9m에서의 파고(H_{s, x = 9 m})의 경우 입력파고(H_{s, input})와 같거나 근소하게 작음을 확인할 수 있다. 한편, x = 30 m에서의 파고(H_{s, x = 30 m})는 x = 10~20m 구간에서의 경사면 및 x = 20~30 m 구간에서의 평탄면을 거치면서 일어나는 천수 및 쇄파의 영향으로 x = 9 m에서의 파고(H_{s, x = 9m})에 비해 근소하게 증가하거나 감소하게 된다. 이처럼 H_{s, x =30m}와 H_{s, input} 사이의 관계가 비선형적인 관계를 나타내며 파랑의 주기 및 바닥 지형에 따라 영향을 받기 때문에 수리실험에서 x = 30m에서의 목표파고를 재현하기 위한 입력파고를 설정할 때 시행착오를 겪게 된다.

3. 자료 분석

본 연구에서는 조파수조 내 불규칙파 입력파고를 예측하는 모델 수립을 위해 Oh and Oh(2022)와 마찬가지로 인공신경망과 가우시안 과정 회귀 모델 두 가지를 각각 적용하고 그 결과를 비교하였다.

3.1 인공신경망(NN) 모델

인공신경망은 인간 두뇌의 신경망 구조에서 영감을 받아 개발된 알고리즘으로, 데이터의 패턴을 학습하고 예측 또는 분류하는 데 사용된다(Jordan and Mitchell, 2015). 인공신경망의 기본 구성 요소는 뉴런(또는 노드)이며, 이들은 서로 연결되어 입력층, 은닉층, 출력층을 형성하며, 각 계층을 거치면서 데이터에 대한 복잡한 패턴을 학습할 수 있다. 입력층은 네트워크로 들어오는 데이터를 받아들이는 역할을 하고, 은닉층은 데이터를 처리하면서 점차 복잡한 특성을 학습하며, 출력층은 최종 예측 결과를 제공한다.

본 연구에서는 입력층과 출력층 사이에 10개의 노드를 가지는 1개의 은닉층으로 구성된 인공신경망을 구성하였다. 입력층의 자료로는 x = 30 m 에서의 불규칙파 파고(H_{s, x = 30 m}) 및 수심(d_{x = 30 m}), 조파판 위치에서의 수심(d_{x = 3.4 m}) 및 입력파랑의 첨두주기(T_{p, input})를, 출력층의 자료로는 입력파랑의 파고(H_{s, input})를 사용하였다. Fig. 3에는 이렇게 구성된 인공신경망의 개념도를 나타내었다. 활성함수로는 미분식이 간단하다는 장점으로 인공신경망에 자주 사용되는 시그모이드(sigmoid) 함수를 사용하였다.

확보된 196개의 전체 자료 중 80%에 해당하는 157개의 자료를 인공신경망의 학습(training) 및 검증(validation)을 통한 모델 구축에 사용하였으며, 나머지 20%에 해당하는 39개 자료를 예측(prediction)에 사용하였다. Fig. 4에는 H_{s, input} 및 H_{s, x = 30 m} 자료에 대하여 학습 및 검증에 사용한 데이터와 모델 예측에 사용한 데이터를 구분하여 나타내었다.

3.2 가우시안 과정 회귀(GPR) 모델

Oh and Oh(2022)에 언급된 것처럼 실험이나 관측 데이터로부터 어떠한 경향성을 찾아낼 때 흔히 사용하는 회귀(regression) 분석도 넓은 관점에서 보면 출력변수와 하나 이상의 입력변수 사이의 관계를 도출해내는 지도학습(supervised learning)의 일종으로 해석할 수 있다. 최근 여러 분야에서 활발하게 적용되고 있는 가우시안 과정 회귀 모델은 비선형 회귀 분석의 일종으로 함수의 특정 형태를 가정하지 않고 데이터 자체에 의해 모델이 학습되는 방식이므로 데이터 수가 상대적으로 많지 않을 경우에 좋은 성능을 발휘한다는 장점이 있다(Rasmussen and Williams, 2006).

가우시안 과정 회귀 모델에서는 데이터 포인트 간의 유사도를 측정하는 커널(kernel) 함수가 중요한 역할을 하며, 이를 통해 모델은 관측된 데이터와 유사한 특성을 갖는 새로운 데이터에 대해 예측을 수행하게 된다. 커널 함수를 어떻게 선택하느냐에 따라 모델의 유연성과 성능이 달라질 수 있게 되는데 본 연구에서는 Oh and Oh(2022)와 동일하게 방사상 기반함수(radial basis function)를 채택하였다.

(1)

k(x,x′)=σf2exp[-(x-x′)2σm2]

여기에서 k(x, x')는 임의의 두 데이터 사이의 공분산을 구하는 커널 함수이고 σ_m은 입력변수 간 상대거리에 따른 상관성을 나타내는 커널모수, σ_f는 출력변수의 크기를 조절하는 커널모수이다. 본 연구에서 GPR 모델 적용 시 최적화된 커널모수의 값은 σ_m = 152.52, σ_f = 19.76이었다.

가우시안 과정 회귀 모델도 인공신경망 모델을 구축할 때와 동일하게 157개의 불규칙파 자료를 이용하여 구축하였다. 또한, 모델 수립 시 활용되지 않은 나머지 39개의 자료를 이용하여 모델의 성능을 예측하였다.

4. 분석 결과

Fig. 5(a)에는 NN 모델에 의해 계산된 조파기 입력파고(H_{s, input})와 x = 30 m에서의 파고(H_{s, x = 30 m})를 서로 비교한 결과를 제시하였다. 조파수조 내에서 계측된 데이터는 ○ 기호로, NN 모델에 의한 결과는 파란색 ● 기호로 나타내었다. 이 그림으로부터 NN 모델에 의해서 H_{s, input}과 H_{s, x = 30 m}의 상관관계가 전반적으로 잘 재현되어 나타남을 확인할 수 있다. 이러한 특성은 모델 구축에 사용되지 않은 나머지 39개의 자료에 대해서 NN 모델로 예측한 결과를 나타낸 Fig. 5(b)에서도 확인할 수 있다. 이 그림에서는 계측 데이터는 ○ 기호로, NN 모델의 예측 결과는 빨간색 ● 기호로 표시되었으며, 구축된 NN 모델은 조파기 입력파고를 비교적 잘 예측하는 성능을 나타내었다.

Fig. 6에는 NN 모델에 의해 계산된 조파기 입력파고 값과 수리실험에서 관측된 조파기 입력파고 값을 1:1로 비교한 결과를 나타내었다. 그림에서 파란색 점은 157개의 자료를 이용하여 구축된 모델의 결과에 해당하며 빨간색 점은 나머지 39개의 자료에 대하여 예측된 결과에 해당한다. 그림에서 알 수 있는 것처럼 모델과 실험자료의 적합도가 매우 높게 나타났다.

한편, Fig. 7에는 GPR 모델에 의한 조파기 입력파고(H_{s, input})와 x = 30 m에서의 파고(H_{s, x = 30 m})의 비교 결과를 제시하였다. GPR 모델의 경우 NN 모델에 비해서 H_{s, input}과 H_{s, x = 30 m}의 상관관계가 더욱 명확하게 재현됨을 확인할 수 있다. NN 모델에서 약간의 편차를 보인 데이터의 경우에도 GPR 모델에서는 거의 정확하게 계측 데이터의 경향을 재현하는 것으로 나타났다. 모델 구축에 사용되지 않은 나머지 39개의 자료에 대해서 GPR 모델을 적용한 결과를 나타낸 Fig. 7(b)에서도 NN 모델에 비해서 더 개선된 결과가 도출됨을 확인할 수 있다.

Fig. 8에는 GPR 모델에 의해 계산된 조파기 입력파고 값과 수리실험에서 관측된 조파기 입력파고 값을 1:1로 비교한 결과를 나타내었다. Fig. 6에 보인 NN 모델에 비해서 실험 자료와의 편차가 훨씬 작아졌다. 이러한 경향은 Table 2에 제시된 평균제곱근오차(NRMSE) 및 결정계수(R²) 값에서도 확인된다. 즉, GPR 모델이 전반적으로 NN 모델보다 더 우수한 예측 성능을 나타내었다.

이상의 결과로부터 규칙파의 조파기 입력파고를 추정한 선행 연구(Oh and Oh, 2022)와 마찬가지로 불규칙파 조파 시 입력파고를 추정하는 데 있어서도 GPR 모델과 NN 모델이 우수한 결과를 나타내었으며, 두 모델 중에서는 GPR 모델이 일관되게 더 나은 예측 성능을 보였다. 선행 연구와의 한 가지 차이점은 Oh and Oh(2022)에서는 쇄파와 비쇄파 자료를 구분하지 않았을 때는 모델의 예측 성능이 크게 저하되었기 때문에 쇄파와 비쇄파 자료에 대하여 각각의 모델을 수립하였던 반면, 본 연구에서는 이러한 구분을 하지 않았음에도 두 모델 모두 비교적 좋은 결과를 나타내었다. 그 이유는 본 연구에서 사용된 불규칙파 자료의 경우 상대적으로 강한 쇄파가 발생하는 경우의 자료는 수집되지 않았기 때문인 것으로 추정되며, 향후 이러한 자료에 대하여 모델의 성능을 추가로 검증해 볼 필요가 있다.

5. 결 론

본 연구에서는 단면 조파수조에서 불규칙파 실험을 수행할 때 목표 파고를 조파하기 위한 입력파고를 예측하는 데이터 기반 모델을 수립하고 그 성능을 평가하였다. 규칙파 조파 시 입력파고를 예측하는 선행연구(Oh and Oh, 2002)와 마찬가지로 인공신경망(NN) 모델에 비해서 가우시안 과정 회귀(GPR) 모델의 성능이 더 우수한 것으로 나타났다.

GPR 모델은 본 연구에서처럼 데이터의 개수가 상대적으로 많지 않은 비선형 회귀 분석에서 상당히 좋은 예측 성능을 나타낸다고 알려져 있으며(Knudde et al., 2020), 본 연구에서도 NN 모델에 비해 더 나은 성능을 보인다는 점이 다시 한번 확인되었다. 다만, 계산 복잡도가 데이터 수의 세제곱에 비례하여 증가하므로 오히려 데이터의 수가 많아지면 계산 시간이 많이 소요되며 예측 정확도가 낮아지는 단점이 있다고 보고되고 있다(Wang et al., 2019). 해안공학 분야 연구에서는 보통 수백~수천 개의 데이터를 이용한 회귀 분석 또는 상관관계 분석이 빈번하게 이루어지므로 GPR 기법을 활용하기에 적합할 것으로 기대된다.

규칙파와 불규칙파를 이용하는 조파실험에서 GPR 모델의 활용성에 대한 검증이 이루어졌으므로 향후 해당 조파수조에서 수리실험을 수행할 때 조파기 입력파고 설정에 본 모델을 활용하는 것이 가능하며, 실험파 생성 시 시행착오를 줄이고 실험 시간을 단축하는 효과를 거둘 수 있을 것으로 기대된다. 즉, 계측 위치에서 희망하는 파고를 재현해 내기 위해 여러 차례의 조파를 통한 시행착오를 거치게 되는데 GPR 모델 적용을 통해 시행착오를 줄임으로써 실험파 생성에 소요되는 시간을 단축시킬 수 있기 때문이다. 선행연구(Oh and Oh, 2022)에서 언급되었던 것처럼 근본적으로 본 연구를 통해 수립된 모델은 실험이 수행된 조파수조에만 사용 가능하지만 조파수조 또는 수치파동수조를 활용하는 다른 환경에서도 유사한 GPR 모델을 구축하여 시간 및 비용 효율적인 연구를 수행하는 것이 가능할 것으로 기대된다.

감사의 글

이 논문은 2023~2024년도 국립창원대학교 자율연구과제 연구비 지원으로 수행된 연구결과이며, 이에 감사드립니다.

Fig. 1.

Locations of the wave board (blue) and wave gauges (red) along the wave flume.

Fig. 2.

Comparison of the significant wave heights between the input values to the wave generation system and the measured values at x = 9 m and x = 30 m.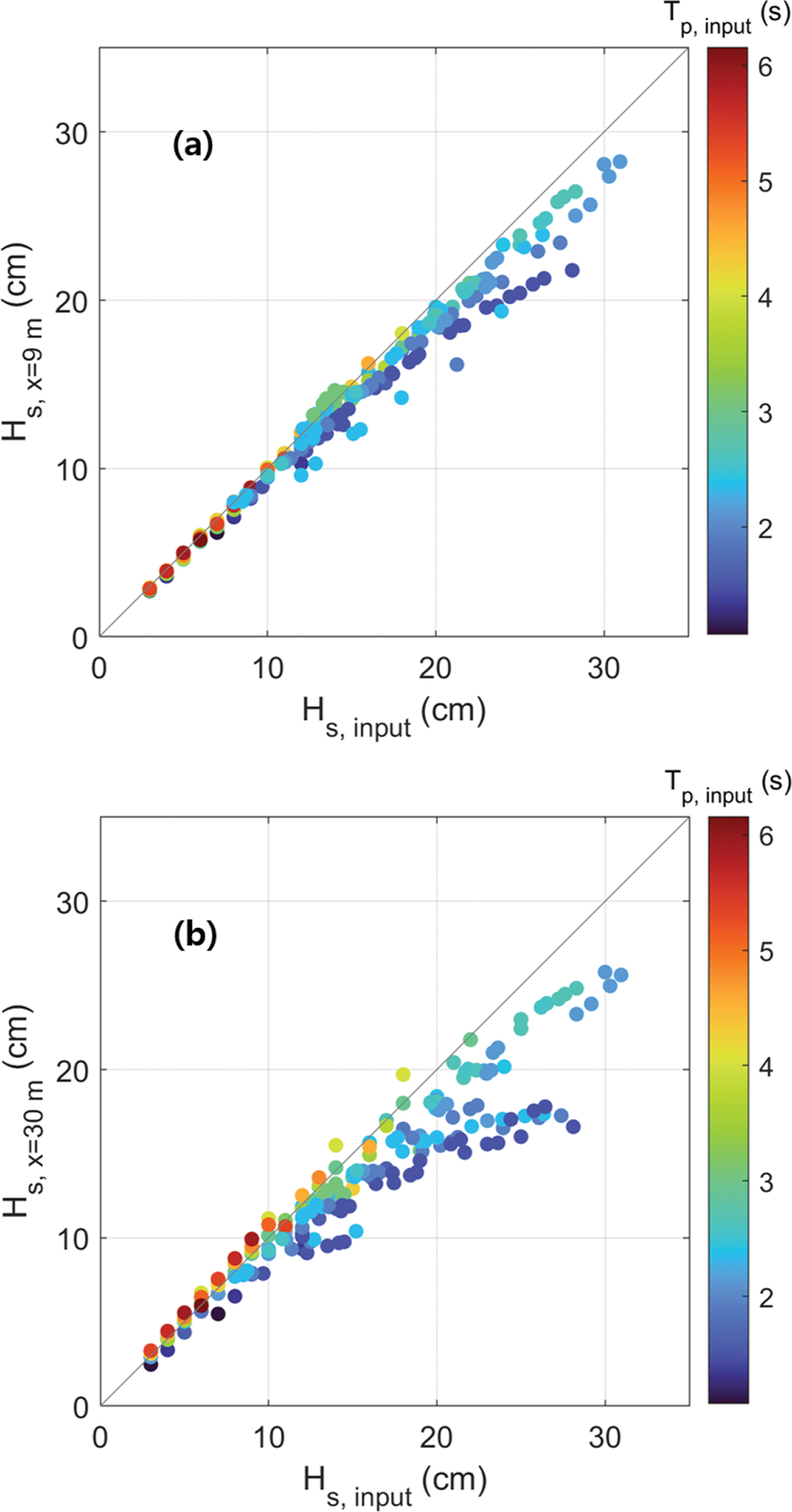

Fig. 3.

Conceptual diagram of the artificial neural network.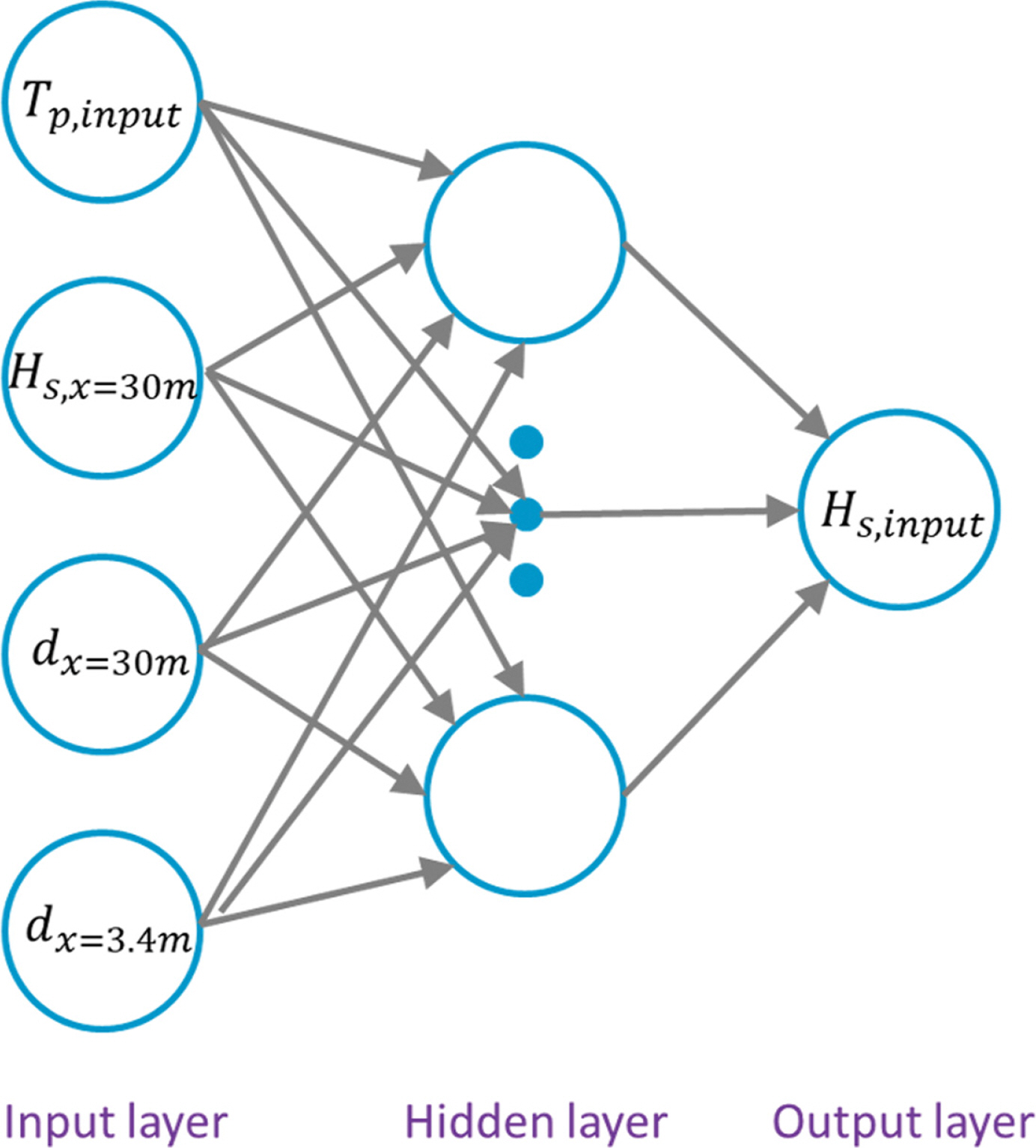

Fig. 4.

Distinction of the data used for model training and validation with the data used for model prediction.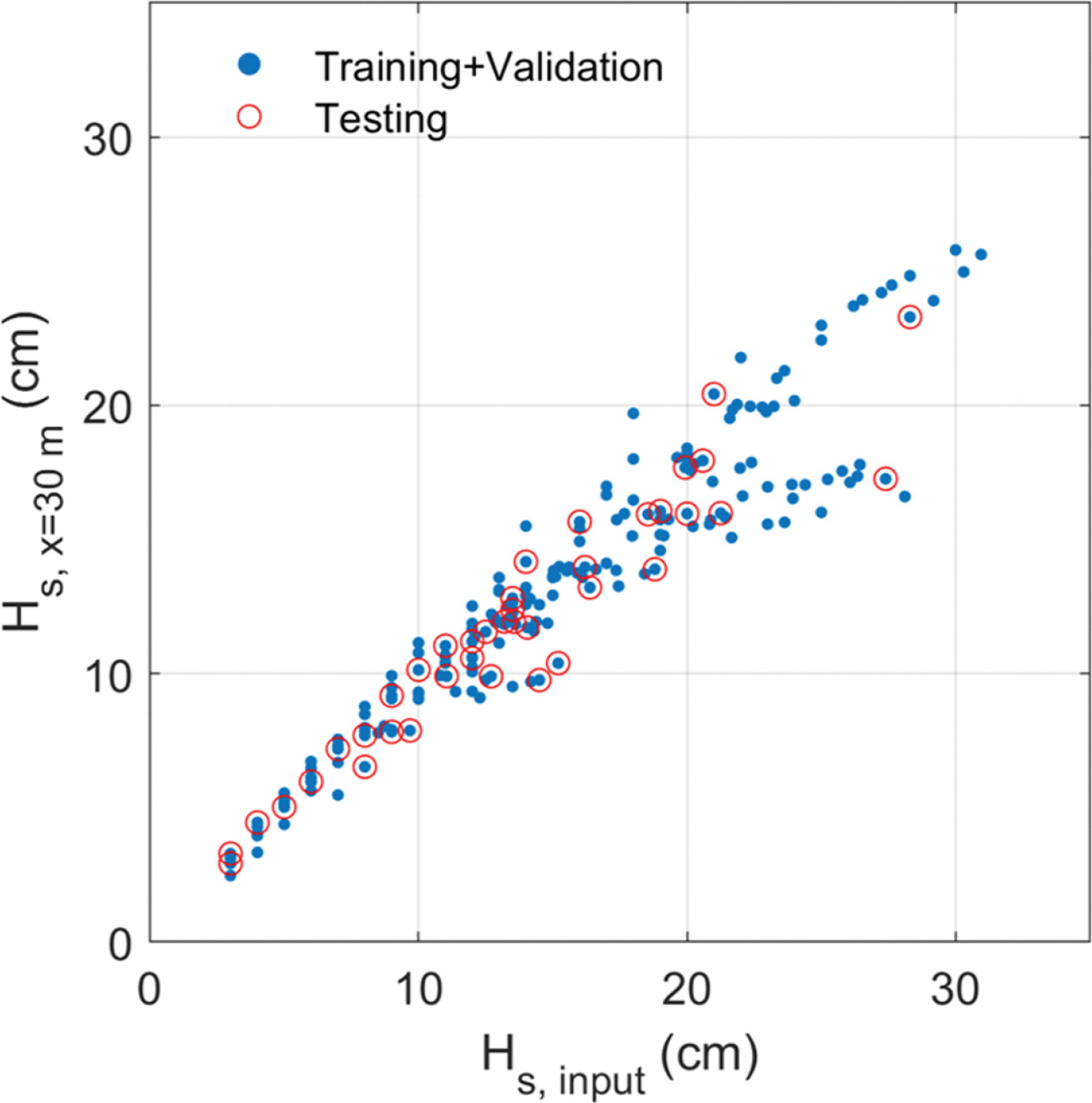

Fig. 5.

Relationship between H_{s, input} and H_{s, x} _{= 30 m} corresponding to the measured data (gray open dot), the builded NN model (blue solid dot), and the predicted result (red solid dot) by the NN model.

Fig. 6.

Comparison of H_{s, input} from the measured data and the NN model. Blue and red dots correspond to the results of model building and prediction, respectively.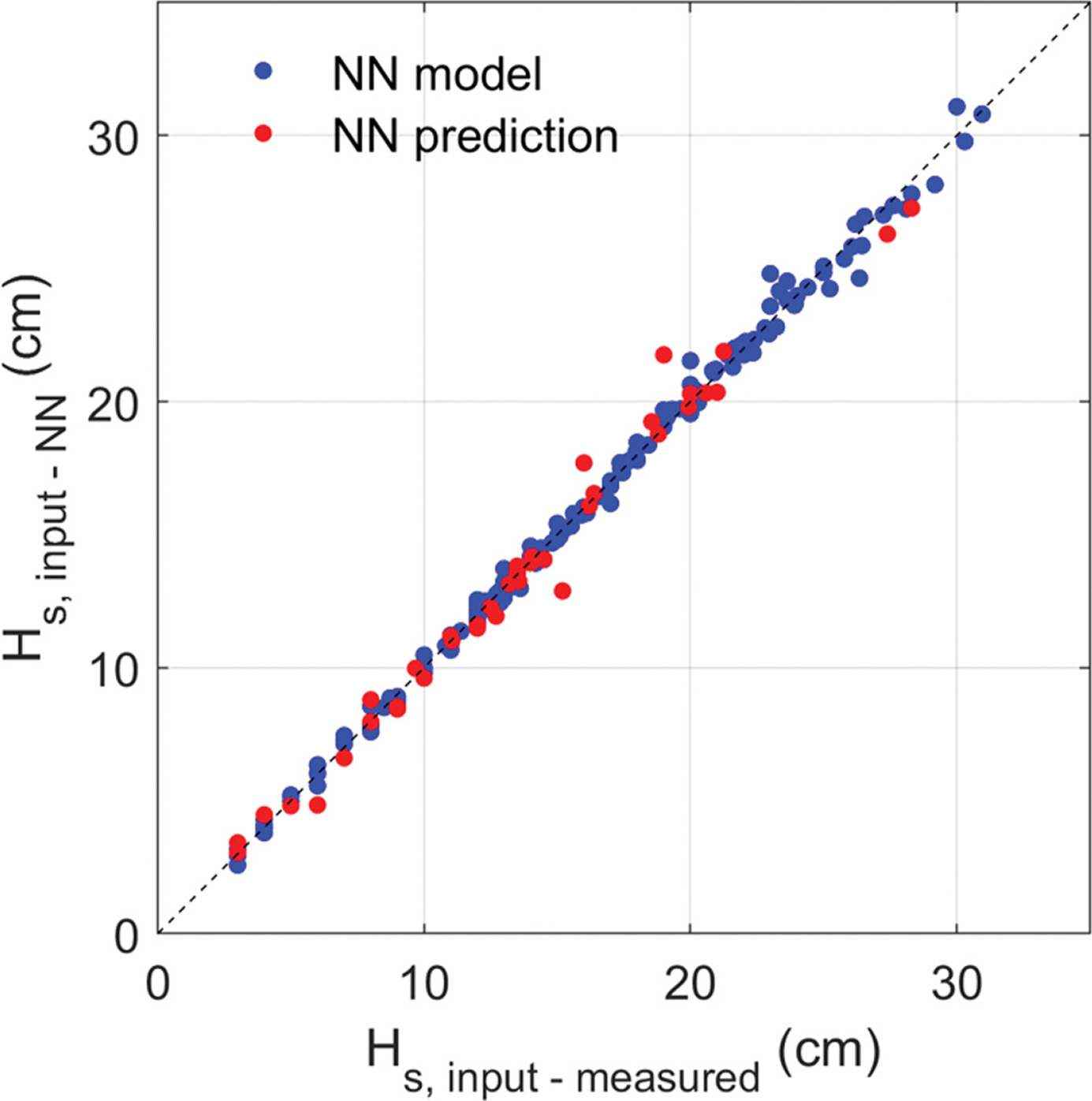

Fig. 7.

Relationship between H_{s, input} and H_{s, x} _{= 30 m} corresponding to the measured data (gray open dot), the builded GPR model (blue solid dot), and the predicted result (red solid dot) by the GPR model.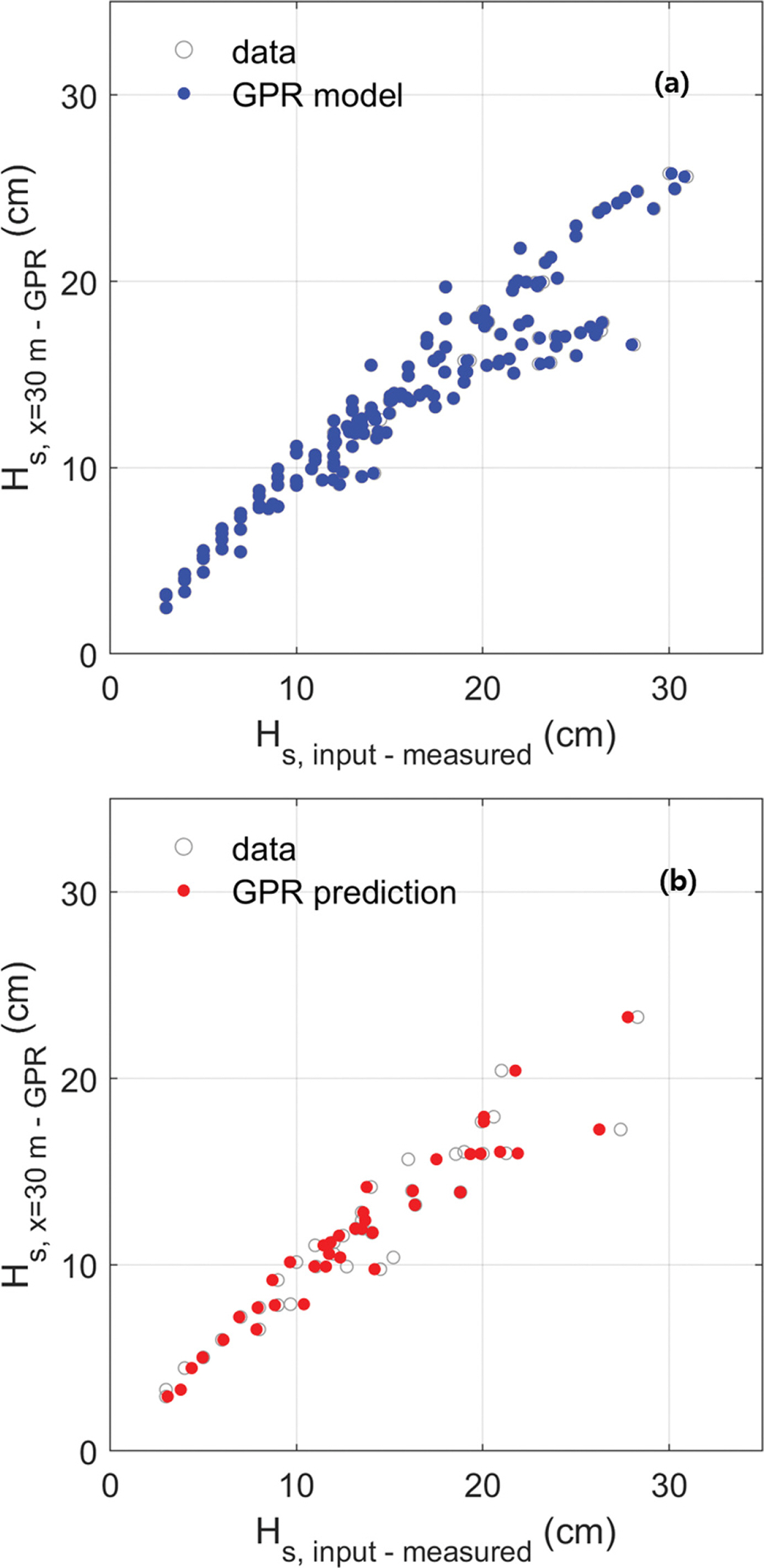

Fig. 8.

Comparison of H_{s, input} from the measured data and the GPR model. Blue and red dots correspond to the results of model building and prediction, respectively.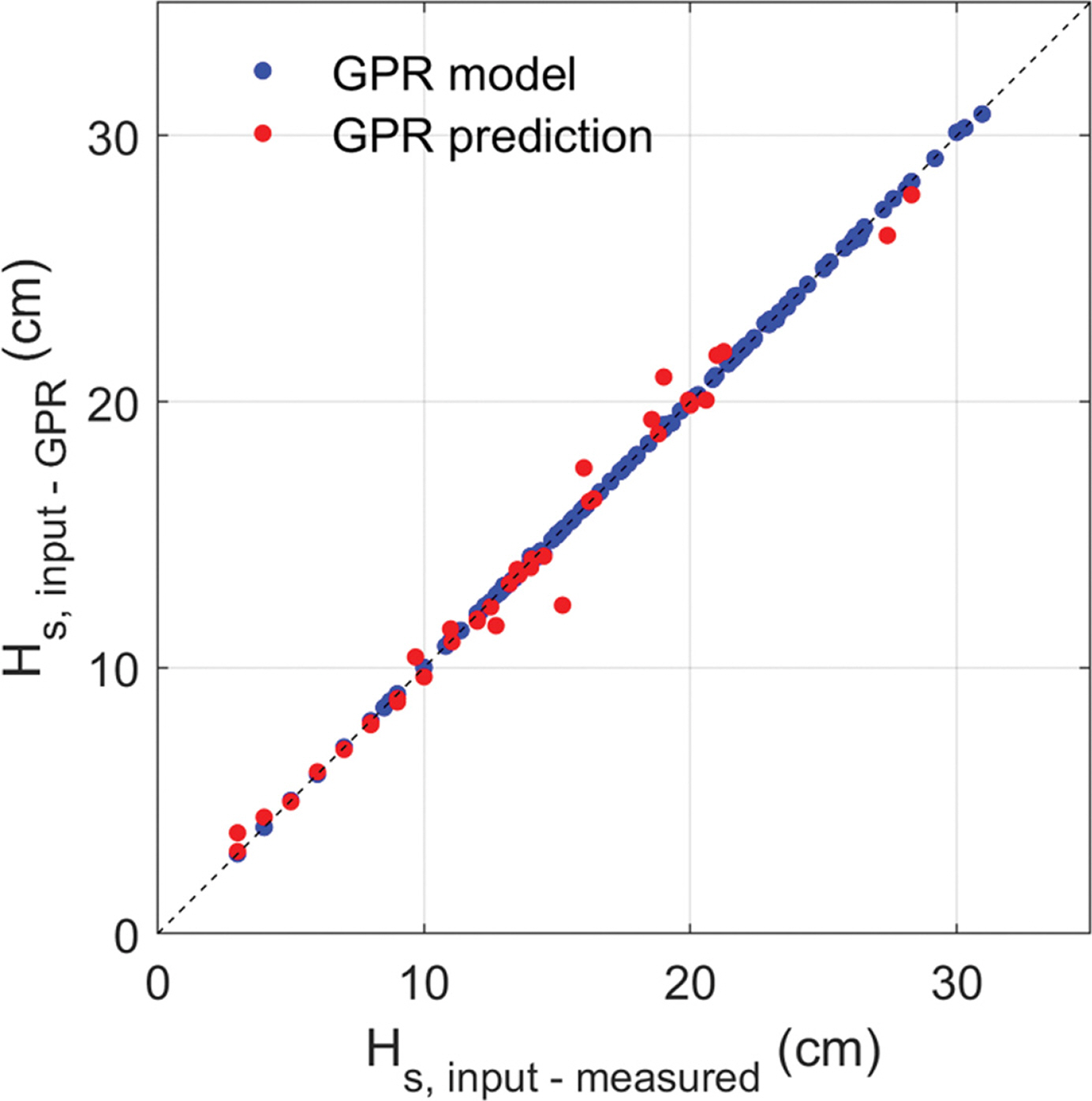

Table 1.

Ranges of the water depth, significant wave height, and peak wave period of the data measured at x = 9 m

d(cm)	H_s(cm)	T_p(s)
55~115	2.7~28.2	1.07~6.15

Table 2.

Indicators representing the performance of the NN and GPR models

		NRMSE	R²
NN	Model	0.411	0.986
NN	Prediction	0.791	0.973

GPR	Model	0.046	0.995
GPR	Prediction	0.533	0.985

부록 Table 3.

Experimental data used for establishing the NN and GPR models

d_x _{= 3.4m}	d_x _{= 30m}	T_{p, input}	H_{s, input}	H_{s, x} _{= 30 m}
70.0	34.6	1.07	3.00	2.48
70.0	34.6	1.07	7.00	5.48
70.0	34.6	2.14	3.00	2.92
70.0	34.6	2.14	7.00	6.69
70.0	34.6	2.14	11.00	10.39
70.0	34.6	2.14	15.00	13.58
70.0	34.6	2.14	19.00	16.06
70.0	34.6	2.14	23.00	16.96
70.0	34.6	3.21	3.00	3.20
70.0	34.6	3.21	7.00	7.32
70.0	34.6	3.21	11.00	11.04
70.0	34.6	3.21	15.00	13.64
70.0	34.6	3.21	19.00	15.18
70.0	34.6	4.28	3.00	3.12
70.0	34.6	4.28	7.00	7.19
70.0	34.6	4.28	11.00	10.63
70.0	34.6	4.28	15.00	12.92
70.0	34.6	5.35	3.00	3.29
70.0	34.6	5.35	7.00	7.55
70.0	34.6	5.35	11.00	10.68
80.0	44.6	1.34	4.00	3.34
80.0	44.6	1.34	8.00	6.53
80.0	44.6	1.34	12.00	9.34
80.0	44.6	2.41	4.00	4.04
80.0	44.6	2.41	8.00	7.99
80.0	44.6	2.41	12.00	11.87
80.0	44.6	2.41	16.00	15.66
80.0	44.6	2.41	20.00	18.40
80.0	44.6	2.41	24.00	20.17
80.0	44.6	3.48	4.00	3.96
80.0	44.6	3.48	8.00	7.85
80.0	44.6	3.48	12.00	11.67
80.0	44.6	3.48	16.00	14.93
80.0	44.6	3.48	20.00	17.98
80.0	44.6	4.55	4.00	4.29
80.0	44.6	4.55	8.00	8.48
80.0	44.6	4.55	12.00	12.52
80.0	44.6	4.55	16.00	15.41
80.0	44.6	5.62	4.00	4.45
80.0	44.6	5.62	8.00	8.78
90.0	54.6	1.61	5.00	4.38
90.0	54.6	1.61	9.00	7.83
90.0	54.6	1.61	13.00	11.14
90.0	54.6	1.61	17.00	14.11
90.0	54.6	2.68	5.00	5.03
90.0	54.6	2.68	9.00	9.06
90.0	54.6	2.68	13.00	13.06
90.0	54.6	2.68	17.00	16.98
90.0	54.6	2.68	21.00	20.42
90.0	54.6	2.68	25.00	22.98
90.0	54.6	3.75	5.00	5.12
90.0	54.6	3.75	9.00	9.18
90.0	54.6	3.75	13.00	13.13
90.0	54.6	3.75	17.00	16.66
90.0	54.6	4.82	5.00	5.27
90.0	54.6	4.82	9.00	9.48
90.0	54.6	4.82	13.00	13.58
90.0	54.6	5.89	5.00	5.55
90.0	54.6	5.89	9.00	9.92
100.0	64.6	1.87	6.00	5.63
100.0	64.6	1.87	10.00	9.31
100.0	64.6	1.87	14.00	12.90
100.0	64.6	1.87	18.00	16.47
100.0	64.6	2.94	6.00	6.14
100.0	64.6	2.94	10.00	10.14
100.0	64.6	2.94	14.00	14.17
100.0	64.6	2.94	18.00	18.00
100.0	64.6	2.94	22.00	21.78
100.0	64.6	4.01	6.00	6.73
100.0	64.6	4.01	10.00	11.15
100.0	64.6	4.01	14.00	15.50
100.0	64.6	4.01	18.00	19.70
100.0	64.6	5.08	6.00	6.47
100.0	64.6	5.08	10.00	10.78
100.0	64.6	6.15	6.00	5.97
70.3	25.4	2.33	8.00	7.70
70.3	25.4	2.33	13.00	11.91
70.3	25.4	2.33	13.20	11.84
70.3	25.4	2.33	13.50	12.27
70.3	25.4	2.33	13.20	11.94
70.3	25.4	2.33	13.40	12.03
70.3	25.4	3.07	14.00	12.58
70.3	25.4	3.07	14.16	12.79
70.3	25.4	2.33	13.50	12.38
70.3	25.4	3.07	14.50	12.57
73.9	29.0	2.33	12.10	11.38
73.9	29.0	2.33	12.84	12.09
73.9	29.0	2.33	12.50	11.56
73.9	29.0	2.33	13.50	12.62
73.9	29.0	3.07	12.72	12.21
73.9	29.0	3.07	13.30	12.52
73.9	29.0	3.07	13.50	12.81
73.9	29.0	3.07	14.00	13.21
55.4	20.0	1.50	9.68	7.88
55.4	20.0	1.50	12.29	9.10
55.4	20.0	1.50	13.50	9.52
55.4	20.0	1.50	14.18	9.70
55.4	20.0	1.50	14.50	9.76
55.4	20.0	1.93	9.00	7.91
55.4	20.0	1.93	11.38	9.33
55.4	20.0	1.93	12.50	9.76
55.4	20.0	2.35	8.50	7.79
55.4	20.0	2.35	8.72	8.05
55.4	20.0	2.35	12.70	9.90
55.4	20.0	2.35	15.20	10.39
72.4	37.0	1.50	12.00	10.07
72.4	37.0	1.50	14.30	11.59
72.4	37.0	1.50	14.81	11.88
72.4	37.0	1.50	17.45	13.26
72.4	37.0	1.50	18.42	13.72
72.4	37.0	1.50	18.80	13.89
72.4	37.0	1.50	21.66	15.07
72.4	37.0	1.50	23.00	15.57
72.4	37.0	1.50	23.63	15.64
72.4	37.0	1.50	25.00	16.01
72.4	37.0	1.50	28.11	16.60
72.4	37.0	1.93	12.00	10.58
72.4	37.0	1.93	13.61	11.83
72.4	37.0	1.93	16.11	13.58
72.4	37.0	1.93	16.61	13.89
72.4	37.0	1.93	19.13	15.14
72.4	37.0	1.93	20.22	15.49
72.4	37.0	1.93	20.88	15.72
72.4	37.0	1.93	21.25	15.98
72.4	37.0	1.93	23.94	16.53
72.4	37.0	1.93	26.07	17.13
72.4	37.0	2.35	12.00	11.20
72.4	37.0	2.35	12.86	11.92
72.4	37.0	2.35	15.10	13.62
72.4	37.0	2.35	15.52	13.83
72.4	37.0	2.35	17.96	15.13
72.4	37.0	2.35	18.99	15.74
72.4	37.0	2.35	19.31	15.75
72.4	37.0	2.35	20.00	15.96
72.4	37.0	2.35	22.07	16.62
72.4	37.0	2.35	23.90	17.05
72.4	37.0	2.35	25.23	17.24
72.4	37.0	2.35	26.35	17.36
81.4	46.0	1.50	12.00	10.25
81.4	46.0	1.50	14.05	11.72
81.4	46.0	1.50	14.38	11.94
81.4	46.0	1.50	16.38	13.21
81.4	46.0	1.50	17.36	13.85
81.4	46.0	1.50	19.00	14.59
81.4	46.0	1.50	20.84	15.57
81.4	46.0	1.50	21.41	15.84
81.4	46.0	1.50	24.40	17.04
81.4	46.0	1.50	25.77	17.55
81.4	46.0	1.50	26.44	17.79
81.4	46.0	1.93	12.00	10.62
81.4	46.0	1.93	13.56	11.93
81.4	46.0	1.93	15.91	13.75
81.4	46.0	1.93	16.20	13.97
81.4	46.0	1.93	18.55	15.94
81.4	46.0	1.93	20.95	17.16
81.4	46.0	1.93	21.98	17.66
81.4	46.0	1.93	22.40	17.87
81.4	46.0	2.35	12.00	11.21
81.4	46.0	2.35	12.85	11.97
81.4	46.0	2.35	15.03	13.84
81.4	46.0	2.35	17.38	15.74
81.4	46.0	2.35	17.67	15.96
81.4	46.0	2.35	19.93	17.68
81.4	46.0	2.35	20.29	17.82
115.4	80.0	2.14	20.00	18.20
115.4	80.0	2.14	23.34	21.01
115.4	80.0	2.14	23.63	21.29
115.4	80.0	2.14	22.80	19.93
115.4	80.0	2.14	30.95	25.62
115.4	80.0	2.68	20.00	18.09
115.4	80.0	2.68	21.59	19.52
115.4	80.0	2.68	22.35	19.96
115.4	80.0	2.68	25.00	22.43
115.4	80.0	2.68	27.24	24.20
115.4	80.0	2.68	27.62	24.48
115.4	80.0	2.68	28.30	24.83
115.4	80.0	2.14	30.00	25.79
115.4	80.0	2.14	10.00	9.05
115.4	80.0	2.14	11.05	9.91
115.4	80.0	2.14	15.61	13.97
115.4	80.0	2.14	20.12	17.59
115.4	80.0	2.14	20.59	17.94
115.4	80.0	2.14	22.95	19.76
115.4	80.0	2.14	23.23	19.96
115.4	80.0	2.14	28.30	23.29
115.4	80.0	2.14	29.18	23.90
115.4	80.0	2.57	10.00	9.25
115.4	80.0	2.57	10.82	9.94
115.4	80.0	2.57	15.24	13.99
115.4	80.0	2.57	19.63	18.05
115.4	80.0	2.57	21.69	19.84
115.4	80.0	2.57	21.86	20.03
115.4	80.0	2.57	26.20	23.70
115.4	80.0	2.57	26.53	23.93

References

Abouhalima, M., das Neves, L., Taveira-Pinto, F., Rosa-Santos, P. (2024). Machine learning in coastal engineering: applications, challenges, and perspectives, Journal of Marine Science and Engineering, 12(4):638.

Cheng, H., Cheng, Y., Zheng, Y., Zhang, J., Lyu, X. (2023). Prediction of irregular wave (current)-induced pore water pressure around monopile using machine learning methods, Coastal Engineering, 182, 104291.

Giaremis, S., Nader, N., Dawson, C., Kaiser, C., Nikidis, E., Kaiser, H. (2024). Storm surge modeling in the AI era: Using LSTM-based machine learning for enhancing forecasting accuracy, Coastal Engineering, 191, 104532.

Goldstein, E.B., Coco, G., Plant, N.G. (2019). A review of machine learning applications to coastal sediment transport and morphodynamics, Earth-science Reviews, 194, 97-108.

Jordan, M.I., Mitchell, T.M. (2015). Machine learning: Trends, perspectives, and prospects, Science, 349(6245):255-260.

Kim, T., Lee, W.D. (2022). Review on applications of machine learning in coastal and ocean engineering, Journal of Ocean Engineering and Technology, 36(3):194-210.

Knudde, N., Raes, W., De Bruycker, J., Dhaene, T., Stevens, N. (2020). Data-efficient gaussian process regression for accurate visible light positioning, IEEE Communications Letters, 24(8):1705-1709.

Liu, Z., Carr, M.L., Nadal-Caraballo, N.C., Yawn, M.C., Taflanidis, A.A., Bensi, M.T. (2024). Machine learning motivated data imputation of storm data used in coastal hazard assessments, Coastal Engineering, 190, 104505.

Lucero, F., Stringari, C.E., Filipot, J.F. (2023). Improving WAVEWATCH III hindcasts with machine learning, Coastal Engineering, 185, 104381.

Oh, J.-E., Oh, S.-H. (2022). Estimation of the input wave height of the wave generator for regular waves by using artificial neural networks and Gaussian process regression, Journal of Korean Society of Coastal and Ocean Engineers, 34(6):315-324 (in Korean)..

Oh, S.-H., Lee, D.S. (2018). Two-dimensional wave flume with water circulating system for controlling water level, Journal of Korean Society of Coastal and Ocean Engineers, 30(6):337-342 (in Korean)..

Parker, K., Ruggiero, P., Serafin, K.A., Hill, D.F. (2019). Emulation as an approach for rapid estuarine modeling, Coastal Engineering, 150, 79-93.

Pourzangbar, A., Jalali, M., Brocchini, M. (2023). Machine learning application in modelling marine and coastal phenomena: a critical review, Frontiers in Environmental Engineering, 2, 1235557.

Rasmussen, C.E., Williams, C.K.. (2006). Gaussian processes for machine learning. MIT press, Cambridge, Massachusetts.

Shashank, V.G., Sriram, V., Schüttrumpf, H., Sannasiraj, S.A. (2024). A new surge index with the incorporation of cyclone track approach angle information for the Bay of Bengal, Coastal Engineering, 188, 104429.

Wang, K., Pleiss, G., Gardner, J., Tyree, S., Weinberger, K.Q., Wilson, A.G. (2019). Exact Gaussian processes on a million data points, Advances in Neural Information Processing Systems, 32.