1. 서 론
1.1 연구배경 및 필요성
우리나라는 좁은 국토에 삼면이 바다로 둘러싸여 있어 해안공간 활용의 필요성이 대단히 높다. 해안을 따라 주요 공단, 기관시설들이 배치되어 있을 뿐만 아니라 국민소득 증가와 함께 레저 및 친수공간으로서의 해안의 중요성이 부각됨에 따라 해안의 이용률은 나날이 높아지고 있다. 해안의 이용률 증가와 함께 반드시 고려되어야 할 부분이 인명 및 시설의 안전이다. 기후 온난화의 효과가 가장 크게 나타나는 곳이 해양이며 이미 강력한 태풍의 빈발과 이로 인한 폭풍해일 피해, 도시 홍수의 빈발 등이 전 세계적으로 보고되고 있다. 우리나라는 태풍 매미 이후 보다 안전한 해안 공간 확보를 위해 여러 가지 기상인자에 대한 체계적이고 장기적인 해안방재 대책이 수립되고 있다. 이 연구에서는 외해에서 발생하여 갑작스런 내습과 함께 인명과 시설에 피해를 끼치는 너울성 고파를 대상으로 그 처오름 특성을 분석하고자 한다.
최근 몇 년간 우리나라 동해안에는 너울성 고파의 반복적인 내습이 빈발하고 있다. 이러한 너울성 고파는 중국 내륙 및 우리나라 부근에서 특별히 강하게 발달한 온대성 저기압이 동해로 진출하여, 강한 바람이 불어서 생성된 폭풍파가 우리나라 동해안까지 전파하여 내습하게 됨에 따라 발생한 것이다(Jeong et al., 2007). 즉 동해상 먼 바다에서 생성된 고파가 우리나라 동해안 쪽으로 오랜 시간 동안 전파해온 것이며, 너울성 고파가 해안에 도달할 무렵의 국지적 날씨는 양호한 경우가 많아서 갑작스런 높은 파도의 출현과 함께 방파제 또는 호안에서의 월파로 인해 인명 및 재산피해가 크게 발생하고 있다. 2005년 이후 동해안 너울성 고파의 내습으로 인해 해상과 해안에서 사망하거나 실종된 사람은 집계된 것만 45명에 달하며, 재산 피해 규모는 연평균 백억 원을 상회한다(Jeong and Oh, 2009).
서해안에서도 2008년 5월 충남 보령에서 갑작스레 발생한 너울성 고파로 인해 인명 및 재산피해가 발생한 바 있다. 국립해양조사원에서는 당시 서해 먼 바다에서 우리나라로 이동하던 발달된 저기압에 의해 높이 50 cm, 주기 50분 정도인 너울이 만들어지고 있었으며, 연안으로 접근하면서 얕은 수심과 지형 등의 영향으로 파고가 2~4 m로 커지게 되어 피해가 발생한 것으로 추정하였다(Choi and Lee, 2010).
이러한 너울성 고파에 대해서는 아직 그 특성이 명확히 규명되어 있지 않으며, 해안구조물 설계에서도 따로이 정의되어 그 특성을 반영하고 있지는 않다. 이를 위해서는 먼저 너울성 고파의 스펙트럼을 분석하여 그 파랑 특성을 확인하고 특히 처오름 및 월파와의 상관성을 검토하는 연구가 필요하다. 본 연구에서는 파랑관측 자료의 분석을 통해 파랑 스펙트럼을 구성하는 인자들을 확인하고 스펙트럼 형상을 결정하는 인자들과 유의파고, 첨두주기의 상관관계 분석을 통해 처오름 높이나 월파에 기여하는 스펙트럼 인자들의 특성을 확인하고자 한다. 기존의 설계에 사용되는 파랑 스펙트럼은 유의파고와 첨두주기에 따라 정해지는 표준 스펙트럼이어서 갑자기 발생하는 이상파의 특성을 반영하기에는 한계가 있다. 이 연구를 통해 특정지역이나 이상파가 자주 발생하는 지역에 대해서는 단순 월파가 아닌 스펙트럼 형상에 따른 월파를 고려함으로써 해안구조물 설계의 타당성과 신뢰도를 제고할 수 있는 기초자료를 제공하고자 한다.
1.2 연구내용 및 방법
동일한 파고와 주기를 가지는 파랑이라도 불규칙파의 스펙트럼 형태에 따라 피해가 달라질 수 있음을 고려하여 다음의 연구를 수행하였다. 한국해양과학기술원에서 관측한 장기 파랑자료를 대상으로, 유의파고 및 첨두주기와 같은 기본 파랑정보 외에도 스펙트럼 형상을 함께 분석하였고 이를 통해 가장 적절한 형상인자를 선정하였다. 스펙트럼 특성에 따른 처오름의 변화를 확인하기 위해 수치실험을 수행하였다. MIKE21 BWM(Boussinesq Wave Module)을 이용하여 파형경사, 바닥경사에 따른 처오름 실험을 수행하여 스펙트럼 형상에 따른 상대 처오름 높이의 변화를 확인하였고, 이를 통해 너울성 고파의 처오름에 영향을 미치는 유의파고, 첨두주기, 스펙트럼 형상 등 주요 인자들의 특성을 분석하였다.
2. 파랑자료 분석
2.1 파랑 스펙트럼 형상모수
파랑 스펙트럼의 형상이 광대역(wide) 또는 협대역(narrow) 인가는 파랑의 특성을 나타내는 매우 중요한 요소이다. 파랑 스펙트럼을 잘 묘사하기 위해서는 파고 및 주기와 관련된 3개의 인자(Hm0, fp, Tp)외에 스펙트럼 형상을 결정하는 인자가 필요하다. 스펙트럼 형상을 결정하는 인자들에 대한 여러 제안들이 있었고 대표적인 3가지 스펙트럼 형상인자는 다음과 같다.
Cartwright and Longuett-Higgins(1956)는 파랑스펙트럼모멘트 m0, m2, m4를 이용하여 주파수 폭대역 모수(spectral bandwidth parameter) ε을 아래 식 (1)과 같이 정의하였다.
차 파랑스펙트럼 모멘트는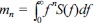 
로 정의되며 f와 S( f )는 각각 주파수와 파랑에너지 스펙트럼을 나타낸다. 이 인자는 0에서부터 1사이의 값으로 0에 가까울수록 협대역이고 1에 가까울수록 광대역이 된다. 또한, Longuett-Higgins(1975)는 파랑스펙트럼 모멘트 m0, m1, m2등을 이용하여 파랑스펙트럼 폭 모수(spectral width parameter) ν를 제안하였다.
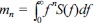로 정의되며 f와 S( f )는 각각 주파수와 파랑에너지 스펙트럼을 나타낸다. 이 인자는 0에서부터 1사이의 값으로 0에 가까울수록 협대역이고 1에 가까울수록 광대역이 된다. 또한, Longuett-Higgins(1975)는 파랑스펙트럼 모멘트 m0, m1, m2등을 이용하여 파랑스펙트럼 폭 모수(spectral width parameter) ν를 제안하였다.
그리고 Goda(1970)는 형상인자로 다음의 파랑스펙트럼 첨두모수(peakedness paramter) Qp를 제안하였다.
Rye(1977)는 JONSWAP 스펙트럼과 스펙트럼 형상인자들과의 상관관계에 관한 연구를 통해 스펙트럼 형상을 결정하는 모수들 중에서 Qp가 스펙트럼의 형상이 광대역인지 협대역인지를 가장 잘 표현하고 있음을 확인하였다.
2.2 파랑자료 분석
동해 연안역에서의 파랑특성을 파악하기 위해 한국해양과학기술원(구 한국해양연구원)에서 관측한 장기 파랑자료를 분석하였으며, 유의파고 및 첨두주기와 같은 파랑정보 외에도 스펙트럼 형상을 함께 분석하였다. 이들 파랑자료는 수압식 파고계를 이용하여 관측되었고, 파랑관측 자료에는 방향 성분이 포함되어 있지 않다. 대상 지역은 너울성 고파의 피해가 가장 심했던 강릉(구 안목)항과 묵호항을 대상으로 분석하였다. 강릉항 파랑자료는 2006년 7월부터 2012년 6월까지 약 6년에 걸쳐 관측된 자료이며, 묵호항 파랑자료는 2004년 3월부터 2012년 6월까지의 약 8년 3개월간의 자료를 활용하였다.
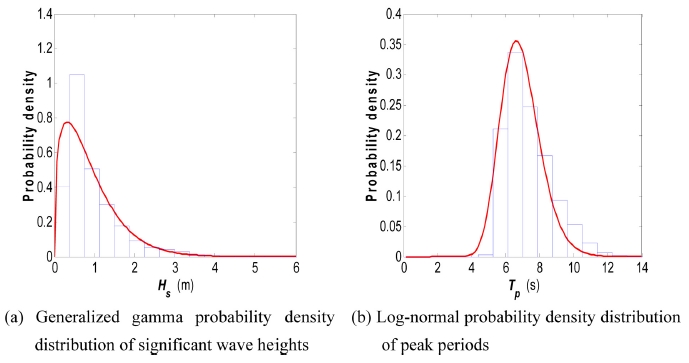
유의파고 및 첨두주기의 분포를 보기 위해 이들의 확률밀도분포를 산정하고, 유의파고는 일반화 감마(generalized gamma)분포 함수, 첨두주기는 대수정규(log-normal) 분포에 적용하였다. 유의파고에 사용한 일반화 감마분포 함수식은 식(4)와 같다.
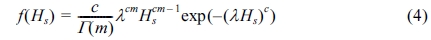
여기서 c, m, λ는 일반화 감마분포 함수의 모수이다. 위의 식에서 모수 c, m은 Newton-Raphson 법을 이용하여 식 (5), 식 (6)을 풀어 계산하였다.
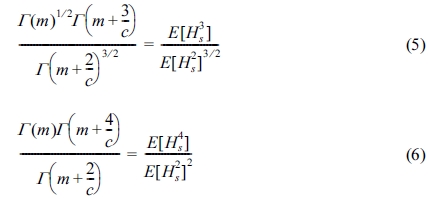
여기서 E[ ]는 조화(ensemble)평균을 의미한다.
첨두주기의 확률밀도는 대수정규분포를 따르는 것으로 알려져 있으며(Ochi, 1998) 대수정규분포 함수식은 식 (7)과 같다.
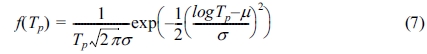
여기서 μ와 σ는 첨두주기의 평균과 표준 편차를 의미하는게 아니라, 대수정규분포의 평균과 표준편차를 의미하며(Ochi, 1992), 식 (8), 식(9)를 이용하여 계산한다.
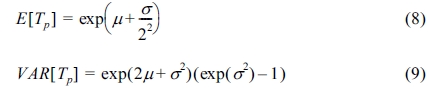
여기서 VAR[ ]는 분산이다.
강릉항 및 묵호항의 유의파고 및 첨두주기의 확률밀도분포를 Fig. 1과 Fig. 2에 나타내었다. Fig. 1(Gangneung)에 있는 유의파고의 확률밀도분포함수에서 일반화 감마 분포함수의 모수는 각각 λ = 1.13, m = 1.10, c = 1.23 이며, 첨두주기 확률밀도분포함수에서 대수정규 분포함수의 모수는 각각 μ = 1.92, σ = 0.17로서 두 함수 모두 유의수준 0.05에서 K-S 및 χ2 검정을 통과하였다. 그리고 Fig. 2(Mukho)의 확률밀도분포 함수에서 일반화 감마분포함수의 모수는 각각 λ = 1.14, m = 1.10, c = 1.23이고, 첨두주기 확률밀도분포함수에서 대수정규 분포함수의 모수는 각각 μ = 1.95, σ = 0.17로 이 경우 역시 유의수준 0.05에서 K-S 및 χ2 검정을 통과하였다.
유의파고 및 첨두주기 분석과 함께 파랑 스펙트럼의 형상도 분석하였다. 파랑 스펙트럼의 형상 모수로는 파랑스펙트럼 첨두모수(Qp), 파랑스펙트럼 주파수 폭대역 모수(ε), 파랑스펙트럼 폭 모수(ν)를 검토하였다. 파랑스펙트럼 모수들과 유의파고 및 첨두주기의 상관관계분석을 하여 그 결과를 Fig. 3(Gangneung)과 Fig. 4(Mukho)에 나타내었다. Qp는 유의파고 및 첨두주기와 반비례 관계에 있고, 및 ε는 ν유의파고 또는 첨두주기와 비례관계에 있다. Table 1, Table 2와 Fig. 3, Fig. 4에 의하면 ε과 유의파고의 상관관계가 가장 높고, 반대로 Qp와 유의파고의 상관관계가 가장 낮은 것으로 분석되었다. 첨두주기와 파랑 스펙트럼 형상인자와의 상관관계는 유의파고에 비해 높지 않은 것으로 파악된다. Ahn et al.(2013)의 확률모의 실험을 통한 파랑 스펙트럼 형상 모수의 특성 분석 결과에 의하면, 첨두모수 Qp는 유의파고 및 첨두주기와 상관관계가 거의 없으며 ε및 ν는 유의파고와 첨두주기에 비례하는 결과를 나타내었다. 확률모의실험 결과는 특정 파랑스펙트럼 모형을 가정하고 있어 실제 파랑관측자료와는 어느 정도 차이가 있음을 고려할 때 두 결과는 대체적으로 일치하고 있다.
Fig. 3.
The relationships between the wave spectral shape parameters and the significant wave heights, peak periods in Gangneung.
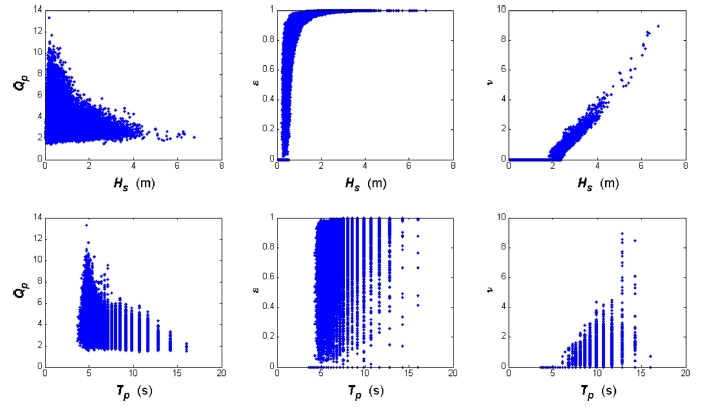
Fig. 4.
The relationships between the wave spectral shape parameters and the significant wave heights, peak periods in Mukho.
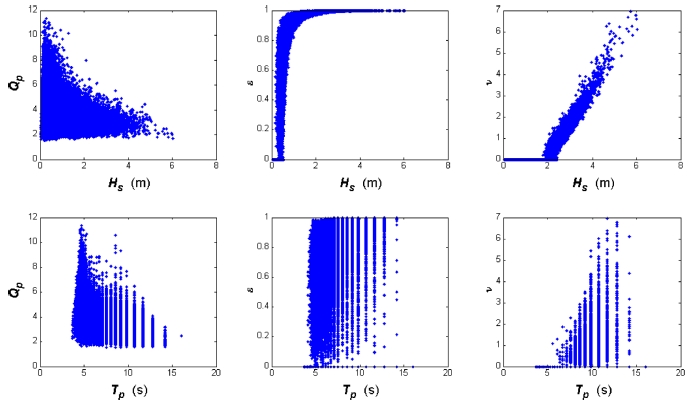
Table 1.
Correlation coefficients between the wave spectral shape parameters and the significant wave heights, peak periods in Gangneung
| Wave information | Qp | ε | ν |
|---|---|---|---|
| Hs | -0.31 | 0.75 | 0.59 |
| Tp | -0.55 | 0.56 | 0.31 |
Table 2.
Correlation coefficients between the wave spectral shape parameters and the significant wave heights, peak periods in Mukho
| Wave information | Qp | ε | ν |
|---|---|---|---|
| Hs | -0.26 | 0.72 | 0.66 |
| Tp | -0.51 | 0.60 | 0.35 |
세 형상모수 모두 스펙트럼의 형상을 표현하는 수학적 표현으로 널리 이용되지만, 파랑 스펙트럼을 설명하는 기본 변수인 파고 및 주기에 더하여 형상모수를 도입한다면 기존 변수인 파고 및 주기와 상관관계가 가장 낮은 변수를 도입하는 것이 보다 적절할 것이다. 따라서, 이 연구에서는 파고와의 상관관계가 가장 낮은 Qp를 추가적인 형상 변수로 채택하였다.
3. 수치모형 실험
앞서 분석한 결과에 따르면, 파랑 스펙트럼의 형상을 정량화하기 위해 도입한 Qp, ε, ν 모수들의 경우, ε혹은 ν는 파랑스펙트럼의 형상 모수로 적절하기는 하나, 유의파고 혹은 첨두주기와 상관성이 상대적으로 높은 반면, Qp는 유의파고와의 상관성이 가장 낮아 독립변수로 보다 적절함을 보여주었다. 형상모수에 따른 파랑의 특성변화 확인을 위해 같은 유의파고와 첨두주기에서 Qp 값만 변동하여 스펙트럼의 형상을 조절하였을 때, 처오름 현상의 차이가 어떻게 나타나는지 MIKE21 BW 모듈을 이용하여 수치모형 실험을 통해 확인하였다. Rye(1976)는 JONSWAP 스펙트럼의 첨두 모수 γ와 스펙트럼 형상 모수 Qp와의 상관관계를 아래의 Table 3과 같이 나타내었다.
Table 3.
Relations between the spectral peakedness parameter and JONSWAP peak shape parameter
| JONSWAP peak shape parameter (γ) | 1.0 | 3.3 | 7.0 |
| spectral peakedness parameter (Qp) | 2.0 | 3.15 | 4.65 |
3.1 실험단면 구성
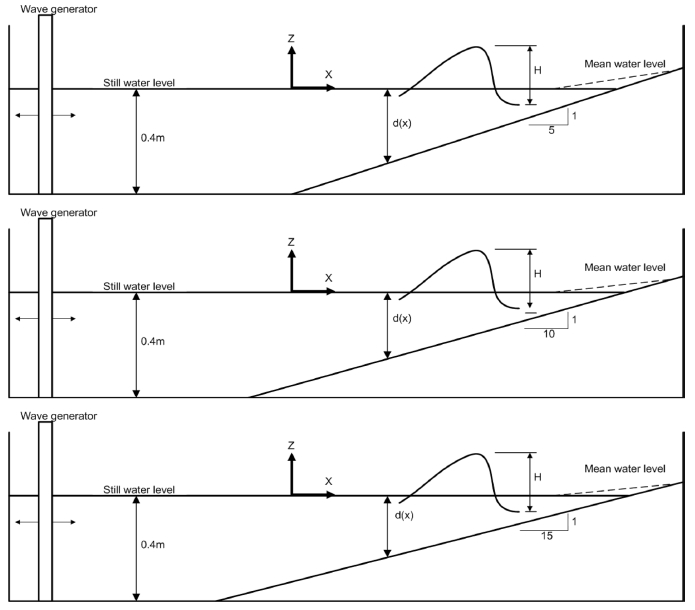
실험단면은 Ting and Kirby(1994)의 파의 쇄파와 처오름 실험단면을 바탕으로 구성하였으며, 원 실험보다 완만한 1/5, 1/10, 1/15의 경사로 바꾸어 구성하였다. 완경사의 해안으로 접근해오는 파랑에 대한 처오름을 알아보는 단면으로 실제 구조물에 대한 처오름 단면보다 경사가 완만하다. 보통 해안구조물 단면의 경사는 1:1.5 ~ 1:3.0까지로 설계되고 있다. 하지만, 수치실험에서는 이런 급경사의 단면에 대한 처오름 계산이 가능한 수치모형이 많지 않고 MIKE21 BW 모듈도 계산 가능한 경사에 한계가 있다. 따라서 본 수치실험에서는 완경사를 대상으로 바닥경사에 따른 처오름 높이의 변화를 검토하였다.
길이 27.5 m의 수조에 격자간격 Δ = 0.02m로 격자개수(n)는 1375개로 구성되었다. 바닥경사는 10 m 지점부터 1/5, 1/10, 1/15의 경사로 이루어져있고, 경사면은 불투수층으로 투수성을 고려하지 않는 단면을 구성하였다. 수면과 경사가 만나는 지점에서 처오름 높이를 확인하였고, 실험단면은 Fig. 5에 나타내었다.
3.2 실험방법 및 조건
모듈은 1차원 Boussinesq Wave Module을 선택하였고, 분산계수는 0.0667을 사용하였다. 계측시간은 1/200Hz(0.005 sec) 간격으로 600 sec간, 총 120001 time step으로 실시하였다. 파랑은 불규칙 파랑으로 파랑 스펙트럼은 각 파고별로 3개씩 JONSWAP 스펙트럼의 γ값을 조정하여 구성하였다. Goda(2000)에 의하면, 풍파의 파형경사는 0.035보다 크고, 너울성 파랑의 파형경사는 0.005~0.02 사이가 된다. 따라서, 이 실험은 파형경사가 0.005~0.02에 해당되는 파고와 주기를 각 3개씩 선택하여 실험을 실시하였다. 너울성 파랑의 주기를 고려하여 T = 2.2 s, 2.4 s, 2.6 s로 고정하고, 해당 파형경사에 해당되는 파고를 찾는 방법으로 파를 선정하였다. 파의 조파는 내부조파 기법을 사용하여 수치수로의 102번째 격자에서 조파되도록 설정하였다. 파의 간섭으로 인한 불안정한 파를 제어하기 위해 필터링을 실시하였다.
3.3 실험결과
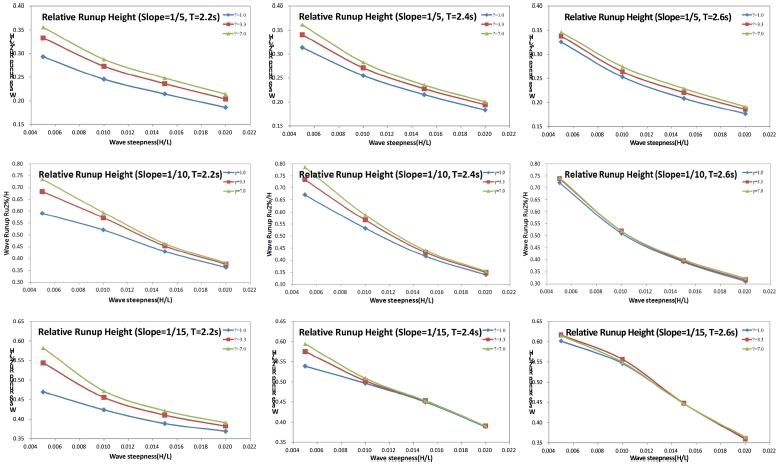
바닥경사 1/5, 1/10, 1/15에서의 상대 처오름 높이를 Table 4, Fig. 6에 나타내었다. 일반적으로 처오름은 파형경사가 작을수록 크게 나타나는데(CERC, 1984) 이러한 경향은 실험결과에서도 잘 나타나고 있다. 동일한 파고 및 주기를 가지는 파랑도 스펙트럼의 형상에 따라 처오름이 달라진다. 결과를 보면 같은 파고, 주기값을 가져도 값에 따라 처오름이 달라지며 γ값이 클수록 큰 처오름 값을 보여준다. 이는 같은 유의파고라도 넓은 주파수대에 에너지가 분산되어 있는 경우 보다는 좁은 주파수대에 에너지가 집중되어 있을 경우 상대적으로 큰 파고를 가지는 성분파가 많아지므로 처오름 값도 커지게 되는 것이다.
Table 4.
Runup heights with the variations of wave spectral shape
수치실험 조건에 따라 일부 실험에서는 쇄파가 발생하였는데 모든 파형경사에서 주기가 2.6 s인 파에서는 쇄파가 발생하였고, 파형경사 0.02에서는 모든 파랑에서 쇄파가 일어났다. 또한 가장 완경사인 1/15의 바닥경사에서는 모든 실험에서 쇄파가 발생하였다.
Fig. 6을 보면 바닥경사가 1/5인 경우에는 주기 2.2 s, 2.4 s 그리고 2.6 s 모두에서 형상 모수 γ에 따른 처오름 높이의 변화가 뚜렷이 나타난다. 하지만 바닥경사 1/10, 1/15의 경우 주기가 커짐에 따라 이러한 차이가 작아지며, 특히 주기 2.6 s의 경우 거의 차이가 없음을 볼 수 있다. 이는 앞서 언급한대로 이 실험 조건에서 쇄파가 대규모로 발생하여 지배적인 성분파들의 운동 형태가 변형되어 나타난 결과이다. 처오름 높이에 미치는 스펙트럼 형상의 영향은 파형경사가 작을수록 더욱 크게 작용하였다.
처오름 자체의 크기는 같은 파랑에 대해서도 바닥경사가 완만해질수록 처오름 높이가 증가하는 것을 알 수 있다. 이러한 너울의 처오름 특성을 감안하면 우리나라 서해안이 동해안처럼 너울성 고파랑이 발생할 조건들이 많지는 않지만 이 실험결과를 통해 나타난 것처럼 스펙트럼의 집중도가 높은 파랑이 바닥경사가 완만한 해안으로 진행해 오면 갑작스러운 이상 고파가 발생할 수 있으므로 서해안에서도 너울성 고파에 대한 검토 및 주의가 필요할 것이다.
4. 결 론
외해에서 발생하여 갑작스런 내습과 함께 인명과 시설에 피해를 끼치는 너울성 고파를 대상으로 그 처오름 특성을 확인하였다. 한국해양과학기술원의 파랑자료를 이용하여 동해 연안역의 파랑관측자료를 분석하였다. 파랑 스펙트럼의 형상을 정량화하기 위해 스펙트럼 형상모수 Qp, ε, ν등을 도입하여 이들 모수들과 유의파고 및 첨두주기와의 상관관계를 검토하였다. 세 형상모수 모두 스펙트럼의 형상을 표현하는 수학적 표현으로 널리 이용되지만 파랑 스펙트럼을 설명하는 기본 변수인 파고 및 주기에 더하여 형상모수를 도입한다면 기존 변수인 파고 및 주기와 상관관계가 가장 낮은 변수를 도입하는 것이 보다 적절할 것이다. 본 연구에서는 파고와의 상관관계가 가장 낮은 것으로 나타난 Qp를 추가적인 형상 모수로 채택하였다.
MIKE-21 BW 모듈을 사용하여 완경사 해안에 대한 처오름 수치실험을 수행하였다. 스펙트럼의 형상모수 Qp 값과 JONSWAP 스펙트럼의 γ값과의 상관관계를 이용하여 형상모수에 따른 처오름 높이를 확인하였다. 유의파고와 첨두주기가 같아도 스펙트럼의 형상에 따라 처오름 높이가 달라지며 스펙트럼이 협대역일수록 처오름 높이가 커지는 것을 수치실험을 통해 확인하였다. 파형경사에 따른 변화를 보면 파형경사가 작을수록 처오름이 크게 나타났으며 이러한 특성은 스펙트럼 형상 변화에 상관없이 전 파형에 걸쳐 일관되게 나타났다. 그리고 바닥경사가 완만해질수록 같은 파에 대해서도 처오름 높이가 증가하는 것도 확인할 수 있었다.
이처럼 파고와의 상관관계가 가장 낮은 Qp를 추가적인 형상 변수로 채택하여 파랑 스펙트럼의 형상 변화에 따라 처오름 높이가 달라지는 것을 확인하였다. 기존의 설계에 사용되는 파랑 스펙트럼은 유의파고와 첨두주기에 따라 정해지는 표준 스펙트럼이어서 갑자기 발생하는 이상파의 특성을 반영하기에는 한계가 있다. 따라서, 특정지역이나 이상파가 자주 발생하는 지역에 대해서는 단순 처오름이 아닌 스펙트럼 형상에 따른 처오름을 고려하게 함으로써 해안구조물 설계의 신뢰도를 높일 수 있을 것이다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation 
Print 
