Characteristic Analysis on the Wind Data in the Pohang Coastal Zone

Weon Mu Jeong; Hongyeon Cho; Wondae Baek

doi:10.9765/KSCOE.2015.27.3.190

Abstract

The estimation method of the sea wind information using the nearby land wind data have been widely used. However, it is insufficient to examine the limitation of the method based on the characteristics of the wind data. In this study, the characteristics of the wind data are analysed and compared to check the limitation of the existing conventional method. The data are observed at the same time period in the land and sea stations in Pohang coastal zone. In particular, the analysis are focused on the direction data simply overlooked in the analysis target. The method is suggested as a useful tool for the various analysis of the wind direction data. The results show that the statistical informations between the land and sea wind data are quite different though the lineal distance between stations are not large (≒ 3.8 km). The difference is attributed to come from the geometrical gradient and elevation difference between land and sea areas. As a consequence, the quantitative estimation error should be checked preliminarily using the land-sea monitoring data sets because the sea wind estimation using land data is essentially unacceptable.

핵심용어: wind data, wind direction data analysis, density estimation, statistical characteristics, Pohang coastal zone, 바람 자료, 풍향자료 분석, 분포 추정, 통계적인 특성, 포항 연안

Abstract

육상의 바람정보를 이용하여 해상 바람을 추정하는 방법은 매우 빈번하게 사용되어 왔다. 그러나 자료의 특성에 근거하여 그 방법의 한계를 검토하는 연구는 매우 미흡하다. 본 연구에서는 육상자료를 이용한 해상자료 추정의 정량적인 한계를 검토하기 위하여 포항 연안의 육상과 바다에서 관측한 바람자료의 특성을 비교·분석하였다. 특히 기존에 간과되던 방향 자료 분석에 중점을 두고 연속적인 풍향 자료 분석 기법을 제안하였다. 분석 결과, 연안 해상의 바람자료는 육상과 매우 인접한 지점에 위치하고 있음에도 불구하고 바람정보의 통계적인 분포 특성이 크게 차이가 나는 것으로 파악되었다. 따라서 육상정보를 이용한 해상 바람정보 추정은 지형적인 영향으로 특성 차이가 커서 근본적인 한계가 있기 때문에 관측 자료를 이용한 정량적인 오차 한계가 반드시 검토되어야 한다.

1. 서 론

연안역의 바람 정보는 연안 흐름 순환, 파랑 발달 등에 직접적인 영향을 미치며, 최근 부각되고 있는 해상풍력에너지 평가·분석 및 해상구조물 건설에서 고려하여야 하는 설계 인자로 매우 중요하다. 또한 연안의 증발잠열 및 대기와 해상의 물질교환에도 직접적인 영향을 미치고 있다. 해상에서 측정한 바람 자료는 설치, 유지비용 및 관리 등의 어려움으로 인하여 그 자료량이 매우 부족하여 일반적으로 육상 기상대 자료를 이용하여 해상자료를 추정하는 경우가 빈번하다(Ko et al., 2012). 그러나 해상에서의 바람과 육상에서의 바람은 바닥 마찰의 영향 및 표면의 변화 정도가 크게 차이를 보이기 때문에 그 차이도 큰 특성을 보일 수 있다. 그럼에도 불구하고 육상과 해상의 풍속 상관관계 분석(회귀분석) 및 간단한 추정 공식 등을 사용하여 연안 해상 바람자료를 추정하는 방법이 그 간편성 때문에 널리 이용되어 왔다(Hsu, 1988; Barthelmie and Palutikof, 1996; Ko et al., 2012). 그러나 육상의 바람 자료를 이용하여 해상의 바람 자료를 추정하는 방법은 지역적인 특성이 매우 중요하기 때문에 해상 관측 자료를 확보하여 상호 비교·분석하는 것을 우선적으로 수행할 필요가 있다. 또한 풍속의 크기만의 비교가 아니라 그 발생빈도와 더불어 풍향에 대한 비교·분석 등 다양한 검토가 필요하다.

본 연구에서는 포항 연안의 육상 기상대와 이에 인접한 해상에서 동시 관측한 4년 동안의 바람 자료를 이용하여 다양한 특성인자에 대한 비교를 수행하였으며, 육상 바람 자료를 이용한 해상 바람 자료 추정의 한계를 제시하였다. 또한 일반적으로 분석에서 제외되는 풍향의 발생빈도 분포도 비교·분석하였으며, 기존의 방법보다 우수한 방향자료의 발생빈도 분석에 대한 기법도 제시하였다.

2. 자료 취득 및 분석방법

2.1 바람 관측 및 포항기상대 자료 취득

본 연구에서는 해상에서의 바람 자료로 포항신항 항내 수역에서 4년간 측정한 바람자료를, 그리고 비교분석을 위한 육상 바람자료로는 동일한 기간의 포항기상대 자료(KMA, 2014)를 이용하여 분석하였다. 관측지점 및 기간 등 기본적인 정보는 Table 1에 제시하였으며, 두 관측지점의 거리 차이는 Fig. 1에 제시한 바와 같이 3.8 km 정도이다. 이 정도의 거리는 육상 기상자료를 해상 기상자료로 환산하는 과정에서 이격 거리가 작은 경우에 해당하기 때문에, 두 지점의 바람 정보가 매우 높은 상관관계를 가질 것으로 기대할 수 있는 상황이다. Ko et al.(2012)에서 사용한 육상과 해상의 바람 자료가 가용한 이격거리는 가장 가까운 영광의 경우에도 37 km, 고창과 부안의 경우에는 각각 45 km, 60 km 정도로 해상풍속과 육상풍속의 결정계수는 0.5~0.7 범위로 제시하고 있다.

Table 1.

Basic information of the wind monitoring data

Contents	Pohang New Port	KMA (Pohang)
Monitoring periods	2008. 9. 4. - 2012. 12. 31	2009. 1. 1.- 2012. 12. 31
Monitoring intervals	10 minutes	1 hour
Locations	36°01'N, 129° 25'E (sea)	36°02'N, 129° 23'E (land)
Height above the ground (m)	10.0	15.4
No. of data	210,384	35,064

Fig. 1.

Monitoring stations of the coastal wind information and the photo of AWS installed in the Pohang New Port (Solid red circle = KMA station, Ted circle = Pohang New Port station).

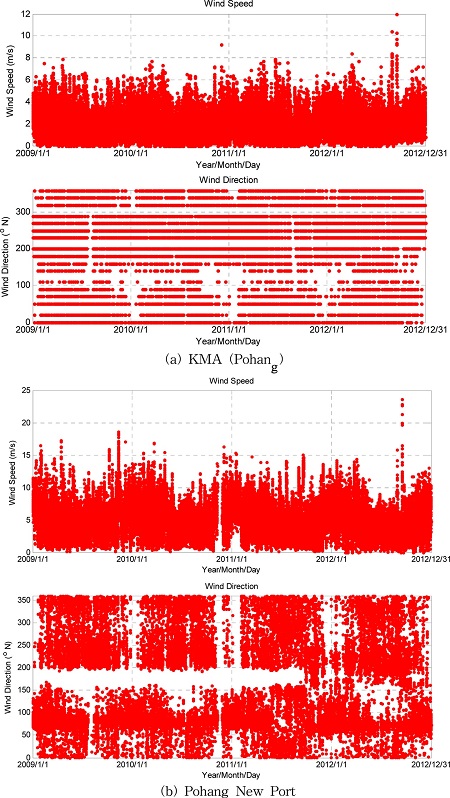
포항기상대에서는 바람 자료가 포항기상대가 건설된 이후 지속적으로 측정되고 있으며, 1시간 간격 관측 자료(매시 10분 동안 관측한 자료를 평균)를 취득하여 사용하였다. 포항신항 내부에서 측정한 자료는 바람의 연중 변화 특성이 뚜렷하기 때문에 2009년 1월 1일부터 2012년 12월 31일까지 4년 동안의 자료만을 본 연구에서 이용하였다. 자료 분석 시에는 작은 시간 규모의 변동성분을 저감시키기 위하여 모든 평균풍속 관측 자료를 시간(hourly)/일(daily) 단위로 평균하여 분석을 수행하였으며, 분석 자료의 전반적인 시간변동 양상은 풍속 및 풍향자료의 시간단위 시계열 도시(time-series plots)를 통하여 파악할 수 있다(Fig. 2. 참조).

Fig. 2.

Time series plots of the wind data sets.

2.2 포항기상대 자료의 풍향 보정

포항기상대에서 제공되는 방향자료는 22.5°간격으로 1/10의 축척으로 변환한 후 반올림되어 16방위에 대해서만 제시(0~360°범위의 방향자료가 0~36° 정보로 제공, 즉 0, 2, 5, 7, 9, 11, 14, 16, 18, 20, 23, 25, 27, 29, 32, 34, 36)되고 있다. 따라서 그 간격이 2 또는 3이 불연속적으로 반복되기 때문에 적절한 처리가 필요하다. 여기서는 방향 정보에 포함된 반올림과 축척계수에 의한 영향을 제거하고, 불연속적인 자료를 연속적인 자료로 변환하기 위하여 ±22.5°/2 구간에 대하여 균일분포(uniform distribution)를 이용한 흐트림(jittering) 기법을 이용하여 방향자료를 다시 구성하고 그 결과를 Fig. 3에 제시하였다. 흐트림 기법은 자료의 반올림 등 다양한 원인으로 발생하는 자료의 불연속성을 제거하기 위하여 작은 변동 성분(perturbation, noise)을 자료에 추가하는 방법으로, SAS 등 다양한 통계프로그램에서 활용되는 간단하고 유용한 방법이다. 한편, 포항신항 내에서 관측한 방향자료는 연속자료이기 때문에 별도의 흐트림 기법 등을 이용한 자료 전처리과정은 필요하지 않다.

Fig. 3.

Time-series plots of the original, adjusted and jittered KMA wind direction data.

2.3 바람자료의 분석인자 및 방법

바람 자료는 풍속과 풍향으로 구성되어 있으며, 풍향정보도 매우 중요하지만 풍속정보만을 비교·분석하는 것이 일반적이다. 풍속정보와는 달리 풍향정보는 일정 범위(0~360°) 내에서만 존재하고, 그 경계에서는 연속되는 정보(0°= 360°)이기 때문에 방향자료에 대한 특별한 분석기법을 필요로 한다. 본 연구에서는 Breckling(1989), Fisher(1993) 등이 제안한 방법을 이용하여 방향자료를 분석하였다. 풍향 자료의 발생빈도 분포 분석에는 방향 자료에서 널리 이용되는 다음의 von Mises 분포함수가 이용되고 있다.

(1)

fVMθ;μ,κ=12πI0κexpκcosθ-μ

여기서, θ는 바람 자료의 방향성분, μ, κ는 각각 von Mises 분포함수의 매개변수, I₀(κ)는 Modified Bessel 함수(첨자 0 = 함수의 차수를 의미)를 각각 나타낸다. von Mises 분포함수의 매개변수는 각각 정규분포의 평균, 표준편차에 해당되며, 간단한 방법으로 매개변수 추정이 가능하다(부록 참조). 그러나 다수의 첨두가 존재하는(multi-modal) 분포인 경우에는 혼합(mixture) 분포함수를 사용하여야 하며 매개변수 추정과정이 복잡해지기 때문에 본 연구에서는 비모수(non-parametric) 추정방법에 해당하는 quadratic Kernel 분포함수를 이용하여 분포함수를 추정하였다(Fisher, 1993).

한편, 연간 자료를 모두 이용하는 경우에는 우세한 방향이 하나 이상일 수 있기 때문에 Kernel 분포함수를 이용한 추정이 적절하나, 특정 월 또는 계절에는 하나의 방향이 우세한 경우가 많기 때문에 Kernel 분포함수와 더불어 von Mises 분포함수를 이용한 추정도 가능할 것으로 판단된다.

3. 관측자료 간 상관관계 분석

3.1 풍속 상관관계 분석

바람 자료의 상관관계 분석은 주로 풍속만을 대상으로 수행되어 왔다. 그러나 바람은 크기와 방향을 가지는 인자이기 때문에 다른 정보 하나(전체의 50%)를 무시하는 자료의 손실 효과가 발생하게 된다. 따라서 본 연구에서는 전통적인 방법과 풍속을 성분별로 추출하여 각각 비교하는 방법, 선형조합 방법에 대하여 각각 상관관계를 분석하였다(Table 2. 참조). 전통적인 방법(Conventional method, CM)은 육상 풍속자료와 해상 풍속자료의 상관관계를 도출하고, 육상풍속만으로 해상 풍속을 추정하는 방법이다. 각각의 풍속성분으로 추정하는 방법(New Method 1, NM1)은 바람자료의 동서방향 성분과 남북방향 성분을 각각 추출하고, 각각의 풍속성분에 대한 상관관계를 도출하고, 육상 바람자료의 각각의 풍속 성분으로 해상 풍속 성분을 각각 추정하는 방법이다. 반면 새로운 선형조합 방법(New Method 2, NM2)은 육상의 각각의 풍속 성분에 대한 해상의 풍속 성분 모두(동서 및 남북방향 성분)를 이용하여 최적 조합을 도출하고, 도출된 선형함수 관계를 이용하여 해상의 풍속을 추정하는 방법으로 각각의 추정방법을 식으로 표현하면 다음과 같다.

Table 2.

Correlation coefficient and root-mean-squared errors of the sea-wind speed estimation using three different methods

Month	Mean wind speed		CM		NM1		NM2
Month	Land	Sea	Corr. coeff	RMSE	Corr. coeff	RMSE	Corr. coeff	RMSE
1	2.25	7.00	0.55	1.94	0.41	2.25	0.57	1.97
2	1.73	5.01	0.49	2.27	0.42	2.71	0.45	2.64
3	1.78	5.27	0.45	2.45	0.51	2.88	0.48	2.83
4	1.92	4.79	0.28	2.81	0.32	3.35	0.28	3.33
5	1.57	3.91	0.32	2.27	0.26	3.00	0.27	2.96
6	1.49	3.70	0.54	1.92	0.51	2.59	0.50	2.60
7	1.58	3.93	0.43	2.08	0.31	3.16	0.31	3.00
8	1.51	3.59	0.42	1.86	0.41	2.81	0.33	2.67
9	1.37	3.63	0.72	2.06	0.72	2.72	0.70	2.73
10	1.51	4.37	0.51	1.98	0.30	2.66	0.24	2.70
11	1.97	5.51	0.63	2.25	0.50	2.77	0.58	2.53
12	2.19	6.63	0.47	2.22	0.32	2.72	0.37	2.63
Mean	1.74	4.78	0.48	2.18	0.41	2.80	0.42	2.72

Ref. CM, NM1, NM2 methods are described in Sec. 3.1, respectively. Corr. coeff = Pearson correlation coefficient, RMSE = Root-mean squared error

CM : W_S = αW_L + β

NM1 : (W_S)_x = α_x(W_L)_x + β_x(W_S)_y = α_y(W_L)_y + β_y

MM2 :(W_S)_x = α_xL(W_L)_x + β_xL + β_xL(W_L)_y + γ_xL

　　　(W_S)_y = α_yL(W_L)_x + β_yL + β_yL(W_L)_y = γ_yL

여기서, W_S, W_L은 각각 해상, 육상에서의 풍속이며, 풍속에 포함된 첨자 x, y는 각각 동서방향의 풍속, 남북방향의 풍속을 의미한다. 또한 매개변수 α, β, α_x, β_x, α_y, β_y, α_xL, β_xL, γ_xL, γ_xL는 육상자료와 해상자료의 선형 그리고 다중 회귀분석 계수에 해당한다.

상관계수는 풍속만을 대상으로 한 경우가 0.48 정도로 약간 크게 나타나고 있으나, 이는 풍속이 우세한 영향으로 판단된다. 월별 상관계수 변화에서 4월, 5월이 상대적으로 작은 이유는 작은 평균 풍속에 비하여 풍속의 변동정도가 크기 때문으로 판단되며, 9월의 결정계수가 뚜렷하게 큰 이유는 일부 큰 풍속(Fig. 2 (b) 참조)이 상관계수를 높이는 역할, 즉 영향자료(influential observations)의 역할을 한 것으로 판단된다. 다른 방법도 0.41~0.42 정도로 상관계수가 크지 않기 때문에 상관관계를 이용하여 육지의 바람 자료로 바다의 바람 정보를 추정하는 오차는 큰 차이가 없는 것으로 파악되었다. 정량적인 평균 RMS 오차는 2.2~2.8 정도이다. 기존의 방법이 오차가 적은 이유는 추가로 풍향 성분을 고려하는 경우의 추정오차 증가가 반영되지 않았기 때문으로 판단된다.

3.2 풍향 통계정보 및 발생빈도 분포함수 비교분석

일반적으로 풍향은 풍속보다는 간과되는 인자이지만, 바람 자료의 반을 차지하는 중요한 정보이다. 풍향은 방향 자료라는 특성을 가지고 있기 때문에 풍속과 더불어 제시되는 바람 장미도(rose diagram)라는 기본적인 분석을 제외하고는 통계적인 분석이 간과되어 왔다. 본 연구에서는 풍향의 기본적인 정보에 해당하는 평균방향 및 크기, 방향의 분산을 육지와 바다의 바람자료를 대상으로 추정하여 비교·분석하였다.

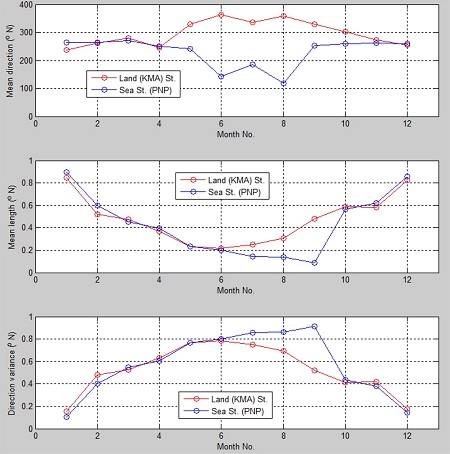
Fig. 4에는 육상과 해상 자료의 평균풍향, 분산 정보 등을 월별로 추정하여 비교·분석하였다. 그림에서 볼 수 있는 바와 같이 하계에 해당하는 5~9월의 기간에는 평균풍속은 큰 변화가 없으나, 평균풍향의 차이가 크게 나타나고 있다. 그리고 풍향자료의 분산은 전반적으로 동계에 감소하고 하계에 증가하는 계절변화가 뚜렷하게 나타나고 있으며, 하계에는 육상과 해상 자료의 방향 분산에서 차이가 크게 발생하고 있음을 알 수 있다. 대표적인 방향정보 인자인 평균 풍향단위 길이(mean resultant length)는 분산에 반비례하는 인자로(계산 과정은 부록 참조), 방향 분산 변화와 반대되는 양상을 보이고 있다.

Fig. 4.

Directional statistical information of the wind direction data sets.

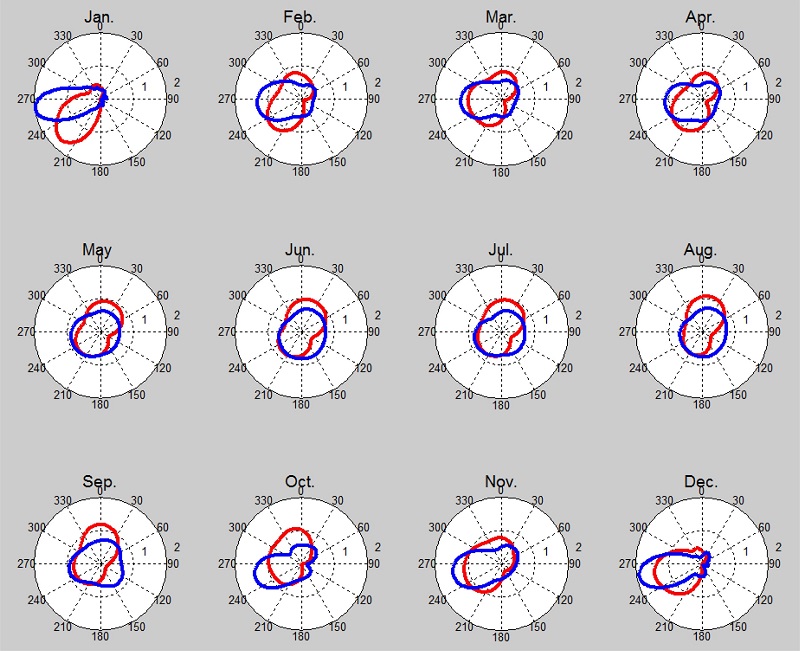
풍향의 발생빈도 분포함수는 quadratic Kernel 함수를 이용하여 월별로 추정하였으며, 추정 결과는 Fig. 5에 제시하였다. Fig. 5는 월별 풍향 발생빈도 분포를 보여주는 그림으로, 동계에 해당하는 12월, 1월에는 특정 풍향으로 발생빈도가 집중되는 양상을 볼 수 있으나, 하계에는 아주 우세한 방향도 없고 풍속도 작게 나타나고 있음을 알 수 있다. 또한 정도의 차이는 있으나 모든 기간에 걸쳐 육상과 바다에서의 풍향 분포가 뚜렷한 차이를 보이고 있음을 알 수 있다. 이러한 차이는 바다는 수면의 고도변화가 매우 작은 평평한 형태를 보이는 반면, 육지는 해안에서부터 내륙으로의 고도변화 및 고도 분포 변화가 매우 심한 영향에 기인되는 것으로 판단된다.

Fig. 5.

Monthly distribution function of the wind direction data sets (Blue line = Sea wind direction data, Red line = Land wind direction data).

3.3 풍속-풍향 결합 확률분포 비교 분석

바람 정보는 기본적으로 풍속과 풍향이 모두 필요한 정보이기 때문에 어느 한 항목만을 분석하면 한 쪽으로 치우친 분석이 될 우려가 크다. 따라서 풍속과 풍향을 모두 포함하는 결합 확률분포에 대한 검토가 필요하다. 전통적인 바람장미도가 불연속적인 결합확률분포의 형태로 간주될 수 있으나, 풍속 및 풍향에 대한 분석의 해상도를 개선시키기가 곤란하기 때문에 본 연구에서는 연속적인 분포형태를 제시하는 비모수적 Kernel 분포함수를 이용하였다.

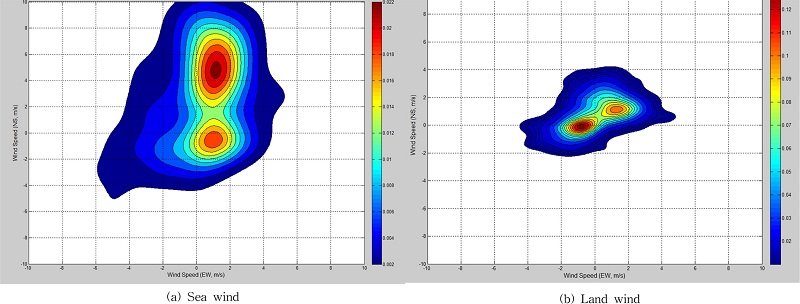
Kernel 분포함수를 이용하여 추정된 결합 확률분포 형태를 Fig. 6에 제시하였다. 그림에서 보면 육지와 바다에서 취득된 자료들이 모두 뚜렷한 2개의 첨두(peak)를 보여준다. 이러한 첨두는 연간 자료에서 나타나는 특정 시기의 우세한 풍향의 영향으로 간주할 수 있다. 또한 첨두 및 분포의 퍼짐 정도를 살펴보면, 육지와 바다의 바람 분포가 뚜렷한 차이를 보이고 있음을 알 수 있다. 이러한 차이는 육상의 바람 자료를 이용하여 해상의 바람 정보를 추정하는 방법은 전체적으로 지형 분포를 고려하는 기상 모형의 도움 없이 상관관계만을 이용하는 추정에는 근본적인 한계가 있음을 의미한다.

Fig. 6.

Joint probability distribution function of the wind speed and direction (The volumes of each joint pdf should be one(1), respectively).

4. 결론 및 제언

포항신항 연안에서 관측한 바다 바람자료와 육상 바람자료의 통계적인 특성을 비교·분석하여 도출된 결론은 다음과 같다.

(1) 자료의 상관관계를 이용한 바다에서의 바람정보 추정은 풍속의 크기만을 이용하는 경우, 풍속의 성분을 각각 이용하는 경우, 각각의 성분을 선형 조합하는 경우 등 보다 개선된 방법을 사용하여도 추정 정도는 개선되지 않았다.
(2) 우세한 풍향이 있는 바람 자료는 von Mises 분포함수가 방향 분포의 양상을 적절하게 반영하는 것으로 나타났다.
(3) 육지와 바다에서의 바람의 방향 분포는 계절적인 차이를 보이고 있었으며, 평균 풍속이 감소할수록 풍향의 분산은 증가하는 경향을 보였다.
(4) 풍향과 풍속의 결합 확률분포함수에서 육상과 바다의 바람자료 모두 2개의 첨두를 가지는 형태를 보였으나, 방향과 크기에는 뚜렷한 차이를 보였다.

따라서 육상 자료를 이용한 바다의 바람자료 추정은 육상의 바람자료 측정지점에 따라 바다 바람자료와의 상관계수가 크게 변할 수 있고, 한계가 있기 때문에 불가피한 경우 정량적인 추정 오차 분석이 반드시 수행되어야 한다. 한편 바다의 바람정보 추정은 단기간의 관측 자료가 가용한 경우, 기상모형을 이용한 검증과정을 거쳐 오차분석을 수행하여야 하며, 이러한 과정이 장기간의 추정 오차 감소에 기여할 것으로 판단된다.