Reliability Analysis of the Long Caisson Breakwater Considering to the Wave Force Reduction Parameter

Gee Nam Lee; Woo Sun Park; Dong Hyawn Kim

doi:10.9765/KSCOE.2017.29.2.121

Journal of Korean Society of Coastal and Ocean Engineers > Volume 29(2); 2017 > Article

파력감소계수를 고려한 장대케이슨 방파제의 신뢰성해석

Article

J Korean Soc Coast Ocean Eng 2017; 29(2): 121-127.

Published online: April 30, 2017

DOI: https://doi.org/10.9765/KSCOE.2017.29.2.121

파력감소계수를 고려한 장대케이슨 방파제의 신뢰성해석

이기남^*, 박우선^**, 김동현^***

^*군산대학교 해양산업공학과

^**한국해양과학기술원 연안공학연구본부

^***군산대학교 건축·해양건설융합공학부

Reliability Analysis of the Long Caisson Breakwater Considering to the Wave Force Reduction Parameter

Gee Nam Lee^*, Woo Sun Park^**, Dong Hyawn Kim^***

^*Ocean Science and Engineering, Kunsan National University

^**Coastal Engineering Division, Korea Institute of Ocean Science & Technology

^***School of Architecture and Coastal Construction Engineering, Kunsan National University, 558 Daehak-ro, Gunsan-si, Jeollabuk-do, 54150, Korea

Corresponding author: Dong Hyawn Kim, School of Architecture and Coastal Construction Engineering, Kunsan National University, 558 Daehak-ro, Gunsan-si, Jeollabuk-do, 54150, Korea, Tel: +82-63-469-1862, Fax: +82-63-469-7449, welcomed@naver.com

Received January 17, 2017 Revised April 25, 2017 Accepted April 25, 2017

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

요약

구조물에 작용하는 실제 파랑은 다방향 불규칙파로써 장대 구조물의 경우 파의 위상차로 인해 파력의 감 소효과가 발생한다. 본 연구에서는 이러한 효과가 파괴확률에 기여하는 정도를 파악하고 기존의 모듈형 방파제에 비 해 어느 정도의 안정성이 확보되는지 확인하고자 기존 방파제 및 파력감소계수를 이용한 장대케이슨 방파제의 활 동 파괴모드에 대해 신뢰성해석을 수행하였다. 그 결과 기존의 모듈형 케이슨 방파제보다 장대케이슨 방파제의 신 뢰도지수가 더 높게 나타났고, 설계변수 중 유의파고가 가장 높은 영향을 미치는 것으로 확인되었다. 추가로 파력 감소계수의 산정에 사용되는 변수들의 평균값 변화에 따른 신뢰성해석을 수행하였으며, 해석 결과 각 변수 값과 파 력감소계수의 관계에서 확인된 경향이 평균값 변화에 따른 신뢰도지수 결과의 경향에 나타나는 것을 확인할 수 있었다.

핵심용어: 다방향 불규칙파, 장대 케이슨, 파력감소계수, 신뢰성해석, 하중면 기법

Abstract

The actual wave is multi-direction irregular wave. In the case of a long structure, a reduction effect of the wave occurs. In this study, in order to grasp the extent to which these influences contribute to the failure probability and compare the existing modular breakwaters to the stability, we used existing modular breakwaters and long caisson breakwaters using wave force reduction parameter to analysis the reliability. As a result, the reliability index of the long caisson breakwater was higher than that of the existing modular caisson breakwater, and it was confirmed that the significant wave height of the design variables had the highest influence. In addition, the reliability analysis was performed according to the change of the mean value of the variables used in the calculation of the wave force reduction parameter. It is confirmed that the relationship between each variable value and the wave force reduction parameter appears in the analysis results.

Keywords: multi-directional random waves, long caisson, wave force reduction parameter, reliability analysis, force surface method

1. 서론

다양한 항만구조물의 붕괴는 사회적 및 경제적으로 그 파급효과가 매우 크게 작용하고, 때문에 이러한 주요 시설물들은 안정성에 대한 정확한 평가가 요구된다. 기존에는 설계 및 평가 시 결정론적 방법이 주로 사용되어 왔지만, 구조물의 설계에 사용되는 다양한 변수들은 일정한 값으로만 이루어지지 않고 변동성을 갖게 된다. 각 변수들의 평균값만으로 설계 또는 평가할 경우 과다 또는 과소설계로 인해 안전성이나 경제적으로 문제점이 발생할 수 있다. 따라서 주요 시설물 설계 시 다양한 설계변수들의 통계적 특성을 고려하여 과소·과다설계를 예방할 수 있는 설계 방법이 필요하며, 이에 대한 방법으로 각 설계변수들의 변동성을 확률적으로 고려할 수 있는 신뢰성기반 설계를 들 수 있다. 이미 선진국에서는 설계 기준에 신뢰성기반 성능설계(또는 한계상태설계)를 도입하여 다양한 사회기반 시설에 대해 적용하고 있고, 국내의 경우 항만구조물에 대해 안전율을 사용하는 결정론적 설계를 신뢰성 기반 성능설계로 개정하고자 활발한 연구가 진행되고 있다(Lee, 2008; Kim, 2009; Kim et al., 2009; Kim et al., 2012; Huh et al., 2010a, b, 2015). 이러한 연구들에서는 대상 구조물에 대해 활동, 전도, 마운드 및 지반의 활동 등 다양한 파괴모드 중 주로 활동파괴를 선정하여 연구가 수행되었는데, 이는 직립식 방파제에서 실제 발생된 파괴모드들과 많은 연구로부터 활동파괴가 가장 지배적인 모드로 확인되었기 때문이며(Goda and Takagi, 2000; Takahashi et al., 2001; Takayama and Higashira, 2002), 활동파괴는 케이슨 전면에 작용하는 파력이 케이슨과 마운드 사이의 마찰력보다 커짐에 따라 케이슨이 밀려나는 파괴모드이다.

일반적으로 직립식 방파제의 활동파괴에서는 파력과 마찰력이 구조물의 안전성을 결정짓는 주요한 변수로 작용하며, 상기 연구들에서는 구조물에 작용하는 파력에 대해 Goda(1974)의 연구를 이용하여 규칙파가 작용할 때의 최대파력을 사용하였다. 그러나 실제 해역에서 발생하는 파랑은 다양한 주파수를 포함함에 따라 불규칙적이며, 다방향의 특성을 갖기 때문에 단순히 최대파력을 이용하는 방법은 정확하지 않을 수 있다. 다방향 불규칙 파랑의 파력에 관한 연구 중 국외의 경우 Battjes(1982)는 최초로 단봉파 특성의 파랑 내습 시 장대 구조물에 작용하는 파력에 대해 연구한 바 있으며, 규칙파 및 다방향 불규칙파에 대한 파력감소계수를 제시하였다. 국내의 경우 Jung et al.(2010)은 JONSWAP 주파수 스펙트럼(Hasselmann et al., 1973) 및 방향 스펙트럼(Mitsuyasu et al., 1975)을 고려하여 장대 케이슨 방파제에 작용하는 파력감소계수를 계산한 바 있다. 상기 연구는 파의 위상차로 인해 감소된 파력이 작용한다는 개념을 이용하기 위해 장대 구조물을 대상 모델로 사용하였으며, 최근 이러한 장대 구조물 중 인터로킹 방파제에 대한 연구가 활발히 수행되고 있다. Kim et al.(2010)은 인접케이슨과의 맞물림 효과를 이용하여 일체 거동이 가능한 인터로킹 방파제에 대해 연구한 바 있으며, 포항 영일만항 외곽시설 2-1단계 축조공사 대안설계 시 인터로킹에 의한 장대 케이슨 방파제가 실제로 적용되었다. 또한 Park et al.(2016)은 다양한 형식의 인터로킹 방파제의 실용화를 위해 연구 중에 있다.

본 연구에서는 앞서 언급한 바와 같이 실제 발생하는 파랑인 다방향 불규칙파랑을 해석에 적용하고 파력감소계수를 산정해 이를 사용하고자 Jung et al.(2010)의 연구를 활용하였다. 대상 구조물은 실제 적용되었던 포항 영일만항의 방파제 제원을 활용하였으며, 유의파고 및 유의주기 등과 같은 환경 조건은 MOF(2005)에서 제시한 자료를 사용하였다. 다방향 불규칙파에 대한 파력감소계수 산정을 위해 주파수 스펙트럼 및 방향분산함수를 고려하고, 이를 불확실성의 반영이 가능한 신뢰성해석에 접목하기 위해 하중면기법을 이용하여 신뢰함수를 구성하였다. 정의된 신뢰함수에 대해 수치해석을 수행하여 파력감소효과로 인한 장대 케이슨 방파제의 파괴확률 및 파괴점, 민감도를 산정하여 기존의 모듈형 케이슨 방파제와 비교하였으며, 파력감소계수 산정에 사용되는 주파향각(θ_p), 첨두증대계수(γ), 최대방향분포계수(s_max)의 모수에 범위를 주어 각 모수의 변화에 따른 신뢰성 평가를 수행하였다.

2. 연구 이론

2.1 규칙파 및 다방향 불규칙파의 파력감소계수

먼저 단순한 규칙파에 대해 케이슨 장대화에 따른 파력감소계수는 식(1)과 같이 정의되고(Battjes, 1982), 이는 Fig. 1의 우측 그림과 같이 파력 첨두(P _max)가 전체 케이슨에 작용하는 것이 아니라 위상차가 생김에 따라 분산되어 청색 선과 같이 전체 구조물에 감소된 파력(P)이 작용한다.

(1)

δ=|sin(πLBLsinθ)πLBLsinθ|

여기서, δ, LB, θ, L은 각각 파력감소계수, 케이슨의 길이, 입사각, 입사 파랑의 파장을 의미한다.

불규칙파랑의 스펙트럼은 주로 JONSWAP 주파수 스펙트럼이 사용되고 여기에 방향분산함수를 적용하여 다방향을 고려한다. 다방향 불규칙파랑을 구성하는 방향분산함수는 Lee et al.(2009)이 제안한 방향에 대한 비대칭을 고려하여 수정된 방향분산함수를 사용하였다. 비대칭계수(μ)가 음수인 경우에는 주파향각을 기준으로 음의 방향(우측 방향)에 대한 분산 정도가 양의 방향(좌측 방향)에 대한 분산 정도에 비해 더 크게 나타나고, 비대칭계수가 양수인 경우에는 이와 반대되는 경향이 나타난다. Lee et al.(2009)은 cos^2s 함수 내의 변수 값의 범위(− π/2 ≤ (θ − θp)ξ/2 ≤ π/2)로부터 파향각의 상한(θ_u, upper limit) 및 하한(θ_l, lower limit)을 산정하고, 해당범위는 μ ≠ 0인 경우 360^o를 초과하는 문제점이 발생함에 따라 식(2)와 같은 조건을 적용하여 최종적으로 θ_max와 θ_min을 식(3)과 같이 결정하였다.

(2)

θu−θl=2πθu2exp(−μ)=−θl2exp(−μ)

(3)

θmin=θp=2π1+exp(2μ)θmax=θp=2π1+exp(−2μ)

JONSWAP 주파수 스펙트럼과 방향스펙트럼을 이용하여 다방향 불규칙파랑의 에너지 분포를 식(4)와 같이 표현할 수 있다.

(4)

S(f,θ)=S(f)G(f,θ)

장대 케이슨 방파제에 대한 파력감소계수(δ_r)는 파고의 ((H_s)_r/H_s)를 이용하여 정의할 수 있다. 파고는 다시 각각의 주기 및 파향에 대한 성분파의 진폭을 의미하는 a(f_i, θ_j)로 표현할 수 있고, 다방향 불규칙파랑의 각 성분파에 대한 진폭과 파력감소효과를 고려한 진폭을 식(6)과 (7)에 나타내었다. 식(7)에서 δ(f_i, θ_j)는 각각의 주파수 및 파향에 대한 규칙파의 파력감소계수를 의미한다. 식(6)과 식(7)을 이용하여 파력감소계수를 정의하면 식(8)과 같다.

(5)

Hs⋍4.004ηrms=η¯2=8∑i=1imax∑j=1jmaxa(fi,θj)2

(6)

a(fi,θj)=2S(fi)G(fi,θj)ΔfΔθ

(7)

ar(fi,θj)=2δ(fi,θj)S(fi)G(fi,θj)ΔfΔθ

(8)

δr=∫θminθmax∫fminfmaxδ2(f,θ)S(f)G(f,θ)dfdθ∫θminθmax∫fminfmaxS(f)G(f,θ)dfdθ

2.2 신뢰성이론

신뢰도 기반 한계상태설계법(limit state design, LSD)은 하중 및 저항에 대한 불확실성을 구조물 설계에 반영하는 설계기법 중 하나로써 구조물의 안전성 또는 성능수준 등에 대하여 그 정도를 평가하는 방법이며, 설계자가 원하는 수준에 따라서 다음의 3가지 단계로 분류된다.

첫 번째, Level I 방법은 설계에 사용되는 저항 및 하중에 대한 요인들에 부분안전계수(partial safety factor)를 직접적으로 적용하여 각 설계변수(design variable)들의 불확실성이 반영되는 방법이다. 두 번째, Level II 방법은 신뢰도 지수(reliability index) 개념이 도입된 방법으로 한계상태함수가 명시적(explicit)인 양함수로 표현된 경우 적용이 가능하며, 각 설계변수들의 민감도를 확인할 수 있고 참값에 근접한 결과를 얻을 수 있으므로 주로 사용되는 방법이다. 세 번째, Level III 방법은 일반적으로 MCS(Monte-Carlo Simulation)가 사용되며, 비교적 정확한 결과를 보이나 안전성이 높은 경우 비례적으로 많은 추출횟수가 요구되므로 적용에 어려움이 따른다(Haldar et al., 2000).

2.3 하중면 기법

신뢰성해석 시 앞서 언급한 바와 같이 한계상태함수는 명시적인 양함수 형태로 표현되어야만 적용이 가능하다. 그러나 해석에 사용되는 설계변수들은 Goda 파압식 및 상기 파력감소계수 산정식의 입력 값으로 사용되고, 해당 식 내의 다양한 조건들로 인해 한계상태함수는 음함수(implicit function) 형태를 나타내게 된다. 이러한 경우 일종의 회귀분석(regression analysis)인 하중면 기법(force surface method)이라는 방법을 이용함으로써 간단히 양함수 형태로 근사할 수 있고, 저항과 하중으로 이루어진 한계상태함수를 하중면을 이용하여 표현하면 식(9)와 같다(Scheuller et al., 1987; Raymond et al., 2002).

(9)

g(X)=R(Xr1,Xr2,…,Xrn)−S(Xs1,Xs2,…,Xsm)

위와 같이 음함수 형태로 가정된 한계상태함수가 주어진 경우 하중면 기법을 적용함으로써 하중함수를 식(10)과 같이 양함수 형태로 근사할 수 있다.

(10)

S(Xs1,Xs2,…,Xsm)=b0+∑ibiXsi +∑ijbijXsiXsj+∑ijkbijkXsiXsjXsk

하중함수의 근사에 사용되는 계수 벡터 b는 표본점에 대한 하중을 계산함으로써 구할 수 있으며, 각 표본점의 위치는 식(11)로부터 선정된다. 즉, 중심으로부터 일정 간격의 표본점을 선정하고, 해당 표본점에서 하중을 계산한다.

(11)

Xi=XiC±hiσXiIi

여기서, XiC, h_i, σ_{X_i}, I_i는 각각 중심점, 확장폭, 설계변수의 표준편차, scattering index matrix를 의미한다.

하중면 구성 시 근사의 정도 및 근사를 위해 필요한 계산 횟수를 고려하여 표본점 선정 방법이 결정되어야 한다. 일반적으로 사용되는 표본점 선정 방법은 BBD(bucher-bourgund besign), SD(saturated design), CCD(central composite design) 방법이 있다(Bucher and Bourgund, 1987; Haldar and Mahadevan, 2000; Box and Wilson, 1951). BBD 방법은 설계변수 간의 연성항을 제외하여 표본점의 수를 줄임으로써 하중면 추정에 필요한 계산 횟수를 줄이는 목적으로 제안된 방법이며, 설계변수의 개수가 n이라고 할 때 표본점의 개수는 2n+1이다. SD 방법은 BBD 방법에서 설계변수의 중심점으로부터 +h_iσ_{X_i} 방향의 연성항을 고려한 방법으로 BBD 방법에 비해 보다 정확한 근사가 가능하며, 표본점의 개수는 N = (n + 1)(n + 2)/2이다. CCD 방법은 설계변수 간의 모든 방향에 대한 연성항을 고려하는 방법으로 상기 두 방법보다 정확한 근사가 가능하다. 그러나 표본점의 개수는 N+2ⁿ+ⁿ+1로 비교적 많은 계산이 필요한 단점이 있다(Haldar et al., 2000).

3. 수치해석

본 장에서는 앞서 언급한 파력감소계수의 산정과 신뢰성 해석이 수행되고, 이러한 수치계산에는 Matlab R2015b(MathWorks Inc., 2015)을 이용하였다. 먼저 설계변수의 변화에 따라 파력감소계수가 산정될 수 있도록 계산 절차를 구축하고, 이를 신뢰성해석 알고리즘에 접목함으로써 반복된 계산을 수행할 수 있도록 한다. 기존의 모듈형 케이슨과 장대 케이슨에 대해 각각 신뢰성해석을 수행하여 그 결과를 분석하고, 파력감소계수를 구성하는 주요 설계변수들의 모수를 변화시키며 신뢰성해석을 수행하였다.

3.1 파력 계산

구조물에 작용하는 파력은 Goda(1974)의 파압 산정식을 사용하며, 파력 계산에 사용된 Table 1의 설계치는 MOF(2005)에서 제시한 자료를 분석하여 유의파고, 유의주기, 주파향각 등 파랑 특성에 관련된 설계변수를 사용하였으며, 구조물에 대한 제원은 포항 영일만항 케이슨식 방파제의 제원을 참고하였다(Hyundai DVP. company, 2009).

3.2 파력감소계수를 고려한 신뢰성해석

신뢰성해석을 위한 한계상태함수는 상기 하중면 기법을 이용함으로써 양함수로의 근사가 가능하다. 본 연구에서는 하중면 구성을 위한 표본점 선정 방법으로 연성항을 고려하되 계산 횟수가 CCD보다는 적은 SD 기법을 이용하였다. 하중면기법 및 파력감소계수를 고려한 한계상태함수는 식(12)와 같이 정의할 수 있다. 수치해석에 사용된 설계변수들 중 유의파고, 주파향각, 첨두증대계수, 방향분포계수에 대해 MOF(2005)에서 제시한 자료를 분석하여 통계특성을 활용하였고, 그 외에 케이슨 중량, 마찰계수, Goda 파압식의 불확실성은 기존 문헌에서 활용되어진 특성치를 사용하였다(Kim, 2009; Lee, 2002). 각 설계변수에 대한 특성치는 Table 2에 나타내었다. Table 2에서 Weibull 분포의 매개변수 중 k_w, σ_w, μ_w는 각각 shape, scale, location parameter를 의미하고, Log-normal 분포의 매개변수에서 σ_l, μ_l은 각각 대수표준편차와 대수평균이다.

(12)

g(X)=X6{X5−Bu−X7Fl(X1,X2,X3,X4)} −X7Fh(X1,X2,X3,X4)

기존의 모듈형 케이슨 방파제와 장대 케이슨 방파제에 대해 Level II 신뢰성해석을 수행하였다. 그 결과 모듈형과 장대 케이슨의 수렴된 신뢰도지수는 각각 2.2와 2.8이고, Fig. 2에 수렴곡선을 도시하였다. 신뢰도지수(β)는 파괴확률(P_f)과 P_f=Φ(−β)의 관계를 가지고 있고 Φ() 는 표준정규분포의 누적확률분포함수이다. 신뢰도지수가 커질수록 파괴확률은 작아지며, 해당 관계와 상기 결과로부터 파력감소효과가 고려된 장대 케이슨(β = 2.8)이 기존 모듈형 케이슨(β = 2.2)에 비해 안전성이 높다고 할 수 있다. 신뢰도지수가 높게 산정된 것은 다양한 원인이 있을 수 있으나 민감도로 보아 파력감소계수가 고려됨에 따라 방파제에 작용하는 파력이 낮아짐이 가장 큰 영향을 미친것으로 판단되며, 각 설계변수들의 민감도를 살펴보면 파력감소계수를 고려한 장대 케이슨 방파제(No. 1)와 기존 모듈형 케이슨 방파제(No. 2)의 유의파고가 각각 −0.7과 −0.9509로 다른 확률변수에 비해 높은 영향을 보이는 것으로 나타났다. 일반적으로 직립식 케이슨 방파제는 마찰계수의 영향이 큰 것으로 나타나지만 이는 파력을 확률변수로 고려한 경우이며(Lee, 2002), 파고를 이용하여 신뢰함수를 정의하면 상기 결과와 마찬가지로 마찰계수에 비해 파고의 영향이 크게 나타난다(Kim, 2009). 그러나 해석 조건, 신뢰성해석의 적용 방법 등에 따라 민감도는 달리 나타날 수 있으므로 일반적인 결과로 해석하는 것은 잘못된 판단이 될 수 있다.

3.3 모수 변화에 따른 신뢰성해석

주파향각, 첨두증대계수, 최대방향분포계수의 평균 변화에 따른 신뢰도평가를 수행하기 위해 Table 4와 같이 각각의 설계변수의 평균에 범위를 주어 신뢰성해석을 수행하였다.

주파향각의 평균(μ_{θ_p}) 변화에 따른 신뢰도지수(Case 1)는Fig. 3과 같이 평균이 증가함에 따라 신뢰도지수도 함께 증가하는 경향을 확인할 수 있다. 특이한 것은 μ_{θ_p} 이 40^o를 기준으로 급격히 증가하다가 완만하게 증가하는 것을 볼 수 있는데, 이는 주파향각 값의 변화에 따른 파력감소계수를 산정하여 그 경향을 살펴봤을 때 상기와 같은 경향이 나타나는 것이 확인되었다. 즉, 평균변화에 따른 신뢰도지수의 경향은 파력감소계수가 큰 영향을 미치고, 파력감소계수의 산정에는 주파향각이 높은 영향을 준다. 또한 상기 결과로부터 μ_{θ_p}가 40^o를 초과할 경우 파력감소효과 증가율이 40^o 이하에 비해 급격히 낮아짐을 알 수 있다. 반면 Fig. 4~5에서 첨두증대계수(γ) 및 최대방향분포계수(s_max)의 평균이 증가함에 따라 신뢰도지수(Case 2 & 3)는 감소하는 경향이 나타났다. γ 및 s_max의 값이 증가함에 따라 파력감소계수는 증가하게 되는데, 이와 같은 경향이 상기 결과에서도 나타난 것으로 판단된다. 그리고 μ_γ 및 μ_Smax의 변화에 대한 β의 변화량이 μ_{θ_p}의 변화에 따른 β의 변화량에 비해 작은 것을 볼 수 있는데, 이는 장대 케이슨의 신뢰성해석(No. 2) 결과인 민감도에서 확인할 수 있듯이 θ_p의 영향이 γ나 S_max에 비해 높기 때문이다.

4. 결론

장대 케이슨식 방파제에 대해 파력감소계수를 고려하여 신뢰성해석을 수행하여 기존의 모듈형 케이슨식 방파제와 비교하고, 파력감소계수의 산정에 사용되는 주요 인자를 확률변수로 고려하여 모수 변화에 따른 신뢰도지수를 각 변수별로 수행하였다. 이에 얻어진 결과는 다음과 같다.

장대 케이슨(No. 1)과 모듈형 케이슨(No. 2)의 신뢰도지수가 각각 2.8과 2.2로 수렴되었고, 장대화로 인한 파력의 감소효과가 나타남으로써 비교적 안전함을 알 수 있었다.
파력감소계수 산정에 사용되는 확률변수들의 평균값 증가에 따른 신뢰도지수의 증감 경향을 확인하였고, 파력감소계수가 신뢰성해석 결과에 주된 영향을 줌으로써 각 변수와 파력감소계수간의 관계가 결과에 나타나는 것으로 판단되었다.
주파향각, 첨두증대계수, 최대방향분포계수의 평균 변화에 따른 신뢰도지수의 변화량은 주파향각의 평균 변화 시 가장 크게 나타났으며, 이는 주파향각이 해석이 미치는 영향이 가장 큰 것으로 판단되고 민감도계수에서도 같은 영향도를 보이는 것으로 확인되었다.

감사의 글

본 연구는 2014년도 산업통상자원부 재원으로 한국에너지 기술평가원(KETEP)의 지원을 받아 수행한 연구과제입니다(NO. 20144030200590).

Fig. 1.

Wave force reduction effect.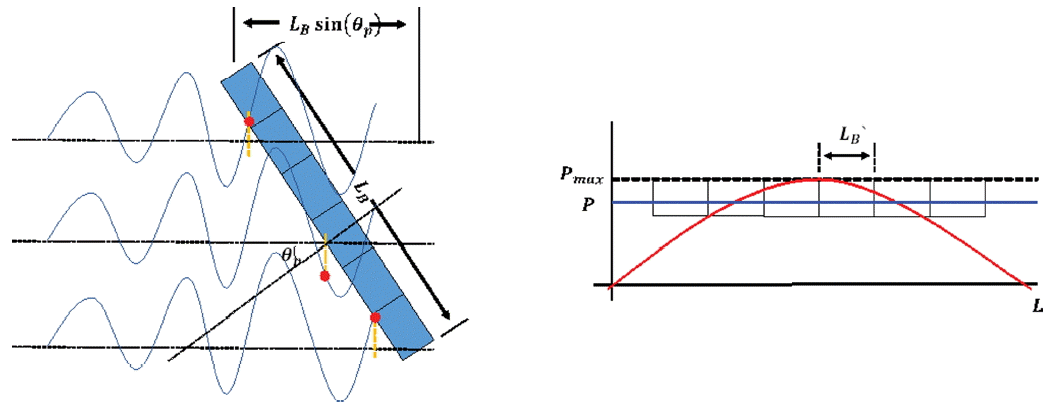

Fig. 2.

Convergence of reliability index (β).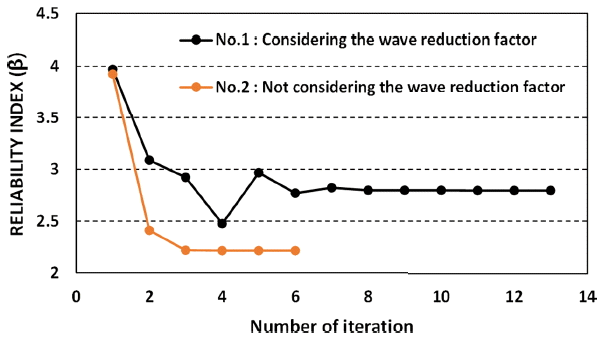

Fig. 3.

Reliability index according to parameter (Case 1: Principal wave direction).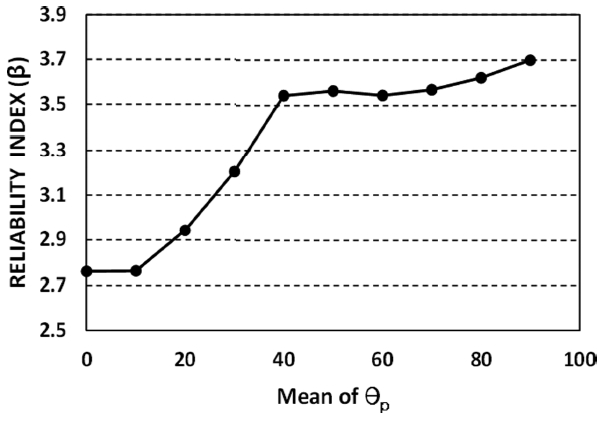

Fig. 4.

Reliability index according to parameter (Case 2: Peak enhancement factor).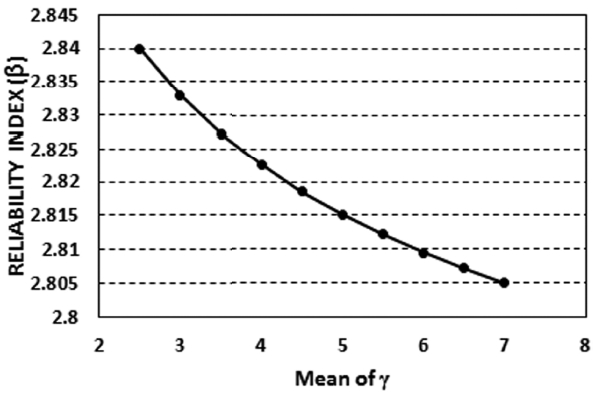

Fig. 5.

Reliability index according to parameter (Case 3: Maximum spreading factor).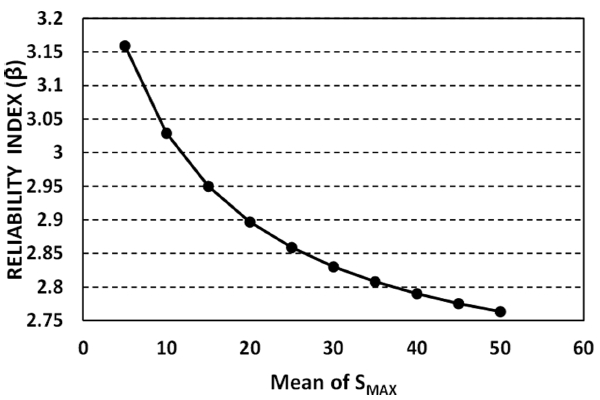

Table 1.

Design parameters

Symbol	Description	Value
H_s	Significant wave height	10.34 m
T_s	Significant wave period	14.38 s
θ_p	Principal wave direction	0°
H	Front water depth	23.10 m
H_w	Front tide level	0.12 m
L	Wave length	200.14 m
h′	Body bottom water depth	21.12 m
H_c	Height of caisson	25.00 m
B	Width of caisson	28.51 m
d	Crest water depth of armour-layer	6.00 m
λ_i	Correction factor of wave pressure	1.0
μ_g	Mean slope of sea-bed	1.75 × 10⁻⁴
L_b	Caisson length	500.00 m
γ	Peak enhancement factor	2.94
s_max	Maximum spreading factor	30.211
μ	Asymmetry parameter	0

Table 2.

Characteristic of random variables

Symbol	Description		Std.	Dist.	Parameters	Mean value
X₁	Significant wave height	H_s	3.2422	Weibull	k_w = 0.0125 σ_w = 1.3665 μ_w = 4.8798	10.344 m
X₂	Principal wave direction	θ_p	38.3946	Normal	-	15°
X₃	Peak enhancement factor	γ	1.7297	Log-normal	σ_l = 0.49 μ_l = 1.08	3.3203
X₄	Maximum spreading paramter	s_max	19.1046	Log-normal	σ_l = 0.58 μ_l = 3.24	30.2110
X₅	Weight of caisson	W	33.3980	Normal	-	1669.9 tonf/m
X₆	Friction coefficient	f_c	0.0900	Normal	-	0.6
X₇	Uncertainty of Goda Eq.	a_i	0.1729	Normal	-	0.91

Table 3.

MPFPs and Sensitivity index

Symbol	Description	MPFP		Sensitivity index

		No. 1	No. 2	No. 1	No. 2
X₁	Significant wave height	9.7040 m	10.5333 m	−0.7000	−0.9509
X₂	Principal wave direction	13.1914°	-	0.5302	-
X₃	Peak enhancement factor	2.8338	-	0.0280	-
X₄	Maximum spreading paramter	20.4874	-	0.1358	-
X₅	Weight of caisson	1664.8 tonf	1667.8 tonf	0.0547	0.0285
X₆	Friction coefficient	0.4789	0.5610	0.4815	0.1955
X₇	Uncertainty of Goda Eq.	0.9784	1.0014	−0.1415	−0.2385

Table 4.

Range of mean values

Description	Case No.	Range	Interval	Std.
Principal wave direction	1	0° ∼ 90°	10°	38.3946°
Peak enhancement factor	2	2.5∼7.0	0.5	1.7297
Maximum spreading paramter	3	5.0∼50.0	5.0	19.105

References

Battjes, J A. (1982). Effects of short-crestedness on wave loads on long structures, Applied Ocean Research, 4(3):165-172.

Box, J, Wilson, W. (1951). Central composites design, JR Stat Soc., 1, 1-35.

Bucher, CG, Bourgund, U. (1987). Efficient use of response surface methods. Universität Innsbruck, Institut für Mechanik.

Goda, Y. (1974). New wave pressure formulae for composite breakwaters, In Proceedings of the 14th International Coastal Engineering Conference, 3, 1702-1720.

Goda, Y, Takagi, H. (2000). A reliability design method of caisson breakwaters with optimal wave heights, Coastal Engineering Journal, 42(4):357-387.

Hasselmann, K, Barnett, TP, Bouws, E, Carlson, H, Cartwright, DE, Enke, K, Ewing, JA, Gienapp, H, Hasselmann, DE, Kruseman, P, Meerburg, A, Müller, P, Olbers, DJ, Richter, K, Sell, W, Walden, H. (1973). Measurements of windwave growth and swell decay during the Joint North Sea Wave Project (JONSWAP), Deutches Hydrographisches Zeitschrift, 8(12):1-95.

Haldar, A, Mahadevan, S. (2000). Reliability assessment using stochastic finite element analysis. John Wiley & Sons, New York.

Huh, JW, Park, OJ, Kim, YS, Hur, DS. (2010a). Reliability analysis of a quay wall constructed on the deep-cement-mixed ground (Part I: External stability of the improved soil system), Journal of Korean Society of Coastal and Ocean Engineers, 22(2):79-87 (in Korean).

Huh, JW, Park, OJ, Kim, YS, Hur, DS. (2010b). Reliability analysis of a quay wall constructed on the deep-cement-mixed ground (Part II: Internal stability of the improved soil system), Journal of Korean Society of Coastal and Ocean Engineers, 22(2):88-94 (in Korean).

Huh, JW, Jung, HW, Ahn, JH, An, SW. (2015). Probabilistic risk assessment of coastal structures using LHS-based reliability analysis method, Journal of the Korea Institute for Structural Maintenance and Inspection, 19(6):72-79 (in Korean).

Hyundai DVP. Company.. (2009). Report of Alternative-design of Counter Facilities Construction at Yeongil Bay Port in Pohang (Stage 2–1) (in Korean).

Jung, JS, Kim, BH, Kim, HJ, Cho, YS. (2010). Calculation of the peak-delay force reduction parameter of multi-directional random waves acting on a long caisson breakwater, Journal of Korea Water Resources Association, 43(10):843-850 (in Korean).

Kim, BH, Lee, JW, Park, WS, Jung, JS. (2010). Making long caisson breakwater using interlocking system, KSCE J. Civil Engrg, 58(12):65-71 (in Korean).

Kim, DH. (2009). Reliability analysis of caisson type breakwater using load surface, Journal of Korean Society of Coastal and Ocean Engineers, 21(3):209-215 (in Korean).

Kim, DH, Yoon, GL. (2009). Application of importance sampling to reliability analysis of caisson quay wall, Journal of Korean Society of Coastal and Ocean Engineers, 21(5):405-409 (in Korean).

Kim, SW, Cheon, S, Suh, KD. (2012). Development of Timedependent reliability-based design method based on stochastic process on caisson sliding of vertical breakwater, Journal of Korean Society of Coastal and Ocean Engineers, 24(5):305-318 (in Korean).

Lee, C, Jung, JS, Haller, MC. (2009). Asymmetry in directional spreading function of random waves due to refraction, Journal of Waterway, Port, Coastal, and Ocean Engineering, 136(1):1-9.

Lee, CE. (2002). Probability of failure on sliding of monolithic vertical caisson of composite breakwaters, Journal of Korean Society of Coastal and Ocean Engineers, 14(2):95-107 (in Korean).

Lee, CE. (2008). Reliability analysis and evaluation of partial safety factors for wave run-up, Journal of Korean Society of Coastal and Ocean Engineers, 20(4):355-362 (in Korean).

Ministry of Oceans and Fisheries (MOF). (2005). Estimation report of deep-sea design wave in the whole sea area (II). Korea Institute of Ocean Science & Technology (KIOST), (in Korean)..

Mitsuyasu, H, Tasai, F, Suhara, T, Mizuno, S, Ohkusu, M, Honda, T, Rikiishi, K. (1975). Observations of the directional spectrum of ocean waves using a cloverleaf buoy, Journal of Physical Oceanography, 5(4):750-760.

Park, WS, Park, SH, Jang, SC. (2016). An interlocking caisson breakwater with fillers, KSCE Journal of Civil Engineering, 64(8):28-32 (in Korean).

Raymond, HM, Douglas, CM. (2002). Response surface methodology: Process and product optimization using designed experiments. John Wiley & Sons, New York.

Schuëller, GI, Bucher, CG, Bourgund, U, Ouypornprasert, W. (1987). On efficient computational schemes to calculate structural failure probabilities, In Stochastic structural mechanics. Springer Berlin Heidelberg, p 388-410.

Takahashi, S, Shimosako, KI, Kimura, K, Suzuki, K. (2001). Typical failures of composite breakwaters in Japan, In COASTAL ENGINEERING CONFERENCE. ASCE AMERICAN SOCIETY OF CIVIL ENGINEERS, 2, 1899-1910.

Takayama, T, Higashira, K. (2002). Statistical analysis on damage characteristics of breakwaters, In PROCEEDINGS OF CIVIL ENGINEERING IN THE OCEAN. Japan Society of Civil Engineers, 18, 263-268 (in Japanese).

The MathWorks, Inc.. (2015). Matlab R2015b. Natick, USA.