Stability Formula for Rakuna-IV Armoring Rubble-Mound Breakwater

Kyung-Duck Suh; Tae Hoon Lee; Hiroshi Matsushita; Hong Ki Nam

doi:10.9765/KSCOE.2013.25.4.181

Abstract

In this study, a total of 51 cases of hydraulic model tests has been conducted for various wave conditions and slope angles of breakwater to develop a stability formula for Rakuna-IV armoring a rubble-mound breakwater. The stability number of the formula is expressed as a function of relative damage, number of waves, structural slope, and surf similarity parameter. The stability formula is derived separately for plunging and surging waves, the greater of which is used. The transitional surf similarity parameter from plunging waves to surging waves is also presented. Lastly, to explain the stability of Rakuna-IV to the engineers who are familiar with the stability coefficient in the Hudson formula, the required weight of Rakuna-IV is calculated for varying significant wave height for typical plunging and surging wave conditions, which is then compared with those of the Hudson formula using several different stability coefficients.

핵심용어: stability formula, Rakuna-IV, rubble-mound breakwater, hydraulic experiment, 안정공식, 사석방파제, 수리실험

Abstract

본 연구에서는 사석 방파제 위에 피복한 Rakuna-IV에 대하여 파랑조건과 구조물의 경사를 변화시키며 51 가지 실험을 수행하여 안정공식을 유도하였다. 안정공식에서 안정수는 상대피해, 파의 개수, 구조물 경사 및 surf similarity parameter의 함수로 표시된다. 안정공식은 권파와 쇄기파에 대하여 따로따로 유도되었으며, 둘 중 안정수를 크게 계산하는 공식을 사용한다. 또한 권파와 쇄기파의 경계가 되는 critical surf similarity parameter를 제시하였다. 마지막으로, Hudson 공식에서 사용되는 안정계수에 익숙한 기술자들에게 Rakuna-IV의 안정성을 설명하기 위하여, 대표적인 권파와 쇄기파 조건에 대하여 유의파고의 변화에 따른 Rakuna-IV의 소요중량을 계산하고, 이를 몇몇 다른 안정계수를 사용한 Hudson 공식의 결과와 비교하였다.

핵심용어: stability formula, Rakuna-IV, rubble-mound breakwater, hydraulic experiment, 안정공식, 사석방파제, 수리실험

1. 서 론

사석 방파제나 호안은 가장 오래 된 형태의 해안구조물이지만 아직도 널리 사용되고 있다. 사석 구조물을 파랑에 의한 침식으로부터 보호하기 위하여, 그 경사면에 피복층을 설치한다. 피복재로 큰 사석을 구할 수 없는 곳에서는 콘크리트 피복블록이 자주 사용된다. 1950년 프랑스 Neyrpic 사에서 Tetrapod를 처음 개발해 특허를 낸 후로 수많은 콘크리트 피복블록들이 개발되었다. 우리나라에서도 Tetrapod를 두 개 연결한 형태의 Octopus가 개발된 바 있으며, 수리모형실험 결과 충분한 수리학적 안정성을 확보하고 있음에도 불구하고(Hong and Chun, 1999), 실제 현장에 사용되지는 못하였다. Kim and Suh(2010)에 의하면 우리나라 경사제의 피복재는 59.1%가 Tetrapod이고 34.2%가 사석으로 되어 있으며, 최근에는 Sealock이나 Dimple 등의 사용이 증가하고 있는 추세이다

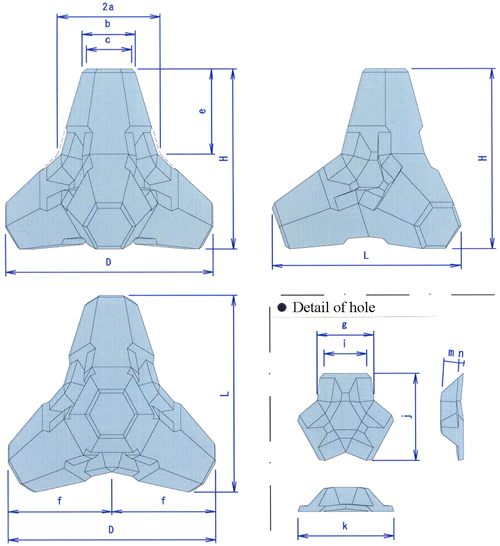
최근 일본 니켄공학주식회사(Nikken Kogaku Co., Ltd.)에서 Tetrapod와 비슷한 형태를 보이는, Rakuna-IV라는 이름의 피복블록을 개발하였다. 이 블록의 형상 특성과 제원을 Fig. 1과 Table 1에 제시하였다. 전체적인 모양은 Tetrapod와 비슷하지만, 다리가 각이 져 있으며 블록 간의 맞물림 효과를 증대시키기 위하여 다리가 만나는 부분에 4개의 홈을 가지고 있다. 또한 이 홈들은 공극률을 높여줌으로써 경제성과 안정성을 향상시킨다. 참고로 Tetrapod의 공극률은 50.0%이며, Rakuna-IV의 공극률은 56.5%이다.

Yasuda et al.(2008, 2009)과 Mase et al.(2011)은 케이슨 전면에 Rakuna-IV만을 난적하거나 사석을 쌓고 그 위에 Rakuna-IV를 피복한 경우에 대하여 실험을 수행하여 Hanzawa et al.(1996)이 제안한 형태의 안정공식을 제안하였다. 제안된 안정공식에는 폭풍지속시간과 상대피해, 파형경사 및 구조물경사 등이 고려되었다. 한편 Vietnam Water Resources University(이하 VWRU, 2011)에서는 일반 사석 방파제 위에 2층으로 피복한 Rakuna-IV에 대하여, Tetrapod의 안정공식을 제안한 Van der Meer (1988)와 같이 쇄기파(surging wave)조건에서 파의 주기, 상대피해 및 폭풍지속시간을 고려한 안정공식을 제안하였다. 하지만 권파(plunging wave)의 조건과 구조물 경사에 의한 영향을 고려하지 않았으며, 평평한 수조 바닥 위에 구조물을 설치하여 실험함으로써 바닥 경사의 영향이 배제되었다.

본 연구에서는 일반적인 사석 경사제 위에 2층으로 피복한 Rakuna-IV에 대하여 파랑 조건과 구조물의 경사를 변화시켜가면서 51 가지 경우에 대한 실험을 실시하여 Tetrapod에 대한 Suh and Kang (2012) 공식의 형태로 안정공식을 제안한다. 바닥 경사는 1:25를 사용하였으며, 안정공식은 상대피해, 파의 개수, 구조물의 경사, 파형경사의 함수로 권파와 쇄기파에 대하여 제안된다.

Fig. 1.

Specification of Rakuna-IV (Use with Table 1).

Table 1.

Specification of Rakuna-IV (Use with Fig. 1)

Nominal weight (ton)	Real weight (ton)	Volume (m³)	Dimension (mm)
Nominal weight (ton)	Real weight (ton)	Volume (m³)	H	L	D	a	b	c	e	f	g	i	j	k	m	n
6	6.25	2.716	2,112	2,315	2,553	630	658	555	1,008	1,277	706	525	1,032	1,176	189	63
8	7.85	3.415	2,280	2,499	2,756	680	710	599	1,088	1,378	762	567	1,114	1,269	204	68
12	11.85	5.154	2,615	2,866	3,161	780	814	687	1,248	1,581	874	651	1,278	1,455	234	78
16	15.89	6.908	2,884	3,160	3,486	860	898	758	1,376	1,743	963	717	1,409	1,605	258	86
20	20.09	8.736	3,118	3,417	3,769	930	971	819	1,488	1,885	1,042	776	1,523	1,735	279	93
25	24.98	10.861	3,353	3,675	4,053	1,000	1,044	881	1,600	2,027	1,120	834	1,638	1,866	300	100
32	32.35	14.065	3,655	4,005	4,418	1,090	1,138	960	1,744	2,209	1,221	909	1,785	2,034	327	109
40	40.92	17.792	3,956	4,321	4,783	1,180	1,181	1,039	1,888	2,391	1,322	984	1,933	2,202	354	118
50	49.82	21.661	4,225	4,614	5,107	1,260	1,261	1,110	2,016	2,554	1,411	1,051	2,064	2,351	378	126
64	59.92	26.055	4,493	4,907	5,431	1,340	1,341	1,180	2,144	2,716	1,501	1,118	2,195	2,500	402	134
80	80.74	35.104	4,962	5,420	5,999	1,480	1,481	1,304	2,368	2,999	1,658	1,234	2,424	2,762	444	148

2. 수리실험

실험은 서울대학교 건설환경공학부 수리해안공학실험실에서 수행하였다. Fig. 2는 실험수조의 단면과 파고계의 위치를 나타낸다. 조파수조는 총 36m의 길이, 폭 1.0m, 그리고 1.2 m의 깊이이다. 조파기는 피스톤 타입으로 수조의 왼쪽에 설치되어 있으며 수조의 양 끝에는 곡면으로 된 소파제가 설치되어 있다. 바닥경사의 영향을 포함시키기 위하여 1/25 경사의 바닥경사가 조파기로부터 20m 거리부터 5 m 길이로 설치되어 있다. 방파제는 바닥경사가 끝나는 지점에서 10 cm 뒤에서부터 설치되었다. 조파기로부터 12m 떨어진 지점부터 수로를 폭 0.6m와 0.4 m로 분할하여, 방파제는 폭 0.6m 수로에 설치하고 입사파를 측정하기 위한 파고계는 폭 0.4 m 수로에 설치하였다. 비록 폭 0.4m 수로에는 방파제가 설치되지 않아도 바닥경사나 소파제로부터 오는 반사파가 생기므로 세 개의 파고계를 이용해 수면변위를 측정하고 Suh et al. (2001)의 방법을 이용해 입사파와 반사파를 분리해 입사파를 취득하였다. 수심은 방파제 위치에서 0.4m로 일정한 값을 사용하였다. 파는 수심이 0.6m인 구간에서 조파되어 방파제 전면 0.4m의 수심까지 전파된다.

연구에 사용된 Rakuna-IV는 두 층으로 피복하여 실험을 수행하였고, 제원은 공칭치수 D_n=3.81 cm; 단위중량 ρ_a=2.3 g/cm³; 무게 W=127.1 g; 공극률(porosity)은 56.5%이다. 코어는 쇄석으로 구성되어 공칭치수와 평균중량이 각각 D₅₀=0.72 cm, W₅₀=1.03 g 이며, 필터층은 D₅₀=1.6~1.8 cm, W₅₀=13.5 g 으로 구성되어 있다. 세 가지의 사면 경사각을 사용하여 실험을 수행하였다: cotθ =1.33, 1.5 및 2.0이며, θ는 수평면으로부터 사면의 경사각이다.

Fig. 3은 실험에 사용된 1:1.5 경사의 방파제 단면도이다. 위 단면은 Suh and Kang (2012)의 Tetrapod 수리실험에 사용된 단면과 유사한 제원을 보이고 유의파고가 18 cm 보다 큰 경우에 약간의 월파현상이 관측되었다. Rakuna-IV는 두 층으로 피복하여 실험을 진행하였다. 콘크리트 블록에 대한 일반적인 방법대로 아래 층은 정적하였고 위 층은 난적하여 피복하였다. 실험구간에 포함되는 Rakuna-IV의 경우 수평방향으로 두 열씩 색을 다르게 피복하여 피해를 관측하기 용이하도록 하였다. 피복한 Rakuna-IV 중 실험수조 벽면에 맞닿아 블록간 맞물림 효과를 기대하기 어려운 블록의 경우 다른 색을 사용하고 고정시켜서 피해가 발생하지 않도록 하였으며, 피해 계산 면적에도 포함시키지 않았다. 구조물 경사 1.33, 1.5 및 2.0의 단면적은 788, 848, 1036 cm² 이고, 블록의 개수는 374, 407, 495개를 각각 사용하였다.

실험은 Table 2에 나타낸 바와 같이 평균주기를 T_z=1.1~2.1 s, 유의파고를 H_s=8.5~20.5 cm의 범위 내에서 변화시켜 가면서, 각 구조물 경사 별로 17 가지씩 수행하여 총 51 가지 실험을 수행하였다. 실험에 사용한 파형경사의 범위는 s_z=H_s/L₀=0.025~0.057, surf similarity parameter의 범위는 2.13~5.19로서 권파와 쇄기파 조건을 모두 포함하도록 실험조건을 설정하였다. 여기서 L₀=gT_z²/(2π)는 평균주기에 대한 심해파장이며, surf similarity parameter는 ξ_z=tanθ/√s_z로 정의된다. 한편 Table 2에서 N_s=H_s/ΔD_n는 안정수이며, 여기서 Δ=ρ_a/ρ_w−1은 Rakuna-IV의 상대밀도이고, ρ_w는 물의 밀도이다.

구조물 전면에서 파랑의 거동은 매우 복잡하여 방파제 위치에서의 입사파랑을 관측하기 어렵다. 파고는 조파기로부터 15 m 떨어진 지점(Fig. 2)에서 관측하고 여기에 천수효과를 곱하여 방파제 위치에서의 파고를 계산하였다. 천수효과는 방파제를 설치하지 않은 상태에서 보정된 스펙트럼을 파랑조건별로 조파하고 바닥경사를 지난 후 측정한 유의파고와 바닥경사를 지나기 전에 측정한 유의파고의 비로 계산하였다.

실험에 적용된 스펙트럼은 modified Bretschneider-Mitsuyasu spectrum (Goda 2010)이 사용되었다. 이는 Pierson-Moskowitz spectrum과 동일하며 다음과 같다.

Fig. 2.

Sketch of wave flume and experimental setup.

Fig. 3.

Cross-section of breakwater (slope=1:1.5, unit=mm).

Table 2.

Test results

Case	Slope	(s)	T_z (s)	H_s (m)	s_z	ξ_z	N_s	N₀
Case	Slope	(s)	T_z (s)	H_s (m)	s_z	ξ_z	N_s	N=1000	N=3000
1	1:4/3	1.10	1.088	0.095	0.051	3.31	1.92	0.07	0.15
2			1.113	0.087	0.045	3.54	1.76	0.01	0.01
3			1.097	0.089	0.047	3.45	1.80	0.01	0.15
4		1.17	1.181	0.111	0.051	3.33	2.25	0.15	0.36
5			1.131	0.102	0.051	3.33	2.06	0.01	0.01
6			1.192	0.115	0.052	3.30	2.33	0.15	0.22
7		1.29	1.176	0.106	0.049	3.39	2.15	0.01	0.15
8			1.131	0.089	0.045	3.56	1.80	0.01	0.01
9			1.572	0.157	0.041	3.73	3.18	0.65	8.63
10		1.42	1.499	0.151	0.043	3.62	3.06	0.44	1.23
11			1.444	0.139	0.043	3.64	2.81	0.22	0.8
12			1.389	0.120	0.040	3.77	2.43	0.15	0.29
13			1.367	0.103	0.035	4.00	2.09	0.01	0.01
14		2.01	2.035	0.178	0.028	4.53	3.60	7.54	11.02
15			1.987	0.164	0.027	4.61	3.32	0.22	5.8
16			1.979	0.151	0.025	4.78	3.06	0.07	0.51
17			2.025	0.134	0.021	5.19	2.71	0.07	0.29
18	1:1.5	1.16	1.179	0.124	0.057	2.79	2.51	0.07	0.22
19			1.177	0.121	0.056	2.82	2.45	0.01	0.01
20			1.128	0.108	0.054	2.86	2.19	0.01	0.01
21		1.29	1.329	0.155	0.056	2.81	3.14	0.22	0.94
22		1.29	1.255	0.133	0.054	2.87	2.69	0.07	0.07
23		1.33	1.378	0.155	0.052	2.91	3.14	0.29	1.09
24			1.333	0.142	0.051	2.95	2.87	0.22	0.29
25			1.288	0.124	0.048	3.05	2.51	0.22	0.29
26		1.54	1.659	0.205	0.048	3.05	4.15	0.22	0.44
27			1.532	0.152	0.042	3.27	3.08	0.01	0.22
28			1.476	0.137	0.040	3.32	2.77	0.15	0.29
29			1.490	0.116	0.033	3.64	2.35	0.01	0.01
30		1.94	2.037	0.188	0.029	3.91	3.81	1.60	4.64
31			2.100	0.172	0.025	4.22	3.48	0.58	2.18
32			1.944	0.162	0.027	4.02	3.28	0.07	0.29
33			1.895	0.142	0.025	4.19	2.87	0.07	0.15
34			1.743	0.128	0.027	4.06	2.59	0.01	0.01
35	1:2	1.18	1.214	0.113	0.049	2.26	2.29	0.07	0.15
36			1.193	0.102	0.046	2.33	2.06	0.01	0.01
37			1.134	0.088	0.044	2.39	1.78	0.01	0.01
38		1.46	1.533	0.175	0.048	2.29	3.54	1.96	10.95
39			1.502	0.184	0.052	2.19	3.72	1.74	10.23
40			1.453	0.182	0.055	2.13	3.68	1.52	3.77
41			1.354	0.114	0.040	2.50	2.31	0.01	0.01
42		1.68	1.762	0.145	0.030	2.89	2.94	0.87	2.83
43			1.729	0.142	0.030	2.87	2.87	1.02	2.47
44			1.709	0.143	0.031	2.82	2.89	0.15	0.73
45			1.629	0.136	0.033	2.76	2.75	0.15	0.29
46			1.576	0.124	0.032	2.79	2.51	0.07	0.07
47		1.93	2.059	0.174	0.026	3.08	3.52	2.10	5.66
48			2.004	0.160	0.026	3.13	3.24	0.65	1.52
49			1.956	0.149	0.025	3.16	3.02	0.44	1.45
50			1.894	0.132	0.024	3.26	2.67	0.07	0.15
51			1.733	0.121	0.026	3.11	2.45	0.07	0.15

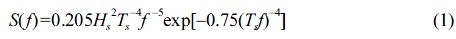
여기서 S(f)=파랑 스펙트럼 밀도함수, f=주파수, H_s=유의파고, T_s=유의주기이다. 각 파랑조건 별로 주파수가 다른 100개의 정현파 성분을 중첩하여 스펙트럼을 재현하였으며, 400 파를 관측하여 스펙트럼 보정을 수행하였다. 실제 피해 실험에서는 더 많은 파를 발생시키게 되는데, 앞에서 관측한 400 파를 반복해서 조파하는 것이 아니라, 보정된 100개의 성분파에 무작위 위상을 부여하고 이들을 중첩하여 원하는 시간만큼 조파하기 때문에 (즉,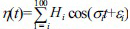

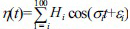; 0 ≤ ε_i<2π)조파 시간이 증가함에 따라 유의파고에 대한 최대파고의 비가 증가한다. 그러나 스펙트럼 자체는 관측된 파의 개수에 따라 변하지 않는다. 한편, 관측된 입사파랑 기록으로부터 유의파고, 유의주기 및 평균주기를 계산하기 위해서는 zero-crossing method를 사용하였다.

각 실험은 주기 T=2 s와 H=5 cm의 규칙파 조건에서 15분간 Rakuna-IV의 안정화를 거친 후 수행되었으며, 실제 실험은 전체 3000파를 조파하여 1000파와 3000파에서의 피해를 측정하였다. 피해는 육안과 캠코더를 이용하여 측정하였다. Rakuna-IV는 공칭치수(D_n) 이상 밀려나거나 이탈한 경우, 이탈하였다가 다시 제 자리로 돌아가는 경우, 그리고 180° 이상 회전하는 경우에 피해로 간주하였다. 한 종류의 실험을 수행할 때마다 피복층을 모두 제거하고 다시 피복하여 수행하였다.

3. 안정공식 유도

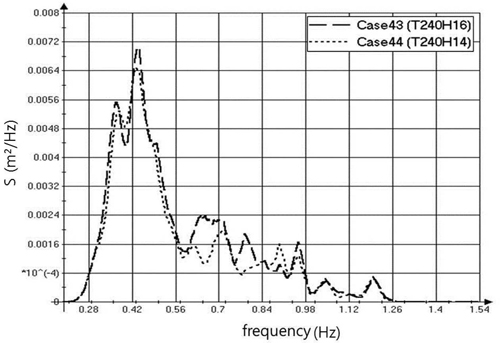
Table 2는 본 연구의 실험 결과이다. N₀는 Van der Meer(1987b)가 제안한 상대피해로서 Rakuna-IV의 공칭치수에 해당하는 방파제 폭 당 이탈하는 Rakuna-IV의 개수로 N₀=N_0d/(B/D_n)로 정의된다. 여기서 N0d는 피해로 간주되는 Rakuna-IV 의 전체 개수이며, B는 전체 수로 폭에서 맞물림 효과가 없는 수로 양측 벽면의 2D_n 만큼을 뺀 실험 단면 폭이다. Table 2를 자세히 살펴보면, 파고와 주기가 거의 같은데 상대피해는 큰 차이를 보이는 경우가 있다 (예로서 Case 18과 19, 43과 44). 이는 방파제 위치에서의 파랑 특성은 거의 같지만 그보다 깊은 수심에서는 파랑 특성이 다르기 때문이다. 예를 들어 Fig. 4는 Case 43과 44에 대하여 바닥 경사가 시작되는 0.6 m 수심에서 관측된 스펙트럼을 비교한 것이다. 전반적으로 Case 43의 에너지가 Case 44보다 더 크며, 유의파고도 16.1 cm 및 15.2 cm로 차이를 보인다. 그러나 이들 파랑이 바닥 경사 위를 전파해 올라오면서 Case 43의 경우가 더 많은 쇄파가 발생하여 방파제 위치에서는 Case 44와 거의 같은 파고를 갖게 된다. 쇄파가 많이 발생한다는 것은 그 만큼 구조물 피해가 커짐을 의미하며, 결국 Case 43의 피해가 Case 44의 피해보다 커지게 된다.

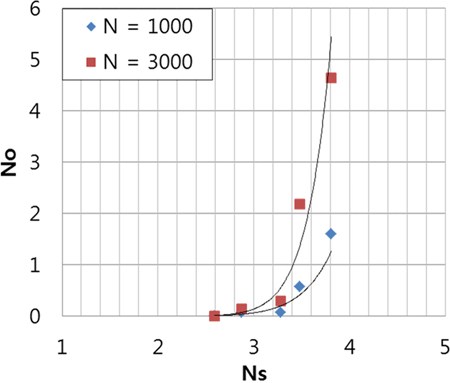
안정공식의 유도는 Suh and Kang (2012)의 Tetrapod의 안정공식 유도방법과 거의 비슷한 방법을 사용하였다. 우선 Table 2의 실험결과의 안정수와 폭풍지속시간에 따른 상대피해를 각 주기별로 나타내고 그 예를 Fig. 5에 나타내었다. 여기서 관측된 주기가 비슷한 자료들을 하나의 그룹으로 간주하였으며, 각 그룹의 평균 주기,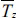

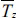를 Table 2에 제시하였다. 예를 들어서 Fig. 5에 나타낸 다섯 개의 자료는 Table 2에서 1:1.5 경사의 T_z=1.743~2.1 s에 해당하는 자료이며, 이들의 평균 주기는 1.94 s이다. Curve-fitting으로 구한 피해곡선에서 피해가 일어나기 시작하는 시점(N₀=0), 피해가 어느 정도 진행된 시점(N₀=0.5), 그리고 피해가 많이 진행된 시점(N₀=1.5)에서의 안정수를 구하고 이에 해당되는 surf similarity parameter를 계산한다.

Fig. 4.

Comparison of frequency spectra between Case 43 and 44 on flat bottom of 0.6-m depth before foreshore slope.

Fig. 5.

Example

Example of damage curve of cotθ =1.5 and

=1.94 s.

Fig. 6.

Stability number versus surf similarity parameter in case of N₀=1.5 and N=1000.

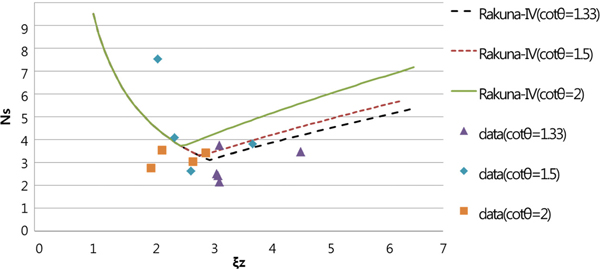
Fig. 6는 surf similarity parameter와 안정수의 관계를 구조물의 경사 별로 나타낸 그림으로 1000파를 조파하였을 때 상대피해가 1.5인 경우이다. Fig. 6와 비슷한 형태의 그림을 N₀(=0, 0.5 및 1.5)와 파의 개수 N(=1000 및 3000)의 여섯 가지 조합에 대하여 그려서 공식 유도에 사용하였다. Fig. 6의 커브들은 이러한 다양한 조합의 자료를 이용하여 본 연구에서 최종적으로 유도되는 안정공식을 나타낸다. 안정공식의 유도 과정은 아래에 기술하였다.

안정공식은 Suh and Kang (2012)의 Tetrapod에 대한 안정공식과 마찬가지로 블록의 안정성과 관련된 무차원 변수들(H_s/ΔD_n, ξ_z, cotθ 및 N₀/√N)의 조합으로 표현하였다. 또한 권파와 쇄기파에 대하여 각각 한 가지씩 총 두 종류의 공식을 제안하였다.

권파의 경우 Fig. 6의 왼쪽에 해당한다. Surf similarity para-meter, ξ_z는 구조물의 경사와 파형경사를 이용해 쇄파 형태를 나타내는 변수이고 surf similarity parameter의 변화에 따른 안정수의 변화를 H_s/ΔD_n=a₁ξ_z^d₁ 과 같은 거듭제곱의 형태로 나타낼 수 있다. 여기서 a₁=f (N₀/√N)이고, 계수 b₁은 Fig. 7에 보인 바와 같이 상대피해 및 파의 개수의 여섯 가지 조합 각각에 대하여 회귀분석을 통하여 구한다. 이렇게 구한 b>₁값들을 Table 3에 제시하였으며, 그 평균값은 약 −1.02이다. 다음으로 파의 개수가 피해에 미치는 영향을 나타내기 위하여 Van der Meer (1987a, 1988), VWRU(2011), Suh and Kang(2012) 등이 사석 및 콘크리트 블록에 사용했던 바와 같이 a₁=a₂N₀^0.5 /N^0.25+a₃의 형태를 가정하고 회귀분석으로 a₃를 구하면 Table 4와 같으며, N₀=0인 경우에 a₃의 평균값은 6.94가 된다. 이제 안정공식은 H_s/ΔD_n=(a₂N₀^0.5 /N^0.25+6.94)ξ_z^−1.02의 형태로 나타낼 수 있다. 회귀분석으로 계수 a₂를 구하기 위하여, 일정한 상대피해에 대해서 피해곡선으로부터 읽어 들인 안정수와 관측된 안정수(즉 Table 2의 자료)를 모두 사용하였다. 각 경우에 이 값은 각각 9.07과 14.48이며 이 두 값의 평균값인 11.78을 사용하였다.

Table 3.

Coefficient b₁ for plunging waves

N₀	b₁(N=1000)	b₁(N=3000)
0	-0.7616	-0.9175
0.5	-1.879	-0.8487
1.5	-1.167	-0.5320

Table 4.

Coefficient a₃ for plunging waves

N₀	a₃(N=1000)	a₃(N=3000)
0	7.39	6.48
0.5	8.32	1.03
1.5	8.30	1.02

쇄기파의 경우 Fig. 6의 오른쪽 곡선에 해당한다. 쇄기파의 경우 구조물의 경사에 따라 다른 거동을 나타낸다. Surf similarity parameter가 구조물의 경사에 의한 영향을 완전히 나타내지는 않지만, 권파와 비슷한 방법으로 쇄기파에 대한 공식을 유도하였다. 파형경사의 영향을 고려하기 위해 H_s/ΔD_n=c₁ξ_z^d₁ 형태로 가정하고 c₁=f(N₀/√N,cotθ)의 형태로 볼 수 있다. 쇄기파의 경우 Fig. 8에 보인 바와 같이 파의 개수, 상대피해, 경사각 등이 각각 다른 18 가지 경우에 대하여 회귀분석을 통해 d₁값을 구하여 Table 5에 나타내고 d₁의 평균값인 0.7을 사용하였다. 구조물의 경사의 영향을 나타내기 위하여 H_s/ΔD_n=c₂(cotθ)^d₂ ξ_z^0.7, c₂=f(N₀/√N)의 형태로 가정할 수 있다. 계수 d2는 일정한 상대피해에 대한 안정수와 관측된 안정수를 사용하여 회귀분석을 통해 구했으며 평균값 d₂=0.71을 결정하였다. 다시 c₂=c₃N₀^0.5/N^0.25+c₄로 가정하고 회귀분석으로 c₄를 구하면 Table 6과 같으며, 피해가 일어나기 시작하는 시점(N₀=0)에서 c₄의 평균값을 구하면 c₄=0.6으로 나타낼 수 있다. 마지막으로 c₃를 권파의 경우와 같은 절차를 통해 구하면 c₃=2.67로 구해진다.

Fig. 7.

Stability number versus surf similarity parameter for various combinations of number of waves and relative damage for plunging waves.

Fig. 8.

Stability number versus surf similarity parameter for various combinations of number of waves, relative damage, and slope angle for surging waves.

Table 5.

Coefficient d₁ for surging waves

N₀	N=1000			N=3000
N₀	1.33	1.5	2	1.33	1.5	2
0	0.5770	0.8100	0.4297	0.5108	0.2650	0.5353
0.5	0.9508	0.8304	0.7188	0.4225	0.5093	0.4563
1.5	0.8950	1.096	1.5090	0.4873	0.8192	0.5876

Table 6.

Coefficient c₄ for surging waves

N₀	c₄(N=1000)	c₄(N=3000)
0	0.67	0.53
0.5	0.91	0.82
1.5	0.97	0.90

따라서 최종적으로 제안된 안정공식은 다음과 같다.

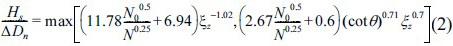
위 공식은 계수들만 다를 뿐 Suh and Kang (2012)의 공식과 동일한 형태를 보인다. Surf similarity parameter가 증가함에 따라 권파에서 쇄기파의 형태로 거동의 형태가 변화하고, 두 값 중 큰 값을 취한다. 권파에서 쇄기파로 변화되는 점에서의 critical surf similarity parameter는 두 공식이 만나는 점에서의 값이며 다음과 같다.

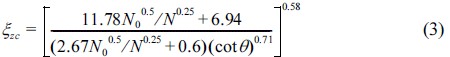
따라서, ξ_z<ξ_zc 이면 권파 공식을 사용하고, ξ_z≥ξ_zc이면 쇄기파 공식을 사용한다.

4. 실험 결과와 제안된 공식의 비교

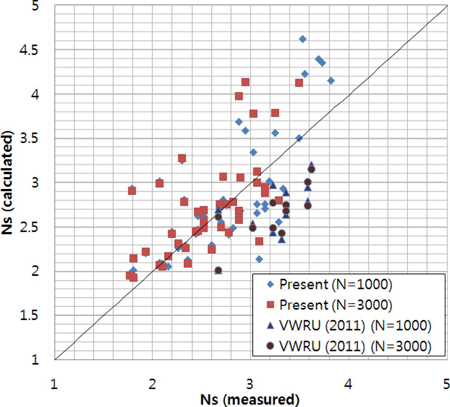
Fig. 9은 실험에서 관측된 안정수와 본 연구에서 제안한 식(2)의 안정공식으로 계산한 안정수를 비교한 그림이다. VWRU(2011)의 자료는 구조물 경사 1:1.5에 대한 쇄기파 조건에 국한된 실험 결과이다. 본 연구에서 수행한 실험의 결과만을 이용하여 일치지수를 구해 보면 0.82의 일치지수를 보인다. 일치지수는 관측치와 계산치의 일치 정도를 나타내기 위해서 Willmott(1981)가 제안한 지수이다. 일치지수는 0과 1사이에서 변화하는데, 0에 가까울수록 계산치와 관측치가 맞지 않는다고 볼 수 있으며, 1에 가까울수록 관측치와 계산치가 일치한다고 볼 수 있다.

Fig. 9.

Comparison of stability number between measurement and prediction by Eq. (2) for present data and Vietnam Water Resources University (2011) data.

Table 7.

Different test conditions between present and VWRU (2011) experiments

	Foreshore slope	Rubble mound	R_c/D_n
Present	1:25	D₅₀(filter)=1.6~1.8 cm	6.57
VWRU(2011)	0 (flat bottom)	No filter layer D₅₀(core)=2.3 cm	8.88

한편, VWRU(2011)의 자료를 포함시켜 계산하면 일치지수가 0.77로 줄어드는데, 이는 Fig. 9에서 볼 수 있듯이 VWRU 자료에 대하여 본 연구에서 구한 안정공식이 안정수를 과소산정하기 때문이다. 식 (2)의 안정공식이 안정수를 과소산정 한다는 것은 동일한 실험조건(파고, 주기, 파의 개수 및 구조물 경사)에 대하여 상대피해(N₀)가 작다는 것을 의미한다. 이에 대한 이유를 알아보기 위해서 본 실험과 VWRU 실험의 차이점을 Table 7에 정리하였다. 이 표에서 R_c는 방파제의 마루높이이다. 평평한 바닥에서 실험한 VWRU 실험은 broken wave 조건인 반면 본 실험은 breaking wave 조건이므로 VWRU 실험에서 피해가 작을 것이다. 마운드 형태에서도 차이를 보이는데, 필터층이 없고 코어 쇄석의 크기가 큰 VWRU 실험이 마운드의 투수성이 크기 때문에 피해가 작을 것이다. 마루높이 측면에서는 VWRU 실험이 마루높이가 높기 때문에 피해가 클 것이다. 이를 종합적으로 판단해 볼 때 마루높이보다 바닥경사와 마운드의 투수성이 더 큰 영향을 미쳐서 본 실험보다 VWRU 실험에서 피해가 작게 관측된 것으로 생각된다.

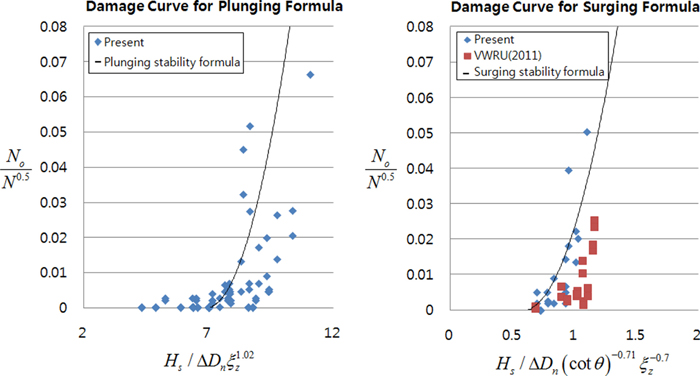
Fig. 10은 실험결과를 권파와 쇄기파로 나누어서 각각의 안정공식과 함께 그린 피해곡선이다. VWRU(2011) 실험은 쇄기파에 대해서만 수행되었다. 권파와 쇄기파는 Eq. (3)을 통해 구분하였다. 쇄기파의 경우 앞에서 설명한 바와 같이 동일한 실험조건에 대하여 VWRU(2011) 실험에서는 피해가 작게 관측되었다. 본 실험 결과만을 안정공식과 비교했을 때, 쇄기파에 대해서는 공식과 실험결과가 비교적 잘 맞는 반면, 권파에 대해서는 다소 산포도가 큰 것을 알 수 있다.

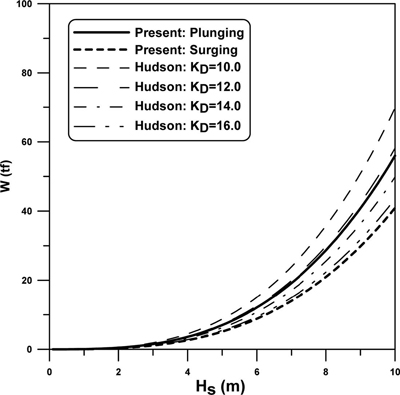
마지막으로, Hudson 공식에서 사용되는 안정계수(K_D)에 익숙한 기술자들에게 Rakuna-IV의 안정성을 설명하기 위하여, Fig. 11에 보인 바와 같이 대표적인 권파와 쇄기파 조건에 대하여 유의파고의 변화에 따른 Rakuna-IV의 소요중량을 계산하고, 이를 몇몇 다른 안정계수를 사용한 Hudson 공식의 결과와 비교하였다. ρ_a= 2,300 kg/m³, cotθ =0.5, N=1,000 을 사용하였으며, 상대피해는 Hanzawa et al.(1996)이 설계값으로 제시한 N₀=0.3을 사용하였다. 파형경사 s_z는 권파와 쇄기파에 대하여 각각 0.05와 0.03을 사용하였으며, 이에 상응하는 surf similarity parameter는 각각 2.98 및 3.85이다. 식 (3)으로 계산되는 ξ_zc는 3.10이다. Fig. 11에서 보듯이, 권파와 쇄기파에 대한 Rakuna-IV의 중량은 Hudson 공식의 K_D 값, 12 및 17의 결과와 비슷하므로 Rakuna-IV의 안정성이 우수함을 보인다. 하지만 이와 같은 방법으로 계산한 안정계수는 상대피해에 따라 매우 민감하게 변화하며, 피해가 발생하기 시작하는 N₀=0.0 을 사용하면 이보다 훨씬 작은 값이 계산된다. 통상적으로 사용되는 안정계수는 백분율 피해(percent damage) 5% 이내를 기준으로 하고 있는데, 백분율 피해와 상대피해의 관계가 명확하지 않기 때문에 위와 같은 방법으로 안정계수를 산정하는 데는 한계가 있다. 보다 정확한 안정계수를 산정하기 위해서는 입사파고를 단계적으로 증가시켜 가면서 실험을 계속하여 피해가 발생하기 시작하는 파고를 Hudson 공식에 대입하여 안정계수를 계산해야 한다. 한편, Rakuna-IV를 개발한 니켄공학에서는 K_D=9.44를 제안하고 있다.

Fig. 10.

Comparison of present stability formula against present and Vietnam Water Resources Univercity (2011) data: Plunging wave formula (left); Surging wave formula (right).

Fig. 11.

Relation between required weight and significant wave height.

5. 결 론

본 연구에서는 다양한 파랑조건과 구조물 경사에 대한 수리실험을 수행하여 사석 방파제 위에 피복한 Rakuna-IV에 대한 안정공식을 유도하였다. 안정공식은 surf similarity parameter의 값에 따라 권파와 쇄기파에 대한 두 개의 공식으로 되어 있으며, 둘 중 안정수를 크게 계산하는 공식을 사용한다. 또한 사용자의 편의를 위하여 권파와 쇄기파의 경계가 되는 critical surf similarity parameter를 제시하였다.

안정공식의 정확성을 검토하기 위하여, 본 실험 결과 및 VWRU 실험 결과와 비교하였다. 본 실험 결과와는 일치지수 0.82로 높은 정확성을 나타냈다. 한편, VWRU 실험 결과에 대해서는 본 연구에서 구한 안정공식이 안정수를 과소산정하는 경향을 보였는데, 이는 VWRU 실험이 평평한 바닥에서 실시되어 쇄파의 영향이 포함되지 않았고, 또한 마운드의 투수성이 크기 때문인 것으로 판단된다. 마지막으로, Hudson 공식에서 사용되는 안정계수에 익숙한 기술자들에게 Rakuna-IV의 안정성을 설명하기 위하여, 대표적인 권파와 쇄기파 조건에 대하여 유의파고의 변화에 따른 Rakuna-IV의 소요중량을 계산하고, 이를 몇몇 다른 안정계수를 사용한 Hudson 공식의 결과와 비교하였다. 그 결과, 상대피해 N₀=0.3의 경우 권파와 쇄기파에 대한 Rakuna-IV의 중량은 Hudson 공식에서 안정계수 12 및 17을 사용한 결과와 비슷하였다. 그러나, 보다 정확한 안정계수를 산정하기 위해서는 입사파고를 단계적으로 증가시켜 가면서 피해가 발생하는 파고를 찾아내는 추가적인 실험이 필요하다.