1. 서 론
수중에 잠겨 있는 바닥 지형이 움직일 때 발생하는 파랑의 생성과 전파에 대해서는 과거부터 많은 연구가 수행되어 왔다. 특히 지진해일은 지진에 의한 해저 지형의 급격한 변화에 의해 발생하는 것으로 알려져 있어, 지진해일의 초기 파형을 결정하기 위해 바닥의 움직임에 따른 파랑 생성에 대한 다양한 연구들이 수행되었다. 최근에는 바닥의 움직임을 이용한 조파장치의 개발을 위해 바닥이 규칙적으로 움직이는 경우의 파랑 생성에 대한 연구도 수행되고 있다.
바닥의 움직임에 따른 파랑 생성에 대한 연구는 많은 연구자들에 의해 수행되었는데, 크게 해석적인 방법과 수치적인 방법으로 구분할 수 있다. 해석적인 방법으로는 Hammack (1973)이 연속방정식 및 자유수면 경계조건, 바닥 경계조건을 공간에 대해서는 푸리에 변환(Fourier transformation), 시간에 대해서는 라플라스 변환(Laplace transformation)하여 평평한 바닥이 1회 움직이는 경우에 대해 선형의 해석해를 제시하였다. Dutykh et al.(2006)은 Hammack(1973)의 해를 3차원으로 확장하였다. Lu et al.(2017a, 2017b)은 경사진 바닥이 1회 움직이는 경우에 대해 Hammack(1973)과 같은 기법을 이용하여 선형의 해석해를 제시하였으며, Boussinesq 방정식을 이용한 비선형 수치해석 모델과 수리모형실험을 통해 비교 검토하였다. Jung et al.(2018)은 Hammack(1973)과 동일한 기법을 적용하여 삼각형 형상의 바닥이 규칙적으로 움직이는 경우에 대한 해석해를 제시하였다. Jung and Son (2021)은 Hammack(1973)의 해석해를 이용하여 두 지점에서 시간 차이를 두고 바닥이 변형되는 경우의 파랑 생성 및 전파에 대해 검토하였다. Mahjouri et al.(2021)은 고유함수전개법을 이용하여 삼각형 및 사각형 형상의 바닥이 규칙적으로 움직이는 경우에 대한 선형의 2차원 해석해를 제시하였다. Jung and Lee(2022a)는 Jung et al.(2018)의 연구를 3차원 영역으로 확장하였으며, 바닥의 움직임을 이용하여 비스듬히 전파하는 파랑의 생성에 대한 선형의 해석해를 제시하였다.
바닥의 움직임에 따른 파랑의 변화를 검토하기 위해 다양한 수치해석 모델들이 개발되었다. Wu(1987)는 시간의 흐름에 따른 바닥 변형의 효과를 포함하는 Boussinesq 방정식을 제시하였다. Cecioni and Bellotti(2010)는 바닥 움직임을 포함하는 완경사방정식을 제시하였으며, Jung et al.(2023)은 바닥 움직임을 포함하는 확장형 완경사방정식을 제시하였다. 스펙트럼 법을 이용한 연구도 수행된 사례가 있는데, Donmmermuth and Yue(1987)는 고차 스펙트럼법을 이용하여 바닥의 움직임을 포함하는 강비선형 모델을 제시하였다. 하지만, 그들은 수식의 형태만 제시하였고 그 결과는 제시하지 않았다. Gyuenne and Nicholls(2007)는 고차 스펙트럼법을 이용하여 시간과 공간에 따른 수심의 변화를 모두 고려하는 강비선형 수치해석 모델을 제시하였다.
본 연구에서는 Hammack(1973)의 방법과 스펙트럼법의 장점을 이용하여 바닥의 변화에 따른 파랑의 생성을 해석할 수 있는 간편한 선형 수치해석 모델을 제시한다. 연속방정식, 선형의 운동학적 및 동역학적 자유수면 경계조건, 그리고 운동학적 바닥 경계조건은 푸리에 변환을 통해 파수(wave number) 영역에서 해석된다. 파수 영역에서 상미분 방정식의 형태를 갖는 연속방정식의 해에 존재하는 계수는 스펙트럼법과 유사한 방법을 통해 파수 영역에서 찾을 수 있다. 본 수치해석 모델은 파수 영역에서 해석되기 때문에 각 변수의 공간미분항은 계산할 필요가 없어 공간적인 수치 오차는 거의 발생하지 않는다.
2. 수치해석 기법
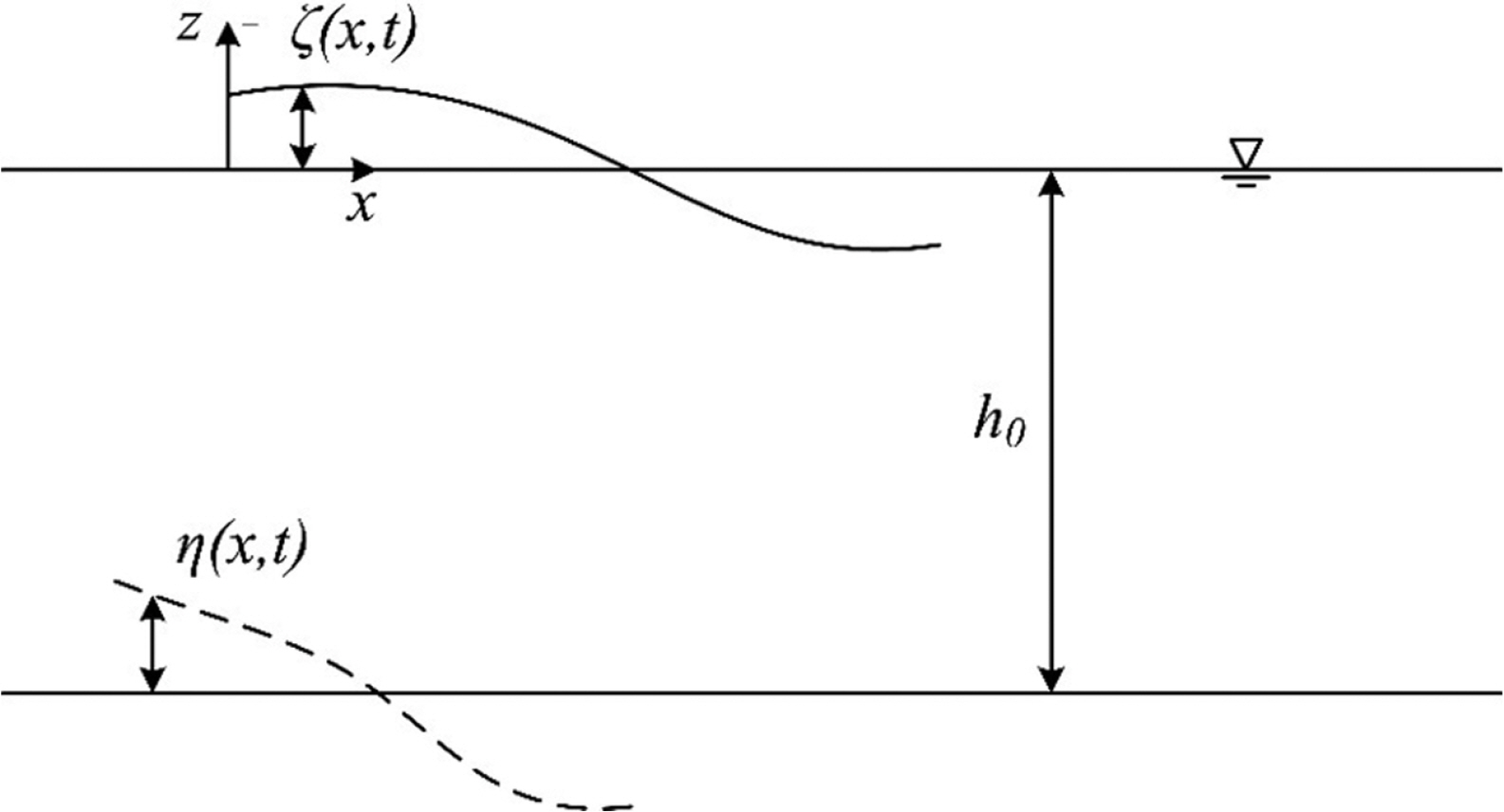
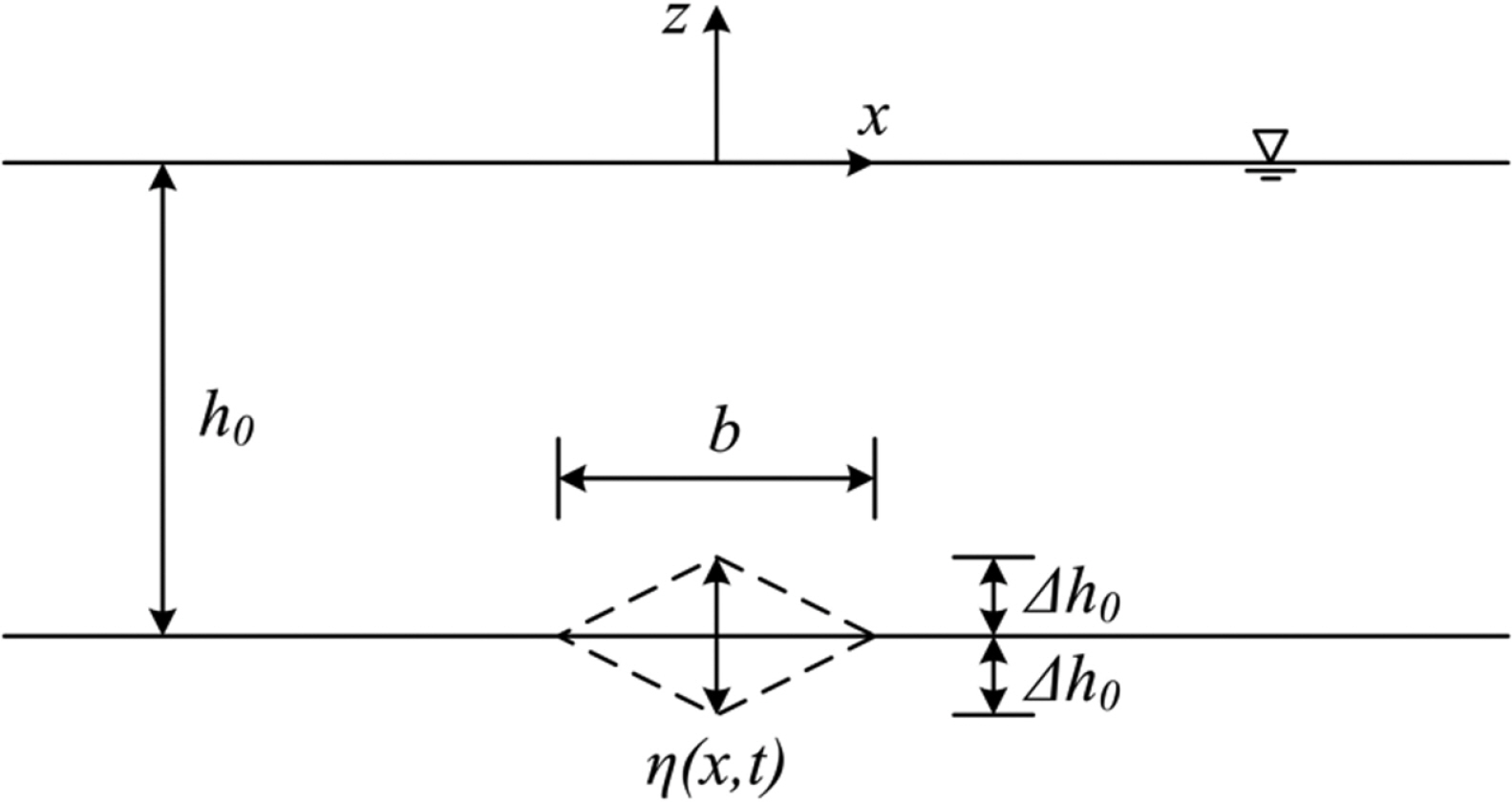
본 연구에서는 Fig. 1과 같은 x-z 2차원 공간에 대해 고려하였다. x-z 2차원 공간에서 연속방정식은 다음과 같이 라플라스 방정식(Laplace equation)의 형태를 갖는다.
여기서, ϕ는 속도포텐셜(velocity potential)이다.
운동학적 자유수면 경계조건 및 동역학적 자유수면 경계조건은 다음과 같다.
여기서, ζ는 자유수면변위(free surface displacement)이며, t는 시간을 뜻한다.
바닥의 시간에 따른 움직임을 포함하는 운동학적 바닥 경계조건은 다음과 같다.
여기서, h0는 평균수심을 나타내며, η는 바닥의 움직임과 공간적인 변화를 나타내는 함수이다.
식(1)-(4)를 푸리에 변환하고 비선형항들을 소거하면 다음과 같다.
여기서, k는 파수(wave number)를 뜻한다. 연속방정식인 식(5)는 상미분 방정식으로 해는 다음과 같이 표현된다.
식(9)를 운동학적 바닥 경계조건 식(8)에 대입하여 정리하면 다음과 같다.
여기서,
따라서, 평균수면(z = 0)에서의 속도포텐셜은 식(9)를 이용하여 다음과 같이 나타낼 수 있다.
연속방정식의 해인 식(9) 및 (12)에서 미지함수는 A(k, t) 하나뿐이다. 따라서, 바닥 움직임에 따른 A(k, t) 함수만 정의할 수 있으면 자유수면 경계조건을 이용하여 파랑 생성을 해석할 수 있다. 자유수면에서 수직방향 속도포텐셜의 변화율은 식(9)를 z 방향으로 미분하여 다음과 같이 나타낼 수 있다.
본 연구에서는 Zakharov(1968)나 Donmmermuth and Yue(1987), Craig and Sulem(1993) 등 스펙트럼 법을 적용한 다른 많은 연구들과 같이 운동학적 및 동역학적 자유수면 경계조건을 수치적으로 해석하여 파랑의 생성 및 변형을 해석한다. 자유수면 경계조건인 식(6)과 (7)은 다음과 같이 차분식으로 표현할 수 있다.
여기서, n은 n번째 시간 step을 나타내며, i는 i번째 파수 성분(k)을 의미한다. ∆t는 계산시간 간격을 나타낸다. 식(14)와 (15)는 파수 영역에서의 식이기 때문에 공간미분항이 없어 수치해석을 매우 간단하게 수행할 수 있다. 식(14)와 (15)를 통해 계산되는 각 시간 단계에서의 속도포텐셜은 식(9)와 같은 운동학적 바닥 경계조건을 만족하는 연속방정식의 해로 표현되어야 한다. 따라서, 각 시간단계에서의 속도포텐셜과 식(9) 및 (12)를 이용하여 미지함수인 A(k, t)를 구할 수 있으며, 이는 다음 식과 같다.
식(16)을 이용하여 미지함수 A(k, t)를 구하고, 식(13)에 대입하여 자유수면에서 속도포텐셜의 수직방향 변화율인 W
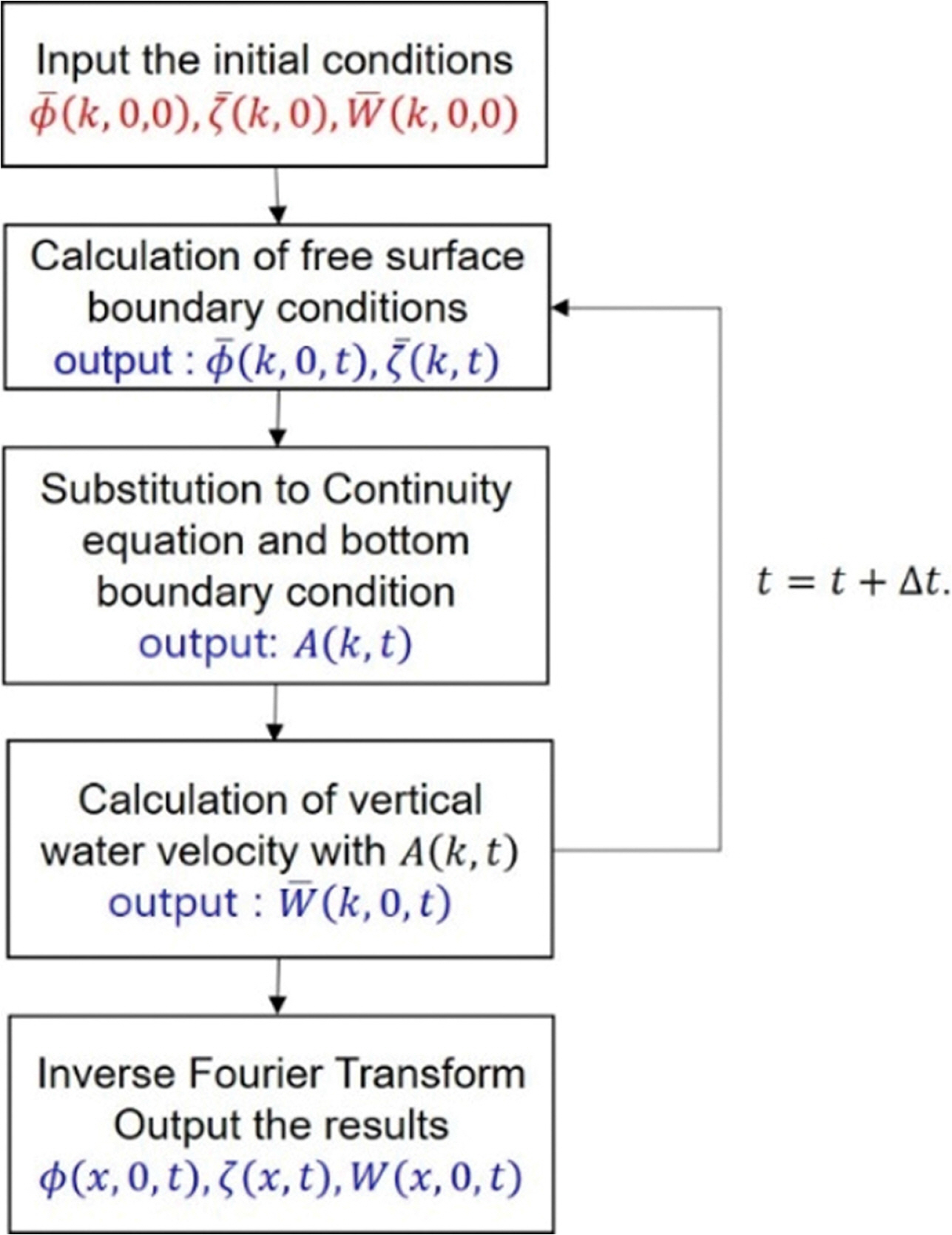
본 연구에서 제시하는 수치해석 기법은 기존의 해석해에 비해 시간에 대한 라플라스 변환 및 역변환을 수행하지 않으므로 매우 간단하고 빠르게 계산할 수 있다. 본 연구에서 제안하는 수치해석 기법에 대한 알고리즘은 Fig. 2와 같다.
3. 수치해석 결과
3.1 사각형 형상 바닥이 주기적으로 움직이는 경우
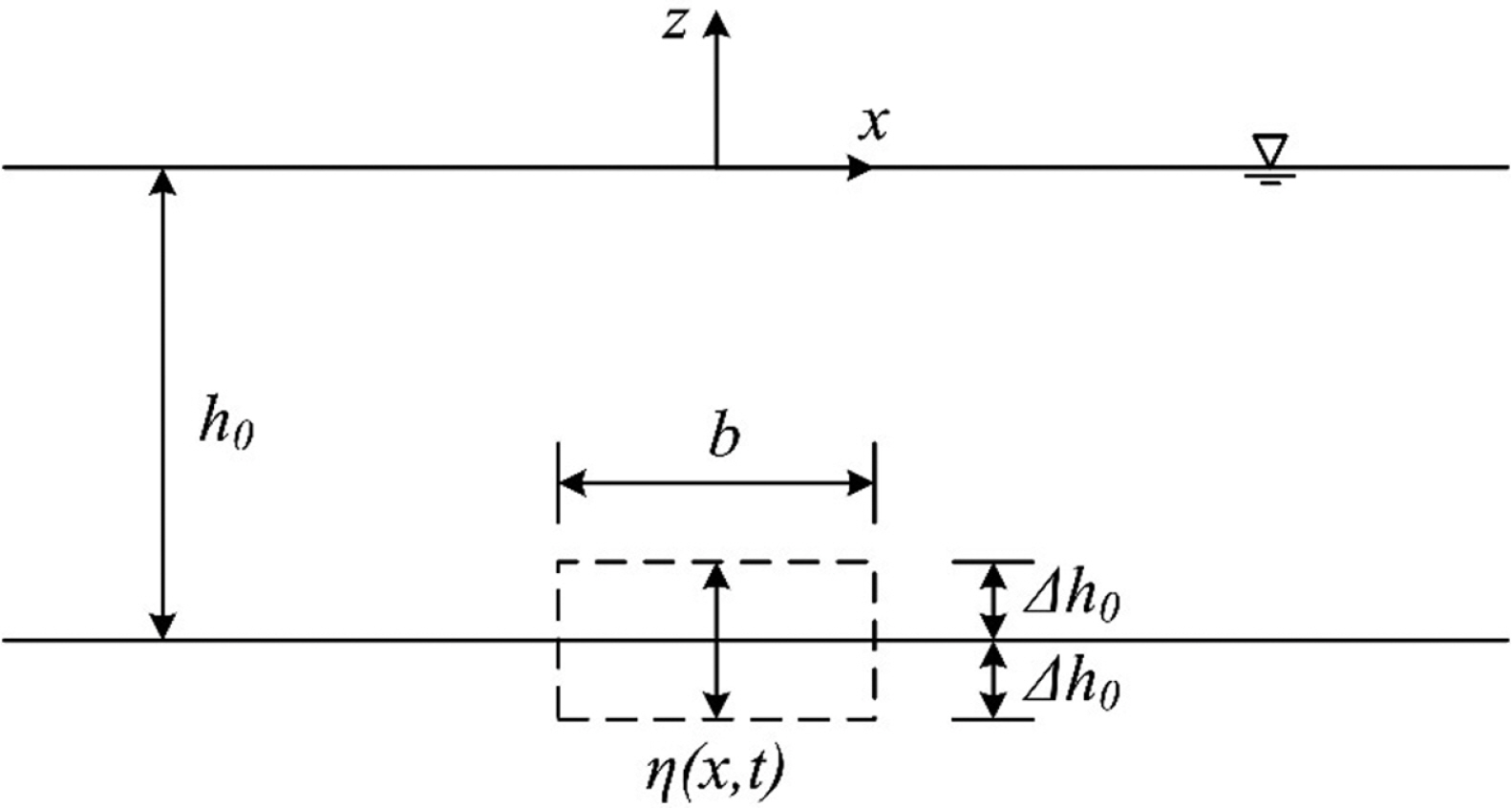
평평한 바닥이 사각형 형상으로 움직이는 경우에 대해 검토하였다. 움직이는 바닥의 형태 및 변수의 정의는 Fig. 3과 같다. 바닥의 움직임은 Jung and Lee(2022b)와 마찬가지로 다음과 같이 정의하였다.
여기서, H는 Heaviside 계단함수를 나타내며, ∆h0는 움직이는 바닥의 진폭, b는 움직이는 바닥의 폭, 그리고 ω0는 규칙적으로 움직이는 바닥의 각진동수를 각각 나타낸다. Jung and Lee(2022b) 및 Jung et al.(2023)은 식(19)와 같이 정의되는 바닥 움직임에 대한 자유수면변위에 대한 해석해를 다음 식과 같이 제시하였다.
여기서,
식(21)에서 k0는 규칙적으로 움직이는 바닥에 의해 생성되는 파랑의 파수를 의미한다.
수치해석을 위한 초기조건은 식(12) 및 (13)을 이용하여 다음과 같이 정의하였다.
본 수치모델에서는 바닥의 움직임을 나타내는 함수 η(x, t)를 푸리에 변환하여 적용하여야 한다. 식(19)와 같이 표현되는 η의 푸리에 변환한 형태는 다음 식과 같다.
수치해석을 위해 수심(h0)은 1.0 m, 움직이는 바닥의 진폭(∆h0)은 0.1 m, 바닥의 폭(b)은 5.0 m 및 10.0 m로 설정하였으며, 바닥이 움직이는 주기(T)는 생성되는 파랑의 파장(wave length, L)이 움직이는 바닥 폭의 2배가 되도록 3.39 s 및 6.50 s를 각각 적용하였다. 수치해석에서 파수 영역에서의 계산범위는 단주기 성분들을 충분히 포함할 수 있는 범위인 k = – 2π에서 k = 2π이며, 파수의 계산간격은 ∆k = π/100, 계산 시간간격은 ∆t = T/1000으로 각각 설정하였다.
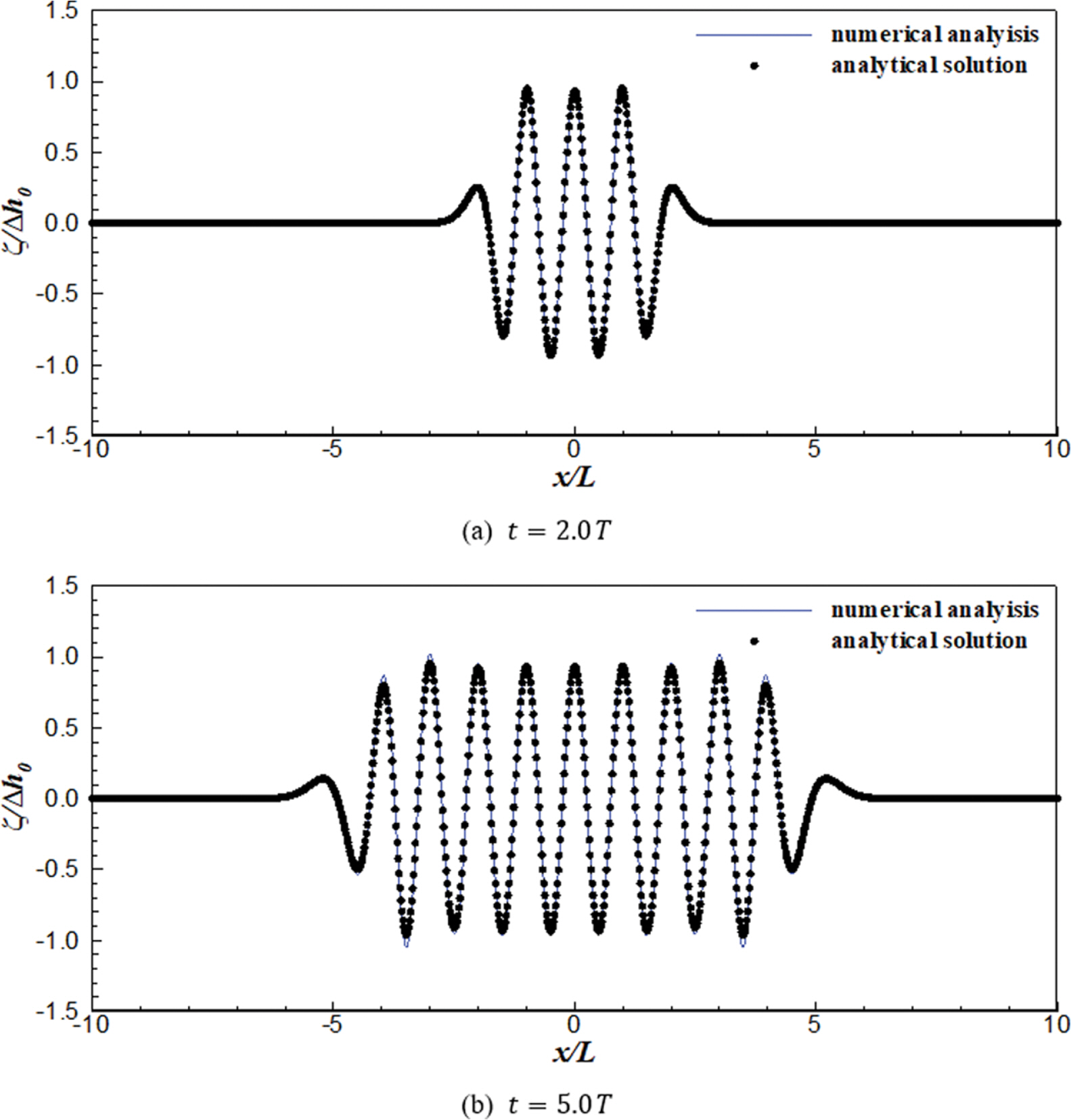
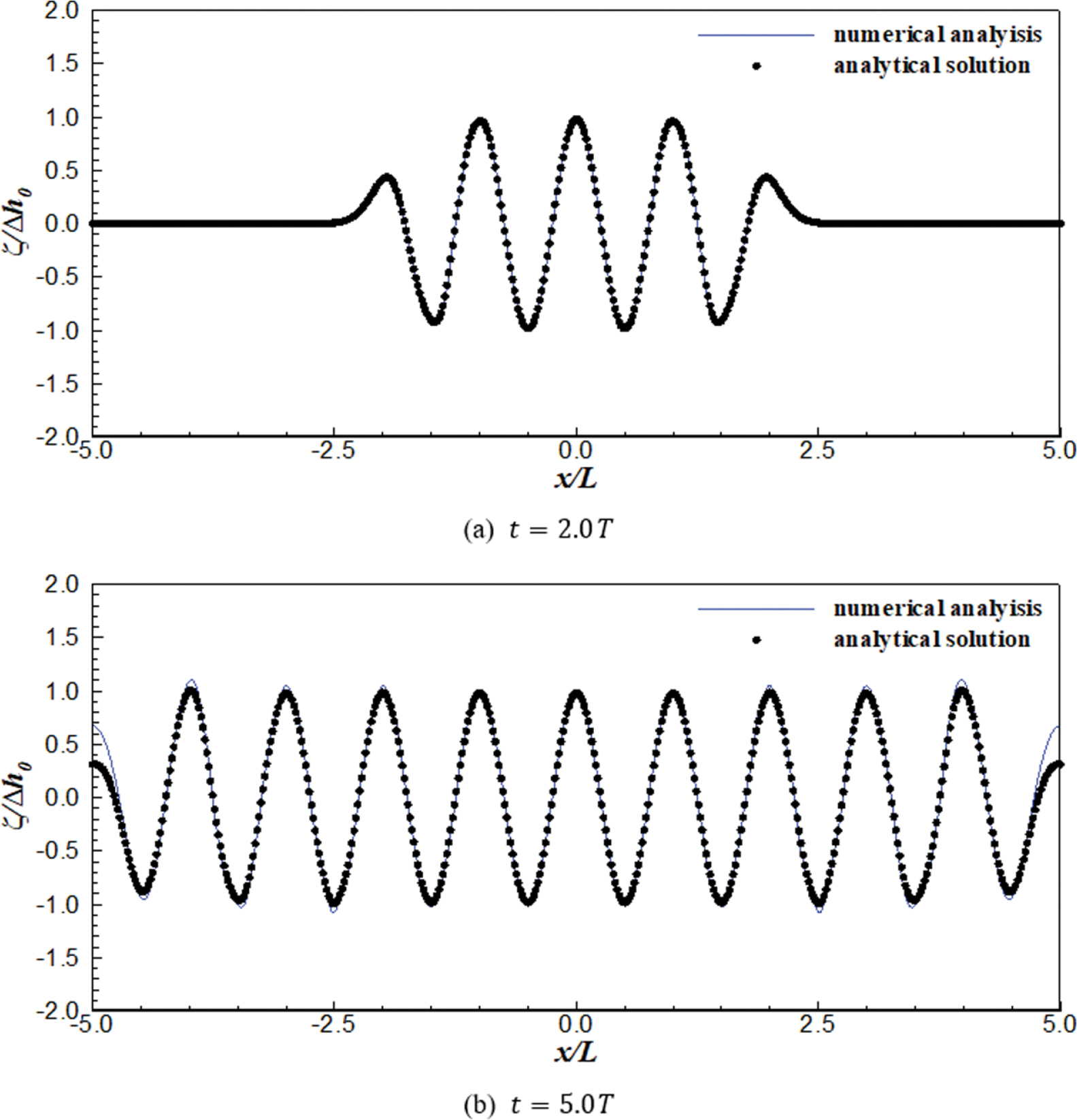
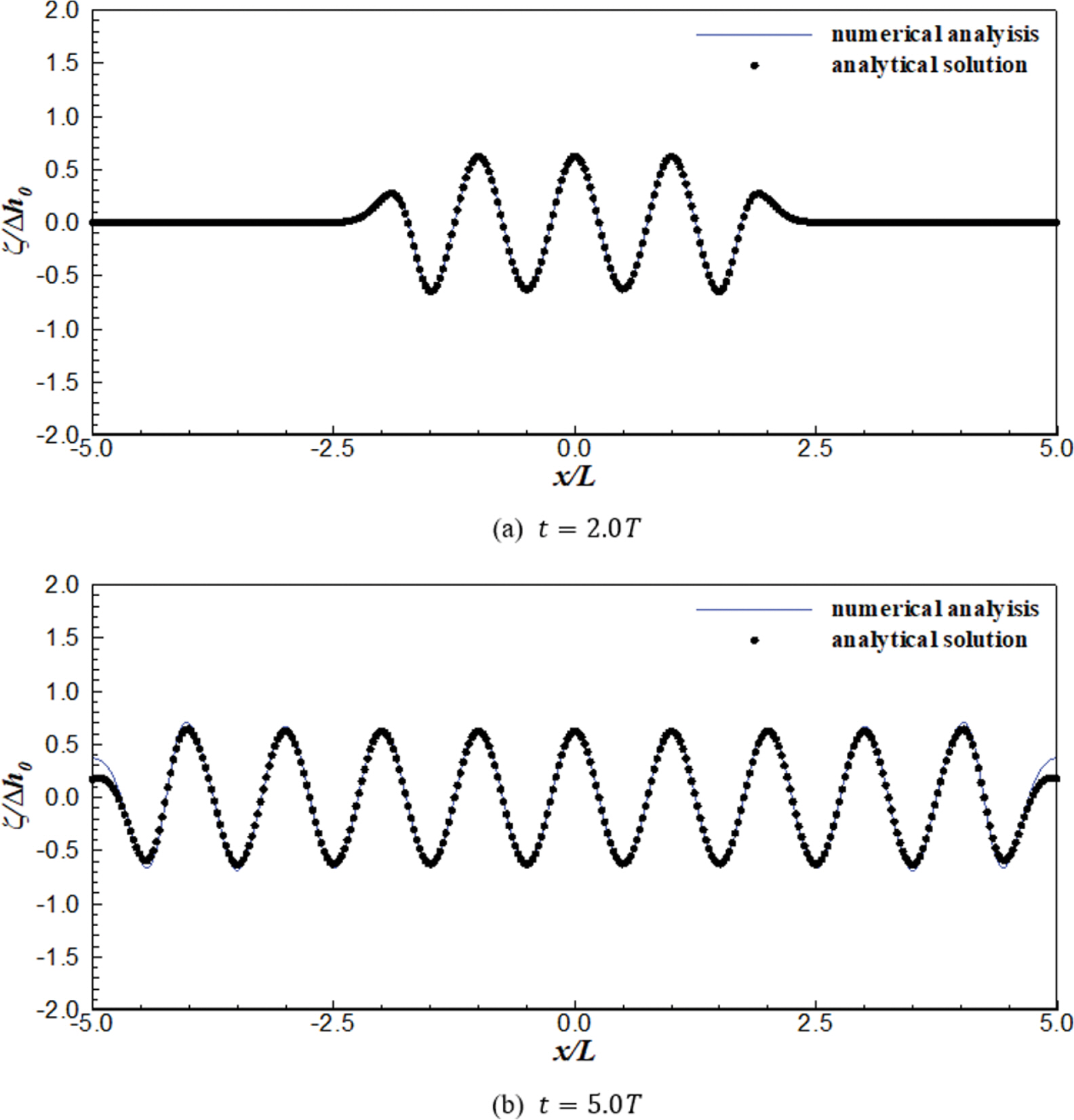
바닥 움직임에 따른 자유수면변위의 변화는 Fig. 4 및 Fig. 5와 같다. Fig. 4는 바닥의 폭이 5.0 m이고 바닥이 움직이는 주기가 3.39 s인 경우(L = 10 m)이며, Fig. 5는 바닥의 폭이 10.0 m이고 주기가 6.50 s인 경우(L = 20 m)이다. 그림에서 실선은 수치해석 결과이며, symbol은 해석해의 결과이다. 비교 결과 수치해석 결과와 Jung and Lee(2022b)의 해석해에 의한 결과는 큰 차이가 없음을 알 수 있다. 각 검토 조건에 대한 수치해석 결과와 해석해 사이의 평균제곱근 오차(RMSE) 및 무차원 평균파고(H/∆h0)는 Table 1과 같다. Table 1에서 평균파고는 파랑의 형성이 충분히 되지 않은 첫번째 파랑을 제외한 나머지 파랑에 대해 공간상에서 zero up crossing 법으로 검토한 결과이며, H는 파고(wave height)를 뜻한다.
3.2 삼각형 형상 바닥이 주기적으로 움직이는 경우
본 절에서는 바닥이 삼각형 형상으로 주기적으로 움직이는 경우에 대해 검토하였다. 삼각형 형상으로 움직이는 바닥의 형태 및 변수의 정의는 Fig. 6과 같으며, 바닥의 움직임은 Jung and Lee(2022b)와 같이 다음 식으로 정의하였다.
Jung and Lee(2022b) 및 Jung et al.(2023)은 식(27)과 같이 정의되는 바닥 움직임에 대한 자유수면변위의 해석해를 다음 식으로 제시하였다.
수치해석을 위한 초기조건은 식(12) 및 (13)을 이용하여 ζ k , 0 = 0 ϕ k , 0 , 0 = 0 W k , 0
삼각형 형상의 바닥 움직임을 나타내는 함수 η(x, t)와 ∂η(x, t)/∂t를 푸리에 변환한 형태는 다음 식과 같다.
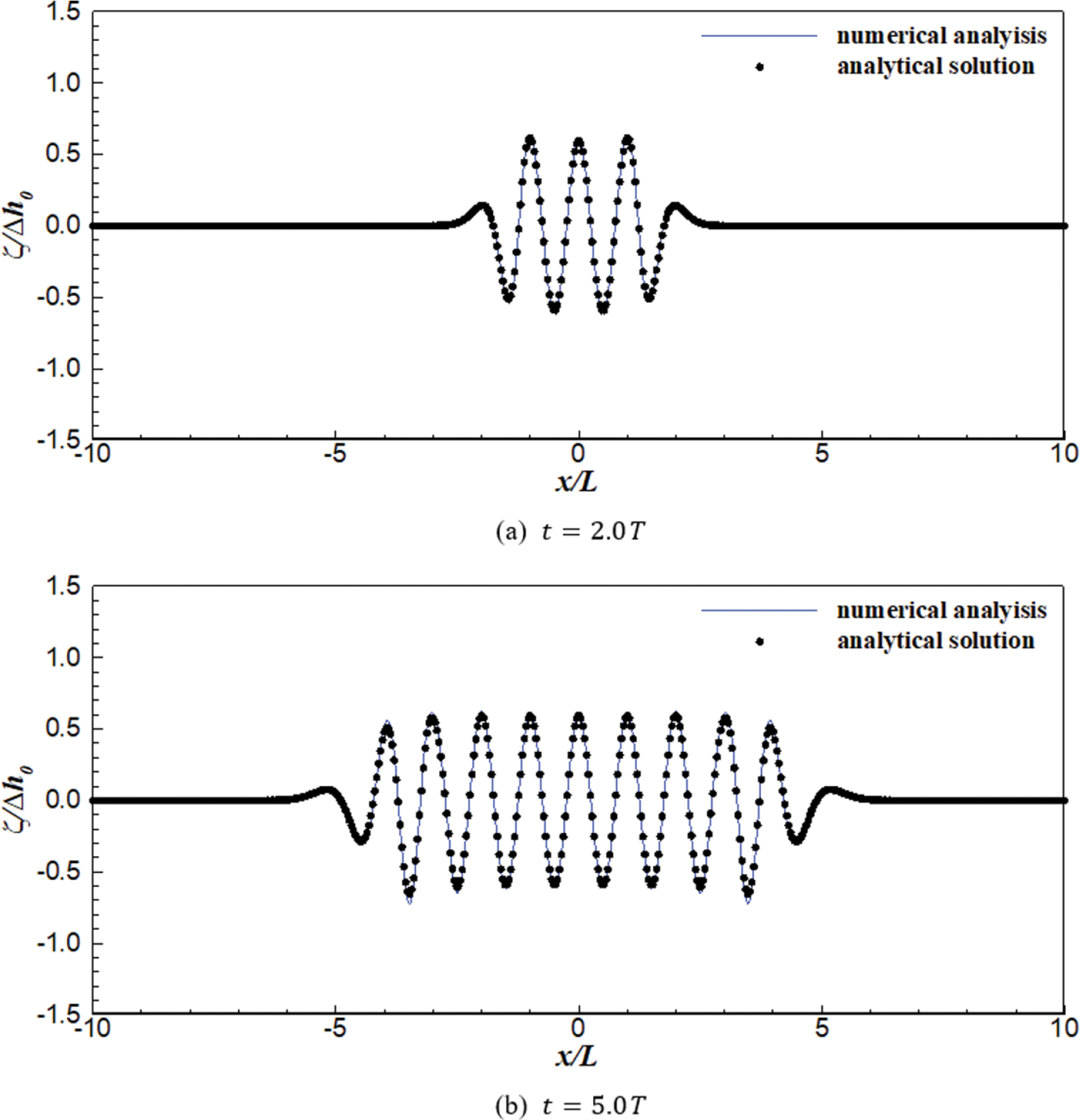
삼각형 형상의 바닥이 움직이는 경우의 수치해석 조건은 사각형 형상과 동일하게 설정하였다. 수치해석 결과는 Fig. 7 및 Fig. 8과 같다. Fig. 7은 움직이는 바닥의 폭이 5.0 m이고 바닥이 움직이는 주기가 3.39 s인 경우(L = 10 m)이며, Fig. 8은 움직이는 바닥의 폭이 10.0 m이고 주기가 6.50 s인 경우(L = 20 m)이다. 비교 결과 삼각형 형상의 바닥이 움직이는 경우에도 수치해석 결과는 Jung and Lee(2022b)의 해석해에 의한 결과와 큰 차이가 없었다. 각 검토 조건에 대한 수치해석 결과와 해석해 사이의 평균제곱근 오차(RMSE) 및 무차원 평균파고는 Table 2와 같으며, 무차원 평균파고의 검토 방법은 3.1절의 사각형 형상 바닥이 움직이는 경우와 동일하다.
4. 수치해의 안정성 분석
4.1 계산 시간간격에 대한 분석
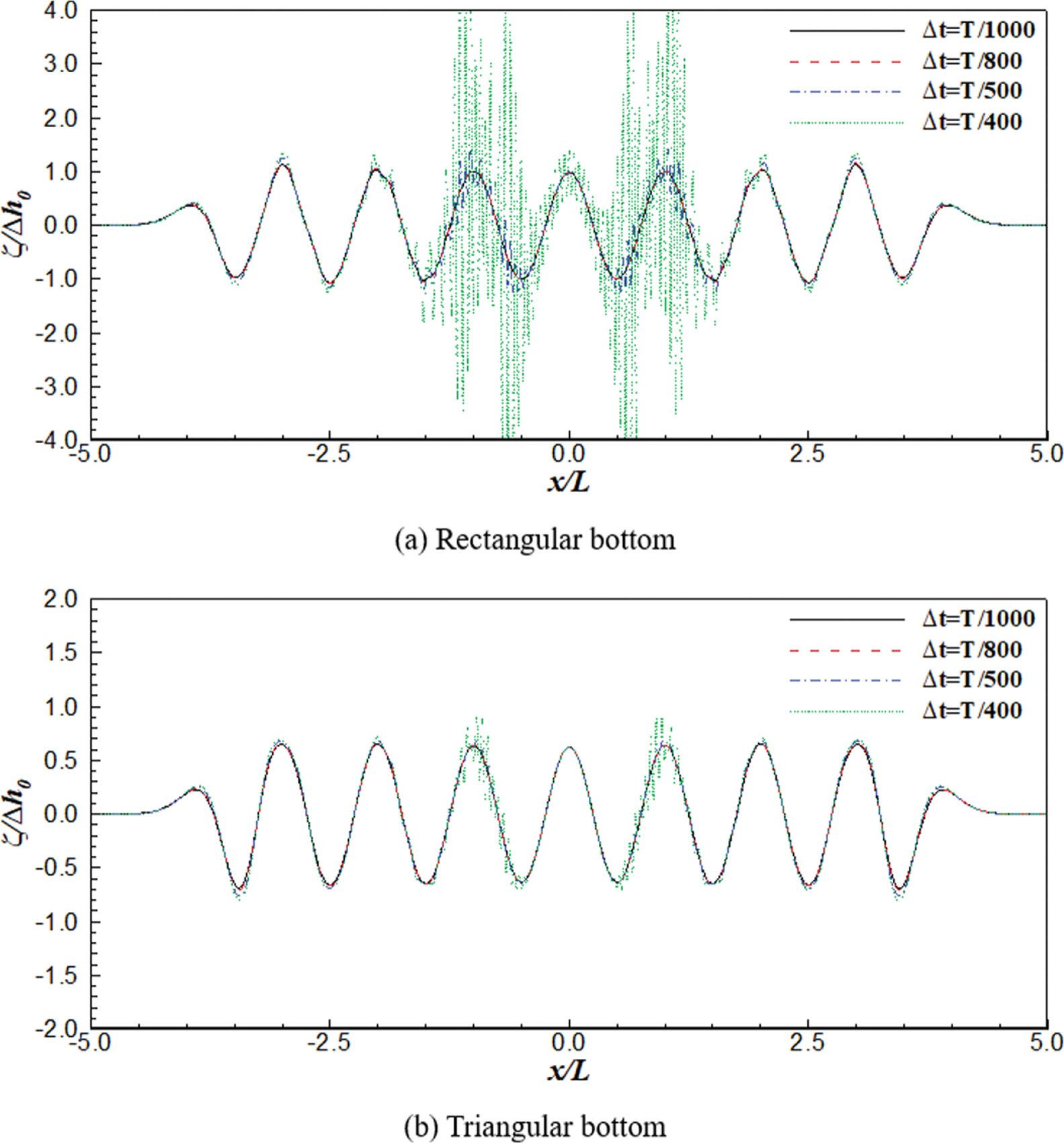
본 절에서는 계산 시간간격(∆t)의 변화에 따른 수치해석 결과 변화를 사각형 및 삼각형 형상 바닥이 움직이는 경우를 대상으로 검토하였다. 검토조건으로 수심(h0)은 1.0 m, 움직이는 바닥의 진폭(∆h0)은 0.1 m, 바닥의 폭(b)은 10.0 m, 바닥이 움직이는 주기(T)는 6.50 s를 각각 적용하였다. 시간이 t = 4.0 T 일 때의 수치해석 결과를 Fig. 9에 나타내었다. 계산 시간간격(∆t)은 T/1000, T/800, T/500, T/400인 경우를 대상으로 하였다. 계산 파수간격(∆k)은 모든 경우에 대해 π/100을 적용하였다.
Fig. 9(a)는 사각형 형상의 바닥이 주기적으로 움직이는 경우에 대한 결과이다. 그림에서 ∆t = T/500에서부터 해가 불안정해지기 시작하고, ∆t = T/400인 경우에는 매우 불안정한 해가 도출되었다. 반면, ∆t = T/800 및 ∆t = T/1000인 경우에는 해가 안정적으로 도출되었으며, 두 결과 사이의 차이도 거의 없었다.
Fig. 9(b)는 삼각형 형상의 바닥이 주기적으로 움직이는 경우에 대한 결과이다. Fig. 9(b)에서 ∆t = T/400인 경우 불안정한 해가 도출되었으며, ∆t = T/500보다 작은 경우에는 비교적 안정한 해가 도출되었다. 바닥이 사각형 형상으로 움직이는 경우에는 바닥에서 불연속인 지점이 존재하며, 삼각형 형상에 비해 파고도 크게 생성되기 때문에 삼각형 형상보다 작은 시간간격(∆t)을 적용해야 해가 안정적으로 도출되는 것으로 생각된다. 바닥 형상에 관계없이 ∆t = T/1000인 경우에는 수치해석에 의한 결과가 적절하게 도출되었다.
4.2 계산 파수간격에 대한 분석
본 절에서는 계산 파수간격(∆k)의 변화에 따른 수치해석 결과 변화를 사각형 및 삼각형 형상 바닥이 움직이는 경우를 대상으로 검토하였다. 본 연구의 수치해석 기법은 파수 영역에서 수치해석을 수행하기 때문에 계산 파수간격(∆k)도 매우 중요한 인자 중의 하나이다. 만약 계산 파수간격(∆k)을 너무 크게 한다면 주파수 성분의 해상도를 낮추는 효과가 있어서 위 신호 발생에 의해 실제 공간영역에서 파랑을 제대로 묘사하지 못할 가능성이 크다. 따라서, 계산 파수간격이 적정한 크기 이하가 되도록 해야 공간영역에서의 파랑을 제대로 재현할 수 있을 것이다.
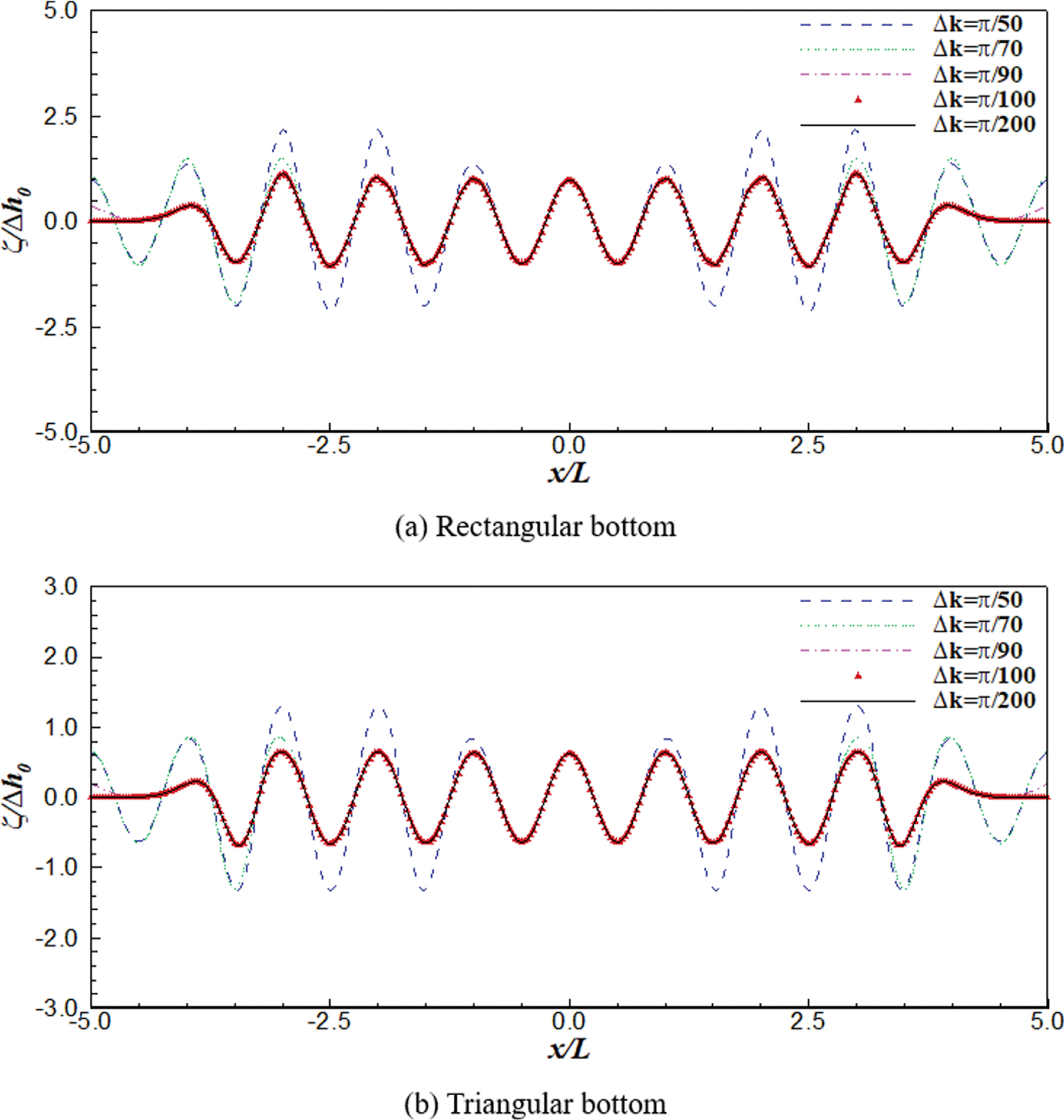
적정한 계산 파수간격(∆k)을 찾기 위한 수치해석 검토조건은 3.3절과 동일하게 수심(h0)은 1.0 m, 움직이는 바닥의 진폭(∆h0)은 0.1 m, 바닥의 폭(b)은 10.0 m, 바닥이 움직이는 주기(T)는 6.50 s, 계산 시간간격(∆t)은 T/1000을 각각 적용하였다. 시간이 t = 4.0 T 일 때의 수치해석 결과를 Fig. 10에 나타내었으며, 계산 파수간격(∆k)은 π/50, π/70, π/90, π/100 및 π/200을 적용하였다. Fig. 10(a)는 사각형 형상의 바닥이 움직이는 경우이며, Fig. 10(b)는 삼각형 형상의 바닥이 움직이는 경우에 해당한다. 검토 결과 계산 파수간격(∆k)이 π/100보다 큰 경우에는 삼각형 및 사각형 형상의 바닥이 움직일 때의 실제 파랑이 전파하는 특성을 제대로 재현하지 못하였다. 반면 ∆k가 π/100 및 π/200인 경우에는 계산 결과가 거의 동일하게 나타났다. 즉, 본 연구에서 제안하는 수치해석 기법을 적용할 때 계산 파수간격(∆k)은 최대 π/100 이하로 설정해야 함을 알 수 있다.
5. 결 론
본 연구에서는 바닥의 움직임에 따른 파랑의 생성 및 변화를 모의할 수 있는 간단한 선형 수치해석 기법을 개발하였다. 연속방정식과 선형의 자유수면 경계조건 및 운동학적 바닥 경계조건을 공간에 대해 푸리에 변환한 후 파수 영역에서 수치해석을 수행하였다. 동역학적 자유수면 경계조건과 운동학적 자유수면 경계조건이 파수 영역에서 수치적으로 계산되며, 이때 평균수면에서의 속도포텐셜은 연속방정식과 운동학적 바닥 경계조건을 만족해야 한다. 계산된 결과는 푸리에 역변환을 통해 공간영역에서 나타내었다. 바닥의 움직임은 삼각형 및 사각형 형상이 주기적으로 움직이는 경우를 선택하였다. 본 연구에서 제안하는 간편한 수치해석 기법에 의한 결과는 기존 연구자들에 의해 제시된 해석해와 비교하였으며, 결과는 거의 일치하였다. 계산 시간간격(∆t)과 계산 파수간격(∆k)에 따른 수치해석 결과의 안정성에 대해서도 검토하였다. 검토 결과 ∆t ≤ T/1000, ∆k ≤ π/100 일 때 수치해석에 의한 결과가 적절하게 도출되는 것으로 나타났다.
본 연구에서는 파수 영역에서 선형의 미분방정식을 해석하는 간단한 방법에 대해 소개하였다. 하지만 본 연구에서는 선형인 경우에 대해서만 결과를 제시하였다. 따라서, 향후에는 비선형까지 포함한 해석 방법에 대해서도 추가 연구가 필요할 것으로 생각된다.