A High-order Spectral Method for Simulation of Nonlinear Wave Generation due to Bottom Movement

Jae-Sang Jung; Changhoon Lee

doi:10.9765/KSCOE.2024.36.6.217

요약

본 연구에서는 바닥의 움직임에 따른 비선형 파랑 생성을 모의할 수 있는 고차 스펙트럼법을 제시하였다. 동역학적 및 운동학적 자유수면 경계조건을 지배방정식으로 하였으며, 각 경계조건의 비선형항은 유사 스펙트럼법을 이용하여 실제 공간에서 연산한 후 Fourier 공간에서 다시 정의하였다. 지배방정식의 시간 적분은 4차 Runge-Kutta법을 적용하여 해석하였다. 계산된 속도포텐셜은 Taylor 급수 전개를 통해 평균수면에서 다시 정의하였으며, 이는 연속방정식과 운동학적 바닥경계조건을 항상 만족한다. 실제 공간과 Fourier 공간에서의 연산을 위해 고속 Fourier 변환을 이용하였다. 모델의 정확도를 검증하기 위해 기존의 실험결과와 비교하였으며, 선형의 결과에 비해 실험결과와 더욱 일치하였다. 최대 섭동차수(M)를 3차 이상 적용할 경우 결과는 거의 수렴하였다.

핵심용어: 바닥의 움직임, 고차 스펙트럼법, 비선형 파랑, 파랑 생성

Abstract

In this study, we presented a high-order spectral method capable of simulating the generation of nonlinear waves due to bottom movement. The governing equations were based on dynamic and kinematic free surface boundary conditions, and the nonlinear terms of each boundary condition were calculated in physical space using a pseudo-spectral method, then redefined in Fourier space. The time integration of the governing equations was analyzed using the fourth-order Runge-Kutta method. The computed velocity potential was redefined at the mean water level through Taylor series expansion, which always satisfies the continuity equation and kinematic bottom boundary condition. Fast Fourier Transform was used for calculations in both physical and Fourier spaces. To verify the model's accuracy, we compared it with existing experimental results, which showed a closer match to experimental data than the linear results. When applying maximum perturbation order (M) of 3 or more, the results converged closely.

Keywords: moving bottom, high-order spectral method, nonlinear waves, wave generation

1. 서 론

일반적으로 지진해일은 해저지진에 의한 단층파괴나 해저사면사태 등에 의해 발생하는 것으로 알려져 있다. 즉, 해저 지형이 순간적으로 움직일 때 자유수면에서의 변동이 발생하게 되고, 이 때 발생한 파랑이 천해역으로 전파하면서 지진해일이 발생하게 된다. 따라서, 지진해일의 생성과 전파를 근본적으로 이해하기 위해서는 해저지형의 순간적인 움직임에 의한 파랑의 생성과 전파를 직접 해석하기 위한 수학적인 모델이 필요하다.

해저지형의 움직임에 따른 파랑 생성을 해석하기 위해 Hammack(1973)은 수리실험과 선형의 해석해를 제시하였다. Lee(1985)는 원호 형상의 바닥이 경사면에서 움직일 때 파랑 생성에 대해 수리실험을 수행하였으며, 이를 해석할 수 있는 Boussinesq 방정식 모델과 KdV(Korteweg-de Vries) 방정식 모델을 제시하였다. Wu(1987)는 KdV 방정식 모델을 이용하여 Lee(1985)의 실험결과를 자세히 검토하였다. Dutykh(2006)는 바닥의 움직임에 따른 파랑생성에 대한 선형의 해석해를 제시하였다. Fuhrman and Madsen(2009)은 바닥 움직임에 따른 파랑의 생성, 전파 및 처오름을 해석할 수 있는 고차 Boussinesq 방정식 모델을 제시하였다. Lu et al.(2017)은 고립파보다 더욱 파장이 긴 지진해일 파의 재현을 위해 경사 바닥 조파장치(bottom tilting wavemaker)를 제시하였으며, 수리실험과 선형의 해석해 및 Boussinesq 방정식을 이용해 이를 검토하였다. Pham and Lee(2022)는 해저 사면사태에 따른 파랑 생성을 모의하기 위해 (b, s) 좌표계와 유한체적법을 이용한 천수방정식(Shallow water equations) 모델과 Boussinesq 방정식 모델을 결합하여 제시하였다. Jung et al.(2023)은 규칙파 생성을 위한 바닥 조파기를 연구하였으며, 바닥이 규칙적으로 움직일 때 생성되는 파랑의 해석을 위해 선형의 해석해와 이를 모의할 수 있는 확장형 완경사방정식(Extended mild-slope equations) 모델을 제시하였다. 이와 같이 바닥 움직임에 따른 파랑생성에 대해 매우 많은 연구들이 수행되었다. 이들은 주로 선형 이론, Boussinesq 방정식, KdV 방정식, 천수방정식, 완경사방정식 등을 이용하여 이를 해석하였다.

본 연구에서는 바닥의 움직임에 따른 파랑의 생성과 전파를 해석할 수 있는 고차 스펙트럼법(HOS, High-order spectral method) 모델을 제시하였다. 일반적으로 고차 스펙트럼법을 활용한 파랑 모델은 비선형파의 변형을 해석하기 위해 주로 사용된다. 비선형 파랑의 해석을 위한 고차 스펙트럼법은 Zakharov(1968)가 자유수면 경계조건으로부터 Hamilton 방정식을 유도한 이후, Zakharov(1968)의 방정식을 이용하여 Dommermuth and Yue(1987)와 West et al.(1987)에 의해 각각 최초로 제안되었다. Dommermuth and Yue(1987)는 수심이 유한한 경우에 대한 모델을 제시하였고, West et al.(1987)은 수심이 무한한 경우에 대한 모델을 제시하였다. Liu and Yue(1998)는 정현파형 지형에서 Bragg 반사 해석을 위해 Dommermuth and Yue(1987)의 모델을 공간적인 수심변화에 따른 파랑 변형 모의가 가능하도록 확장하였다. 이후 Craig and Sulem(1993)이 자유수면과 바닥에서의 경계조건을 동시에 고려할 수 있는 Dirichlet-Neumann 연산자를 새롭게 정의한 고차 스펙트럼법을 제안하였다. Craig et al.(2005)은 Craig and Sulem(1993)의 연구에 기초하여 수심변화에 따른 파랑 변형을 모의할 수 있는 고차 스펙트럼법을 제안하였으며, Guyenne and Nicholls(2007)는 바닥의 움직임에 따른 파랑 생성을 모의할 수 있는 고차 스펙트럼법을 제안하였다. Gouin et al.(2016)는 Dommermuth and Yue(1987)의 HOS 모형에 Craig et al.(2005)의 방법을 적용하여 수심변화에 따른 파랑 변형 효과를 추가로 고려하였다. Ducrozet et al.(2012)은 피스톤 및 힌지 타입 조파기에 의한 파랑생성 및 변형을 모의할 수 있는 수정 고차 스펙트럼법을 제안하였다. Seiffert and Ducrozet(2018)은 쇄파(wave breaking)를 고려한 고차 스펙트럼 모델을 제안하였다. 최근에는 Klahn et al.(2020)이 계산 효율과 정확성 향상을 위해 기존 스펙트럼법의 양해법이 아닌 Saad and Schultz(1986)의 GMRES(Generalized Minimal REsidual algorithm for Solving nonsymmetric linear systems)를 활용한 Implicit Taylor법을 새로 제안하였다. 국내에서는 Oh et al.(2020)이 비선형을 고려한 규칙파와 불규칙파 모의를 위해 Dommermuth and Yue(1987)의 고차 스펙트럼법을 적용하였으며, Jung(2023)과 Jung and Lee(2024)는 선형 스펙트럼법을 적용하여 바닥조파기에 의한 규칙파의 생성에 대해 연구한 사례가 있다.

이와 같이 고차 스펙트럼법을 이용한 다양한 연구들이 수행되었지만, 바닥의 움직임에 따른 비선형 파랑의 생성에 대해서는 거의 연구가 수행되지 않았다. Guyenne and Nicholls(2007)는 바닥의 움직임에 따른 고차 스펙트럼법을 제안하였지만 평평한 바닥이 순간적으로 움직이는 경우에 대한 하나의 조건에서만 선형이론과 비교하여 제시하였을 뿐 다양한 조건에 대한 결과는 제시하지 않았다. 그리고 Guyenne and Nicholls(2007)는 매우 복잡한 좌표변환 과정을 통해 해를 제시하여 계산효율이 좋지 않음을 그들의 연구에서 밝혔다.

본 연구에서는 Dommermuth and Yue(1987)에 의해 제안된 고차 스펙트럼법을 기초로 하여 비쇄파 조건에서 바닥이 움직일 때 비선형을 고려한 파랑 생성과 변형을 모의할 수 있는 새로운 고차 스펙트럼법을 제안하였다. 일반적으로 고차 스펙트럼법은 5차 이상 고차의 비선형항들을 고려할 수 있으므로 그 정확도가 매우 높다. 바닥 경계조건으로 시간에 따른 해저지형의 변화를 고려할 수 있는 운동학적 바닥경계조건을 적용하였다. 본 연구에서 제시하는 모델에서 운동학적 바닥경계조건은 Fourier 공간에서 해석되므로 계산이 매우 간편하며 효율적이다. 2장에서는 바닥 움직임에 따른 파랑 생성을 모의할 수 있는 고차 스펙트럼법에 대한 이론적인 설명을 기술하였으며, 3장에서는 수치해석 방법, 4장에서는 기존 수리실험 결과와 비교를 통해 모델을 검증하였다. 그리고 5장에서는 결론을 기술하였다.

2. 바닥의 움직임과 수심변화를 고려한 고차 스펙트럼법

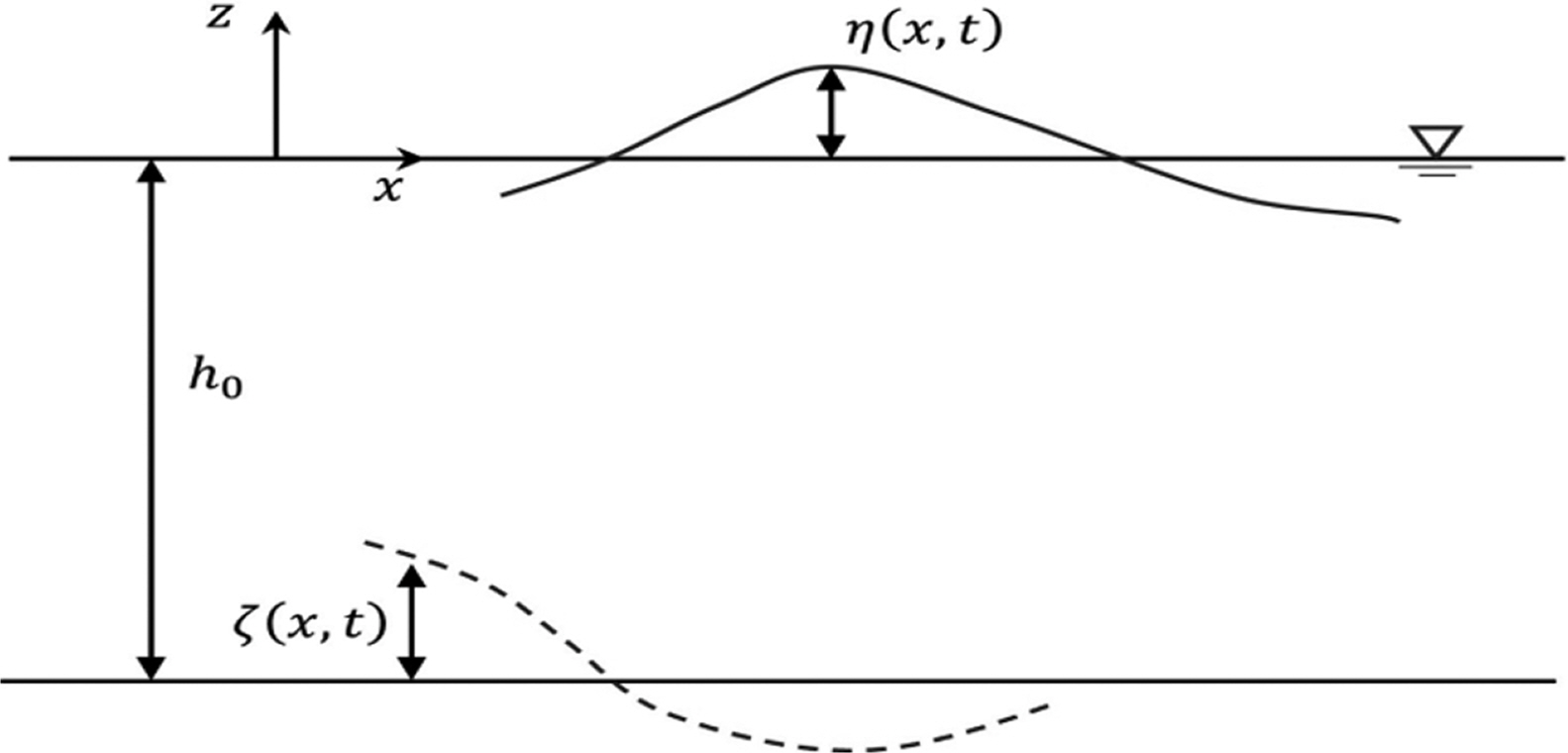
바닥의 움직임에 따른 비선형 파랑 생성 해석을 위해 x - z 2차원 공간을 Fig. 1과 같이 정의한다. 그림에서 η는 자유 수면변위, ζ는 바닥의 변위, h₀는 수심을 뜻한다. 대상 유체가 비압축성, 비점성 및 비회전류라 가정하면, 2차원 공간에서의 연속방정식은 다음과 같이 Laplace 방정식으로 표현된다.

(1)

∂2φ∂x2+∂2φ∂z2=0

여기서, Φ는 속도포텐셜이다. 운동학적 자유수면 경계조건과 동역학적 자유수면 경계조건은 다음과 같이 표현된다.

(2)

∂η∂t=∂φ∂z-∂φ∂x∂η∂xon z=η(x,t)

(3)

∂φ∂t=-gη-12[(∂φ∂x)2+(∂φ∂z)2]on z=η(x,t)

여기서, t는 시간을 뜻한다. 운동학적 바닥경계조건은 다음과 같이 정의하였으며, 본 연구에서는 공간적인 수심의 변화는 고려하지 않았다.

(4)

∂ζ∂t=∂φ∂zon z=-h0

자유수면에서의 속도포텐셜 Φs(x, t) = Φ(x, η(x, t), t)라 하면 자유수면경계조건 식(2) 및 (3)은 다음 식과 같이 나타낼 수 있다(Zakharov, 1968; Dommermuth and Yue, 1987; West et al., 1987).

(5)

∂η∂t=-∂φs∂x∂η∂x+(∂φs∂z){1+(∂η∂x)2}

(6)

∂φs∂t=-gη-12(∂φs∂x)2+12(∂φs∂z)2{1+(∂η∂x)2}

식(2)와 (3)으로부터 식(5)와 (6)을 유도하는 과정에 ∂ϕ∂t=∂ϕs∂t−∂η∂t∂ϕs∂z 및 ∂ϕ∂x=∂ϕs∂x−∂η∂x∂ϕs∂z 의 관계식이 적용되었다. 연속방정식인 식(1)과 운동학적 바닥경계조건인 식(4)를 Fourier 변환하면 각각 다음과 같다.

(7)

∂2φ¯∂z2-k2φ¯=0

(8)

∂φ¯(k,-h0,t)∂z=∂ζ¯∂t

여기서, k는 파수를 나타낸다. 식(8)을 이용하면 바닥지형의 시간적 변동에 따른 파랑 변화의 해석이 가능하다. 본 연구에서 Fourier 변환은 다음과 같이 정의된다.

(9)

f¯(k)=∫-∞∞f(x)eikxdx

식(7)은 상미분방정식으로 해는 다음과 같이 표현된다.

(10)

φ¯(k,z,t)=A(k,t)coshkz+B(k,t)sinhkz

식(10)과 같은 상미분방정식의 해는 z = 0에서 자유수면 경계조건인 Dirichlet 경계조건을 만족해야 하며, z = -h₀에서 바닥 경계조건인 Neumann 경계조건을 만족해야 한다. 식(10)을 운동학적 바닥경계조건인 식(8)에 대입하여 정리하면 다음과 같다.

(11)

B(k,t)=A(k,t)sinhk(z+h0)coshkh0+∂ζ¯∂tkcoshkh0

식(11)을 식(10)에 대입하여 정리하면 다음과 같은 Fourier 공간에서 Laplace 방정식과 운동학적 바닥경계조건을 만족하는 속도포텐셜이 정의된다.

(12)

φ¯=Acoshk(z+h0)coshkh0+∂ζ¯∂tsinhkzkcoshkh0

식(12)에서 첫번째 항은 진행파에 대한 속도포텐셜이고, 두번째 항은 바닥 움직임에 따른 파랑 변형의 속도포텐셜을 의미한다. 해석의 편의를 위해 식(12)는 다음과 같이 다시 쓸 수 있다.

(13)

φ¯=A(ek(z+h0)+e-k(z+h0))2coshkh0+∂ζ¯∂t(ekz-e-kz)2kcoshkh0

ϕ¯의 z 방향 1차 도함수와 n차 도함수는 각각 다음과 같다.

(14)

∂φ¯∂z=A(kek(z+h0)-ke-k(z+h0)2coshkh0+∂ζ¯∂t(ekz+e-kz)2coshkh0

(15)

∂nφ¯∂zn=A[knek(z+h0)+(-k)ne-k(z+h0)]+∂ζ¯∂t[kn-1ekz+(-k)n-1e-kz]2coshkh0

평균 수면인 z = 0에서 Fourier 공간의 속도포텐셜 ϕ¯와 ϕ¯의 z 방향 n차 도함수는 각각 다음과 같이 쓸 수 있다.

(16)

φ¯(k,0,t)=A(k,t)

(17)

∂nφ¯(k,0,t)∂zn=A[knekh0+(-k)ne-kh0]+∂ζ¯∂t[kn-1+(-k)n-1]2coshkh0

실제 공간에서 속도포텐셜은 Fourier 공간에서의 속도포텐셜을 Fourier 역변환하여 구할 수 있다.

(18)

φ(x,z,t)=12π∫-∞∞[A(ek(z+h0)+e-k(z+h0)2coshkh0+∂ζ¯∂t(ekz-e-kz)2kcoshkh0]e-ikxdk

식(18)과 같은 속도포텐셜의 해는 -h₀ ≤ z ≤ 0에서 타당하며, 실제 공간에서 속도포텐셜은 다음과 같이 섭동 전개(perturbation expansion)로 표현할 수 있다.

(19)

φ(x,z,t)=∑m=1Mφ(m)(x,z,t)

여기서, M은 최대 섭동차수(maximum perturbation order)로서 고려할 수 있는 최대 비선형 차수를 뜻한다.

자유수면경계조건 식(5) 및 식(6)에서 Φ_s(x, t)는 다음과 같은 Taylor 급수로 나타낼 수 있다(Dommermuth and Yue, 1987).

(20)

φs(x,t)=∑m=1M∑n=0M-mηnn!∂n∂znφ(m)(x,0,t)

여기서,

∂n∂znφ(1)(x,0,t)=12π∫-∞∞[A(1)[knekh0+(-k)ne-kh0]+∂ζ¯∂t[kn-1+(-k)n-1]2coshkh0]e-ikxdk,

(21)

∂n∂znφ(m)(x,0,t)=12π∫-∞∞[A(m)[knekh0+(-k)ne-kh0]2coshkh0]e-ikxdk

식(19) 및 (20)을 이용하여 z = 0에서의 속도포텐셜을 다음과 같이 쓸 수 있다.

(22)

φ(x,0,t)=∑m=1Mφ(m)(x,0,t)=φs(x,t)-∑m=1M∑n=1M-mηnn!∂n∂znφ(m)(x,0,t)

따라서,

(23)

φ(1)(x,0,t)=φs(x,t),φ(m)(x,0,t)=-∑n=1m-1ηnn!∂n∂znφ(m-n)(x,0,t)

위 식을 이용하여 Φ^(m)(x, 0, t)을 구한 후 이를 Fourier 변환하고, 식(16)과 같은 Φ^(m)(k, 0, t) = A^(m)(k, t)의 관계식을 이용하여 계수 A^(m)(k, t)를 구할 수 있다. A^(m)(k, t)을 구하는 과정에서 실제 공간에서 식(20)과 같은 Taylor 급수를 해석해야 하며, A^(m)(k, t)은 Fourier 공간에서 해석해야 하므로 고속 Fourier 변환을 이용하였다. A^(m)(k, t)을 구한 이후 다음 식과 같이 Taylor 급수 전개를 통해 ∂ϕs(x,t)∂z를 구할 수 있다.

(24)

∂φs(x,t)∂z=∑m=1M∑n=0M-mηnn!∂n+1∂zn+1φ(m)(x,0,t)

3. 수치해석 방법

3.1 시간 적분의 해석

수치해석은 운동방정식인 식(5) 및 (6)을 이용하여 실제 공간에서 수행한다. 다만 식(5) 및 (6)에서 비선형항들은 유사 스펙트럼법(pseudo-spectral method)을 이용하여 Fourier 공간에서 정의한 후 Fourier 역변환을 통해 실제 공간에서 연산한다. 실제 공간에서 비선형 항들은 식(25)~(27)과 같이 표현된다.

(25)

∂φs∂x∂η∂x=14π2∫-∞∞-ikφ¯s(k,t)e-ikxdk⋅∫-∞∞-ikη¯(k,t)e-ikxdk

(26)

(∂η∂x)2=14π2[∫-∞∞-ikη¯(k,t)e-ikxdk]2

(27)

(∂φs∂x)2=14π2[∫-∞∞-ikφ¯s(k,t)e-ikxdk]2

식(5) 및 (6)은 4차 Runge-Kutta 방법을 이용하여 계산할 수 있다. 기존 연구들에서 4차 Runge-Kutta 방법의 수치적 안정성은 충분히 입증되었다(Dommermuth and Yue, 1987; Guyenne and Nicholls, 2007; Klahn et al., 2020). 자유수면 경계조건의 시간 적분을 위한 4차 Runge-Kutta 방법은 다음 식으로 정의된다.

(28)

C1(x)=∂η(φs,η)∂t,D1(x)=∂φs(φs,η)∂t

(29)

C2(x)=∂η(φs+D1Δt2,η+C1Δt2)∂t,D2(x)=∂φs(φs+D1Δt2,η+C1Δt2)∂t

(30)

C3(x)=∂η(φs+D2Δt2,η+C2Δt2)∂t,D3(x)=∂φs(φs+D2Δt2,η+C2Δt2)∂t

(31)

C4(x)=∂η(φs+D3Δt,η+C3Δt)∂t,D4(x)=∂φs(φs+D3Δt,η+C3Δt)∂t

(32)

η(x,t+Δt)=η(x,t)+Δt6(C1+2C2+2C3+C4)

(33)

φs(x,t+Δt)=φs(x,t)+Δt6(D1+2D2+2D3+D4)

3.2 고속 Fourier 변환의 적용

본 연구에서 고속 Fourier 변환(Fast Fourier Transform)을 적용하기 위해 2ⁿ개의 격자를 공간 및 주파수 영역에서 동일하게 구성하였다. x 방향으로 -NΔx/2 및 NΔx/2 사이의 실제 공간에서 격자수 N = 4096이 적용되었다. Fourier 공간에서도 -π/Δx 및 π/Δx 사이의 영역에서 파수(wave number) 격자수 N = 4096 및 파수 간격 Δk = 2π/(NΔx)가 적용되었다. 여기서, Δx는 공간 격자간격을 뜻하며, Δk는 Fourier 공간에서 파수간격을 각각 뜻한다. 고속 Fourier 변환은 복소수를 대상으로 Cooley et al.(1969)이 제안한 알고리즘을 적용하였다.

3.3 Low-pass filter의 적용

일반적으로 고차 스펙트럼법을 통해 비선형 파랑을 해석할 때, 자유수면 경계조건에서 비선형 항의 곱 연산을 식(25)~(27)과 같이 실제 공간에서 수행한다. 이 때 Fourier 변환 과정에서 위신호(aliasing error)가 발생한다(Dommermuth and Yue, 1987; Guyenne and Nicholls, 2007; Oh et al., 2020; Klahn et al., 2020). Dommermuth and Yue(1987)와 Guyenne and Nicholls(2007)는 ideal low-pass filter를 사용하여 고주파수에서의 위신호를 제거하였으며, Oh et al.(2020)과 Klahn et al.(2020)은 zero padding method를 적용하여 위신호를 제거하였다. Zero padding method는 Fourier 공간의 확장에 따라 계산 효율이 저하되기 때문에, 본 연구에서는 다음과 같은 ideal low-pass filter를 적용하였다.

(34)

γ(kn,ν)={1 for|km|/|kN|≤ν0 for|km|/|kN|>ν, 0<ν≤1

여기서, γ(k_n, ν)는 filter의 전달함수(transfer function)이고, ν는 상대 임계 파수(relative cutoff wavenumber)이다. 본 모델에서 최대 파수(k_max)는 Δx에 의해 결정되기 때문에, ν도 Δx의 크기에 따라 값을 결정하여야 한다. 본 연구에서는 계산 공간격자 크기를 고려하여 ν = 0.2를 적용하였다.

3.4 측면 감쇠영역(relaxation zone)의 적용

스펙트럼법을 이용한 수치해석 수행 시, 스펙트럼법의 특성 상 좌측 경계나 우측 경계를 통과한 파랑은 우측 및 좌측 경계에서 다시 나타나게 된다. 따라서, 장기간의 수치해석 수행을 위해서는 좌우측 경계에 파랑 흡수층을 둘 필요가 있다. 일반적으로 자유수면 경계조건에 별도의 감쇠항을 두거나(Oh et al., 2020), 감쇠영역에서 속도포텐셜 및 자유수면 변위에 감쇠계수를 곱하여 좌우측 경계에서 파랑 흡수를 할 수 있다(Guyenne and Nicholls, 2007; Gouin et al., 2016). 본 연구에서는 Guyenne and Nicholls(2007)의 방법을 적용하여 측면 감쇠영역을 설정하였다. 본 연구에서 감쇠계수(λ)는 다음 식과 같이 정의된다.

(35)

λ={12+12tanh[2π(x-xminl-12)],xmin≤x≤xmin+l12+12tanh[2π(xmax-xl-12)],xmax-l≤x≤xmax

여기서, l은 파랑 감쇠구간의 길이를 나타내며 xmin은 좌측 경계에서의 x 좌표, x_max는 우측 경계에서의 x 좌표를 각각 뜻한다.

4. 수치모형의 검증

본 연구에서 제시하는 수치모형의 검증을 위해 Reeve et al.(2024)의 실험 결과와 비교하였다. Reeve et al.(2024)은 30 m 길이의 수로에 바닥 조파기를 설치하고, 조파기가 1회 +z 방향으로 움직일 때 파랑의 생성 및 전파에 대해 수리실험을 수행하였다. 본 연구의 고차 스펙트럼법 모델과 비교하기 위한 실험 조건은 2개로 Table 1과 같다.

Table 1에서 T₀는 조파기가 움직이는 시간을 나타내며, 따라서 Δh₀/T₀는 조파기가 움직이는 평균 속도를 의미한다. 파고계의 위치는 조파기의 중앙에서 x 축 방향으로 떨어진 거리이다. Reeve et al.(2024)의 실험에서 바닥조파기의 조파판 길이 b = 0.305 m이며, 바닥의 공간적 형상 및 시간적 움직임은 다음 식과 같이 정의된다.

(36)

ζ(x,t)=Δh0[12(1-cosκt)H(T0-t)+H(t-T0)]H(b2-x2)

여기서, H는 Heaviside 계단함수를 나타내며, κ는 바닥 조파 기의 움직임을 정의하는 변수로 κ = π/T₀으로 정의된다. 고차 스펙트럼법을 이용한 수치모형에서 Δx = 0.01 m, Δt = 0.01 s를 적용하였으며, N = 4096을 적용하여 -20.48 m ≤ x ≤ 20.47 m의 범위에서 모형을 구축하였다. 최대 섭동차수(M)는 5를 적용하였다. 비선형을 고려한 결과와 비교를 위해, 선형 스펙트럼법을 이용한 수치모형은 Jung(2023)이 제시한 모형을 이용하였다.

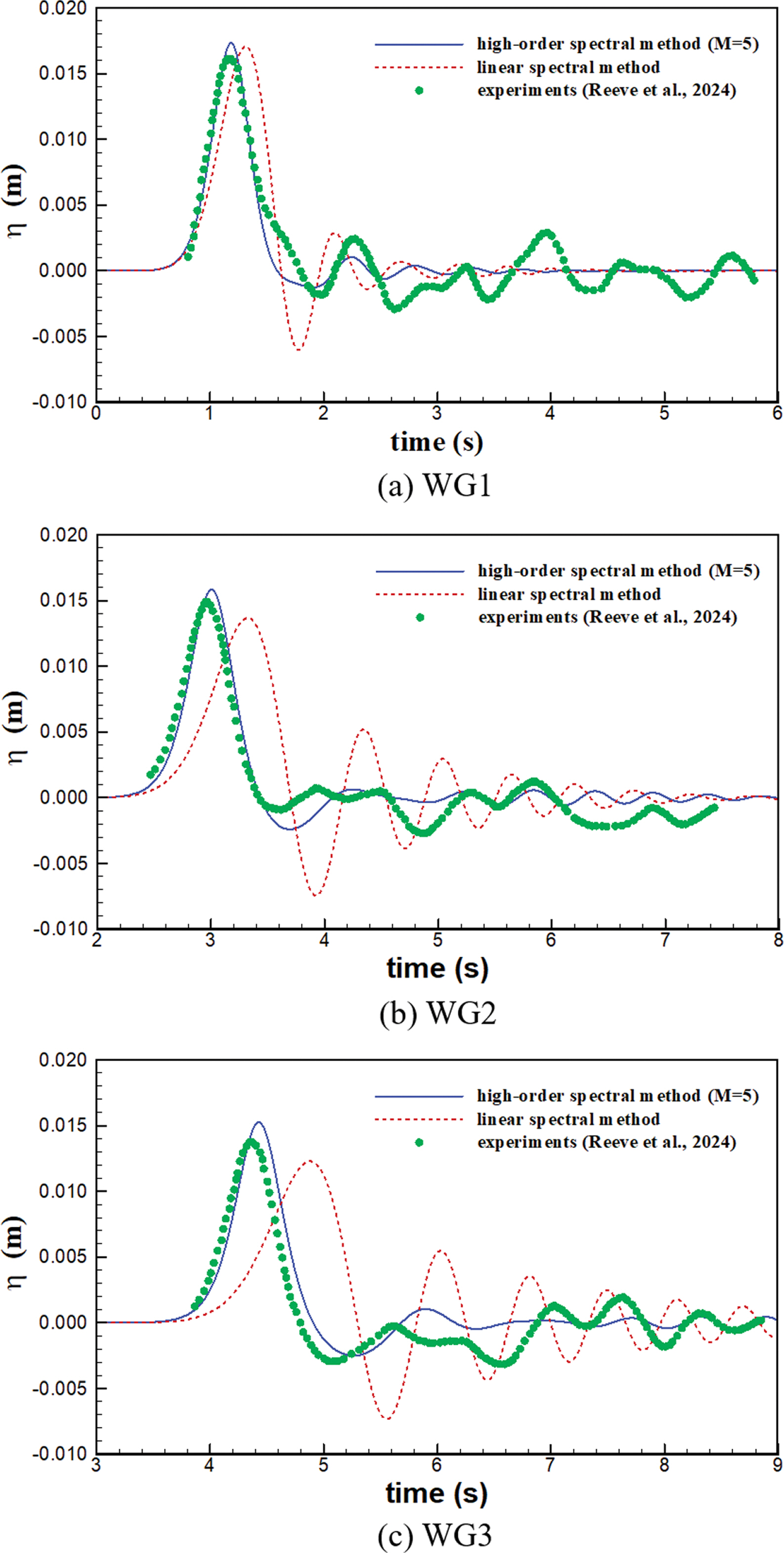
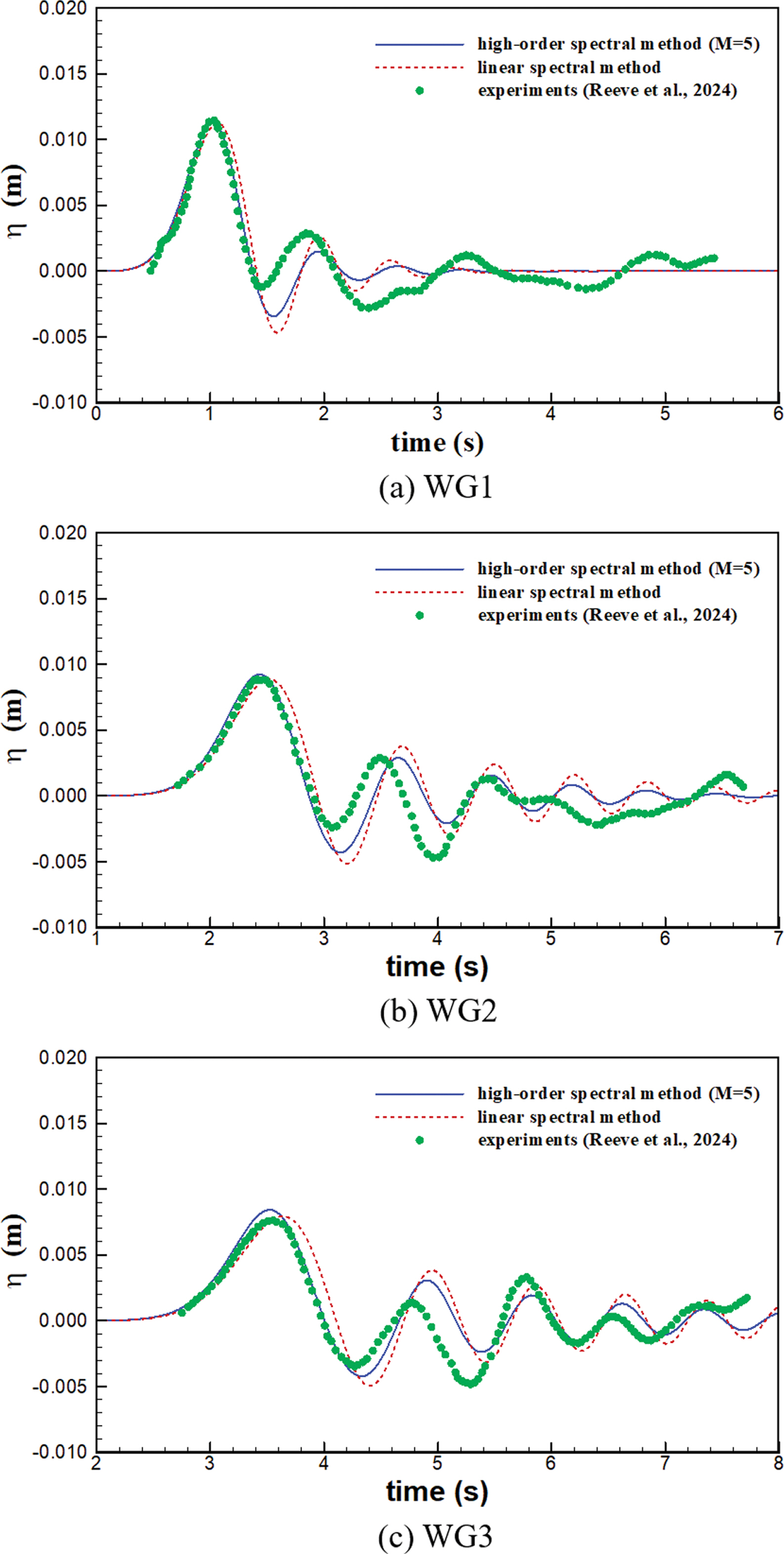
수치모형의 검증을 위해 Reeve et al.(2024)이 수행한 실험 중 2가지 조건과 비교하였다. 비교 결과는 Fig. 3~4에 나타내었다. 각 그림에서 파란색 실선은 본 연구에서 제시한 고차 스펙트럼법 모형의 결과이며, 빨간색 파선은 Jung(2023)의 선형 스펙트럼법 모형의 결과이다. 그리고, 녹색 심볼은 Reeve et al.(2024)의 수리실험 결과이다. Fig. 2는 수심(h₀)이 0.1 m이고, 조파기의 진폭(Δh₀)이 0.0476 m 및 Δh0h0=0.476으로 비선형성이 상당히 큰 경우이며, 조파기가 +z방향으로 움직이는 조건이다(case1). Fig. 2에서 선형의 결과는 첫번째 파가 지나간 이후에 두번째 파, 세번째 파가 생성되어 전파되는 것으로 계산된다(Fig. 2(b), Fig. 2(c)). 반면, 고차 스펙트럼법을 이용한 비선형 결과와 수리실험 결과에서는 첫번째 파는 강하게 생성되지만, 두번째 이상의 파의 진폭은 매우 작은 것으로 나타났다. 전체적인 파형(wave shape)도 고차 스펙트럼법의 결과가 실험결과와 매우 유사함을 볼 수 있으며, 전반적으로 비선형을 고려한 고차 스펙트럼법 모형이 선형 모형에 비해 실험결과와 더욱 일치하였다. WG1 파고계에서 최대 자유수면변위는 고차 스펙트럼법 모형에서 0.01733 m로 계산되었다.

Fig. 3은 Δh0h0=0.241로 비선형성이 case1에 비해 크지 않으며, 조파기가 +z방향으로 움직이는 조건이다(case2). 비선형성이 크지 않으므로 고차 스펙트럼법의 결과, 선형 스펙트럼법의 결과 및 실험결과는 모두 유사하게 나타났다. 바닥 조파기의 움직이는 진폭이 case1의 절반 정도이므로, WG1 파고계에서 최대 자유수면변위는 고차 스펙트럼법 모형에서 0.01129 m로 계산되었다.

본 연구에서 제시한 고차 스펙트럼법을 이용한 수치모형은 Reeve et al.(2024)의 실험결과와 비교하여 검증하였다. 검증 결과 고차 스펙트럼법 모형은 수리실험 결과와 거의 일치하는 결과를 보였다. 특히 비선형성이 큰 case1의 경우 선형의 결과에 비해 실험 결과와 더욱 일치하였다. 반면, 비선형성이 비교적 작은 case2의 경우에는 고차 스펙트럼법 모형의 결과와 선형의 결과는 모두 실험결과와 일치하였다.

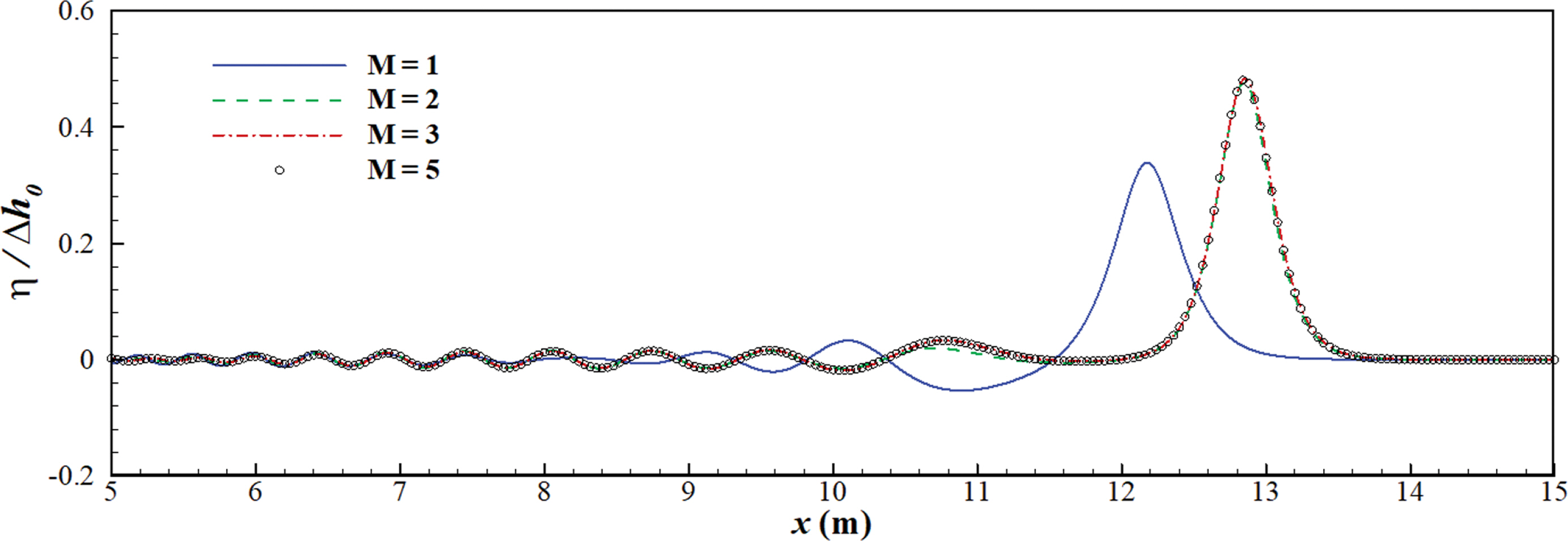
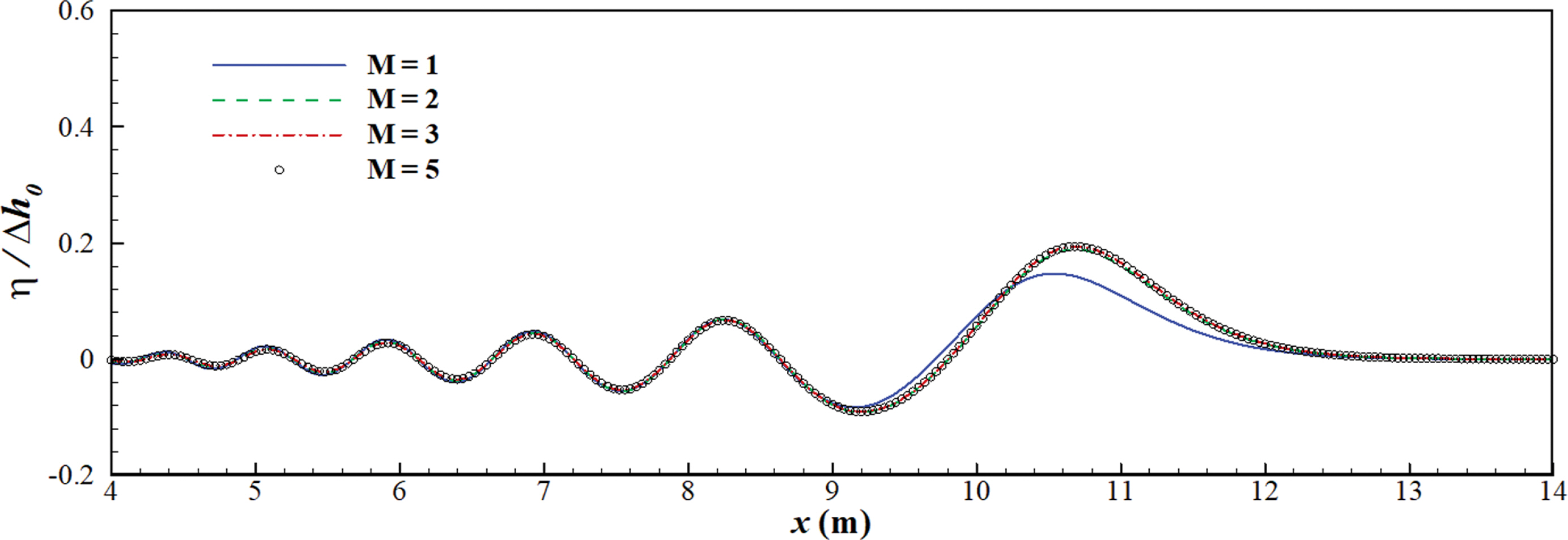
최대 섭동차수(M)의 변화에 따른 해의 수렴성을 검토하였다. case1에 대한 결과는 Fig. 4와 같고, case2의 결과는 Fig. 5와 같다. Fig. 4에서는 시간 t = 12 s일 때, Fig. 5에서는 시간 t = 8 s일 때 공간적인 파형을 도시하였다. 그림에서 파란색 실선은 M = 1인 경우, 녹색 파선은 M = 2, 빨간색 일점쇄선은 M = 3 및 심볼은 M = 5인 경우의 결과이다. M = 1인 경우와 M = 2 이상인 경우는 결과에 큰 차이를 보였다. M = 2인 경우(녹색파선) 첫번째 파랑은 거의 일치하였으나 두번째 파랑에서 M = 3 이상인 결과와 차이를 보였다(Fig. 4). 그리고, M = 3 이상인 경우에는 해가 수렴하는 결과를 보였다. 즉, Reeve et al.(2024)의 실험조건에서는 최대 섭동차수 M = 3 이상을 적용하면 신뢰성 있는 결과가 도출되는 것으로 보인다.

5. 결 론

본 연구에서는 바닥 조파기에 의해 생성되는 비선형파의 모의를 위한 고차 스펙트럼법 모델을 제시하였다. 본 연구에서 제안하는 모델은 Dommermuth and Yue(1987)의 고차 스펙트럼법 모델을 바탕으로 하여 바닥의 움직임에 따른 파랑 생성을 모의할 수 있도록 확장하였다. 모형의 검증을 위해 Reeve et al.(2024)의 실험 결과와 비교하였다. 비교 결과 고차 스펙트럼법 모형은 수심에 비해 바닥 움직임의 진폭(Δh₀/h₀)이 큰 경우, 즉 비선형성이 큰 경우에는 선형 스펙트럼법 모형에 비해 수리실험 결과와 더욱 일치하는 결과를 보였다. Reeve et al.(2024)이 실험을 수행한 조건에서는 최대 섭동차수(M)가 3 이상이면 수치모델의 해는 거의 수렴하였다.

본 연구에서는 x - z 2차원 평면에서 바닥이 움직이는 경우 비선형 파랑의 생성을 모의할 수 있는 고차 스펙트럼법 모형을 제시하였다. 향후에는 본 모델을 3차원으로 확장하여, 바닥의 3차원적인 형상이 변화할 때 생성되는 비선형파에 대한 검토도 필요할 것으로 생각된다. 그리고, 해저 지형의 공간적 변동을 고려하여 모델을 확장할 필요가 있을 것이다.

바닥의 움직임에 따른 비선형 파랑 생성의 모의를 위한 고차 스펙트럼법